Пи на 2 разделить на пи: «Как решить пример пи разделить на 3 минус пи разделить на 6?» — Яндекс Кью

Содержание

Пространства с иным числом Пи / Хабр

Недавно на Хабре в одной статье упомянули про вопрос «Что было бы с миром, если бы число Пи равнялось 4?» Я решил слегка поразмышлять на эту тему, используя некоторые (пусть и не самые обширные) знания в соответствующих областях математики. Кому интересно – прошу под кат.

Чтобы представить такой мир, нужно математически реализовать пространство с иным соотношением длины окружности к ее диаметру. Это я и попытался сделать.

Попытка №1.

Оговорим сразу, что рассматривать я буду только двумерные пространства. Почему? Потому что окружность, собственно, определена в двумерном пространстве (если рассмотреть размерность n>2, то отношение меры (n-1)-мерной окружности к ее радиусу даже не будет константой).
Так что для начала я попытался придумать хоть какое-то пространство, где Пи не равно 3.1415… Для этого я взял метрическое пространство с метрикой, в которой расстояние между двумя точками равно максимуму среди модулей разности координат (т. е. расстояние Чебышева).

Какой же вид будет иметь единичная окружность в этом пространстве? Возьмем точку с координатами (0,0) за центр этой окружности. Тогда множество точек, расстояние (в смысле заданной метрики) от которых до центра равно 1, есть 4 отрезка, параллельных осям координат, образующих квадрат со стороной 2 и с центром в нуле.

Да, в некоторой метрике это — окружность!

Посчитаем здесь Пи. Радиус равен 1, тогда диаметр, соответственно, равен 2. Можно также рассмотреть определение диаметра как наибольшего расстояния между двумя точками, но даже так оно равно 2. Осталось найти длину нашей «окружности» в данной метрике. Это сумма длин всех четырех отрезков, которые в данной метрике имеют длину max(0,2)=2. Значит, длина окружности равна 4*2=8. Ну а тогда Пи здесь равно 8/2=4. Получилось! Но нужно ли сильно радоваться? Результат этот практически бесполезен, ведь рассматриваемое пространство абсолютно абстрактно, в нем даже не определены углы и повороты. Вы можете представить себе мир, где по факту не определен поворот, и где окружностью является квадрат? Я пытался, честно, но у меня не хватило воображения.

Попытка №2.

Осознав, что я получил хоть и интересный, но абсолютно бесполезный (в смысле понимания строения мира с иным числом Пи) результат, я решил попытаться построить модель пространства с определенными понятиями углов и поворотов (то есть пространство с заданным невырожденным скалярным произведением). Разумеется, мне хотелось, чтобы метрика осталась метрикой в классическом понимании этого слова (т.е. чтобы расстояние между двумя точками было вещественным и неотрицательным). Но тогда скалярное произведение должно быть положительно определено, откуда вытекает, что пространство должно быть евклидовым. Или хотя бы локально евклидовым, то есть многообразием. Можно не забивать себе голову всеми этими понятиями, а просто читать дальше 🙂

Признаюсь, я убил некоторое время, пытаясь придумать хитрую евклидову метрику с нехорошим числом Пи.

Я считал длины получившихся «окружностей», вспоминая различные интегральные формулы, пока до меня не дошел очевидный факт: если пространство евклидово, то заменой координат можно получить наше обычное пространство , в котором число Пи известно. Значит и в другом евклидовом пространстве оно не изменит своего значения. Печаль.

Попытка №3.

Раз нам по-прежнему желательно наличие углов и поворотов, но евклидово пространство нас не устраивает, попробуем рассмотреть псевдоевклидово типа (1,1) (т.к. нас интересуют только двумерные). От обычного евклидового пространства оно отличается тем, что в нем квадрат расстояния между двумя точками (а, как следствие, и скалярное произведение двух векторов) может быть отрицательным. Чтобы особо не мучиться, я взял метрику в которой скалярное произведение в декартовых координатах будет иметь вид . Какой же вид примет окружность единичного радиуса? Это будет множество точек, задаваемых уравнением , то есть… Гипербола.

Да-да! В определенном пространстве и это — окружность.

Радиус равен 1, а вот с нахождением длины этой «окружности» есть некоторые сложности. После некоторых поисков информации в интернете, я пришел к выводу, что в псевдоевклидовом пространстве такое понятие как «число Пи» вообще не может быть определено, что, безусловно, плохо.

Если кто-нибудь в комментариях расскажет мне, как формально считать длину кривой в псевдоевклидовом пространстве, я буду очень рад, ибо моих познаний в дифференциальной геометрии, топологии (а также усердного гугления) для этого не хватило.

Выводы:

Не знаю, можно ли писать о выводах после таких не сильно продолжительных исследований, но кое-что сказать можно. Во-первых, попытавшись представить пространство с иным числом Пи, я понял, что оно будет слишком абстрактно, чтобы быть моделью реального мира. Во-вторых, когда если попытаться придумать более удачную модель (похожую на наш, реальный мир), выходит, что число Пи останется неизменным.

Если принять за данность возможность отрицательного квадрата расстояния (что для обычного человека — просто абсурд), то Пи не будет определено вовсе! Все это и наводит на мысль, что, возможно, мира с другим числом Пи и вовсе быть не могло? Ведь не зря же Вселенная именно такая, какая она есть. А может быть, это и реально, только обычной математики, физики и человеческого воображения для этого недостаточно. А вы как считаете?

Upd. Узнал точно. Длина кривой в псевдоевклидовом пространстве может быть определена только на каком-либо его евклидовом подпространстве. То есть, в частности, для получившейся в попытке N3 «окружности» вовсе не определено такое понятие как «длина». Соответственно, Пи там тоже посчитать нельзя.

Математическое значение пи. Таинственное число «пи»

Чему равно число Пи мы знаем и помним со школы. Оно равно 3.1415926 и так далее… Обычному человеку достаточно знать, что это число получается, если разделить длину окружности на ее диаметр.

Но многим известно, что число Пи возникает в неожиданных областях не только математики и геометрии, но и в физике. Ну а если вникнуть в подробности природы этого числа, то можно заметить много удивительного среди бесконечного ряда цифр. Возможно ли, что Пи скрывает самые сокровенные тайны Вселенной?

Бесконечное число

Само число Пи возникает в нашем мире как длина окружности, диаметр которой равен единице. Но, несмотря на то, что отрезок равный Пи вполне себе конечен, число Пи начинается, как 3.1415926 и уходит в бесконечность рядами цифр, которые никогда не повторяются. Первый удивительный факт состоит в том, что это число, используемое в геометрии, нельзя выразить в виде дроби из целых чисел. Иначе говоря, вы не сможете его записать отношением двух чисел a/b. Кроме этого число Пи трансцендентное. Это означает, что нет такого уравнения (многочлена) с целыми коэффициентами, решением которого было бы число Пи.

То, что число Пи трансцендентно, доказал в 1882 году немецкий математик фон Линдеман. Именно это доказательство стало ответом на вопрос, можно ли с помощью циркуля и линейки нарисовать квадрат, у которого площадь равна площади заданного круга. Эта задача известна как поиск квадратуры круга, волновавший человечество с древнейших времен. Казалось, что эта задача имеет простое решение и вот-вот будет раскрыта. Но именно непостижимое свойство числа Пи показало, что у задачи квадратуры круга решения не существует.

В течение как минимум четырех с половиной тысячелетий человечество пыталось получить все более точное значение числа Пи. Например, В Библии в Третьей Книги Царств (7:23) число Пи принимается равным 3.

Замечательное по точности значение Пи можно обнаружить в пирамидах Гизы: соотношение периметра и высоты пирамид составляет 22/7. Эта дробь дает приближенное значение Пи, равное 3.142… Если, конечно, египтяне не задали такое соотношение случайно. Это же значение уже применительно к расчету числа Пи получил в III веке до нашей эры великий Архимед.

В папирусе Ахмеса, древнеегипетском учебнике по математике, который датируется 1650 годом до нашей эры, число Пи рассчитано как 3. 160493827.

В древнеиндийских текстах примерно IX века до нашей эры наиболее точное значение было выражено числом 339/108, которое равнялось 3,1388…

После Архимеда почти две тысячи лет люди пытались найти способы рассчитать число Пи. Среди них были как известные, так и неизвестные математики. Например, римский архитектор Марк Витрувий Поллион, египетский астроном Клавдий Птолемей, китайский математик Лю Хуэй, индийский мудрец Ариабхата, средневековый математик Леонардо Пизанский, известный как Фибоначчи, арабский ученый Аль-Хорезми, от чьего имени появилось слово «алгоритм». Все они и множество других людей искали наиболее точные методики расчета Пи, но вплоть до 15 века никогда не получали больше чем 10 цифр после запятой в связи со сложностью расчетов.

Наконец, в 1400 году индийский математик Мадхава из Сангамаграма рассчитал Пи с точностью до 13 знаков (хотя в двух последних все-таки ошибся).

Количество знаков

В 17 веке Лейбниц и Ньютон открыли анализ бесконечно малых величин, который позволил вычислять Пи более прогрессивно – через степенные ряды и интегралы. Сам Ньютон вычислил 16 знаков после запятой, но не упомянул это в своих книгах – об этом стало известно после его смерти. Ньютон утверждал, что занимался расчетом Пи исключительно от скуки.

Примерно в то же время подтянулись и другие менее известные математики, предложившие новые формулы расчета числа Пи через тригонометрические функции.

Например, вот по какой формуле рассчитывал Пи преподаватель астрономии Джон Мэчин в 1706 году: PI / 4 = 4arctg(1/5) – arctg(1/239). С помощью методов анализа Мэчин вывел из этой формулы число Пи с сотней знаков после запятой.

Кстати, в том же 1706 году число Пи получило официальное обозначение в виде греческой буквы: его в своем труде по математике использовал Уильям Джонс, взяв первую букву греческого слова «периферия», что означает «окружность». Родившийся в 1707 великий Леонард Эйлер популяризовал это обозначение, нынче известное любому школьнику.

До эры компьютеров математики занимались тем, чтобы рассчитать как можно больше знаков. В связи с этим порой возникали курьезы. Математик-любитель У. Шенкс в 1875 году рассчитал 707 знаков числа Пи. Эти семь сотен знаков увековечили на стене Дворца Открытий в Париже в 1937 году. Однако спустя девять лет наблюдательными математиками было обнаружено, что правильно вычислены лишь первые 527 знаков. Музею пришлось понести приличные расходы, чтобы исправить ошибку – сейчас все цифры верные.

Когда появились компьютеры, количество цифр числа Пи стало исчисляться совершенно невообразимыми порядками.

Один из первых электронных компьютеров ENIAC, созданный в 1946 году, имевший огромные размеры, и выделявший столько тепла, что помещение прогревалось до 50 градусов по Цельсию, вычислил первые 2037 знаков числа Пи. Этот расчет занял у машины 70 часов.

По мере совершенствования компьютеров наше знание числа Пи все дальше и дальше уходило в бесконечность. В 1958 году было рассчитано 10 тысяч знаков числа. В 1987 году японцы высчитали 10 013 395 знаков. В 2011 японский исследователь Сигеру Хондо превысил рубеж в 10 триллионов знаков. 2.

Пи появляется в задаче Бюффона о бросании иглы, сформулированной в 18 веке: какова вероятность того, что брошенная на расчерченный лист бумаги игла пересечет одну из линий. Если длина иглы L, а расстояние между линиями L, и r > L то мы можем приблизительно рассчитать значение числа Пи по формуле вероятности 2L/rPI. Только представьте – мы можем получить Пи из случайных событий. И между прочим Пи присутствует в нормальном распределении вероятностей, появляется в уравнении знаменитой кривой Гаусса. Значит ли это, что число Пи еще более фундаментально, чем просто отношение длины окружности к диаметру?

Мы можем встретить Пи и в физике. Пи появляется в законе Кулона, который описывает силу взаимодействия между двумя зарядами, в третьем законе Кеплера, который показывает период обращения планеты вокруг Солнца, встречается даже в расположении электронных орбиталей атома водорода. И что опять же самое невероятное – число Пи прячется в формуле принципа неопределенности Гейзенберга – фундаментального закона квантовой физики.

Тайны числа Пи

В романе Карла Сагана «Контакт», по которому снят одноименный фильм, инопланетяне сообщают героине, что среди знаков Пи содержится тайное послание от Бога. С некоторой позиции цифры в числе перестают быть случайными и представляют себе код, в котором записаны все секреты Мироздания.

Этот роман на самом деле отразил загадку, занимающую умы математиков всей планеты: является ли число Пи нормальным числом, в котором цифры разбросаны с одинаковой частотой, или с этим числом что-то не так. И хотя ученые склоняются к первому варианту (но не могут доказать), число Пи выглядит очень загадочно. Один японец как то подсчитал, сколько раз встречаются числа от 0 до 9 в первом триллионе знаков Пи. И увидел, что числа 2, 4 и 8 встречаются чаще, чем остальные. Это может быть одним из намеков на то, что Пи не совсем нормальное, и цифры в нем действительно не случайны.

Вспомним всё, что мы прочли выше, и спросим себя, какое еще иррациональное и трансцендентное число так часто встречается в реальном мире?

А в запасе имеются еще странности. Например, сумма первых двадцати цифр Пи равна 20, а сумма первых 144 цифр равна «числу зверя» 666.

Главный герой американского сериала «Подозреваемый» профессор Финч рассказывал студентам, что в силу бесконечности числа Пи в нем могут встретиться любые комбинации цифр, начиная от цифр даты вашего рождения до более сложных чисел. Например, на 762-ой позиции находится последовательность из шести девяток. Эта позиция называется точкой Фейнмана в честь известного физика, который заметил это интересное сочетание.

Нам известно также, что число Пи содержит последовательность 0123456789, но находится она на 17 387 594 880-й цифре.

Все это означает, что в бесконечности числа Пи можно обнаружить не только интересные сочетания цифр, но и закодированный текст «Войны и Мира», Библии и даже Главную Тайну Мироздания, если таковая существует.

Кстати, о Библии. Известный популяризатор математики Мартин Гарднер в 1966 году заявил, что миллионным знаком числа Пи (на тот момент еще неизвестным) будет число 5. Свои расчеты он объяснил тем, что в англоязычной версии Библии, в 3-й книге, 14-й главе, 16-м стихе (3-14-16) седьмое слово содержит пять букв. Миллионную цифру получили спустя восемь лет. Это было число пять.

Стоит ли после этого утверждать, что число Пи случайно?

Число Пи — одно из самых популярных математических понятий. О нем пишут картины, снимают фильмы, его играют на музыкальных инструментах, ему посвящают стихи и праздники, его ищут и находят в священных текстах.

Кто открыл π?

Кто и когда впервые открыл число π, до сих пор остается загадкой. Известно, что строители древнего Вавилона уже вовсю пользовались им при проектировании. На клинописных табличках, которым тысячи лет, сохранились даже задачи, которые предлагали решить с помощью π. Правда, тогда считалось, что π равно трем. Об этом свидетельствует табличка, найденная в городе Сузы, в двухстах километрах от Вавилона, где число π указывалось как 3 1/8 .

В процессе вычислений π вавилонцы обнаружили, что радиус окружности в качестве хорды входит в нее шесть раз, и поделили круг на 360 градусов.

А заодно сделали то же самое с орбитой солнца. Таким образом, они решили считать, что в году 360 дней.

В Древнем Египте π было равно 3,16.
В древней Индии – 3,088.
В Италии на рубеже эпох считали, что π равно 3,125.

В Античности самое раннее упоминание π относится к знаменитой задаче о квадратуре круга, то есть о невозможности при помощи циркуля и линейки построить квадрат, площадь которого равна площади определенной окружности. Архимед приравнивал π к дроби 22/7 .

Ближе всего к точному значению π подошли в Китае. Его вычислил в V веке н. э. знаменитый китайский астроном Цзу Чунь Чжи. Вычислялось π довольно просто. Надо было дважды написать нечетные числа: 11 33 55, а потом, разделив их пополам, поместить первое в знаменатель дроби, а второе – в числитель: 355/113 . Результат совпадает с современными вычислениями π вплоть до седьмого знака.

Почему π – π?

Сейчас даже школьники знают, что число π — математическая константа, равная отношению длины окружности к длине её диаметра и равняется π 3,1415926535 … и далее после запятой – до бесконечности.

Свое обозначение π число обрело сложным путем: сначала этой греческой буквой в 1647 году математик Оутрейд обозвал длину окружности. Он взял первую букву греческого слова περιφέρεια — «переферия». В 1706 году английский преподаватель Уильям Джонс в работе «Обозрение достижений математики» уже называл буквой π отношение длины окружности к ее диаметру. А закрепил название математик XVIII века Леонард Эйлер, перед авторитетом которого остальные склонили головы. Так π стало π.

Уникальность числа

Пи — поистине уникальное число.

1. Ученые считают, что количество знаков в числе π бесконечно. Их последовательность не повторяется. Более того, найти повторения не удастся никому и никогда. Так как число бесконечно, оно может заключать в себе абсолютно все, даже симфонию Рахманинова, Ветхий Завет, ваш номер телефона и год, в котором наступит Апокалипсис.

2. π связано с теорией хаоса. К такому выводу пришли ученые после создания вычислительной программы Бэйли, которая показала, что последовательность чисел в π абсолютно случайна, что соответствует теории.

3. Вычислить число до конца практически невозможно – это заняло бы слишком много времени.

4. π – иррациональное число, то есть его значение нельзя выразить дробью.

5. π – трансцедентное число. Его нельзя получить, произведя какие-либо алгебраические действия над целыми числами.

6. Тридцать девять знаков после запятой в числе π достаточно для того, что вычислить длину окружности, опоясывающей известные космические объекты во Вселенной, с погрешностью в радиус атома водорода.

7. Число π связано с понятием «золотого сечения». В процессе измерений Великой пирамиды в Гизе археологи выяснили, что ее высота относится к длине ее основания, так же как радиус окружности — к ее длине.

Рекорды, связанные с π

В 2010 году сотрудник компании «Yahoo» математик Николас Чже смог вычислить в числе π два квадрильона знаков после запятой (2×10). На это ушло 23 дня, и математику понадобилось множество помощников, которые работали на тысячах компьютеров, объединенных по технологии рассеянных вычислений. Метод позволил произвести расчеты с такой феноменальной скоростью. Чтобы вычислить то же самое на одном компьютере, потребовалось бы больше 500 лет.

Для того, чтобы просто записать все это на бумаге, потребуется бумажная лента больше двух миллиардов километров длиной. Если развернуть такую запись, ее конец выйдет за пределы Солнечной системы.

Китаец Лю Чао установил рекорд по запоминанию последовательности цифр числа π. В течение 24 часов 4 минут Лю Чао назвал 67 890 знаков после запятой, не допустив ни одной ошибки.

У π много поклонников. Его воспроизводят на музыкальных инструментах, и оказывается, что «звучит» оно превосходно. Его запоминают и придумывают для этого различные приемы. Его ради забавы скачивают себе на компьютер и хвастаются друг перед другом, кто больше скачал. Ему ставят памятники. Например, такой памятник есть в Сиэтле. Он находится на ступенях перед зданием Музея искусств.

π используют в украшениях и в интерьере. Ему посвящают стихи, его ищут в святых книгах и на раскопках. Есть даже «Клуб π».
В лучших традициях π, числу посвящен не один, а целых два дня в году! В первый раз День π празднуют 14 марта. Поздравлять друг друга надо ровно в 1час, 59 минут, 26 секунд. Таким образом, дата и время соответствуют первым знакам числа- 3,1415926.

Во второй раз праздник π отмечают 22 июля. Этот день связывают с так называемым «приближенным π», который Архимед записывал дробью.
Обычно в этот день π студенты, школьники и ученые устраивают забавные флэш-мобы и акции. Математики, забавляясь, с помощью π вычисляют законы падающего бутерброда и дарят друг другу шуточные награды.
И между прочим, π в самом деле можно найти в святых книгах. Например, в Библии. И там число π равно… трем.

Значение числа (произносится «пи» ) — математическая константа, равная отношению

Обозначается буквой греческого алфавита «пи». Старое название — лудольфово число .

Чему равно число пи? В простых случаях хватает знать первые 3 знака (3,14). Но для более

сложных случаев и там, где нужна бОльшая точность необходимо знать больше, чем 3 цифры.

Какое число пи? Первые 1000 знаков числа пи после запятой:

3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989. ..

В обычных условиях приблизительное значение числа пи можно вычислить следуя пунктам,

приведенным ниже:

Берем круг , обматываем по его краю нить один раз.
Измеряем длину нити.
Измеряем диаметр круга.
Делим длину нити на длину диаметра. Получили число пи.

Свойства числа Пи.

пи — иррациональное число , т.е. значение числа пи не возможно точно выразить в виде

дроби m/n , где m и n являются целыми числами . Из этого видно, что десятичное представление

числа пи никогда не заканчивается и оно не является периодическим.

пи — трансцендентное число, т.е. оно не может быть корнем какого-либо многочлена с целыми

коэффициентами. В 1882 году профессор Кёнигсбергский доказал трансцендентность числа пи , а

позднее, профессором Мюнхенского университета Линдеманом. Доказательство упростил

Феликс Клейн в 1894 году.

так как в евклидовой геометрии площадь круга и длина окружности — это функции числа пи,

то доказательство трансцендентности пи дало конец спору о квадратуре круга, длившемуся более

2,5 тысяч лет.

пи является элементом кольца периодов (то есть, вычислимым и арифметическим числом).

Но никто не знает, принадлежит ли к кольцу периодов.

Формула числа пи.

Франсуа Виет:

Формула Валлиса:

Ряд Лейбница:

Другие ряды:

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «НОВОАГАНСКАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ CРЕДНЯЯ ШКОЛА №2»

История возникновения

числа Пи.

Выполнила Шевченко Надежда,

ученица 6 «Б» класса

Руководитель: Чекина Ольга Александровна, учитель математики

пгт. Новоаганск

2014

План.

Ведение.

Цели.

II. Основная часть.

1)Первый шаг к числу пи.

2)Не разгаданная загадка.

3)Интересные факты.

III. Заключение

Использованная литература.

Введение

Цели моей работы

1)Найти историю происхождения пи.

2)Рассказать интересные факты числа пи

3)Сделать презентацию и оформить доклад.

4) Подготовить выступление на конференцию.

Основная часть.

Пи (π) — буква греческого алфавита, применяемая в математике для обозначения отношения длины окружности к диаметру. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр. Оно стало общепринятым после работы Л. Эйлера, относящейся к 1736г., однако впервые оно было употреблено английским математиком У. Джонсом (1706г.). Как и всякое иррациональное число, π представляется бесконечной непериодической десятичной дробью:

π = 3,141592653589793238462643.

Первый шаг в изучении свойств числа π сделал Архимед. В сочинении «Измерение круга» он вывел знаменитое неравенство: [формула]
Это означает, что π лежит в интервале длиной 1/497. В десятичной системе счисления получаются три правильных значащих цифры: π = 3,14…. Зная периметр правильного шестиугольника и последовательно удваивая число его сторон, Архимед вычислил периметр правильного 96-угольника, откуда и следует неравенство. 96-угольник визуально мало отличается от окружности и является хорошим приближением к ней.
В том же сочинении, последовательно удваивая число сторон квадрата, Архимед нашел формулу площади круга S = π R2. Позднее он дополнил ее также формулами площади сферы S = 4 π R2 и объема шара V = 4/3 π R3.

В древнекитайских трудах попадаются самые разные оценки, из которых самая точная — это известное китайское число 355/113. Цзу Чунчжи (V век) даже считал это значение точным.
Лудольф ван Цейлен (1536-1610) затратил десять лет на вычисление числа π с 20-ю десятичными цифрами (этот результат был опубликован в 1596 году). Применив метод Архимеда, он довёл удвоение до n-угольника, где n=60·229. Изложив свои результаты в сочинении «Об окружности», Лудольф закончил его словами: «У кого есть охота, пусть идёт дальше». После смерти в его рукописях были обнаружены ещё 15 точных цифр числа π. Лудольф завещал, чтобы найденные им знаки были высечены на его надгробном камне. В честь него число π иногда называли «лудольфовым числом».

Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, хотя по-прежнему волнует ученых. Попытки математиков полностью вычислить всю числовую последовательность часто приводят к курьезным ситуациям. Например, математики братья Чудновские в Политехническом Университете Бруклина специально с этой целью сконструировали суперскоростной компьютер. Однако установить рекорд им не удалось – пока рекорд принадлежит японскому математику Ясумаса Канада, который смог вычислить 1,2 биллиона чисел бесконечной последовательности.

Интересные факты
Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3/14, что соответствует приближённому значению числа Пи.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи», так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
Мировой рекорд по запоминанию знаков числа π принадлежит японцу Акира Харагути (Akira Haraguchi). Он запомнил число π до 100-тысячного знака после запятой. Ему понадобилось почти 16 часов, чтобы назвать всё число целиком.
Германский король Фридрих Второй был настолько очарован этим числом, что посвятил ему… целый дворец Кастель дель Монте, в пропорциях которого можно вычислить Пи. Сейчас волшебный дворец находится под охраной ЮНЕСКО.

Заключение
В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Всё это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.

Мою работу можно использовать на уроках математики.

Итоги моей работы:

Нашла историю происхождения числа пи.
Рассказала о интересных фактах числа пи.
Узнала много нового о числе пи.
Оформила работу и Выступила на конференции.

13 января, 2017

π= 3,
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989. .

Не нашли? Тогда посмотрите .

Вообще это может быть не только номер телефона, а любая информация, закодированная с помощью цифр. К примеру, если представить все произведения Александра Сергеевича Пушкина в цифровом виде, то они хранились в числе Пи еще до того, как он их написал, даже до того, как он родился. В принципе, они хранятся там до сих пор. Кстати, ругательства математиков в π тоже присутствуют, да и не только математиков. Словом, в числе Пи есть всё, даже мысли, которые посетят вашу светлую голову завтра, послезавтра, через год, а может, через два. В это очень трудно поверить, но даже если мы представим, что поверили, еще труднее будет получить оттуда информацию и расшифровать её. Так что вместо того, чтобы копаться в этих цифрах, может проще подойти к понравившейся девушке и спросить у неё номер?.. Но для тех, кто не ищет легких путей, ну или просто интересующихся, чему же равно число Пи, предлагаю несколько способов его вычисления. Считайте на здоровье.

Чему равно число Пи? Методы его вычисления:

1. Экспериментальный метод. Если число Пи это отношение длины окружности к её диаметру, то первый, пожалуй, самый очевидный способ нахождения нашей загадочной константы будет вручную произвести все измерения и вычислить число Пи по формуле π=l/d. Где l — длина окружности, а d — её диаметр. Все очень просто, необходимо лишь вооружится ниткой для определения длины окружности, линейкой для нахождения диаметра, и, собственно, длины самой нитки, ну и калькулятором, если у вас проблемы с делением в столбик. В роли измеряемого образца может выступить кастрюля или банка из под огурцов, неважно, главное? чтоб в основании была окружность.

Рассмотренный способ вычисления самый простой, но, к сожалению, имеет два существенных недостатка, отражающихся на точности полученного числа Пи. Во-первых, погрешность измерительных приборов (в нашем случае это линейка с ниткой), а во-вторых, нет никакой гарантии, что измеряемая нами окружность будет иметь правильную форму. Поэтому не удивительно, что математика подарила нам множество других методов вычисления π, где нет нужды производить точные измерения.

2. Ряд Лейбница. Существует несколько бесконечных рядов, позволяющих точно вычислять число Пи до большого количества знаков после запятой. Одним из самых простых рядов является ряд Лейбница. π = (4/1) — (4/3) + (4/5) — (4/7) + (4/9) — (4/11) + (4/13) — (4/15) …
Все просто: берем дроби с 4 в числителе (это то что сверху) и одним числом из последовательности нечетных чисел в знаменателе (это то что снизу), последовательно складываем и вычитаем их друг с другом и получаем число Пи. Чем больше итераций или повторений наших нехитрых действий, тем точнее результат. Просто, но не эффективно, к слову, необходимо 500000 итераций чтоб получить точное значение числа Пи с десятью знаками после запятой. То есть, нам придется несчастную четверку разделить аж 500000 раз, а помимо этого полученные результаты мы должны будем 500000 раз вычитать и складывать. Хотите попробовать?

3. Ряд Нилаканта. Нет времени возится с рядом Лейбница? Есть альтернатива. Ряд Нилаканта, хотя он немного сложнее, но позволяет быстрее получить нам искомый результат. π = 3 + 4/(2*3*4) — 4/(4*5*6) + 4/(6*7*8) — 4/(8*9*10) + 4/(10*11*12) — (4/(12*13*14) … Думаю, если внимательно посмотреть на приведенный начальный фрагмент ряда, все становится ясным, и комментарии излишни. По этому идем дальше.

4. Метод «Монте-Карло» Довольно интересным методом вычисления числа Пи является метод Монте Карло. Столь экстравагантное название ему досталось в честь одноименного города в королевстве Монако. И причина тому случайность. Нет, его не назвали случайно, просто в основе метода лежат случайные числа, а что может быть случайней чисел, выпадающих на рулетках казино Монте Карло? Вычисление числа Пи не единственное применение этого метода, так в пятидесятых годах его использовали при расчетах водородной бомбы. Но не будем отвлекаться.

Возьмем квадрат со стороной, равной 2r , и впишем в него круг радиусом r . Теперь если наугад ставить точки в квадрате, То вероятность P того, что точка угодит в круг, есть отношение площадей круга и квадрата. P=S кр /S кв =πr 2 /(2r) 2 =π/4 .

Теперь отсюда выразим число Пи π=4P . Остается только получить экспериментальные данные и найти вероятность Р как отношение попаданий в круг N кр к попаданиям в квадрат N кв . В общем виде расчетная формула будет выглядеть следующим образом: π=4N кр / N кв.

Хочется отметить, что для того, чтобы реализовать этот метод, в казино идти необязательно, достаточно воспользоваться любым более или менее приличным языком программирования. Ну а точность полученных результатов будет зависеть от количества поставленных точек, соответственно, чем больше, тем точнее. Желаю удачи 😉

Число Тау ( Вместо заключения).

Люди, далекие от математики, скорее всего не знают, но так сложилось, что число Пи имеет брата, который больше его в два раза. Это число Тау(τ) , и, если Пи — это отношение длины окружности к диаметру, то Тау — это отношение этой длины к радиусу. И на сегодняшний день есть предложения некоторых математиков отказаться от числа Пи и заменить его на Тау, так как это во многом более удобно. Но пока это только предложения, и как говорил Лев Давидович Ландау: «Новая теория начинает господствовать тогда, когда вымрут сторонники старой».

14 марта объявлен днем числа «Пи», так как в этой дате присутствуют три первые цифры этой константы.

ЧЕМУ РАВНО ЧИСЛО ПИ? | Ньютонов

***

Что общего между колесом от Лады Приоры, обручальным кольцом и блюдцем вашего кота? Вы, конечно, скажете красота и стиль! Но я осмелюсь с вами поспорить. Число Пи! Это число, объединяющее все окружности, круги и округлости, к коим в частности можно отнести и мамино кольцо, и колесо от любимой папиной машины и даже блюдце любимого кота Мурзика. Готов поспорить, что в рейтинге самых популярных физических и математических констант число Пи несомненно займет первую строчку. Но что скрывается за ним? Может какие-то страшные ругательства математиков? Давайте попробуем разобраться в этом вопросе.

Что же такое число «Пи»

_{и откуда оно взялось?}

Современное обозначение числа π (Пи) появилось благодаря английскому математику Джонсу в 1706 году. Это первая буква греческого слова περιφέρεια (периферия, или окружность).

Для тех, кто проходил математику давно, да и к тому же мимо, напомним, что число Пи — это отношение длины окружности к её диаметру. Величина является константой, то есть постоянна для любой окружности, независимо от её радиуса. Люди знали об этом еще в древности. Так в древнем Египте число Пи принимали равным отношению ²⁵⁶/₈₁, а в ведических текстах приводится значение ³³⁹/₁₀₈, Архимед же предлагал соотношение ²²/₇. Но ни эти, ни многие другие способы выражения числа Пи не давали точный результат.

Оказалось, что число Пи трансцендентное, соответственно, и иррациональное. А это значит, его нельзя представить в виде простой дроби. Если же его выразить через десятичную, то последовательность цифр после запятой устремятся в бесконечность, к тому же периодически не повторяясь. Что все это значит? Очень просто. Хотите узнать номер телефона понравившейся девушки? Его наверняка можно найти в последовательности цифр после запятой числа Пи.

Телефон можно посмотреть здесь ↓

Число Пи с точностью до 1000 знаков.

_{π= 3,}
_{1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989. .}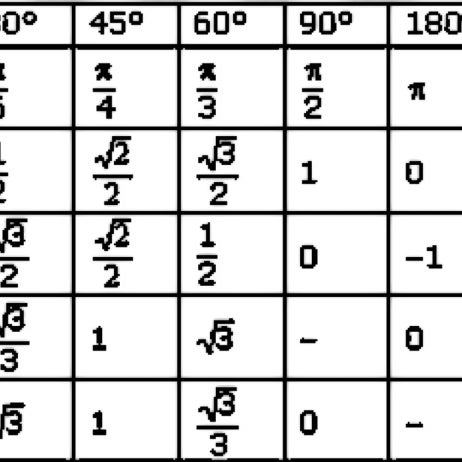

Не нашли? Тогда посмотрите здесь.

Все в числе «Пи»

Словом, в числе Пи есть всё, даже мысли, которые посетят вашу светлую голову завтра, послезавтра, через год, а может, через два. В это очень трудно поверить, но даже если мы представим, что поверили, еще труднее будет получить оттуда информацию и расшифровать её. Так что вместо того, чтобы копаться в этих цифрах, может проще подойти к понравившейся девушке и спросить у неё номер?.. Но для тех, кто не ищет легких путей, ну или просто интересующихся, чему же равно число Пи, предлагаю несколько способов его вычисления. Считайте на здоровье.

Чему равно число Пи?

_{Методы его вычисления:}

Экспериментальный метод.

Если число Пи это отношение длины окружности к её диаметру, то первый, пожалуй, самый очевидный способ нахождения нашей загадочной константы будет вручную произвести все измерения и вычислить число Пи по формуле π=l/d. Где l — длина окружности, а d — её диаметр. Все очень просто, необходимо лишь вооружится ниткой для определения длины окружности, линейкой для нахождения диаметра, и, собственно, длины самой нитки, ну и калькулятором, если у вас проблемы с делением в столбик. В роли измеряемого образца может выступить кастрюля или банка из под огурцов, неважно, главное? чтоб в основании была окружность.

Ряд Лейбница.

Существует несколько бесконечных рядов, позволяющих точно вычислять число Пи до большого количества знаков после запятой. Одним из самых простых рядов является ряд Лейбница. π = (4/1) — (4/3) + (4/5) — (4/7) + (4/9) — (4/11) + (4/13) — (4/15) …

Все просто: берем дроби с 4 в числителе (это то что сверху) и одним числом из последовательности нечетных чисел в знаменателе (это то что снизу), последовательно складываем и вычитаем их друг с другом и получаем число Пи. Чем больше итераций или повторений наших нехитрых действий, тем точнее результат. Просто, но не эффективно, к слову, необходимо 500000 итераций чтоб получить точное значение числа Пи с десятью знаками после запятой. То есть, нам придется несчастную четверку разделить аж 500000 раз, а помимо этого полученные результаты мы должны будем 500000 раз вычитать и складывать. Хотите попробовать?

Ряд Нилаканта

Нет времени возится с рядом Лейбница? Есть альтернатива. Ряд Нилаканта, хотя он немного сложнее, но позволяет быстрее получить нам искомый результат. π = 3 + 4/(2*3*4) — 4/(4*5*6) + 4/(6*7*8) — 4/(8*9*10) + 4/(10*11*12) — (4/(12*13*14) … Думаю, если внимательно посмотреть на приведенный начальный фрагмент ряда, все становится ясным, и комментарии излишни. По этому идем дальше.

Метод «Монте-Карло»

Довольно интересным методом вычисления числа Пи является метод Монте Карло. Столь экстравагантное название ему досталось в честь одноименного города в королевстве Монако. И причина тому случайность. Нет, его не назвали случайно, просто в основе метода лежат случайные числа, а что может быть случайней чисел, выпадающих на рулетках казино Монте Карло? Вычисление числа Пи не единственное применение этого метода, так в пятидесятых годах его использовали при расчетах водородной бомбы. Но не будем отвлекаться.

Возьмем квадрат со стороной, равной 2r, и впишем в него круг радиусом r. Если наугад ставить точки в квадрате, то вероятность P того, что точка угодит в круг, есть отношение площадей круга и квадрата. P=S_кр/S_кв=πr²/(2r)²=π/4.

Теперь отсюда выразим число Пи π=4P. Остается только получить экспериментальные данные и найти вероятность Р как отношение попаданий в круг N_кр к попаданиям в квадрат N_кв. В общем виде расчетная формула будет выглядеть следующим образом: π=4N_кр / N_кв.

Число Тау

_{(Вместо заключения).}

14 марта объявлен днем числа «Пи», так как в этой дате присутствуют три первые цифры этой константы.3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

davidbau.

com Тайна 355/113483 : 5371151992734
2851718461558 : 895529372127380727 010529372127760737 010711151992734
2851718461558: 336851849443403
324521540032945 : 1019514486099146 и т.

д.

И затем он указывает, что последняя пара представляет число пи с точностью до 25 знаков после запятой.

Ламберт пришел к выводу, что число пи иррационально. Это часть доказательства, но из-за моего плохого понимания немецкого языка я не могу понять, откуда он взял эту серию рациональных приближений.

Автор: Бернард Грининг, 26 июля 2012 г., 16:22

в вашем разделе
Другие хорошие рациональные приближения для числа Пи

Я думаю, что один из этих трех правилен, но вы должны исправить два других:
1/3748629
1/3748269
1/3748259

Дилсексуальный момент?

Разместил: scottm 27 июля 2012 г., 12:52

3141592654:1000000000 🙂

Размещено: 3 августа 2012 г., 18:15

Aqu en la tierra exists dos personajes Que han dicho ser Dios. Эллос, сын Иеговы и Кришны. Es obvio Que эль Creador эс уно соло.
Cual de los dos es el mentiroso? Y cul es el verdadero? О сын лос душ фальсос? Yo s quien es el Dios verdadero y te lo voy a decir despus de. .. 95 + 3/11)/(2*5 + 3/11)

3/11 — отношение радиуса Луны к радиусу Земли.

Размещено: Тревор Стритон 18 апреля 2013 г., 07:58

Если вы запрограммируете компьютер искать 2 трехзначных числа, соотношение которых находится между 223/71 и 22/7, возникают только 4 возможности.

(300 + 22*k)/(100 + 7*k) для k = от 1 до 4.

(я все еще пытаюсь понять, как древние могли количественно определить точность любого приближения с помощью дробей). Из этих 4-х вариантов надо было выбрать Ву 355/113, все лучше исходных 2.95 + 3/11)/(2*5 + 3/11). Красиво, правда?

Вычеркните все цифры из правой части слева, и у вас останется 1 1 2 2.
Вы можете увидеть это как 11 22 или как 11 11 11 три одиннадцати?

Теперь дополнительные цифры в 355/113, полученные по сравнению с двумя начальными значениями, составляют 1592.

Вот странная числовая синхронность, соединяющая PI, 22/7 и число Эйлера e, где эти цифры оказываются перевернутыми.

Первые 9 цифр числа e (включая целую часть) можно найти в последовательности 228118278 на позициях 21, 33, 34, 37, 49., 52, 63, 66 и 68 ФИ.

Только 2 из этих цифр расположены правильно, первая 2 и 8 на 6-м месте. Необходимо четыре перестановки, первая — перестановка 2-й и 8-й цифр. Четыре кода подкачки, читающиеся зигзагообразно, образуют символ PI, повернутый на 180 градусов.

Цифры e в этих позициях равны
024795741. Игнорируя начальный 0 и удаляя 2591, вы получаете 4774, палиндром. Сумма цифр = 22. (Я родился в 1947 г.)

Также 355/113 = 3*[360 — (3+7)/2]/(360 — 3*7).

Мне кажется, что отношение является артефактом самой структуры числа, а не аналитически полученным.

Размещено: 5 мая 2013 г., 14:29

Посмотрите на Иоганна Генриха Ламберта, 1792 г., на http://j.mp/16wYL1d Fritz

Разместил: Fritz Jrn 31 мая 2013 г., 18:02

Обратите внимание, что первое приближение числа пи, которое даже БЛИЖЕ, чем 355/113, равно 52163/16604 (3,14159238. ..). Обратите внимание, что 52163/16604pi, так что, просто добавив 355 к 52163 и 113 к 16604, мы получим 52518/16717, немного более близкое приближение, чем 52163/16604. Это может продолжаться до тех пор, пока 104348/33215=3,14159265392.

Разместил: Джастин 28 ноября 2013 г., 21:36

С Новым годом!

Я понял, что 355/113 использует всего шесть цифр, а 3,141592920354… содержит шесть знаков после запятой, очень высокая степень точности. Скорее всего, это потому, что в непрерывной дроби числа пи 355/113 стоит прямо перед 292! Следующая дробь этого товара — 21053343141/6701487259, за которой следует 2646693125139304345/842468587426513207!

Разместил: Джастин 2 января 2014 г., 20:00 909:20

283 разделить на 90
6352 разделить на 2023
13308 разделить на 4235 = 3,14238488784 = тоже очень близко к Пи….

Разместил: Джейми Паттон 4 января 2014 г. , 10:52

Вы можете получить число Пи, используя любое число!
(например,
254,46

94077325 9094077325 чехол (81)…
вы можете сделать это с любым номером. Я люблю математику, но когда вы действительно вникаете в нее, это довольно абсурдно. все числа могут быть равны нулю или бесконечности, так что в чем смысл, например, у вас может быть бесконечное количество чисел между любыми двумя числами. поэтому все числа имеют возможность иметь одинаковое количество чисел между каждым числом, в основном они компенсируют друг друга. вы могли бы просто использовать только числа 12 и 3, но, став действительно конкретными десятичными знаками, вы могли бы бесконечно продолжать всего с тремя числами, не нуждаясь в 456789. вы можете проделать ту же работу с тремя числами, но у людей есть склонность к излишней сложности. если все числа могут иметь бесконечное значение, то есть ли какое-либо число больше или меньше другого числа, и я включаю 0.

Герои на самом деле мое любимое число, кажется, что оно мало что делает, но оно бесконечно, для меня это странное совпадение это круг. если уж математика надоела, то как должно быть у людей, когда у меня с ней много проблем. это в основном сводится к математикам и людям, что с большим эго математика проста, если вы можете сосчитать до трех, вы можете сосчитать что угодно. подумайте о простой арифметике

1 x 0 = 0….. хорошо, скажем, у меня была одна карта в руке, я умножаю количество карт(ы) на ноль, сколько карт у меня есть.. да, я получаю число один так какого черта 0 стал принятым ответом. математика похожа на магию, это иллюзия.

Разместил: JOSKi 15 августа 2014 г., 16:54

Не то, что вы спросили, а
В японском языке дроби читаются в обратном порядке от английского: знаменатель _бун нет_ числитель.
Итак, 355/113 — это «113 булочек № 355», что особенно запоминается, если читать цифру за цифрой (здесь с заглавной буквы): «Ичи, Ичи, Сан бун но Сан, иди, иди».
(«Бун» означает «часть [ы]», а «нет» — притяжательный маркер.)
Эта система чтения дробей заимствована из китайского языка и также используется в корейском языке.

Тем временем я заметил, что в системе счисления 11 355/113 получается как 2X3/X3 (где X означает число после 9), что, на мой взгляд, довольно аккуратно в любом порядке.

Сообщение от: Джереми Уиппл 9 ноября 2015 г., 05:00

Я нашел наиболее приближенное дробное число.
117766625/(113×331737) =3,1415926535897…

Разместил: Нага Санджай 12 января 2016 г., 11:38

pi варьируется от 3,1416 до 3,164

посмотри Aetzbar на амазоне

Разместил: Aetzbar 5 февраля 2016 г., 18:30

Я разработал определенную непрерывную дробь для 1/pi, которая имеет 7/22 как одну из сходящихся. Пожалуйста, проверьте это в этом посте http://math.stackexchange.com/questions/1446792/a-conjectured-continued -фракция-для-кроватки-левый-фракз-pi4z2n-правый-что

Сообщение от: mandelbrot 17 апреля 2016 г. , 10:11 909:20

Разместил: Мандела 17 апреля 2016 г., 10:12

Из самого первого комментария—

«является ли их любая другая дробь, очень близкая к пи…»

На ум приходит одно, дающее выдающиеся результаты, это превосходное приближение Шринивасы Рамануджана 9(1/2).

[Прошу прощения за дублирование, но я не читал эту статью полностью]

Разместил: jimmike 26 мая 2016 г., 23:08

нержавеющая сталь

Размещено: 1 июля 2016 г., 01:00

ПРОМЕЖУТОЧНЫЙ; Schade, dass ihr die Quadratur des LdV nicht zeichnet knnt, wie in scmar beschrieben. Lesen geht hoffentlich noch. Allerdings muss man sich die paar Seiten ausdrucken. Es ist meine Version, kein Buch zu finanzieren.

Либе Гре, Удо

PS, Viren sind nicht drin, kann ich nicht-

Разместил: Удо Шмидт 12 августа 2016 г., 18:24

Тайна числа 355/113

Сегодняшняя дата — хороший повод запомнить еще несколько цифр числа 3,1415926 53589793 23846264 33832795….

И все же десятичное приближение к пи — артефакт нашей десятипалой анатомии. Дробные приближения к пи более удовлетворительны, и они обещают научить нас чему-то более универсальному относительно числа пи.

Все мы знаем, что 22/7 — очень хорошее приближение к числу Пи. Но эта хорошо известная дробь на самом деле на 1/791 больше, чем немного менее известная, но гораздо более загадочная рациональная аппроксимация числа пи:

Воспоминание 355/113

Дробь 355/113 невероятно близка к пи, в пределах одной трети миллионной от точного значения. Этот уровень точности выходит далеко за рамки права дроби с таким маленьким знаменателем и вызывает различные странности в других областях математики. Например, используйте любой научный калькулятор для вычисления cos(355) в радианах. Странный результат связан с причудливой близостью числа 355/113 к числу пи.

Симпатичная мнемоника позволяет нашим видам с основанием 10 легко запомнить эту полезную дробь. Дважды запишите первые три нечетных числа: 1 1 3 3 5 5. Затем разделите десятичное число, представленное тремя последними цифрами, на десятичное число, представленное первыми тремя цифрами.

Загадка: почему эта дробь так близка к пи? Чем глубже вы смотрите, тем более уникальным и необъяснимым кажется 355/113.

Необычность 355/113

В лекции 2000 года о рациональных приближениях числа пи Фриц Бойкерс определяет «качество» рационального приближения p / q как число M такое, что

На словах качество Бьюкера M есть отношение количества цифр точности к количеству цифр знаменателя.

Неудивительно, когда мы находим дробь, которая приближает число пи с M около 1: для любого q будет p / q в пределах 1/ q любого значения. Но редко можно найти M больше 2. Два лучших приближения для пи, которые мы видели:

Обе эти аппроксимации имеют качество M > 3, что необычно хорошо. Обе эти дроби дают аппроксимацию с точностью примерно втрое больше, чем можно было бы ожидать для их малых знаменателей.

Другие хорошие рациональные приближения для Пи

Дробь 355/113 завышает число пи менее чем на .

Нелегко аппроксимировать число Пи так же экономично, как 355/113, но попробовать можно. Если у вас достаточно хорошая память, чтобы запомнить число 3748629, то вам может быть полезно знать, что следующая разница еще ближе к pi:

Другими словами, вычитание 1/3748629 из 355/113 даст приближение числа пи, которое находится в пределах 10 ^-14 от истинного значения. Вычитая пару дробей, вы приближаетесь к пределу 10 ^-15 арифметики двойной точности IEEE 754. Эта новая дробь — отличный и экономичный способ аппроксимировать число Пи как разницу между двумя дробями.

С другой стороны, эта новая дробь не так примечательна, как 355/113:

В то время как M > 1 говорит нам о том, что точность лучше, чем дал бы нам случайный знаменатель, M все еще намного ниже, чем качество 355/113.

Поиск 355/113 в рациональном выражении Уоллиса

Близкие совпадения в математике обычно намекают на нечто более глубокое. Итак, давайте взглянем на некоторые вычислимые последовательности рациональных чисел, которые сходятся к pi, чтобы увидеть, встречается ли 355/113 на каком-то объяснимом пути к pi.

Есть несколько прекрасно вычислимых и хорошо известных последовательностей рациональных чисел, которые сходятся к пи. В 1655 году, незадолго до появления исчисления, английский математик Джон Уоллис кропотливо вычислил расширенное рациональное выражение для площади круга и получил одно из самых запоминающихся рациональных выражений для числа пи:

Частичные разложения этой бесконечной дроби:

Этот ряд сходится очень медленно, несмотря на огромные знаменатели, и нашей эффективной дроби 355/113 нигде не видно.

Ищем 355/113 серии Taylor

Развивая современное исчисление, Грегори и Лейбниц систематически вычисляли то, что мы называем разложением Тейлора для арктангенса. Эта формула приводит к другому довольно рациональному расширению числа пи:

Частичные разложения дают нам сходящуюся последовательность рациональных чисел:

К сожалению, эта последовательность снова сходится медленно, и 355/113 не появляется.

Ищем 355/113 в непрерывной дроби Гаусса

Гаусс разработал умную обобщенную непрерывную дробь для арктангенса, которая дает нам быстро сходящееся выражение:

Это расширяется до последовательности рациональных чисел, которая сходится гораздо быстрее, чем в предыдущих примерах:

Ах, ха! Здесь мы видим, что гауссовское расширение arctan оправдывает рациональное приближение 22/7, которое появляется как третье приближение в последовательности. Кажется, это побочный эффект эффективности последовательности рациональных чисел Гаусса, которая становится намного ближе к пи для знаменателя любого заданного размера.

Но 355/113 все еще вне досягаемости этой последовательности. Это не появляется здесь.

Поиск 355/113 в последовательности Ланге

В 1999 году Ланге вывел еще одно элегантное выражение для числа пи, основанное на непрерывной дроби для арксинуса:

Последовательность неполных дробей начинается:

Это еще одна быстро сходящаяся последовательность, включающая режим 22/7. Но опять же 355/113 не появляется.

Квест не закончен; Математики все еще ищут более быстро сходящиеся последовательности рациональных приближений числа пи. Лекцию Бьюкерса на эту тему стоит прочитать. Но число 355/113 естественным образом не появляется ни в одной из этих последовательностей, которые можно использовать для получения числа пи.

Откуда берется 355/113?

Так откуда же взялось 355/113? Является ли его близость к числу пи простым совпадением? Математическая случайность? Чудо природы?

Возможно.

Или это может быть намеком на то, что существует какая-то еще не открытая последовательность рациональных чисел, которая гораздо быстрее сходится к пи, для которой высокоточное число 355/113 — лишь одно замечательное число среди многих.

Размещено Дэвидом 14 марта 2010 г., 04:03

это их любая другая дробь, очень близкая к пи…

Разместил: pi master 1 октября 2010 г., 20:36

Это действительно очень интересные мысли, но не искать ли чего-то особенного в 355/113 не то же самое, что привязывать
к самим числам и семиотическим свойствам десятичной системы?

Как бы все это выглядело, если бы у нас было шестнадцать пальцев и мы бы считали в шестнадцатеричном формате, как в натуральном?

Пожалуйста, пересчитайте для меня HEX! 😉

Для начала, 22/7 в шестнадцатеричном формате будет 16/7, а
355/113 будет 163/71.. но я не могу вычислять дроби в шестнадцатеричном формате, так каким же тогда будет число пи?

*сбитый с толку*

Размещено: 24 октября 2010 г. , 09:13

Привет, Дэвид,
посмотрите на эту непрерывную дробь: http://numbers.computation.free.fr/Constants/Pi/piApprox.html#tth_sEc1.1.1
Выглядит очень хорошо, как 22/7, так и 355/113 появляются в последовательность приближений…

Разместил: GuidoB, 9 декабря, 2010 18:02

Гвидо — последовательность непрерывных дробей 3 7 15 1 292 1 1 1 2 1… аналогия непрерывной дроби десятичной последовательности 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 и т. д.: обе они гарантированы -существовать последовательности последовательно лучших приближений для числа пи, которые исходят из действительного значения числа пи. Ни один из способов получить или вычислить пи, если у вас еще нет точного значения.

Другими словами, если вы хотите вычислить последовательность непрерывных дробей, вам придется начать с вычисления почти точного значения числа пи, а затем вернуться к аппроксимациям непрерывных дробей.

Что было бы замечательно, если бы существовал какой-то прямой способ вывести последовательность 3 7 15 1 292 1 1 1 2 1, начиная только со счетных чисел, без эффективного вычисления пи каким-либо другим способом. До сих пор не известно ни одной естественной последовательности, которая так экономично сходится к числу пи.

Особая загадка 113/355 такая же, как и вопрос: «Почему число 292 в последовательности непрерывных дробей такое необычно большое?»

Разместил: Дэвид 20 декабря 2010 г., 06:53

Приветствую вас, Дэвид,

Однажды одна француженка сделала мне ОТЛИЧНЫЙ подарок на день числа PI. Что было подарком? Что ж, это действительно было PI ~= 355/113 со ссылкой на мои открытия простых чисел в священной книге ислама, Коране.

Коран состоит из 114 глав, первая из которых называется Открывающая (Ключ), а остальные 113 — Послание (Прямой Путь к БОГУ).

В Послании я нашел главу, которая указывает на 2012 год (точнее, на 1433 год по исламскому календарю), но я не мог убедить людей, что это число было 1433 годом хиджры, пока не обнаружил, что количество слов в главе было 355. ! Это точно такое же количество дней в исламском високосном году, каким должен быть 1433 год хиджры.

Короче говоря, 113 — это Прямой Путь к БОГУ (Диаметр), а 355 — это количество дней в исламском году (Окружность).

Теперь, зная, что арабы использовали 22/7, в то время как китайцы использовали 355/113, мы подразумеваем только то, что китайцы больше мусульмане (покорны воле БОГА), чем арабы 🙂

Али Адамс
Бог > бесконечность
www.heliwave.com

Автор: Али Адамс, 19 марта 2011 г., 21:52

Следующая дробь после 355/113, которая приближает число пи с такой же точностью, это 52163/16604. Усреднение двух дает вам 3,14159265386526 — с точностью до 9-го знака после запятой. Эквивалентная дробь (ох!) 11788839/3752504.

Разместил: Джо 27 апреля 2011 г., 01:07

используйте этот метод:
3/1 = 3
4/1 = 4
сложите числа
7/2 = 3,5
11/3 = 3,3
я сделал это, и оно ДЕЙСТВИТЕЛЬНО содержало
22/7
157/50
и 355/113.
я делаю это, когда у меня есть свободное время 😀

Разместил: pimasterfromhk 8 ноября 2011 г. , 08:22

pimasterfromhk должен объясниться, тем более что 11/3 = 3,666… Теперь 10/3 = 3,33… Итак, если вы начнете с 4/1 = 4 и 3/1 = 3, вы получите первые два новых члена 7/ 2 и 10/3, но эта последовательность сходится к 3,38196…

Автор: Крис Стаффа, 29 февраля 2012 г., 15:42

Я знаю, что это немного запоздало, но: /1 22/7
3/1 25/8

25/8 47/15
47/15 69/22
69/22 91/29
91/29 113/36
113/36 135/43 935073 /43 157/50
157/50 179/57
179/57 201/64
201/64 223/71
223/71 245/78
245/78 267/85
269/85 981073 289/92 311/99
311/99 333/106
333/106 355/113

Сообщение от: flatfly 24 июля 2012 г., 10:20

ммм… ваш блог не принимает знаки больше и меньше, поэтому они отсутствуют в моем предыдущем посте… ок, опубликую позже

Сообщение от: flatfly 24 июля 2012 г., 10:22

Рациональное выражение Уоллиса начинается с повторения каждого знаменателя дважды.

Если вы прикрепите 1/1 перед ним, так что 1 также повторится дважды, тогда знаменатели будут 1,1,3,3,5,5 и т. д.

1,1,3,3,5,5 — это «симпатичная мнемоника», которую вы велели нам записать и запомнить выше, а также, согласно АА, прямой путь к БОГУ и количество дней в исламском високосном году. . Ясно, что Уоллис читала священную книгу, но упустила единственную истинную, чтобы сбить нас с толку.

Разместил: Skeuomorph 24 июля 2012 г., 10:35

Попробуйте этот рубиновый код:

def force(x, y)
diff = Math::PI — ((1.0 * x)/y)
return — Math::log(diff.abs) / Math::log( у)
конец

прочность(22, 7)
прочность(355, 112)
прочность(1330631944, 423553267)

Автор: Хью Браун, 24 июля 2012 г., 11:19

Арх. Каким-то образом я вырезал и вставил опечатку в код.

сила защиты (x, y)
разница = Math::PI — (x.to_f / y)
возврат — Math::log(diff. abs) / Math::log(y)
конец

сила (22, 7)
прочность(355, 113)
прочность(1330631944, 423553267)

Автор: Хью Браун, 24 июля 2012 г., 11:25 92/22)

Размещено: 24 июля 2012 г., 14:03

Говорят, что в Ветхом Завете (3 Царств 7:23) число пи равно точно трем. дает следующее объяснение: Еврейское слово, обозначающее линию или окружность, записано в Библии как трехбуквенное еврейское слово, транслитерированное как kaveh, английские буквы которого эквивалентны KVH (kof, vav, hei). Тем не менее, это слово читается как 2-буквенное еврейское слово, эквивалентным английским буквам которого являются KV.

Буквы иврита имеют числовые значения, а рассматриваемые буквы имеют значения kof = 100, vav = 6 и hei = 5. Таким образом, KVH = 100 + 6 + 5 = 111 и KV = 100 + 6 = 106. Отношение отношение KVH к KV составляет 111/106, что при умножении на значение 3, подразумеваемое 3 Царств 7:23, дает 3,141509 (округленное), что опять-таки довольно близко к числу пи. Разместил: tao of me 24 июля 2012 г., 15:18

Существуют математические факты, которые верны без всякой причины, как показал Курт Гдель в 1931. За 355/113 нет тайны.

Разместил: KurtGodel 24 июля 2012 г., 19:16

Отличная информация. Возможно, вам придется позаботиться о небольших опечатках вокруг числа 3748629. В следующей строке это 3748269, а в следующей — 3748259. Действительно, это число нелегко запомнить.

Разместил: Маной Р. 25 июля 2012 г., 00:10

Итак, если я вспомню шесть цифр числа 355/113, это даст мне первые шесть десятичных знаков числа пи. Не похоже на большую экономию.

Автор: Пол Линтон, 25 июля 2012 г., 01:24

Курт Гедель не делал ничего подобного. Он доказал существование неразрешимых предложений в логических системах, таких как теория множеств.

Разместил: Gaus 25 июля 2012 г. , 06:17

Это называется диофантовым приближением.
http://en.wikipedia.org/wiki/Diophantine_ приблизительно
p.s. Взгляните на часть «Результат Лиувилля».

Сообщение от: Wandspiegel 25 июля 2012 г., 07:26

92 = 2х это 2? Spoookkkyyy…

Разместил: Lancem 25 июля 2012 г., 10:17

Вот еще один способ «измерить», насколько случайна эта точность.

Когда вы выбираете знаменатель q, пи-аппроксимация с этим знаменателем будет в пределах 1/(2q) от числа пи. По всем случайно выбранным q эта ошибка должна быть равномерно распределена между 0 и 1/(2q).

Выразите это как точность относительно 1/(2q) — т. е. u = |p/q — pi| / (1/(2q)), так что u распределяется как Uniform(0,1).

Для 355/113, u=60e-6. Если вы выберете один знаменатель наугад, у вас будет только 60 шансов на миллион получить этот уровень точности.

Но, конечно, вы можете просмотреть достаточное количество знаменателей, чтобы в конце концов найти что-то столь же хорошее или лучше. 1000).

В статистике говорят, что почти, но не совсем, статистически значимо.

Разместил: Лонни 25 июля 2012 г., 12:59

Я не специалист по математике, но постараюсь ответить на несколько вопросов, поднятых в комментариях.

@Lancem Правда, нет ничего примечательного в том, чтобы найти дробь, близкую к пи, но интересно найти дробь, которая удивительно близка к пи, учитывая ее маленький числитель и знаменатель. Обычно они должны быть намного больше, чтобы дробь была хорошим приближением.

@tao_of_me @Ali_Adams Я почти уверен, что Коран и Библия достаточно длинные, чтобы вы могли найти любые числа, которые вы хотите, подсчитывая различные подмножества глав, слов, букв и т. д. Если нет окончательной причины, по которой одно из этих значений *должен* равняться важному числу в математике, это похоже на чистое совпадение. Но люди любят находить смысл в совпадениях, так что все равно интересно посмотреть.

@(парень, который пишет о шестнадцатеричных числах) Мне нравится ваше замечание о произвольности десятичной точки. Шестнадцатеричный так же хорош. Или любую другую базу. Тем не менее, кажется, что точка зрения, сделанная в этой статье, в равной степени верна для любой базы. Независимо от основания, числа с большим значением требуют для записи больше цифр и наоборот. Итак, если число короче и его легче запомнить в десятичном виде, то же самое верно и в шестнадцатеричном. Например, 162/71 — это 355/113 в шестнадцатеричном формате и короче, чем 4F4FD508/19.3EE8F3, то есть 1330631944/423553267 в шестнадцатеричном формате.

Автор: FishDawg, 25 июля 2012 г., 14:56

Самый близкий, который я нашел до сих пор, это
9999999/3183101.

9999999/3183101 = 3,1415

150760000000
355/113 = 3,1415929203539800000
22/7 = 3,142857142857140000000

= 3,142857142857140000000

Хм, было бы точнее для
число 7 должно быть числом отдыха, поскольку Бог
отдыхал от Своей работы в седьмой день,
и заповедь соблюдать субботу в святости
, в которой также говорится: «Шесть дней работай
, а в седьмой отдыхай».

Число 9 является уникальным числом в самом
и для самого числа:

9 = Сумма ( произведение [ ] ) = x * 9;

Ditil складывает цифры продукта
, пока не получится одна цифра.
В этом случае дистилляция всегда будет равна 9.

Следующий псевдокод может создать этот эффект
:

product = 9 * x

While ( count( product [ ] ) ) > 1 )
{

foreach ( product as digit )
{

newProduct += digit

}

product = newProduct

}

Будьте осторожны.

Скотт А. Тови

Разместил: Скотт 25 июля 2012 г., 18:20

Это отличные комментарии, и я почти все их понимаю.

Или, может быть, это говорит текила….

В любом случае, я ценю комментарии.

спасибо,
патрон

Размещено: 25 июля 2012 г., 19:49

Эта дробь является хорошей аппроксимацией числа пи: Автор: Исаак Тесла, 25 июля 2012 г. , 21:56

http://openlibrary.org/books/OL23278656M/Archimedes_Huygens_Lambert_Legendre.

Архимед, Гюйгенс, Ламбер, Лежандр.
Vier Abhandlungen ber die Kreismessung. Дойч ХРСГ. und mit einer bersicht ber die
Geschichte des Problemes von der Quadratur des Zirkels
Опубликовано в 1892 г. Б.Г. Тойбнера в Лейпциге.
Написано на немецком языке.

Страницы 146-147 имеют таблицу рациональных приближений PI

1: 3
7:22
106: 333
113: 355
33102: 103993
33215: 104348
66317: 20113
33215. 833719
364913 : 1146408
1360120 : 4272943
1725033 : 5419351
25510582 : 80143857
52746197 : 165707065
78256779 : 245850922
131002976 : 411557987
340262713 : 1068966896
811528438 : 2549491779
1963319607 : 6167950454
4738167652 : 14885392687
6701487259 : 21053343141
567663097408 : 1783366216531
1142027682075 : 3587785776203
17096

4077325 / 81 = 3,141592653589793,…

это довольно просто просто получить число, умножив его на PI…

{81pi} = 254,46

пи до 10 000 цифр

Понимание математики по Питер Альфельд, кафедра математики, Университет Юты

pi=3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 01133 05305 48820 46652 13841 46951 94151 16094 33057 27036 57595 91953 09218 61173 81932 61179 31051 18548 07446 23799 62749 56735 18857 52724 89122 79381 83011 94912 98336 73362 44065 66430 86021 39494 63952 24737 19070 21798 60943 70277 05392 17176 29317 67523 84674 81846 76694 05132 00056 81271 45263 56082 77857 71342 75778 96091 73637 17872 14684 40901 22495 34301 46549 58537 10507 92279 68925 89235 42019 95611 21290 21960 86403 44181 59813 62977 47713 09960 51870 72113 49999 99837 29780 49951 05973 17328 16096 31859 50244 59455 34690 83026 42522 30825 33446 85035 26193 11881 71010 00313 78387 52886 58753 32083 81420 61717 76691 47303 59825 34904 28755 46873 11595 62863 88235 37875 93751 95778 18577 80532 17122 68066 13001 92787 66111 95909 21642 01989 38095 25720 10654 85863 27886 59361 53381 82796 82303 01952 03530 18529 68995 77362 25994 13891 24972 17752 83479 13151 55748 57242 45415 06959 50829 53311 68617 27855 88907 50983 81754 63746 49393 19255 06040 09277 01671 13900 98488 24012 85836 16035 63707 66010 47101 81942 95559 61989 46767 83744 94482 55379 77472 68471 04047 53464 62080 46684 25906 94912 93313 67702 89891 52104 75216 20569 66024 05803 81501 93511 25338 24300 35587 64024 74964 73263
92726 04269 92279 67823 54781 63600 93417 21641 21992 45863 15030 28618 29745 55706 74983 85054 94588 58692 69956 2107975093 02955 32116 53449 87202 75596 02364 80665 49911 98818 34797 75356 63698 07426 54252 78625 51818 41757 46728

77279 38000 81647 06001 61452 49192 17321 72147 72350 14144 19735 68548 16136 11573 52552 13347 57418 49468 43852 33239 07394 14333 45477 62416 86251 89835 69485 56209 92192 22184 27255 02542 56887 67179 04946 01653 46680 49886 27232 79178 60857 84383 82796 79766 81454 10095 38837 86360 95068 00642 25125 20511 7392984896 08412 84886 26945 60424 19652 85022 21066 11863 06744 27862 20391 94945 04712 37137 86960 95636 43719 17287 46776 46575 73962 41389 08658 32645 99581 33904 78027 59009 94657 64078 95126 94683 98352 59570 98258 22620 52248 94077 26719 47826 84826 01476 99090 26401 36394 43745 53050 68203 49625 24517 49399 65143 14298 09190 65925 09372 21696 46151 57098 58387 41059 78859 59772 97549 89301 61753 92846 81382 68683 86894 27741 55991 85592 5245953959 43104 99725 24680 84598 72736 44695 84865 38367 36222 62609

08051 24388 43904 51244 13654 97627 80797 71569 14359 97700 12961 60894 41694 86855 58484 06353 42207 22258 28488 64815 84560 28506 01684 27394 52267 46767 88952 52138 52254 99546 66727 82398 64565 96116 35488 62305 77456 49803 55936 34568 17432 41125 15076 06947 94510 96596 09402 52288 79710 89314 56691 36867 22874 89405 60101 50330 86179 28680 92087 47609 17824 93858 14909 67598 52613 65549 78189 31297 84821 68299 89487 22658 80485 75640 14270 47755 51323 79641 45152 37462 34364 54285 84447 95265 86782 10511 41354 73573 95231 13427 16610 21359 69536 23144 29524 84937 18711 01457 65403 59027 99344 03742 00731 05785 39062 19838 74478 08478 48968 33214 45713 86875 19435 06430 21845 31910 48481 00537 06146 80674 91927 81911 97939 95206 14196 63428 75444 06437 45123 71819 21799 98391 01591 95618 14675 1426

7 48940 64942 31961 56794 52080 95146 55022 52316 03881 93014 20937 62137 85595 66389 37787 08303 92077 34672 21825 62599 66150 14215 03068 03844 77345 49202 60541 46659 25201 49744 28507 32518 66600 21324 34088 19071 04863 31734 64965 14539 05796 26856 10055 08106 65879 69981 63574 73638 40525 71459 10289 70641 40110 97120 62804 39039 75951 56771 57700 42033 78699 36007 23055 87631 76359 42187 31251 47120 53292 81918 26186 12586 73215 79198 41484 88291 64470 60957 52706 95722 09175 67116 72291 09816

28017 35067 12748 58322 28718 35209 35396 57251 21083 57915 13698 82091 44421 00675 10334 67110 31412 67111 36990 86585 16398 31501 97016 51511 68517 14376 57618 35155 65088 49099 89859 98238 73455 28331 63550 76479 18535 89322 61854 89632 13293 30898 57064 20467 52590 70915 48141 65498 59461 63718 02709 81994 30992 44889 57571 28289 05923 23326 09729 97120 84433 57326 54893 82391 19325 97463 66730 58360 41428 13883 03203 82490 37589 85243 74417 02913 27656 18093 77344 40307 07469 21120 19130 20330 38019 76211 01100 44929 32151 60842 44485 96376 69838 95228 68478 31235 52658 21314 49576 85726 24334 41893 03968 64262 43410 77322 69780 28073 18915 44110 10446 82325 27162 01052 65227 21116 60396 66557 30925 47110 55785 37634 66820 65310 98965 26918 62056 47693 12570 58635 66201 85581 00729 36065 98764 86117

33488 50346 11365 76867 5324944166 80396 26579 78771 85560 84552 96541 26654 08530 61434 44318 58676 97514 56614 06800 70023 78776 59134 40171 27494 70420 56223 05389 94561 31407 11270 00407 85473 32699 39081 45466 46458 80797 27082 66830 63432 85878 56983 05235 80893 30657 57406 79545 71637 75254 20211 49557 61581 40025 01262 28594 13021 64715 50979 25923 09907 96547 37612 55176 56751 35751 78296 66454 77917 45011 29961 48903 04639 94713 29621 07340 43751 89573 59614 58901 93897 13111 79042 97828 56475 03203 19869 15140 28708 08599 04801 09412 14722 13179 47647 77262 24142 54854 54033 21571 85306 14228 81375 85043 06332 17518 29798 66223 71721 59160 77166 92547 48738 98665 49494 50114 65406 28433 66393 79003 97692 65672 14638 53067 36096 57120 91807 63832 71664 16274 88880 07869 25602 47210 40317 21186 08204 19000 42296 61711 96377 92133 75751 14959 50156 60496 31862 94726 54736 42523 08177 03675 15906 73502 35072 83540 56704 03867 43513 62222 47715 89150 49530 98444 89333 09634 08780 76932 59939 78054 19341 44737 74418 42631 29860 80998 88687 41326 04721 56951 62396 58645 73021 63159 81931 95167 35381 29741 67729 47867 24229 24654 36680 09806 76928 23828 06899 64004 82435 40370 14163 14965 89794 09243 23789 69070 69779 42236 25082 21688 95738 37986 23001 59377 64716 51228 93578 60158 81617 55782 97352 33446 04281 51262 72037 34314 6531977774 16031 99066 55418 76397 92933 44195 21541 34189 94854 44734 56738 31624 99341

14809 27777 10386 38773 43177 20754 56545 32207 77092 12019 05166 09628 04909 26360 19759 88281 61332 31666 36528 61932 66863 36062 73567 63035 44776 28035 04507 77235 54710 58595 48702 79081 43562 40145 17180 62464 36267 94561 27531 81340 78330 33625 42327 83944 97538 24372 05835 31147 71199 26063 81334 67768 79695 97030 98339 13077 10987 04085

46414 42822 77263 46594 70474 58784 77872 01927 71528 07317 67907 70715 72134 44730 60570 07334 92436 93113 83504 93163 12840 42512 19256 51798 06941 13528 01314 70130 47816 43788 51852

54520 11658 39341 96562 13491 43415 95625 86586 55705 52690 49652 09858 03385 07224 26482 93972 85847 83163 05777 75606 88876 44624 82468 57926 03953 52773 48030 48029 00587 60758 25104 74709 16439 61362 67604 49256 27420 42083 20856 61190 62545 43372 13153 59584 50687 72460 29016 18766 79524 06163 42522 57719 54291 62991 93064 55377 99140 37340 43287 52628 88963 99587 94757 29174 64263 57455 25407 51357 11136 94109 11939 32519 10760 20825 20261 87985 31887 70584 29725 91677 81314 96990 09019 21169 71737 27847 68472 68608 49003 37702 42429 16513 00500 51683 23364 35038 95170 29893 92233 45172 20138 12806 96501 17844 08745 19601 21228 59937 16231 30171 14448 46409 03890 64495 44400 61986 85160 26327 50529 83491 87407 86680 88183 38510 22833 45085 04860 82503 93021 33219 71551 84306 35455 00766 82829 49304 13776 55279 39751 75461 39539 84683 39363 83047 46119 96653 85815 38420 56853 38621 86725 23340 28308 71123 28278 92125 07712 62946 32295 63989 89893 58211 67456 27010 21835 64622 01349 67151 88190 97303 81198 00497 34072 39610 36854 06643 19395 09790 19069 96395 52453 00545 05806 85501 95673 02292 19139 33918 56803 44903 98205 95510 02263 53536 19204 19947 45538 59381 02343 95544 95977 83779 02374 21617 27111 72364 34354 39478 22181 85286 24085 14006 66044 33258 88569 86705 43154 70696 57474 58550 33232 33421 07301 54594 05165 53790 68662 73337 99585 11562 57843 22988 27372 31989 87571 41595 78111 96358 33005 94087 30681 21602 87649 62867 44604 77464 91599 50549 73742 56269 01049 03778 19868 35938 14657 41268 04925 64879 85561 45372 34786 73303 83834 36346 5537949864 19270 56387 29317 48723 32083 76011 23029
79386 27089 43879 93620 16295 15413 37142 48928 30722 01269 01475 46684 76535 76164 77379 46752 00490 75715 55278 19653 62132 39264 06160 13635 81559 07422 02020 31872 77605 27721 61484 25551 87925 30343 51398 44253 22341 57623 36106 42506 39049 75008 65627 10953 59194 65897 51413 10348 22769 30624 74353 63256 91607 81547 81811 52843 66795 70611 08615 33150 44521 27473 92454 49454 23682 88606 13408 41486 37767 00961 20715 12491 40430 27253 86076 48236 34143 34623 51897 57664 52164 13767 96903 14950 19108 57598 44239 19862 91642 19399 49072 36234 64684 41173 94032 65918 40443 78051 33389 45257 42399 50829 65912 28508 55582 15725 03107 12570 12668 30240 29295 25220 11872 67675 62204 15420 51618 41634 84756 51699 98116 14101 00299 60783 86909 29160 30288 40026

40792 88621 50784 24516 70908 70006 99282 12066 04183 71806 53556 72525 32567 53286 12910 42487 76182 58297 65157 95984 70356 22262 93486 00341 58722 98053 49896 50226 29174 87882 02734 20922 22453 39856 26476 69149 05562 84250 39127 57710 28402 79980 66365 82548 89264 88025 45661 01729 67026 64076 55904 29099 45681 50652 65305 37182 94127 03369 31378 51786 09040 70866 71149 65583 43434 76933 85781 71138 64558 73678 12301 45876 87126 60348
95620 09939 36103 10291 61615 28813 84379 09904 23174 73363 94804 57593 14931 40529 76347 57481 19356 70911 01377 51721 00803 15590 24853 09066 92037 67192 20332 29094 33467 68514 22144 77379 39375 17034 43661 99104 03375 11173 54719 18550 46449 02636 55128 16228 82446 25759 16333 03910 72253 83742 18214 08835 08657 39177 15096 82887 47826 56995 99574 49066 17583 44137 52239 70968 34080 05355 98491 75417 38188 39994 46974 86762 65516 58276 58483 58845 31427 75687 09517 02835 29716 34456 21296 40435 23117 60066 51012 41200 65975 58512 76178 58382 92041 97484 42360 80071 93045 76189 32349 22927 96501 98751 87212 72675 07981 25547 09589 04556 35792 12210 33346 69749 92356 30254 94780 24901 14195 21238 28153 09114 07907 38602 51522 74299 58180 72471 62591 66854 51333 12394 80494 70791 19153 26734 30282 44186 04142 63639 54800 04480 02670 49624 82017 92896 47669 75831 83271 31425 17029 69234 88962 76684 40323 26092 75249 60357 99646 92565 04936 81836 09003 23809 29345 95889 70695 36534 94060 34021 66544 37558 63288 22505 45255 64056 44824 65151 87547 11962 18443 96582 53375 43885 69094 11303 15095 26179 37800 29741 20766 51479 39425 96959 46995 56576 12186 56196 73378 62362 56125 21632 08628 69222 10327 48892 18654 36480 22967 80705 76561 51446 32046 92790 68212 07388 37781 42335 62823 60896 32080 68222 46801 22482 61177 18589 63814 09183 36722 20888 32151 37556 00372 79839 40041 52970 02878 30766 70944 47456 01345 56417 25437 09069 79396 12257 14298 94671 54357 84687 88614 44581 23145 93571 98492 25284 71605 04922 12424 70141 21478 05734 55105 00801 96033 02763 47870 81081 75450 11930 71412 23390 86639 38339 52942 57869 05076 43100 63835 19834 38934 15961 31854 34754 64955 69781 03829 30971 64651 43840 70070 73604 11237 35998 43452 25161 05070 27056 23526 60127 64848 30840 76118 30130 52793 20542 74628 65403 60367 45328 65105 70658 74882 25698 15793 67897 66974 22057 50596 83440 86973 50201 41020 67235 85020 07245 22563 26513 41055 92401 21624 84391 40359 98953 53945 07046

14093 87001 26456 00162 37428 80210 92764 57931 06579 22955 24988 72758 46101 26483 69998 92256 95968 81592 05600 10165 52563 7567 .
No related posts.