ГИПР — Чётное или нечётное число на экране, видеотест 9, средний темп смотреть онлайн видео от ГИПР
12+
1 год и 1 месяц назад
ГИПР — Говорит и показывает репетитор24 подписчика
Категория 12+.
Этот видеоролик — основа эпизода игры в репетитора и ученика и позволяет тренироваться отличать чётные и нечётные числа.
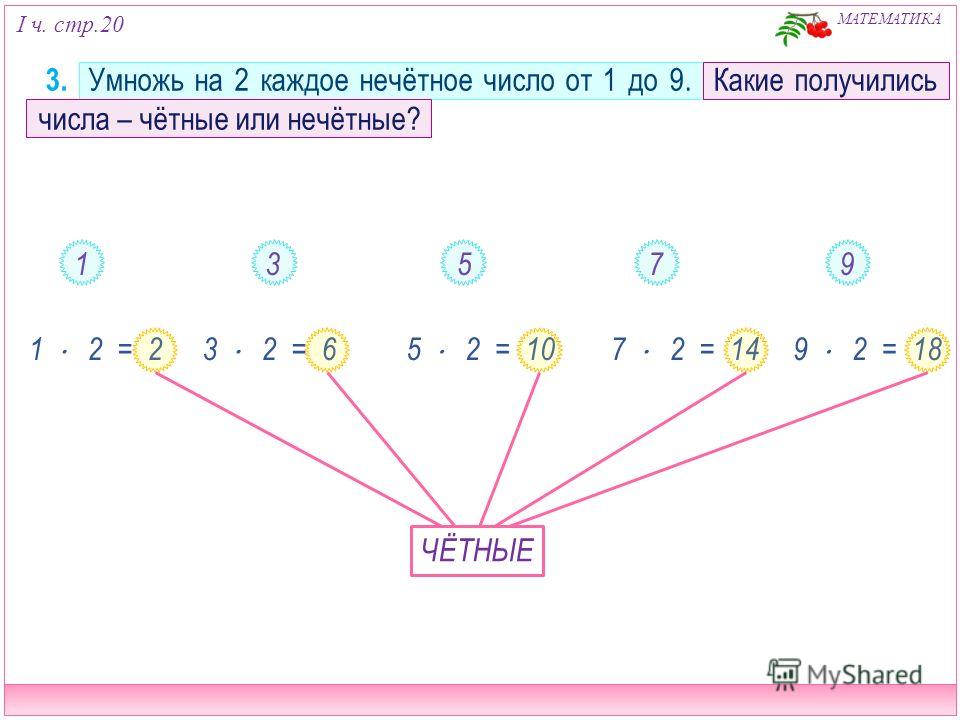
Правила игры в этом эпизоде такие: после запуска видео репетитор-компьютер (планшет, смартфон, телевизор) показывает (отображает) на экране число, а вопрос репетитора следующий: «Чётное или нечетное число изображено на экране?». Игрок-ученик должен дать ответ (вслух или про себя). Через некоторое время на экране появляется правильный ответ, с которым нужно сравнить свой собственный. Затем показывается следующее число и т. д.
Цель игрока-ученика — дать как можно больше правильных ответов. Если все ответы верные, это считается абсолютной победой ученика в этом эпизоде игры.
Я рекомендую это видео в первую очередь детям, осваивающим тему «Чётность/нечётность чисел».
Таким образом, ролик представляет собой игровой видеотест, имеющий общие черты с программой-тренажером, дающей онлайн примеры и ответы на них.
Показ числа длится 1,4 секунды, а ответа — 1,2 секунды. Это, на мой взгляд, средний темп. Если тема игры Вам интересна и Вы добились успехов, рекомендую попробовать свои силы при помощи других видеотестов на эту же тему в среднем или даже в быстром темпе, а если Вам кажется, что вопросы задаются очень часто и Вы не успеваете продумывать ответы, то попробуйте потренировать навыки при помощи видеотестов на эту тему в медленном темпе. Если же тема не интересна, то не забывайте — это игра и она не должна идти по принуждению.
При создании ролика мной преследовалась следующая цель: дать ненавязчивый игровой материал, помогающий повторять пройденную тему детям, с которыми я, как репетитор, индивидуально вживую проводил занятия по арифметике и алгебре. При выборе примеров, времени показа примера, количества примеров в одном ролике, продолжительности ролика, используемых цветов и других параметров в первую очередь я полагался на результаты собственных наблюдений, полученных в процессе указанных занятий.
ru/plst/53373
в среднем темпе: https://rutube.ru/plst/53374
в быстром темпе: https://rutube.ru/plst/53375
Большая коллекция моих видеороликов: https://rutube.ru/channel/23724933/
Подборки роликов, структурированные по темам и темпам: https://rutube.ru/channel/23724933/playlists/
Адрес моей группы: https://ok.ru/giprgovorit
Мои каналы на других ресурсах: https://zen.yandex.ru/giprgovorit и https://yarus.ru/u/5776747Новый инвариант числа. Исследование натурального ряда чисел (НРЧ) / Хабр
          В арифметике натуральных чисел иногда возникает необходимость поиска делителей составного числа N. Простая операция, обратная умножению чисел, на сегодняшний день неизвестна. Ее отсутствие создает определенные трудности при решении некоторых практических задач, особенно, если манипулировать приходится с числами высокой и очень высокой разрядности (сотни и даже тысячи цифр, представляющих числа).
          В работе «Фундаментальные структуры натурального ряда чисел» Ваулин А.
Е., Пилькевич С.В.– Интеллектуальные системы. Труды Седьмого международного симпозиума. Под ред. К.А. Пупкова.– М.: РУСАКИ, 2006. – с.384-387. Приводятся сведения об оригинальной концепции моделирования натурального ряда чисел и отдельного числа с целью установления свойств, слабо зависящих или вообще не зависящих от разрядности чисел. Дальнейшему развитию и уточнению деталей этого подхода посвящена настоящая работа.
          Независимость некоторых свойств чисел от их разрядности явилась одной из основных идейных посылок предлагаемого аналитического подхода к моделированию чисел. Наличие таких свойств у чисел подтверждает существование признаков делимости чисел. Например, какой бы величины не было заданное число, если свертка (сумма) его цифр делится на три, то и исходное число делится на три. От разрядности числа делимость на три практически не зависит. Аналогично и для других признаков делимости. Это свидетельство того, что некоторые свойства чисел могут не зависеть от их разрядности.
Поиск таких свойств и разработка теории их использования в различных направлениях, в частности, при разработке алгоритмов факторизации, установлении простоты числа, и других не менее трудных задач является актуальной и важной проблемой современной математики.
          В работе описывается новый обнаруженный признак-свойство чисел. Этот признак оказывается полезным для разработки алгоритмов решения как новых, так и традиционных задач теории и практики. Приведем вначале качественные содержательные рассуждения о сущности предлагаемой работы.
          Натуральный ряд. Будем далее рассматривать натуральный ряд чисел как математический объект, имеющий сложное строение. НРЧ можно рассматривать как совокупность различных рядов с разными свойствами, например, составленным из двух арифметических прогрессий четных и нечетных чисел. Эти прогрессии имеют совпадающие разности d, равные d=2, но с разными начальными элементами: а=1 для прогрессии нечетных чисел и а=2 для прогрессии четных чисел.
Загрузим все числа НРЧ в ячейки (разряды) регистра и тогда НРЧ можно представить регистром с бесконечным числом ячеек. Обратим внимание на ряд нечетных чисел.
          Рассмотрим в НРЧ три смежных последовательных числа 2n–1, 2n, 2n+1, среднее из которых четное. Возведем их в квадрат. Между квадратами крайних нечетных чисел всегда лежит четное число разрядов регистра вида 8k, которое четным квадратом разбивается на два последовательных (смежных) нечетных числа вида 4k–1 слева и 4k+1 справа. Ячейку самого четного квадрата отнесем к правому числу.
          Таким образом, любое нечетное число вида N=4k±1, k>0 – произвольное натуральное число, в НРЧ лежит всегда между квадратами чисел N=x12–x02 с разной четностью. В определенных ячейках НРЧ размещаются квадраты натуральных чисел. Такому размещению соответствует ряд закономерностей.
Нечетные квадраты чередуются с четными квадратами. При этом, если больший квадрат x12 четный, то N=4k–1 и N≡3(mod4), а если больший квадрат x12 нечетный, то N=4k+1 и N≡1(mod4).
          Представим регистр НРЧ линейкой с движком по типу логарифмической. Для заданного числа N в движке создадим окно размером в N+1 позиций (разрядов). Путем перемещения движка вдоль НРЧ-линейки будем находить и фиксировать его положения парой чисел (x02, x12), которые размещены в крайних позициях окна (x02 – левая и x12 – правая) и оба значения будут соответствовать числовым квадратам. Разность между квадратами в крайних позициях окна, очевидно, будет совпадать с числом N=x12–x02.
          Контуры НРЧ.
Расстояние между квадратами двух последовательных нечетных чисел назовем контуром. Расстояние между ячейками с квадратами несмежных чисел назовем интервалом в НРЧ. Если сумма смежных нечетных чисел кратна числу 8, то она образует длину интервала, называемого контуром, а значение k является номером этого контура. Так смежные числа 11 и 13 образуют контур (11+13=24=3•8) с номером k=3 и длиной L(k)=24=k•8, а смежные нечетные числа 13 и 15 контур не образуют (13+15=28≠k•8).
          Расстояния между нечетными квадратами-границами смежных чисел всегда образуют контуры и содержат число регистровых ячеек, равное 8k. Контуры в НРЧ образуют непрерывную последовательность с номерами k=1(1)∞, т.е. НРЧ образован заполненными числами ячейками последовательности контуров, длины которых кратны числу 8. Первый контур имеет длину L(1)=32–12=1•8, второй контур – L(2)=52–32=2•8=16, и т.
д. Длины контуров образуют арифметическую прогрессию с разностью d=8 и а=8.
          Заполнение всех позиций окна числами (интервалов) в каждом из фиксированных парой чисел (x02, x12) положений обладает закономерностью и характеризуется некоторым числовым инвариантом, устанавливаемым в работе. Так как пар (x02, x12) может быть больше одной, то будем снабжать ее числа индексом i.
         
Пример 1
          Для N=105 (размер окна — 1) имеется 4 положения (4 пары квадратов разной четности), которые фиксируются. Контролировать будем положение левой границы окна. Начинаем перемещение движка от 1 вправо. Первое положение (остановка) возникает с появлением на левой границе окна числа x02=4, но правая граница при этом равна 109 – не квадрат, затем на левой границе окна оказывается квадрат x02=9, но справа число 114 – не квадрат, после прохода позиции с числом 15 в окне слева появляется число x02=16 – квадрат.
Останавливаемся и проверяем число на правой границе окна. Там видим число x12=121 – тоже квадрат. Фиксируем это положение с контролем разности между квадратами:
.
          Продолжаем движение до прихода левого края окна в позиции 25, 36, 49 и видим, что для них правая граница на квадрат не попадает. Но когда в окне слева появляется число 64, справа видим число 169 – квадрат. Фиксируем это положение и выполняем контроль
.
          Следующее фиксируемое положение окна: слева число xо2=256, а справа x12=361, оба квадраты.
.
          И, наконец, четвертое положение окна дает разность квадратов равную
.
          Дальнейшее движение прекращается, так как больше не существует пары квадратов, разность между которыми равна числу N=105, разность всех пар будет больше 105. Четвертую пару x142, x042 назовем предельной парой.
          Полуконтуры. Место каждого четного квадрата вида (2k) 2 во внутренней ячейке k-го контура. Эта ячейка делит длину L(k) контура на два m(k)=4k–1 и М(k)=4k+1 смежных нечетных числа (левое и правое), называемых полуконтурами.
Заметим, что контуры и полуконтуры – это множества ячеек, заполненных натуральными числами, а m(k) и M(k) – мощности этих множеств. Множества ячеек последовательно следующих полуконтуров формируют НРЧ. Все множество нечетных чисел образуют два класса: левые числа N≡3(mod4) и правые числа N≡1(mod4). Длины полуконтуров первого контура, левое нечетное число 4•1–1=3 и правое нечетное число 4•1+1=5, в сумме образуют длину L(k=1)=3+5=8 контура с номером k=1.
          Границы контура. При заданном номере k контура он полностью определяется, полуконтуры с длиной
          Действительно, разность границ Гп(k)–Гл(k)=(2k+1)2–(2k–1)2=
          Предельный контур. Любое нечетное число N можно представить как полуконтур в некотором контуре с номером kп. Такой контур единственный, так как контур слева от предельного имеет полуконтуры меньшие N, а справа — большие N. Число N левое или правое определяется с использованием четного квадрата предельного контура. Для левогоN=x12–x02, и x1 четное, для правого N=x12–x02 и x1 нечетное. Здесь роль границ полуконтуров играют значения x12 и x02. Эти границы определяются из выражений x1=(N+1)/2 и xо=(N–1)/2.
Длина предельного контура с номером kп для числа N определяется по формуле
          Номер kп предельного контура числа N вычисляется через длину предельного контура kп=L(kп)/8. Теперь самое время пояснить введенные понятия числовым примером. Это специально подобранный пример, очень простой, способствующий лучшему пониманию изучаемого явления.
         
Пример 2
          Пусть задано составное нечетное натуральное число (сннч)
N=105=3•5•7. Для этого числа требуется найти предельный контур, его границы и определить его номер kп. Указать все пары квадратов
(xi12, xi02), i=1(1).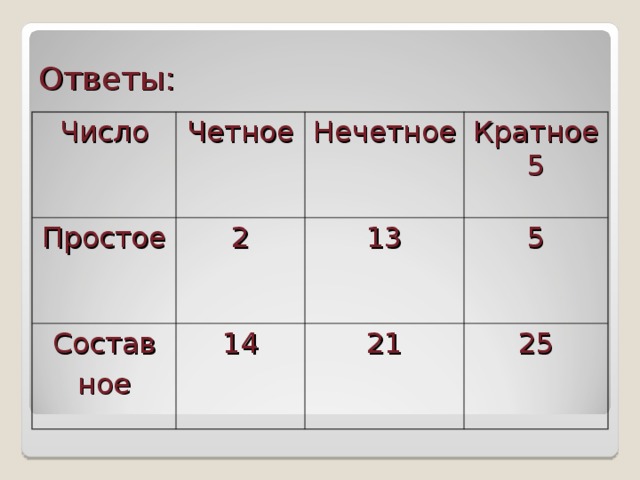
.. разной четности, разность между которыми равна числу N=105.
          Решение. Для лучшего усвоения содержания примера рекомендуется воспользоваться карандашом и бумагой. Известно, что сннч лежит между квадратами разной четности N=x12–x02. Определим левое или правое число заданногоN=105≡1(mod4). Число N правое, т.е. это больший полуконтур в предельном контуре. Определим границы предельного контура через значение N, x1=(N+1)/2=(105+1)/2=53 и xо=(N–1)/2=(105–1)/2=52. Квадраты чисел 52 и 53 являются границами полуконтура.
          Длина контура L(kп)=2•105–2=208=8•kп, откуда kп=208/8=26. Меньший (левый) полуконтур имеет длину m(kп)=L(kп)–М(kп)=208–105=103, является простым числом.
          Находим через kп границы предельного контура: левая Гл(kп)=(2kп–1)2=(2•26–1)2=512=2601 и правая Гп(kп)=(2kп+1)2=(2•26+1)2=532=2809. Длина контура через его границы определяется выражением L(kп)=Гп(kп)–Гл(kп)=2809–2601=208=8kп.
          Поскольку заданное сннч N=105 является полуконтуром в предельном контуре, то будем полагать, что ему соответствует лишь половина номера предельного контура, т.е. kп(N)/2=26/2=13.
          Инвариант числа. Характеристику числа N в форме kп(N)/2 назовем инвариантом числа N, а дальше покажем, почему выбрано такое название.
Инвариант может быть целым или дробным числом в зависимости от четности номера kп предельного контура.
          Интервалы НРЧ для числа N. Далее рассмотрим возможности представления сннч N=105 разностями других пар квадратов разной четности. Число 105, как впрочем, и любое другое нечетное число можно представить суммой нечетного количества меньших смежных нечетных чисел. Полезность такого представления N следует из того, что границы всех нечетных чисел в НРЧ – квадраты, следовательно, и непрерывный интервал, представляющий N=105 из смежных нечетных чисел, будет иметь на границах квадраты. Количество слагаемых в сумме должно быть нечетным числом.
- Допустим, что таких слагаемых будет три. Очевидно, 105:3=35 и первое слагаемое будет равно 35–2=33, второе 35, а третье 35+2=37. Числа 33, 35, 37 образуют непрерывную последовательность нечетных смежных чисел, а 35 и 37 являются полуконтурами одного контура, так как их сумма 35+37=72 кратна 8.
Этот контур имеет номер k=72/8=9. Число 33 принадлежит другому предшествующему контуру с номером k=8 и в нем является правым, т.е. большим. Этому числу 33 соответствует половина номера его контура, т.е. k/2=8/2=4. Интервалу из трех примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров в виде kп(N)/2=8/2+9=4+9=13.Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=9, т.е. Гп(k)=(2•k+1)2=(2•9+1)2=192=x12=361. Меньшая граница интервала совпадает с левой границей меньшего из трех полуконтура, т.е. числа 33, находящегося в контуре с номером k=8, его граница – это четный квадрат удвоенного номера контура Гч(k)=Гл(k)=(2k)2=(2•8)2=x02=256. Проверка: N=Гп(9)–Гл(8/2)=361–256=105.
Теперь для N=105 можем записать факторы N=x12–x02=(19+16)(19–16)=35•3=105. - Пусть представление N имеет полуконтурами в сумме пять нечетных слагаемых. Очевидно, 105:5=21 и первое слагаемое будет равно 21–4=17, второе 21–2=19, третье 21, четвертое 21+2=23 и, наконец, пятое 21+4=25. Числа 17, 19, 21, 23, 25 образуют непрерывную последовательность нечетных смежных чисел, а 19, 21 и 23, 25 из них являются полуконтурами двух смежных контуров, так как их сумма 19+21=40=5•8 и 23+25=48=6•8 кратна 8. Эти контуры имеют номера k=40/8=5 и k=48/8=6.
Число 17 является большим (правым) полуконтуром предшествующего контура с номером k=(15+17)/8=4. Этому числу соответствует половина номера меньшего контура k/2=4/2=2. Интервалу из пяти примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров kп(N)/2=4/2+5+6=2+5+6=13.
Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=6, т.е. Гп(k)=(2•k+1)2=(2•6+1)2=132=x12=169. Меньшая левая граница интервала совпадает с левой границей меньшего полуконтура, т.е. числа 17, находящегося в контуре с номером k=4. Меньшая граница – это четный квадрат удвоенного номера контура Гч(k)=Гл(k)=(2k)2=(2•4)2=x02=64.Проверка на разность квадратов: N=Гп(6)–Гч(4)=169–64=105. Теперь для N=105 можем записать факторы N=x12–x02=(13+8)(13–8)=21•5=105.
- Пусть слагаемых в представляющей число N сумме будет семь. Очевидно, 105:7=15 и первое слагаемое будет равно 15–6=9, второе 15–4=11, третье 15–2=13, четвертое 15, пятое 15+2=17, шестое 15+4=19 и, наконец, седьмое 15+6=21. Числа 9, 11, 13, 15, 17, 19, 21 образуют непрерывную последовательность нечетных смежных чисел, а 11, 13; 15, 17 и 19, 21 являются полуконтурами трех смежных контуров, так как их суммы 11+13=24=3•8; 15+17=32=4•8 и 19+21=40=5•8 кратны 8. Эти контуры имеют номера k=24/8=3, k=32/8=4 и k=40/8=5.
Число 9 является большим (правым) полуконтуром предшествующего контура с номером k=(7+9)/8=2. Этому числу соответствует половина номера меньшего контура, т.е. k/2=2/2=1. Интервалу из семи примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров kп(N)/2=2/2+3+4+5=1+3+4+5=13.
Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=5, т.е. Гп(k)=(2•k+1)2=(2•5+1)2=112=x12=121.
Меньшая граница интервала совпадает с левой границей меньшего полуконтура, т.е. числа 9, находящегося в контуре с номером k=2, это четный квадрат удвоенного номера контура Гч(k)=Гл(k)=(2k)2=(2•2)2=x02=16.Проверка: N=Гп(5)–Гч(2)=121–16=105.
Теперь для N=105 можем записать факторы N=x12–x02=(11+4)(11–4)=15•7=105.
Этот контур имеет номер k=72/8=9. Число 33 принадлежит другому предшествующему контуру с номером k=8 и в нем является правым, т.е. большим. Этому числу 33 соответствует половина номера его контура, т.е. k/2=8/2=4. Интервалу из трех примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров в виде kп(N)/2=8/2+9=4+9=13.
Числа 9, 11, 13, 15, 17, 19, 21 образуют непрерывную последовательность нечетных смежных чисел, а 11, 13; 15, 17 и 19, 21 являются полуконтурами трех смежных контуров, так как их суммы 11+13=24=3•8; 15+17=32=4•8 и 19+21=40=5•8 кратны 8. Эти контуры имеют номера k=24/8=3, k=32/8=4 и k=40/8=5.
Меньшая граница интервала совпадает с левой границей меньшего полуконтура, т.е. числа 9, находящегося в контуре с номером k=2, это четный квадрат удвоенного номера контура Гч(k)=Гл(k)=(2k)2=(2•2)2=x02=16.Проверка: N=Гп(5)–Гч(2)=121–16=105.          Рассмотренный пример показывает, что для числа N=105 существуют четыре пары квадратов разной четности, расстояние в НРЧ между которыми равно 105. Каждая из найденных пар квадратов позволяет решить задачу факторизации сннч N=105, исключая предельную пару – она дает тривиальное разложение на множители.
          Остается открытым очень важный вопрос, где брать, как получать для произвольного числа N пары (xо2, x12) квадратов?
          Анализ результатов примера 2 показывает, что разные пары квадратов (xоi2, x1i2), i=1(1)4, получаются при разных представлениях инвариантаkп(N)/2=13 в виде суммы с разным числом слагаемых.
Сами такие суммы можно рассматривать как разбиения числа 13 специального вида. Все слагаемые суммы представляют собой отрезок НРЧ, в котором одно из крайних слагаемых в сумму включается лишь своей половиной. Определение такого слагаемого диктуется принадлежностью числа N к классу левых или правых нечетных чисел.
Если N – левое, то половина берется от большего слагаемого:
- N=183 – левое нечетное, 183≡3(mod4), половина берется от большего слагаемого в представлении инварианта суммой kп(183)/2=23=15+16/2; инвариант целое число;
- N=203 – левое нечетное, 203≡3(mod4), половина берется от большего слагаемого в представлении инварианта суммой kп(203)/2=25.5=6+7+8+9/2; инвариант не целое число;
Если N – правое, то половина берется от меньшего слагаемого:
- N=213 – правое нечетное, 213≡1(mod4), половина берется от меньшего слагаемого в представлении инварианта суммой kп(213)/2=26. 5=17/2+18; инвариант не целое число;
- N=217 – правое нечетное, 217≡1(mod4), половина берется от меньшего слагаемого в представлении инварианта суммой kп(217)/2=27=6/2+7+8+9; инвариант целое число;
Таким образом, из рассмотренных фактов следует алгоритм решения задачи факторизации чисел:
- Для заданного сннч N найти инвариант kn/2.
- Инвариант представить разбиением специального вида kn/2=a+(a+1)+(a+2)+…+(a+t-1)+kд/2, где kд – дополнительный номер крайнего контура, левый или правый.
- Для крайних слагаемых вычислить границы: левую Гл=x02 и правую Гп=x12.
- Разность границ представить произведением скобок N=x12–x02=(x1+x0)(x1–x0)=pq.
Рассмотренный материал позволяет сделать следующие выводы.
- Модель составного нечетного натурального числа, представляемого в понятиях контуров – полуконтуров НРЧ позволяет установить инвариант такого числа, как функцию номеров представляющих число контуров. Инвариант kп(N)/2 сохраняет значение независимо от того разностью какой пары квадратов ( при наличии нескольких пар квадратов ) представляется сннч N=xi12–xi02, i=1(1)t, где t – число представляющих пар. N=105=xi12–xi02=532–522=192–162=132–82=112–42
- Значение инварианта устанавливается элементарной обработкой заданного числа N при установлении номера предельного контура. Инвариант может быть как целым, так и дробным числом. Относительно предельного контура сформулированы и доказаны теоремы, которые в посте не приводятся, но используются.
- Предлагаемая модель НРЧ в терминах и понятиях контуров – полуконтуров открывает возможность формулирования и исследования задачи факторизации нечетных чисел за приемлемое для практических приложений время.
Определение четных и нечетных чисел
Ключевые понятия
- Определение четных и нечетных чисел
Четные и нечетные числа
Введение
Сосчитайте числа от 1 до 10.
Вот 6 игрушек. Теперь разделите их на две части.
Разделите игрушки, представленные на картинке, на две равные части.
Вот 3 расчески. Теперь разделите их на две части.
Здесь мы не можем разделить 3 соты на две равные части, потому что остается одна сота.
Четные числа
Числа, которые мы можем разделить поровну на две части, называются четными числами.
Числа, в которых 0, 2, 4, 6, 8 стоят на месте, считаются четными.
Четные числа можно разделить на две равные части.
Здесь четыре кубика вверху и внизу четыре кубика.
4 кубика + 4 кубика = 8 кубиков
Итак, всего 8 кубиков, и мы знаем, что 8 — четное число.
Пример:
Укажите, является ли количество объектов на изображении четным или нечетным.
Решение:
На изображении присутствуют два объекта. Мы можем разделить 2 на две равные части. Итак, 2 четно.
Пример:
Укажите, является ли число четным или нечетным.
Решение:
Мы можем разделить 12 на две равные части.
6 + 6 = 12
Итак, 12 четно.
Пример:
Укажите, является ли количество тортов на изображении четным или нечетным.
Решение:
На изображении четыре торта. Мы можем разделить 4 на две равные части. Итак, 4 четно.
Нечетные числа
Числа, которые нельзя разделить поровну на две части, называются нечетными.
Здесь мы не можем разделить 9 кусков пиццы на две равные части. Итак, 9 — нечетное число.
Числа, имеющие 1, 3, 5, 7, 9на своих местах можно рассматривать как нечетные числа.
Пример:
Укажите, является ли количество объектов на изображении четным или нечетным.
Решение:
Сложите кубики, чтобы узнать, четное это число или нечетное.
10 кубов + 9 кубов = 19 кубов
Мы не можем разделить 19 на две равные части. Итак, 19 — нечетное число.
Пример:
Подсчитайте количество точек на рисунке ниже и напишите, четное это число или нечетное.
Решение:
На изображении присутствуют девять объектов. Мы не можем разделить 9 на две равные части.
Итак, 9 — нечетное число.
Пример:
Укажите, является ли количество объектов на изображении четным или нечетным.
Решение:
На изображении присутствуют три объекта. Мы не можем разделить 3 на две равные части. Значит, 3 нечетное.
Пример:
Укажите, является ли количество объектов на изображении четным или нечетным.
Решение:
На изображении присутствует семь объектов. Мы не можем разделить 7 на две равные части. Итак, 7 нечетное.
Пример:
Укажите, является ли число четным или нечетным.
Решение:
Мы не можем разделить 5 на две равные части. Итак, 5 нечетное.
Упражнение
- Напишите, четное или нечетное число
- Напишите, четное или нечетное количество объектов на изображении
- Укажите, является ли число четным или нечетным
- Укажите, является ли количество объектов, присутствующих на изображении, четным или нечетным
- Укажите, является ли количество объектов, присутствующих на изображении, четным или нечетным
- Напишите, четное или нечетное число
- Напишите, четное или нечетное количество объектов, присутствующих на изображении
- Напишите, четное или нечетное число
- Напишите, является ли количество объектов на изображении четным или нечетным
Концептуальная карта
Чему мы научились
- Различать четные и нечетные числа
Нечетные числа Определения, типы, свойства и примеры
Числа являются строительными блоками математики. Их можно использовать для подсчета или измерения чего-либо. Он играет очень важную роль в нашей повседневной жизни и математике .
Десять математических цифр (от 0 до 9) используются для представления возраста, веса, дней рождения, времени, результатов, банковских счетов и телефонных номеров. Без этих десяти чисел невозможно представить свою жизнь.
Числа бывают различных типов, такие как натуральные числа (N), целые числа (W), целые числа (Z), рациональные числа (Q), действительные числа (R) и т. д.
Натуральные числа, целые числа и целые числа могут быть далее классифицируются на нечетные и четные числа.
Четные и нечетные числа играют важную роль в изучении многих математических понятий. Понимание четных и нечетных чисел важно для освоения некоторых из самых сложных математических понятий.
ЧТО ТАКОЕ НЕЧЕТНЫЕ НОМЕРА?
Нечетные числа — это целые числа, которые не делятся на 2. Если мы разделим нечетное число на 2, то в остатке останется 1. Нечетные числа оканчиваются цифрами 1, 3, 5, 7 или 9. Нечетные числа противоположны четным числам. Нечетные числа не могут быть расположены парами. Нечетные числа не кратны 2.
Примерами нечетных чисел являются 1, 3, 5, 7,31, 43 и т. д. разделите его на 2, и оно оканчивается на 3. Итак, 13 — нечетное число.
СПИСОК НЕЧЕТНЫХ ЧИСЕЛ ОТ 1 до 100:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35 , 37, 39, 41, 43, 45, 47, 49,51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85 , 87, 89, 91, 93, 95, 97, 99
ПРИМЕЧАНИЕ.
- Наименьшее нечетное число – 1.
- Каждое число, следующее за четным, является нечетным.
- Каждое число, следующее за нечетным, является четным числом.
- Дроби и десятичные дроби не являются четными или нечетными числами, потому что они не являются целыми числами.
ЧТО ТАКОЕ ЧЕТНЫЕ ЧИСЛА?
Четные числа — это те числа, которые точно делятся на 2. Четные числа всегда заканчиваются последней цифрой 0, 2, 4, 6 или 8. Любое число, которое делится на 2 без остатка, называется четным числом. .
Примеры четных чисел: 24, 56, 88, 102 и т. д.
Что такое собственность?
Свойство целого числа, независимо от того, является ли оно четным или нечетным, называется четностью.
Целое число является четным, если оно делится на два без остатка, и его четность является нечетной, если оно не делится на 2 и его остаток равен 1.
Любые два последовательных целых числа имеют противоположную четность.
Четные и нечетные числа имеют противоположную четность.
Например, 15 — нечетное, а 16 — четное имеет противоположные четности
29нечетно, а четное 14 имеет противоположные четности.
ОБЩАЯ ФОРМА НЕЧЕТНЫХ ЧИСЕЛ
Нечетное число – это целое число вида 2k+1, где k ∈ Z (т.е. целые числа) называются нечетными числами.
Если мы подставим любое значение k, мы получим нечетное число.
Например: если мы возьмем k за 2, получим 2 x 2 + 1 = 5, что является нечетным числом.
Четное число — это целое число вида 2k, где k ∈ Z (т. е. целые числа) называются нечетными числами.
Если мы подставим любое значение k, мы получим четное число.
Например: Если мы возьмем k за 2, получим 2 x 2 = 4, что является четным числом.
КАК ПРОВЕРИТЬ ЧЕТНОЕ ИЛИ НЕЧЕТНОЕ ЧИСЛО?
Существует два метода определения четности или нечетности числа. Это:
1. Проверяя цифру числа на месте единицы:
Чтобы проверить, является ли число нечетным или четным, мы должны проверить число на «единицы» или «единицы». «место или конечная цифра числа.
Числа, оканчивающиеся цифрами 1,3,5,7 и 9, являются нечетными.
Пример: 7,11,283,5735,9859 и т.д.
Поскольку число 2835 оканчивается цифрой 5 (нечетное число), данное число является нечетным.
А,
Числа, оканчивающиеся цифрами 0,2,4,6 и 8, являются четными числами.
Поскольку число 2838 заканчивается цифрой 8 (четное число), данное число является четным числом.
2. По группировке:
Здесь у нас всего 11 точек. Все точки не спарены. Одна точка остается непарной. Такие числа, которые нельзя составить парами, называются 9.0201 нечетные числа.
Те числа, которые не делятся точно на 2, называются нечетными.
Теперь
12 точек. Мы видим, что все точки спарены и не осталось непарных точек, поэтому 12 — четное число.
Мы можем сделать вывод, что все те числа, которые можно сложить в пары, называются четными числами.
СВОЙСТВА НЕЧЕТНЫХ ЧИСЛА
- Свойство сложения двух нечетных чисел
- Когда мы складываем два нечетных числа, результаты всегда четные.
Пример: 7(нечетное) + 5(нечетное) = 12 (четное)
- Когда мы складываем одно нечетное число и одно четное, результат всегда будет нечетным.
Пример: 9(нечетное) + 2(четное) = 11(нечетное)
- Свойство вычитания нечетных чисел
- Когда мы вычитаем два нечетных числа, результаты всегда четные.
Пример: 9(нечетное) – 3(нечетное) = 6(четное)
- Когда мы вычитаем одно нечетное число и одно четное, результат всегда будет нечетным.
Пример: 15(нечетное) – 10(четное) = 5(нечетное)
- Свойство умножения нечетных чисел
1. При умножении двух нечетных чисел результат всегда нечетный.
Пример: 3(нечетное) x 5(нечетное) = 15(нечетное)
2. Когда мы умножаем одно нечетное число на одно четное, результат всегда будет четным.
Пример: 5(нечетное) x 2(четное) = 10(четное)
- Свойство деления нечетных чисел
1. При делении двух нечетных чисел получается нечетное число, только если знаменатель является множителем числителя.
Пример: Когда мы делим 15 на 5 и 5 делим на 15, мы получаем 3, что является целым числом.
- Когда мы делим два нечетных числа и знаменатель не является множителем числителя, результат может быть дробным или десятичным (конечным или неконечным).
Пример: когда мы делим 5 на 15, мы получаем 1/3 (дробь) или 0,3333 (неконечная десятичная дробь). .
- Составные нечетные числа : Составные числа, которые нельзя разделить на 2, являются составными нечетными числами, а все положительные целые числа, имеющие множитель, отличный от 1, называются составными числами. Эти типы нечетных чисел образованы произведением двух меньших положительных нечетных целых чисел.
Список составных нечетных чисел от 1 до 50 выглядит следующим образом.
9, 15, 21, 25, 27, 33, 45, 49.
- Последовательные нечетные числа : Последовательные нечетные числа — это нечетные числа, следующие друг за другом в последовательном порядке. Между ними разница 2. Если n нечетное число, то числа n и n+2 являются последовательными нечетными числами.