| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
§ Стандартный вид числа.
Записать число в стандартном видеВ задачах по физике часто приходится работать с очень большими и очень малыми величинами.
Как вести вычисления в атомной физике? Или записать радиус электрона? Если потребуется сравнить массу электрона и массу планеты Земля, как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?
Физики и математики, столкнувшись с такими задачами, поняли, что для решения подобных задач требуется привести числа к единому стандартному виду. Так появилось понятие стандартный вид числа.
Прежде чем переходить к объяснению, как записать число в стандартном виде, нужно вспомнить определение степени. Особенно хорошо нужно помнить, чему равняется число «10» в различных степенях.
- 10−2 = = = 0,01 (более подробно об отрицательной степени можно прочитать в уроке 9 класса «Отрицательная степень»)
- 10−1 = = = 0,1
- 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1000
- …
Вспомним, что при умножении целого числа на 10, 100, 1000 и т.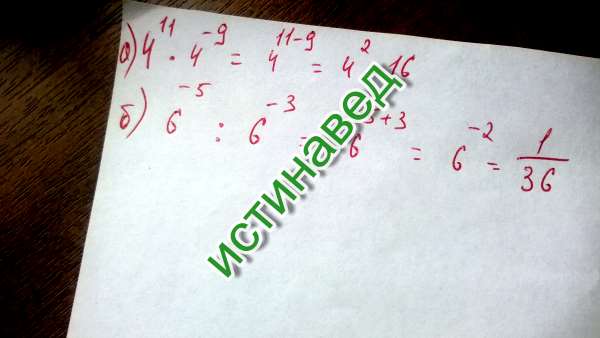
д. мы
просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..
- 5 · 10 = 50
- 27 · 100 = 2 700
- 18 · 1000 = 18 000
Теперь запишем тоже самое, используя определение степени.
- 5 · 10 = 5 · 101 = 50
- 27 · 100 = 27 · 102 = 2 700
- 18 · 1000 = 18 · 103 = 18 000
При делении целого числа на 10, 100, 1000 и т.д. мы убирали нули.
- 13 000 : 100 =
= 13013 000 100 - 50 : 10 = = 5
Для десятичных дробей действует схожее правило умножения на 10, 100, 1000. При умножении десятичной дроби на 10, 100, 1000 и т.д. мы перемещаем запятую вправо на количество нулей, что и в 10, 100, 1000 и т.д…
- 5,7 · 100 = 570
- 7,013 · 10 = 70,13
- 68,3 · 1000 = 68 300
С помощью степени можно записать вычисления выше следующим образом:
- 5,7 · 100 = 5,7 · 102 = 570
- 7,013 · 10 = 7,013 · 101 = 70,13
- 68,3 · 1000 = 68,3 · 103 = 68 300
При делении на 10, 100, 1000 и т.
д. перемещаем запятую влево.
- 6,7 : 10 = = 0,67
- 0,15 : 100 =
= 0,00150,15 100
С помощью определения отрицательной степени можно записать вычисления выше следующим образом:
- 6,7 : 10 = = 6,7 · 10−1 = 0,67
- 0,15 : 100 =
= 0,15 · 10−2 = 0,00150,15 100
Стандартный вид числа
Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.
Запомните!
Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:
a · 10n,
где 1 ≤ a < 10
и n — натуральное число.
Такая запись называется — стандартный вид числа.
При этом число
«n»
называют порядком числа «a».
Из определения выше важно понять, что степень, в которой стоит «10», в стандартном
виде числа называется порядком.
Теперь к примеру. Пусть нам дано число «5 600» и требуется записать его в стандартном виде.
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от «1» до «9».
В числе «5 600» первая цифра справа — «5». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.
Значит, чтобы из «5,600» получить «5600» нам нужно умножить «5,600» на «1000». Запишем полученное преобразование.
5 600 = 5,600 · 1000
Теперь запишем «1000» с использованием степени.
5 600 = 5,600 · 1000 = 5,600 · 103
Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.
5 600 = 5,600 · 1000 = 5,600 · 103
=
5,6 · 103
Таким образом «5 600» в стандартном виде будет выглядеть следующим образом:
5 600 = 5,6 · 103
Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно.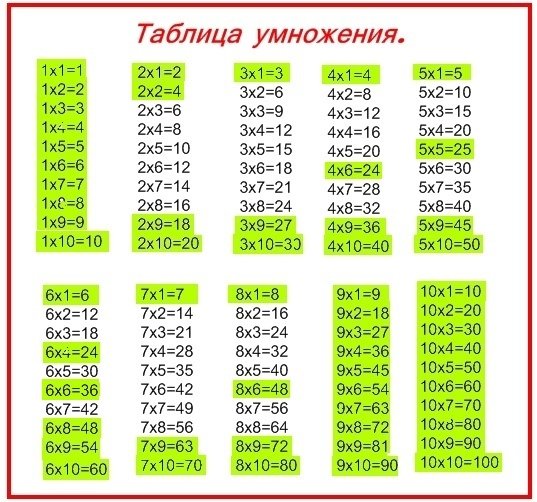
Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.
5,6 · 103 = 5 600
Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь «0,017».
Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от «1» до «9».
В десятичной дроби «0,017» вначале идет «0». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от «0».
Это цифра «1». Посчитаем сколько знаков (цифр) стояло от запятой до цифры «1», включая саму цифру «1».
Получается два знака. Начнем записывать «0,017» в стандартном виде. Перенесем запятую и поставим ее справа от «1».
0,017 = 1,7 · 10…
Ответим себе на вопрос: «На что нужно умножить или разделить «1,7», чтобы получить изначальное число
«0,017» ?».
Напоминаем, что при делении на 10, 100, 1000 и т.
д. запятая переносится
Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится
влево.
Выходит, чтобы из «1,7» сделать 0,017», нужно «1,7 разделить на «100» (чтобы перенести запятую на два знака влево).
0,017 = 1,7 : 100
Запишем это деление на «100», используя обыкновенную дробь.
0,017 = 1,7 : 100 = 1,7 ·
С помощью отрицательной степени запишем окончательный вид числа «0,017» в стандартном виде.
0,017 = 1,7 : 100 = 1,7 · =
1,7 · 10−2
Примеры решения задач
на запись числа в стандартном виде
Разбор примера
Определить порядок числа, выражающего значение физической константы:
1) масса покоя электрона
me = 9,1093897 · 10−31
Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень,
в которой стоит «10».
В данном примере «10» стоит в
степени
«−31».
Значит, порядком массы покоя электрона является «−31».
Разбор примера
Записать в стандартном виде и определить порядок числа k, выражающего физического константу:
2) постоянная Фарадея
F = 96485,309 Кл/моль;
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от «1» до «9».
Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра «9».
96485,309 = 9,6485309 · 10…
Зададим себе вопрос: «На что нужно умножить «9,6485309», чтобы получить «96485,309» ?» Посчитаем количество знаков (цифр), на которое требуется перенести запятую в «96485,309», чтобы получить «96485309».
Получается «4» знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим образом:
96485,309 = 9,6485309 · 104
Порядком числа «9,6485309 · 104» является степень, в которой стоит
«10». Следовательно, порядок
«k = 4».
3) Постоянная Лошмидта
n0 = 2686763 · 10 26
Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:
2686763 · 10 26 =
2,686763 · 10 26 · 10…
Рассчитаем, на какое количество знаков (цифр) требуется перенести запятую, чтобы из «2,686763» получить «2686763».
Значит, чтобы получить из «2,686763» нужно изначальное число «2686763» умножить на «106».
2686763 =
2,686763 · 10 26 · 106
Завершим решение и запишем окончательный ответ, используя свойство «Произведение степеней».
2686763 = 2,686763 · 10 26 · 106 = 2,686763 · 10 26 + 6 = 2,686763 · 10 32
Другие примеры записи чисел в стандартном виде
- 0,52 = 5,2 · 10 −1
- 401 = 4,01 · 10 2
- 60,756 = 6,0756 · 101
- 0,00123 = 1,23 · 10
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
-12.
Калькулятор экспоненциального представления
Используйте приведенный ниже калькулятор для выполнения вычислений с использованием экспоненциального представления.
Научное обозначение
Научное представление — это способ представления чисел в форме, которая делает слишком маленькие или слишком большие числа более удобными для записи и выполнения вычислений. Он обычно используется в математике, технике и естественных науках, так как помогает упростить арифметические операции. В научной записи числа записываются как основание, b , называемая мантиссом, умноженная на 10, возведенная в целочисленную степень, n , которая называется порядком величины:
b × 10 n
Ниже приведены некоторые примеры записанных чисел в десятичной системе счисления по сравнению с экспоненциальной записью:
Вычисления с экспоненциальной записью
Экспоненциальная запись может упростить процесс вычисления основных арифметических операций вручную.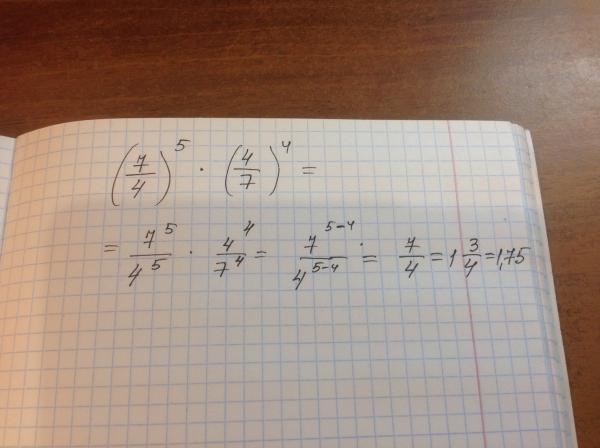
Сложение и вычитание:
Чтобы складывать и вычитать в экспоненциальном представлении, убедитесь, что каждое число преобразовано в число с той же степенью 10. Например, 100 можно записать как 1×10 2 , 0,01×10 4 , 0,0001 ×10 6 и так далее. Как только все числа будут записаны в одной степени 10, добавьте каждую соответствующую цифру. Рассмотрим задачу. 2 + 800×10 -1 – 0,001×10 5
Умножение: 90 005
Чтобы умножить числа в экспоненциальном представлении, разделите степени 10 и цифры. Цифры умножаются обычным образом, а показатели степени числа 10 складываются, чтобы определить новую степень числа 10, применяемую к произведению цифр.
Рассмотрим 1,432×10 2 × 800 × 10 -1 × 0,001 × 10 5 :
1,432 × 800 × 0,001 = 1,1456
10 2 × 10 -1 × 10 5 = 10 2+ (-1)+5 = 10 6
Таким образом:
1,432×10 2 ×800×10 -1 ×0,001×10 5 90 021 = 1,1456×10 6
Деление :
Чтобы разделить числа в экспоненциальном представлении, разделите степени 10 и цифры. Разделите цифры нормально и вычтите показатели степени 10. По соглашению частное записывается так, чтобы слева от десятичной дроби была только одна ненулевая цифра. Рассмотрим (1,432×10 2 ) &дел; (800×10 -1 ) &дел; (0,001×10 5 ):
1,432 &дел; 800 &дел; 0,001 = 1,79
10 2 &дел; 10 -1 ÷ 10 5 = 10 (2-(-1)-5) = 10 -2
Таким образом:
(1,432×10 2 ) ÷ (800×10 -1 ) &дел; (0,001×10 5 ) = 1,79×10 -2
Если бы, например, решение было 0,179×10 -2 , по соглашению, мы должны сдвинуть десятичную дробь влево так, чтобы первая цифра слева от десятичной точки не была равна 1, а затем соответствующим образом изменить показатель степени:
0,179×10 -2 = 1,79×10 -3
Инженерная запись
Инженерная запись аналогична научной записи, за исключением того, что показатель степени n ограничен числом, кратным 3, например: 0, 3, 6, 9, 12, -3 , -6 и т.
д. Это сделано для того, чтобы числа соответствовали префиксам SI и могли быть прочитаны как таковые. Например, 10 3 будет иметь префикс килограмм, 10 6 будет иметь префикс мега, а 10 9 будет иметь префикс гига. Обратите внимание, что десятичный разряд числа можно переместить, чтобы преобразовать научную запись в инженерную запись. Например:
1,234 × 10 8 (научная запись)
можно преобразовать в:
123,4 × 10 6 (техническая запись)
Электронная запись
Электронная нотация почти такая же, как научная обозначения, за исключением того, что «× 10» в экспоненциальном представлении заменено просто «E». Он используется в тех случаях, когда экспонента не может быть удобно отображена. Пишется так:
bEn
, где b — основание, E указывает «x 10», а n пишется после E . Ниже приведено сравнение научной записи и электронной записи:
«Е» также может быть записано как «е», что и используется в этом калькуляторе.