В каких случаях ставится скобки. Калькулятор онлайн.Упрощение многочлена.Умножение многочленов
Везде. Везде и всюду, куда ни глянь, встречаются вот такие конструкции:
«Конструкции» эти у грамотных людей вызывают неоднозначную реакцию. Как минимум типа «неужели так — правильно?».
Вообще лично я не могу понять, откуда пошла «мода» не закрывать внешние кавычки. Первая и единственная приходящая по этому поводу аналогия — аналогия со скобками. Никто же не сомневается, что две скобки подряд — это нормально. Например: «Оплатить весь тираж (200 шт. (из них 100 — брак))». А вот в нормальности постановки двух кавычек подряд кто-то засомневался (интересно, кто первый?)… И теперь все поголовно стали с чистой совестью плодить конструкции типа ООО «Фирма «ПупковЪ и Ко».
Но даже если вы в жизни не видели правила, о котором речь пойдет чуть ниже, то единственным логически обоснованным вариантом (на примере скобок) был бы следующий: ООО «Фирма «ПупковЪ и Ко»».
Итак, непосредственно правило:
Если в начале или в конце цитаты (то же относится к прямой речи) встречаются внутренние и внешние кавычки, то они должны различаться между собой рисунком (так называемые «елочки» и «лапочки»), причем внешние кавычки не должны опускаться, например: С борта парохода передали по радио:«„Ленинград“ вошел в тропики и следует дальше своим курсом».О Жуковском Белинский пишет: «Современники юности Жуковского смотрели на него преимущественно как на автора баллад, и в одном своем послании Батюшков называл его „балладником“».
© Правила русской орфографии и пунктуации. — Тула: Автограф, 1995. — 192 с.
Соответственно… если у вас нет возможности набрать кавычки-«елочки», то, что уж поделаешь, придется пользоваться такими «» значками. Однако, невозможность (или нежелание) использовать русские кавычки отнюдь не является причиной, по которой можно не закрывать внешние кавычки.Таким образом с неверностью констукции ООО «Фирма «ПупковЪ и Ко» вроде бы разобрались. Встречаются еще конструкции вида ООО «Фирма «ПупковЪ и Ко».
Из правила совершенно понятно, что и такие конструкции безграмотны… (Правильно: ООО «Фирма „ПупковЪ и Ко“»Однако!
В «Справочнике издателя и автора» А. Э. Мильчина (издание 2004 года) указано, что можно использовать два варианта оформления в подобных случаях. Использование «елочек» и «лапок» и (при отсутствии технических средств) использование только «елочек»: двух открывающих и одной закрывающей.
Справочник это «свежий» и лично у меня тут сразу появляется 2 вопроса. Во-первых, с какой все же радости можно использовать одну закрывающую кавычку-елочку (ну нелогично это, см. выше), а во-вторых, особо обращает на себя внимание фраза «при отсутствии технических средств». Это как, простите? Вот откройте Notepad и наберите там «только елочки: две открывающие и одну закрывающую». На клавиатуре таких символов нет. Напечатать «елочку» не получается… Сочетание Shift + 2 выдает знак » (который, как известно, и кавычкой-то не является). А теперь откройте Microsoft Word и снова нажмите Shift + 2. Программа исправит » на « (или »). Что же, получается что существовавшее не один десяток лет правило взяли и переписали под Microsoft Word? Мол, раз ворд из «Фирма «ПупковЪ и Ко» делает «Фирма «ПупковЪ и Ко», то пусть теперь это будет допустимо и корректно???Похоже, что так. А если это так, то есть все основания усомниться в правильности подобного нововведения. Да, и еще одно уточнение.
Все специальные символы шрифта можно легко набрать, зная соответствующий номер этого символа. Достаточно зажать Alt и набрать на NumLock-клавиатуре (NumLock нажат, индикаторная лампочка горит) соответствующий номер символа:
„ Alt + 0132 (левая «лапка»)
“ Alt + 0147 (правая «лапка»)
« Alt + 0171 (левая «елочка»)
» Alt + 0187 (правая «елочка»)
.. про то самое «отсутствие технических средств». Дело в том, что на любом компьютере с Windows всегда имеются «технические средства» для ввода и «елочек», и «лапок», так что это новое «правило» (для меня оно — именно в кавычках) неверно изначально!Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.
Раскрыть скобки означает избавить выражение от этих скобок.
Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок.
Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.
И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).
Правило раскрытия скобок при сложении
При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.
Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.
2 + (7 + 3) = 2 + 7 + 3
Правило раскрытия скобок при вычитании
Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.
Пример. Раскрыть скобки в выражении 2 − (7 + 3)
Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.
2 − (7 + 3) = 2 − (+ 7 + 3)
При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3) , а знаки, которые были в скобках, меняем на противоположные.
2 − (+ 7 + 3) = 2 − 7 − 3
Раскрытие скобок при умножении
Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками.
При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.
Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.
(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5
На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Раскрываем скобки при делении
Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.
3 \)Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.
Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т.
2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму. Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.
Если вы хотите включить информацию, связанную с основным текстом, но эта информация не вписывается в основную часть предложения или абзац, вам необходимо взять эту информацию в скобки. Взяв ее в круглые скобки, вы тем самым уменьшаете ее значимость, так что она не отвлекает от основного смысла в тексте.
- Пример: Дж. Р. Р. Толкин (автор «Властелин колец») и К. С. Льюис (автор «Хроники Нарнии») были постоянными членами литературной дискуссионной группы, известной как «Инклинги».
Примечания в скобках. Часто, когда вы пишете прописью численное значение, полезно также указывать это значение в цифрах.
- Пример: Она должна заплатить семьсот долларов ($700) за аренду до конца этой недели.
Использование цифр или букв при перечислении. Когда вам нужно перечислить ряд информации внутри абзаца или предложения, нумерация каждого пункта может сделать список менее запутанным. Вы должны взять цифры или буквы, используемые для обозначения каждого пункта, в скобки.
- Пример: Компания ищет кандидата на работу, который (1) дисциплинирован, (2) знает все, что нужно знать о последних тенденциях в редактировании фотографий и улучшения программного обеспечения и (3) имеет, минимум, пять лет профессионального стажа в данной области.
- Пример: Компания ищет кандидата на работу, который (А) дисциплинирован, (Б) знает все, что нужно знать о последних тенденциях в редактировании фотографий и улучшения программного обеспечения и (В) имеет, минимум, пять лет профессионального стажа в данной области.
Обозначение множественного числа. В тексте, вы можете говорить о чем-то в единственном числе, в то же время подразумевая и множественное число. Если заведомо известно, что читатель получит пользу, зная, что вы имеете в виду как множественное, так и единственное число, вы можете обозначить свое намерение, указав в скобках сразу после существительного соответствующее окончание, свойственное данному существительному во множественном числе, если существительное имеет такую форму.
- Пример: Организаторы фестиваля в этом году надеются на большое количество зрителей, поэтому не забудьте приобрести дополнительный(ые) билет(ы).
Обозначение сокращений. При написании названия организации, продукта или других объектов, которые, как правило, имеют общеизвестные сокращения, вам необходимо указать полное имя объекта в первый раз, как вы его упоминаете в тексте. Если далее вы собираетесь обращаться к объекту, используя общеизвестную аббревиатуру, вы должны указать эту аббревиатуру в скобках, так чтобы читатели знали что искать позже.
- Пример: Сотрудники и волонтеры Лиги Зашиты Животных (ЛЗЖ) надеются уменьшить и, в конечном счете, ликвидировать случаи жестокого обращения с животными и ненадлежащего обращения в рамках сообщества.
Упоминание знаменательных дат. Хотя это не всегда необходимо, в определенных контекстах, вам может потребоваться указать дату рождения и/или дату смерти определенного лица, о котором вы упоминаете в тексте. Такие даты нужно заключить в скобки.
- Пример: Джейн Остин (1775-1817) известна своими литературными работами «Гордость и предубеждение» и «Разум и чувства»
- Джордж Мартин (д.р. 1948) является человеком, положившим начало популярного сериала «Игра престолов».
Использование вводных цитат. В научной литературе, вводные цитаты должны быть включены в текст, когда вы напрямую или косвенно цитируете другую работу. Эти цитаты содержат библиографическую информацию и должны быть заключены в скобки сразу после заимствованной информации.
- Пример: Исследования показывают, что существует связь между мигренью и клинической депрессией (Смит, 2012).
- Пример: Исследования показывают, что существует связь между мигренью и клинической депрессией (Смит 32).
- Для получения дополнительной информации о правильном использовании в тексте вводных цитат смотрите «Как правильно использовать цитаты в тексте».
Основная функция скобок – менять порядок действий при вычислениях значений . Например , в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).
Пример. Раскройте скобку: \(-(4m+3)\).
Решение : \(-(4m+3)=-4m-3\).Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение : \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).Пример. Раскройте скобки \(5(3-x)\).
Решение : В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей .Пример. Раскройте скобки \(-2(-3x+5)\).
Решение : Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).Пример. Упростить выражение: \(5(x+y)-2(x-y)\).
Решение : \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).Осталось рассмотреть последнюю ситуацию.
При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:
\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)
Пример. Раскройте скобки \((2-x)(3x-1)\).
Решение : У нас произведение скобок и его можно раскрыть сразу по формуле выше. Но чтобы не путаться, давайте сделаем всё по шагам.
Шаг 1. Убираем первую скобку — каждый ее член умножаем на скобку вторую:Шаг 2. Раскрываем произведения скобки на множитель как описано выше:
— сначала первое…Потом второе.
Шаг 3. Теперь перемножаем и приводим подобные слагаемые:
Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.
Примечание ко всему разделу. На самом деле, вам нет необходимости запоминать все четыре правила, достаточно помнить только одно, вот это: \(c(a-b)=ca-cb\) . Почему? Потому что если в него вместо c подставить единицу, получиться правило \((a-b)=a-b\) . А если подставить минус единицу, получим правило \(-(a-b)=-a+b\) . Ну, а если вместо c подставить другую скобку – можно получить последнее правило.
Скобка в скобке
Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).
Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.При этом важно при раскрытии одной из скобок не трогать все остальное выражение , просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение :
\(-(x+3(2x-1\)\(+(x-5)\) \())\)
Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается.
\(-(x+3(2x-1\)\(+x-5\) \())\)
Теперь нужно раскрыть вторую скобку, промежуточную.
\(=-(x\)\(+3(3x-6)\) \()=\)
Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него.
\(=-(x\)\(+9x-18\) \()=\)
И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные.
Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.
Долой калькулятор! Техника счета на уроках математики – Учительская газета
Много ли ученики считают устно на уроках? «Немало»,- ответят учителя начальных классов. «Порядочно», – скажут математики средней школы.
На самом деле, считаем мы мало. Причин несколько: перегруженность программы, отсутствие системы приемов рациональных вычислений, недостаточность осознания конечных целей обучения математике. В наших учебниках много определений, правил, алгоритмов, которые надо понять, усвоить и научиться применять. Так много, что большинство учеников просто не в состоянии запомнить чересчур обширный материал. Обилие теоретических сведений, немалое количество тупиковых тем, в которых рассматриваются бесконечно оторванные от реальной жизни примеры, – еще одна причина трудностей восприятия учебного предмета. Между тем очень часто можно наблюдать знакомую картину – ученики старших классов не могут быстро и точно выполнить простейшие вычисления в уме. На это приходится тратить драгоценное время, вместо того чтобы заняться решением более трудных задач.
В средних классах мы недостаточно внимания уделяем педагогическому проектированию – видению содержания будущего материала с точки зрения материала текущего.
Несколько примеров. Начало 10-го класса. Изучение тригонометрии. Простейшие вычисления с углами. Ученики не могут найти значения выражений типа p + n/4; 2n – n/6.
Эти проблемы возникают у них при упрощении выражений, вычислении значений тригонометрических функций, решении уравнений, построении графиков. Навыки, не сформированные в свое время, на каждом шагу дают о себе знать. И тогда на уроках приходится возвращаться к счету, начиная решение задач с простейших устных вычислений.
Еще один пример. Решение разных уравнений, изучаемых в старших классах, так или иначе сводится к решению квадратных уравнений. А много ли учеников применяют теорему Виета, знают формулу корней квадратного уравнения со вторым четным коэффициентом, помнят о разложении квадратного трехчлена на множители? Подобных «мелочей» наберется немало.
Формирование прочных вычислительных навыков – то, что мы часто забываем, увлекаясь текущими делами. Владение системой вычислительных приемов – основа для восприятия и понимания материала каждого урока. С учеником просто общаться и легко обучать, если он хорошо считает, помнит простейшие вычислительные правила. Правда, приемов рациональных вычислений в учебниках очень мало. Их недостаток заставляет учителей задумываться о формировании системы рациональных вычислений, полезных правил, которые облегчают вычисления и которые в конечном итоге помогают формировать вычислительную культуру учеников.
И как свидетельство этому – письмо в «УГ» учителя математики И.
( 9+1).
Возможно, что с первого раза у учеников не получится быстро, с ходу выполнять эти или другие подсчеты. Пусть сначала не получится использовать прием, показанный учителем. Не беда. Нужна постоянная вычислительная тренировка. Из урока в урок, из года в год. Она поможет приобрести полезные навыки устного счета. Тренировочные минутки-считалки, сопроводительные пояснения в подходящих «числовых ситуациях», вычислительные мини-бои – далеко не полный перечень учебных форм, которые полезно включать в учебный процесс.
Вычислительную культуру помогают формировать и другие приемы. Учителям известно, что, складывая довольно простые числа, дети часто испытывают трудности. Они не могут сложить, например, устно 253 и 198. Но если объяснить, что при сложении таких чисел можно использовать прикидку, то дело будет обстоять лучше. Ученик без труда это поймет и в дальнейшем будет пользоваться прикидкой (или упрощением). В данном примере для того, чтобы сложить, например, 253 и 198, надо сначала сложить 253 и 200 (мы как бы округляем второе слагаемое до 200), а потом из полученной суммы 453 вычесть два.
Подобная прикидка используется и при умножении чисел, близких к 100. Предположим, надо умножить 94 на 98. Найдем те слагаемые, которые дополняют каждое число до сотни. Это 6 и 2 соответственно. Далее из любого множителя вычтем дополнение второго множителя до сотни, т.е., например, 98-6=92. Потом найдем произведение дополнений и к разности множителя и дополнения припишем слева произведение дополнений. В результате получим 9212. Просто? Конечно. Возьмите на вооружение этот прием. А если с первого раза покажется трудно, повторите несколько раз. Еще один похожий пример: найти произведение 99 х 95. Вот последовательность мыслительных действий. Цепочка рассуждений состоит из нескольких простых примеров.
1) 99 – 5=95 -1=94; 2)5 х 1= 5 ; 3)99 х 95=9405. Все это легко находится в уме. Операции проходят значительно быстрее, чем письменное умножение столбиком.
Привычка выполнять подобные примеры устно формирует устойчивый навык, который не раз сыграет добрую службу при изучении более сложного материала.
Очень часто на уроках математики требуется быстро найти квадрат целого числа. Надо приучать учеников и эти действия выполнять в уме. Вот лишь некоторые из приемов, которые можно использовать при возведении двузначного числа в квадрат.
Для того, чтобы найти квадрат числа n, если известен или легко вычисляется квадрат числа (n+2), необходимо из числа (n+2)2 вычесть сумму чисел n+(n+2), умноженную на 2.
Покажем это правило на примере: 382 = 402 – (38+40)х2 = 1600-156=1444.
А для того, чтобы найти квадрат числа n, если известен или легко вычисляется квадрат числа n-2, необходимо к числу (n-2)2, прибавить удвоенную сумму чисел n и n-2.
Например, 422 = 402+(40+42)х2 = 1600 + 164 = 1764. И еще несколько примеров, иллюстрирующие последние два правила.
522 = 2500 + (50+52) х 2 = 2704,
482 = 2500 – (48+50) х 2 = 2304,
572 = 3025 + (55+57) х 2 = 3249,
532 = 3025 – (53+55) х 2 = 2809.
Вот так, систематически и ненавязчиво, красиво и последовательно надо показывать ученикам практическую значимость математики.
Как комбинировать одинаковые термины
Калькулятор комбинирования похожих терминов помогает упростить выражение алгебраических терминов путем объединения похожих терминов. Мы знаем, что алгебраическое выражение состоит как из одинаковых, так и из разных членов. Должно быть довольно интересно упростить, объединив одинаковые термины в алгебраических выражениях. Необходимо комбинировать одинаковые термины, чтобы создать эквивалентное выражение, которое облегчает понимание нашего вывода.
Что такое компоненты термина?
Для понимания подобных терминов нам сначала нужно распознать различные части алгебраического термина, такого как \(4x^{2}\).
Упрощайте и комбинируйте одинаковые термины независимо от длины алгебраического выражения и вставляйте значения в калькулятор комбинирования похожих терминов. Когда вам предоставляется возможность использовать такой простой в использовании калькулятор, это также немного облегчает вам задачу.
Последовательности операций Like Term Правила:
Существуют определенные правила, применяемые при упрощении выражения путем объединения одинаковых терминов. Мы постараемся последовательно изучить все правила последовательности операций. Следующие аббревиатуры обычно используются в математических расчетах, и их лучше понять. Используйте калькулятор комбинирования похожих терминов, чтобы упростить алгебраическое выражение.
PEMDAS:
PEMDAS означает P арентез, E экспонент, M умножение, D ivision, а затем 906 S9 030 S
вычитание.
BEMDAS:
BEMDAS означает B арентез, E экспонент, M умножение, D ivision и затем 9036 A 9003 9036 A 9003 7 вычитание.
BODMAS:
BODMAS означает «скобки, порядок, деление и умножение, сложение и вычитание»
GEMDAS:
GEMDAS расшифровывается как «Группировка, экспоненты, деление и умножение, сложение и вычитание». Это означает «Умножение и деление, сложение и вычитание». алгебраические термины путем объединения подобных терминов калькулятор.
Ассоциативность операторов:
Умножение, деление, сложение и вычитание являются левоассоциативными операциями. Когда вы решаете вышеупомянутые четыре оператора, вы фактически исходите из левой стороны. Когда вы добавляете и вычитаете одинаковые термины, вы следуете ассоциативному свойству операторов. Калькулятор комбинированных терминов автоматически решает, должен ли он использовать левоассоциативное свойство или правоассоциативное свойство.
Лево-ассоциативное свойство:
9(з/н))
Сначала нам нужно решить самые внутренние скобки, а затем решить внутренние скобки или скобки. Для решения правильного ассоциативного свойства мы используем PEMDAS, и мы можем проверить значения с помощью калькулятора комбинированных терминов.
Правила сложения, вычитания, умножения и деления:
Существуют определенные правила сложения, вычитания, умножения и деления, которые применяются при использовании калькулятора комбинирования подобных терминов.
Эти правила являются стандартными для следующих операторов и заключаются в следующем:
Правила добавления операций(+):
При добавлении двух одинаковых терминов с одинаковыми символами сохраняйте символы и упрощайте и комбинируйте похожие термины. Примеры объединения подобных терминов с операциями сложения следующие:
(-)+(-) = (-) (+)+(+) = (+) (-15х)+(-5х) = (-20х) (+12х)+(+8х) = (+20х) Если символы отличаются, вычтите термины и сохраните символы большего термина.
(-большой)+(+маленький) = (-) (-маленький)+(+большой) = (+) (-15х)+(+5х) = (-10х) (-6л)+(+8л) = (+2г)
Правила операций вычитания (-):
Сохраните знак первого члена, затем измените все остальные знаки, а затем примените те же правила сложения для решения задачи:
(- )-(-) = (-)-(+) = (+)-(-) = (-15x)-(-5x) (+12x)-(+8x) (+5x)-(-6x ) -15x+5x= -10x +12x-8x= +4x +5x+6x= +11x Правила операций умножения (* или × ):
Когда мы комбинируем одинаковые члены для создания эквивалентного выражения умножения, тогда отрицательные и отрицательные значения дают положительные значения. Умножение отрицательных и положительных результатов дает отрицательный результат, а положительные и положительный термин дает положительный результат.
(-)*(-) = (-)*(+) = (+)*(-) = (+)*(+) (-5)*(-5) =25 (-5)*(+8)= -40 (+5)*(-6 )=-30 (+5)*(+7)=35 Правила операции деления (/ ):
Операции деления используются так же, как мы использовали для умножения. Отрицательное и отрицательное деление дает положительные значения, тогда как деление отрицательного и положительного дает отрицательный результат. Положительный и положительный термин дают положительный результат, как объединить подобные термины с операциями деления следующим образом:
(-)/(-) = (-)/(+) = (+)*(-) = (+)*(+) (-10)/(-10) =+1 (-10)/(+2)= -5 (+15)*(-3 )=-5 (+7)*(+7)=+1 Вы можете использовать проверку всех расчетов, комбинируя подобные термины калькулятор.
Работа калькулятора комбинированных терминов:
Чтобы найти ответы на комбинированные подобные термины, нам нужно понять работу калькулятора комбинированных уравнений. Давай сделаем это!
Ввод:
- Добавьте коэффициент, переменные и операторы в поле ввода.
- Вы можете добавлять дробные, мономиальные, полиномиальные и экспоненциальные значения и т.д.
- Нажмите кнопку расчета
Вывод:
Объединитель одинаковых членов выполняет следующие вычисления:
- Все одинаковые члены отображаются соответствующей операцией.
- Все шаги показаны для нашего понимания
- Нажмите кнопку пересчета
Часто задаваемые вопросы
Как объединить одинаковые термины, чтобы создать эквивалентное выражение?
Упростить, комбинируя коэффициенты одинаковых членов, например, 3x и 5x становится (3+5) x= 8x
Какова последовательность решения операций?
Простая последовательность операций: сначала решить скобки, затем решить деление, умножение, затем сложение и, наконец, вычитание.
Вывод:
Подобные члены — это алгебраические члены, имеющие одинаковые степени и степени, но разные коэффициенты. Калькулятор комбинированных членов помогает нам записать полином в идеальном порядке, чтобы упростить наши вычисления.
Ссылки:
Из источника Википедии: Обобщение, Упрощение выражения, Подобные термины
Из источника Академии Хана: Что такое эквивалентные выражения? Какие навыки проверяются? Как мы переставляем формулы?
Из источника ixl.com: Равнозначные выражения, Объединение подобных терминов, Распределяющее свойство
Калькулятор объединения подобных терминов шаг за шагом
Калькулятор объединения похожих терминов шаг за шагомКалькулятор объединения одинаковых членов
Введите математическое выражение…
РАДДЕГ
Триггерные функции
Решить для:xyztabcdfghjklmnopqrsuvw
Решить для: xyztabcdfghjklmnopqrsuvw
Привет! Вы устали пытаться упростить алгебраические выражения самостоятельно? Вам нужна дополнительная помощь в понимании процесса объединения похожих терминов? Если да, то вам повезло! Калькулятор объединения похожих терминов с шагами здесь, чтобы помочь.
Этот калькулятор разработан специально для того, чтобы помогать таким пользователям, как вы, упрощать алгебраические выражения, комбинируя похожие термины. Он содержит пошаговые инструкции, чтобы вы могли легко понять процесс, связанный с объединением похожих терминов.
Чтобы использовать калькулятор, просто введите алгебраическое выражение, которое вы хотите упростить, в поле ввода. Калькулятор объединения похожих терминов затем проанализирует выражение и предоставит пошаговую разбивку процесса, связанного с объединением похожих терминов. С помощью этого полезного инструмента упростить алгебраические выражения будет проще простого.
Содержание
- 1 Калькулятор комбинирования подобных терминов
- 2 Определение комбинирования подобных терминов
- 3 Как сочетать одинаковые термины
Определение объединения сходных терминов
Объединение сходных терминов представляет собой математический процесс, при котором сходные термины в алгебраическом выражении объединяются или упрощаются.
Как объединить одинаковые термины
Чтобы объединить похожие термины, выполните следующие действия:
Определите похожие термины в выражении. Подобные термины — это термины, которые имеют одну и ту же переменную и показатель степени. Например, «3x» и «5x» — такие же термины, как и «2y» и «4y».
Сложите или вычтите коэффициенты при одинаковых условиях. Коэффициент — это число, которое стоит перед переменной. В примере «3х+5х» коэффициенты равны «3» и «5». Чтобы объединить эти условия, сложите коэффициенты вместе, чтобы получить «8x».
Вы можете указать численную форму, поместив ее в скобки.
Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке.
И нетрудно предположить, какой ответ будет у тех учителей, кто преподает в старшей школе…
Это приводит к тому, что в средней школе бывают упущены те узловые моменты учебного содержания, которые в дальнейшем дают возможность более эффективно формировать практические навыки школьников.
Они, как тяжелые гири, висят на ногах у старшеклассников, мешая им твердыми и размеренными шагами двигаться вперед по пути изучения серьезных разделов предмета. Все это происходит оттого, что в свое время этим вопросам не уделили достаточно внимания, не отработали практические навыки на простом и стандартном материале. А потом то, что упустили, вновь дает о себе знать.
С.Плужникова из села Дунайка Белгородской области. Иван Степанович постоянно пополняет свою методическую копилку, собирая остроумные приемы, которые значительно упрощают вычислительную работу. Некоторые из них учителя начальных классов используют на уроках. Так, например, при умножении числа 11 на двузначное число, они пользуются следующим алгоритмом. 37 х 11 = 37 х 10 + 37 х1 = 370 + 37 = 407. Однако автор письма приводит и более простой способ умножения в подобных случаях. Чтобы умножить двузначное число на 11, надо в произведении по краям числа записать цифры десятков и единиц соответственно, а в середине – сумму цифр данного числа. Например: 27 х 11 = 297. Как видим, в результате по краям стоят цифры 2 и 7, а «в середине» – сумма 2+7=9. Возьмем еще один пример, в котором двузначные числа больше предыдущих: 95 х 11 = 1045. Видно, что здесь этот прием не проходит, поэтому учитель предлагает другое правило. В тех случаях, когда сумма цифр двузначного числа больше 9, в середине пишут только цифру единиц, а к цифре десятков числа прибавляют единицу и записывают полученные число впереди произведения.
В нашем последнем примере, 4 – в середине, а перед ней – 10
Это воспринимается ими так же естественно и понятно, как свежий воздух или восход солнца. Уроки математики должны учить считать, должны тренировать мышление, разум и волю. Не только в начальной школе, но в средней и старшей. И тогда наши дети чаще будут выглядеть перед нами способными, уверенными и культурными. Ведь своя голова, согласитесь, все-таки надежней, чем самые современные калькуляторы.
Мы разработали различные части алгебраического термина, такие как: 9{2}\), который объединяет похожие термины ответов.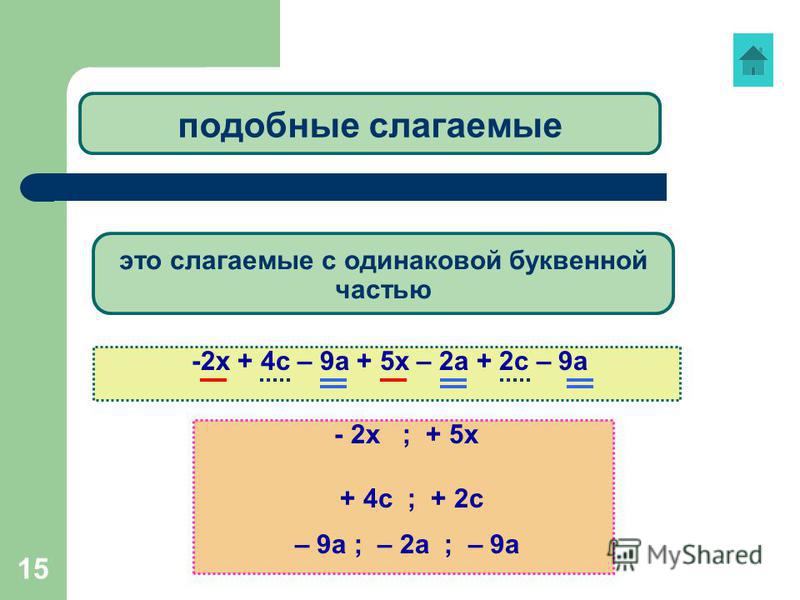
Как объединить подобные термины с операциями умножения, выглядит следующим образом:
Обычно это делается путем добавления или вычитания коэффициентов членов и оставления переменных без изменений. Например, если выражение содержит термины «3x» и «5x», эти термины можно объединить, чтобы сформировать упрощенное выражение «8x». Точно так же термины «2y» и «4y» могут быть объединены для образования «6y». Объединение одинаковых терминов может помочь упростить сложные алгебраические выражения и облегчить работу с ними.