А b 2 формула: Формулы сокращённого умножения

Содержание

таблица, примеры использования с ответами по алгебре для 7 класса

В математике есть формулы, которые просто необходимо держать всегда в памяти, так как большинство заданий ЕГЭ не могут обойтись без их применения. Это формулы сокращенного умножения. Изучать ФСУ начинают в 7-м классе. Тема считается непростой, но знание их поможет избежать утомительных вычислений и снизить вероятность ошибки.

Что такое формула сокращенного умножения

Из названия следует, что эти формулы позволяют проводить умножение, возведение в степень чисел и многочленов сокращенно, то есть быстрее при более компактной записи решения. Эти тождества служат для разложения многочленов на множители, упрощения выражений и приведения многочленов к стандартному виду.

Таблица формул сокращенного умножения

Для удобства мы собрали все формулы сокращенного умножения в одну таблицу. Ее можно использовать при выполнении домашних заданий по алгебре. При решении задач вы можете заменить буквы a и b числами, переменными или даже целыми выражениями.

Квадрат суммы	(a + b)²= a² + 2ab + b²
Квадрат разности	(a – b)²= a² – 2ab + b²
Разность квадратов	a² – b²=(a – b)·(a + b)
Сумма кубов	a³ + b³=(a + b)·(a² – ab + b²)
Разность кубов	a³ – b³=(a – b)·(a² + ab + b²)
Куб суммы	(a + b)³= a³ + 3a²b + 3ab² + b³
Куб разности	(a – b)³= a³ – 3a²b + 3ab² – b³

Формулы сокращенного умножения следует выучить. Без первой тройки формул о «тройке» и мечтать нельзя, без остальных — о «четверке» и «пятерке».

Как запомнить все эти, на первый взгляд, сложные формулы? Можно использовать метод аналогии. Присмотритесь к ФСУ внимательнее и вы увидите, что формула квадрата суммы очень похожа на формулу квадрата разности: здесь нужно запомнить только одно отличие — «плюс» меняется на «минус».

Также легко запомнить куб суммы и куб разности: их формулы практически одинаковы, снова поменялись только знаки. Сумма кубов и разность кубов тоже похожи, к тому же они напоминают первые две формулы.

И еще: научитесь правильно проговаривать формулы сокращенного умножения. Очень частая ошибка учеников — говорить «формула суммы квадратов». Такой формулы не существует!

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7-го класса по алгебре и добавим еще несколько формул.

Формула возведения в квадрат суммы трех, четырех и большего количества слагаемых:

(a₁+a₂+…+a_n)²=a₁²+a₂²+…+a_n−1²+a_n²+2·a₁·a₂+2·a₁·a₃+2·a₁·a₄+…+2·a₁·a_n−1+2·a₁·a_n+ +2·a₂·a₃+2·a₂·a₄+…+2·a₂·a_n−1+2·a₂·a_n+…+2·a_n−1·a_n.

Квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых. Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых x, y и z. Имеем: (x+y+z)²=x²+y²+z²+2·x·y+2·x·z+2·y·z. В частном случае при n=2 эта формула становится уже известной нам формулой квадрата суммы двух слагаемых.

Формула возведения в квадрат суммы трех, четырех и большего количества слагаемых:

aⁿ−bⁿ=(a−b)·(aⁿ⁻¹+aⁿ⁻²·b+aⁿ⁻³·b²+…+a²·bⁿ⁻³+a·bⁿ⁻²+bⁿ⁻¹)

Частными случаями этой формулы являются: разность квадратов (при n=2), разность кубов (при n=3) и сумма кубов (при n=3 и если b заменить на −b).

Важно!

При выполнении заданий необходимо знать некоторые свойства формул:

(a – b)²ⁿ = (b – a)²ⁿ, где n ∈ N
(a – b)²ⁿ⁺¹ = –(b – a)²ⁿ⁺¹, где n ∈ N

N – множество натуральных чисел

Примеры использования формул сокращенного умножения

Лучше всего формулы запоминаются на практике. Решайте как можно больше примеров, и все формулы запомнятся сами собой, а вы избавитесь от скучной и малоэффективной зубрежки. Итак, рассмотрим примеры и их решения с помощью формул сокращенного умножения.

Пример №1

Упростим выражение:

Применим формулу разности квадратов и получим:

Пример №2

Найдем значение выражения:

Применим формулы квадрата разности и квадрата суммы, раскроем скобки, приведем подобные слагаемые, сократим дробь и получим:

это интересно

Тригонометрические формулы

Таблица с основными тригонометрическими формулами, которые помогут при решении задач на ЕГЭ

ПОДРОБНЕЕ

Презентация на тему: «Познакомиться с формулами сокращённого умножения 1) (а + b) 2 = а 2 + 2аb + b 2 2) (а — b) 2 = а 2 — 2аb + b 2 3) (b –а ) 2 = а 2

4 Познакомиться с формулами сокращённого умножения 1) (а + b) 2 = а 2 + 2аb + b 2 2) (а — b) 2 = а 2 — 2аb + b 2 3) (b –а ) 2 = а 2 — 2аb + b 2 4) (-а — b) 2 = а 2 + 2аb + b 2

5 Вывести формулы сокращённого умножения Рассмотреть их применение при возведении в квадрат суммы или разности выражений Выработать навыки возведения в квадрат двучлена преобразуя его в многочлен стандартного вида Развивать логическое мышление и устный счёт Рассмотреть проблемную ситуацию для перехода к теме Разложение на множители с помощью формул квадрата суммы и квадрата разности

6 Устная работа Задание 1. Представьте в виде произведения и вычислите : а) 3², 7², 9². 3² = 3·3 = 9 ; 7² = 7·7 =…; 9² = …. б) 11², 25², 77². 11² = 11·11 = 121 ; 25² = 25·25 = … ; 77² =…. в) 103², 292², 195². 103² =…; 292² =…; 195² =….
7 Задание 2. Представьте в виде произведения и раскройте скобки : а)( 5 – а )²; б)( x + 10 )²; в)( y – 7 )²; г)( 9 + z )². а) ( 5 – а )² = ( 5 – а ) · ( 5 – а ) = 25 – 5а – 5a + а² = 25 – 10а + а² ; б) ( x + 10 )² = ( x + 10 ) · ( x + 10 ) = х² + 10х +10x = х² + 20х ; в) ( y – 7 )² = ( y – 7 ) · ( y – 7 ) = y²– 7y – 7у + 49 = … ; г) ( 9 + z )² = ( 9 + z ) · ( 9 + z ) = ….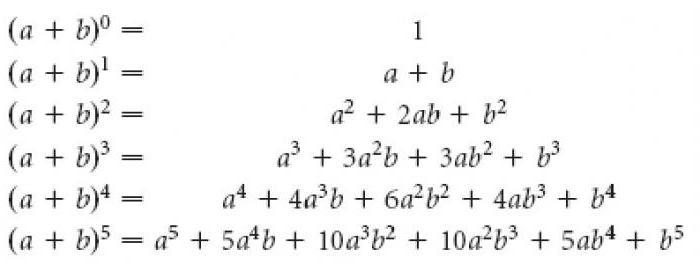

8 Задание 3. Представьте в виде произведения и вычислите : а) 199² = ( 200 – 1 ) ( 200 – 1 ) = 200² – ² = – = ; б) 702² = ( ) ( ) = 700² ² = =… ; в) 999² = ( 1000 – 1 ) ( 1000 – 1 ) =… ; г) 10,5² =….

9 Мы выполнили ряд примеров в которых, чтобы возвести в квадрат число или двучлен, раскрывали скобки, выполняя умножение.
702² = ( )·( ) = 700² ² = = Заметьте, что в каждом примере второго задания умножаются одинаковые двучлены и в результате из четырёх слагаемых два являются квадратами одночленов, а два их произведениями. Причем, удвоенное произведение имеет знак двучлена ( + или — ) ( y – 7 )² = ( y – 7 )·( y – 7 ) = y²– 7y – 7у + 7² = y²– 2·7y + 7² = y²– 14y + 49
10 Итак, если двучленом является сумма или разность одночленов, то можно сформулировать правила возведения их в квадрат. Квадрат суммы двух одночленов равен сумме их квадратов плюс их удвоенное произведение (а + b)² = a² + b² + 2ab = a² + 2ab +b² Квадрат разности двух одночленов равен сумме их квадратов минус их удвоенное произведение (а — b)² = a² + b² — 2ab = a² — 2ab +b²

11 Эти тождества называются формулами сокращённого умножения и если их запомнить, то можно с успехом использовать при возведении в квадрат суммы или разности двух выражений.
При использовании этих формул нужно знать, что (b –a)² = (a – b)² и (- a –b)² = (a + b)², так как (-а )² = а². Это можно проверить умножением двучленов при раскрытии скобок.
12 Запомните ! ( а + b )² — квадрат суммы двух выражений представим в виде произведения и раскроем скобки, выполнив умножение двучлена (а + b) на себя, приведём подобные слагаемые и получим многочлен стандартного вида а² + 2 а b + b² ( а + b )² = ( а + b )·( а + b ) = а² + а b + а b + b² = а² + 2 а b + b² Сократим запись! ( + )² = ( )² + 2· · + ( )² Перерисуйте схему в тетрадь !

13 (а – b )² — квадрат разности двух выражений представим в виде произведения и раскроем скобки, выполнив умножение двучлена (а — b) на себя, приведём подобные слагаемые и получим многочлен стандартного вида а² — 2 а b + b² ( а – b )² = ( а – b )·( а – b ) = а² — а b — а b + b² = а² — 2 а b + b² Сократим запись! ( — )² = ( )² — 2· · + ( )² Перерисуйте схему в тетрадь !

14 ( b – а )² — квадрат разности двух выражений представим в виде произведения и раскроем скобки, выполнив умножение двучлена ( b – а ) на себя, приведём подобные слагаемые и получим многочлен стандартного вида а² — 2 а b + b² ( b – а )² = (b – а)·(b – а) = b² — а b — а b + а² = b² — 2 а b + а² = а² — 2 а b + b² Так как, от перемены мест слагаемых значение суммы не изменяется, видно, что (b –a)² = (a – b)²

15 ( — а – b )² — квадрат разности двух выражений представим в виде произведения и раскроем скобки, выполнив умножение двучлена (- а — b) на себя, приведём подобные слагаемые и получим многочлен стандартного вида а² + 2 а b + b² (- а – b )² = (- а – b )·(- а – b ) = (- а)² + а b + а b + b² = а² + 2 а b + b², так как (- а )² = (-а )·(-а ) = а² Следовательно, (- a –b)² = (a + b)² = а² + 2 а b + b² Выучите эти формулы и учитесь их правильно читать ! (см. учебник стр.65 )
16 Отмечу, что на этих формулах основаны некоторые математические фокусы, позволяющие производить вычисления в уме. Что мы и попытались сделать в начале урока. 103² = ( )² = 100² + 2·100·3 + 2² = = ² = ( )² = 300² — 2·300·8+ 8² = = 94864
17 Но самый элегантный фокус связан с возведением в квадрат чисел, оканчивающихся цифрой 5. Приведём пример: 85² = (80 + 5)² =80² +2·80·5 + 5² = 80·( ) + 25 = 80· = = 7225 Заметьте, что для вычисления 85² достаточно было умножить 8 на 9 и к полученному результату приписать справа 25. Аналогично поступаем и в других случаях. Например, 105² = (10·11 =110 и к полученному результату приписали справа 25 ).
18 При использовании формул квадрата суммы и квадрата разности для раскрытия скобок в упрощении выражений, необходимо твердо установить какая формула используется и привести сумму или разность, возводимую в квадрат в соответствие с формулой.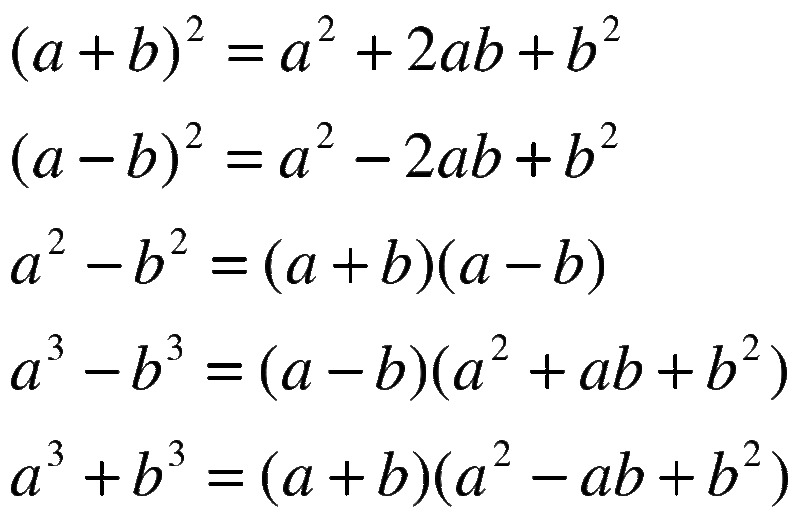 Например : а) (-3а + 5x)² = (5x – 3a)² = (5x)² — 2·5x·3a +(3a)² = 25x² – 30ax +9a² б) (-1,5x – 4,5y)² = (1,5x+4,5y)² = (1,5x)² + 2·1,5x·4,5y + (4,5y)² = …
19
20 А теперь попробуйте использовать полученные знания, выполнив в тетради задания по образцу : Задание 4. Используя формулы, раскройте скобки: Образец: а) (c + d)² = c² + 2cd + d² б) (m – n)² = m² — 2mn + n² в) (c + 8)² = c² +2·c·8 + 8² = c² + 16c + 64 г) (12 – p)² = 12² – 2·12 · p + p² = 144 – 24p + p² Выполните самостоятельно: а) (a + x)² = б) (b – y)² = в) (9 + b)² = г) (a – 5)² =
21 Задание5.Раскройте скобки: Образец : а)(- n + 8)²=(8 – n)²=8² –2·8·n+ n² =64 –16n+ n² б)(- m – 10)² = (m + 10)² = m² +2·m·10+10² = m² + 20m в) (- 3a + 5x)² = (5x – 3a)² = (5x)² – 2·5x·3a + (3a)² = 25x² – 30ax + 9a² г) (- 6y – 2z)² = (6y + 2z)² = (6y)² + 2·6y·2z + (2z)² = 36y² + 24yz + 4z² Выполните самостоятельно: а) (-x + 1)² = б) (-z – 3)² = в) (-3n + 4v)² = г) (-12z – 3t)² =
22 Задание 6. Используя формулы, раскройте скобки : Образец : Выполните самостоятельно: а) б) в)
23 Задание 7. Используя формулы квадрата суммы и квадрата разности, вычислите: Образец : Выполните самостоятельно: а) б) в) При решении можно использовать таблицу квадратов ( справочник стр. 179 )
24 Правильные ответы: Устная работа Задание 1. б) 121; 625; в) 11609; ; ; Задание 2. в) y² – 14y + 49 г) z + z² Задание 3. б) в) г) 110,25
25 Применение на практике: б) 2,25x² +13,5x y+20,25y² Практикум Задание 4. а) a² +2ax +x² б) b² – 2by + y² в) b + b² г) a² – 10a + 25 Задание 5. а) 1 – 2x +x² б) z² + 6z + 9 в) 16v ² -24nv + 9n² г) 144z² + 72tz + 9t²
26 Правильные ответы: Задание 6. а) б) в) Задание 7. а) б) в)
27 А теперь, ребята, я предлагаю вам ответить на вопрос: Можете ли вы применить полученные знания при выполнении заданий такого вида : Задание 1. Разложите на множители : а) m² + 2mk + k² ; б) a² — 10a + 25 ; Задание 2. Решите уравнение : а) 25 – 10a + a² = 0 ; б) x² – 6x + 9 = 0 ; Задание 3. Сократите дробь : ?
28 Ребята, понравился ли вам урок? Чем конкретно ? Какие моменты урока вызвали у вас затруднения ? Итак, сегодня на уроке вы познакомились с двумя формулами сокращенного умножения. Если вы заинтересовались, то остальные формулы можно найти в справочнике на странице 180. Домашнее задание : задачник — страница 73,
29
30
a — b доказательство формулы целого квадрата
@ : Домашний > Бесплатные рабочие листы для печати > Математика > (а — б) ²
Идентификатор: (a — b) ² = a ² + b ² — 2ab

Как достигается это тождество?
Посмотрим, как.
Взятие LHS тождества:
(a — b) ²
Это также может быть записано как:
= (а — б) (а — б)
Умножайте так же, как мы делаем умножение двух двучленов или используем F.O.I.L. методом и получаем:
= а(а — б) — б(а — б)
= a ² — ab — ab + b ²
При сложении подобных членов получаем:
= a ² — 2ab + b ²
Переставляя слагаемые, получаем:
= a ² + b ² — 2ab
Следовательно, мы получаем тождество, т.е. личность.

Пример 1: Решить (2x — 3y) ²
Решение: Это происходит следующим образом:
Данный многочлен (2x — 3y) ² представляет тождество (a — b) ²
Где а = 2х и б = 3у
Применяя значения a и b к тождеству, т. е. (a — b) ² = a ² + b ² — 2ab, получаем:
(2x — 3y) ² = (2x) ² + (3y) ² — 2(2x)(3y)
Разложим экспоненциальные формы и получим:
= 4x ² + 9 лет ² — 2(2x)(3y)
Решая процесс умножения, получаем:
= 4x ² + 9y ² — 12xy
Следовательно, (2x — 3y) ² = 4x ² + 9y ² — 12xy

Пример 2: Решить (6m — 9n) ²
Решение: Это происходит следующим образом:
Данный многочлен (6m — 9n) ² представляет тождество (a — b) ²
Где a = 6m и b = 9n
При применении значений a и b к тождеству, т. е. (a — b) ² = a ² + b ² — 2аб получаем:
(6м — 9н) ² = (6м) ² + (9н) ² — 2(6м)(9н)
Разложим экспоненциальные формы и получим:
= 36м ² + 81н ² — 2(6м)(9н)
Решая процесс умножения, получаем:
= 36м ² + 81н ² — 108мн
Следовательно, (6m — 9n) ² = 36m ² + 81n ² — 108mn
Пожалуйста, включите JavaScript для просмотра комментарии на базе Disqus.
prep4paper.com

Подпишитесь на нас: Facebook
Подпишитесь на нашу рассылку новостей
(A + B) ²
A ² — B ²
(A + B) ³
(A — B) ³
(A + B + C) ²
3 а ³ + б ³ + в ³ — 3абв
Линейные уравнения с одной переменной
Различные алгебраические формулы и свойства
Различные алгебраические формулы и свойства

Алгебра — это раздел математики, который имеет дело с числами и буквами. Значение чисел фиксировано, а буквы или алфавиты представляют неизвестные величины в алгебраической формуле. Ниже приведены некоторые различные алгебраические формулы и свойства.
Комбинация чисел, букв, факториалов, матриц и т. д. используется для формирования алгебраического уравнения или алгебраической формулы.
Вот список всех важных алгебраических формул:
a ² – b ² = (a – b)(a + b)
(a+b) 4 =1 2 a3 ² + 2AB + B ²
A ² + B ² = (A — B) ² + 2AB
(A — B) ² = A ²7 — 2AB + — 2AB + — 2 — 2 — 2 (A — B) ² = A
(A — B) ² = 2AB
б ²
(а + б + в) ² = а ² + б ² + в ² + 2аб + 2ас + 2бс
(а – б 0 – в) ² + b ² + c ² – 2ab – 2ac + 2bc
(a + b) ³ = a ³ + 3a ² b + 3ab ² + b ³ ; (a + b) ³ = a ³ + b ³ + 3ab(a + b)
(a – b) ³ = a ³ – 3a ² B + 3AB ² — B ³
A ³ — B ³ = (A — B) (A ² + AB + B ²)
A ³ 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 ). ³ = (а + b)(а ² – ab + b ² )
(а + b) ³ = а ³ + 3а ^{2 901 3ab 9 + 1 3ab 90 + 1 3ab 90 ³}
(а – б) ³ = а ³ – 3а ² б + 3аб ² – б ³
а (0013 4 = A ⁴ + 4A ³ B + 6A ² B ² + 4AB ³ + B ⁴)
(A — B) ⁴ = — — ⁴⁰²⁵²
(A — B) ⁴)
(A — B) ⁴⁰⁰¹⁴⁾
(A — B) ^{40014) 4A ³ B + 6A ² B ² — 4AB ³ + B ⁴)}
A ⁴ — B ⁴ = (A B) (A + B) (A ² + б ² )
а ⁵ – б ⁵ = (а – б)(а ⁴ + а ³ б + а ² б ² + ab ³ + b ⁴ )
प्राकृतिक संख्या (Natural Numbers) – a ⁿ – b ⁿ = (a – b)(a ^n-1 + ^N-2 +… + B ^N-2 A + B ^N-1)
सम संख्या (даже)- (n = 2K), A ^N + B ^N = A ^N + B ^N = A ^N + B ^N = A (a + b)(a ^n-1 – a ^n-2 b +…+ b ^n-2 a – b ^n-1 )
विषम संख् संख् संख् = 2k + 1), а ⁿ + b ⁿ = (a + b)(a ^n-1 – a ^n-2 b +…- b ^n-2 a + b ^n-1 )
( A + B + C +…) ² = A ² + B ² + C ² +… + 2 (AB + AC + BC +….
घात ंक नियम. )
1. (A ^M) (A ^N) = A ^M+N 2. (AB) ^M = A ^M B ^M 3. 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333н. ^м) ^N = A ^MN
Немного алгебраических свойств

ADDECTING ADIMITION + ADIND + ADIMIFITION + AD AID + AID + АД AISIMIFITION + IS AISIFITION + . , сумма выражения не меняется. В качестве элементов могут использоваться выражения или числа.
Коммутативное свойство умножения –
a x b = b x a
Произведение не меняется при изменении порядка множителей. В качестве этих факторов могут использоваться числа или фразы.
Ассоциативное свойство сложения –
(a + b)+ c = a + (b + c)
Свойство утверждает, что когда два или более числа объединяются для выполнения основного арифметического сложения, порядок цифры не имеют никакого отношения к результату.
Умножение обладает ассоциативным свойством:
(a x b) x c = a x (b x c)
Когда два или более множителя объединяются вместе в основном арифметическом умножении, порядок элементов не влияет на конечный результат . Кроме того, в этой ситуации круглые скобки используются для организации элементов.
Сложение и умножение обладают распределительными свойствами –
a × (b + c) = a × b + a × c и (a + b) × c = a × c + b × c
Распределительное Свойство утверждает, что умножение каждого элемента на одно слагаемое, а затем сложение и вычитание произведений — это то же самое, что умножение каждого элемента на одно слагаемое, а затем сложение и вычитание произведений.
No related posts.