A b c квадратное уравнение: Решение: Решить квадратное уравнение — Pascal ABC (23704)

Содержание

Решение квадратных уравнений в среде программирования Паскаль-ABC

Оглавление

1. ВВЕДЕНИЕ 3

2. ОСНОВНАЯ ЧАСТЬ 4

2.1. История квадратных уравнений и методы их решений 4

2.2. Решение квадратных уравнений по формуле корней 7

2.3. Интегрированная среда программирования Паскаль – ABC. Разработка и тестирование программы 10

3. ЗАКЛЮЧЕНИЕ 12

Список использованных источников 13

ВВЕДЕНИЕ

Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений, неравенств и их систем.

Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.

Практически все, что окружает современного человека-это все так или иначе связано с математикой. Последнее достижения в физике ,технике и информационных технологиях не оставляют никакого сомнения , что и в дальнейшем данная тенденция сохранится. Решение многих практических задач сводится к решению различных видов уравнений. При этом актуальным является использование ЭВМ и специального ПО при решении уравнений.

Цель работы: Разработка программы, нахождения корней уравнения второй степени в среде программирования Паскаль — АВС.

Гипотеза: Возможно ли создание программы, для нахождения корней уравнения второй степени в среде программирования Паскаль – АВС с полным выводом решения, а так же нахождение корней при отрицательном D.

Задачи:

ознакомиться с историей квадратных уравнений и методами их решения;
освоить приемы программирования в интегрированной среде Паскаль — АВС;
разработать алгоритм и блок-схему нахождения корней квадратных уравнений;
создать программу нахождения корней и протестировать ее.

Объект исследования: уравнения второй степени.

Предмет исследования: Паскаль — программа решения уравнений второй степени в среде программирования Паскаль — АВС.

Практическая значимость нашего проекта заключается в том, что результаты исследования могут быть использованы в курсе математики для проверки решения квадратных уравнений, а так же для запоминания алгоритма действий при решении.

Научная новизна исследования состоит в том, что:

— разработана универсальная программа, понятная каждому пользователю;

— охарактеризована структура программы по всем трём ветвям программирования;

— определены основные сложности и возможные проблемы при решение квадратных уравнений при отрицательном дискриминанте.

ОСНОВНАЯ ЧАСТЬ
1. История квадратных уравнений и методы их решений

Необходимость решать уравнения не только первой степени, но и второй еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков с развитием астрономии, военного дела и нуждами самой математики. Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся ко второму тысячелетию до н.э. это эпоха расцвета Вавилона и Древнего Египта.

Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются ,кроме неполных, и полные квадратные уравнения. Правила решения этих уравнений, изложенные в вавилонских источниках, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.[2]

Герон Александрийский — греческий математик и механик. Времени жизни предположительно отнесено ко второй половине I века н.э. «Метрика» Герона и извлеченные из нее «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике.

Среди содержащихся в «Метрике» сведений: формулы для площадей правильных многоугольников, формула Герона для расчета площади треугольника по длинам его сторон, правила численного решения квадратных уравнений, алгоритмы извлечения квадратных и кубических корней. В основном изложение в математических трудах Герона не рационально — правила часто не выводятся, а только показываются на примерах. Герон вывел формулу для решения квадратного уравнения умножением всех членов на а и прибавлением к обеим половинам уравнения выражения .[2]

Древнегреческие математики могли решать некоторые виды квадратных уравнений, сводя их решения к геометрическим построениям. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский(III в.н.э.). В дошедших до нас шести из 13 книг «Арифметика» содержит задачи с решениями. Способ решения полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились. Его трактат «Арифметика» содержит ряд задач, решаемых при помощи квадратных уравнений.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при составлении уравнений разных степеней.

Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году н.э. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому ученому Брахмагупте (около 598 г.). Брахмагупта изложил универсальное правило решения квадратного уравнения, приведенного к каноническому виду: ; притом предполагалось, что в нем все коэффициенты, кроме а, могут быть отрицательными. Сформулированное ученым правило по своему существу совпадает с современным.

Абу Абдуллах (или Абу Джафар) Мухаммад ибн Муса аль-Хорезми (ок. 783 — ок.850) — один из крупнейших средневековых персидских ученых IX века, математик, астроном, географ и историк.

Аль — Хорезме впервые представил алгебру как самостоятельную науку об общих методах решения линейных и квадратных уравнений, дал классификацию этих уравнений. Труды аль-Хорезми переводились с арабского на латинский язык, а затем на новые европейские языки. На их основе создавались различные учебники по математике. Аль-Хорезми известен, прежде всего, своей «Книгой о восполнении и противопоставлении» («Аль-китаб аль-мухтасар фи хисаб аль-джабр ва-ль-мукабала»), которая сыграла важнейшую роль в истории математики. От названия этой книги произошло слово «алгебра». Подлинный арабский текст утерян, однако содержание известно по латинскому переводу 1140 года английского математика Роберта Честерского. Рукопись, которую Роберт Честерский озаглавил как «Книга об алгебре и ал-мукабале» хранится в Кембредже. Другой перевод книги выполнен испанским евреем Иоанном Севильским. Задумывавшаяся как начальное руководство по практической математике «Китаб аль-джабр ….» в первой (теоретической) своей части начинается с рассмотрения уравнений первой и второй степени, а в двух заключительных разделах переходит к практическому применению алгебры.

Слово аль-джабр («восполнение») означало перенесение отрицательного члена из одной части уравнения в другую, а аль-мукабала («противопоставление») — сокращение равных членов в обеих частях уравнения.[2]

Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в книге «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи (он же Леонардо из Пизы или Леонардо Пизанский 1180-1240гг.). Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франция и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники 16 – 17 вв. и частично 18 веке.

В XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет (1540-1603)впервые вводит в обращение буквенные обозначения не только для не известных величин, но и для данных, то есть коэффициентов уравнения. Франсуа Виет — замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчесления. Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие эпохи Возрождения в математике, и подготовил почву для появления результатов Ферма, Декарта, Ньютона.

Общее правило решения квадратных уравнений, было сформулировано немецким математиком М.Штифелем (1487-1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет.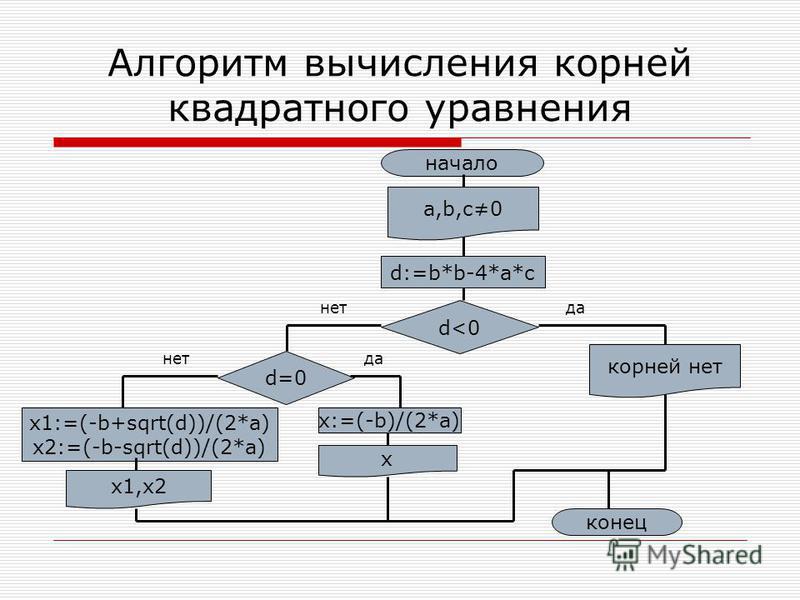 Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591г. Однако свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А. Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.[2]

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных равнений, которые позволяют очень быстро и рационально решать многие уравнения. Перечислим десять способов решения квадратных уравнений:

Метод выделения полного квадрата.
Решение квадратных уравнений по формулам.
Теорема Виета.
Свойства коэффициентов.
Разложение левой части на множители.
Способ «переброски».
Графический способ.
Метод монограммы.
Геометрические способы. Решение квадратных уравнений с помощью циркуля и линейки.
Тригонометрический способ.

Решение квадратных уравнений по формуле корней

Квадратное уравнение – алгебраическое уравнение общего вида

где x – свободная переменная; a,b,c – коэффициенты, причём a ≠ 0.[1]

Выражение называют квадратным трёхчленом.

Корень уравнения – это значение переменной x, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.[1]

Элементы квадратного уравнения имеют собственные названия:

а называют первым коэффициентом;
b называют вторым коэффициентом;
с называют свободным членом.

Приведенным называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент:

; , .

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

Квадратное уравнение с вещественными коэффициентами a, b, c имеет ровно два комплексных корня, о чём гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта , как один, так и оба корня могут не иметь мнимой части и быть вещественными:

при D

Приведем алгоритм решения квадратного уравнения по формуле корней.

Алгоритм – четкое описание последовательности действий, которые необходимо выполнить при решении задачи. Можно сказать, что алгоритм описывает процесс преобразования исходных данных в результат, т.к. для решения любой задачи необходимо:

Ввести исходные данные.
Преобразовать исходные данные в результат.
Вывести результат.

Разработка алгоритма решения задачи – это разбиение задачи на последовательно выполняемые этапы, причём результаты выполнения предыдущих этапов могут использоваться при выполнении последующих. При этом должны быть четко указаны как содержание каждого этапа, так и порядок выполнения этапов. Отдельный этап алгоритма представляет собой либо другую, более простую задачу, алгоритм решения которой известен (разработан заранее), либо должен быть достаточно простым и понятным без пояснений. Разработанный алгоритм можно записать несколькими способами:

Рассмотрим пример алгоритма на естественном языке:

Ввести в компьютер числовые значения переменных a, b, c.
Вычислить дискриминант по формуле .
Если D 0, то вычислить и напечатать значения и перейти к п. 6. иначе перейти к п. 4.
Если D = 0, то вычислить и напечатать значение и перейти к п. 6. иначе перейти к п. 5.
Вычислить действительную и мнимую части комплексных корней и напечатать значения пары комплексных корней и напечатать значения пары комплексно-сопряженных корней.
Прекратить вычисления.

Представим разработанный алгоритм в виде блок-схемы.

Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур – блоков, а связи между этапами (последовательность выполнения этапов) указывается при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19. 701-90.

Рис. 1 — Блок – схема решения квадратного уравнения с комплексно сопряженными корнями

Интегрированная среда программирования Паскаль – ABC. Разработка и тестирование программы

Наиболее распространенным в настоящее время языком программирования для компьютеров серии IBM PC Паскаль. Это язык высокого уровня, отличающийся простотой синтаксиса, структурированный и удобный для начального обучения программированию.

Учебная система программирования Паскаль – ABC представляет собой диалект стандартного языка Паскаль. Система создавалась на факультете математики, механики и компьютерных наук ЮФУ как учебная среда программирования.

Система Паскаль – ABC предназначена для обучения программированию на языке Паскаль и ориентирована на школьников и студентов младших курсов. По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близкими к стандартным и иметь богатые и современные библиотеке подпрограмм.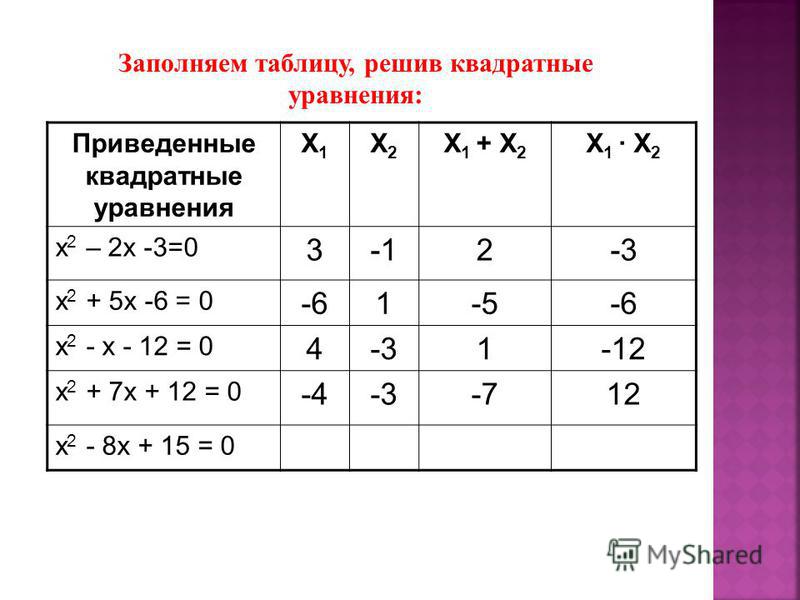

Система программирования Паскаль – ABC представляет собой единство компилятора языка программирования Паскаль и инструментальной программной оболочки, называемой средой. Среда предоставляет необходимые сервисные услуги и способствует повышению эффективности процессов разработки, отладки и испытаний программ, что облегчает труд программиста.

На рис. 2 представлен скриншот разработанной программы решения квадратных уравнений в среде Паскаль – ABC. Так как программа имеет три выбора, то протестируем каждую из ветвей.

Решим квадратное уравнение, имеющее два действительных корня (D 0):

Здесь a=1, b=3, c=-4, поэтому формула корней квадратного уравнения имеет вид:

Тогда вычисленные корни имеют вид:

Скриншот полученного результата представлен на рис. 3.

Рис. 2 – Скриншот разработанной программы решения квадратных уравнений в среде Паскаль – ABC

Рис. 3 – Скриншот результата вычислений действительных различных корней

Решим квадратное уравнение, имеющее один действительный корень (D = 0):

Здесь a=1, b=-4, c=4, поэтому формула корней квадратного уравнения имеет вид:

т.е:

Скриншот полученного результата представлен на рис.4.

Рис. 4 – Скриншот результата вычислений действительных различных корней

Решим квадратное уравнение, имеющее пару комплексно-сопряженных корней (D

Здесь a=1, b=-4, c=8, поэтому формула корней квадратного уравнения имеет вид:

Тогда вычисленные корни имеют вид:

Скриншот полученного результата представлен на рис. 5.

Рис. 5 – Скриншот результата вычислений двух комплексно-сопряженных корней

ЗАКЛЮЧЕНИЕ

В результате выполнения нашей научно-исследовательской работы достигнута цель исследования – разработана универсальная и понятная каждому пользователю программа нахождения корней уравнения второй степени в среде программирования Паскаль – ABC. Программа протестирована по всем трём ветвям вычислительного процесса: решения квадратного уравнения в случае двух действительных различных корней, случая двух действительных равных (кратных) корня и при наличии двух комплексно-сопряженных корней. При этом я ознакомился с историей квадратных уравнений и различными методами их решения. Освоил некоторые приемы программирования в интегрированной среде Паскаль – ABC (оператор выбор, вывод числа в форматном виде). Разработал алгоритм и блок-схему нахождения корней квадратного уравнения. Надеюсь, что полученные знания и навыки помогут мне в дальнейшем изучении языка программирования Паскаль, а так же привлечёт других учащихся к данному предмету информатики и программирования, а программа поможет учащимся 8-11 классов при проверки решения квадратного уравнения.

Список использованных источников

Энциклопедический словарь юного математика [Текст] / Сост. А. П. Савин, гл.ред. Б. В. Гнеденко, ред. В. Д. Белоусов и др. − 2-е изд., перераб. и доп. − М: Педагогика, 1989. – 352 с.
Смышляев В. К. Все о великих математиках [Текст] / В. К. Смышляев. − 2-е изд., перераб. и доп. − М: Марийское книжное издательство, 1977. − 224 с.
Википедия − свободная энциклопедия. Квадратное уравнение [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Квадратное_уравнение (Дата обращения: 3.03.2018)

Проектная работа по теме «Квадратные уравнения».

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ –

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА с. МЕЧЁТНОЕ

СОВЕТСКОГО РАЙОНА САРАТОВСКОЙ ОБЛАСТИ

Проектная работа по теме: «Решение квадратных уравнений различными способами. »

Работу выполнили : Ученики 10 класса.
Руководитель : Давыдова Е.В.

2018-2019уч. год

Содержание

1.Определение понятия «Квадратное уравнение»……………… 3

2.История квадратных уравнений…………………………………. 4

3.Неполные квадратные уравнения……………………………… 5

4.Способы решений квадратных уравнений
4.1.Разложение левой части уравнения на множители………… 5
4.2.Метод выделения полного квадрата………………………… 5
4.3.Решение квадратных уравнений по формуле………………. 5
4.4.Решение квадратных уравнений с помощью теоремы Виета. 7
4.5.Решение уравнений с помощью переброски……………… 8
4.6.Свойства коэффициентов квадратного уравнения…….…… 9

4.7. Геометрический метод ……………………………………… 10

4.8. Неполные квадратные уравнения ………………………….. 12

5.Дидактические материалы……………………………………….. 13
6. Литература………………………………………………………. 14

Определение понятия «Квадратное уравнение».

Квадратное уравнение — уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0), x — неизвестное.
Числа a.b.c называются коэффициентами квадратного уравнения.
a- называется первым коэффициентом;
b- называется вторым коэффициентом;
c- свободным членом
Приведенное квадратное уравнение — уравнение вида , первый коэффициент которого равен единице ().

Если в квадратном уравнении коэффициенты и не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение . Если один из коэффициентов или равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным.
Например, .

Значение неизвестного , при котором квадратное уравнение обращается в верное числовое равенство, называется корнем этого уравнения. Например, значение является корнем квадратного уравнения , потому что или — это верное числовое равенство.

Решить квадратное уравнение — это значит найти множество его корней.

Решить уравнения.

Пример 1. 2x·(x+3)=6x-x2.

Решение. Раскроем скобки, умножив 2х на каждое слагаемое в скобках:

2×2+6x=6x-x2; переносим слагаемые из правой части в левую:

2×2+6x-6x+x2=0; приводим подобные слагаемые:

3×2=0, отсюда x=0.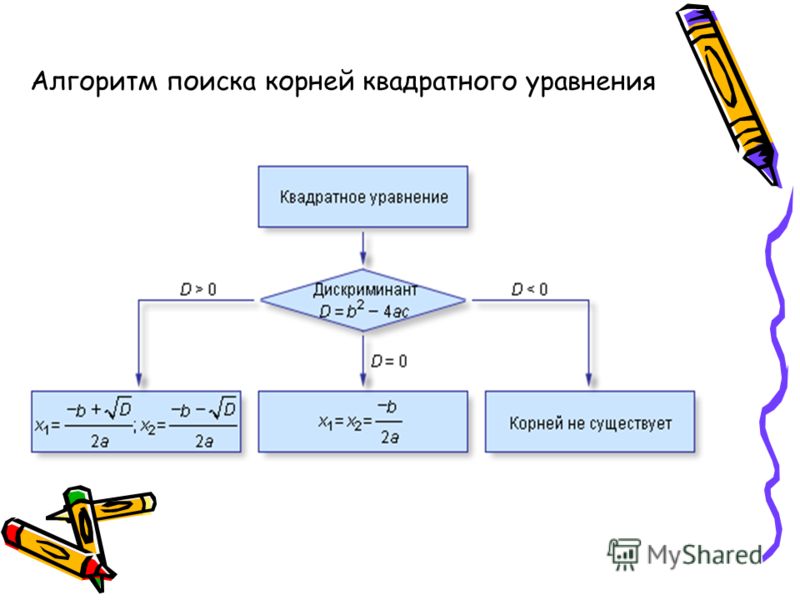

Ответ: 0

(Материал предоставила Иванова П.)

История Квадратных уравнений.

        Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.
        Древнеиндийский математик Баудхаяма в VIII столетии до н.э. впервые использовал квадратные уравнения в форме ax² = c и ax² + bx = c и привел методы их решения.
        Вавилонские математики примерно с IV века до н.э. и китайские математики примерно со II века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения.
        Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был Брахмагупта (Индия, VII столетие нашей эры). (Материал подготовила Яковлева Ю. ).

СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

Разложение левой части уравнения на множители.

(Материал предоставила Никулина Д.)

1. Решим уравнение х2 + 10х – 24 = 0.

Разложим левую часть уравнения на множители:

х2 + 10х – 24 = х2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).

Следовательно, уравнение можно переписать так: (х + 12)(х – 2) = 0.

Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = — 12. это означает, что числа 2 и – 12 являются корнями уравнения х2 + 10х – 24 = 0.

Ответ: -12; 2.

Метод выделения полного квадрата.

(Материал предоставила Сергеева М.)

Выделение полного квадрата — это такое тождественное преобразование,
при котором заданный трехчлен представляется в виде (a±b)2(суммы или разности квадрата двучлена и некоторого числового или буквенного выражения).

Пример:
Решить уравнение x² + 14x + 45 = 0
Решение:
Разложим многочлен на множители методом выделения полного квадрата.
Для применения первой формулы необходимо получить выражение
x²+ 14x + 49 = 0.
Поэтому прибавим и отнимем от многочлена x² + 14x + 45 число 4, чтобы выделить полный квадрат
x² + 14x + 45+4−4 =0

(x² + 14x + 45+4)−4=0

(x² + 14x + 49)−4=0

(x+7)2−4=0
Применим формулу «разность квадратов» a²−b²= (a−b)⋅(a+b)
(x+7)2 − 22=0

( x + 7 – 2 ) ( x + 7 + 2 ) = 0

( x + 5 ) ( x + 9 ) = 0

x + 5 = 0, x + 9 = 0

x1 = – 5, x2 = – 9 Ответ: –9;–5.

Решение квадратных уравнений по формуле.

(Материал предоставил Чжен Д.)

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.

Эту формулу надо знать наизусть. Важно знать: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

x2 − 8x + 12 = 0;
5×2 + 3x + 7 = 0;
x2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

Задача. Решить квадратные уравнения:

x2 − 2x − 3 = 0;
15 − 2x − x2 = 0;
x2 + 12x + 36 = 0.

Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Решение уравнений с помощью теоремы Виета.

(Материал предоставил Сисекенов С.)

Теорема Виета (точнее, теорема, обратная теореме Виета) позволяет сократить время на решение квадратных уравнений. Только надо уметь ею пользоваться. Как научиться решать квадратные уравнения по теореме Виета? Это несложно, если немного порассуждать.

Сейчас мы будем говорить только о решении по теореме Виета приведенного квадратного уравнения. Приведенное квадратное уравнение — это уравнение, в котором a, то есть коэффициент перед x², равен единице. Не приведенные квадратные уравнения решить по теореме Виета тоже можно, но там уже, как минимум, один из корней — не целое число. Их угадывать сложнее.
Теорема, обратная теореме Виета, гласит: если числа x1 и x2 таковы, что
x1 + x2 = -p

x1 * x2 = q

то x1 и x2 — корни квадратного уравнения x2 + px + q = 0
При решении квадратного уравнения по теореме Виета возможны всего 4 варианта. Если запомнить ход рассуждений, находить целые корни можно научиться очень быстро.

I. Если q — положительное число,

это означает, что корни x1 и x2 — числа одинакового знака (поскольку только при умножении чисел с одинаковыми знаками получается положительное число).

I.a. Если -p — положительное число, (соответственно, p

I.b. Если -p — отрицательное число, (соответственно, p>0), то оба корня — отрицательные числа (складывали числа одного знака, получили отрицательное число).

II. Если q — отрицательное число,

это значит, что корни x1 и x2 имеют разные знаки (при умножении чисел отрицательное число получается только в случае, когда знаки у множителей разные). В этом случае x1 и x2 является уже не суммой, а разностью (ведь при сложении чисел с разными знаками мы вычитаем из большего по модулю меньшее). Поэтому x1 + x2 показывает, на сколько одно отличаются корни x1 и x2, то есть, на сколько один корень больше другого (по модулю).

II.a. Если -p — положительное число, ( то есть p

II. b. Если -p — отрицательное число, (p>0), то больший (по модулю) корень — отрицательное число.

Рассмотрим решение квадратных уравнений по теореме Виета на примерах.

Решить приведенное квадратное уравнение по теореме Виета:

1). x2 -7x + 12 = 0
Здесь q=12>0, поэтому корни x1 и x2 — числа одного знака. Их сумма равна -p=7>0, поэтому оба корня — положительные числа. Подбираем целые числа, произведение которых равно 12. Это 1 и 12, 2 и 6, 3 и 4. Сумма равна 7 у пары 3 и 4. Значит, 3 и 4 — корни уравнения.
Ответ: 3; 4.

2). х2 + 10x + 16 = 0

В данном примере q=16>0, значит, корни x1 и x2 — числа одного знака. Их сумма

-p=-10

Ответ: -8; -2.

3)x2 — 2x — 15 = 0

Здесь q=-150, то большее число положительно. Значит, корни 5 и -3.

Ответ: -3; 5.

4) x2 + 5x — 36 = 0

q= -36

Ответ: -9; 4.

Решение квадратных уравнений способом переброски.
(МАТЕРИАЛ ПРЕДОСТАВИЛА ЯНЮШКИНА П.)

Рассмотрим квадратное уравнение

ах2 + bх + с = 0, а ≠ 0.

Умножая обе его части на а, получаем уравнение

а2 х2 + а bх + ас = 0.

Пусть ах = у, откуда х = у/а ; тогда приходим к уравнению

у2 + by + ас = 0,

равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = и х1 = . При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Примеры :

Решим уравнение 2х2 – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у2 – 11y +30 = 0.

Согласно теореме Виета

Ответ: 2,5;3.

Свойства коэффициентов квадратного уравнения
(Материал предоставил Денисов Д..)

Свойство 1
Дано квадратное уравнение ax² + bx + c = 0. Если a + b + c = 0 (сумма коэффициентов), то
x1 = 1, x2 = c/a

Свойство 2
Дано квадратное уравнение ax² + bx + c = 0.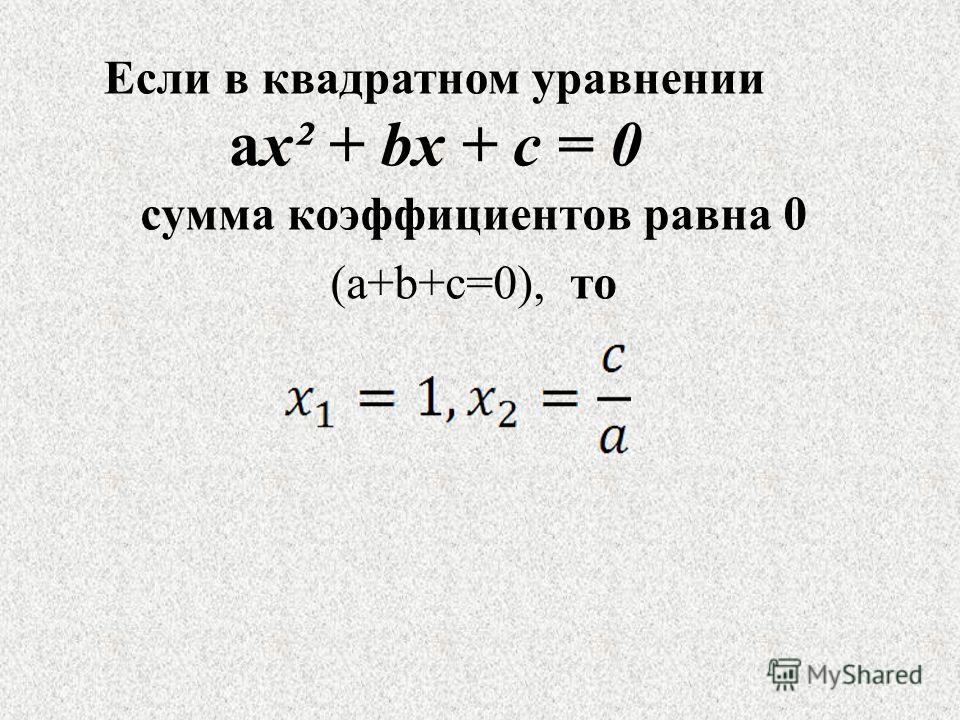 Если a — b + c = 0 (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то
x1 = -1, x2 = -c/a

Пример:
341x² + 290x — 51 = 0
Решение:
Здесь, a = 341, b = 290, c = -51.
Проверим удовлетворяют ли коэффициенты условию
свойства 2
341 — 51 = 290. Получим а + с = b. Следовательно, мы
можем воспользоваться свойством 2.
x1 = -1 и х2 = 51/341
Ответ: -1; 51/341.
Свойство 3
Если в квадратном уравнении ax² + bx + c = 0. Коэффициент b представлен в виде 2k, т.е. является четным числом, то формулу корней уравнения можно переписать в более простом виде
D = (b/2)2 + a*c

Пример:
3x² + 2,2x — 0,16 = 0
Решение:
Коэффициент b = 2,2
D = 1,12 + 3 * (-0,16) = 1,69
x1.2= (-1,1 ± 1,3)/3

Квадра́тное уравне́ние — алгебраическое уравнение общего вида
ax²+bx+c=0, ax²+bx+c=0,
где x — неизвестное, a, b,c — коэффициенты.
Выражение ax²+bx+c называют квадратным трёхчленом.
Корень — это значение переменной x, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство.
Элементы квадратного уравнения имеют собственные названия.
a называют первым или старшим коэффициентом,
b называют вторым, средним или коэффициентом при x,
c называют свободным членом.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент a.

x²+px+q=0,
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Геометрический способ решения квадратных уравнений.
(Материал предоставил Платонова К)

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

* Примеры.

1) Решим уравнение х2 + 10х = 39.

В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис. 15).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4* 2,5х = 10х) и четырех пристроенных квадратов (6,25* 4 = 25), т.е. S = х2 + 10х + 25. Заменяя х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у2 + 6у — 16 = 0.

Решение представлено на рис. 16, где

у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.

Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис. 16).

3) Решить геометрически уравнение у2 — 6у — 16 = 0.

Преобразуя уравнение, получаем у2 — 6у = 16.

На рис. 17 находим «изображения» выражения у2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16, получаем: (у — 3)2 = 16 + 9, т.е.

у — 3 = ±

или у — 3 = ± 5, где у1 = 8 и у2 = — 2.

Неполные квадратные уравнения.

(Материал предоставила Иванова П.)

Неполные квадратные уравнения бывают трёх видов.
1)Неполные квадратные уравнения, в которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0. Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю.
2)Неполные квадратные уравнения, в которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0). Если знаки a и c — разные, уравнение имеет два корня.
3)Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0. Уравнение такого рода имеет единственный корень x=0

II. Неполные квадратные уравнения, к которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0).

Раскладываем левую часть уравнения по формуле разности квадратов:

Это уравнение — типа «произведение равно нулю».приравниваем к нулю каждый множитель:

Ответ: 7; -7.

Ответ: 2,25; -2,25.

III. Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0.

Пример 1. 2x·(x+3)=6x-x2.

Решение. Раскроем скобки, умножив 2х на каждое слагаемое в скобках:

2×2+6x=6x-x2; переносим слагаемые из правой части в левую:

2×2+6x-6x+x2=0; приводим подобные слагаемые:

3×2=0, отсюда x=0.

Ответ: 0.

Дидактические материалы.

1. Решите квадратное уравнение, разлагая его левую часть на множители:

а) х2 – х = 0;

б) х2 + 2х = 0;

в) 3 х2 – 3х = 0

2. Решите уравнения по формуле:

а) 2х2 – 5х + 2= 0

б) 6х2 + 5х + 1=0

в) 3х2 – 7х – 1 = 0

3. Решите уравнения, используя метод «переброски»:

2х2 – 9х +9 = 0
3х2 +11х +6 = 0
4х2 +12х + 5 = 0

4. Решите уравнения, используя свойства коэффициентов:

5х2 – 7х + 2 = 0
3х2 + 5х – 8 = 0
11х2 + 25х – 36 = 0

5. Решите графически уравнения:

1) х2 – х – 6 = 0;

2) х2 – 4х + 4 = 0
3) х2 + 4х +6 = 0;

ЛИТЕРАТУРА

https://infourok.ru/issledovatelskaya-rabota-po-teme-reshenie-kvadratnih-uravneniy-razlichnimi-sposobami-571792.html

http://www.grandars.ru/student/vysshaya-matematika/kvadratnoe-uravnenie.html

https://multiurok.ru/files/issledovatelskaia-rabota-10-sposobov-resheniia-kva. html

https://www.berdov.com/docs/equation/quadratic_equations

http://kvadur.info

Математика. Алгебра. Функции. Анализ данных. 8 класс: Учебник для общеобразовательных учреждений / Г. В. Дорофеев и др. – М.: Дрофа, 2004

Гусев В. А., Мордкович А. Г. Математика: Справочные материалы:

Книга для учащихся. – М.: Просвещение, 1988

Глейзер Г. И. История математики в школе. – М.: просвещение, 1982

Брадис В. М. Четырехзначные математические таблицы для средней школы. – м., просвещение, 1990

Окунев А. К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. – М.: Просвещение, 1972

Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. М., Квант, №4/72. С.34.

Дидактические материалы по алгебре.

Квадратные уравнения (abc-формула)

Квадратное уравнение имеет следующий общий вид:

Конечно имеем , иначе уравнение было бы не квадратным, а линейным.

В разделе Квадратные уравнения (разложение на множители) мы объяснили, при каких условиях мы можем решить квадратное уравнение с помощью факторизации. Преимущество этого метода в том, что он может быстро найти решение. Однако этот способ не всегда возможен и также требует определенных навыков.

Если у вас нет навыков или вы не хотите применять этот метод , есть другой подход, который всегда работает и широко известен как -формула. Обычно для этого требуются дополнительные расчеты. С другой стороны, решение гарантировано.

Решение квадратного уравнения дает не более двух (действительных) решений: или :

Здесь мы использовали обозначение, но мы также можем написать:

или:

не более двух решений. Это зависит от значения дискриминанта , т. е. формулы под корневым обозначением:

Мы различаем три случая:

В этом случае решения и различны, и тогда мы говорим, что уравнение имеет два решения.

В этом случае решения и равны, и тогда мы говорим, что уравнение имеет только одно решение (на самом деле 2 совпадающих решения).

В этом случае уравнение не имеет действительных решений, и тогда мы говорим, что уравнение не имеет решений.
Приведем ряд примеров.

Пример 1

Решение:

Мы немедленно заметили, что левая сторона может быть факторирована:

и уравнение:

имеет следующее решение:

из

Для сравнения, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение, сравнение. мы также решаем это уравнение с -формулой:

и находим, как и ожидалось:

из

Когда мы используем -формулу? Когда у вас будет достаточно навыков, чтобы попробовать метод факторизации, вы предпочтете его, хотя знаете, что это не всегда вам поможет. Если этот метод не дает результатов достаточно быстро, вам следует применить -формулу.

Пример 2

Решите:

В этом случае не просто использовать факторизацию (и если вы разделите обе части на, вы получите дроби в виде коэффициентов). Таким образом, мы должны применить -формала:

и найти следующие решения:

или

Пример 3

Решение:

Применение -формала. решение есть. У уравнения два совпадающих решения, иногда говорят, что уравнение имеет только одно решение.

Обратите внимание, что решение также можно найти, применив следующий специальный продукт:

Применяя эту формулу к приведенному выше уравнению, мы замечаем, что en . Тогда мы можем написать:

Пример 4

Решить:

Если мы применим -формулу, мы немедленно заметим, что:

Таким образом, уравнение не имеет решения.

Пример 5

Решите:

Это уравнение не имеет стандартной общей формы и должно быть переписано. Убираем скобки:

и факторизуем результат:

Решения:

или

Формула дает тот же результат.

ABC формула — Photomath

Изучите квадратные уравнения

Вы уже знаете о важности ваших A-B-C, но вы, вероятно, только сейчас изучаете значение формулы ABC. К сожалению, для этой азбуки нет запоминающейся песни (но если вы ее напишете, дайте нам знать!).

На самом деле это не так сложно, как вы думаете, особенно если разбить его на части. 92-4ac}}{2a}$$

Чем так полезна формула ABC?

Формула ABC обеспечивает более простой и удобный способ решения квадратных уравнений.

Вот что делает этот метод отличным:

Ваша цель при решении уравнения — изолировать переменную с одной стороны. Это легко, когда переменная (также известная как неизвестная) не возводится ни в какую степень — но это не так в квадратных уравнениях, где переменная возводится во вторую степень.

Другие методы решения квадратных уравнений (разложение на множители, завершение квадрата и т. д.) требуют гораздо большего количества манипуляций и поэтому могут очень быстро привести к путанице.

Однако формула ABC намного чище и эффективнее. Все, что вам нужно сделать, это определить коэффициенты, вставить их в формулу и оценить выражение!

Видите, почему мы такие большие фанаты?

Как использовать формулу ABC

Теперь, когда мы знаем, что такое формула ABC и почему она полезна, пришло время увидеть ее в действии! Давайте вместе разберемся с проблемой.

Пример

Решим это квадратное уравнение по формуле ABC: 92-4\cdot2\cdot3}}{2\cdot2}$$

Теперь оценим мощность. Помните: отрицательное основание, возведенное в четную степень, равно положительному.

$$x=\frac{7\pm \sqrt{49-4\cdot2\cdot3}}{2\cdot2}$$

Вычислить произведение чисел под квадратным корнем и в знаменателе.

$$x=\frac{7\pm \sqrt{49-24}}{4}$$

Вычтите числа под квадратным корнем.

$$x=\frac{7\pm \sqrt{25}}{4}$$

Время извлекать квадратный корень!

$$x=\frac{7\pm 5}{4}$$

Напишите решения, одно со знаком $$+$$ и одно со знаком $$-$$.

$$x=\frac{7+ 5}{4}$$

$$x=\frac{7- 5}{4}$$

Теперь мы просто выполним основные операции для расчета нашего конечного решения.

$$x=3$$

$$x=\frac{1}{2}$$

Вот они — наши окончательные решения! Как видите, уравнение имеет два решения. Мы можем проиндексировать их, если захотим, вот так:

$$x_1=\frac{1}{2},x_2=3$$

Это было не так уж и плохо, правда? Теперь, когда мы рассмотрели подробный пример, давайте рассмотрим весь процесс в целом, чтобы вы могли научиться использовать его с любая проблема :

Резюме исследования

Перепишите квадратное уравнение в стандартной форме (если это еще не сделано).
Определите коэффициенты.
Подставьте коэффициенты в формулу ABC.
Упростите выражение, чтобы получить решения вашего квадратного уравнения. 92+х=0$$

Решения:

$$x_1=-6, x_2=5$$
$$t_1=-\frac{1}{2}, t_2=2$$
$$x_1=-5, x_2=5$$
$$x_1=-\frac13, x_2=0$$

Если вы все еще боретесь с процессом решения, ничего страшного! Несколько раз спотыкаться полезно для обучения. Если вы слишком застряли или заблудились, отсканируйте проблему с помощью приложения Photomath, и мы проведем вас на другую сторону!

Вот краткий обзор того, что вы увидите:

00:00 / 00:00

Дополнительные баллы

Контекст очень важен для получения всестороннего опыта обучения. Если вам интересно узнать больше, узнайте, как математики изначально вывели квадратичную формулу (спойлер: это очень круто!).