| Дата: 20.11.2014 Таблица производных.Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств. Это знакомство позволит: Понимать суть несложных заданий с производной; Успешно решать эти самые несложные задания; Подготовиться к более серьёзным урокам по производной. Сначала — приятный сюрприз.) Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний! Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. Приступим к знакомству?) Термины и обозначения.В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках. Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная. Дифференцирование — действие над функцией. Производная — результат этого действия. Так же, как, например, сумма — результат сложения. Или частное — результат деления. Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т. Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее. Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…) Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем. Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного. Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. 1. Таблица производных (формулы дифференцирования). 3. Производная сложной функции. Начнём по порядку. В этом уроке рассмотрим таблицу производных. Таблица производных.В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п. Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.) Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету… Рассмотрим несколько примеров: 1. Найти производную функции y = x 3 Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат: (x 3) » = 3·x 3-1 = 3x 2 Вот и все дела. Ответ: y» = 3x 2 2. Найти значение производной функции y = sinx в точке х = 0. Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция. По табличке находим синус и соответствующую производную: y» = (sin x)» = cosx Подставляем ноль в производную: y»(0) = cos 0 = 1 Это и будет ответ. 3. Продифференцировать функцию: Что, внушает?) Такой функции в таблице производных и близко нет. Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает… Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается! Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем: Ответ: y» = — sin x . Пример для продвинутых выпускников и студентов: 4. Найти производную функции: Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так: А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем: Вот и всё. Это будет ответ. Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования. |
Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по
nx. Формулы производных высших порядков.
Для этого нам понадобятся следующие факты:
Производная от числа равна нулю 
Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
Производная переменной под корнем произвольной степени 
И всё. Это радует.
п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
Вот они эти три кита:
Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
По формуле косинуса двойного угла:
64. Вывод табличных производных. Производная постоянной.
При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :
Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения.
Производная степенной функции.
Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем
пользоваться определением производной.
Запишем предел отношения приращения
степенной функции к приращению
аргумента:
Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:
Следовательно,
Этим доказана формула производной степенной функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним подстановку в исходный предел:
Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:
Производная логарифмической функции.
Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:
Как
Вы заметили, при доказательстве
преобразования проводились с использованием
свойств логарифма.
Равенство справедливо
в силу второго замечательного предела.
Производные тригонометрических функций.
Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.
По определению производной для функции синуса имеем .
Воспользуемся формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким образом, производная функции sin x есть cos x.
Абсолютно аналогично доказывается формула производной косинуса.
Следовательно, производная функции cos x есть –sin x.
Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.
Производная обратной функции.
Перед началом изучения данной статьи рекомендуем вспомнить определение и свойства обратной функции.
Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, — это производная функции f(x) по x.
Теперь сформулируем правило нахождения производной обратной функции.
Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x), то в точке существует конечная производная обратной функции g(y), причем . В другой записи .
Можно это правило переформулировать для любого x из промежутка , тогда получим .
Давайте проверим справедливость этих формул.
Найдем
обратную функцию для натурального
логарифма (здесь y –
функция, а x—
аргумент). Разрешив это уравнение
относительно x,
получим (здесь x –
функция, а y –
ее аргумент).
То есть, и взаимно
обратные функции.
Из таблицы производных видим, что и .
Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:
Как видите, получили такие же результаты как и в таблице производных.
Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.
Начнем с производной арксинуса.
Для обратной функцией является . Тогда по формуле производной обратной функции получаем
Осталось провести преобразования.
Так как областью значений арксинуса является интервал , то (смотрите раздел основные элементарные функции, их свойства и графики). Поэтому , а не рассматриваем.
Следовательно, . Областью определения производной арксинуса является промежуток (-1; 1).
Для арккосинуса все делается абсолютно аналогично:
Найдем производную арктангенса.
Для обратной функцией является .
Выразим
арктангенс через арккосинус, чтобы
упростить полученное выражение.
Пусть arctgx = z, тогда
Следовательно,
Схожим образом находится производная арккотангенса:
чему равна, формула, примеры решения задач
Понятие производной, чему равна Х* корня из Х
Определение
Производной функции \(y=f(x)\) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует).
Говоря проще, производная есть скорость изменения функции в конкретной точке. Скорость оценивается с помощью вычисления отношения изменения функции \(\triangle y\) к изменению аргумента \(\triangle x\). Данное отношение рассматривается в пределе, где \(\triangle x\rightarrow0.\)
Обычно производную обозначают как f'(x).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
{-\frac12}=\frac1{2\sqrt g}\)
\(g'(x)=3\)
Комбинируем найденные произведения по правилу дифференцирования сложных функций.
Таким образом:
\(y’=\frac1{2\times\sqrt g}\times3=\frac1{2\sqrt{(3x+2)}}\times3=\frac3{2\times\sqrt{(3x+2)}}\)
Ответ: \(y’=\frac3{2\times\sqrt{(3x+2)}}.\)
С помощью упрощенного правила дифференцирования корня
Определение
Производная квадратного корня, под которым стоит переменная или фукнция, будет равна производной подкоренного выражения, поделенной на удвоенный первоначальный квадратный корень
или
\(f'(x)=\frac{u’}{2\times\sqrt u},\) если \(f(x)=\sqrt u\).
Рассмотрим на примере производной функции \(\sqrt{5x+2}.\)
В ней подкоренным выражением будет \((5x+2)\), а его производной — \(5\).
Вспомним определение производной корня. Получим:
\(f(x)=\sqrt{5x+2}\)
\(f'(x)=\frac5{2\times\sqrt{5x+2}}\)
По правилу дифференцирования квадратных корней нужно было делить числитель на удвоенное произведение первоначального корня, что мы и сделали для получения ответа.
Примеры решения задач по теме «Производная корня»
Задача 1
Найти производную функции \(y(x)=2\sqrt x.\)
Решение
\(y'(x)=(2\sqrt{x)}’\)
Применим уже изученные правила. Получим:
\(y'(x)=2\times(\sqrt{x)’}=2\times\frac1{2\times\sqrt x}=\frac1{\sqrt x}\)
Ответ: \(y'(x)=\frac1{\sqrt x}.\)
Задача 2
Найти производную функции \(y(x)=\sqrt{2x}.\)
Решение
\(y'(x)=(\sqrt{2x})’\)
Применим уже изученные правила. Получим:
\(y'(x)=(\sqrt{2x})’=\frac1{2\times\sqrt{2\times x}}\times(2x)’\)
\(y'(x)=\frac1{2\times\sqrt{2\times x}}\times2\times\;(x)’=\frac1{\sqrt{2x}}\times1=\frac1{\sqrt{2x}}\)
Ответ: \(y'(x)=\frac1{\sqrt{2x}}.\)
Задача 3
Попробуем решить производную частного случая \(x\times\sqrt x\).
Найти производную от \(x\times\sqrt x.\)
Решение
Применим уже изученные правила и получим:
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | 92)|||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производные экспоненциальной и логарифмической функций
Подход
к
C A L C U L U S
Содержание | Главная
14
Производная от ln x
Производная e с функциональным показателем
г.
Производная от ln u ( x )
Общее силовое правило
В СИСТЕМЕ НАТУРАЛЬНЫХ ЛОГАРИФМОВ в качестве основания используется число, называемое e; это система, которую мы используем во всей теоретической работе. (В следующем уроке мы увидим, что e приблизительно равно 2 . 718.) Система натуральных логарифмов отличается от системы десятичных логарифмов, в основе которой лежит 10 и которая используется в большинстве практических работ.
г.Мы обозначаем логарифмическую функцию с основанием e как «ln x ».
ln x = log e x .
y = ln x подразумевает e y = x .
Другими словами, эта логарифмическая функция —
у = пер х
— имеет обратную экспоненциальную функцию,
г.у = е х .
Вот обратные соотношения:
ln e x = x и e ln x = x .
А логарифм самого основания всегда равен 1:
ln е = 1.
(Тема 20 предварительного исчисления.)
Функция y = ln x является непрерывным и определяется для всех положительных значений x . Оно будет подчиняться обычным законам логарифмов:
1 . ln ab = ln a + ln b .
| 2 . номер | а б | = ln a − ln b . |
3 . ln a n = n ln a .
(Тема 20 предварительного исчисления.)
Как и все правила алгебры, они подчиняются правилу симметрии.
Например,
n ln a = ln a n .
Производная от ln x
Теперь применим определение производной, чтобы доказать:
г.
| д дх | л х | = | 1 х |
В ходе доказательства будет значительно упрощено, если мы определим основание системы натуральных бревен, число, которое мы называем e, как следующий предел:
г.Предел в доказательстве будет иметь такой же вид.
Позже мы будем называть переменную x , а не v . А на следующем уроке, при замене переменной с на на , следует знакомое определение.
Вот коэффициент разности:
| по 2-му закону; | |||
| = | при умножении на x / x ; | |
| = | в соответствии с 3-м законом. | |
Теперь мы принимаем предел, поскольку ч приближается к 0.
| = |
| Ограничение не распространяется на | 1 х | , потому что ч это переменная |
| приближается к 0. | 1 х | – постоянный коэффициент. |
Теперь мы определим этот предел как основание натуральных логарифмов, число, которое мы будем называть e. (Этот предел указан выше, с v = ; когда 0, 0.)
Следовательно,
| = | ||
| = | ||
| = | ||
Что мы и хотели доказать.
Чтобы убедиться, что этот предел —
— то есть e существует, поскольку x приближается к 0, вот график
y имеет определенное значение, так как x приближается к 0. И в следующем уроке мы увидим, что это приблизительно 2,718.
Производная от e x
Теперь докажем:
г.| д дх | е х | = e x |
«Производная от е х по отношению к х
равно е x ».
С г = е x является обратным y = ln x , мы можем получить его производную следующим образом:
| г | = | е х | ||
| подразумевает | п г | = | ln e x | = x . |
Следовательно, взяв производную от обеих сторон относительно x и применив цепное правило к ln y :
| = | 1. | ||
| г’ | = | и . | |
| То есть | |||
| = | e x . | ||
e x является собственной производной.
Что это значит? Это подразумевает значение экспоненциального роста. Ибо мы говорим, что количество растет «экспоненциально», когда оно растет в 9 раз.1823 скорость , что пропорционально его размеру. Чем он больше в любой момент времени, тем быстрее он растет в это время. Типичным примером является население. Чем больше будет индивидуумов, тем больше будет рождений и, следовательно, тем больше скорость изменения населения — число рождений в каждом году.
Все экспоненциальные функции имеют вид a x , где a — основание. Следовательно, сказать, что скорость роста пропорциональна его размеру, значит сказать, что производная a x пропорционально a x .
| д дх | а x | = тыс. лет назад x | , |
, где k — константа пропорциональности. (Урок 39алгебры.) Когда мы вычислим эту производную ниже, мы увидим, что эта константа становится ln a .
| д дх | а x | = ln a · a x | . |
В системе натуральных логарифмов, в которой e — это основание, у нас есть самая простая возможная константа, а именно 1.
| д дх | е х | = e x . |
Производная от e с функциональным показателем
Когда y = e u ( x ) , то по цепному правилу:
То есть
«Производная от e с функциональным показателем
равно e с показателем степени, умноженным на производную от этого показателя, умноженную на
».
Пример 1. Вычислить производную e 2 x + 3 .
| Решение . |
Задача 1. Вычислить производную e x 2 .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
e x 2 · 2 x = 2 x e x 2
Задача 2. Вычислите производную от следующего.
а) e sin x . e sin x cos x
б) e −x . e − x (−1) = −e − x
c) x 2 e x . х 2 e x + 2 x e x
В соответствии с правилом продукта.
| г) | Согласно частному правилу: |
Производная от ln u ( x )
Когда y = ln u ( x ), то по цепному правилу:
г.То есть
| Пример 2. |
Пример 3. | д дх | ln sin x | = | 1 sin x | · потому что x | = | cos x sin x | = детская кроватка x . |
Пример 4. Найдите производную от ln x 2 .
Решение . Мы можем применить законы логарифмов:
| д дх | л x 2 | = | д дх | 2 ln x , 3-й закон, | |||
| = | 2 | д дх | л х | ||||
| = | 2 х | . | |||||
| Пример 5. Найти производную от ln | . x 3 x − 4 | . |
Решение . По 2-му закону:
| д дх | в | x 3 x − 4 | = | д дх | [ln x — ln (3 x — 4)] |
| = | |||||
| = | |||||
| = | |||||
Задача 3. Дифференцируйте следующее.
а) в x 3 . | д дх | ln x 3 = | д дх | 3 дюйма x | = | 3 х |
| b) (ln x ) 3 . | 3 (пер. x ) 2 · | 1 х | = | 3(ln x ) 2 x |
| c) ln (3 x 2 − 4 x ). | 1 3 x 2 − 4 x | · (6 х — 4) | = | 6 x − 4 3 x 2 − 4 x |
| d) ln (3 x − 4) 2 . | 1 (3 x − 4) 2 | · 2(3 x − 4) · 3 | = | 6(3 x — 4) (3 x — 4) 2 | = | 6 3 x − 4 |
e) ln cos x . | 1 cos x | (−sin x ) | = | − | sin x cos x | = | −загар x |
| Задача 4. Вычислить производную от ln | . 2 х | . |
| д дх | п | 2 х | = | д дх | (ln 2 — ln x ) = 0 — | 1 х | = − | 1 х |
Задача 5. Производная от log a x .
Согласно правилу перехода с базы e на другую базу a :
г.Тема 20 предварительного исчисления.
Вычислите предел этой производной
а) когда x больше 1 и становится больше.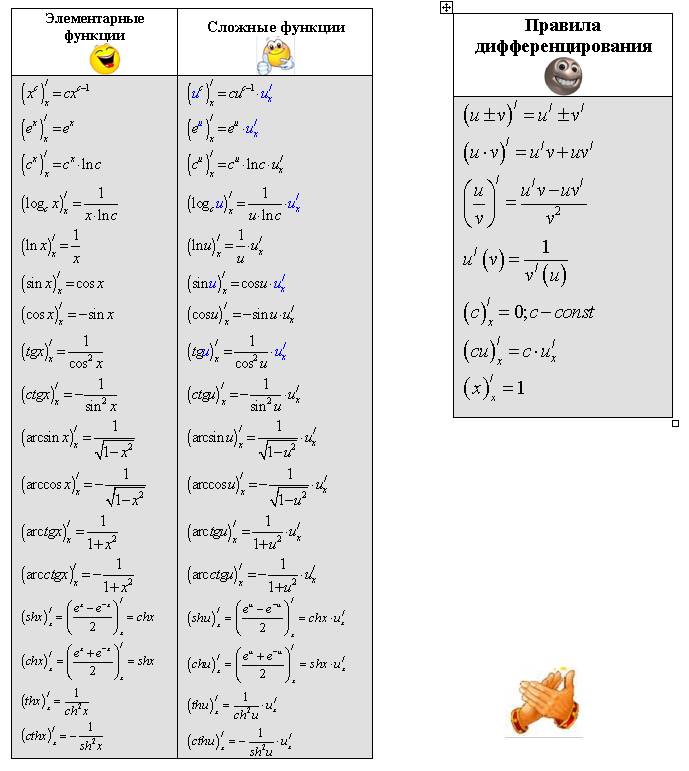
Эта производная приближается к 0, то есть становится меньше.
б) когда x меньше 1 и становится меньше.
г. Эта производная становится больше.
Общее силовое правило
Теперь мы можем доказать, что производная от f ( x ) = x n , где n — любой рациональный показатель, имеет следующий вид:
| д дх | х п | = n x n −1 |
Пусть
| г | = | x n . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Затем | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п г | = | n ln x (3-й закон). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поэтому, взяв производную по x : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | нет x | |||
| так что | ||||
| у’ | = | нет x | · г | |
| = | нет x | · x n | ||
| = | n x n −1 . | |||
Именно это мы и хотели доказать.
(Если n равно 0, то x 0 = 1, константа; ее производная равна 0.
Если n иррационально, потребуется рациональное приближение.)
| Задача 6. Вычислить производную от |
Производная от a x
Докажем:
| д дх | а x | = первая a · a x |
«Производная экспоненциальной функции с основанием a
равно натуральному логарифму основания
экспоненциальная функция умножается на«.
Пусть
| г | = | х . | |||
| Тогда при натуральном логарифмировании обеих частей: | |||||
| ln y | 4 | = | x ln a . (3-й закон) | ||
| Следовательно, | |||||
| = | |||||
| Но по правилу цепочки: | |||||
| = | |||||
| Следовательно, | |||||
| = | по и . | ||||
| = | по и | ||||
| г’ | = | ln a · y | |||
| То есть | |||||
| = | ln a · a x . | ||||