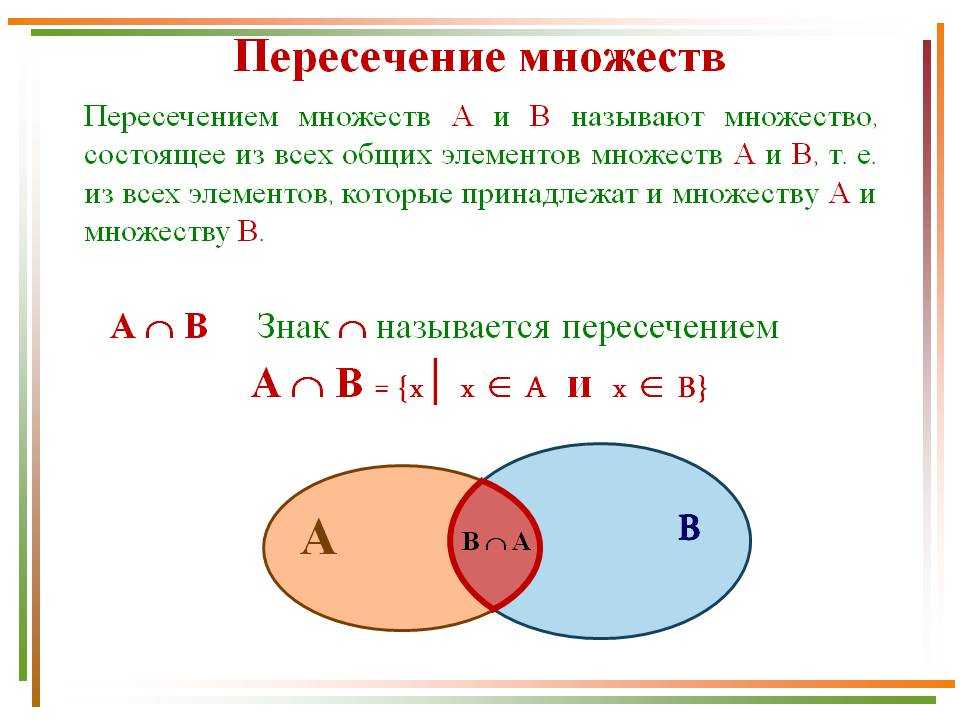
«Не широкая река, а множество ручейков…». Беседу вела А. Ямпольская
Ярким событием последних лет стал масштабный проект «Русские в Италии». В 2010 году его координаторы профессор Салернского университета Антонелла д’Амелия и профессор Венецианского университета Даниела Рицци «за вклад в изучение связей русской культурной эмиграции с итальянской культурой и обществом в первой половине XX века» были удостоены Премии Н. Гоголя в Италии. С Антонеллой д’Амелией и Даниелой Рицци беседует Анна Ямпольская.
— Несмотря на целый ряд исследований, посвященных присутствию русских в вашей стране (вспомним фундаментальный труд «Русские в Италии» Этторе Ло Гатто (1971), сборник «Русские и Италия» под редакцией Витторио Страды (1995), работы историков Тамборры, Вентури, Комоловой, Талалая и других), до сих пор мы знаем об этом очень мало — пожалуй, за исключением отдельных ярких фигур, таких как Вячеслав Иванов, Николай Бенуа, Паоло Трубецкой или Максим Горький. Почему, на Ваш взгляд, русская эмиграция в Италии долгое время оставалась в тени? Правомерно ли говорить о ней как o заметном и цельном явлении, сопоставимом с русским Парижем, Берлином или Прагой?
А. д’А.: Действительно, во второй половине XX века внимание итальянских исследователей главным образом привлекали отдельные факты, касающиеся русской эмиграции, а также видные представители мира литературы (Горький, Иванов, Амфитеатров, Осоргин) и политики. Особенность нашего проекта в том, что он опирается на изучение государственных и частных архивов. Это позволило собрать обширные, доселе неизвестные сведения, которые затем описывались и анализировались. Мы преследовали три основные цели: воссоздать подробную картину эмиграции русских в Италию; восстановить малоизвестные или забытые страницы жизни русской общины — как ее внутренней жизни, так и взаимодействия с итальянским обществом и культурой; лучше представить себе роль русских, оказавшихся в Италии, и понять, насколько плодотворными были их связи с миром литературы, изобразительного искусства, театра, кино, музыки и танца. Успех нашего начинания объясняется, прежде всего, тем, что проект с самого начала задумывался как коллективный: в отличие от прошлого, когда русской эмиграцией занимались отдельные ученые, сосредотачивавшие внимание на том или ином персонаже, мы организовали целую команду, работающую по всей стране и методично изучающую архивы и библиотеки.
д’А.: Действительно, во второй половине XX века внимание итальянских исследователей главным образом привлекали отдельные факты, касающиеся русской эмиграции, а также видные представители мира литературы (Горький, Иванов, Амфитеатров, Осоргин) и политики. Особенность нашего проекта в том, что он опирается на изучение государственных и частных архивов. Это позволило собрать обширные, доселе неизвестные сведения, которые затем описывались и анализировались. Мы преследовали три основные цели: воссоздать подробную картину эмиграции русских в Италию; восстановить малоизвестные или забытые страницы жизни русской общины — как ее внутренней жизни, так и взаимодействия с итальянским обществом и культурой; лучше представить себе роль русских, оказавшихся в Италии, и понять, насколько плодотворными были их связи с миром литературы, изобразительного искусства, театра, кино, музыки и танца. Успех нашего начинания объясняется, прежде всего, тем, что проект с самого начала задумывался как коллективный: в отличие от прошлого, когда русской эмиграцией занимались отдельные ученые, сосредотачивавшие внимание на том или ином персонаже, мы организовали целую команду, работающую по всей стране и методично изучающую архивы и библиотеки. Финансовая поддержка со стороны государства стала предпосылкой и необходимым условием проведения подобной работы.
Финансовая поддержка со стороны государства стала предпосылкой и необходимым условием проведения подобной работы.
Возвращаясь к сравнению с русским Парижем, Прагой или Берлином, нельзя не признать, что там эмиграция из России стала куда более заметным явлением, а наличие русских организаций в сфере культуры и других областях какое-то время позволяло эмигрантам сохранять за границей собственную, «настоящую» Россию. Эмиграция в Италию по своему характеру иная: она куда скромнее в количественном отношении, также не стоит забывать, что наша страна в скором времени превратилась в тоталитарное государство. Многие эмигранты пробыли здесь несколько лет, а затем уехали в другие страны Европы или в США. Те же, кто осели в Италии, не столько стремились создать сплоченную общину, сколько, оставаясь русскими, вливались в итальянское общество, однако при этом их вклад в наши культуру и искусство оказался, возможно, даже весомее, чем в других странах.
— Как возник замысел вашего проекта? Кто его участники? Какие материалы вы исследуете и в каких временных рамках? Проект существует в виде Интернет-сайта или вы планируете издать собранные материалы в печатном виде?
Д. Р.: Проект «Русские в Италии» был создан в 2005 году славистами четырех университетов, которые задались целью восстановить подробную картину присутствия русских в нашей стране в первой половине XX века, осветив связь русских эмигрантов с обществом и культурой Италии. Координаторы проекта — Антонелла д’Амелия (Салерно), Эльда Гаретто (Милан), Стефано Гардзонио (Пиза) и Даниела Рицци (Венеция). Вместе с ними работает большая команда, объединившая преподавателей и научных сотрудников разных университетов Италии. Основная задача проекта — заполнить лакуну и восстановить общую картину присутствия русских в Италии, создав справочный Интернет-ресурс (сайт «Russi in Italia»), где предполагается выложить как можно больше информации. В отличие от Франции, Германии или славянских стран, где русские создавали собственные организации, образовательные учреждения, органы печати, издательства и библиотеки, диаспору в Италии можно сравнить не с широкой рекой, а с множеством ручейков, разбежавшихся по стране и затерявшихся среди холмов и долин итальянской истории первой половины XX века.
Р.: Проект «Русские в Италии» был создан в 2005 году славистами четырех университетов, которые задались целью восстановить подробную картину присутствия русских в нашей стране в первой половине XX века, осветив связь русских эмигрантов с обществом и культурой Италии. Координаторы проекта — Антонелла д’Амелия (Салерно), Эльда Гаретто (Милан), Стефано Гардзонио (Пиза) и Даниела Рицци (Венеция). Вместе с ними работает большая команда, объединившая преподавателей и научных сотрудников разных университетов Италии. Основная задача проекта — заполнить лакуну и восстановить общую картину присутствия русских в Италии, создав справочный Интернет-ресурс (сайт «Russi in Italia»), где предполагается выложить как можно больше информации. В отличие от Франции, Германии или славянских стран, где русские создавали собственные организации, образовательные учреждения, органы печати, издательства и библиотеки, диаспору в Италии можно сравнить не с широкой рекой, а с множеством ручейков, разбежавшихся по стране и затерявшихся среди холмов и долин итальянской истории первой половины XX века.
А. д’А.: Изначально мы планировали ограничиться отрезком между первой русской революцией 1905 года и началом Второй мировой войны, однако со временем проект охватил весь прошлый век. Расширилась и область исследования: после архивов Фонда Джорджо Чини (Венеция), Римского архива Вячеслава Иванова (Рим) и Государственного архива (Рим) были изучены важнейшие государственные и частные архивы. Мы занимались как отдельными персонажами, так и организациями — теми, что создавали сами русские, и итальянскими учреждениями, в которых сотрудничали эмигранты. Затем мы соединили собранные данные с информацией, которую нашли в периодической печати тех лет, а также с результатами архивных исследований, проводившихся в России, США и других странах Европы. Кроме того, была составлена библиография книг, статей и переводов, опубликованных русскими в Италии в 1900-1940 годах.
Д. Р.: Работая над проектом, мы, например, сосредоточили внимание на контактах русских писателей и интеллигентов с издательским миром: именно им итальянская публика во многом обязана знакомством с русской литературой и культурой. Почти ничего не было известно о связи русских художников с миром искусства, а они много работали у нас в театре, кино и музыкальной сфере. Наконец, изучение архивных документов и систематизация собранных данных позволили точнее представить себе численность русской общины и деятельность ее членов. Параллельно со сбором информации мы описывали найденные материалы, наиболее важные из которых планируем напечатать.
Почти ничего не было известно о связи русских художников с миром искусства, а они много работали у нас в театре, кино и музыкальной сфере. Наконец, изучение архивных документов и систематизация собранных данных позволили точнее представить себе численность русской общины и деятельность ее членов. Параллельно со сбором информации мы описывали найденные материалы, наиболее важные из которых планируем напечатать.
После развала СССР российские ученые активно занялись воссозданием истории своей страны (доказательство тому — большое число публикаций об эмиграции, появившихся за последние годы). Это подтолкнуло их зарубежных коллег из стран, принимавших русских, также начать восстанавливать общую картину эмиграции. Во Франции, Германии и славянских странах, куда в основном шел поток эмигрантов, это уже сделано, так что наш проект преследовал еще и цель поднять исследование русской эмиграции в Италии на европейский уровень.
По своей природе изучение архивов предполагает, что в процессе работы горизонты исследования постоянно расширяются. В итоге масса отдельных фактов, каждый из которых по отдельности обречен на забвение, постепенно складывалась в цельную, исторически достоверную картину, позволив в полной мере представить себе русскую эмиграцию как особое явление. Достаточно зайти на сайт www.russinitalia.it, на котором мы постоянно выкладываем новые материалы. Хотя работа над сайтом еще не завершена, его новаторский характер очевиден уже сейчас:
В итоге масса отдельных фактов, каждый из которых по отдельности обречен на забвение, постепенно складывалась в цельную, исторически достоверную картину, позволив в полной мере представить себе русскую эмиграцию как особое явление. Достаточно зайти на сайт www.russinitalia.it, на котором мы постоянно выкладываем новые материалы. Хотя работа над сайтом еще не завершена, его новаторский характер очевиден уже сейчас:
Хотите продолжить чтение? Подпишитесь на полный доступ к архиву.
Уже подписаны? Авторизуйтесь для доступа к полному тексту.
3.Перечислите элементы следующих множеств: А — множество натуральных чисел, меньших 20; В — множество натуральных чисел, больших 30; С
Математика, 26.02.2021 23:52, ktdgegrbyfk
6. Какие из следующих множеств являются пустыми? Какие из них числовые множества?
А — множество городов России с население более 15 млн.;
В — множество параллелограммов с неравными противоположными сторонами;
С — множество двузначных чисел, меньших 6;
D — множество натуральных чисел, меньших 1 ;
Е= {х/х N, 6 <х<7};
К= {х/х Z, х2-4=0} ;
L = {х/х R, х2 +25=0}. 3=125 s1-s2=486-150=336 v1-v2= 729-125= 604
3=125 s1-s2=486-150=336 v1-v2= 729-125= 604
Ответ разместил: Гость
Турист прошёл за первый день 18 км, что составляет шесть пятых пути, который он должен пройти во второй день. сколько км пройдет турист за два дня? 18 км это 6/5 18/6*5=15км пройти во второй день 18+15=33 км
Ответ разместил: Гость
округляем до десятков
3482 = 3480
586 = 590
67509 = 67510
125,67 = 130
Ответ разместил: Гость
2/3=16 часов
5/6=20 часов
3/8=9 часов
7/12=14 часов
3/5 от 35 =21 больше 11/18 от 18=11
Другие вопросы по: Математика
Вкаких из нижеперечисленных случаев совершается механическая работа; девочка играет на пианино; вода давит на стенку сосуда; вода падает с плотины?…
Опубликовано: 27.02.2019 13:40
Ответов: 2
Определения отрезка первый признак равенства тпеугольника…
Опубликовано: 28. 02.2019 07:30
02.2019 07:30
Ответов: 2
Продолжительность дня а часов. чему равна продолжительность ночи? составить выражение. найти его значение при а=8; 10; 12…
Опубликовано: 28.02.2019 19:10
Ответов: 3
Лодка по озеру движется со скоростью 12км\ч. сколько времени понадобится, чтобы отплыть по реке на 70 км и вернуться назад, если бревно по реке проплывает за час 2 км?…
Опубликовано: 01.03.2019 02:00
Ответов: 1
На доске записано некоторое число. один ученик уменьшил это число на 7, а второй увеличил записанное на доске число в 3 раза. результат второго ученика оказался на 39 больше, чем р…
Опубликовано: 01.03.2019 14:20
Ответов: 3
Какой путь пройдёт свободно тело за четвёртую секунду?. ..
..
Опубликовано: 02.03.2019 07:10
Ответов: 1
Знаешь правильный ответ?
3.Перечислите элементы следующих множеств: А — множество натуральных чисел, меньших 20; В — множеств…
Популярные вопросы
На сколько меньше сумма чисел8и2,чем их произведения?…
Опубликовано: 27.02.2019 21:30
Ответов: 3
Найдите площадь круга, вписанного в квадрат со стороной 4 см….
Опубликовано: 28.02.2019 06:50
Ответов: 1
Вставить слова вместо пропусков. fill in: survived, violent, humped, mythical, rustling, torture, dull, glimpse, illusion. 1 many old castles used to have chambers. 2 as the wind…
Опубликовано: 01.03.2019 17:50
Ответов: 1
1) дано: 4 киломоль водорода, найти v и m 2) что тяжелее 5 л углекислого газа или 5 л so2(диоксид серы) заранее : ).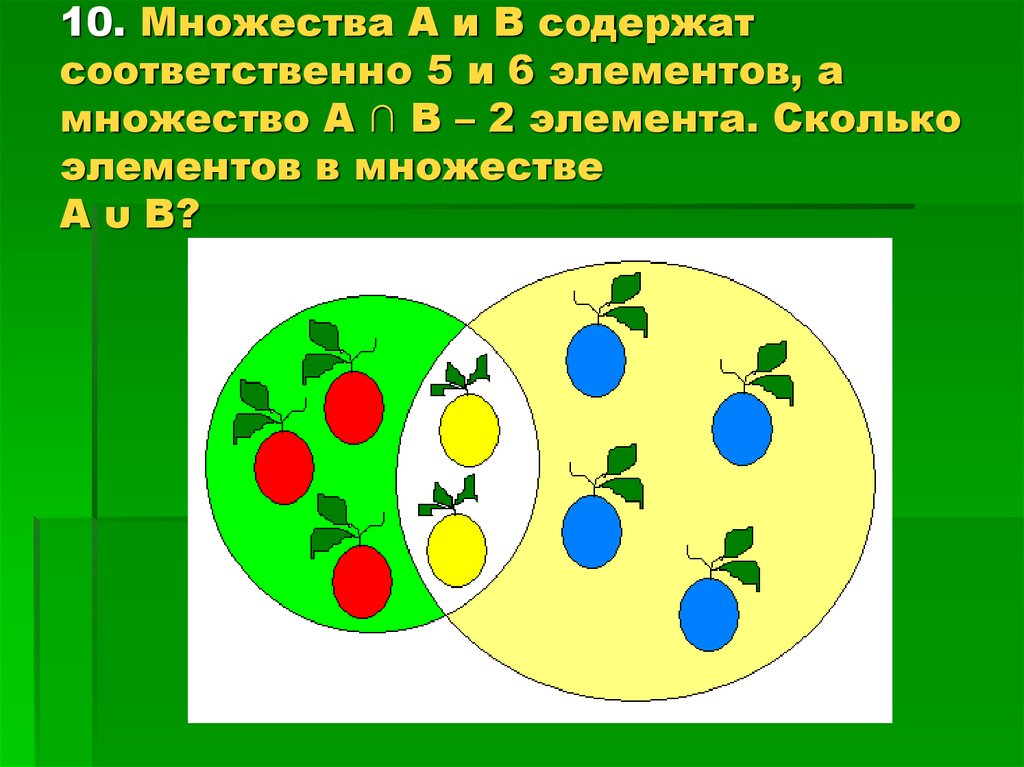 ..
..
Опубликовано: 01.03.2019 19:10
Ответов: 3
Найдите боковую сторону и площадь равнобедренного треугольника если основание равно 12 см а высота проведенная к основанию рвна 8 см…
Опубликовано: 02.03.2019 00:50
Ответов: 3
Сделать крассворд по музыке. 1(6 букв), 10(5букв). — части песен. 2(10 букв), 3(11 букв) 7(11 букв) — название форм по кол-ву частей. 4(9 букв) — форма используемая в песнях. 5(8 б…
Опубликовано: 02.03.2019 13:50
Ответов: 3
Определить площадь круга, если площадь вписанного в него квадрата равна 144см…
Опубликовано: 02.03.2019 14:50
Ответов: 3
Вспахали 6/7 поля, что составило 210 га. каковаплощадь всего поля?…
Опубликовано: 03. 03.2019 13:20
03.2019 13:20
Ответов: 2
У=2х(в квадрате)+3х-2.нужно вычислить абсциссу точки а…
Опубликовано: 03.03.2019 14:50
Ответов: 2
Какие пословици , поговорки , метафоры , связанные с телосложением человека вы знаете ? запишите ваши примеры…
Опубликовано: 03.03.2019 20:00
Ответов: 3
Случайные вопросы
Множества и операции над ними презентация, доклад
Множества и операции над ними
Множество и его элементы
Пустое множество
Способы задания множеств Подмножества данного множества
Операции над множествами
Понятия теории множеств
Множество- совокупность объектов, обладающих определенным свойством, объединенных в единое целое.
Например:
Множество цифр:
0;1;2;3;4;5;6;7;8;9
Множество букв русского алфавита
Например:
1). Цифра 6 – элемент множества цифр.
2). Буква Л – элемент множества букв
русского алфавита
Предметы, из которых состоит множество, называются его ЭЛЕМЕНТАМИ
Для обозначения множеств используют большие
буквы латинского алфавита или фигурные скобки,
внутри которых записывают элементы
множества(при этом порядок элементов не имеет
значения).
Например:
1). А— множество цифр: А={0;1;2;3;4;5;6;7;8;9}.
2). W— множество букв русского алфавита:
W={А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;Ц;Ч;Ш;Щ; Ь;Ы;Ъ;Э;Ю;Я }
Для обозначения элементов множества используют малые буквы латинского алфавита
Например:
1). f = 6 – элемент множества цифр
f = 6 – элемент множества цифр
2). а = Р – элемент множества букв русского алфавита
Принадлежность предмета данному множеству обозначается
Например:
1). f = 6 ; 6 є А, где А— множество цифр.
2). К є W, где W— множество букв русского алфавита
Непринадлежность – символом
Множество может быть:
1). Конечное :
Например: А— множество цифр
2). Бесконечное:
Например: N – множество натуральных чисел
3). Пустое:
ø- множество, в котором нет ни одного элемента
Например: X – множество решений уравнения
На диаграмме Эйлера-Венна утверждение «множество А является подмножеством множество В» изображают так
Если множество В состоит из некоторых элементов множества А
(и только из них),
то множество В называется ПОДМНОЖЕСТВОМ
множества А
Например:
1). В= {5;9;0 }, А= { 0;1;2;3;4;5;6;7;8;9 }, то
В= {5;9;0 }, А= { 0;1;2;3;4;5;6;7;8;9 }, то
(читается В содержится в А)
2). С= { Л;Е;Т;О },
W= {А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;Ц;Ч;Ш;Щ;Ь;Ы;Ъ;Э;Ю;Я },
(читается С содержится в W)
Подмножеством данного множества А является и само множество А
Пустое множество, по определению, считают подмножеством всякого множества
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ
Перечислением элементов множества;
с помощью некоторого свойства, объединяющего элементы;
описанием получения множества.
Например:
1). К = {х : -5 ≤ х ≤ 6 }-описанием характеристического свойства элементов
2). Т = {х : 0 ≤ х ≤ 9, х є N } –описанием характеристического свойства элементов
3). Множество учеников данного класса определяется их списком в классном журнале — перечислением элементов
4). Множество цифр: А = {0,1,2,3,4,5,6,7,8,9} — перечислением элементов
L=М «>
Множества называются РАВНЫМИ, если они состоят из одних и тех же элементов
Например:
1). Равными являются все пустые множества
Равными являются все пустые множества
Равенство множеств А и В записывают в виде А=В
Отношение «=» называется отношением равенства
2). Множество корней уравнения х²=49; L= {-7; 7 },
Множество корней уравнения | х |=7; M= {-7; 7 },
=> L=М
Решение задач
1.Задайте перечислением элементов множества:
а) А—множество гласных букв русского алфавита.
Решение
А = {а, е, ё, и, о, у, ы, э, ю, я }
б) В—множество корней уравнения х³-4х=0.
Решение
х (х²-4)=0
х=0 или х= ±2
В={-2; 0; 2 }
Решение
С = { 2 }
в) С—множество простых четных чисел.
3. Какие из следующих множеств являются пустыми?
множество решений уравнений х²-4=0
множество решений уравнений х=х+2
множество решений уравнений х+1 = х+1
множество кругов, у которых диаметр меньше радиуса
5. Даны множества:
Даны множества:
а) множество А всех трапеций.
б) множество В всех прямоугольников.
в) множество С всех четырехугольников.
г) множество D всех квадратов.
д) множество H всех параллелограммов.
е ) множество F всех многоугольников.
Запишите с помощью знака эти множества в таком порядке,
чтобы каждое предыдущее множество являлось подмножеством последующего.
Решение
A
F
C
H
B
D
Суммой, или объединением произвольного конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А,В.
На диаграмме Эйлера-Венна объединение двух множеств выглядит так
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.
Операции над множествами
ОБЪЕДИНЕНИЕ МНОЖЕСТВ А и В
Например:
L= { 5;7;9;3;1},
W= { 1;0;8;2;4;5;6 } =>
LUW={0;1;2;3;4;5;6;7;8;9}
С =А U B К U M
Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.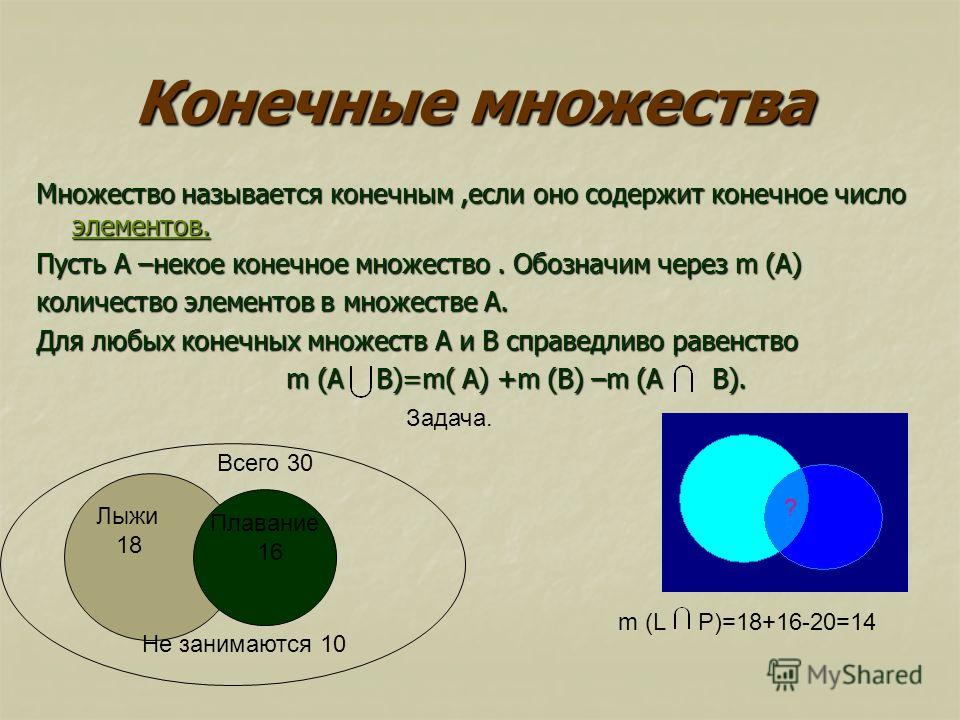
Пересечение множеств обозначается
На диаграмме Эйлера-Венна пересечение двух множеств выглядит так
П р и м е р : {1,2,3} {2,3,4} = {2,3}
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ А и В
С= А ∩ В К ∩ М = ø
Например:
L= { 5;7;9;3;1},
W= { 1;0;8;2;4;5;6 }
=> К = L ∩ W= { 1;5 }
Разностью между множеством В и множеством А называется множество всех элементов из В , не являющихся элементами из А .
Разность двух множеств обозначается
На диаграмме Эйлера-Венна разность двух множеств выглядит так
РАЗНОСТЬ МНОЖЕСТВ А и В
Решение задач:
1. Дано: M = { a;b;c;d } , N = { b;d } .
Найти: а) M \ N; б) N \ M; в) (M \ N) U (N \ M)
2. Найти разность множеств К = {1;2;3;7;8;9;) } и М = {2;0;8 }.
Дополнением множества А называется множество, состоящее из всех элементов, не принадлежащих множеству А
(но принадлежащих универсальному множеству U)
Дополнение множества А обозначается (можно читать: «А с чертой»)
A
U
.
.
A
Задача. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Решение:
Пусть А- множество учащихся изучающих английский язык, Ф — множество учащихся изучающих французский язык, О — множество учащихся изучающих английский и французский язык.
Ответ: в классе 34 ученика.

21-110: Наборы
21-110: НаборыПонятие множества — одна из самых фундаментальных идей математики. По сути, набор — это просто набор объектов. Область математики которая изучает множества, названная теорией множеств , была основана немецким математик Георг Кантор во второй половине XIX в. Сегодня концепция наборов пронизывает почти всю современную математику; почти любой другой математический концепция (включая кажущуюся фундаментальной концепцию чисел!) была определяются прямо или косвенно в терминах множеств.
Основные определения и обозначения
Набор представляет собой набор объектов, рассматриваемых как математический
объект сам по себе. (Полезная метафора для набора — картонная
коробка — коробка может содержать предметы, и мы можем думать о том,
объекты в коробке по отдельности или думать о коробке и ее содержимом
вместе как единый объект.) Объекты в наборе называются элемента (или элемента ) множества; говорят элементы
до принадлежат набору (или быть в наборе ), а набор
Говорят, что содержат элемента. Обычно элементы множества
другие математические объекты, такие как числа, переменные или геометрические
точки.
Обычно элементы множества
другие математические объекты, такие как числа, переменные или геометрические
точки.
Письменные наборы
Набор часто записывается путем перечисления его элементов между фигурными фигурные скобки { }. Например, набор, содержащий числа 1, 2, и 3 будет записано как {1, 2, 3}.
Когда элементы набора следуют очевидному шаблону, но их слишком много
из них для явного перечисления, обычно перечисляются первые несколько элементов (чтобы
установить шаблон) и последний элемент (чтобы указать, где шаблон
останавливается) с многоточием (…) между ними, чтобы указать, что
элементы в середине были опущены. Например, чтобы записать множество положительных
целые числа от 1 до 100, мы можем написать
{1, 2, 3, …, 100}. Если ни один элемент не написан после
многоточие, предполагается, что шаблон будет продолжаться вечно; так набор написан
{1, 2, 3, …} содержит все положительные целые числа.
Иногда элементы множества продолжаются бесконечно в обоих случаях.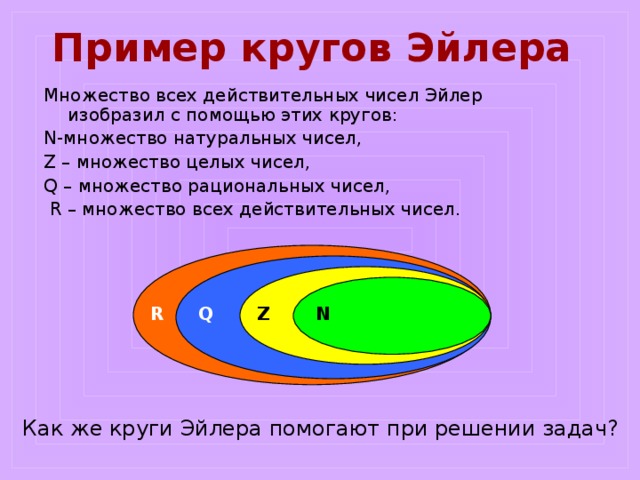
Множество также можно описать на естественном языке с помощью английских фраз. За
Например, «множество всех положительных целых чисел» описывает конкретное
установлен. Важно, чтобы описание было точным, чтобы не было сомнений.
о том, является ли тот или иной объект элементом множества. Обычный
Примером неточного описания является такая фраза, как «числа
от 1 до 10». В этой фразе есть несколько неясностей. Являются ли
числа 1 и 10 сами являются элементами множества или они исключены? Находятся включены все действительных чисел от 1 до 10 или только целые числа?
Наконец, фраза, вероятно, должна быть более ясной в отношении того факта, что эти
числа следует рассматривать как набор, а не по отдельности. Более точный
описанием этого набора может быть «множество положительных целых чисел, не превышающих
чем 10” (если в наборе есть числа 1 и 10 и только
включены целые числа) или «множество действительных чисел между 1
и 10, исключая» (если в наборе есть числа с дробной
части, но не сами цифры 1 и 10).
Символ ∈ используется для обозначения «является элементом», просто поскольку символ = используется для обозначения «равно». Например, чтобы сказать что число 2 является элементом множества {1, 2, 3}, мы можем напишите 2 ∈ {1, 2, 3}. Чтобы выразить обратное, «не является элементом», мы ставим косую черту через символ и напишите ∉. Например, мы можем написать 4 ∉ {1, 2, 3}.
Часто полезно присваивать имена наборам. Эти имена обычно выбирают
быть одиночными буквами, аналогично использованию букв для представления чисел в
алгебра. Очень распространенным соглашением является использование заглавных букв в именах
наборы и строчные буквы для представления элементов наборов. Таким образом, для
например, если мы присвоим букву А к комплекту
{1, 2, 3}, написав A = {1, 2, 3}, мы
тогда можно сказать, что 2 ∈ A . Мы также можем написать a ∈ A , под которым мы подразумеваем, что a – число (возможно, неизвестное), являющееся элементом
установить A — другими словами, значение a должно
быть либо 1, 2, либо 3.
Равенство множеств
Два набора называются равными , если каждый элемент первого набора является элементом второго множества, и наоборот. Например, если A = {1, 2, 3} и B = {2, 3, 1}, тогда наборы A и B равны. Каждый элемент A также является элемент B , и каждый элемент B также является элемент A . Мы выражаем равенство множеств знаком равенства, поэтому в этом случае мы пишем A = B . Когда два набора равны, они считаются одним и тем же набором. Важно помнить, что равенство между множествами — это другое понятие, чем равенство между числами.
Одним из следствий этого определения равенства является то, что порядок, в котором
перечисление элементов множества не имеет значения. Мы заботимся только о том, какие
объекты являются элементами множества, а не порядком их появления. Так, например,
выражения {1, 2, 3} и {2, 3, 1} описывают
тот же набор.
Другим последствием является то, что количество раз, когда элемент перечисляется, не имеющий отношения. Набор {1, 2, 1, 3, 3, 3} равен набор {1, 2, 3}, поскольку каждый элемент первого набора является элементом второго, и наоборот. (Неважно, что числа 1 и 3 перечислены несколько раз в первом наборе.)
[Иногда нам нужно использовать набор объектов, в котором порядок равен важный. Такой набор называется последовательностью или последовательностью . заказанный список . Примером может служить использование упорядоченных пар форма ( x , y ) для представления точек в
двумерная плоскость; точка (2, 5) отличается от
точка (5, 2). Точно так же нам иногда нужна коллекция объектов в
что имеет смысл, чтобы элемент появлялся более одного раза. Такой
сборник называется мультимножество . Когда
мы ссылаемся на набор , однако следует понимать, что порядок и
повторение элементов не имеет значения. ]
]
Наборы, содержащие другие наборы
Элементами набора может быть что угодно — даже другие наборы. Например, предположим, что у нас есть два множества: A = {1, 2, 3} и B = {2, 3, 4, 5}. Думайте о A как о коробка с цифрами 1, 2 и 3 и B в качестве коробка с цифрами 2, 3, 4 и 5. Ничто не мешает нам поставить коробку A и коробка B вместе в большой коробке C . Точно так же мы можем сделать набор C , содержащий набор A и установите B в качестве элементов. Мы можем записать набор C как { A , B } или, если хотите, мы можем сказать
C = { {1, 2, 3}, {2, 3, 4, 5} }.
Набор, содержащий другие наборы, подобен коробке, содержащей другие коробки. В этом
случай, набор C имеет два элемента , которые являются двумя
наборы A и B . Эти элементы
set C сами являются наборами; набор A состоит из трех
элементов, а набор B состоит из четырех элементов.
Следовательно, верно, что A ∈ C , потому что A является элементом C . Точно так же верно что B ∈ C . Конечно, это тоже верно что, скажем, 1 ∈ A , потому что число 1 является элемент набора А .
Однако верно , а не , что 1 ∈ C , потому что 1 не является элементом множества C . только два элемента из C являются наборы A и B , и ни один из этих двух элементов не является числом 1. (Набор A содержит номер 1, но А сам по себе не является номер 1.)
Возвращаясь к метафоре коробки, мы должны думать об элементах множества (a
коробка) как объекты, которые прямо внутри коробки.
номер 1 не находится непосредственно внутри коробки C ; вместо этого это
спрятан внутри коробки A . Таким образом, 1 не является элементом
set C , но 1 – это элемент
набор А .
Аналогично, хотя верно, что 2 ∈ A и также верно, что 2 ∈ B , это , а не верно, что 2 ∈ C , потому что число 2 напрямую не внутри коробки C .
Теперь рассмотрим набор
D = {1, 2, 3, 2, 3, 4, 5},
, который совпадает с набором {1, 2, 3, 4, 5}, поскольку
порядок и повторение элементов значения не имеют. Набор D отличается от набора C — эти наборы не
равный. Чтобы убедиться в этом, достаточно найти один элемент в одном множестве, который
не является элементом другого множества. Ну, например, число 1 – это
элемент D , но (как объяснялось выше) не является элементом
из С ; поэтому наборы не равны. Думая о C и D в виде коробок, мы видим, почему они не совпадают:
set C — это блок, содержащий два блока (которые сами по себе бывают
содержать несколько чисел), тогда как набор D представляет собой коробку,
непосредственно содержит пять чисел (и никаких ящиков).
В качестве другого примера рассмотрим два набора E = {1} и F = {{1}}. Эти множества не равны. В наборе E есть один элемент, номер 1; в установить F также имеет один элемент, но один элемент из F — это другой набор, а не число. Таким образом, тогда как set E – это поле, содержащее число 1, set F – это поле, содержащее поле, содержащее число 1. (Другими словами, набор F представляет собой коробку содержащий E — вы видите это?) Оба они отличается от самого числа 1. Так что это правда, что 1 ∈ E , а на самом деле E ∈ F (поскольку единственный элемент из F — это набор E ), но это , а не . что 1 ∈ F .
Множества, содержащие другие множества, распространены в некоторых областях математики, но мы не будет видеть их очень часто в этом курсе. (Математики, работающие в эти области часто называют множество, содержащее другие множества, «набором наборы» или «семейство наборов», чтобы избежать неловкой фразы «набор наборов»)
Мощность
Мощность множества — это количество элементов,
содержит.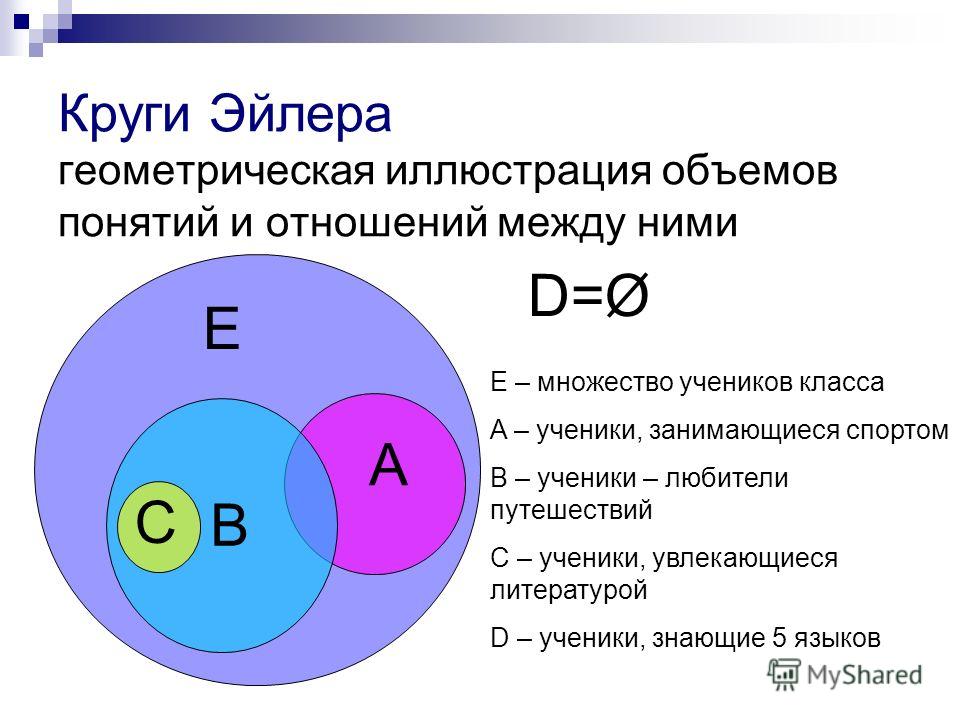 (Иногда мощность множества называют просто
«размер» набора, потому что размер
более короткое слово; но «мощность» — технически правильный термин.)
(Иногда мощность множества называют просто
«размер» набора, потому что размер
более короткое слово; но «мощность» — технически правильный термин.)
Обычно пишут | А | означать мощность набор А . Например, если A = {1, 4, 8}, тогда | А | = 3, потому что A состоит из трех элементов. Это та же запись, что и для абсолютного значения числа, но контекст поясняет, что имеется в виду: если набор окружают вертикальные полосы, они относятся к мощности множества.
Мощность множества может быть бесконечной. Например, мощность набор положительных целых чисел {1, 2, 3, …} равен бесконечный.
Пустой набор
Мы думали о наборах как о коробках. Какой набор соответствует
идея пустой коробки? Ясно, что это должно быть множество, не содержащее ни одного элемента
все. Мы называем такое множество пустым множеством . Так как любые два пустых множества
содержат точно такие же элементы (точнее, вообще не содержат элементов), мы
считать любые два пустых множества равными и, следовательно, одним и тем же множеством. Так что мы обычно
обратитесь к пустому набору , потому что на самом деле он только один.
Так что мы обычно
обратитесь к пустому набору , потому что на самом деле он только один.
Существует два распространенных способа записи пустого множества. Первый способ, как вы можно ожидать, { }. Другое обозначение — круг или ноль с прорежьте его, что выглядит как ∅. Оба { } и ∅ – символы пустого множества.
Обратите внимание, что между ∅ и {∅} есть разница. во-первых, это пустой набор, который представляет собой пустой ящик. Второй — коробка , содержащее , является пустой коробкой, поэтому вторая коробка не пуста — у нее есть коробка в нем! Не пишите {∅}, когда имеете в виду пустой набор, потому что {∅} относится к набору, содержащему пустой набор, который не является как и само пустое множество.
Кардинальность пустого множества равна 0, что логично, поскольку
пустое множество не содержит элементов. Заявление x ∈ ∅ всегда ложно, несмотря ни на что х есть, потому что нет такой вещи как пустой элемент
установлен.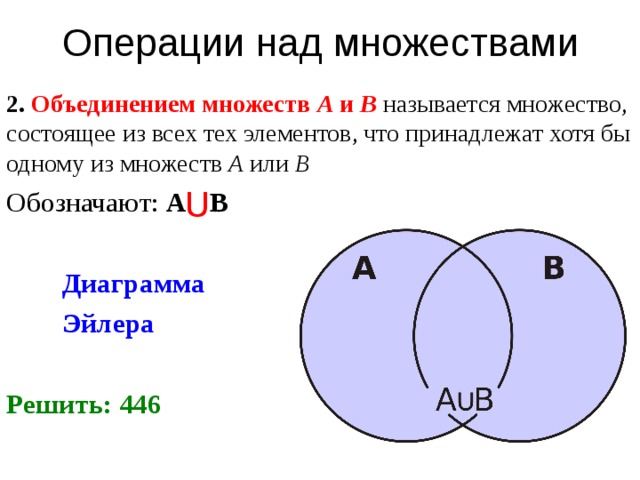
Подмножества
Выше мы определили два набора A и B равными, если каждый элемент A является элементом B , и наоборот наоборот Если убрать из этого определения «наоборот», то получим определение подмножества.
Мы говорим, что множество A является подмножеством установите B , если каждый элемент A также является элементом B . Мы используем символ ⊆ для обозначения «является подмножеством
из»; например, A ⊆ B означает
« A является частью B ». Мы также можем
поверните этот символ в другую сторону и запишите множества в другом порядке, чтобы получить В ⊇ А ; это значит то же самое, что А ⊆ В . Чтобы написать, что А это
не является подмножеством B , мы рисуем косую черту через символ подмножества: А ⊈ В . Интуитивно, подмножество B является «частью» B .
Интуитивно, подмножество B является «частью» B .
Например, рассмотрим наборы C = {1, 2} и D = {1, 2, 3, 4}. Набор C является подмножеством D , потому что каждый элемент C является также элемент D . Итак, мы можем написать C ⊆ D . У данного набора есть много подмножеств; за например, другое подмножество D — это {1, 3, 4}.
Чтобы запомнить, в каком направлении писать символ ⊆, подумайте о мощностей множеств и символа неравенства ≤. Если А является подмножеством B , то B должно содержать не менее много элементов, как A (просто потому, что B содержит все элементы A ), поэтому мощность из B должно быть больше или равно количеству элементов из А . Другими словами,
А ⊆ В подразумевает, что
| А | ≤ | Б |.
Обратите внимание, что символы выше «указывают» в одном направлении.
Существует очень важное различие между символами ∈ и ⊆. Символ ∈ используется для обозначения элемента . набора, тогда как символ ⊆ используется для обозначения подмножества . Например, рассмотрим набор
Д = {1, 2, 3, 4}.
Набор {2, 4} является подмножеством D , потому что каждый
элемент {2, 4} также является элементом D , поэтому он
правильно писать {2, 4} ⊆ D . Но
set {2, 4} – это , а не элемент набора D ,
потому что четыре элемента множества D — это числа.
( D не содержит наборов в качестве элементов), поэтому некорректно
напишите {2, 4} ∈ D . С другой стороны,
число 2 является элементом D , поэтому правильно писать
2 ∈ D ; но число 2 равно не подмножество
из D (поскольку число 2 – это число, а не набор), поэтому
неправильно писать 2 ⊆ D .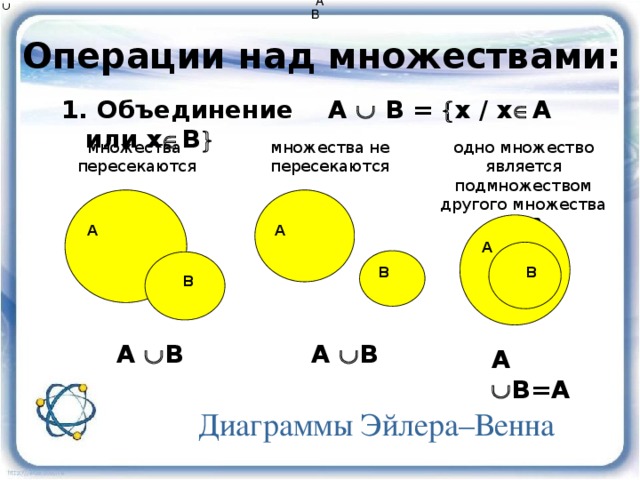 Если мы хотим обратиться к
подмножество D , содержащее только число 2, мы должны
напишите {2}, то есть набор, содержащий 2 (обратите внимание, что набор {2}
отличается от числа 2). Набор {2} является подмножеством
из D , то есть {2} ⊆ D ; но это не элемент D , потому что D не является
имеют какие-либо множества в качестве элементов, поэтому некорректно писать
{2} ∈ Д .
Если мы хотим обратиться к
подмножество D , содержащее только число 2, мы должны
напишите {2}, то есть набор, содержащий 2 (обратите внимание, что набор {2}
отличается от числа 2). Набор {2} является подмножеством
из D , то есть {2} ⊆ D ; но это не элемент D , потому что D не является
имеют какие-либо множества в качестве элементов, поэтому некорректно писать
{2} ∈ Д .
Когда A является подмножеством B ,
набор B иногда называют надмножеством .
из А . Мы также можем сказать
« B содержит A в качестве подмножества», но
следует быть очень осторожным со словом «содержит», потому что, как
отмечено в предыдущем абзаце, есть большая разница между высказыванием
« B содержит A в качестве элемента»
(что означает A ∈ B ) и сказать B содержит A в качестве подмножества» (значение А ⊆ В ). попробую использовать слово
содержит только для ссылки на элементы, а не на подмножества.
попробую использовать слово
содержит только для ссылки на элементы, а не на подмножества.
Внимательное прочтение определения подмножества показывает, что каждое множество является
подмножество самого себя. Например, используя указанный выше набор D ,
очевидно верно, что «каждый элемент D также является
элемент D », поэтому по определению D является
подмножество D . Мы часто хотим исключить этот случай, поэтому мы определяем правильное подмножество набора B быть подмножеством B , который не является самим B . Мы пишем A ⊂ B означает, что A является
правильное подмножество B . [Это использование символов ⊆
и ⊂ означает «является подмножеством (или равным)» и «является
правильное подмножество», соответственно, соответствует использованию неравенства
символы ≤ и < означают «меньше или равно» и
«строго меньше» соответственно. ]
]
Пустое множество считается подмножеством любого множества (включая его самого). Это может показаться довольно странным соглашением. Пожалуй, лучшее оправдание это происходит от того, что мы переворачиваем определение подмножества с ног на голову и задаемся вопросом, что оно средства для набора A не быть подмножеством B . Из определения это должно означать, что существует некоторое элемент в A , который не является элементом B . Так что значит сказать, что пустое множество не является подмножеством из B ? Это означало бы, что в пустом множестве есть какой-то элемент это не элемент B — но это не может быть правдой, потому что в пустом наборе нет элементов! Итак, с этого момента точки зрения, имеет смысл сказать, что пустое множество является подмножеством каждый набор.
[Следует отметить, что использование символов ⊆ и ⊂
описанное выше не является универсальным. Некоторые авторы используют символ ⊂ для
означает «является подмножеством» (для которого мы используем
символ ⊆) и ввести новый символ ⊊, символ подмножества
с перечеркнутой полосой «равно», что означает «является правильным
подмножество» (для которого мы используем символ ⊂).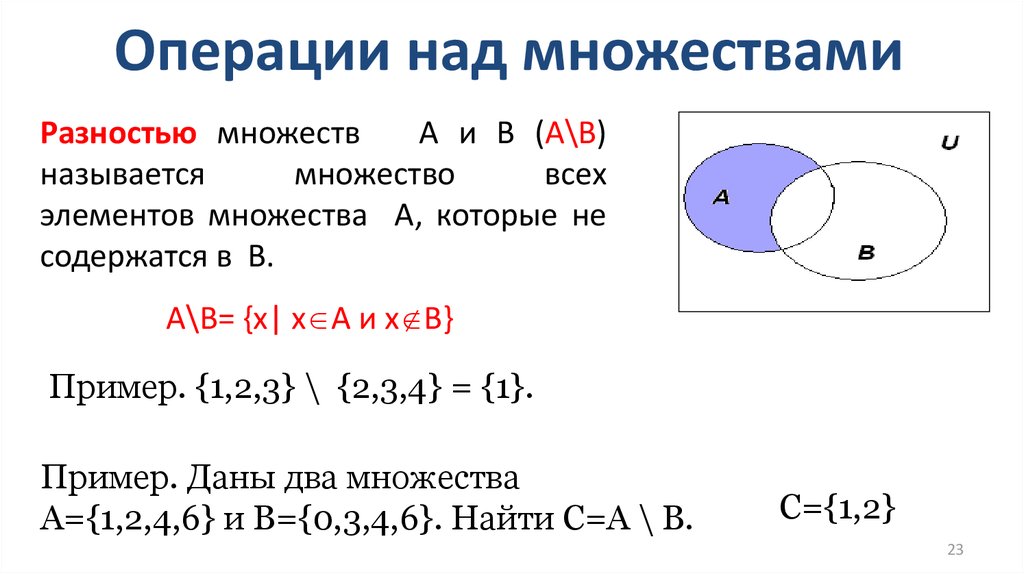 ]
]
Наборы цифр
Есть несколько наборов чисел, которые настолько часто используются, что их специальные символы. Двойные прописные буквы, иногда называемые жирным шрифтом на доске. часто используются буквы (в частности, буквы ℝ, ℤ, ℕ и ℚ). В качестве альтернативы буквы могут быть просто набраны в полужирный. [Из-за возможности того, что необычные символы, такие как классная доска, жирным шрифтом, может отображаться не во всех веб-браузерах, я буду использовать простое полужирное начертание буквы здесь.]
Множество всех действительных чисел, как положительных, так и отрицательных (и нулей), равно называется R (от «настоящего»). Множество действительных чисел включает все числа, обычно встречающиеся в алгебре, тригонометрии или исчислении курс. (Он не содержит комплексных чисел, таких как как √−1.)
Набор целых чисел (положительных, отрицательных и нулевых) называется Z (от немецкого слова Zahlen, означающего
«числа»). Другими словами, Z = {…, –3, –2, –1, 0, 1, 2, 3, …}.
Набор натуральных чисел называется N (для
«естественный»). Множество натуральных чисел содержит все положительные
целые числа и никаких отрицательных целых чисел. К сожалению, нет единого мнения о
следует ли считать ноль натуральным числом. Некоторые авторы включают 0
в комплекте N , а других нет. Причина этого отсутствия
согласованность заключается в том, что иногда полезно включать ноль, а иногда нет,
в зависимости от ситуации. Таким образом, математики используют любое определение, которое подходит
их лучше всего в то время, но они знают о различиях в использовании, поэтому
они всегда очень тщательно указывают, какое именно определение они используют
в каждом конкретном случае, чтобы избежать какой-либо путаницы или двусмысленности, и как только они
выбрав определение, они придерживаются его. Для этого класса давайте договоримся
что 0 равно не натуральное число, если не указано иное. В
другими словами, если не указано иное, мы будем использовать символ N для
представляют набор {1, 2, 3, …}.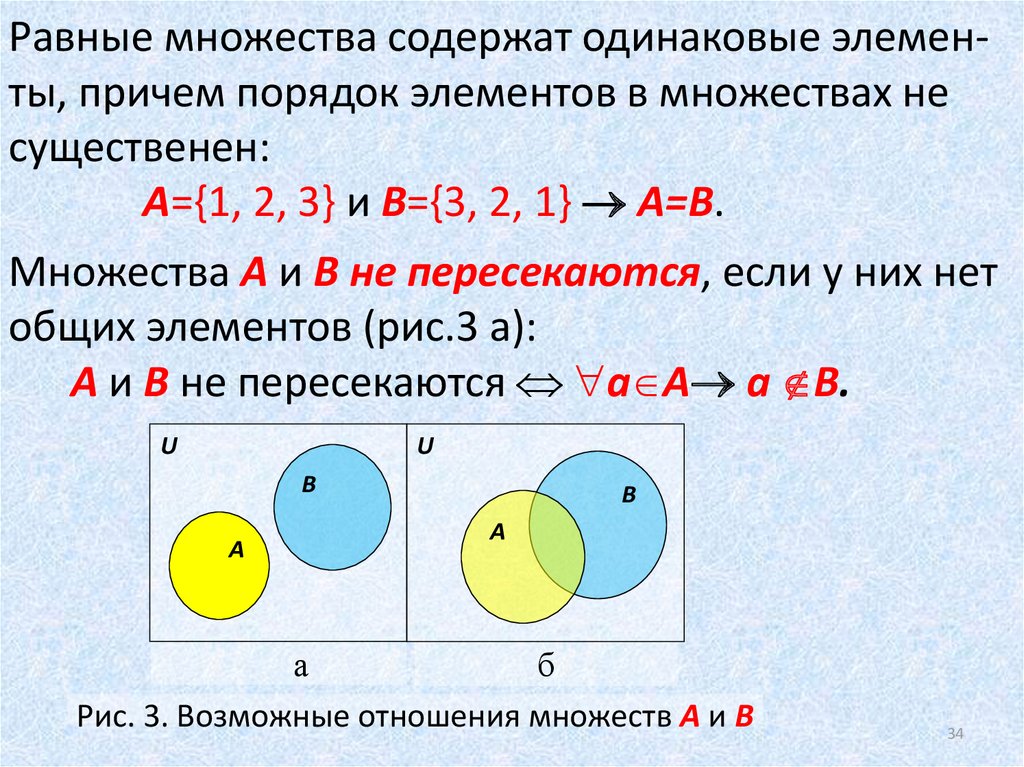 Если мы хотим обратиться к
набор {0, 1, 2, 3, …}, когда мы используем это
определение N , мы всегда можем написать N ∪ {0}
(о значении символа ∪ мы поговорим чуть позже).
В качестве альтернативы, термины положительное целое число и неотрицательное число
целых всегда однозначны: ноль не положителен, но он
неотрицательный. Следовательно, другой способ обратиться к множеству
{1, 2, 3, …} — это «множество положительных
целые числа», а {0, 1, 2, 3, …} – это
множество неотрицательных целых чисел».
Если мы хотим обратиться к
набор {0, 1, 2, 3, …}, когда мы используем это
определение N , мы всегда можем написать N ∪ {0}
(о значении символа ∪ мы поговорим чуть позже).
В качестве альтернативы, термины положительное целое число и неотрицательное число
целых всегда однозначны: ноль не положителен, но он
неотрицательный. Следовательно, другой способ обратиться к множеству
{1, 2, 3, …} — это «множество положительных
целые числа», а {0, 1, 2, 3, …} – это
множество неотрицательных целых чисел».
Наконец, множество рациональных чисел называется Q (от слова
«частное»). Рациональное число — это число, которое можно
записывается точно как дробь или частное двух целых чисел. Например,
число 2/3 является рациональным числом, как и число –7/2. Все
целые числа являются рациональными числами, потому что любое целое число можно записать в виде дроби
со знаменателем 1; например, целое 5 можно записать
как 5/1. Другие примеры рациональных чисел включают числа, которые могут быть
записывается как завершающая десятичная дробь (например, число 8,13 может быть
записывается как 813/100) или как повторяющаяся десятичная дробь (например,
число 0,333… можно записать как 1/3). Не все действительные числа
однако рациональны. Примеры вещественных чисел, которые нельзя записать точно
как дробь двух целых чисел включает
√2
и π ; десятичные расширения этих чисел продолжаются вечно
и никогда не повторять. В этом курсе у нас не будет особой необходимости различать
рациональные числа из действительных чисел, поэтому мы редко (если вообще когда-либо) будем использовать
символ Q .
Не все действительные числа
однако рациональны. Примеры вещественных чисел, которые нельзя записать точно
как дробь двух целых чисел включает
√2
и π ; десятичные расширения этих чисел продолжаются вечно
и никогда не повторять. В этом курсе у нас не будет особой необходимости различать
рациональные числа из действительных чисел, поэтому мы редко (если вообще когда-либо) будем использовать
символ Q .
Обратите внимание, что эти четыре набора чисел являются (правильными) подмножествами друг друга: N ⊂ Z ⊂ Q ⊂ R .
Обозначение конструктора наборов
Перечислить все элементы набора можно, если набор не слишком
большой. Для больших наборов мы можем пропустить некоторые элементы, написав
многоточие (…), как мы видели, но это возможно только тогда, когда
элементы следуют шаблону, который хорошо виден в первых нескольких элементах.
Это не всегда так. Например, множество всех простых чисел между
100 и 500 можно было бы записать как
{101, 103, 107, …, 499}, но это не очень
полезно написать, потому что очень трудно угадать правильный
закономерность только из этих цифр (и это выражение не исключает
неправильные шаблоны, такие как «набор всех нечетных чисел между 100
и 500, кроме кратных 5″).
В подобных ситуациях часто лучше описать набор, указав условие для членства. (Наше английское описание набора выше делает именно это; фактически он говорит, что условие для числа Элемент набора состоит в том, что число должно быть простым и лежать в пределах 100. и 500.) Когда мы хотим таким образом описать множество, мы можем использовать нотация построителя набора .
Когда мы используем нотацию построителя наборов, мы должны сначала установить универсальный набор (иногда называемый доменом дискурса или вселенная дискурса ), представляющая собой множество всех возможных объектов
на рассмотрении. Например, можно сказать, что универсальное множество R , множество всех действительных чисел; или, возможно, Z ,
набор целых чисел. Другая возможность состоит в том, чтобы использовать ранее определенный набор в качестве
универсальный набор. Если мы определили А = {1, 2, 3},
например, мы можем использовать A в качестве универсального набора.
После того, как мы выбрали универсальный набор, мы можем «построить» набор, выбор всех элементов универсального множества, удовлетворяющих заданному условие. Например, если универсальный набор равен R , мы можем определить установить B , скажем, как набор всех элементов R , которые больше 17. (Таким образом, B содержит числа 18 и 29,4, например, но не содержит 11,26 или -30.) Это установить B можно записать, используя нотацию конструктора наборов, как
.B = { x ∈ R | x > 17 }.
В системе построения наборов вертикальная черта | следует читать как «такой, что» или «удовлетворяющий условию, что». Итак Вышеприведенное выражение можно прочитать как « B — это набор, который содержит все элементы x универсального набора R удовлетворяющее условию, что x > 17».
Обратите внимание, что универсальный набор указан слева от вертикальной
bar, и дается имя для представления произвольного элемента универсального множества
с помощью символа ∈. Справа от полосы находится условие
которым элемент должен удовлетворять, чтобы быть членом множества, которое мы
строительство. Имя произвольного элемента ( x в примере
выше) может быть любым; приведенный выше пример означает то же самое, что и, скажем,
Справа от полосы находится условие
которым элемент должен удовлетворять, чтобы быть членом множества, которое мы
строительство. Имя произвольного элемента ( x в примере
выше) может быть любым; приведенный выше пример означает то же самое, что и, скажем,
B = { z ∈ R | z > 17 },
или даже
B = { ♣ ∈ R | ♣ > 17 },
, хотя ♣ не очень распространенное имя переменной (и оно, вероятно, вызовет некоторое недоумение, поэтому его, вероятно, следует избегать).
Почему важен универсальный набор? Ответ состоит в том, что множество, описанное с помощью Нотация создателя множества всегда будет подмножеством универсального множества. Рассмотрим набор
C = { x ∈ N | x > 17 },
, который определяется точно так же, как набор B выше.
за исключением того, что универсальный набор был изменен на N .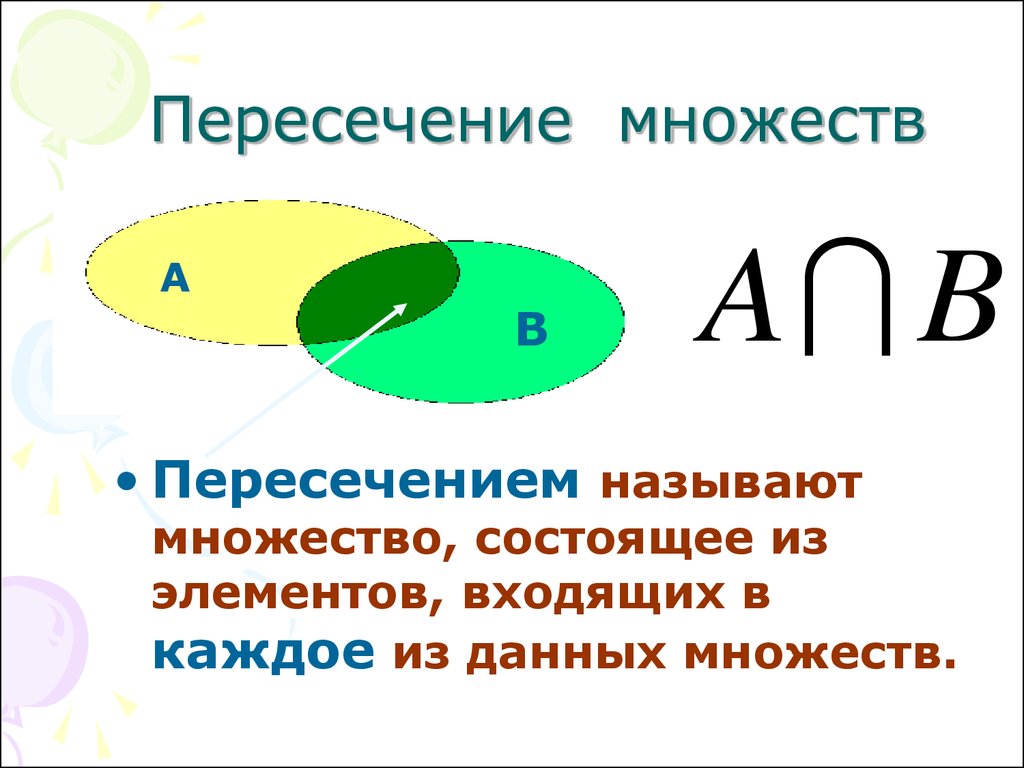 Наборы B и C имеют много общего; Например,
число 20 является элементом как B , так и C .
Однако, начиная с , C состоит из элементов N .
а не элементы R , набор C содержит только
(положительные) целые числа и не содержит чисел с дробной частью. Так,
например, число 23,456 является элементом B , но не элемент C .
Наборы B и C имеют много общего; Например,
число 20 является элементом как B , так и C .
Однако, начиная с , C состоит из элементов N .
а не элементы R , набор C содержит только
(положительные) целые числа и не содержит чисел с дробной частью. Так,
например, число 23,456 является элементом B , но не элемент C .
В качестве другого примера нотации конструктора наборов рассмотрим набор
.D = { n ∈ N | n ≤ 10 }.
Что это значит? Читая слева направо по одному символу за раз, мы читай « D – это набор, содержащий все элемент N в универсальном наборе N удовлетворяющий при условии, что n ≤ 10». Здесь универсальный набор есть множество N натуральных чисел (которое, как мы договорились, не include 0), поэтому мы видим, что
D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Обратите внимание, что набор, описанный с помощью нотации конструктора наборов, может быть пустым, если нет элементы универсального множества удовлетворяют указанному условию! Например, набор
E = { n ∈ N | n < 0 }
— пустое множество, потому что натуральных чисел меньше нуля не существует. А несколько более тонкий пример набора, который оказывается пустым, это
F = { n ∈ N | 8 < n < 9 },
, которое пусто, потому что нет натурального числа n , которое удовлетворяет неравенству 8 < n < 9. (Напомним, что 8 < n < 9 — сокращение для «8 < n и n < 9». Ни одно натуральное число не удовлетворяет этому условию, потому что каждое натуральное число либо меньше или равно 8, либо больше или равно 9.)
Вариации нотации конструктора наборов
Условие в нотации построителя набора не нужно записывать в
математические символы. Обычно условие записывается как
английская фраза. Например, мы можем определить S как набор
совершенные квадраты, написав
Обычно условие записывается как
английская фраза. Например, мы можем определить S как набор
совершенные квадраты, написав
S = { t ∈ Z | t — полный квадрат}.
(Здесь в качестве универсального набора мы использовали Z вместо N , даже хотя никакое отрицательное целое число не является полным квадратом, потому что ноль равен a идеальный квадрат, и мы хотели включить его в набор S . Этот пример, в котором было бы удобно, чтобы 0 был в N . Ну ладно.)
Если универсальный набор указан явно в словах до или после использование нотации построителя наборов, он часто опускается в нотации построителя наборов сам. Например, при определении нескольких наборов мы можем сказать:
Пусть
К = { x | x ≠ 0 }, L = { x | −6 ≤ x < 1 }, M = { x | x ≥ 50 и x идеально}, , где универсальный набор — это набор действительных чисел.
В этом случае, поскольку универсальный набор указан как набор реальных чисел, мы должны читать определение множества K как » K это множество, содержащее все действительные число x , удовлетворяющее условию, что x ≠ 0». Другими словами, K – это набор всех действительных чисел, кроме 0. Можете ли вы понять определения L и M ?
Иногда вместо вертикальной черты используется двоеточие (:). нотация построителя множества. Это особенно распространено, когда состояние включает в себя выражение абсолютного значения, потому что вертикальные полосы, используемые в абсолютном значении обозначение можно легко спутать с вертикальной чертой, используемой в конструкторе наборов. обозначение.
Набор операций
Есть несколько операций, которые можно выполнить над множествами, чтобы получить
новые комплекты из старых. Эти операции столь же фундаментальны для теории множеств, как и
сложение и умножение относятся к арифметике.
Соединения и пересечения
Рассмотрим наборы
| A | = | {1, 2, 3, 5, 8, 13}, | |
| B | = | B= | B. |
Одна полезная вещь, которую можно сделать с этими наборами, — это «поместить их вместе» — другими словами, создать новый набор, содержащий все элемент A , а также каждый элемент B . Такой набор называется соединением из A и B , и записывается A ∪ B . В этом примере мы есть
A ∪ B = {1, 2, 3, 4, 5, 6, 8, 13}.
Обратите внимание, что числа 2 и 8 содержатся в обоих А и B , но каждый из них указан только один раз. in A ∪ B , потому что количество раз элемент, указанный в наборе, не имеет значения.
Какими бы ни были наборы A и B , всегда
правда что А ⊆ ( А ∪ В ) и B ⊆ ( A ∪ B ). Делать
понимаешь почему?
Делать
понимаешь почему?
Еще одна полезная операция — выбрать элементы, которые A и B имеют общее. Это называется пересечение A и B , и написано А ∩ В . В нашем текущем примере у нас есть
А ∩ В = {2, 8}.
Какими бы ни были наборы A и B , всегда правда что ( A ∩ B ) ⊆ A и ( A ∩ B ) ⊆ B . Делать понимаешь почему?
Если наборов A и B не имеют общих элементов, они называются непересекающимися . В этом случае пересечение A ∩ B пусто установлен.
Предположим, что одно из двух множеств, с которыми мы работаем, является пустым множеством. Независимо от того
что такое набор A , всегда верно, что А ∪ ∅ = А и А ∩ ∅ = ∅. Вы понимаете, почему?
Вы понимаете, почему?
Дополняет
Еще одна полезная вещь, которую можно сделать с набором, — рассмотреть все, что есть. вместо в комплекте. Для того, чтобы иметь точное значение для «все», нам нужно указать универсальный набор (как мы сделали, когда используя нотацию конструктора наборов). Совокупность всех элементов универсального множества, не являются элементами множества называется дополнением A , и написано А . (Еще один распространенный обозначение дополнения A А в .)
Например, предположим, что универсальный набор равен Н . Пусть P быть набором простых чисел; то есть
P = { n ∈ N | n простое } = {2, 3, 5, 7, 11, 13, 17, …}.
Затем P , дополнение P , это набор составных чисел (и число 1, который не является ни простым, ни составным):
P = {1, 4, 6, 8, 9, 10, 12, …}.
Установить разницу
Иногда нам нужно обратиться ко всем элементам в некоторых установить A , которые являются , а не элементами какого-либо другого набор B . Эта операция называется набором разности . (иногда называется относительным дополнением ) и пишется А \ В . (Некоторые авторы используют стандартный знак минус и напишите A − B , но операция множества разница сильно отличается от обычной идеи вычитания, поэтому обратная косая черта более распространена.)
Например, если у нас есть наборы
| A | = | {3, 4, 5, 10, 14, 17}, | |||||||||||||||||||||||||||||||||||||||||
| B | = | B | = | . установленная разница A \ B равна А \ В = {3, 10, 14}, , потому что это элементы A , которые не являются элементами B . Нет необходимости, чтобы один набор был подмножеством другого. Например, рассмотреть наборы
Ни один из этих наборов не является подмножеством другого. Операция установки разницы однако по-прежнему имеет смысл. У нас есть C \ D = {3, 15}, , потому что это элементы C , которые не являются элементами из D ; и D \ C = {4, 5, 20}, , потому что это элементы D , которые не являются элементами C . Обратите внимание, что если универсальное множество называется U , то мы можем выразить дополнение множества A как разность множеств: А = U \ А . Давайте подумаем, как ведет себя пустой набор с разницей в наборе операция. Независимо от того, какой набор A это всегда верно, что А \ ∅ = А и ∅ \ A = ∅. Вы понимаете, почему? СкобкиКогда мы выполняем две или более операции над множествами, нам часто нужно включать круглые скобки, чтобы сделать порядок вычислений однозначным. Например, предположим у нас есть наборы
Рассмотрим выражение ( A ∪ B ) ∩ C . Мы сначала оцените A ∪ B , потому что это в скобки. Мы видим, что А ∪ В = {1, 2, 3, 4}, так ( A ∪ B ) ∩ C = {1, 2, 3, 4} ∩ C = {3, 4}. С другой стороны, предположим, что у нас есть выражение А ∪ ( B ∩ C ), который точно так же, за исключением размещения скобок. Мы тут сначала оцените B ∩ C , что {3, 4}, поэтому мы получаем A ∪ ( B ∩ C ) = A ∪ {3, 4} = {1, 2, 3, 4}. Этот пример показывает, что размещение скобок важно. Скобки свободны — если вы не уверены, нужны ли вам круглые скобки в выражении, поместите их на всякий случай. Диаграммы Веннадиаграммы Венна, введенные английским математиком Джоном Венном в 1881 году очень полезны для понимания отношений между наборы. На диаграмме Венна наборы представлены перекрывающимися формами.
самая внешняя форма, которая обычно представляет собой прямоугольник, представляет собой универсальный
установлен. Внутри этого прямоугольника находятся другие формы (часто круги), представляющие
различные наборы. Эти формы могут перекрываться, указывая на возможность того, что две или
несколько наборов могут иметь некоторые общие элементы. Ниже показан наиболее распространенный способ построения диаграммы Венна для двух наборов. A и B . Здесь универсальный набор по телефону U . Например, предположим, что универсальный набор равен .U = {1, 2, 3, …, 12} и мы определяем наборы
На приведенной ниже диаграмме Венна показаны целые числа от 1 до 12 в
соответствующие места. Например, число 1 находится внутри круга.
обозначен A , но вне круга B ,
потому что 1 является элементом A , но не B .
число 7 находится внутри обоих кругов, потому что оно является элементом обоих A и B . Число 5 находится внутри прямоугольника,
потому что это элемент универсального множества, но он вне обоих кругов,
потому что это ни в A или B . Из этой диаграммы легко увидеть, например, что A ∩ B = {3, 7, 11}. Диаграмма Венна особенно полезна, когда мы думаем об абстрактных или неизвестные наборы, а не конкретные примеры, такие как наборы выше. В этом случай, когда мы не можем явно выписать элементы множеств; вместо этого мы представляем различные области самой диаграммы как метафоры для различных наборов, которые мы работают с. Полезно заштриховать или раскрасить части диаграммы, чтобы выделить определенные области. Заштрихованные области на диаграммах ниже показывают области, соответствующие указанные наборы.
Одним из способов использования диаграмм Венна является проверка того, что два выражения действительно описывают
тот же набор. ( A ∪ B ) \ ( A ∩ B ) а также ( A \ B ) ∪ ( B \ A ). Нарисуем диаграммы Венна для этих наборов. Мы начнем с выражение слева. Диаграммы Венна для А ∪ В и A ∩ B показаны ниже.
Теперь заштрихованная область на диаграмме Венна для ( A ∪ B ) \ ( A ∩ B ) должны включать области, заштрихованные на диаграмме Венна для A ∪ B , но , а не , заштрихованы Венном схема для A ∩ Б . Итак, диаграмма Венна для ( A ∪ B ) \ ( A ∩ B ) выглядит так:
Теперь рассмотрим другое выражение:
( A \ B ) ∪ ( B \ A ).
Теперь заштрихованная область на диаграмме Венна для ( A \ B ) ∪ ( B \ A ) должна включать заштрихованную область на диаграмме Венна для A \ B а также заштрихованная область в Венне схема для B \ A . Итак, диаграмма Венна для ( А \ В ) ∪ ( В \ А ) выглядит так:
Обратите внимание, что это точно такая же диаграмма Венна, которую мы получили для
( A ∪ B ) \ ( A ∩ B ).
Это показывает, что эти два выражения представляют собой разные способы именования одного и того же
установлен. ( A ∪ B ) \ ( A ∩ B ) = ( A \ B ) ∪ 9 ( B 3 0 0 \ 090). (Этот набор иногда называют симметричной разностью A и B , письменный А ∆ В .) вопросовВот несколько вопросов о наборах, чтобы проверить ваше понимание.
Назад на стр. 21-110 Последнее обновление: 19 марта 2010 г. Брайан КеллНаборы и операции с наборамиНаборы и операции с наборами Раздел 2.1 Комплект: а коллекция предметов Элементы: члены принадлежность к набору Наборы могут быть четко определенными (без двусмысленности) или нет четко определенный. Обозначения: S = {а, б, в } представляет список, реестр. Множество S равно множеству элементов: а, б, в. Обозначение конструктора набора: г = {х | х > 0 } гласит: «Набор G равен набору значений x, таких что х это больше 0.» Итак, G — это множество всех положительных чисел, т. е. невозможно перечислить, поэтому необходима нотация компоновщика. средство является элементом (принадлежит) значит не является элементом (не является ли не принадлежит) Кардинальное число набора — это количество элементов в
набор. n(S) = 3, Каково кардинальное число набора G выше? п(Г) = с {а, б, в} в S е { а, б, в} ф S Т = {с, б, а} Т = С Два набора равны тогда и только тогда, когда каждый элемент в одном наборе находится в другом. Таким образом, каждый элемент T должен быть в S и каждый элемент в S находится в Т. Пустой набор: Набор, не содержащий элементов, обозначается , нулевой набор. п( ) = 0 Если Е = { } Затем п(Е) = 0 Примечание: набор Z = { 0 } не является пустым множеством. п (Z) = 1, в множестве Z есть один элемент, и это элемент 0. Универсальные наборы: U — набор всех возможных используемых элементов в проблеме. Пример 1: Пусть U знак равно { Икс | x учится в этом классе } Пусть А знак равно { Икс | x — студент в первом ряду } В знак равно { Икс | x учится на факультете гуманитарных наук } С знак равно { Икс | x — студент ростом более 7 футов } Подмножество — это набор, который содержится в универсальном наборе. A, B, C являются подмножествами У. А У, Б У, С У И вообще U, или любой другой набор. Диаграммы Венна: Операции с множествами. Пересечение и соединение: Пересечение двух наборов является перекрытием наборов; что у них обоих есть общего. А В знак равно { Икс | х А и х Б } Союз из двух комплектов состоит из всех элементов в А или Б или оба. А В знак равно { Икс | х А или х Б } Взаимоисключающие наборы не имеют ничего общего. Если Вт = {1, 2, 3} и S = {а, б, в} Тогда В S = Кардинальное число союза наборов: п(А B ) = n(A) + n(B) n(A Б) , в противном случае некоторые элементы учитываются дважды. Дополнение к набору A: Обозначается A (простой), Элементы, которые есть в Универсальном наборе, но отсутствуют в специальный комплект, А.
Пример 2: Пусть U знак равно { Икс | Икс это буква алфавита } А знак равно { Икс | х — согласная} А знак равно { Икс | х не согласная } Кардинальное число дополнений n(А) + n(А) = n(U) Так n(A) = n(U) n(A) Найти n(A). п (и) n(A) = n(A) 26 5 = 21
Назад на главную страницу подсчета и вероятности Вернуться к Обзор домашней страницы математических идей Назад на главную страницу математического факультета электронная почта Вопросы и предложения
реальный анализ — Разница между номером и набором с одним номером Наборы — это наборы объектов. Это концептуальный блок для многих студентов. Если набор является коллекцией и в нем есть коллекции, то, спрашивают они, не должны ли элементы в подколлекциях также быть в коллекции? И ответ на это — громкое и абсолютное !!!!! НЕТ !!!!!!. А причина простой базовый нет концепт, нет интерпретация, нет вычисление. Набор представляет собой список объектов с интерпретацией NO . Если в наборе есть: русалка, пакет с собачьим кормом и английский алфавит, то в наборе три вещи. 1) русалка, 2) мешок собачьей еды и 3) английский алфавит. В , а не в есть несколько кусочков корма; у него нет A, K, Q и P. У него , а не есть «слегка ядовитая соленая слюна» и «дыхательная система, функционирующая как под водой, так и на воздухе» — хотя эти вещи содержатся в объекты, их а не объектов в самом наборе. Возможно, было бы проще думать о наборе как о «списке». Думаю, вы все это понимаете. Для ответов на ваши вопросы:
Действительно, да.
Довольно много. …. Я думаю, что главное в Тао:
Есть проблема, что — это натуральное число. Ну, может быть, он собирается проникнуть в конструктивистскую идею построения натуральных чисел из множеств. $0$ — пустой набор. $1$ — набор, содержащий пустой набор. Если вы определили $n$ как определенное множество, тогда будет установлено $n+1$, являющееся объединением этого множества и множества, содержащего это множество. Итак, $0 = \emptyset$ $1 = \emptyset \cup \{\emptyset\}=\{\emptyset\}=\{0\}$ $2 = 1 \cup \{1\} = \ {\emptyset\} \cup \{\{\emptyset\}\} = \{\emptyset, \{\emptyset\}\}=\{0,1\}$. $3 = 2\cup \{2\} = \{\emptyset, \{\emptyset\}\}\cup \{ \{\emptyset, \{\emptyset\}\} \}= \{ \emptyset , \{\emptyset\}\},\{\emptyset, \{\emptyset\}\} \}=\{0,1,2\}$ и так далее. И хотя я стал ценить и полагаться на эту концепцию натуральных чисел, я искренне надеюсь твоя реакция «Что за #@&! ты говоришь!» Натуральные числа не являются множествами. Но что такое натуральных чисел ? Или, если уж на то пошло, что такое… что-нибудь . С точки зрения теоретика множеств все — это концепция множеств. Мы начинаем с идеи множества, в котором ничего нет, и идеи размещения вещей в множествах, и мы можем построить последовательностей объектов (а «последовательность» эквивалентна , считая вещей одну за другой), поместив предыдущий объект в себя, чтобы сделать следующий объект. Фу!…… Но, как указывает Тао… натуральные числа на самом деле не наборов , которые мы делаем таким образом, а концепция мощности того, сколько элементов в комплекты, которые мы создаем. Наш первый набор — $K_0 = \emptyset = \{\}$ — набор, в котором ничего нет. И наше первое натуральное число — это $0 = |K_0|$ количество элементов в нем. В $K_0$ нет элементов. Наш следующий набор $K_1 = \{K_0\}$ набор с одним набором в нем. Наш следующий набор $K_2 = K_1 \cup \{K_1\} = \{K_0, K_1\}$ и $2 = |K_2|$ содержит два элемента. И $K_3 = \{K_0,K_1,K_2\}$ и $3=|K_3|$. И так далее. Итак, я подозреваю, что Тао пытается добраться до двух зайцев: 1) Множество может иметь множества как элементы, но элементы внутри этих множеств не являются элементами «верхнего» множества. 3) Натуральные числа могут быть элементами множеств, но не самими множествами, но могут представлять мощности множеств. Итак, $|\{3\}| = 1$. Но $|\{0,1,2\}| = 3$ и $|\{0,1,\{0,1\}\}|= 3$ и $|\{\emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\ }\}\}| = 3$. Это приводит к первоначальному, казалось бы, круговому, но на самом деле правильному определению: натуральное число $n$ определяется как мощность множества $\{0,1,2,3,…..,n- 1\}$. (Иногда математику стоит взять выходной, сходить в зоопарк и посмотреть на слонов, а на следующий день начать все заново. |

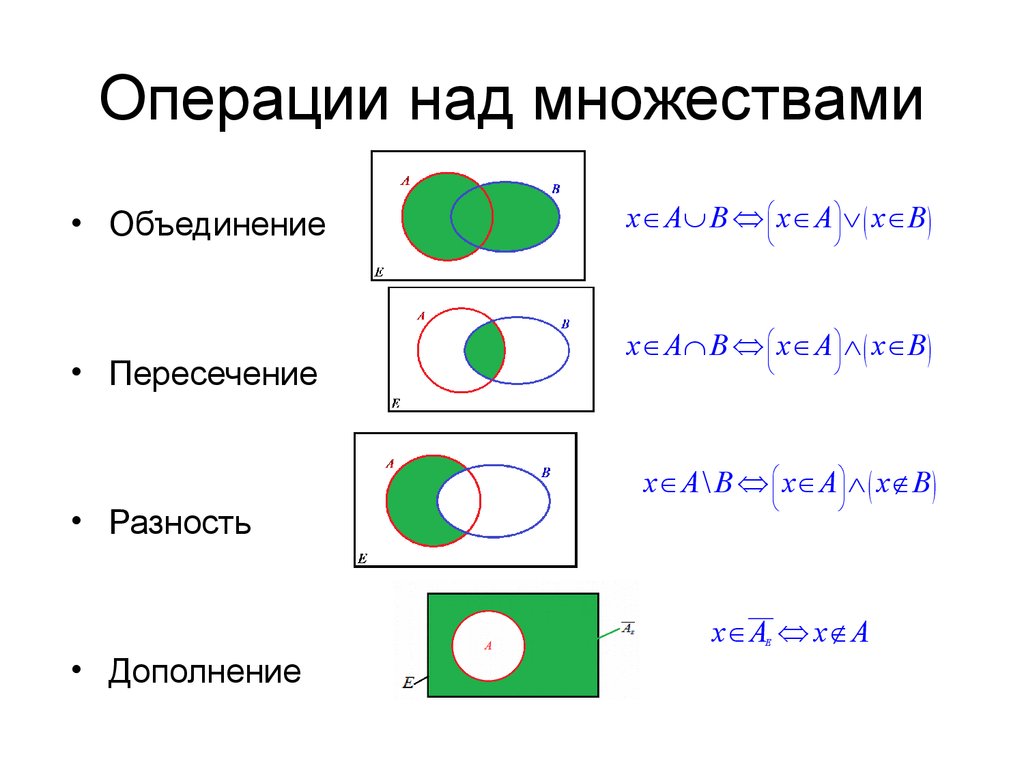





 Например, рассмотрим два выражения
Например, рассмотрим два выражения Диаграммы Венна для A \ B и B \ A показаны ниже.
Диаграммы Венна для A \ B и B \ A показаны ниже. Другими словами, для любых двух наборов A и B будет
правда что
Другими словами, для любых двух наборов A и B будет
правда что
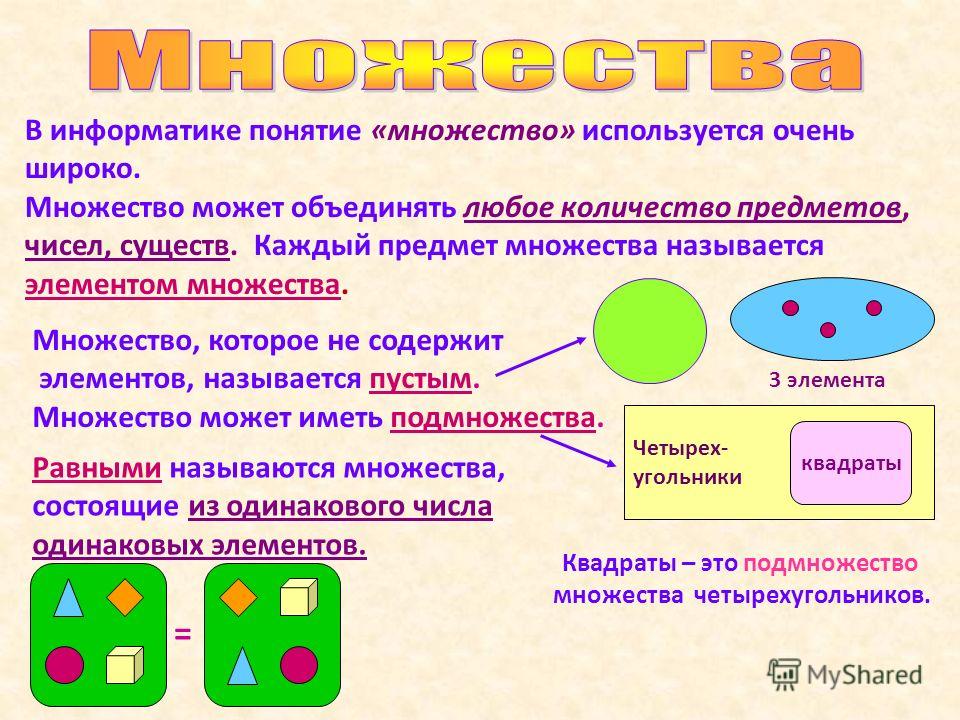 )
) Что такое кардинал
номер набора S выше?
Что такое кардинал
номер набора S выше?

 Предметы, которые можно собирать в наборы, сами могут быть наборами.
Предметы, которые можно собирать в наборы, сами могут быть наборами. Если у вас есть список из трех пунктов: слон Бабар, начальная школа Рузвельта Франклина и стартовый состав нью-йоркских янки 1942 года; тогда в списке есть три вещи. Компоненты элементов в списке сами по себе не входят в список. НО тогда… список подразумевает вещи, которые не являются необходимыми; порядок не имеет значения, определение не имеет значения. Набор в основном сбрасывает вещи в сумку и носит их.
Если у вас есть список из трех пунктов: слон Бабар, начальная школа Рузвельта Франклина и стартовый состав нью-йоркских янки 1942 года; тогда в списке есть три вещи. Компоненты элементов в списке сами по себе не входят в список. НО тогда… список подразумевает вещи, которые не являются необходимыми; порядок не имеет значения, определение не имеет значения. Набор в основном сбрасывает вещи в сумку и носит их. Математика начинается с… как можно меньшего, и что мы делаем, когда считаем?
Математика начинается с… как можно меньшего, и что мы делаем, когда считаем? Наборы есть наборы. Верно?
Наборы есть наборы. Верно? И наше следующее натуральное число — это $1 = |K_1|$ количество элементов в нем.
И наше следующее натуральное число — это $1 = |K_1|$ количество элементов в нем.