А в 0 степени равно: Степень с показателем 0 — урок. Алгебра, 7 класс.

0=?» — Яндекс Кью

Алгебра 7-9 классы. 3. Степень с натуральным показателем. Свойства степени

Подробности: Категория: Алгебра 7-9 классы

СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

ОПРЕДЕЛЕНИЕ СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

Произведение нескольких одинаковых множителей можно записать в виде степени. Например,

Выражение 5⁷ читают по-разному: «Пять в седьмой степени», «Седьмая степень числа пять», «Степень числа пять с показателем семь».

Определение. Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.

Степень числа а с показателем n обозначают так: аⁿ. Выражение аⁿ называют степенью, число а — основанием степени, число n — показателем степени.

По определению степени:

Вообще,

Нахождение значения степени называют возведением в степень. Приведем примеры возведения в степень:

При возведении в степень отрицательного числа может получиться как положительное число, так и отрицательное. Например,

Степень отрицательного числа с четным показателем есть число положительное, так как произведение четного числа отрицательных множителей положительно. Степень отрицательного числа с нечетным показателем есть число отрицательное, так как произведение нечетного числа отрицательных множителей отрицательно.

Квадрат любого числа есть число положительное или нуль, т. е. при любом а.

Вычислим значения нескольких выражений, содержащих степени.

Пример 1. Найдем значение выражения :

Значит,

Пример 2. Найдем значение выражения

Значит,

УМНОЖЕНИЕ И ДЕЛЕНИЕ СТЕПЕНЕЙ

Выражение а²а³ представляет собой произведение двух степеней с одинаковыми основаниями. Это произведение можно записать в виде степени с тем же основанием:

Значит,

Мы видим, что произведение а²а³ равно степени с тем же основанием и показателем, равным сумме показателей перемножаемых степеней.

Докажем, что для любого числа а и произвольных натуральных чисел m и n

Для этого, используя определение степени и свойства умножения, представим выражение а^mаⁿ сначала в виде произведения множителей, каждый из которых равен а, а затем в виде степени:

Таким образом,

Доказанное равенство выражает свойство произведения степеней. Его называют основным свойством степени. Оно распространяется на произведение трех и более степеней.

Например,

Отсюда следует правило умножения степеней: при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

Приведем примеры:

Выражение а⁷:а³ является частным двух степеней с одинаковыми основаниями. Это частное при можно представить в виде степени с тем же основанием. Действительно, так как , то по определению частного

Мы видим, что частное а⁷:а³ равно степени с тем же основанием и показателем, равным разности показателей делимого и делителя.

Докажем, что для любого числа и произвольных натуральных чисел тип, таких, что ,

Покажем, что .

Действительно, по основному свойству степени

Значит, по определению частного

Итак, при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя

Приведем примеры:

Мы вывели правило деления ат на а^m для случая, когда . Если это правило применить к частному aⁿ:aⁿ, то получится

Степень с нулевым показателем не была определена. Так как при всяком и любом натуральном n

то считают, что при

Определение. Всякое число (кроме нуля) в нулевой степени равно единице.

Например, 2° — 1, (— 3,5)° =1. Выражение 0° не имеет смысла.

Теперь, после введения нулевой степени, мы можем применять формулу и в том случае, когда m = 0 или n = 0 (при ). Точно так же формула справедлива и тогда, когда или .

ВОЗВЕДЕНИЕ В СТЕПЕНЬ ПРОИЗВЕДЕНИЯ И СТЕПЕНИ

Выражение является степенью произведения множителей а и b. Это выражение можно представить в виде произведения степеней а и b:

Значит,

Мы видим, что четвертая степень произведения аb равна произведению четвертых степеней множителей а и b.

Докажем, что для любых а и b и произвольного натурального числа n

По определению степени

Сгруппировав отдельно множители а и множители b, получим :

Воспользовавшись определением степени, находим:

Следовательно,

Свойство степени произведения, выраженное равенством , распространяется на степень произведения трех и более множителей. Например,

Отсюда следует правило: (пpu возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

Выражение есть степень, основание которой само является степенью. Это выражение можно представить в виде степени с основанием а:

В результате возведения степени а⁵ в третью степень мы получили степень с тем же основанием и показателем, равным произведению показателей 5 и 3.

Докажем, что для любого числа а и произвольных натуральных чисел m и n

По определению степени

Согласно основному свойству степени

Заменим сумму произведением mn.

Тогда получим:

Следовательно,

Из равенства следует правило: при возведении степени в степень основание оставляют тем же, а показатели перемножают.

Свойства степеней, выраженные формулами и , имеют место и для степеней с нулевым показателем (если основания отличны от нуля).

Чему равно 0 в 0 степени? — IronSet

Plan

1 Чему равно 0 в 0 степени?
2 Сколько будет 0 в любой степени?
3 Сколько будет 1 в 0 степени?
4 Как возвести число в степень?
5 Как возвести число в степень в Паскале?
6 Что нужно сделать чтобы возвести одночлен в степень?
7 Как перевести дробь в степень?
8 Как возводить отрицательные дроби в степень?
9 Что происходит с показателями при возведении степени в степень?
10 Как умножать числа в степени?
11 Как сократить число в степени?
12 Как сокращать степени с разными основаниями?
13 Как умножать дроби 5 класс?
14 Что нужно сделать чтобы сократить дробь?
15 Как правильно сокращать обыкновенные дроби?
16 Что нужно сделать для сокращения дроби?
17 Как сократить дробь 5 15?

Чему равно 0 в 0 степени?

Известно, что абсолютно любое число в нулевой степени равно единице. Почему 0 в степени 0 равно 1? Доказать это просто, при умножении степеней с одинаковым основанием их показатели складываются, а при делении – вычитаются.

Сколько будет 0 в любой степени?

Любое число в нулевой степени равно единице. Ноль в любой натуральной степени равен нулю.

Почему любое число в степени 0 равно 1?

Таким образом нулевой показатель степени как бы говорит о том, что число не умножается само на себя, а делится само на себя. …

Сколько будет 1 в 0 степени?

Любое число в нулевой степени (за исключением 0) равно 1.

Как возвести число в степень?

Как возвести число в натуральную степень Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем.

Как быстро возвести число в степень?

Это можно записать так: Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем.

Как возвести число в степень в Паскале?

Чтобы возвести число в степень, его надо умножить само на себя количество раз, равное показателю степени. Т. е.

Что нужно сделать чтобы возвести одночлен в степень?

При возведении одночленов в степень: — каждый коэффициент одночлена возводится в степень по отдельности; — показатели переменных множителей одночлена (буквы) умножаются на показатель степени, в которую надо возвести одночлен.

Как получить число в квадрате?

Квадрат числа a обозначают a². Читают: «a в квадрате». Выражение a² назвали квадратом числа a, так как именно такой формулой выражается площадь квадрата со стороной a. Таким образом, чтобы найти квадрат некоторого числа, надо это число взять множителем два раза и вычислить произведение.

Как перевести дробь в степень?

Для того, чтобы возвести дробь в степень, необходимо возвести её числитель и знаменатель в эту же степень. При возведение в степень смешанной дроби, сначала нужно эту дробь преобразовать в неправильную, а затем возвести в степень её числитель и знаменатель.

Как возводить отрицательные дроби в степень?

Степень с дробным показателем определена только для положительных a (a>0). Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени. Дробь в минус первой степени — это «перевернутая» дробь.

Как умножать дроби с разными степенями?

Умножение дробей. Возведение дроби в степень

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

Что происходит с показателями при возведении степени в степень?

При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.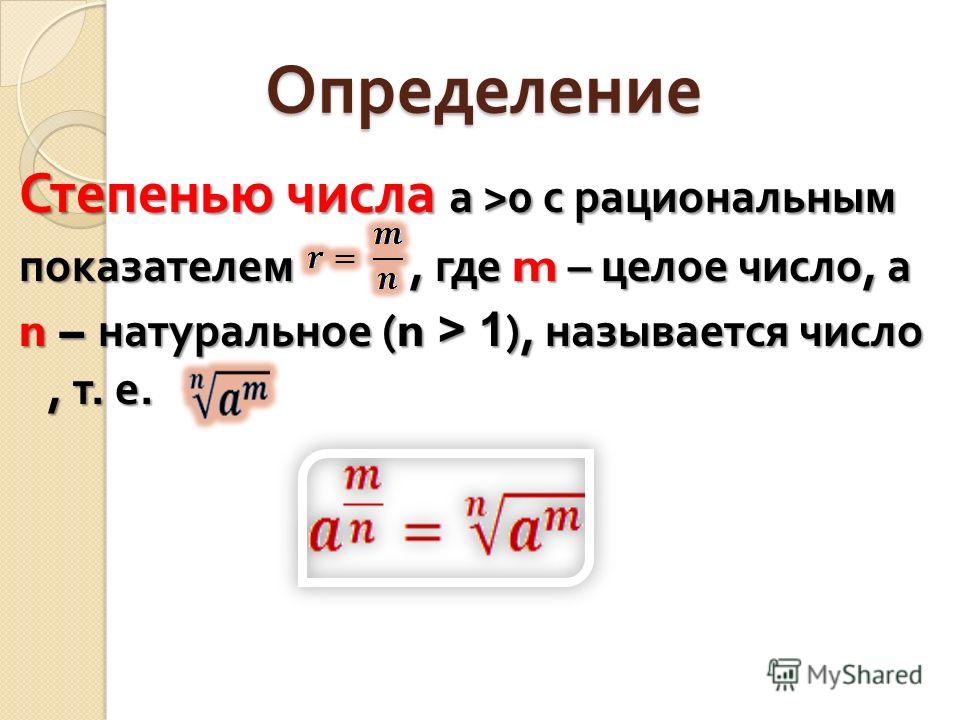 (an)m = an · m, где «a» — любое число, а «m», «n» — любые натуральные числа.

Как умножать числа в степени?

Чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным: an · bn = (a · b)n , гд

Как произведение двух множителей возвести в степень?

Свойство степени произведения распространяется на степень произведения двух и более множителей: (3a2b)2 = 9a4b2. Отсюда следует правило: Чтобы возвести произведение в степень, можно отдельно возвести в эту степень каждый множитель и полученные результаты перемножить.

Как сократить число в степени?

Степени сокращаем на степень с наименьшим показателем. Сократить дробь — значит, разделить числитель и знаменатель на один и тот же делитель, а при делении степеней показатели вычитаем. a² и a⁷ сокращаем на a².

Как сокращать степени с разными основаниями?

1) Если надо умножить два числа с одинаковыми основаниями, но разными показателями степеней, то общее основание возводится в сумму степеней. 2) Если основания разные, а показатели одинаковые, то нужно возводить в степень произведение оснований.

Когда нельзя сокращать дроби?

Если числитель и знаменатель представлены числовыми или буквенными выражениями, то на слагаемое сокращать нельзя. Сумму (разность), если возможно, надо преобразовать в произведение и сократить на общий множитель числителя и знаменателя дроби.

Как умножать дроби 5 класс?

Чтобы умножить дробь на дробь, надо:

числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;
знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;

Что нужно сделать чтобы сократить дробь?

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы. В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби. К примеру, возьмем обыкновенную дробь 624 и сократим ее.

Как сократить дробь с разными знаменателями?

Сокращение дробей — СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ — ОБЫКНОВЕННЫЕ ДРОБИ С помощью признаков делимости найти общий делитель числителя и знаменателя дроби. Делить числитель и знаменатель дроби на общий делитель до тех пор, пока не получится несократимая дробь.

Как правильно сокращать обыкновенные дроби?

Деление и числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби.

Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.
Сократим дробь на 3 (делим числитель на 3;
Сокращаем дробь на 7.

Что нужно сделать для сокращения дроби?

Для примера, проведем сокращение обыкновенной дроби 8/24, разделив ее числитель и знаменатель на 2. Иными словами, сократим дробь 8/24 на 2. Так как 8:2=4 и 24:2=12, то в результате такого сокращения получается дробь 4/12, которая равна исходной дроби 8/24 (смотрите равные и неравные дроби).

Можно ли сократить дробь?

Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД. Найдем НОД, разложив числитель и знаменатель на простые множители.

Как сократить дробь 5 15?

Ответ, проверенный экспертом Ответ: 1/3. Пошаговое объяснение: 5/15 = (5:5)/(15:5) = 1/3.

Показатель степени в математике с примерами решения и образцами выполнения

Оглавление:

При введении понятия о степени подразумевалось, что показатель степени — целое положительное число. Все правила действий над степенями были выведены в этом предположении.

В математике наряду со степенями с целыми положительными показателями рассматриваются также и степени с нулевым, отрицательным и дробным показателями. Более того, исследование некоторых вопросов, имеющих очень большое значение, требует рассмотрения степеней с иррациональными показателями.

В этой главе будет введено понятие о степени с любым вещественным показателем и будет показано, что все правила действий над степенями, выведенные для целых положительных показателей, сохраняются и для любых вещественных показателей.

Понятие о степени с нулевым и отрицательным показателем

Определение. Если а ≠ 0, то а⁰ = 1. Нулевая степень числа, отличного от нуля, равна единице.

Например, 2°= 1; (0,75)°= 1; (—√3)° = 1. Выражение 0° смысла не имеет.

Определение:

Если а ≠ 0 и q — целое положительное число, то

Целая отрицательная степень числа, отличного от нуля, равна единице, деленной на степень того же числа с показателем, равным абсолютной величине отрицательного показателя. Например,

Теорема:

При любых целых положительных m и n справедливо правило деления степеней

Доказательство:

Если m > n, утверждение в доказательстве не нуждается.

Если m = n, справедливость утверждения вытекает из определения нулевого показателя.

Если m < n, справедливость утверждения вытекает из определения целого отрицательного показателя.

Теорема доказана.

Определение нулевого и отрицательного показателей возникло в связи с желанием обобщить установленное ранее правило деления степеней одной и той же величины. Это правило

было выведено в предположении, что m и n— целые положительные числа и что m > n.

Допустим, что правило деления степеней можно применять и.тогда, когда показатель степени делимого равен показателю степени делителя и когда» показатель степени делимого меньше показателя степени делителя.

Пусть m = n, тогда

С другой стороны,

Сравнение результатов (1) и (2) показывает, что a° = 1

Пусть m < n , т. е. n = m + q, где q — положительное число.

Тогда имеем

С другой стороны, посредством сокращения получаем

Сравнение результатов (3) и (4) показывает, что целесообразно считать

где q — целое положительное число.

Рассуждения, которые приведены выше, не являются, конечно,

доказательствами того, что Эти рассуждения проведены только для того, чтобы показать, что принимаемые нами определения нулевого и отрицательного показателя подсказаны нам опытом деления степеней с одним и тем же основанием и единственно возможны, если мы желаем сохранить правило деления степеней для случая, когда показатель степени делимого не превосходит показателя степени-делителя.

Замечание:

Не следует думать, что введением отрицательного показателя дробное выражение превращается в целое . Выражение является лишь другой формой записи выражения

Понятие о степени с дробным показателем

Определение:

Если a > 0 и числа m и n натуральные, то

Пример:

Определение дробного показателя возникло в связи с желанием обобщить правило извлечения корня на случай, когда показатель подкоренного количества не делится на показатель корня. Правило

было выведено в предположении, что m и n натуральные и m делится на n. Теперь, это правило можно применять и тогда, когда m и n— любые натуральные числа.

Известно, что рациональная дробь может быть представлена в различных видах. Например, может быть представлена как и т. п. Выражение с дробным показателем не зависит oт того, в каком виде представлен показатель. Пусть

Тогда

В силу (1) правые части равенств (2) и (3) тождественны. Поэтому

Определение дробного показателя не распространяется на степени с отрицательными основаниями, так как тогда выражения с дробными показателями не обладали бы столь простым и важным свойством, которое указано.

Пример:

Допустим, что определение дробного показателя распространено на степени с отрицательным основанием. Тогда

В то же время

Замечание:

Не следует думать, что введением дробного показателя иррациональное выражение превращается в рациональное . Если выражение иррациональное, то и выражение тоже иррациональное. Выражение является лишь другой формой записи выражения

Понятие о степени с дробным отрицательным показателем

Определение:

Если а — положительное число, то

где m и n— любые натуральные числа.

То есть дробная отрицательная степень положительного числа равна единице, деленной на степень того же числа с показателем, равным абсолютной величине отрицательного показателя. Например,

Теорема:

При любом целом х

Доказательство:

Если x > 0 справедливость утверждения вытекает из определения дробного показателя.

Если х = 0, то

С другой стороны,

Пусть x < 0. Положим х = — m,m > 0. Имеем :

Действия над степенями с рациональными показателями

В этом параграфе буквы m, n, р, q обозначают целые положительные числа, буква r, а также r₁— любые рациональные числа.

Теорема:

Произведение степеней с одинаковыми основаниями равно степени с тем же основанием и с показателем, равным сумме показателей.

Короче: при умножении степеней с одинаковыми основаниями показатели степеней складываются, т. е.

Доказательство:

Переместительный закон умножения справедлив для любых действительных чисел. При любых рациональных r и r₁ степени —действительные числа, поэтому

Для доказательства теоремы достаточно рассмотреть следующие случат

Случай 1. r = 0; r₁ — любое рациональное число. Имеем

Случай 2.Имеем

Случай 3. Имеем

Случай 4. имеем

На основании доказанного в случае 2

Значит,

Методом математической индукции можно показать, что теорема верна для любого количества множителей.

Пример:

Теорема:

Частное от деления степеней с одинаковыми основаниями равно степени с тем же основанием и с показателем, равным разности показателей делимого и делителя.

Короче; при делении степеней с одинаковыми основаниями показатели степеней вычитаются, т. е.

Доказательство:

На основании правила умножения степеней

Отсюда по определению деления

Пример:

Теорема:

Степень произведения двух чисел равна произведению степеней сомножителей, т. е.

Доказательство:

Возможны три случая:

Случай 1. r = 0. Имеем

Следовательно,

Случай 2. . Имеем

Случай 3. Имеем

На основании доказанного в случае 2

Значит,

Методом математической индукции можно показать, что теорема верна для любого количества множителей.

Теорема:

Степень дроби равна частному от деления степени числителя с показателем, равным показателю дроби на степень знаменателя с показателем, равным показателю дроби.

Короче: степень дроби равна частному от деления степени числителя на степень знаменателя, т. е.

Доказательство:

Возможны три случая:

Случай 1. r = 0. Имеем

Следовательно,

Случай 2. Имеем

Случай 3. Имеем

На основании доказанного в случае 2

Значит,

Пример:

Теорема:

Результат возведения степени в степень равен степени с тем же основанием и с показателем, равным произведению показателей, участвующих в действии.

Короче: при возведении степени в степень показатели перемножаются, т. е.

Доказательство:

Возможны шесть случаев:

Случай 1. r = 0. Имеем

Случай 2. r₁=0. Имеем

Случай 3. r > 0; r₁ > 0. Положим Тогда

Случай 4, r < 0, r₁ > 0. Положим r = — r₂r₂, > 0. Тогда

На основании теоремы 4 и доказанного в случае 3

Значит,

Случай 5. r > 0; r₁ < 0. Положим r₁ = — r₃, r₃, > 0. Тогда

На основании доказанного в случае 3

Значит,

Случай 6. r < 0; r₁ < 0. Положим r = -r₂, r₁ = — r₃, r₂ > 0, r₃ >0. Тогда

На oсновании доказанного в случае 4

Значит,

Следствие.

Пример:

Из доказанных теорем вытекает, что для степеней с любыми рациональными показателями справедливы следующие правила, которые были ранее установлены для степеней с натуральными показателями:

1) правило умножения степеней;

2) правило деления степеней;

3) правило возведения произведения в степень;

4) правило возведения дроби в степень;

5) правило возведения степени в степень.

Пример:

Вычислить при а = 2,5 и b= 20

Решение:

При а = 2,5; b = 20 имеем

Ответ. А = 4

Степень с рациональным показателем

Теорема:

Пусть r рационально, тогда

1) если а > 1 и r > 0, то > 1; .

2) если 0 < a < 1 и r > 0 , то < 1

3) если а > 1 и r < 0, то < 1;

4) если 0 < a < 1 и r < 0, то > 1

Доказательство:

1) Пусть а > 1 и , где m и n— натуральные числа. Тогда

Так как

2) Пусть а< 1 и . Положим тогда a₁ > 1. Имеем

так как по доказанному в п. 1)

3) Пусть а > 1 и , тогда

так как по доказанному в п. 1)

4) Пусть а < 1 и , тогда

так как < 1 (по доказанному в п; 2).

Теорема:

Если а > 1 и рациональное r больше рационального r₁, то если же 0 < а < 1, то , т. е. если а > 1 то при возрастании r возрастает и степень , а если 0 < a < 1, то при возрастании r степень убывает.

Доказательство:

Пусть a > 1 и r > r₁ Рассмотрим разность

Так как и, следовательно, , т. е.

Пусть а < 1 и r > r₁. Рассмотрим разность

Так как

Теорема:

Если c > 0, то последовательность имеет пределом единицу, т. е.

Доказательство:

Имеем последовательность

При с = 1 утверждение проверяется легко. Остается рассмотреть два случая: c > 1 и c < 1.

Предположим сначала, что с > 1. Тогда каждый член последовательности (3) больше единицы. Обозначим

Тогда последовательность (3) может быть переписана так:

где при любом n.

Пусть теперь n >1 тогда (см. теорему 1 § 9 гл. V)

Но значит,

Последнее неравенство показывает, что по любому заданному положительному e можно указать столь большой номер N, что при всех n >N число будет меньше e. Действительно, чтобы было меньше е, достаточно, чтобы Таким образом, за N можно принять любое целое число, бoльшее Отсюда вытекает, что а тогда

Пусть теперь подкоренное выражение c₁ меньше единицы. Положим Тогда последовательность

примет такой вид:

или, что все равно,

Последовательность (4), составленная из знаменателей последовательности (7), как показано, стремится к единице, значит, и последовательность (7) стремится к единице, т. е. опять

Понятие о степени с иррациональным показателем

Пусть а — какое-нибудь положительное число и а — иррациональное. Какой смысл следует придать выражению ?

Чтобы сделать изложение более наглядным, проведем его на частном примере. Именно, положим а = 2 и а = 1,624121121112…. Здесь, а — бесконечная десятичная дробь, составленная по такому закону: начиная с четвертого десятичного знака, для изображения а употребляются только цифры 1 и 2, и при этом количество цифр 1, записываемых подряд перед цифрой 2, все время увеличивается на одну. Дробь а непериодическая, так как иначе количество цифр 1, записываемых подряд в его изображении, было бы ограниченным. Следовательно, а — иррациональное число.

Итак, какой же смысл следует придать выражению

Чтобы ответить на этот вопрос, составим последовательности значений а с недостатком и избытком с точностью до . Получим

1,6; 1,62; 1,624; 1,6241; …, (1)

1,7; 1,63; 1,625; 1,6242; … (2)

Составим соответствующие последовательности степеней числа 2:

Последовательность (3) возрастает, так как возрастает последовательность (1) (теорема 2 § 6).

Последовательность (4) убывает, так как убывает последовательность (2).

Каждый член последовательности (3) меньше каждого члена последовательности (4), и, таким образом, последовательность (3) ограничена сверху, а последовательность (4) ограничена снизу.

На основании теоремы о монотонной ограниченной последовательности каждая из последовательностей (3) и (4) имеет предел. Если теперь окажется, что разность последовательностей (4) и (3) сходится к нулю, то из этого будет вытекать, что обе эти последовательности, имеют общий предел.

Разность первых членов последовательностей (3) и (4)

Разность вторых членов

Разность n-х членов

На основании теоремы 3 § 6

Итак, последовательности (3) и (4) имеют общий предел. Этот предел является единственным вещественным числом, которое больше всех членов последовательности (3) и меньше всех членов последовательности (4), его и целесообразно считать точным значением .

Из сказанного вытекает, что и вообще целесообразно принять следующее определение:

Определение:

Если a > 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых есть рациональные приближения а с недостатком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с избытком.

Если a < 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых — рациональные приближения а с избытком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с недостатком.

.Если а= 1, то степенью его с иррациональным показателем а является 1.

Пользуясь понятием предела, это определение можно сформулировать так:

Степенью положительного числа с иррациональным показателем а называется предел, к которому стремится последовательность рациональных степеней этого числа при условии, что последовательность показателей этих степеней стремится к а, т. е.

Пример:

Вычислить с точностью до 0,1 число , если а= 1,624121121112 … (а то же, что и выше).

Решение:

Для приближенного вычисления заметим, что

Далее,

Таким образом, < 3,09.

Испытанием уходим, что (3,03)⁵ = 255,3954324543 < 256. Поэтому . Выходит, что

Число вычислено с точностью до: 0,06.

Свойства степени с любым вещественным показателем

Теорема:

1) Если а > 1 и а > 0, то

2) если 0 < а < 1 и а>0, то

3) если а > 1 и а < 0, то

4) если 0 < а < 1 и а<0, то

Доказательство:

1) Это утверждение доказано для случая, когда о рационально (теорема 1 § 6).

Пусть о иррациональное. Рассмотрим последовательность {} десятичных приближений а с недостатком с точностью до . Среди членов этой последовательности должны находиться, и положительные числа, так как если бы при всех n, то и

Пусть (теорема 1 §6). Но Значит,

2) Положим , тогда a₁ >. 1. По доказанному , значит,

3) Пусть а > 1; а < 0. Положим . Рассмотрим

По доказанному в п. (1) Значит,

4) Пусть а<1; а<0. Положим. Тогда

так как (по доказанному в п. 2).

Теорема:

Если а > 1 и число а больше , то т. е. при а > 1 функция возрастает.

Если 0 < a < 1 и a > то , т. е. при 0 < a < 1 функция убывает.

Доказательство:

Пусть . Рассмотрим разность

Так как , то и, следовательно, . Пусть Рассмотрим

Так как

Решение заданий и задач по предметам:

Математика
Высшая математика
Математический анализ
Линейная алгебра

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Определен ли 0 в степени 0? – Обзоры Вики

Ноль в степени нуля, обозначается 0⁰, Является математическое выражение без согласованного значения. Наиболее распространенные варианты: 1 или оставление выражения неопределенным с обоснованием для каждого, в зависимости от контекста.

Аналогично, можете ли вы поднять мощность от 0 до 0? Таким образом 0 в степени 0 не определено!

0 в любой положительной степени равен 0, поэтому 0 в степени 0 должен быть равен 0. Но любое положительное число в степени 0 равно 1, поэтому 0 в степени 0 должен быть равен 1.

Почему 0-я степень равна 1? Короче говоря, 0 — это единственное число, такое что для любого числа х х + 0 = х. … Итак, причина того, что любое число в нулевой степени равно единице, заключается в том, что любое число в нулевой степени — это просто продукт отсутствия чисел вообще, которое является мультипликативным тождеством, 1.

Каково значение 0 на 0? Отвечать: 0 разделить на 0 не определено.

Мы знаем два факта о нуле: любая дробь с нулем в числителе дает только нулевое десятичное значение. Любая дробь с нулем в знаменателе будет иметь бесконечное значение своей десятичной формы.

Во-вторых, что такое правило нулевой мощности? Правило нулевого показателя: a⁰ = 1, не равно 0. Выражение 0⁰ является неопределенным или неопределенным. В следующем примере, когда мы применяем правило произведения для показателей степени, мы получаем показатель степени, равный нулю.

0 0 существует в пределах?

При простой оценке уравнения 0/0 не определено. Однако, принимая предел, если мы получаем 0/0, мы можем получить множество ответов, и единственный способ узнать, какой из них правильный, — это фактически вычислить предел. … Однако еще раз обратите внимание, что мы получаем неопределенную форму 0/0, если мы пытаемся просто оценить предел.

тогда что такое 1 как степень 2? Ответ: 1 в степени 2 можно представить как 1² = 1 × 1 = 1. Давайте продолжим шаг за шагом, чтобы найти 1². Объяснение: есть два важных термина, которые часто используются в экспонентах: основание и степень.

Как записать 2 в степени 2? Два во второй степени равно 4. Запишем два во второй степени следующим образом: 22.

Является ли квадрат нуля неопределенным?

Любое число, умноженное на ноль, дает ноль, оно никогда не может равняться 2. Поэтому мы говорим деление на ноль не определено. Возможного решения нет.

Что произойдет, если вы спросите Siri 0 разделить на 0? «Сколько ноль разделить на ноль?» Если вы зададите Siri этот вопрос в операционной системе iOS 8, виртуальный помощник iPhone умно скажет вам, что вы не имеете смысла. «Представьте, что у вас нет файлов cookie, — начинает ответ Сири, — и вы поровну делите их между нолью друзей.

Определена ли бесконечность бесконечность?

На это нет ответа. С, бесконечность на самом деле не число, мы не можем обращаться с ним так же, как мы обращаемся с «числами», то есть мы не можем выполнять математические вычисления с Бесконечностью. Из-за вышеизложенного неясно, что именно означает «минус» для бесконечности.

Что такое 10 в степени О? Ответ: 10 в степени 0 равно 10⁰ = 1.

Найдем значение числа 10, возведенного в степень 0. Объяснение: Показатель степени числа показывает, сколько раз число умножается само на себя.

Что такое переменная для степени 0?

Правило для нуля в качестве показателя степени состоит в том, что любое число или переменная (кроме самого нуля), возведенные в степень 0 мощность равна 1.

Как вы объясните 0 0?

0. Ответ: Это верно для любого отличного от нуля знаменателя, но делить на 0 0 0 нельзя независимо от числителя. Опровержение: любое число, деленное на 0 0 0 равно ∞ .

Можете ли вы иметь 0 в качестве предела? Да, предел функции может быть равен 0. Однако, если вы имеете дело с рациональной функцией, убедитесь, что знаменатель не равен 0.

Что делать, если ограничение равно 1 0? В математике такие выражения, как 1/0 не определены. Но предел выражения 1 / x, когда x стремится к нулю, равен бесконечности. Точно так же выражения типа 0/0 не определены. … Таким образом, 1/0 не является бесконечностью, а 0/0 не является неопределенным, поскольку деление на ноль не определено.

Что делать, если лимит равен 0?

Что такое 2-я сила? 1. вторая сила – произведение двух равных членов; «девять — вторая степень числа три»; «гравитация обратно пропорциональна квадрату расстояния»

Что такое 3-я во 2-й степени?

Пояснение: 3 во второй степени можно записать как 3² = 3 × 3, так как 3 умножается на себя в 2 раза. Здесь 3 называется «основанием», а 2 — «показателем» или «степенью». В общем, xⁿ означает, что x умножается на себя n раз. 3 × 3 = 3² = 9.

Является ли 0 целым числом? Целые числа — это числа 0, 1, 2, 3, 4 и т. д. (натуральные числа и нуль). Отрицательные числа не считаются «целыми числами». Все натуральные числа являются целыми числами, но не все целые числа являются натуральными числами, так как ноль — это целое число но не натуральное число.

Как написать во 2-й степени?

Первый способ выразить 10 во второй степени — это написать две десятки со знаком умножения между, например: 10 x 10. Это указывает на два множителя (то есть — вторую степень) 10, умноженные на себя.

Что такое 2-я сила? Когда число описывается как возведенное в степень, это сигнал для вас, что вы собираетесь повторять умножение. … Когда говорят, что число находится во «второй степени», это также называется «в квадрате.

Циклы в программировании. Цикл while. Урок 10 курса «Python. Введение в программирование»

Циклы являются такой же важной частью структурного программирования, как условные операторы. С помощью циклов можно организовать повторение выполнения участков кода. Потребность в этом возникает довольно часто. Например, пользователь последовательно вводит числа, и каждое из них требуется добавлять к общей сумме. Или нужно вывести на экран квадраты ряда натуральных чисел и тому подобные задачи.

Цикл while

«While» переводится с английского как «пока». Но не в смысле «до свидания», а в смысле «пока имеем это, делаем то».

Можно сказать, while является универсальным циклом. Он присутствует во всех языках, поддерживающих структурное программирование, в том числе в Python. Его синтаксис обобщенно для всех языков можно выразить так:

while логическое_выражение {
    выражение 1;
    …
    выражение n;
}

Это похоже на условный оператор if. Однако в случае циклических операторов их тела могут выполняться далеко не один раз. В случае if, если логическое выражение в заголовке возвращает истину, то тело выполняется единожды. После этого поток выполнения программы возвращается в основную ветку и выполняет следующие выражения, расположенные ниже всей конструкции условного оператора.

В случае while, после того как его тело выполнено, поток возвращается к заголовку цикла и снова проверяет условие. Если логическое выражение возвращает истину, то тело снова выполняется. Потом снова возвращаемся к заголовку и так далее.

Цикл завершает свою работу только тогда, когда логическое выражение в заголовке возвращает ложь, то есть условие выполнения цикла больше не соблюдается. После этого поток выполнения перемещается к выражениям, расположенным ниже всего цикла. Говорят, «происходит выход из цикла».

Рассмотрите блок-схему цикла while.

На ней ярко-голубыми прямоугольниками обозначена основная ветка программы, ромбом – заголовок цикла с логическим выражением, бирюзовым прямоугольником – тело цикла.

С циклом while возможны две исключительные ситуации:

Если при первом заходе в цикл логическое выражение возвращает False, то тело цикла не выполняется ни разу. Эту ситуацию можно считать нормальной, так как при определенных условиях логика программы может предполагать отсутствие необходимости в выполнении выражений тела цикла.
Если логическое выражение в заголовке while никогда не возвращает False, а всегда остается равным True, то цикл никогда не завершится, если только в его теле нет оператора принудительного выхода из цикла (break) или вызовов функций выхода из программы – quit(), exit() в случае Python. Если цикл повторяется и повторяется бесконечное количество раз, то в программе происходит зацикливание. В это время она зависает и самостоятельно завершиться не может.

Вспомним наш пример из урока про исключения. Пользователь должен ввести целое число. Поскольку функция input() возвращает строку, то программный код должен преобразовать введенное к целочисленному типу с помощью функции int(). Однако, если были введены символы, не являющиеся цифрами, то возникает исключение ValueError, которое обрабатывается веткой except. На этом программа завершается.

Другими словами, если бы программа предполагала дальнейшие действия с числом (например, проверку на четность), а она его не получила, то единственное, что программа могла сделать, это закончить свою работу досрочно.

Но ведь можно просить и просить пользователя корректно вести число, пока он его не введет. Вот как может выглядеть реализующий это код:

n = input("Введите целое число: ")
 
while type(n) != int:
    try:
        n = int(n)
    except ValueError:
        print("Неправильно ввели!")
        n = input("Введите целое число: ")
 
if n % 2 == 0:
    print("Четное")
else:
    print("Нечетное")

Примечание 1. Не забываем, в языке программирования Python в конце заголовков сложных инструкций ставится двоеточие.

Примечание 2. В выражении type(n) != int с помощью функции type() проверяется тип переменной n. Если он не равен int, то есть значение n не является целым числом, а является в данном случае строкой, то выражение возвращает истину. Если же тип n равен int, то данное логическое выражение возвращает ложь.

Примечание 3. Оператор % в языке Python используется для нахождения остатка от деления. Так, если число четное, то оно без остатка делится на 2, то есть остаток будет равен нулю. Если число нечетное, то остаток будет равен единице.

Проследим алгоритм выполнения этого кода. Пользователь вводит данные, они имеют строковый тип и присваиваются переменной n. В заголовке while проверяется тип n. При первом входе в цикл тип n всегда строковый, то есть он не равен int. Следовательно, логическое выражение возвращает истину, что позволяет зайти в тело цикла.

Здесь в ветке try совершается попытка преобразования строки к целочисленному типу. Если она была удачной, то ветка except пропускается, и поток выполнения снова возвращается к заголовку while.

Теперь n связана с целым числом, следовательно, ее тип int, который не может быть не равен int. Он ему равен. Таким образом логическое выражение type(n) != int возвращает False, и весь цикл завершает свою работу. Далее поток выполнения переходит к оператору if-else, находящемуся в основной ветке программы. Здесь могло бы находиться что угодно, не обязательно условный оператор.

Вернемся назад. Если в теле try попытка преобразования к числу была неудачной, и было выброшено исключение ValueError, то поток выполнения программы отправляется в ветку except и выполняет находящиеся здесь выражения, последнее из которых просит пользователя снова ввести данные. Переменная n теперь имеет новое значение.

После завершения except снова проверяется логическое выражение в заголовке цикла. Оно даст True, так как значение n по-прежнему строка.

Выход из цикла возможен только тогда, когда значение n будет успешно конвертировано в число.

Рассмотрим следующий пример:

total = 100
 
i = 0
while i < 5:
    n = int(input())
    total = total - n
    i = i + 1
 
print("Осталось", total)

Сколько раз «прокрутится» цикл в этой программе, то есть сколько итераций он сделает? Ответ: 5.

Сначала переменная i равна 0. В заголовке цикла проверяется условие i < 5, и оно истинно. Тело цикла выполняется. В нем меняется значение i, путем добавления к нему единицы.
Теперь переменная i равна 1. Это меньше пяти, и тело цикла выполняется второй раз. В нем i меняется, ее новое значение 2.
Два меньше пяти. Тело цикла выполняется третий раз. Значение i становится равным трем.
Три меньше пяти. На этой итерации i присваивается 4.
Четыре по прежнему меньше пяти. К i добавляется единица, и теперь ее значение равно пяти.

Далее начинается шестая итерация цикла. Происходит проверка условия i < 5. Но поскольку теперь оно возвращает ложь, то выполнение цикла прерывается, и его тело не выполняется.

«Смысловая нагрузка» данного цикла – это последовательное вычитание из переменной total вводимых чисел. Переменная i в данном случае играет только роль счетчика итераций цикла. В других языках программирования для таких случаев предусмотрен цикл for, который так и называется: «цикл со счетчиком». Его преимущество заключается в том, что в теле цикла не надо изменять переменную-счетчик, ее значение меняется автоматически в заголовке for.

В языке Python тоже есть цикл for. Но это не цикл со счетчиком. В Питоне он предназначен для перебора элементов последовательностей и других сложных объектов. Данный цикл и последовательности будут изучены в последующих уроках.

Для while наличие счетчика не обязательно. Представим, что надо вводить числа, пока переменная total больше нуля. Тогда код будет выглядеть так:

total = 100
 
while total > 0:
    n = int(input())
    total = total - n
 
print("Ресурс исчерпан")

Сколько раз здесь выполнится цикл? Неизвестно, все зависит от вводимых значений. Поэтому у цикла со счетчиком известно количество итераций, а у цикла без счетчика – нет.

Самое главное для цикла while – чтобы в его теле происходили изменения значений переменных, которые проверяются в его заголовке, и чтобы хоть когда-нибудь наступил случай, когда логическое выражение в заголовке возвращает False. Иначе произойдет зацикливание.

Примечание 1. Не обязательно в выражениях total = total - n и i = i + 1 повторять одну и ту же переменную. В Python допустим сокращенный способ записи подобных выражений: total -= n и i += 1.

Примечание 2. При использовании счетчика он не обязательно должен увеличиваться на единицу, а может изменяться в любую сторону на любое значение. Например, если надо вывести числа кратные пяти от 100 до 0, то изменение счетчика будет таким i = i - 5, или i -= 5.

Примечание 3. Для счетчика не обязательно использовать переменную с идентификатором i. Можно назвать переменную-счетчик как угодно. Однако так принято в программировании, что счетчики обозначают именами i и j (иногда одновременно требуются два счетчика).

Практическая работа

Измените последний код из урока так, чтобы переменная total не могла уйти в минус. Например, после предыдущих вычитаний ее значение стало равным 25. Пользователь вводит число 30. Однако программа не выполняет вычитание, а выводит сообщение о недопустимости операции, после чего осуществляет выход из цикла.
Используя цикл while, выведите на экран для числа 2 его степени от 0 до 20. Возведение в степень в Python обозначается как **. Фрагмент вывода:
```
...
  32
  64
 128
 256
 512
1024
...
```

Примеры решения и дополнительные уроки в android-приложении и pdf-версии курса

0 (E в степени 0)?

Что такое e ⁰ ? Если вы помните свои показатели, ответ на этот вопрос прост. Для всех чисел возведение этого числа в 0-ю степень равно единице. Итак, мы знаем, что:

e ⁰ = 1

Этот ответ основан на внутреннем свойстве способа, которым определяется возведение в степень. Возведение в степень определяется как итеративное умножение, поэтому выражение x ⁿ означает, что вы умножаете x на себя n раз. Следовательно, любое выражение вида x ⁰ означает умножение x на себя 0 раз. Умножение числа само на себя 0 раз должно возвращать один и тот же элемент, который аналогичен умножению элемента на 1, мультипликативной идентичности. Таким образом, для всех чисел x, x ⁰ вы должны получить мультипликативное тождество, равное 1 (за исключением случаев, когда x=0, что является особым случаем, который мы рассмотрим позже).

«Сам по себе ноль — ничто, но без нуля ничего нельзя сосчитать; следовательно, ноль — это что-то, но ноль». — Далай-лама

Приведенные выше рассуждения основаны на определении операции возведения в степень. Давайте посмотрим на общее определение возведения в степень и на то, как мы можем обосновать утверждение, что x ⁰ = 1.

Что такое возведение в степень?

Возведение в степень — это математическая операция, в которой участвуют два числа: основание b и показатель степени n. Если n является положительным числом, то возведение в степень соответствует итеративному умножению основания. Таким образом, экспоненциальное выражение означает, что вы умножаете n копии базы b вместе. Другими словами, выражение

b ⁿ

означает произведение n оснований b вместе. Мы можем увидеть, как это работает, подставив фактические числа вместо переменных. Например, 2 ³ можно переписать как (2×2×2)=8. Другими словами, 2 ³ равно числу два, умноженному на себя 3 раза. Аналогично, 4 ⁴ равно (4×4×4×4)=256.

Наоборот, если N является отрицательным числом, то экспоненты, определенное как:

B ^-N = 1/ B ^N

Участник с отрицательным показателем -N соответствует на достопримечательно обратное число b ⁿ . Это конкретное определение отрицательного возведения в степень является следствием полезного правила объединения показателей степени, которое мы рассмотрим чуть позже. А пока просто запомните два определения возведения в степень положительными и отрицательными целыми числами:

b ⁿ = ( b ₁ × b ₂ × b ₃ ×…. × b _n )

b ^{— n} = 1/ b ⁿ

Возведение в степень можно рассматривать как обратную операцию логарифмирования

Проверка концепции!

Взгляните на эти задачи, связанные с возведением в степень, чтобы убедиться, что вы понимаете основную концепцию. Для каждой задачи попробуйте переписать задачу в виде расширенной серии итеративного умножения:

5 ⁶
7 ^-2
1 ^-1

Растворы

5 ⁶ = (5 × 5 × 5 × 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5 × 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5) 9000). 7 ^-2 = 1/(7×7)
1 ^-1 = 1/1 ¹

Сосредоточившись на задаче 3, мы обнаруживаем интересный факт, касающийся числа 1 и возведения в степень. А именно, для любого показателя n 1 ⁿ = 1. Это легко доказать. Поскольку возведение в степень определяется как итеративное умножение, 1 ⁿ просто означает «умножить n копий 1». Однако произведение 1 на 1 всегда равно 1, сколько бы единиц вы ни умножали. Так что не имеет значения, что такое или ; 1 ⁿ всегда будет равно 1.

Мы можем доказать, что 1 ⁿ =1 верно и для отрицательных показателей. Помните, что b ^-n определяется как 1/ b ⁿ . Следовательно, 1 ^-n должно быть равно 1/1 ⁿ . Поскольку мы только что доказали, что 1 ⁿ =1, 1 ^-n всегда будет равно 1/1, что как раз равно 1. Следовательно, для всех n, 1 ^-n =1.

Дополнительная практика: Посмотрите, сможете ли вы доказать это для всех оснований b , b ¹ = b . Вы должны быть в состоянии сделать это, просто рассуждая о значении операции экспоненты.

«Когда вы превращаетесь в ноль, ваша сила становится непобедимой». — Махатма Ганди

Арифметические операции с показателями степени

Определение операции возведения в степень дает нам алгоритмический способ решения задач, связанных с умножением или делением членов с показателями степени. Сначала мы рассмотрим пример умножения членов экспоненты.

Умножение

Обычно правило умножения членов с показателями степени следующее:0005

Мы можем показать, что это правило должно выполняться, на простом числовом примере. Скажем, у нас есть 2 ⁴ и 2 ³. 2 ⁴ равно (2×2×2×2), а 2 ³ равно (2×2×2), поэтому 2 ⁴ ×2 ³ = (2×2×2×2 )(2×2×2). Поскольку умножение является ассоциативным (неважно, где мы ставим скобки), мы можем объединить все члены в правой части этого уравнения в одно большое выражение в скобках:

2 ⁴ × 2 ³ =(2×2×2×2×2×2×2)=2 ³⁺⁴ =2 ⁷

Мы можем обобщить это рассуждение для любого основания b, и любых показателей m и n . По определению операции по эксплуатации мы знаем, что:

B ¹ = B,

и что

B ^N+1 = B ^N × B ¹

Общие этом случае, установив b ¹ = b ^m дает нам наше окончательное выражение: b ⁿ × b ^m = b ^n+m

Существуют также правила деления для

. В общем, правило таково:

b ⁿ ÷b ^m = b ^n−m

Еще раз, мы можем показать, что это правило верно для конкретного числового примера, скажем, 2 ⁵ и 2 ² . 2 ⁵ совпадает с (2×2×2×2×2) и 2 ² это (2×2). Таким образом, 2 ⁵ ÷ 2 ² равно (2×2×2×2×2)/(2×2). Поскольку мы делим, мы можем сократить пары одинаковых терминов и избавиться от них, что просто оставляет (2 × 2 × 2).

Между прочим, именно это конкретное правило деления возведенных в степень членов дает нам наше определение возведения в степень на 0. В общем, возведение экспоненциального члена в экспоненту:

( b ⁿ ) ^m = b ^n×m

Это конкретное определение вложенной множественности возведения в степень является следствием ассоциативности. условия. Выражение ( b ⁿ ) ^m говорит нам умножить вместе m копии основания b ⁿ . Основание, b ⁿ говорит нам умножить n копий основания б . Итак, все вместе у нас будет m копий b ⁿ , где каждый b ⁿ имеет n копий b . Чтобы вычислить общее количество b s, умноженных вместе, мы можем просто умножить m на n, чтобы получить и получить окончательное выражение степени.

Вот числовой пример, чтобы проиллюстрировать это. Скажем, у нас есть (2 ²) ³. Это выражение говорит нам умножить вместе 3 копии основания 2 ² . Это то же самое, что (2×2)×(2×2)×(2×2). Поскольку умножение ассоциативно, мы можем избавиться от скобок и объединить все члены в одно выражение (2×2×2×2×2×2) = (2 ² ) ³ = 2 ⁶ .

Возведение в степень на 0

Теперь, когда у нас есть некоторые правила возведения в степень, мы можем точно понять, почему возведение любого числа в 0-ю степень всегда равно 1. Вспомним, что при делении возведенных в степень членов действует общее правило:

b ⁿ ÷b ^m = b ^n−m

Это эквивалентно b ⁿ /b ^m . Если мы установили как N , так и M , равные 1, мы получаем:

B ¹ ÷ B ¹ = B ^1-1 = B ¹ /B ¹ = B ⁰

Так как b ¹ равно просто b и любое число, деленное само на себя, равно 1, отсюда обязательно следует, что

B ⁰ = B ¹ /B ¹ = B /B = 1

Это выражение верно для любого ненулевого числа B . Другими словами, b ⁰ соответствует делению b на самого себя, что всегда будет равно 1.

Возведение в степень отрицательными числами может генерировать определение отрицательного возведения в степень, на которое мы намекали ранее. Напомним, что для отрицательного возведения в степень:

B ^-N = 1/ B ^N

Согласно определению экспонента +1 )/ b

Приведенное выше утверждение просто следует из того, что означает применение оператора возведения в степень. Мы также знаем, что это утверждение верно в случае, когда n = 0:

b ⁰ = B ¹ / B = 1

Сейчас, продлив это определение до n = -1 Дает нам:

B ^-1 = B ⁰ /31 B1 = B ^{0 0004 /31 B 1 = B ^{0,0004 / 31 B1 = B ^{0 0004 /319 = B ^{0 0004 /319 = B ^{0,0004 / 319 = B 9003 0 0004 /^{-1 B9004 = B 9003 0 . = 1/ B}}}}}}

Мы можем расширить эту рассуждения на все отрицательные N , чтобы получить наше заявление о личности для отрицательного экспоненты:

B ^-N = 1/ B ^N

Возведение 0 в степень

Все вышеуказанные правила определены с ненулевым основанием b . Что произойдет, если мы допустим b = 0? Операция возведения нуля в степень имеет некоторые особые правила.

Во-первых, когда n положительное, 0 ⁿ =0. Это достаточно легко увидеть; выражение 0 ⁿ означает «умножить n копий 0». 0×0 всегда равно 0, независимо от того, сколько копий 0 у вас есть, поэтому для всех положительных n, 0 ⁿ = 0.

Когда n отрицательно, 0 ⁿ не определено. Причина в том, что возведение 0 в отрицательную степень подразумевает деление на 0, которое не определено. Подумайте об этом так: мы знаем, что для всех b и n b ^-n = 1/ b ⁿ. Если положить b = 0, то получим:

0 ^-n = 1/0 ⁿ = 1/0.

Деление на ноль — неопределенная операция, поэтому возведение 0 в некоторую отрицательную степень — тоже неопределенная операция.

0 В 0-й Степени

Что если оба b и n равны 0, то есть 0 ⁰ ? Здесь мы начинаем добираться до спорной территории. В настоящее время не существует общепринятого значения выражения 0 ⁰ . В зависимости от области математики дадут вам разные ответы. В базовой алгебре 0 ⁰ обычно просто определяется как равное 1, однако это часто делается из соображений простоты, а не логической строгости.

«Ноль-ноль — это большой счет». — Рон Аткинсон

Некоторые математики утверждают, что 0 ⁰ не определено по той же причине, что и возведение 0 в отрицательную степень не определено; они оба подразумевают деление на 0, что является неопределенной операцией в алгебре. Следование обычным правилам для ненулевых показателей степени при замене 0, по-видимому, указывает на то, что выражение 0 ⁰ совпадает с 0/0.

Другие математики утверждают на этом основании, что 0 ⁰ не является неопределенным, просто неопределенный . Причина в том, что выражение 0/0 не дает нам достаточно информации, чтобы определить его значение. Такие выражения, как 0/0, обычно используются в контексте исчисления, когда берется отношение двух производных по мере того, как они приближаются к своим пределам. В этих случаях ответ 0/0 не означает, что ответ не определен, просто нам нужно больше информации, чтобы определить его значение.

Почему что-то в 0-й степени 1?

Экспоненты 0

Энтони В.

спросил 30.05.13
Умножает само на себя ноль раз, значит, должно быть 0?
Подписаться І 6
Подробнее
Отчет
6 ответов от опытных наставников
Лучший Новейшие Самый старый
Автор: ЛучшиеНовыеСамыеСтарые
Бен П. ответил 30.05.13 90 не определено.
Надеюсь, это поможет.
Голосовать за 4 Понизить
Подробнее
Отчет
Аарон С. ответил 30.05.13
Репетитор
Новое в Византе
С помощью Аарона математика проста как число пи
Смотрите таких репетиторов
Посмотреть таких репетиторов
Нет, вот один из способов придумать:
Помните правило:
x ^M /x ^N = x ^M-N (если x ≠ 0)
Итак, если m = n, это говорит:

x ^m / x ^m = x ⁰

Но очевидно, что мы должны иметь x ^{m ^{/x 9 х ⁰ = 1 тоже.}}

Будьте осторожны, когда говорите, что «что угодно» в 0-й степени равно 1, потому что 0 ⁰ не определено.
Голосовать за 4 Понизить
Подробнее
Отчет
Джонни Р. ответил 31.05.13
Репетитор
4,8 (164)
Исключительный репетитор по математике и бухгалтерскому учету
Об этом репетиторе ›
Об этом репетиторе ›
Чтобы понять эту концепцию, давайте рассмотрим правила умножения и деления показателей степени.
Правила возведения в степень гласят, что x ^m /x ⁿ ⁼ x ^m-n
x ^{0 степень — это наименьшая степень для любого числа.}
Давайте в качестве примера воспользуемся степенью числа 7.
7 ⁵ /7 ⁼ 7 ⁵ ^-1 = 7 ⁴ = 16807 /7 = 2401
7 ⁴ /7 = 7 ^4-1 = 7 ³ = 2401 /7 = 243
7 ³ /7 = 7 ^3-1 = 7 ² = 343/7 = 49
7 ² /7 = 7^2-1 = 7 ¹ = 49/7 = 7
7 ¹ /7 = 7 ^1-1 = 7 ⁰       = 7/7= 1
Применение этого закона объясняет, почему 0) в нулевой степени всегда равно 1,
Голосовать за 2 Понизить
Подробнее
Отчет
Джин Г. ответил 31.05.13
Репетитор
5,0 (257)
Инженер-электрик на пенсии. Помогает людям понять алгебру
См. таких репетиторов
9(-n) как (1) разделить на x, n раз.
Голосовать за 1 Понизить
Подробнее
Отчет
Дэвид Л. ответил 30.05.13
Репетитор
5,0 (281)
Доктор философии по физике, Принстонский университет и бакалавр физики, Колледж Харви Мадда
Смотрите таких репетиторов
Смотрите таких репетиторов
Если вы знакомы с дробными степенями, вы можете рассмотреть еще один способ:
Возможно, вы помните, что a ^1/n — это число, которое нужно умножить как n копий, чтобы получить a . Другими словами, (a ^1/n ) ⁿ = a . Рассмотрим следующую систему уравнений:
(16 ¹ ) ¹ = (16,00) ¹ = 16
(16 ^1/2) ² = (4,00) ² = 16
(16 ^1/3) ³ = (2,52) ^{(16 ^1/3) 3} = 16
(16 ^1/4 ) ⁴ = (2,00) ⁴ = 16
. . . и т. д.
Поскольку мощность, присоединенная непосредственно к апельсину 16, становится сколь угодно малой (т. е. 16 ^1/100 , 16 ^1/1000 , 16 ^1/10000 и т. д.), мы получаем величины все ближе и ближе до 1.00. Они должны быть очень близки к 1, иначе мы быстро «превысим» окончательное значение 16, прежде чем закончим умножение всех наших копий оранжевых чисел. Таким образом, когда мощность, приложенная к 16, становится сколь угодно близкой к нулю, оранжевая величина становится сколь угодно близкой к единице, а когда мощность равно нулю, количество равно единице.
Вы понимаете, почему количество приближается к единице, а не к нулю? Предположим, что 16 ^1/000 были не близки к 1, а были небольшим числом, близким к нулю, например 0,01. Если бы это было правдой, то (16 ^1/1000) ¹⁰⁰⁰ = (0,01) ¹⁰⁰⁰, что является очень маленьким числом, намного меньшим, чем единица (0,01, умноженное само на себя во много-много раз, очень мало). Однако это не может быть правдой, потому что (16 ^1/1000 ) ¹⁰⁰⁰ = 16 , что не такое уж и маленькое число. Таким образом, мы не можем интуитивно ожидать, что 16 ⁰ будет равно нулю.

Надеюсь, это было интересно.
Голосовать за 1 Понизить
Подробнее
Отчет
Кэй С. ответил 22.06.13
Репетитор
Новое в Византе
Кей Ди — Репетиторство по английскому языку, ASL, истории
Смотрите таких репетиторов
Смотрите таких репетиторов
Вы не умножаете 3 раза на ноль, вы просто не умножаете саму себя. Число 3 не умножается, поэтому оно остается прежним.
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Степень 0 — Математика GCSE
Здесь вы узнаете все, что вам нужно знать о возведении терминов в степень 0 для математики GCSE и iGCSE (Edexcel, AQA и OCR).
Обратите внимание на рабочие листы законов индексов и экзаменационные вопросы в конце.
Что такое возведение значения в степень 0?
Любое ненулевое значение, возведенное в степень 0, равно 1.
Рабочие листы по законам индексов (включая степень 0)
Получите бесплатно рабочий лист в степени 0, содержащий более 20 вопросов и ответов по законам индексов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс
Рабочие листы по законам индексов (включая степень 0)
Получите бесплатный рабочий лист в степени 0, содержащий более 20 вопросов и ответов по законам индексов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Похожие уроки по законам индексов
Степень числа 0 является частью нашей серии уроков по пересмотру законов индексов . Возможно, вам будет полезно начать с урока основных законов индексов, чтобы получить краткое изложение того, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки этой серии включают:
Законы индексов
Обозначение индексов
Дробные индексы
Отрицательные индексы
Умножение индексов
Индексы деления
Скобки с индексами
Как возвести что-то в степень 0
Возведение члена в нулевую степень означает умножение члена на самого себя ноль раз. Это даст 1.
Давайте посмотрим на это тремя разными способами:
1 Деление
Когда мы делим что-то само по себе, мы получаем 1.
Например.
\[\begin{выровнено} &5 \дел 5=1 \\\\ &\frac{5}{6} \div \frac{5}{6}=1 \\\\ &2 х \дел 2 х=1 \конец{выровнено}\] 9{\frac{1}{3}}=\sqrt [3] {a}\]
Индексы, степени или степени
Индексы также могут называться степенями или показателями.
Возведение любого термина или действительного числа в степень 0 равно 1.
Независимо от того, является ли это целым числом, десятичной дробью или дробью, положительным или отрицательным числом или рациональным числом. число (например, 4, 0,25, ½ и т. д.) или иррациональное число (например, π, √5, e (число Эйлера) и т. д.) возведение основного числа или базовой переменной в степень 0 даст значение 1.
Возведение алгебраических многочленов в степень 0 также равно 1.
Любой индекс, который является ненулевым числом, не будет дайте 1, если базовое значение не равно 1.
Практика в степени 0 вопросы
Это потому, что любая константа или переменная, возведенная в нулевую степень, равна 1
Это потому, что переменная x , возведенная в степень ноль равен 1. Следовательно, у нас есть 8 лотов по 1, что составляет 8. 9{0}
(1 балл)
Показать ответ
Учебный контрольный список
Теперь вы научились:
Упрощать выражения с использованием законов индексов
Вычислять с корнями и дробными индексами
Следующие уроки
Доказательство математики
Функции в алгебре
Последовательности
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Степени и квадратные корни — чайники
Автор: Марк Зегарелли и
Обновлено: 25-04-2016
Математика для реальной жизни Для чайников
0 power — это быстрый способ умножить число само на себя. Например, 2 ⁵ , которое вы читаете как два в пятой степени, означает, что вы умножаете 2 на себя 5 раз:
2 ⁵ = 2 х 2 х 2 х 2 х 2 = 32
Число 2 называется основанием , , а число 5 называется показателем степени .
Степени числа десять — то есть степени с 10 в основании — особенно важны, потому что на них основана система счисления. К счастью, с ними очень легко работать. Чтобы возвести 10 в степень любого положительного целого числа, запишите число 1, за которым следует количество нулей, указанное в показателе степени. Например, 10 ³ это 1000.
Вот несколько важных правил для нахождения степеней, содержащих 0 или 1:
Каждое число, возведенное в степень 1, равно самому этому числу.
Каждое число (кроме 0), возведенное в степень 0, равно 1. Например, 10 ⁰ — это 1, за которой следует , а не 0, то есть 1.
Число 0, возведенное в степень любого числа (кроме 0), равно 0, потому что сколько бы раз вы ни умножали 0 сам на себя, результат будет 0.
Математики решили оставить 0 ⁰ неопределенным, то есть оно не равно никакому числу.
Число 1, возведенное в степень любого числа, равно 1, потому что сколько бы раз вы ни умножали 1 само на себя, в результате получится 1.
Когда вы умножаете любое число само на себя, в результате получается число в квадрате. Итак, когда вы возводите любое число в степень 2, вы получаете в квадрате этого числа. Например, вот 5 ² или пять в квадрате:
5 ² = 5 х 5 = 25
Обратная операция возведения числа в квадрат называется нахождением 90 734 квадратного корня числа из 90 735 (обратные операции отменяют друг друга. Когда вы находите квадратный корень числа, вы обнаруживаете новое число, которое при умножении само на себя равно числу, которое вы начал с. Например, вот квадратный корень из 25:
Примеры вопросов
Что такое 3 ⁴ ?
81. Выражение 3 ⁴ говорит вам умножить 3 само на себя 4 раза:
3 х 3 х 3 х 3 = 81
Что такое 10 ⁶?
1 000 000. Используя правило степени десяти, 10 ⁶ равно 1, за которой следуют шесть нулей, поэтому 10 ⁶ = 1 000 000.
Что дальше?
6. Вы хотите найти число, которое при умножении само на себя равно 36. Вы знаете, что 6 х 6 = 36, поэтому
Что дальше?
16. Вы хотите найти число, которое при умножении само на себя равно 256. Попробуйте угадать, чтобы сузить круг возможных вариантов. Начните с угадывания 10:
10 х 10 = 100
256 > 100, поэтому ответ больше 10. Угадайте 20:
20 х 20 = 400
256 < 400, поэтому ответ находится между 10 и 20. Угадайте 15:
15 х 15 = 225
256 > 225, поэтому ответ между 15 и 20. Угадайте 16:
16 х 16 = 256
Это верно, поэтому
Практические вопросы
Найдите значение следующих степеней:
a. 6 ²
б. 3 ⁵
г. 2 ⁷
д. 2 ⁸ ( Подсказка: Вы можете облегчить себе работу, используя ответ на вопрос c . )
Найдите значение следующих степеней:
а. 10 ⁴
б. 10 ¹⁰
г. 10 ¹⁵
д. 10 ¹
Ниже приведены ответы на практические вопросы:
Найдите значение следующих степеней:
a. 6 ² = 6 х 6 = 36 .
б. 3 ⁵ = 3 х 3 х 3 х 3 х 3 = 243 .
г. 2 ⁷ = 2 х 2 х 2 х 2 х 2 х 2 х 2 = 128 .
д. 2 ⁸ = 2 х 2 х 2 х 2 х 2 х 2 х 2 х 2 = 256 . Вы уже знаете из части c , что 2 ⁷ = 128, поэтому умножьте это число на 2, чтобы получить ответ: 128 x 2 = 256.
Найдите значение следующих степеней:
a. 10 ⁴ = 10 000 . Запишите 1, за которой следуют четыре нуля.
б. 10 ¹⁰ = 10 000 000 000 . Напишите 1, а затем десять нулей.
г. 10 ¹⁵ = 1 000 000 000 000 000 . Напишите 1, а затем пятнадцать нулей.
д. 10 ¹ = 10 . Любое число, возведенное в степень 1, является этим числом.
Об этой статье
Эту статью можно найти в категории:
Базовая математика,
Показатель 0 — Полный курс алгебры
Содержание | Дом
Урок 20 Раздел 2
Назад к Разделу 1
Показатель степени 0
Научное обозначение
Показатель степени 0
Любое число (кроме 0) с показателем степени 0 определяется как означающее 1.
а ⁰ = 1
Задача 8.   Оцените следующее..
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
а) 5 ⁰ = 1. б) (−5) ⁰ = 1, в) −5 ⁰ = −1. г) (½) ⁰ = 1.
д) 3 · 10 ⁰ = 3 · 1 = 3. е) (3 · 10) ⁰ = 1. г) -3 · 10 ⁰ = -3 · 1 = -3.
ч) 5 + 5 ⁰ (5 + 5 ⁰ ) = 5 + 1 (5 + 1) = 5 + 6 = 11.
См. порядок действий.
Почему мы определяем a ⁰ как 1?
Во-первых, у нас есть это правило:
= а ^{м − м} = а ⁰ .
Но (когда а 0),

= 1.
Следовательно, мы должны определить a ⁰ как 1.
Что касается 0 ⁰ , это может быть любое число! За,
= Любой номер. Урок 6
Но
= 0 ⁰ .
Следовательно, мы должны заключить, что 0 ⁰ может быть любым числом.
Задача 9.   Используйте правила экспонент, чтобы оценить следующее.
а) = 10 ^{7 − 2 + 3 − 8} = 10 ⁰ = 1
б) = 2 ^{2 − 8 + 4 + 3 − 6 + 5} = 2 ⁰ = 1
Научное обозначение
«Научная нотация» имеет одну ненулевую цифру слева от десятичной точки.
2,345
Это число записано в экспоненциальном представлении. Слева от запятой стоит одна цифра — 2 — и это не 0.
Обычно число, записанное в экспоненте, умножается на 10, возведенное в степень.
Пример 1.   6,45 × 10 ³ . Это научное обозначение какого числа?
Ответить . Поскольку показатель степени положительный, мы будем умножать на 6,45. Чтобы умножить десятичную дробь на степень 10, переместите запятую вправо на число знаков, указанное в показателе степени:
6,45 × 10 ³ = 6450
Переместите точку на три места вправо. Для этого мы должны добавить 0. (Навык арифметики, урок 4.)
Пример 2.   6,45 × 10 ⁻³ . Это научное обозначение какого числа?
Ответить . Поскольку показатель степени отрицательный, мы будем делить на 6,45. (За,
10 ⁻³ =    1
1000 .) Чтобы разделить десятичную дробь в степени 10, переместите десятичную дробь
точка слева количество мест, указанных в показателе степени:
6,45 × 10 ⁻³ = 0,00645
Переместите точку на три места влево. Для этого нужно добавить 0.
Задача 10. Каждое из них записано в экспоненциальной записи. Умножить.
г.
а) 2,401 × 10 ³ = 2401 б) 1,006 × 10 ² = 100,6

в) 7,01 × 10 ⁵ = 701 000 г) 4,986 × 10 = 49,86

д) 3,85 × 10 ⁻⁴ = 0,000385 е) 1,8 × 10 ⁻¹ = 0,18

ж) 6,0 × 10 ⁻³ = 0,006 ч) 4,3 × 10 ⁻⁸ = 0,000000043
Пример 3.    Запишите в экспоненциальном представлении.
а)   562,4 = 5,624 × 10 ²
Чтобы изменить 562,4 на 5,624, мы переместили десятичную точку на два разряда оставил . Чтобы компенсировать, мы должны умножить на 10 с показателем степени +2.
б)   .00395 = 3,95 × 10 ⁻³
Чтобы изменить .00395 на 3,95, мы переместили десятичную точку на три знака вправо . Чтобы компенсировать, мы должны умножить на 10 с показателем степени -3.
Задача 11.   Запишите в экспоненциальном представлении.
г.
No related posts.
Навигация по записям
Предыдущая статьяГрафик функции y 1 x 2: Mathway | Популярные задачи
Следующая статьяКалькулятор с градусами и минутами онлайн: Калькулятор градусов онлайн ° ’ ”.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта
а) 1234 = 1,234 × 10 ³ б) 12,34 = 1,234 × 10

в) 219 000 000 = 2,19 × 10 ⁸ г) 0,000081 = 8,1 × 10 ⁻⁵

д) 0,00395 = 3,95 × 10 ⁻³