А в 2 степени а в 5 степени: упростите выражение -2а в 5 степени х умножить на 0,5а в 2 степени

Что такое степень с натуральным показателем (В.А. Тарасов) 7 класс онлайн-подготовка на Ростелеком Лицей

Обсуждение, зачем математикам понадобилась степень

 

Откуда появилась степень.

 

Выражение а+а+а в математике можно заменить на а+а+а=3а.

Выражение а+а+а+а+а можно представить в виде а+а+а+а+а=5а.

То есть, если в выражении n одинаковых слагаемых, каждое из которых а, то его можно кратко записать na.  

А умножение , можно кратко записать так: а³, читается: а в кубе или третья степень числа а.

 – а в пятой степени или пятая степень числа а.

А если в выражение n одинаковых сомножителей, каждый из которых а, то мы будем писать:

 = aⁿ – n-ная степень числа а.

 

Определение степени

 

 

Определение. Степенью aⁿ называется произведение n одинаковых сомножителей,  , где n— натуральное число n={2,3,…..}; а – любое число.

 

 

Терминология

 

 

Терминология: aⁿ

 

 а – основание степени,

n – показатель степени,

aⁿ– степень, или а в n-ой степени, или n-ая степень числа а.

 

Решение типовых задач на определение степени

 

 

Пример 1: Записать произведение в виде степени, назвать основание и показатель степени, вычислить, если возможно.

 

1. – это по определению 4 в кубе или третья степень числа 4, 4— основание степени, 3— показатель степени. Результат:

 

Ответ: 64

2. – по определению, это x в четвертой степени, x – основание степени, 4 – показатель степени. Дальше вычислять нельзя, потому что x нужно присвоить конкретное значение.

Ответ: 

3.  

Это в пятой степени,  – это основание степени, 5 – показатель степени, он показывает сколько раз основание умножается на себя. Замечание: от переменных мест сомножителей произведение не меняется, запишем это выражение по-другому:

 

Значит, выражение .

Ответ: .

4. – это в кубе, 3 – это показатель степени, – основание степени.

Ответ: 

5.  

 – вторая степень числа 13 ,  – вторая степень числа 5.

Ответ: 4225

6.

 – третья степень числа 2,  – вторая степень числа 3.

Ответ: 72

 

Примеры на вычисление степени с различными показателями

 

 

В степени aⁿ может отдельно меняться показатель степени или основание степени.

 

Пример 2: Вычислить , если

a) n=2

b) n=3

c) n=4

Решение:

a)  так как стоит четная степень, минус пропадает.

b)

c) – так как стоит четная степень, минус пропадает.

Ответ: a) 25; b)-125; c)625;

В этом примере менялся показатель степени, а основание не менялось. Рассмотрим пример, когда меняется основание.

 

Примеры на вычисление степени с различными основаниями

 

 

Пример 3: Вычислить: b⁴, где

 

a) b=1

b) b=-3

c) b=

d) b=

Ответ:

a)

b)

c)

 

Определение степени с показателем 1

 

 

Вспомним, что натуральные числа — это 1,2,3 и так далее.

 

n={1,2,3,…..}

По нашему определению:

a^{n =} ,                                (1)

n={2,3,…..}

Нужно еще одно определение для случая n=1. Что же такое а¹?

a¹=a                                                   (2)

 

Примеры степеней с показателем 1

 

 

Пример.

 

()¹=)

(-2)¹=-2

3¹=3.

Итак, теперь мы знаем, что такое a^n, ,где n={1,2,3,…..} – любое натуральное число.

 

Геометрические задачи, в которых участвует степень

 

 

Рассмотрим геометрические задачи, в которых участвуют степени.

 

Задача: вычислить площадь квадрата, сторона которого равна а, где

a) а=3 см

b) а=7 см

c) а=1,5 см

Замечание.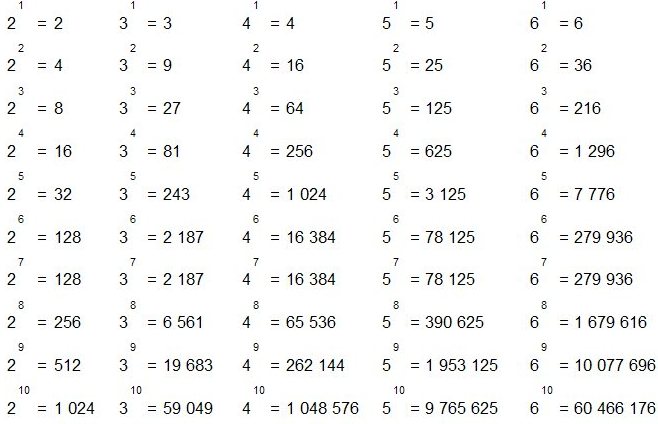 Если у нас есть квадрат со стороной а, то его площадь равна а² или вторая степень числа а.

S=a²

Ответ:

S=3²=9 см²

S=7²=49 см²

S=1,5²=2,25 см²

Итак, геометрическая задача потребовала от нас знание степени.

 

Задачи на вычисление

 

 

И в заключение, несколько примеров на вычисление. Задач много, но ключ к решению – первое и второе определение.

 

Вычислить:

a)   

Как видим, вычисления могут быть разные, но ключ к решению одинаковый.

b) Вычислить при а=1 следующее выражение:

а²=1²=1

а³=1³=1

При а=-1 будет чуть посложнее:

а²=(-1)²=1

а³=(-1³⁾=-1

а⁴=(-1)⁴=1

и т.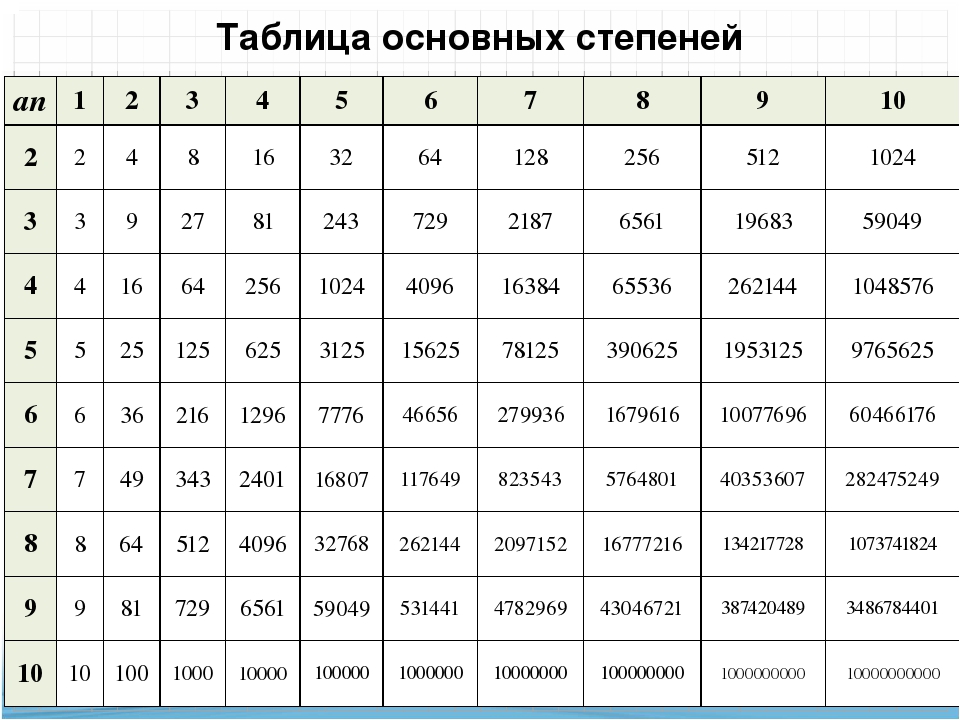 д. -1 будет мерцать то 1, то -1 в зависимости от того четный или нечетный показатель.

 

Подведение итогов урока

 

 

Итак, наша задача была рассмотреть, что такое степень с натуральным показателем. Мы рассмотрели 2 основных определения (1) и (2), выучили терминологию аⁿ, где n – это показатель степени, а – основание степени, n – натуральное число, а – любое число. Затем мы выполнили ряд задач. Далее мы будем изучать свойства степени с натуральным показателем.

 

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет

1. Школьная математика (Источник).
2. Школьный помощник (Источник).

 

Рекомендованное домашнее задание

1. Записать произведение в виде степени, назвать основание и показатель степени, вычислить, если возможно.

а)  

б) 

в)

2. Вычислить (-2)ⁿ, если

а) n=2 б) n=3 в) n=4

3. Вычислить: а⁵, где

а) а=1

б) а=-2

в) а=

4. Вычислить площадь квадрата, сторона которого равна а/2, где

а) а=6 см

б) а=8 дм

в) а=3 м

 

Матемагический 2023: традиционная новогодняя мозговая разминка с подарками.

Мальчики и девочки,

Вдруг заметил, что мы все снова и все вместе унеслись в очередную цикличную аномалию – смену номера года нашего совместного существования. К этой теме все относятся с разной степенью восторженности, демонстрируя и проецируя свои эмоции в самых разных видах Дед-Морозов, ёлок с развесками, да плюс салатами оливье и шубой на селёдке.

Мне же хочется вернуться к нашему заветному сумасшествию – математической игре на магии цифр «2023». Помните такую традиционную мат-новогоднюю забаву (предыдущие серии: 2017, 2018, 2019, 2020, 2021, 2022)?

Что-то меня на графоманию потянуло, посему сразу спойлер:

Из последовательности чисел <10 9 8 7 6 5 4 3 2 1> и четырёх базовых арифметических действий (плюс, минус, умножить, разделить) и любого количества скобок получить число следующего года = 2023. Склеивать и переставлять цифры нельзя.

Например, 10*9*8 + 7*6*5*(4+3) + 2*1 = 2192, а хочется ровно 2023.

Дерзайте! Задачка – ой какая увлекательная, с продолжением! Подробности – ниже.

А для оживления текста надо картинку воткнуть.. Ага, вот мне по заказу дети нарисовали:

В целом по этой картинке, наверное, можно попробовать определить количество этих детей, их пол и примерный возраст — но это отдельная задачка, к математике имеющая лишь косвенное отношение 🙂

/* Сразу мультикультурно извинюсь, что все дальнейшие измышления идут исключительно по Григорианскому календарю. Кто не придерживается этого годоисчисления, те имеют право наблюдать дальнейшие рассуждения отстранённо, но тем не менее желающие могут попробовать спроецировать всю последующую ахинею на свой номер нового или уже давно текущего года.

В Израиле, например, это будет 5782. А вот в Японии традиционный календарь ведёт счёт от начала правления императора, т.е. там сейчас 26й год — и задачка сразу упрощается. */

Итак, едем дальше.

С чего бы начать… Да с того, что мои личные прогнозы совершенно адски не сбываются! Вот ну просто посмотрите, что я ждал от года 2020го -> «Двадцать-двадцать. Чётность, сбалансированность, уравновешенность — я весы по гороскопу, мне приятно равновесие. А по китайскому зодиаку я змей, посему неудивительно, что изгибы двоек и кольца нулей числа 2020 усиливают моё расположение к номеру предстоящего года»

. Ага, уравновесились, чёрт его побери. Закарантинились и наудалёнились…

А про 2019й можно только мечтать, хотя я его предполагал разбалансированным: «Новый Год 2019. Что в цифрах этих нам звучит? Некоторым может почудиться некоторая неуверенность, вроде как «двадцать-девятнадцать», ни то и ни сё. Другие же отметят в этих цифрах плюрализм мнений и приоритет общечеловеческих ценностей: «двадцать — девятнадцать», мы, мол, толерантны к различным мнениям на данный факт и их оценкам. Третьи вообще скажут, что подобное сочетание есть сплошной депрессняк, никаких перспектив, исключительно всеобщий кризис и никаких надежд, ведь это же «двадцать — девятнадцать»»

Посему ничего не буду пророчить и кассандрить про 2023. Просто понадеюсь, что Дедушка Мороз над нами смилуется…

Но глянуть на магию цифр и погадать на их кофейной гуще всё же можно попробовать. Вот, например, как эта картинка выглядит:

2023 = 7 * 17²

Вот что бы это могло значить? Семёрка мне однозначно нравится — просто (и по-китайски тоже) она очень хорошее число. А 17 — это старый-добрый символ моего детства в физмат-школе ФМШ-18, которая нынче называется СУНЦ МГУ. А тут 17, да ещё и в квадрате!

Про 2022 вы всё сами знаете. А в разложении на простые вот так тревожно он и выглядел:

2022 = 2 * 3 * 337

Посткарантинный год 2021 был «ни то, ни сё» — что подтверждается математически:

2021 = 43 * 47

Коронавирусная пандемия — можно ли было что-то подобное сказать про 2020? В целом задним умом мы все крепки. Но ведь можно же было увидеть, что в разложении на множители сквозит очень нехорошее число «404»!

2020 = 2² * 5 * 101 = 5 * 404

Если покопать историю, то выглядела она вот так:

2019 = 3 * 673
2018 = 2 * 1009
2017 = prime
2016 = 2⁵ * 3² * 7

Ну, для меня лично 2017й был совершенно не «простым» годом, а вот с остальным соглашусь. Именно примерно такими бы числами я бы их и охарактеризовал.

Так что же значит «7 * 17²» — будем надеяться, что исключительно что-то хорошее…

Ну как, первый уровень кто-нибудь уже прошёл? Напоминаю, с помощью базовой арифметики и скобок слепить «2023» ->

10 9 8 7 6 5 4 3 2 1 = 2023

У меня первое решение получилось минут за 5. А вот на альтернативный вариант (второе решение) ушло более часа… Ну и ладно, я в конкурсе не участвую, я его организую 🙂 А тем временем, кто первый покажет в комментариях правильное решение — тот молодец. А потом обозначим победителей и обязательно вручим подарки от Деда Мороза.

Тем временем надо усиливать задачку. Далее переходим к работе в более сложных метео- мат-условиях. Выкидываем десятку: то есть в тех же условиях надо собрать «2023» из девяти цифр.

9 8 7 6 5 4 3 2 1 = 2023

Ну и далее всё как обычно, как мы любим — вычёркиваем цифру за цифрой…

8 7 6 5 4 3 2 1 = 2023

Впрочем, вот здесь я не уверен. Не исключаю, что решения для «восьмёрки» может и не существовать. Ну, тогда надо подключать расширенную арифметику:

От «семёрки» точно (а если не получится найти решение от «восьмёрки», то и для неё тоже) можно использовать факториал, степени, корни, сдвиги и прочие логарифмы. Чуть далее (от шестёрки) потребуются кратные, суб- и суперфакториалы.

Пятёрка и ниже наверняка решается только с использованием специальных средств, например, числа Леонардо, Ферма, Фибоначчи, Каталана, Мерсенна и прочих подобных. Короче, для решения более сложных случаев можно вызывать «матемагических демонов».

7 6 5 4 3 2 1 = 2023
6 5 4 3 2 1 = 2023
5 4 3 2 1 = 2023
4 3 2 1 = 2023

Неужели можно получить заветное число из трёх цифр? А из двух? А если найду попробовать? По крайней мере, раньше получалось 🙂 Итак, самое интересное:

3 2 1 = 2023
2 1 = 2023

Ну и, наконец, вишенкой на торте — получить решение только из одной единицы!

Понятно, что чудес не бывает… Однако раньше практически всегда находилось какое-то решение. Итак, самые отважные могут попробовать:

1 = 2023.

При этом решения, которые были найдены в прошлые разы, одноразовые и больше не принимаются.

Итак, вперёд! Все — в комменты!

А впрочем, истинным гурманам имеет смысл сначала немного пощекотать серые клеточки мозга лучшими конструкциями предыдущих серий новогодней матемагики. В смысле залезть в архивы и показать несколько красивых примеров прошлых годов. А заодно и новичкам будет проще разобраться в арифметических ухищрениях, необходимых для достижения обозначенных выше целей. Вот такие, например, красивые решения получались (специально беру древние годы, дабы не искушать на адаптации к нынешнему номеру):

(10 * 9 * 8 — 7 * 6 — 5) * (4 — 3 + 2 * 1) = 2019

Или вот:

9 * 8 * 7 * (6 + 5 — 4 — 3) + 2*1 = 2018
8 * 7 * 6 * (5 + 4 — 3) + 2*1 = 2018

Факториалы и кратные факториалы:

((7 * 6! / 5) + (4 — 3) ) * 2 * 1 = 2018
6! / 5 * (4+3)!!!!! + 2*1 = 2018

Чистая арифметическая красотища 🙂

7! / 6 / 5 * 4 * 3 + 2 + 1 = 2019

А вот пример сдвига:

(7 + 6 * (( 5 << 4 ) + 3) << 2 ) — 1 = 2019

Теперь с использованием прочей мате-магии =>

sf(4) * (3! + !2) +1 = 2017

{
sf(4)=1!*2!*3!*4!=288 — суперфакториал
3!=3*2*1=6 — факториал
!2=1 — субфакториал
}

А вот пришло время вызывать матемагических демонов:

(5! — 4!) * F( F(3!) ) + 2*1 = 2018
{
F(n) — Фибоначчи
5! — 4! = 120 — 24 = 96
F(3!=6) = 8
F(8) = 21
96*21 + 2 = 2016 + 2 = 2018
}

((4!)!!!!!!!!!!!!!!!!!)*(3!)*2+1 = 2017
// 17кратный факторал
{
4!=1*2*3*4=24
24!!!!!!!!!!!!!!!!!=24*(24-17)=24*7=168
3!=6
168*6*2+1=2016+1=2017
}

L( (L(3)) !! ) + !( L(2 + 1) ) = 1973 + 44 = 2017

{
L(n) – Леонардо
L(3) = 5
5!! = 15
L(15) = 1973
L(2 + 1 = 3) = снова 5
!5 = 44 (cубфакториал)
}

L( (L( Fm(F(2)) )) !! ) + !( L( Fm(1) )) = 2017

Но самое интересное, конечно же, «добыть» номер года из единицы. 2 -1 раз (доказательство по ссылке выше).

Что интересно, данный подход универсален. Он позволяет получить из единицы любое натуральное число.

(1) = 2018 =>

2018 получено с помощью матемагических демонов: через числа Вудала и числа Ферма, антисигму, субфакториал и кратный факториал:

(As( W( Fm( !1 ) )!!!!!!!!!!!!!!!!!!!!!) )!!!!!…..!!!!! = 2018

!1 = 0
Fm(0)=3
W(3)=23 // числа Вудала
23!!!!!!!!!!!!!!!!!!!!! = 46 // 21-кратный факториал
As(46) = 1009 // антисигма, как правильно обозначаются мне неизвестно, «As» я сам придумал…
1009!!!…!!! = 1009*2 = 2018 // 1007-кратный факториал, кратными факториалами можно чёрта лысого слепить 🙂

(1) = 2019 =>

2019 выведено через числа Тетраначчи и прочие уже традиционные числа Ферма и разно-факториалы ->

Tcci(( Fm( !1 )! )!!!! ) !!!…!!! (670-кратный факториал) = 673*3 = 2019

!1=0, Fm(0)=3, 3!=6, 6!!!!=12
Tcci(12) = 673
673*3 = 2019, вуаля!

(1) = 2020 =>

2020 получилось логарифмированием числа 10²⁰²⁰.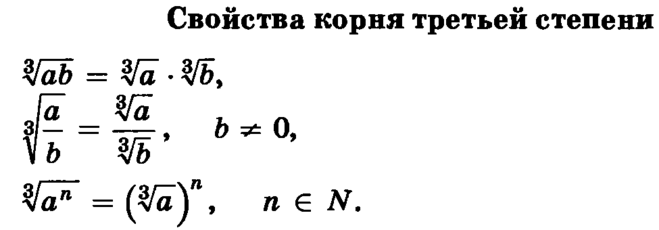 n + 1 =>

2 5 9 17 33 65 129 257 513 1025, за 9 итераций из просто сотни получили 10¹⁰²⁵. При этом каждый кратный факториал приводит только к одному умножению. Каждый очередной X умножается только на X/10. На этом «кратно-факториальные» числа заканчиваются.

Теперь берём !!!…x-кратный…!!! факториал, чтобы добить к числу 10¹⁰²⁵ ещё 995 нулей. Т.е. кратность x = 10¹⁰²⁵ — 10⁹⁹⁵ = 10⁹⁹⁵(10³⁰ — 1). Это число больше (10¹⁰²⁵ — 10¹⁰²⁴), посему повторного умножения кратного факториала и здесь не будет.

Итого получили 10²⁰²⁰.

Кстати, метод этот тоже универсален: им можно получить любое натуральное число, а не только 2020.

В качестве шутки:

2020 можно получить из «вообще ничего». Это достигается элементарно и при помощи тех же кратных факториалов и функций интернета:

2020 = (http://вообще-ничего.ком)!!!…399-кратный-факториал…!!!

🙂

Доказательство:

http://вообще-ничего.ком = 404.
404!!!…399-кратный-факториал. ..!!! = 404 * 5 = 2020

А ещё особенно горжусь получением 2020 через позиции чисел в разложении числа «пи»:

PiSrch( Pi0( PiSrch( Pi0( Fm(1) ) ) ) ) = 2020

где:

Pi0(n): позиции нулей в разложении Pi — A037008
PiSrch(n): позиция числа в разложении Pi.

О как! Сам [придумал] нашёл! Ух да я…

Если для 2020 было найдено аж три разной серьёзности решения, то в дальнейшем наступил какой-то облом и дефицит идей…

(1) = 2021 =>

Год 2021-й как-то кривенько, с хрустом и ударом большого молотка, через 6-ричную систему счисления — получился здесь.

числа Ферма: Fm(1)=5,
5!!!=5*2=10,
числа Рекамана: Rc(10)=11,
числа Фибоначчи: F(11)=89,
89!!!…84-кратный факториал…!!! = 89*5 = 445 = 2021 в 6-ричной системе счисления 🙂

(F(Rc(Fm(1)!!!)))!!!…84-кратный факториал…! = 2021₆

Альтернативно-1 =>

В комментариях в ЖЖ ещё подсказали через округление, но это тоже как-то совсем «на тоненького».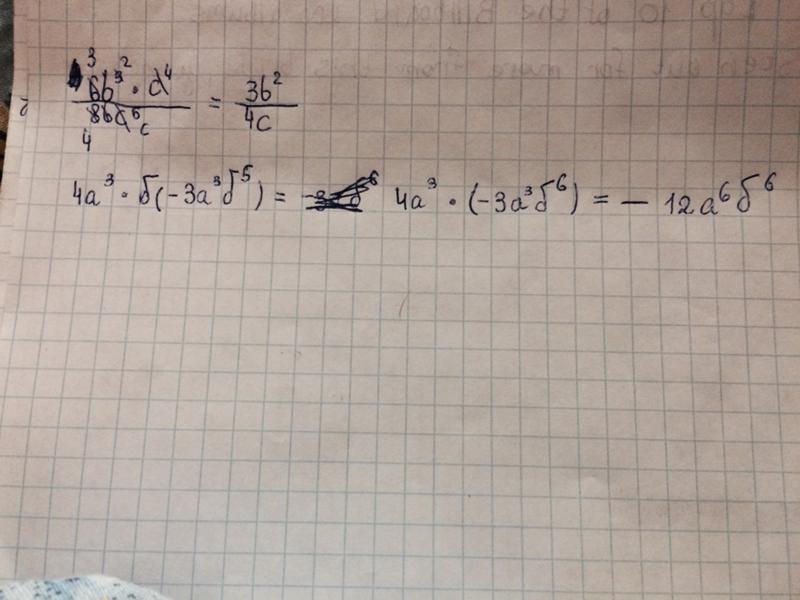 (-N)
5) берем еще раз двоичный логарифм. получаем: -N
6) дописываем еще раз знак —

Ну или итогово вот так:

-(log(-log(√(√(…√(sin (arctg(1)))…)))) = N (если корней взято N штук)

(1) = 2022 =>

Тоже получился далеко не сразу… Но в итоге было принято решение считать решением 🙂 формулу через числа Ченя (поскольку в Википедиях это есть — то данный матдемон допускается к исполнению работ).

( Chen( ( Fm(1)!!! )!!!!! ) )!!…(331-кратный)…! = 2022

Fm(1) = 5
5!!! = 10
10!!!!! = 50
Chen(50) = 337 http://oeis.org/A109611/list
337!!…! (331-кратный) = 337*6 = 2022.

Всё на этом!

Желаю всем отменных успехов в решении самых сложных математических (и не только) задач в наступающем 2023м!

Метки: chtogdekogda, contest, math

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Сколько будет 3 в 5-й степени?

Итак, вы хотите знать, сколько будет 3 в 5-й степени, не так ли? В этой статье мы объясним, как именно выполнить математическую операцию под названием «возведение числа 3 в степень 5». Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.

Что такое возведение в степень?

Давайте сначала зафиксируем наши термины, а затем посмотрим, как вычислить число 3 в 5-й степени.

Когда мы говорим об возведении в степень, все, что мы на самом деле имеем в виду, это то, что мы умножаем число, которое мы называем основанием (в данном случае 3) само по себе определенное количество раз. Показатель степени — это количество раз, которое нужно умножить на 3, что в данном случае равно 5 раз.

3 в степени 5

Есть несколько способов, как это может быть выражено, и наиболее распространенными способами, которые вы увидите, являются следующие:

• 3 ⁵
909) для обозначения показателя степени. Знак вставки полезен в ситуациях, когда вы не хотите или не нуждаетесь в использовании надстрочного индекса.

Итак, мы упомянули, что возведение в степень означает умножение базового числа само на себя для получения показателя степени число раз. Давайте посмотрим на это более наглядно:

3 в 5-й степени = 3 x … x 3 (5 раз)

Итак, каков ответ?

Теперь, когда мы объяснили теорию, стоящую за этим, давайте посчитаем числа и выясним, чему равно 3 в 5-й степени:

3 в степени 5 = 3 ⁵ = 243

Почему мы вообще используем возведение в степень 3 ⁵ ? Что ж, нам намного проще писать умножения и выполнять математические операции как с большими, так и с маленькими числами, когда вы работаете с числами с большим количеством конечных нулей или большим количеством десятичных знаков.

Надеюсь, эта статья помогла вам понять, как и почему мы используем возведение в степень, и дала вам ответ, который вы изначально искали. Теперь, когда вы знаете, что такое 3 в 5-й степени, вы можете продолжить свой веселый путь.

Не стесняйтесь поделиться этой статьей с другом, если вы считаете, что она поможет ему, или перейдите вниз, чтобы найти еще несколько примеров.

Процитируйте, дайте ссылку или ссылку на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.

No related posts.