Перевод в восьмеричную систему счисления
Пример №1. Перевести число 132,26710 в восьмеричное представление.
Решение находим с помощью калькулятора. Переводим целую часть числа, т.е. 132.
| Целая часть от деления | Остаток от деления |
| 132 div 8 = [16].5 = 16 | 132 mod 8 = 4 (132 — 16*8) | 16 div 8 = 2 | 16 mod 8 = 0 | 2 div 8 = 0 | 2 mod 8 = 2 | 0 div 8 = 0 | 0 mod 8 = 0 |
Остаток от деления записываем в обратном порядке. Получаем число в 8-ой системе счисления: 0204
132 = 02048
Для перевода дробной части числа последовательно умножаем дробную часть на основание 8. В результате каждый раз записываем целую часть произведения.
0.267*8 = 2.136 (целая часть 2)
0.136*8 = 1.088 (целая часть 1)
0.088*8 = 0.704 (целая часть 0)
0.704*8 = 5. 632 (целая часть
632 (целая часть
Получаем число в 8-ой системе счисления: 2105
0.267 = 21058
Таким образом, число 132,267 записывается в восьмеричной системе счисления как 204,21058
Пример №2. Перевести число 1000000010,10012 в восьмеричное представление.
Переводим целую часть числа. Для этого разделим исходный код на группы по 3 разряда.
10000000102 = 001 000 000 010 2
Затем заменяем каждую группу на код из таблицы.
| Двоичная СС | Восьмеричная СС |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Переводим дробную часть числа. Для этого разделим исходный код на группы по 3 разряда.
Для этого разделим исходный код на группы по 3 разряда.
10012 = 100 1002
Затем заменяем каждую группу на код из таблицы.
Получаем число: 100 1002 = 448
Таким образом, число 1000000010,10012 в восьмеричной системе счисления записывается как 1002,44.
Пример №3. Перевести число 132,26710 в восьмеричное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.
| Двоичная СС | Шестнадцатеричная СС |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Переводим дробную часть числа.
Получаем число: 3B16 = 001110112
Переводим целую часть числа. Для этого разделим исходный код на группы по 3 разряда.
1010010111112 = 101 001 011 111 2
Затем заменяем каждую группу на код из таблицы.
| Двоичная СС | Восьмеричная СС |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Переводим дробную часть числа. Для этого разделим исходный код на группы по 3 разряда.
001110112 = 001 110 1102
Затем заменяем каждую группу на код из таблицы.
Получаем число: 001 110 1102 = 1668
Таким образом, число A5F,3B16 в восьмеричной системе счисления записывается как 5137,166.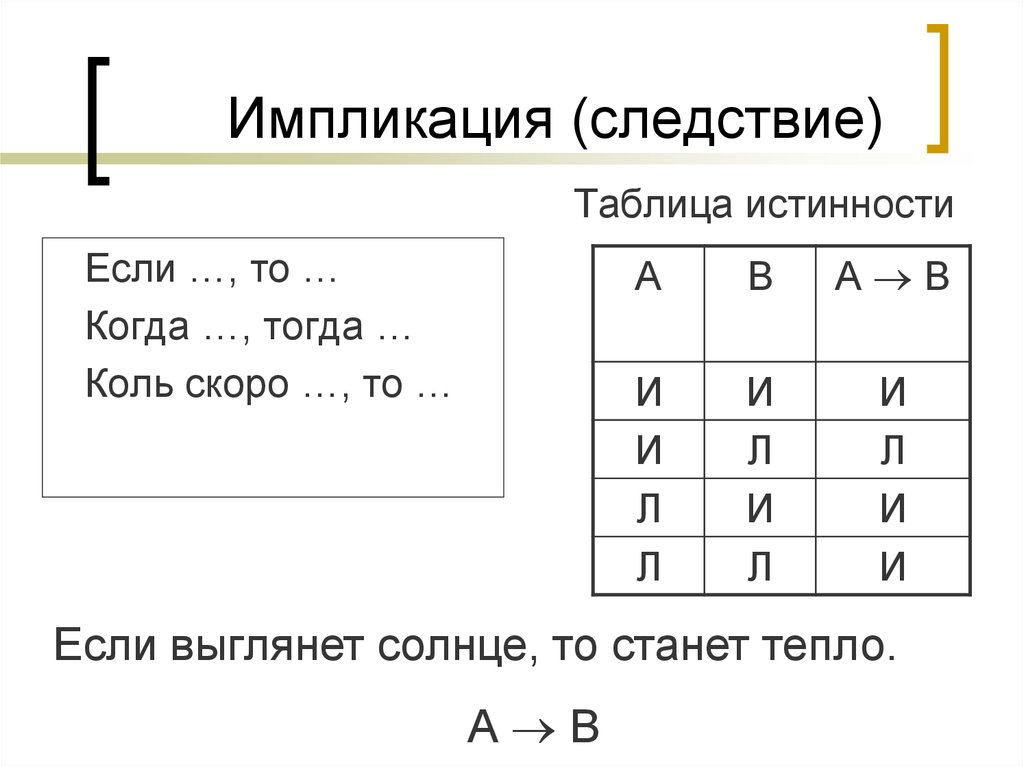
Перейти к онлайн решению своей задачи
отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция, законы де Моргана, тавтология, таблицы истинности
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Законы де Моргана
- Алгоритм доказательства эквивалентности высказываний с помощью таблиц истинности
- Тавтология
- Примеры
п.1. Отрицание
Отрицанием высказывания A называется новое высказывание «не A», принимающее значение «истина», если A ложно, и значение «ложь», если A истинно.
Обозначение отрицания \(\overline{A}\) читается «не A».
Если записать эту операцию с помощью таблицы истинности, где 0 обозначает «ложь», а 1 – «истина», получаем:
A
\(\overline{A}\)
Закон отрицания отрицания. Двойное отрицание \(\overline{\overline{A}}=A\) истинно только в том случае, если истинно исходное высказывание A.
Правило отрицания высказываний с кванторами: $$ \mathrm{ \overline{(\forall x)A(x)}=(\exists x)\overline{A(x)},\ \ \overline{(\exists x)A(x)}=(\forall x)\overline{A(x)} } $$
Расшифровка первого правила: высказывание «неверно, что для любого x выполняется A(x)» совпадает с высказыванием «найдётся x, для которого A(x) не выполняется».
Расшифровка второго правила: высказывание «неверно, что найдётся x, для которого выполняется A(x)» совпадает с высказыванием «для любого x A(x) не выполняется».
п.2. Конъюнкция
Конъюнкция двух высказываний – это высказывание, которое будет истинным, если истинны оба исходных высказывания; а во всех остальных случаях – будет ложным.
Конъюнкция является логическим умножением.
Обозначение конъюнкции A ∧ B, читается «А и В». Таблица истинности:
A
B
A ∧ B
С точки зрения операций над множествами, конъюнкция аналогична пересечению двух множеств (см. 2-1\geq 0} & \\ \mathrm{x\gt\frac12} & \end{array}\right. \Leftrightarrow x\leq -1 \cup x\gt\frac12 $$
2-1\geq 0} & \\ \mathrm{x\gt\frac12} & \end{array}\right. \Leftrightarrow x\leq -1 \cup x\gt\frac12 $$
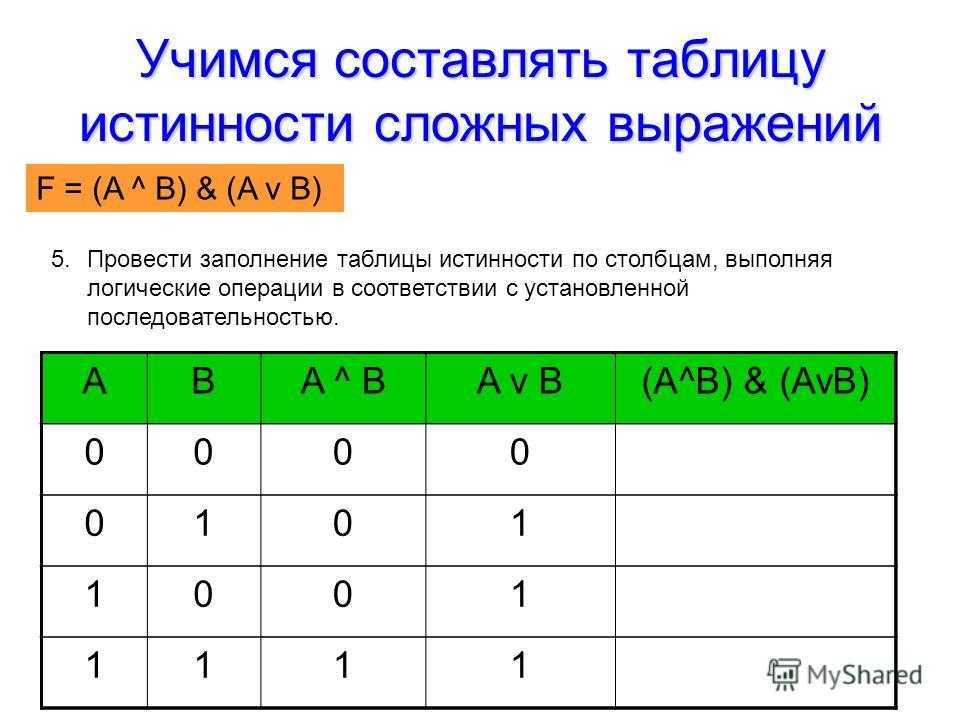
п.4. Импликация
Импликация двух высказываний – это высказывание, которое будет ложным, если первое высказывание истинно, а второе ложно; а во всех остальных случаях – будет истинным.
Обозначение импликации A → B, читается «если A, то B».
Высказывание A называют «посылкой», а высказывание B – «заключением».
Значение импликации зависит от порядка высказываний.
Таблица истинности:
A
B
A → B
п.5. Эквиваленция
Эквиваленция двух высказываний – это высказывание, которое будет истинным только при совпадении истинности обоих высказываний; а при несовпадении – будет ложным.
Обозначение эквиваленции A ↔ B, читается «A то же самое, что B» или «A эквивалентно B».
Таблица истинности:
A
B
A ↔ B
п.
 6. Законы де Моргана
6. Законы де МорганаОтрицание конъюнкции эквивалентно дизъюнкции отрицаний: \(\mathrm{\overline{A\wedge B}=\overline{A}\vee\overline{B}}\)
Докажем эквивалентность с помощью таблиц истинности:
A B A ∧ B \(\mathrm{\overline{A\wedge B}}\) | A B \(\mathrm{\overline{A}}\) \(\mathrm{\overline{B}}\) \(\mathrm{\overline{A}\vee\overline{B}}\) |
Мы видим, что итоговые столбцы слева и справа полностью совпадают.
Значит, высказывания эквивалентны.
Отрицание дизъюнкции эквивалентно конъюнкции отрицаний: \(\mathrm{\overline{A\vee B}=\overline{A}\wedge\overline{B}}\)
Докажем эквивалентность с помощью таблиц истинности:
A B A ∨ B \(\mathrm{\overline{A\vee B}}\) | A B \(\mathrm{\overline{A}}\) \(\mathrm{\overline{B}}\) \(\mathrm{\overline{A}\wedge\overline{B}}\) |
Высказывания слева и справа эквивалентны.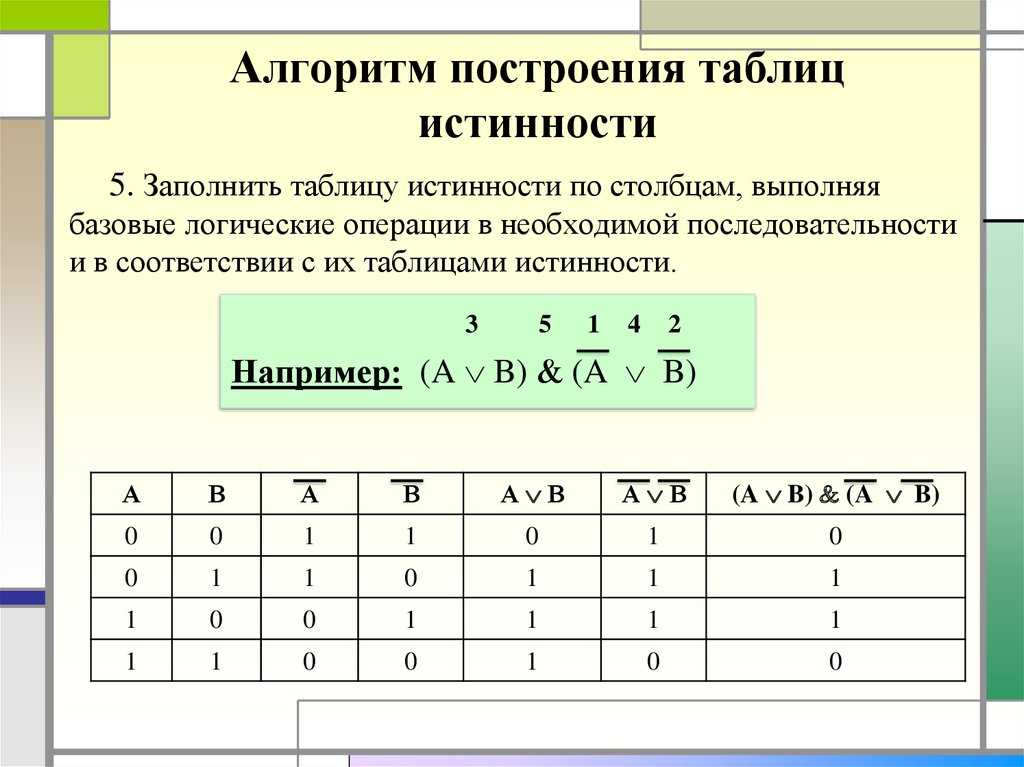
Высказывания называются эквивалентными (равносильными), если соответствующие значения каждого из них совпадают в таблице истинности.
п.7. Алгоритм доказательства эквивалентности высказываний с помощью таблиц истинности
На входе: две формулы алгебры высказываний, соединенные отношением эквивалентности «=».
Шаг 1. Построить таблицу истинности для формулы слева от знака «=».
Шаг 2. Построить таблицу истинности для формулы справа от знака «=».
Шаг 3. Сравнить итоговые столбцы двух таблиц. Если столбцы полностью совпадают, формулы эквивалентны.
Например:
Докажем следующее свойство:
Отрицание импликации эквивалентно конъюнкции посылки и отрицания заключения: $$ \mathrm{ \overline{A\rightarrow B}=A \wedge\overline{B} } $$
A B A → B \(\mathrm{\overline{A\rightarrow B}}\) | A B \(\mathrm{\overline{B}}\) \(\mathrm{A\wedge\overline{B}}\) |
Столбцы совпадают.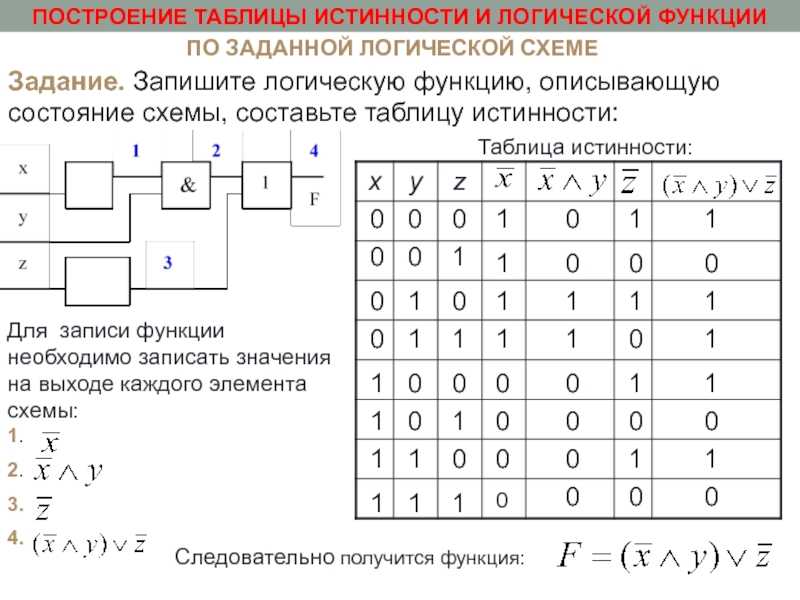 Значит, формулы эквивалентны.
Значит, формулы эквивалентны.
Что и требовалось доказать.
п.8. Тавтология
Тавтологией (или законом логики) называется формула, принимающая значение истины при любых значениях переменных.
Таблица истинности для тавтологии даёт итоговый столбец, заполненный только единицами.
Например: \(\mathrm{A \vee \overline{A}}\)
A
\(\mathrm{\overline{A}}\)
\(\mathrm{A\vee\overline{A}}\)
«Быть иль не быть» — это тавтология.
п.9. Примеры
Пример 1. Для формулы P(x, y)=(∃x∀y)(A(x,y)∧B(x,y))
сформулируйте предложения A и B, при которых:
а) формула всегда истинна; б) формула всегда ложна.
a) A(x,y): квадрат числа x больше y
B(x,y): куб числа x больше y
Пусть x = |y + 1|. Тогда x2 = (y + 1)2 > y – истинно ∀y
x3 = |y + 1|3 > y – ∀y
Таким образом, мы нашли x, при котором A(x,y) ∧ B(x,y) = 1 для любого y, т. е.
е.
P(x,y) = 1.
б) A(x,y): x больше y
B(x,y): x меньше y
A(x,y)∧B(x,y) = 0 – ложно для любого y, т.к. не существует x, который одновременно был бы больше и меньше y.
P(x,y) = 0.
Пример 2. Составьте таблицу истинности для формулы \(P=(\overline{A}\rightarrow B)\vee (A\rightarrow \overline{B})\).
Является ли данная формула тавтологией?
A
B
\(\mathrm{\overline{A}}\)
\(\mathrm{\overline{B}}\)
\(\mathrm{\overline{A}\rightarrow B}\)
\(\mathrm{A\rightarrow \overline{B}}\)
P
0
0
1
1
0
1
1
0
1
1
0
1
1
1
1
0
0
1
1
1
1
1
1
0
0
1
0
1
Это – тавтология.
Пример 3*. Составьте таблицу истинности для формулы
P = (A → B) ∧ (B → C) → (A → C)
Является ли данная формула тавтологией?
A
B
C
A → B
B → C
A → C
(A → B)
∧
(B → C)
P
0
0
0
1
1
1
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
1
0
1
1
1
0
1
0
0
0
1
1
1
1
1
1
1
1
1
Это – тавтология.
[Решено] Таблица истинности для данной логической схемы:
Таблица истинности для данной логической схемы:
A Б С 0 0 0 0 1 1 1 0 0 1 1 1 А Б С 0 0 0 0 1 1 1 0 1 1 1 0 А Б С 0 0 1 0 1 0 1 0 0 1 1 1 А Б С 0 0 1 0 1 0 1 0 1 1 1 0
Опция 4:
| А | Б | С |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Бесплатно
RPMT Тест оптики 1
17,7 тыс. пользователей
пользователей
10 вопросов
40 баллов10 минут
Понятие:
Здесь мы использовали понятия И и НЕ-И вентилей. (1)
входы A и b, то выход: Y = \(\overline{A.B}\) —— (2)
Вычисление:
Дано:
В этой схеме мы обозначили ее как 1,2,3 часть схемы, имеющую выходы Y1, Y2, 1, Y2, и C 900. из первых двух входных элементов И-НЕ, Y2 = решение для вторых двух входных элементов И-НЕ
C = решение для третьего элемента И, соединяющего оба элемента И-НЕ как два входа
Из принципиальной схемы видно, что Y1 = \(\overline{ А.Б}\) —— (3)
и, Y2 = \(\overline{\overline{A}.B}\) —— (4)
Здесь выведите C = Y2.Y1 = \(\overline{A.B}\).\( \overline{\overline{A}.B}\) = \(\overline{\overline{A}.B + AB}\) (по теореме Де Моргана)
Это можно записать как: \(\overline{ (\overline{A} + A)B}\) = \(\overline{1} + \overline{B} = \overline{B}\) (где \(A+ \overline{A} = 1\))
Итак, мы можем записать таблицу истинности как C = \(\overline{B}\) —— (4)
когда B = 0, то C = 1, B = 1, затем C = 0, так что решение совершенно не зависит от A.
Итак, таблица истинности:
| A | Б | С |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
H вариант 4) правильный.
Скачать решение PDFПоделиться в WhatsApp
Последние обновления NEET
Последнее обновление: 21 октября 2022 г.
15 декабря 2022 года Национальное агентство по тестированию опубликовало уведомление о дате экзамена NEET 2023. Экзамен будет проведен 7 мая 2023 года. Расписание консультаций по национальному вступительному экзамену (NEET) было опубликовано для округов Махараштры, Ассама и Карнатаки. Ознакомьтесь с подробным графиком консультирования NEET на связанной странице. Национальное агентство тестирования (NTA) ежегодно проводит экзамен NEET для поступления в медицинские колледжи. Кандидаты могут проверить свои результаты NEET на официальном сайте NTA. Для официального ключа ответов NEET кандидаты должны пройти шаги, упомянутые здесь.
Национальное агентство тестирования (NTA) ежегодно проводит экзамен NEET для поступления в медицинские колледжи. Кандидаты могут проверить свои результаты NEET на официальном сайте NTA. Для официального ключа ответов NEET кандидаты должны пройти шаги, упомянутые здесь.
Предлагаемые экзамены
содержание:
функции пункты меню установка ввод формулы операции ввод таблицы вывод таблицы правила редукции CNF — DNF противоречивость тавтология сохранение и загрузка перевод информации информация сканирования виртуальные термины в работе история
Введение Logic10 — это программа, которая:
 Генерирует таблицы истинности из формул булевой алгебры Генерирует таблицы истинности из формул булевой алгебры . 2. Сокращает таблицы истинности, применяя правила булевой алгебры. Щелкните [ ЗДЕСЬ ] для программирования сокращения таблицы истинности. Logic10 отлично помогает в изучении булевой алгебры, проектировании цифровых электронных схем Это Logic10 версии 2.0 Так Logic10 выглядит в работе:(уменьшенное изображение) 2. вывод (сокращенных) таблиц истинности 3. информация о процессе перевода или сокращения формулы Характеристики Особенности Logic10:
— вывод : Таблица истинности в формате CNF или DNF — сохранить и перезагрузить всех входных и выходных данных — печать входных данных и выходных результатов — по выбору: информация о процессе перевода формулы — по выбору: пошаговая информация о процессе восстановления — In-Line справка информация Пункты меню см. ниже: ниже:Изображения слева направо позволяют
— сохранение таблицы истинности и настроек на диск — распечатать ввод и таблицу истинности — настройка принтера — отображать справочную информацию В верхней части окна вывода можно выбрать выход CNF или DNF. Кроме того, флажок может быть установлен, если необходимо уменьшить таблицу истинности. На вершине Поле Info , два флажка могут быть отмечены: Установка Logic10 написан для Windows. Язык программирования — Delphi.Загрузите Logic10, щелкнув значок загрузки (молния) в верхней части этой страницы. Нет никакой процедуры установки, просто скопируйте Logic10 в папку по выбору.  Реестр Windows не изменен. Ввод формулы ниже подробное изображение поля ввода формулы:Логические переменные представляют собой одиночные символы A..Z Допускается выбор не более 15 различных символов. Круглые скобки (…) могут использоваться на 20 уровнях для определения приоритета операций. Операторы с их приоритетом
Примечания: 1. ABC = ABC А(В+С) = А.(В+С) (А+В)(С+D) + (А+В).(С+D) Примечание: Осторожно: При продолжении формулы на следующей строке символ «.» оператор вставляется между последовательными переменными, поэтому эта формула А+Б С+ГИнтерпретируется как: A+B.C + D Чтобы удалить строку, введите ctrl y Операции В таблице ниже перечислены таблицы истинности для всех операций.
Ввод таблицы истинности Входными данными может быть таблица истинности не более 100 строк.Начните вводить имя переменной (A..Z) в верхней части таблицы. Входная таблица находится в форме CNF, поэтому каждая строка представляет собой операцию И своих переменных, строки объединяются по схеме ИЛИ. Введите «0», если отрицательная переменная должна быть истинной, введите «1», если переменная должна быть истинной.  Итак, эта таблица
А Б В Г
0 1 1
1 1 0
Представляет формулу: /A C D + A B /DВыход таблицы истинности При нажатии кнопки GO формула транслируется в список основных операций в порядке их приоритета.Затем запускается счетчик для генерации всех возможных состояний 0,1 переменных и выполняются операции. Для режима CNF: если окончательный результат дает true, значения переменных добавляются в выходную таблицу истинности. Для режима DNF:
если результат ложный, то значения переменных копируются в выходную таблицу истинности. Правила сокращения Если установлен флажок уменьшить , то для уменьшения выходной таблицы применяются правила логической алгебры.Нет никакой разницы между режимами CNF и DNF. В этом процессе сокращения используются следующие правила:
 ….А + А = А ….А + А = А 2…..А + АВ =А 3…..А/В + АВ = А 4…..А + /АВ = А + В 5…..A/B + BC —> AC Обратите внимание, что такая формула, как A + A, представляет собой структуру 90 388.
он может отображаться как D/F + D/F или как PQ/(X+Y+Z) + PQ/(X+Y+Z) Правило 5. основное изменение по сравнению с предыдущим уровнем 1.2 Оно заменяет старые правила 5. и 6. и устраняет все известные «утечки» в процессе редукции. В правиле 5. AC называется виртуальным термином и лишь временно добавляется в процесс сокращения. Правило 5. означает, что если AC =1, то A/B + BC = 1, однако обратное неверно. . Правила сокращения для виртуальных терминов такие же, как и для обычных терминов, за одним исключением:
 Сам термин удаляется из окончательной таблицы истинности. Добавление термина без родителей изменит формулу. Виртуальный и нормальный термин из таблицы истинности могут быть объединены (по ИЛИ), что может привести к
— сокращение виртуального срока — сокращение или удаление члена таблицы истинности Виртуальные термины, происходящие от других виртуальных терминов, также имеют более двух родителей. Родителями являются все термины, которые внесли свой вклад в виртуальный термин путем редукции или генерации. Ввод таблицы истинности При нажатии GO входная таблица истинности копируется в выходную таблицу.Если уменьшите проверяется таблица сокращена по вышеуказанным правилам 1..5. КНФ и ДНФ Выходная таблица истинности может быть в форме CNF или DNF. CNF означает «конъюнктивную нормальную форму», которая представляет собой ABC + DEF + GHI + ….. . Итак, И отдельных переменных (с предшествующим / или без него), которые объединяются по ИЛИ. ДНФ означает «дизъюнктивную нормальную форму», которая представляет собой (A+B+C)(D+E+F)(G+H+I)(…. В режиме DNF при формировании выходной таблицы истинности Logic10 вводит значения переменных в таблицу для значений Примечание: cnf………AB + BC = (A+C)(A+D)(B+C)(B+D)………dnf Также законы де Моргана иллюстрируют связь между CNF и DNF Несоответствие Логическая формула (предложение) несостоятельна, если она никогда не приводит к истине. Простое несоответствие: ……A./A Logic10 сообщает о несоответствиях. Тавтология Логическая формула (предложение) называется тавтологией, если она всегда истинна.Простая тавтология:……..A + /A Logic10 сообщает о тавтологиях. Сохранить и загрузить При нажатии на значок сохранения (дисковая пластина) открывается диалоговое окно для выбора имени файла.Logic10 не использует расширения имен файлов, так как их и так достаточно. Однако для ясности выбранное имя файла имеет префикс logic10_ (если еще не был). Все данные: входная формула, входная таблица CNF и выходная таблица истинности сохраняются в одном файле. Чтобы перезагрузить сохраненные данные, щелкните значок карты и выберите файл. Перевод информации если xlate флажок установлен, информация о переводе формулы отображается в информационном поле.ниже подробная картинка  Добавляется третий столбец с приоритетом операции. Из этой таблицы составляется таблица переменных . Правильный директор таблицы является окончательным результатом перевода.
2. регистр назначения 3. исходный операнд1, регистр 4. регистр исходного операнда2 При установке переменных на определенные значения и выполнении таблицы директоров формула вычисляется истина или ложь . Информация о сканировании Просмотр таблицы истинности сводится к сравнению ( ИЛИ ing) каждой строки (term) и ed переменных с каждым другим термином.Индексами таблицы истинности являются [i] и [j]. Итак, запись таблицы истинности [i] сравнивается с записью [j].  Анализ пары терминов дает 4 логических результата: привет отверстие-яЭто верно, когда [ i ] удалил переменные, которые присутствуют в [ j ] 906:00 А Б В Г Д Е [i] 0 0 х 0 х х [к] 1 0 х 1 1 0 В приведенной выше таблице переменные E, F исключаются в [ i ], но не в j, поэтому hi верно. хдж Отверстие-jЭто верно, когда [ j ] удалил переменные, которые присутствуют в [ i ]
А Б В Г Д Е
[i] 1 х 1 1 0 0
[j] 0 х 0 х х х
Здесь [ j ] удалил переменные D, E, F, которые не удалены в [ i ], поэтому hj истинно.сб Один бит означает, что разница (исключающее или) между [ i ] и [ j ] имеет только 1 бит.
А Б В Г Д Е
[i] х 1 1 1 0 1
[к] 0 х 1 1 1 1
Отличаются только биты E. Столбцы, имеющие x (удаленная переменная), игнорируются. Итак, сб верно. зб Нулевой результат, также называемый равным или без разницы
А Б В Г Д Е
[i] 0 1 1 1 х 0
[к] 0 1 х 1 1 0
Столбцы с x игнорируются.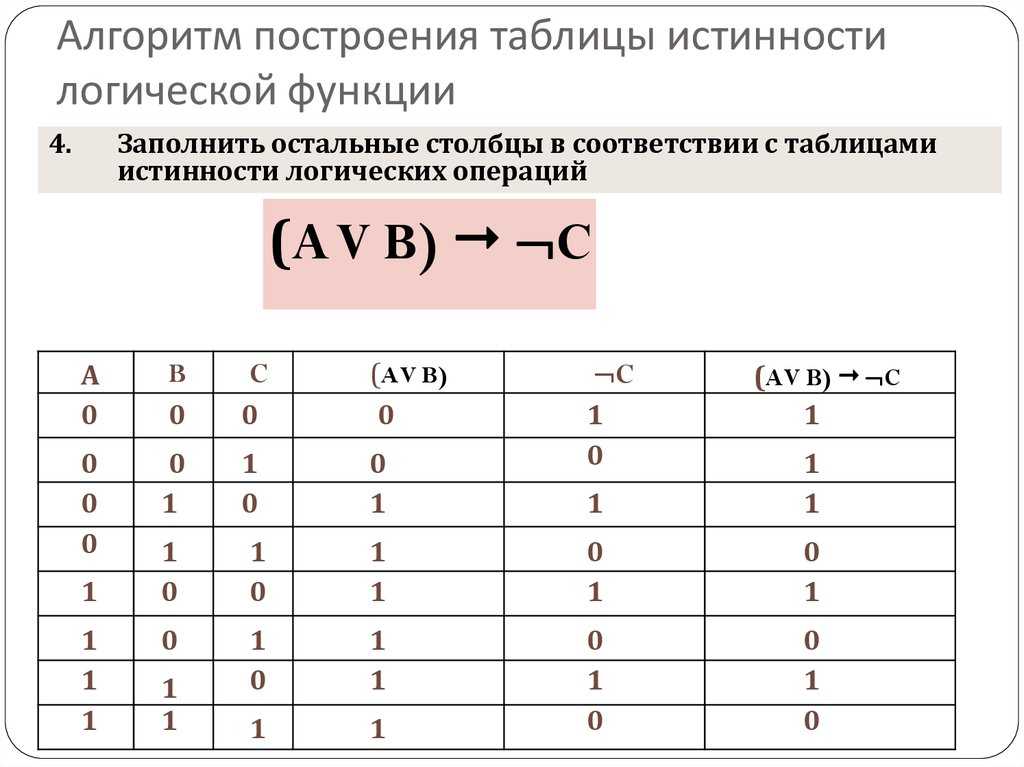 Остальные столбцы должны быть равны. Итак, ЗБ верно. hi(3) hj(2) sb(1) zb(0) — биты 3,2,1,0 в коде. Некоторые примеры: Правило редукции 1 АВ/С + АВ/С = АВ/С
А Б В
[я] 1 1 0
[к] 1 1 0
Разница 0 0 0,hi, hj, sb ложны (0), zb истинны (1). Код действия = 1. Таким образом, член [ j ] удаляется. Правило редукции 2 АВ + АВС/D = АВ
А Б В Г
[i] 0 1 х х
[к] 0 1 1 0
hi истинно, hj ложно, sb ложно, zb истинно. Код действия 1001 = 9 (десятичный). [j] удаляется. Правило редукции 3 А/ВС + АВС = А
А Б В Г Д Е
[i] 1 0 1 х х х
[к] 1 1 1 х х х
привет, hj, zb неверны. sb истинно (различно только B). Код действия 2. Переменная B в [i] удалена, все переменные [j] удалены. 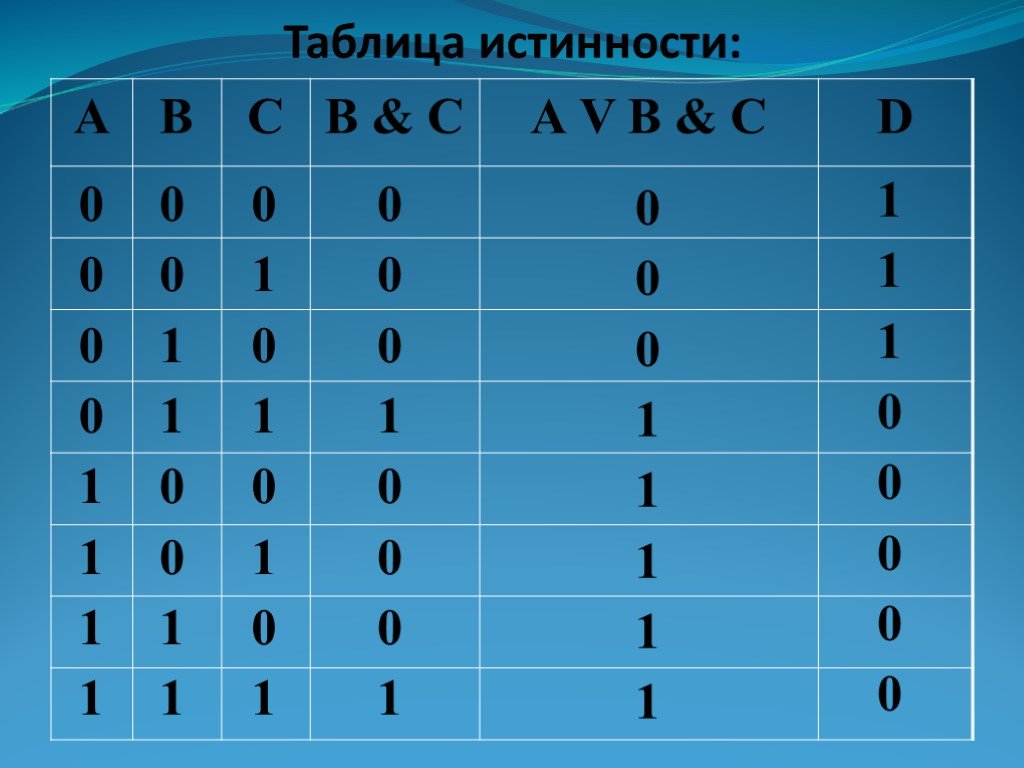 Правило редукции 4 АВ + А/ВС = АВ + АС
А Б В
[я] 1 1 х
[к] 1 0 1
привет, сб правда. zb, hj ложны. Разностный бит B удаляется в [ j ]. Правило редукции 5, виртуальные термины AB + /BC —> AC, где AC — виртуальный термин, используемый только для сканирования. 906:00 А Б В [я] 1 1 х [j] х 0 1 привет, hj, sb верны. зб неверно. Код действия 1110 = 14 десятичных знаков.Действие : Запускается сканирование для сравнения виртуального термина AC с каждым термином в таблице истинности. Правила 1..4 применяются с единственным ограничением, что [i] или [j] не могут быть удалены, потому что они являются родителями. Ниже приведена типичная информация обычного сканирования. k — это индекс в таблице истинности (как i, j для нормального сканирования) Виртуальный термин может (по сравнению с терминами таблицы истинности) генерировать новые виртуальные термины.  Эти термины хранятся в стеке (фактически в буфере FIFO) для последующей обработки. В таблице истинности родительские термины виртуального термина выделены красным. Виртуальные термины в работе Введение виртуальных терминов устраняет все прежние дополнительные правила за пределами 1..4Сначала позвольте мне объяснить, как возникла идея виртуальных терминов. Формула /BQ + /AP + AB привела к /B /P Q + AB + /AP + AQ Этот результат не является ошибочным, но указанный термин жир является избыточным (как и /P в / б/пк) Итак, AQ представляет собой /BQ + AB. Если AQ = 1, то наверняка /BQ + AB = 1 (но не наоборот). В этом случае термины /BQ + AB образуют виртуальный термин AQ. Пример 1: /AZ + /BZ + /CZ + ABC = Z + ABC Пример 2: BC + /BP + ACPQ = BC + /BP Пример 3: /B /P Q + AB + /AP + AQ …………….{см. выше} История Первую версию этого генератора/редуктора таблицы истинности я написал в 1991 году во время изучения математики.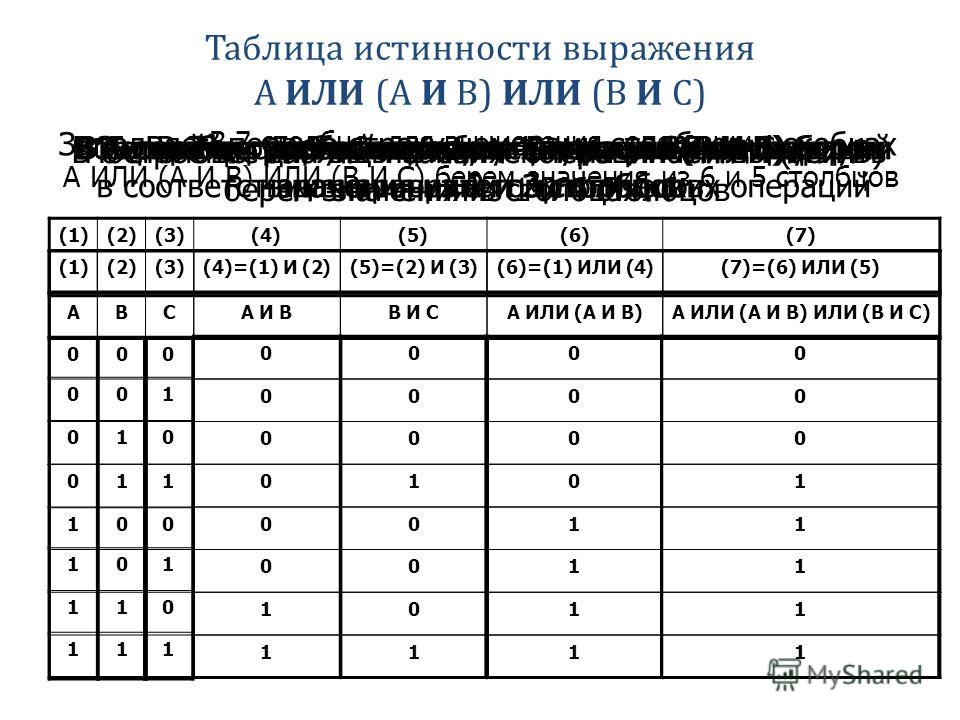 10 (высший балл) предлагалось каждому студенту, который мог написать программу для диагностики . формула логики высказывания как «непоследовательная» или «тавтология». Я написал программу на Turbo Pascal (под MSDOS) и набрал «10». В январе 2013 года, убираясь в своей комнате, я нашел старую дискету. Оказалось, что программа работала нормально, несмотря на старомодный пользовательский интерфейс, но некоторые таблицы где не сводится к пределу. Применялись только правила редукции 1..4. Я снова начал работать над этим. Получилась версия Logic10 1.2 в которой добавлено 2 новых правила
2. АВ + /ВС + АС = АВ + /ВС Однако еще оставались случаи, когда сокращение было не предельным. Версия 2.0 с виртуальными терминами вместе с правилами редукции 1..4 очищает каждую таблицу истинности.  |

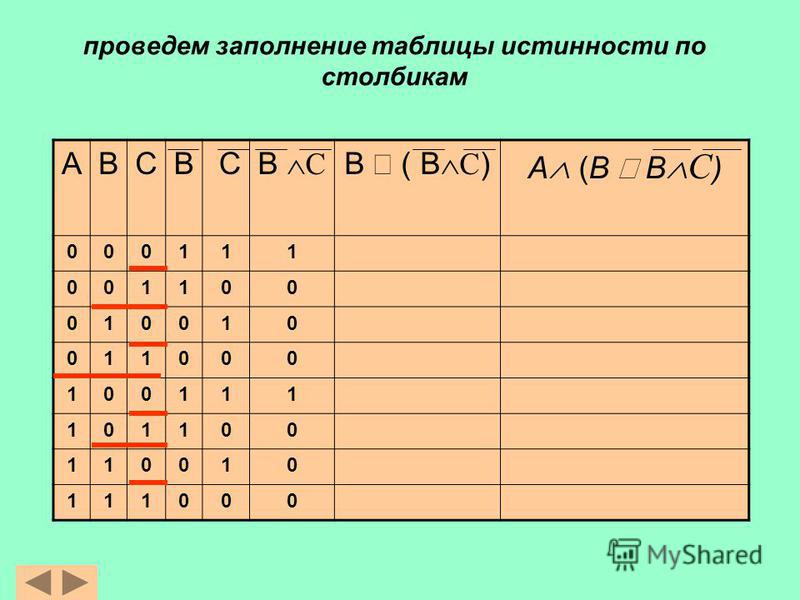 между переменными «.» Оператор И может быть опущен. Программа добавляет «.» автоматически.
между переменными «.» Оператор И может быть опущен. Программа добавляет «.» автоматически.