Сколько вариантов 4 из 20: правила игры, условия выигрыша и что можно выиграть в лотерею «Спортлото «4 из 20»

Как посчитать количество сочетаний

Статьи › Находится › В ящике находится 15 деталей сколькими способами можно взять 4 детали

Количество сочетаний обозначается как C n m (читается: сочетания из \(n\) по \(m\)). Сочетания вычисляются по формуле C n m = n! M! (n − m)!.

1. Как рассчитать количество комбинаций цифр
2. Сколько комбинаций из 8 цифр с повторениями
3. Сколько комбинаций из 3 цифр с повторением
4. Что такое C из n по k
5. Сколько комбинаций из цифр 1 2 3 4
6. Сколько комбинаций из 10 цифр по 4
7. Сколько комбинаций из 4 цифр от 1 до 9
8. Сколько комбинаций из 6 цифр от 1 до 9
9. Сколько комбинаций из 5 цифр от 1 до 5
10. Сколько комбинаций из 3 кубиков
11. Сколько комбинаций из 999 цифр
12. Как посчитать количество вариантов комбинаций без повторений
13. Как найти C по физике
14. Сколько комбинаций из 10 цифр без повторений
15. Сколько комбинаций из 9 цифр без повторений
16. Сколько вариантов кода из 4 цифр
17. Сколько вариантов комбинаций из 24 цифр
18. Сколько комбинаций в игре 4 из 20
19. Сколько комбинаций из 6 вариантов
20. Как посчитать количество перестановок с повторениями
21. Сколько может быть комбинаций из 3 Цветов
22. Сколько четных трехзначных чисел можно составить из цифр 3 4 5 6
23. Сколько различных трехзначных чисел можно составить из цифр 1 2 3 4 5 Если цифры в числе не повторяются
24. Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5
25. Сколько комбинаций из 4 цифр от 1 до 4
26. Сколько комбинаций из 6 цифр от 0 до 9

Как рассчитать количество комбинаций цифр

Формула для определения количества возможных комбинаций выглядит следующим образом: nCr = n! / р! (н-р)!

Сколько комбинаций из 8 цифр с повторениями

N = m ^ k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля. 15.

Сколько комбинаций из 3 цифр с повторением

3 = 60 способов расстановки цифр, т. е. искомое количество трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132, )

Что такое C из n по k

Число сочетаний из n по k (Cnk) — называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми.

Сколько комбинаций из цифр 1 2 3 4

Следовательно комбинаций будет: 4 * 3 * 2 * 1 = 4! = 24.

Сколько комбинаций из 10 цифр по 4

Очевидно, что количество всех возможных комбинаций из 10 цифр по 4 равно 10.000. Число всех возможных комбинаций из 30 букв по две равно.

Сколько комбинаций из 4 цифр от 1 до 9

Можно сказать что это числа от 0 до 9999. Значит всего возможных комбинаций 10 000. Ответ: 10 000 комбинаций.

Сколько комбинаций из 6 цифр от 1 до 9

720 вариантов. Как вывести на экран все 720 комбинаций? Пример: 325614, 236451, 231564 и так далее. 5 = 100,000. Логически подумайте — каждая из комбинаций от 000,001 до 100,000 повышают общее число комбинаций на одну, итого кол-во комбинаций равно собственно числу.

Сколько комбинаций из 3 кубиков

Комбинаторика Число всех достижимых различных состояний кубика Рубика 3x3x3 равно: 43 252 003 274 489 856 000.

Сколько комбинаций из 999 цифр

999). Всего комбинаций из цифр и букв может быть: 676 × 9 999 999 = 6 759 999 324 (6 млрд.

Как посчитать количество вариантов комбинаций без повторений

Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4). Очевидно, что k меньше или равно n, т. к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются).

Как найти C по физике

С = Q / (m * (t2 — t1)).

Сколько комбинаций из 10 цифр без повторений

Можно сказать, что это 10-тизначное число в 36-ричной системе счисления. Количество комбинаций будет равно 3610 или 3,6561584×1015. Если символы не могут повторяться, то мы имеем дело с размещениями.

Сколько комбинаций из 9 цифр без повторений

Это ж порядка 400-410 тясяч комбинаций, если не ошибаюсь. Количество размещений 9 цифр в 9-значном числе 363000 + 8,7,6, значные числа.

Сколько вариантов кода из 4 цифр

Из них 11% составила комбинация 1234, 1111 — 6%, 0000 — 2%, хотя набор возможных комбинаций для PIN-кодов с четырьмя цифрами — от 0 до 9 насчитывает 10 тыс вариантов.

Сколько вариантов комбинаций из 24 цифр

Вы немного ошиблись, комбинаций не 12, а из 24 чисел по 12 есть почти 3 млн. комбинаций, точнее 2 704 156 комбинаций.

Сколько комбинаций в игре 4 из 20

Вероятность выигрыша = 1/4845. Одна правильная комбинация знаков из 4845 возможных.

Сколько комбинаций из 6 вариантов

= 1 * 2 * 3 * 4 * 5 * 6 =720. При условии, что числа могут повторяться, на каждом месте могут быть все 6 чисел и количество таких комбинаций равно: 6 * 6 * 6 * 6 * 6 * 6 = 66 = 46 656.

Как посчитать количество перестановок с повторениями

Такие выборки называются перестановками с повторениями. Их возможное количество вычисляется по формуле: P n ¯ = P n 1, n 2, n k = n! N 1!

Сколько может быть комбинаций из 3 Цветов

Например, при 3 цветах в схеме и 7 цветах в наборе получится 35 сочетаний, а при 4 цветах в схеме и 10 цветах в наличии получится уже 210 различных сочетаний и т. д.

Сколько четных трехзначных чисел можно составить из цифр 3 4 5 6

Ответ: Можно составить 32 трехзначных четных числа. Как добавить хороший ответ?

Сколько различных трехзначных чисел можно составить из цифр 1 2 3 4 5 Если цифры в числе не повторяются

На первое место мы можем выбрать одну из 5 цифр, на второе — только одну из четырех, так как цифры не должны повторяться, а на третье — одну из трех цифр. Общее количество возможных цифр равно произведению вариантов цифр для каждого места: 5 * 4 * 3 = 60 вариантов. Ответ: 60 вариантов трехзначных чисел.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? И сколько из них с неповторяющимися цифрами? = 5× 4×3 = 60. ПРИМЕР 4.

Сколько комбинаций из 4 цифр от 1 до 4

Можно сказать что это числа от 0 до 9999. Значит всего возможных комбинаций 10 000. Ответ: 10 000 комбинаций.

Сколько комбинаций из 6 цифр от 0 до 9

То есть N=6, и число возможных комбинации N!, 6!= 720 вариантов.

Сколько комбинаций формула

Статьи › Карточка › Сколько различных буквосочетаний можно получить перестановкой карточек со следующими буквами колокол

Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: Ckn=n!(n−k)!⋅k!.

1. Сколько комбинаций из цифр 1 2 3 4
2. Сколько вариантов комбинаторика
3. Как посчитать все возможные варианты
4. Сколько комбинаций из 10 цифр по 10
5. Сколько комбинаций из 4 цифр от 1 до 5
6. Сколько комбинаций из 999 цифр
7. Сколько комбинаций из 6 вариантов
8. Сколько вариантов 6 из 6
9. Сколько вариантов 3 цифр
10. Сколько вариантов комбинаций из 24 цифр
11. Как посчитать количество вариантов перестановок
12. Сколько комбинаций из 10 цифр по 4
13. Сколько вариантов пароля из 8 цифр
14. Сколько комбинаций из 9 цифр без повторений
15. Сколько комбинаций из 5 цифр от 1 до 5
16. Сколько вариантов комбинаций из 4 цифр
17. Как посчитать количество вариантов комбинаций без повторений
18. Сколько трехзначных чисел можно составить из цифр 0 1 3 6 7 9
19. Сколько вариантов в 6 из 49
20. Сколько комбинаций можно составить из двух цифр
21. Сколько вариантов на 2 кубиках
22. Что такое сочетание в математике
23. Сколько комбинаций в игре 4 из 20
24. Сколько комбинаций из 3 цифр без повторений
25. Сколько всего комбинаций Трёхзначных чисел
26. Как посчитать количество комбинаций кодового замка
27. Сколько трехзначных чисел можно составить из цифр 1 2 3 4
28. Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5
29. Сколько четырехзначных чисел можно составить из цифр 1 2 3 4 если цифры в числе не повторяются
30. Сколько чисел можно составить из цифр 1 2 3

Сколько комбинаций из цифр 1 2 3 4

Следовательно комбинаций будет: 4 * 3 * 2 * 1 = 4! = 24.

Сколько вариантов комбинаторика

Общее число возможных вариантов выбора 5 из 36 равно С365. Формулы, использующие число сочетаний: CNK = CN-1K-1 + C.

Как посчитать все возможные варианты

Формула для определения количества возможных комбинаций выглядит следующим образом: nCr = n! / р! (н-р)!

Сколько комбинаций из 10 цифр по 10

Можно сказать, что это 10-тизначное число в 36-ричной системе счисления. Количество комбинаций будет равно 3610 или 3,6561584×1015. Если символы не могут повторяться, то мы имеем дело с размещениями.

Сколько комбинаций из 4 цифр от 1 до 5

Ответ: 10 000 комбинаций.

Сколько комбинаций из 999 цифр

999). Всего комбинаций из цифр и букв может быть: 676 × 9 999 999 = 6 759 999 324 (6 млрд.

Сколько комбинаций из 6 вариантов

= 1 * 2 * 3 * 4 * 5 * 6 =720. При условии, что числа могут повторяться, на каждом месте могут быть все 6 чисел и количество таких комбинаций равно: 6 * 6 * 6 * 6 * 6 * 6 = 66 = 46 656. 5 = 100,000. Логически подумайте — каждая из комбинаций от 000,001 до 100,000 повышают общее число комбинаций на одну, итого кол-во комбинаций равно собственно числу.

Сколько вариантов комбинаций из 4 цифр

Из них 11% составила комбинация 1234, 1111 — 6%, 0000 — 2%, хотя набор возможных комбинаций для PIN-кодов с четырьмя цифрами — от 0 до 9 насчитывает 10 тыс вариантов.

Как посчитать количество вариантов комбинаций без повторений

Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4). Очевидно, что k меньше или равно n, т. к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются).

Сколько трехзначных чисел можно составить из цифр 0 1 3 6 7 9

Сколько трёхзначных чисел можно составить из цифр 0 1 3 6 7 9? Если цифры повторно использовать нельзя, то у меня получается следующее: Первую цифру в числе можно выбрать 5-ю способами (0 ведущим быть не может). Ответ:100.

Сколько вариантов в 6 из 49

Вероятность выпадения любых 6 чисел из 49 не «стремится к нулю», а составляет ровно 1/13983816, и не имеет значения, идут эти числа подряд или нет.

Сколько комбинаций можно составить из двух цифр

51, 53, 55, 57, 59. 71, 73, 75, 77, 79. 91, 93, 95, 97, 99. Всего 25 возможных комбинаций.

Сколько вариантов на 2 кубиках

В игре участвуют две игральные кости, и каждая игральная кость имеет 6 граней. Таким образом, возможно всего 36 различных комбинаций с суммами между 2 и 12. В подобных играх (онлайн разных жанров) как правило существует «ранд».

Что такое сочетание в математике

Комбинации, при составлении которых важно знать только то, какие элементы выбраны, но их порядок не имеет значения, называются сочетаниями. В сочетаниях все элементы равноправны. Например, два дежурных, два куска хлеба. Сочетания не являются упорядоченными наборами.

Сколько комбинаций в игре 4 из 20

Вероятность выигрыша = 1/4845. Одна правильная комбинация знаков из 4845 возможных.

Сколько комбинаций из 3 цифр без повторений

3 = 60 способов расстановки цифр, т. е. искомое количество трехзначных чисел есть 60.

Сколько всего комбинаций Трёхзначных чисел

Так как для построения комбинаций всего цифр имеется три (4, 6, 8), и мест для них тоже три (нужны трехзначные числа). При условии, что цифры в одной комбинации не должны повторяться, из трех цифр можно составить трехзначных комбинаций всего: 3!

Как посчитать количество комбинаций кодового замка

Есть два варианта расчета количества комбинаций кодового замка по количеству его цифр. Если имеется линейная зависимость — например, замок чемодана или пин-код карточки — то число сочетаний равно N=K*K*K, то есть 1000 комбинаций, все число в промежутке 1-999 и тысячное число 000.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4

Ответ: 48 трехзначных чисел.

Сколько трехзначных чисел можно составить из цифр 1 2 3 4 5

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? И сколько из них с неповторяющимися цифрами? = 5× 4×3 = 60. ПРИМЕР 4.

Сколько четырехзначных чисел можно составить из цифр 1 2 3 4 если цифры в числе не повторяются

Ответ. Всего из этих цифр можно составить 120 чисел, без повтора цифр внутри них.

Сколько чисел можно составить из цифр 1 2 3

Для того что бы создать трёхзначные числа из чисел 1, 2, 3 нужно каждое число соединить с другими числами. Составляем трехзначные числа: 131, 132, 133, 211, 212, 213, 221, 222, 223, 231, 232, 233, 311, 312, 313, 321, 322, 323, 331, 332, 333. Итого составили 27 трехзначных чисел.

Расчет комбинаций и перестановок в R

Комбинаторика является важным аспектом анализа данных и статистики. Он используется для решения многих проблем, основанных на способностях и реальных жизненных задачах. Хотя перестановки учитывают порядок, комбинации от него не зависят. Следовательно, перестановка считается упорядоченной комбинацией. Язык R позволяет нам вызывать множество пакетов для вычисления комбинаций и перестановок.

Метод 1: Комбинированный пакет

Пакет Combinat на языке программирования R может использоваться для вычисления перестановок и комбинаций чисел. Он предоставляет подпрограммы и методы для выполнения комбинаторики.

combn() Метод на языке R, принадлежащий этому пакету, используется для генерации всех комбинаций элементов x, взятых m за раз. Если x — положительное целое число, возвращает все комбинации элементов seq(x), взятые m за один раз.

Синтаксис:

combn(x, m, fun=NULL, simple=TRUE, …)

Параметры: 

• x – векторный источник для комбинаций
• m –
  6 fun

  количество элементов, которые необходимо взять

  – функция, применяемая к каждой комбинации (может быть нулевой)

• упрощение – логическая, если FALSE, возвращает список, иначе возвращает вектор или массив

Пример 1:

R

9

494

library (combinat)     print ( "Combination of letters two at a time" ) combn ( letters [ 1:4], 2)

Вывод

 [1] "Комбинация букв по две за раз"
> комбн(буквы[1:4], 2)
       [1] [2] [3] [4] [5] [6]
[1,] «а» «а» «а» «б» «б» «в»
[2,] "б" "в" "г" "в" "д" "д" 

Example 2:

R

library (combinat)     print ( "Combination where x=m" )     комбинация (8,8)

Выход

 [1] "Комбинация
> #выбираем 8 элементов из 8
> комбн(8,8)
[1] 1 2 3 4 5 6 7 8 

Приведенный ниже код иллюстрирует метод, где m=1, то есть количество выбранных элементов эквивалентно 1.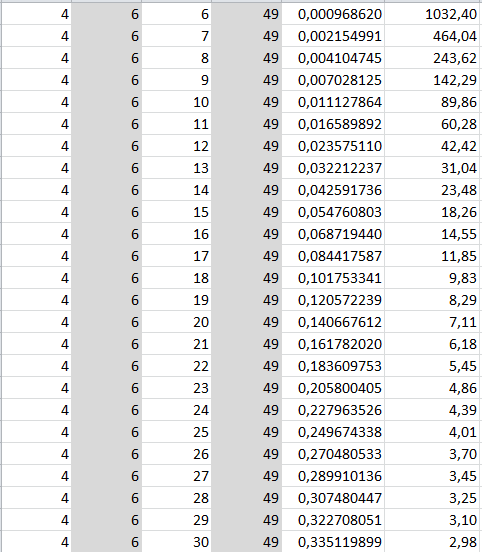 Количество способов выполнить эту операцию эквивалентно общему количеству элементов, поскольку каждый элемент можно выбрать один раз .

Пример 3:

R

Библиотека (Combinat) 9003 . 6966666666666666666. ).0056 COMBN (10,1)

Выход

[1] «Комбинация M = 1”

[1] [1] [1] [1] [1] [1] «Комбинация m = 1”

[1] [1] [1]. ,3] [4] [5] [6] [7] [8] [9] [10] 

[1,]    1    2    3    4    5    6    7    8      9    10

Метод combn() также обеспечивает подсчет количества комбинаций, которые будут сгенерированы в качестве выходных данных. Поскольку вывод получается в виде матрицы, окончательным результатом является количество столбцов в матрице, заданное ncol(res), где res — результат применения метода combn().

Пример 4:

R

Библиотека (Combinat) 966666666666666666666666666666666666 »6666666666666666666666666666666666666666» 66666666666666666666666666666666666666666666666666666666. RES <- COMBN ( Letters [1: 4], 2) Print ( : "Номер ( :" "Номер ( 9005:» Номер ( : "Номер . 0056 ) print ( ncol (res))

Output

 [1] "Number of combinations : "
> печать (ncol(res))
[1] 6 

метод permn() в R генерирует все перестановки элементов x. Если x — положительное целое число, возвращает все перестановки элементов seq(x). Перестановка числа 0 равна 1. 

Синтаксис:

permn(x, fun=NULL, …)

Параметры:

• x – источник вектора для комбинаций 1:

  R

  Библиотека (Combinat) Print ( . LIVERSUTATIONS .9005. .9005. .9005. .9005. . .9005. . 9005. 9005. из . из . из из . . . из из . . . . 9005. из из )0054 permn (3)

  Выход

   [1] "Перестановки 3"
  [[1]] [1] 1 2 3
  [[2]] [1] 1 3 2
  [[3]] [1] 3 1 2
  [[4]] [1] 3 2 1
  [[5]] [1] 2 3 1
  [[6]] [1] 2 1 3 

  Мы также можем вычислить перестановки вектора или списка.

  Пример 2:

  R

  библиотека (комбинированная)     x <- c ( 'red' , 'blue' , 'green' , 'violet' ) Печать ( "перестановки вектора x" ) Permn (x)

  Выход: 9003

     
   . 
  > пермн(х)
  [[1]] [1] "красный" "синий" "зеленый" "фиолетовый"
  [[2]] [1] "красный" "синий" "фиолетовый" "зеленый"
  [[3]] [1] "красный" "фиолетовый" "синий" "зеленый"
  [[4]] [1] "фиолетовый" "красный" "синий" "зеленый"
  [[5]] [1] "фиолетовый" "красный" "зеленый" "синий"
  [[6]] [1] "красный" "фиолетовый" "зеленый" "синий"
  [[7]] [1] "красный" "зеленый" "фиолетовый" "синий"
  [[8]] [1] "красный" "зеленый" "синий" "фиолетовый"
  [[9]] [1] "зеленый" "красный" "синий" "фиолетовый"
  [[10]] [1] "зеленый" "красный" "фиолетовый" "синий"
  [[11]] [1] "зеленый" "фиолетовый" "красный" "синий"
  [[12]] [1] "фиолетовый" "зеленый" "красный" "синий"
  [[13]] [1] "фиолетовый" "зеленый" "синий" "красный"
  [[14]] [1] "зеленый" "фиолетовый" "синий" "красный"
  [[15]] [1] "зеленый" "синий" "фиолетовый" "красный"
  [[16]] [1] "зеленый" "синий" "красный" "фиолетовый"
  [[17]] [1] "синий" "зеленый" "красный" "фиолетовый"
  [[18]] [1] "синий" "зеленый" "фиолетовый" "красный"
  [[19]] [1] "синий" "фиолетовый" "зеленый" "красный"
  [[20]] [1] "фиолетовый" "синий" "зеленый" "красный"
  [[21]] [1] "фиолетовый" "синий" "красный" "зеленый"
  [[22]] [1] "синий" "фиолетовый" "красный" "зеленый"
  [[23]] [1] "синий" "красный" "фиолетовый" "зеленый"
  [[24]] [1] "синий" "красный" "зеленый" "фиолетовый" 

  Как и в методе combn(), количество перестановок также можно определить с помощью метода length() по выходному вектору, сгенерированному метод perm().

  Пример 3:

  R

  Библиотека (сочетание) x <- '95959595959595959595959595959595959595959595959595959595959569569595695959709. ' , 'green' , 'violet' ) print ( "Permutations of vector x" )     res <- permn (x) print ( "Number of possible permutations : " ) print ( length (res)

  Выход

  [1] «Количество возможных перестановков:»

  > Печать (длина (Res))

  [1] 24

  Метод 2: GTOOLS. 0006

  Использование пакета gtools на языке программирования R также может быть использовано для легкого вычисления перестановок и комбинаций как без, так и с повторением. Комбинаторику можно легко выполнить с помощью пакета gtools в R. Метод

  permutations() в R можно использовать для простого вычисления перестановок с заменами и без них. Он возвращает фрейм данных или матрицу возможных перестановок, сформированную при перетасовке элементов заданного вектора с учетом ограничений. Количество таких возможных перестановок можно получить с помощью метода nrow(), который возвращает количество строк в полученном фрейме выходных данных.

  Синтаксис:

  перестановки(n , r, vec, Repeats.allowed=F)

  Параметры: объектов на выбор

• р – нет. объектов на выбор
• vec — атомарный вектор или матрица для перетасовки
• Repeats.allowed — По умолчанию: false. Если true, перестановки генерируются с разрешенным повторением

Возврат:

Кадр данных или матрица с правдоподобными перестановками. Количество строк во фрейме данных эквивалентно значению r.

Пример 1:

R

Библиотека (GTools) . res <- permutations (n=4,r=2,v=vec) print ( "Permutations without replacement" ) print (res)     print ( "Number of permutations without replacement" ) print ( nrow (res)) RES1 <- Пропутания (n = 4, r = 2, v = vec, repets. allowed = t) Print ( »с замены" ( "REMPATION0056 ) print (res1)     print ( "Number of permutations with replacement" ) print ( nrow (res1))

Вывод

 [1] «Перестановки без замены»
     [1] [2]
[1,] «Д» «Э»
[2,] «Д» «Ф»
[3,] «Д» «Г»
[4,] «Э» «Д»
[5,] «Э» «Ф»
[6,] «Э» «Г»
[7,] «Ф» «Д»
[8,] «Ф» «Э»
[9,] «Ф» «Г»
[10,] «Г» «Д»
[11,] «Г» «Э»
[12,] «Г» «Ф»
[1] «Количество перестановок без замены»
[1] 12
[1] «Перестановки с заменой»
     [1] [2]
[1,] «Д» «Д»
[2,] «Д» «Э»
[3,] «Д» «Ф»
[4,] «Д» «Г»
[5,] «Э» «Д»
[6,] «Э» «Э»
[7,] «Э» «Ф»
[8,] «Э» «Г»
[9,] «Ф» «Д»
[10,] «Ф» «Э»
[11,] «Ф» «Ф»
[12,] «Ф» «Г»
[13,] «Г» «Д»
[14,] «Г» «Э»
[15,] «Г» «Ф»
[16,] "Г" "Г"
[1] «Количество перестановок с заменой»
[1] 16 

Аналогичным образом метод комбинаций можно использовать для создания возможных комбинаций из заданного исходного вектора. Все аргументы аналогичны методу permutations().

Синтаксис:

комбинации(n , r, vec, Repeats.allowed=F)

Входной вектор указывать не обязательно.

Пример 2:

R

библиотека (gtools)     print ( "Combination of five objects taken two at a time" ) combinations (5, 2)

Output

 [1] «Комбинация пяти объектов, взятых по два одновременно»
     [1] [2]
[1,] 1 2
[2,] 1 3
[3,] 1 4
[4,] 1 5
[5,] 2 3
[6,] 2 4
[7,] 2 5
[8,] 3 4
[9,] 3 5
[10,] 4 5 

Пример 3:

R

Библиотека (GTOOLS) VEC <- 56955 : 955955: 9005: 95: 9515: .   print («Сочетание четырех предметов, взятых по два раза без повторения ») век) Печать (RES) Печать ( "Количество комбинаций без повторения» 5) 9545955955955955955955955955955955955955955955 9559559559559559559559559559559559559005. )     print ("Комбинация четырех объектов, взятых по два в \ раз с повторением") 1 res0056 Комбинации (n = 4, r = 2, v = vec, repets. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт