А в третьей степени плюс а в третьей степени: A во второй степени плюс А в третьей степени минус А =

Содержание

Что такое дальнозоркость (гиперметропия), степени дальнозоркости.

Особенность рефракции глаза, при которой изображение предметов не фокусируется на сетчатке.

Дальнозоркость (гиперметропия) — это такое устройство оптики глаза, когда фокус изображения от предмета попадает не на сетчатку, а за нее, т.е. за глаз Дальнозоркий глаз имеет короткий размер в 20-22 мм, при нормальной длине глаза в 23,5 мм.

При дальнозоркости глаз имеет меньший размер в длину, чем нормальный. Уменьшение длины глаза на 1 мм от нормы дает +3,0 диоптрии дальнозоркости!

Дальнозоркость — пожалуй, самая «неудобная» оптика для человеческого глаза, потому что он видит плохо и вблизи и вдали. Особенно сильно снижение зрения от гиперметропии проявляется в возрасте после 30 лет, когда ослабевает аккомодация (способность глаза настраиваться на фокус при переводе глаза с дали на близь за счет работы цилиарной мышцы и хрусталика. Всего гиперметропией страдает около 10% населения.

Еще со школы мы с вами помним, что хорошее зрение у человека возможно лишь в том случае, когда лучи света фокусируются в глазу точно на сетчатке. Любое нарушение зрения, будь то близорукость, дальнозоркость или астигматизм, вызвано тем, что свет не фокусируется в макуле, которая имеет максимальное число чувствительных клеток сетчатки.

Дальнозоркость – это «плюс» или «минус»?

При гиперметропии глаз имеет слабую оптику и ей не хватает плюсовых диоптрий, чтобы собрать лучи света в строго определенном месте на сетчатке. Становится понятным, что только дополнительная плюсовая линза может вытащить фокус из-за глаза обратно не сетчатку, чтобы вернуть глазу хорошее зрение.

Если говорить по-простому, то дальнозоркость – это «+» плюс, а не «-» минус

Дальнозоркость — это «+» плюс, потому что оптика глаза слабая и ей не хватает диоптрий, чтобы вытащить фокус из-за глаза. Плюсовые собирательные линзы усиливают оптику гиперметропического глаза.

Степени дальнозоркости (гиперметропии)

В зависимости от оптической силы глаза гиперметропию принято делить на 3 степени:

1 степень — Гиперметропия слабой степени до +2,0 диоптрий
2 степень — Гиперметропия средней степени от +2, 25 до +4,0 диоптрий
3 степень — Гиперметропия высокой степени свыше +4,25 диоптрий

Зрение при дальнозоркости слабой степени практически не изменяется. Дальнозоркость до +2,0 диоптрий может проявляться повышенной утомляемостью глаз при работе на близком расстоянии длительное время. В более раннем возрасте, чем в норме, появляется потребность в очках для чтения.

Чем выше степень дальнозоркости, тем хуже зрение вблизи.

При дальнозоркости средней степени ухудшается зрение вблизь и возникает сильный дискомфорт и напряжение при работе на близком расстоянии.

Зрение при дальнозоркости средней степени вдаль остается хорошим, а вблизи ухудшено. Характерна очень быстрая утомляемость глаз и сильный дискомфорт при работе вблизи.

При дальнозоркости высокой степени пациент имеет очень низкое зрение вблизи и значительное ухудшение зрения вдаль.

Отличие дальнозоркости и близорукости

Мы теперь знаем, что при дальнозоркости лучи света от окружающих предметов собираются за глазом. Это и есть главное отличие дальнозоркости от близорукости.

При миопии глаз в длину больше нормы, и свет фокусируется до сетчатки.

Ведь при миопии все наоборот, т.е. глаз имеет сильную оптику и большие размеры в длину, в результате чего свет фокусируется перед сетчаткой, не доходя до нее. Чтобы получить хорошее изображение, близорукому глазу нужно минусовое рассеивающее стекло, которое отодвинет фокус дальше на сетчатку.

Видео-урок: Законы экспонент над действительными числами

Стенограмма видео

В этом видео мы научимся применять законы показателей для умножения и деления степеней и для вычисления степени возведены в степень над действительными числами. Мы уже должны быть знакомы с что такое степени и основные законы показателей. Но мы кратко их повторим здесь.

Мощность есть выражение преобразуйте 𝑎 в степень 𝑚, где 𝑎 и 𝑚 — действительные числа. 𝑎 называется основанием, а 𝑚 называется показателем. Если мы сможем оценить это степени, поэтому, если мы можем записать 𝑎 в степени 𝑚 равно 𝑐, то 𝑐 — это результат. Например, два в кубе или два в третья степень равна восьми. Для положительных целых показателей степени таких как показатель степени трех, который мы здесь имеем, мы можем думать о степенях как о числе основания, которые мы умножаем вместе. Итак, два в кубе означает дважды два раз два; это три двойки, умноженные вместе.

Существует несколько законов показателей с которым мы уже должны быть знакомы. Каждое из них относится к реальным значениям основания 𝑎. А пока мы просто будем связаны с целыми значениями показателей. Во-первых, у нас есть правило произведения для показатели степени, которые говорят нам, как найти показатель степени, когда у нас есть произведение степеней той же базы. Добавляем мощности. 𝑎 в степени 𝑚, умноженной на 𝑎 в степени 𝑛 равно 𝑎 в степени 𝑚 плюс 𝑛. Так, например, семь в квадрате умножить на семь в кубе будет семь в степени два плюс три; без семи сила пяти. Мы можем продемонстрировать это правило на по крайней мере для положительных целых показателей, написав выражение от руки. 𝑎 в степени 𝑚, умноженной на 𝑎 в степени 𝑛 равно 𝑚 много 𝑎 умножить вместе на 𝑛 много 𝑎 перемножить. В общем, умножаем 𝑚 плюс 𝑛 много 𝑎 вместе. Итак, это показатель степени результат.

Нам нужно быть осторожными, когда работать с этим правилом, потому что есть две действительно распространенные ошибки.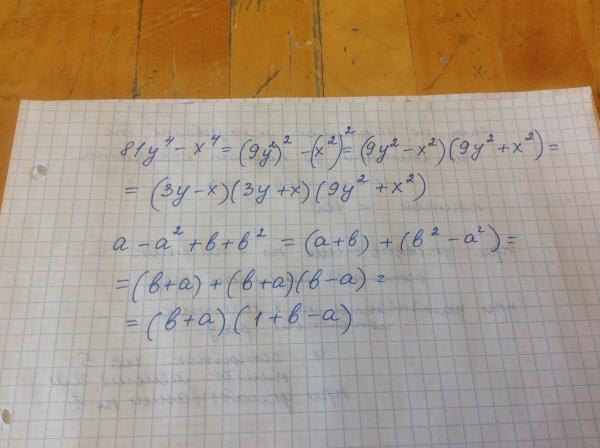 Во-первых, умножить, а чем добавить показатели. Второй — умножить основания или действительно делают обе ошибки и умножают как основания, так и показатели. Но если мы вспомним, почему это правило держится, то мы не должны делать этих ошибок. Теперь, несмотря на то, что мы продемонстрировали логика этого правила, использующая положительные целые показатели степени, на самом деле применяется когда показатели являются любыми действительными значениями.

Затем у нас есть частное правило для показатели степени, которые говорят нам, как найти показатель степени при делении двух степеней той же базы. На этот раз мы вычитаем силы. Мы можем снова продемонстрировать это правило для положительных целых значений 𝑚 и 𝑛, написав частное от руки, а затем сокращая общие множители в числителе и знаменателе. Здесь мы предполагаем, что 𝑚 больше или равно 𝑛, но результат также верен, если 𝑛 больше 𝑚. Далее у нас есть правило мощности для степени, что говорит нам о том, что если мы возводим основание в степень, а затем в другая сила, в общем, мы поднимаем эту базу до произведения этих сил.

Это три основных правила, но есть также некоторые дополнительные, которые нам нужно вспомнить. Если мы обнаружим силу произведения, это то же самое, что возводить каждый множитель в степень, а затем находить товар. И если мы обнаружим силу частное, это то же самое, что поднять и числитель, и знаменатель этого отношение к мощности отдельно. Нам уже должно быть удобно применение каждого из этих правил, когда основание представляет собой целое или дробное значение. В центре внимания этого видео будет расширить наши знания, чтобы применить эти правила ко всему набору действительных чисел. Итак, теперь мы включаем иррациональное числа в качестве основы.

С чем мы будем работать любое действительное число здесь, нам нужно ввести некоторые дополнительные правила для упрощения выражения с квадратными корнями. Они следующие. Для выражения с вещественной основой 𝑎, который должен быть неотрицательным, квадратный корень из 𝑎 в квадрате равен 𝑎, а квадратный корень или 𝑎 в квадрате также равен 𝑎. Важно, чтобы 𝑎 был здесь неотрицательно, так что его квадратный корень корректно определен в первом правиле и, следовательно, что у нас есть уникальный ответ при возведении в квадрат, а затем извлечении квадратного корня в второй. Теперь рассмотрим наш первый пример, в котором мы увидим, как использовать правило произведения для показателей степени, чтобы упростить выражение с вещественной основой.

Заполните пропуск. Корень выражения три умножить на корень из трех в квадрате умножить на корень из трех в кубе упрощает до пустой.

Нам нужно упростить это выражение который состоит из трех степеней одного основания, корня три, умноженного вместе. Таким образом, мы можем применить продукт правило для показателей, которое гласит, что для действительных значений 𝑎, 𝑚 и 𝑛, 𝑎 к степень 𝑚, умноженная на 𝑎 в степени 𝑛, равна 𝑎 в степени 𝑚 плюс 𝑛. Теперь нет экспоненты, написанной для первый член в произведении, но мы знаем, что любое число равно этому числу в первую степень. Таким образом, корень три является корнем три для сила одного. Таким образом, применяя правило произведения и суммируя все три показателя, получаем, что это выражение упрощается до корня три в степени один плюс два плюс три, что составляет корень три в шестой степени. Теперь мы знаем, что у нас есть шесть лотов. корня три, умноженные вместе, которые мы можем написать от руки.

Далее мы видим, что можем сгруппировать термины в этом произведении на пары. И, следовательно, мы можем выразить Произведение как корень три в квадрате умножить на корень три в квадрате умножить на корень три в квадрате. Затем мы можем вспомнить результат, который для неотрицательных значений 𝑎 квадратный корень из 𝑎 в квадрате равен 𝑎. Итак, квадратный корень из трех квадрат равен трем. Таким образом, выражение равно до трех умножить на три умножить на три или три в кубе, что равно 27. Итак, заполнив пропуск, данный выражение упрощается до 27.

Теперь рассмотрим другой пример. в которой мы увидим, как упростить частное двух степеней, в которых основания негативы друг друга.

Каково значение отрицательного корня три в шестой степени разделить на корень три в третьей степени?

Основы в этом выражении почти то же самое, но одно является отрицательным для другого. Мы еще не можем применять законы степени, чтобы упростить это деление, поскольку основания не совсем одинаковы. Так что давайте вместо этого подумаем о том, как мы можно изменить это выражение так, чтобы основания были идентичными.

В первом слагаемом имеем мощность произведения, потому что отрицательный корень из трех равен отрицательному, умноженному на единицу. по корню три. Таким образом, мы можем вспомнить силу правила произведения для показателей, которое гласит, что произведение 𝑎𝑏 в 𝑛-й степени равно 𝑎 в 𝑛-й степени, умноженному на 𝑏 в 𝑛-й степени. Таким образом, мы можем переписать первый член как минус один в шестой степени, умноженный на корень три в шестой степени. Затем мы можем вспомнить, что отрицательное единица в любой четной степени положительна. Так что фактически первый срок упрощает корень три в шестой степени.

Теперь у нас точно такая же база для обеих частей частного. Таким образом, мы можем упростить использование правило частных для показателей, которое говорит нам, что для разделения степеней одного и того же основания, мы вычитаем показатели. Итак, корень три в шестой степени разделить на корень три в третьей степени это корень три в степени шесть минус три, то есть корень три в кубе. Мы можем выразить это сокращенно как корень три умножить на корень три умножить на корень три. И тогда мы можем сгруппировать первые два члены в произведении вместе дают корень три в квадрате, умноженный на корень три.

Вспомним, что для неотрицательных действительные значения 𝑎, квадратный корень из 𝑎 в квадрате равен 𝑎. Итак, квадратный корень из трех квадрат равен трем. И выражение упрощается до три корень три. Мы обнаружили, что значение отрицательного корень три в шестой степени разделить на корень три в третьей степени это корень три три.

Каждый из примеров, которые мы рассмотренные до сих пор включали только положительные показатели. Правила, однако, остаются в силе показатели положительные или отрицательные. Нам нужно вспомнить еще некоторые ключевые свойства, позволяющие нам работать с нулевыми и отрицательными показателями, оба из которых применимы когда основание отлично от нуля. Во-первых, любое ненулевое действительное основание для степень нуля равна единице. Во-вторых, напомним, что отрицательное экспонента определяет обратную величину. 𝑎 в отрицательной степени 𝑛 равно равно единице над 𝑎 в степени 𝑛.

В нашем следующем примере мы собираемся применить закон для отрицательных показателей к задаче, в которой основания дробный. Прежде чем мы это сделаем, мы можем использовать второе правило, чтобы записать дальнейшее свойство. Это называется силой Правило отношения для отрицательных показателей. И в нем говорится, что для ненулевого значений 𝑎 и 𝑏, 𝑎 над 𝑏 до отрицательного 𝑛 равно 𝑏 над 𝑎 до сила 𝑛. Мы можем кратко показать, почему это правило держится. Применение закона об отрицательном степени выражения 𝑎 над 𝑏 до отрицательного 𝑛 дает единицу над 𝑎 над 𝑏 к 𝑛.

Применение степени частного правило в знаменателе, это эквивалентно единице над 𝑎 в 𝑛-й степени над 𝑏 в 𝑛й степени. Но мы знаем, что деление на частное эквивалентно умножению на обратное. Так что это эквивалентно одному умножается на 𝑏 в 𝑛-й степени над 𝑎 в 𝑛-й степени. А затем применяя силу правило отношения в обратном порядке, это равно 𝑏 над 𝑎 в 𝑛-й степени. Давайте теперь посмотрим, как мы можем применить это правило в примере.

Для 𝑎 равно 15 больше четырех и 𝑏 равно пяти больше двух, оцените 𝑎 в квадрате 𝑏 до минус трех.

Начнем с замены числовые значения 𝑎 и 𝑏 в данное выражение. И у нас есть 15 на четыре в квадрате умножить на пять на два с минусом на три. Чтобы упростить второй член в этом произведения, мы можем вспомнить силу правила отношения для отрицательных показателей. Это утверждает, что для 𝑎 и 𝑏 не равен нулю, 𝑎 над 𝑏 в минус 𝑛 равен 𝑏 над 𝑎 в степени 𝑛. Таким образом, оставляя первый член в произведение не изменилось, второй член равен двум пятым в степени три.

Затем мы вспоминаем силу правило частных, которое гласит, что 𝑎 над 𝑏 в 𝑛-й степени равно 𝑎 в 𝑛-й степени над 𝑏 в 𝑛-й степени. Таким образом, применяя это правило к каждому термину, у нас есть 15 в квадрате на четыре в квадрате, умноженное на два в кубе на пять в кубе.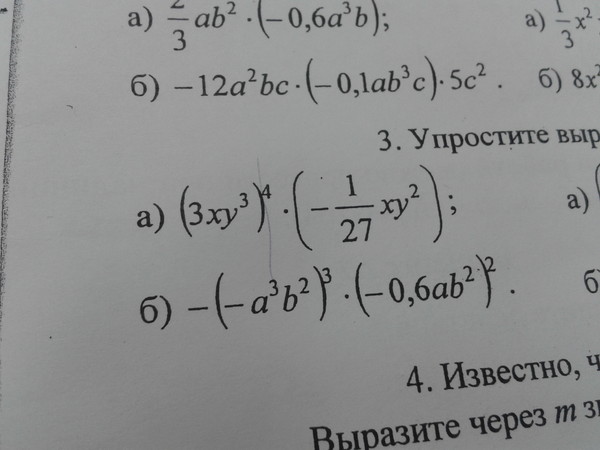 Тогда мы можем написать выражение от руки и сократим общие множители в числителе и знаменателе частное. Когда мы это сделаем, у нас останется три умножить на три в числителе на два умножить на пять в знаменателе, что равно девяти больше 10. Итак, мы обнаружили, что когда 𝑎 равно до 15 на четыре и 𝑏 равно пяти на два, 𝑎 в квадрате 𝑏 до минус три равно девяти десятым.

Последнее, что мы собираемся сделать Рассмотрим, как мы можем решать уравнения, в которых либо основания, либо показатели подобные. Предположим, что у нас есть уравнение два в степени 𝑥 равно двум в степени четыре. В качестве оснований с каждой стороны уравнения одинаковы, единственный способ, которым эти два выражения могут быть равны, состоит в том, что показатели также равны. Итак, приравнивая показатели, имеем решение 𝑥 равно четырем. Аналогично, предположим, что у нас есть уравнение 𝑦 в четвертой степени равно трем в четвертой степени.

Так как на этот раз представители два выражения одинаковы, мы можем подумать, что основания тоже должны быть одинаковыми. Но по факту немного больше сложнее, чем это, потому что это зависит от того, является ли мощность четной или нечетной. Три в четвертой степени равно до 81, но так же отрицательно три в четвертой степени. Так что 𝑦 может быть равно трем, но он также может быть равен отрицательному трем. Мы бы выразили это, сказав абсолютное значение 𝑦 равно трем. Однако, если показатель степени нечетный целое число, поэтому предположим, что у нас есть уравнение 𝑧 в кубе равно трем в кубе, тогда мы не есть эта же проблема. Три в кубе равно 27, но минус три в кубе равен минусу 27. В этом случае мы можем сказать, что если показатели одинаковы, то и основания должны быть одинаковыми.

Мы можем формализовать каждый из этих процессы решения уравнений с использованием следующих правил. Во-первых, если 𝑎 в 𝑚-й степени равно 𝑎 в 𝑛-й степени, где 𝑎 — действительное число, но не отрицательное, ноль, или один, то 𝑚 должно быть равно 𝑛. А во-вторых, если 𝑎 к 𝑛-му мощность равна 𝑏 в 𝑛-й степени, то 𝑎 равно 𝑏, когда 𝑛 — нечетное число. целое число, а абсолютное значение 𝑎 равно абсолютному значению 𝑏, когда 𝑛 четное целое число. В нашем последнем примере мы будем продемонстрировать, как мы можем использовать эти законы для решения уравнения, в котором неизвестное в экспоненте.

Найдите значение 𝑥 в уравнение 16, умноженное на два в степени девять минус 𝑥 равно двум степень 𝑥 минус один в квадрате.

Чтобы найти значение 𝑥, мы можем использовать законы показателей. Но для того, чтобы это сделать, нам нужно сначала выразить каждый член в уравнении в степени одного и того же основания. У нас есть два в степени девяти минус 𝑥 и два в степени 𝑥 минус один все в квадрате. Итак, давайте подумаем, как мы можем перепиши член 16. Ну 16 это два в четвертом сила. Таким образом, заменив 16 на два на четвертой степени, мы имеем все уравнение в терминах того же основания.

Теперь мы можем начать применять некоторые законы показателей. С левой стороны у нас есть произведение степеней одного и того же основания. Таким образом, мы можем применить правило произведения для показателей степени, в котором говорится, что для умножения степеней одного и того же основания мы добавляем экспоненты. Следовательно, левая сторона эквивалентно двум в степени четыре плюс девять минус 𝑥. С правой стороны у нас есть мощность возведена в другую степень. Таким образом, мы можем упростить это, используя степенное правило показателей, которое гласит, что в этом случае мы умножаем степени вместе. Таким образом, правая часть становится двумя в степени двойки, умноженной на 𝑥 минус один. Упрощение экспоненты на каждом стороны, у нас есть два в степени 13 минус 𝑥 равно два в степени два 𝑥 минус два.

Теперь, когда базы с каждой стороны уравнения одинаковы, должно также быть верно, что показатели степени одинаковы. Таким образом, приравнивание показателей дает уравнение 13 минус 𝑥 равно два 𝑥 минус два. Теперь решим это уравнение относительно 𝑥. Добавление двух и 𝑥 с каждой стороны дает 15 равно трем 𝑥. А затем, разделив обе стороны уравнение на три, находим, что 𝑥 равно пяти. Таким образом, значение 𝑥 в данном уравнение равно пяти.

Давайте теперь суммируем ключевые моменты из этого видео. Мы можем использовать законы экспонент, чтобы упростите полномочия с реальными основаниями. Для реальных значений 𝑎 и 𝑏 и целые значения 𝑚 и 𝑛, правило произведения для показателей степени, правило отношения для показатели, правило степени для показателей, мощность правила произведения и мощность частного правила все применяются. Мы также представили мощность Правило отношения для отрицательных показателей. Для ненулевых значений 𝑎 и 𝑏, 𝑎 над 𝑏 до отрицательного 𝑛 равно 𝑏 над 𝑎 в степени 𝑛. Мы также увидели некоторые ключевые правила для Работа с квадратами и квадратными корнями. Для неотрицательных действительных значений 𝑎, квадратный корень из 𝑎 в квадрате равен 𝑎, а квадратный корень из 𝑎 в квадрате равен также равно 𝑎.

Для решения простой экспоненциальной уравнения с вещественными основаниями, мы можем использовать следующие правила, когда либо основания, либо показатели равны. Если 𝑎 к 𝑚 равно 𝑎 к 𝑛, где 𝑎 — действительное число, а не отрицательная единица, ноль или единица, то 𝑚 должно быть равно 𝑛. А если показатели одинаковые, поэтому, если 𝑎 к 𝑛 равно 𝑏 к 𝑛, то 𝑎 равно 𝑏, когда 𝑛 является нечетным целое число, а абсолютное значение 𝑎 равно абсолютному значению 𝑏, когда 𝑛 четное целое число.

какое значение эквивалентно 5 в третьей степени, умноженному на 5 в четвертой степени?

Предварительная алгебра

Бриджит Б.

спросил 17.01.13

, не могли бы вы указать, как получить ответ.

Подписаться І 4

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСамыеСтарые

Натан Дж. ответил 17.01.13

Репетитор

4.9 (11)

Гибкое и адаптивное обучение — подготовка к следующему шагу

См. таких репетиторов

Смотрите таких репетиторов

Я предполагаю, что вы формулируете вопрос следующим образом:

5 ³ • 5 ⁴

Всякий раз, когда вы умножаете идентичные фразы или компоненты (например, числа/константы или переменные) на степени, просто сложите степени, чтобы найти «конечную степень».

В этом случае 5 и 5 являются идентичными константами/числами, поэтому вы можете сложить их степени, что даст вам:
5 ⁷ , что равно 5 • 5 • 5 • 5 • 5 • 5 • 5, что равно 78 125.

Если вы хотите проверить свою работу, разбейте полномочия на:
5 ³ = 125 и 5 ⁴ = 625, а затем подставьте:
125 • 625 = 78 125

Отлично работает! Надеюсь это поможет!

Голосовать за 1 Понизить