Презентация к уроку алгебры в 7 класе по теме «Действия со степенями» | Презентация к уроку (алгебра, 7 класс) по теме:
Презентация разработана к проблемному уроку с элементами исследования.
Скачать:
Подписи к слайдам:
Проблемный урок алгебры в 7 классе По теме «Действия со степенями»
Подготовил: учитель математики МБОУ «Красноярская СОШ»Учитель 1 категории Кумарица Надежда Николаевна.
«Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит». известный учёный Ал – Бируни.
Математический диктант:1.Единицы измерения длины.2. Единицы измерения массы.3.Единицы измерения площади.4.Сколько в 1 километре метров, сантиметров?5.Как найти, во сколько раз одна величина больше или меньше другой? 6. Какова масса земного шара?7. Величину поверхности земного шара.8. Сколько кг весит атмосфера Земли?
Ответы к диктанту1..Миллиметры, сантиметры, дециметры, метры, километры.2. Граммы, килограммы, центнеры, тонны.
3.ммІ,смІ, мІ, кмІ, а, га.4. 1кмІ =1000І мІ=1000000мІ=10№єсмІ5. Большую величину разделить на меньшую. 6. Масса земного шара равна 6 · 1021 т.7. Величина поверхности земного шара равна 51 ·10 17 смІ,8.Вес атмосферы земли — 51 ·10 17 кг
Определим, во сколько раз масса земного шара больше массы всего окружающего воздуха .Сколько квадратных сантиметров содержится в одном квадратном километре?Сколько заключается квадратных сантиметров во всей поверхности земли? Столько же килограммов весит атмосфера Земли.Переведите в килограммы. Определите, во сколько раз планета Земля тяжелее своей воздушной оболочки.
Как умножить степени с одинаковыми основаниями, равными 10?Как делятся степени с одинаковыми основаниями, равными 10?Как возвести степень с основанием 10 в степень?Изменятся ли правила, если придётся выполнять действия с другими основаниями?
Как выполнить умножение, деление и возведение степени в степень? С какими степенями возможны эти действия?Свойства степеней с одинаковыми основаниями.
am
Свойства степеней с одинаковыми основаниями am · аn =am+n am : аn = am-n (am)n=amn (ab)m=ambm
Уровень 21.36=3*3*3*3*3*3=729, а нельзя ли вычислить значение 36, выполнив меньшее число операций. Найдите значения степеней , выполнив как можно меньшее число процедур умножения:(3,1)4= ; (2,2)6= ; 28= .2.Некто продаёт свою лошадь по числу подковных гвоздей, которых у него 16. За первый гвоздь он просит 1 копейку, за вторую – 2, за третий – 4, за четвёртый -8, и всегда за каждый следующий вдвое больше, чем за предыдущий.Запишите цену лошади (выраженную в копейках) в виде суммы степеней числа 2. Можно ли представить эту цену в виде степени с основанием а?Уровень 1№403, 404, 408, № 414, 416, № 430.
Домашнее задание: Можно ли утверждать, чтоА) если а – отрицательное число, то а5а2 отрицательное число?Б)если х – отрицательное число, то хх3 -отрицательное число?В) Может ли сумма квадратов двух чисел быть меньше (равной) разности квадратов этих чисел?Г) Подберите значения х, при которых х4*х6= (х4)6.
Свойства степеней с натуральным показателем
Урок изучения нового материала.
Класс: 7 класс.
Цели:
Образовательная цель: изучение свойств степени с натуральным показателем; совершенствование вычислительных навыков.
Воспитательная цель: воспитание интереса к математике и ее приложениям, активности, общей культуры.
Развивающая цель: развитие математического и общего кругозора, мышления и речи, внимания и памяти; формирование умений применять приемы наблюдения, сравнения, анализа.
Оборудование: компьютер, экран, проектор, тесты на 2 варианта.
Ход урока
1.
Тема урока на доске.Постановка целей урока совместно с учащимися: составление плана урока с помощью примерных карточек.
- Ввести определение степени.
- Закреплять умения применять свойства степеней
на практике.
- Установить закономерность в действиях со степенями.
- Сформулировать закономерность в действиях со степенями.
- Доказать верность закономерностей в действиях со степенями.
- Применить на практике свойства степеней.
- Учится выполнять операцию возведения в степень.
План урока:
- Установить закономерность в действиях со степенями.
- Сформулировать закономерность в действиях со степенями.
- Доказать верность закономерностей в действиях со степенями.
- Применить на практике свойства степеней.
Вопросы по оставшимся карточкам:
– Почему нам не надо вводить определение степени? Сформулируйте его.
– Можем ли мы закреплять умения применять свойства степеней?
– Почему нам не надо учиться выполнять операцию возведения в степень?
2.
Проверка д/з. Получившиеся имена математиков: Симон Стевин, Рене Декарт. Историческая справка.
3.
Работа по теме урока.Установка закономерностей.
Задание по рядам. Вычислить:
| 1 ряд | А) | А) |
| Б) | Б) | |
| 2 ряд | А) | А) |
| Б) | Б) | |
| 3 ряд | А) | А) |
| Б) | Б) |
Трое учащихся выходят к доске.
Обсудить подмеченную закономерность.
Формулировка свойств степеней учащимися.
Проговаривание правил полушопотом.
Перейти от словесных формулировок к символической записи свойств.
Следуя инструкции проведите доказательство свойства умножения степеней.
Инструкция:
- Расписать аn по определению степени.
- Расписать ак по определению степени.
- Умножить аn и ак, т.е. аn • ак.
- Преобразовать полученное выражение к виду аn+к.
Проверим по учебнику.
Работа с учебником (стр. 80-82). Обратите внимание на доказательство: 1), 2), 3), 4).
Посмотреть, как представлены эти свойства в учебнике. В виде чего записаны свойства? / в виде теорем/. Из чего состоит всякая теорема? /условие, заключение, доказательство/.
Доказательство теорем /дифференцированное
домашнее задание/.
4.
Первичное закрепление материала.Мозаика: учащиеся должны составить из предложенного материала задание и предложить ее решить одноклассникам.
5.
Работа с тестами с последующей самопроверкой и выставлениями оценок за урок.Фамилия Вар 1 |
Фамилия Вариант 2 |
| 1. Выполнить преобразование: а) х8 б) х15 в) х2 |
1. Выполнить преобразование: а) х28 б) х11 в) х3 |
| 2. Выполнить преобразование: а) х12 б) х32 в) х4 |
2. Выполнить преобразование: а) х3 б) х54 в) х15 |
3. Выполнить преобразование:а) х10 б) х3 в) х7 |
3. Выполнить преобразование: а) х1 б) х12 в) х7 |
| 4. Упростить: а) а1 б) а15 в) а19 |
4. Упростить: а) а18 б) а2 в) а6 |
| 5. При каком х выполняется
равенство: а) 4 б) 2 в) 6 |
5. При каком х выполняется
равенство: а) 6 б) 5 в) 1 |
| Оценка за тест: Оценка за работу на уроке: |
Оценка за тест: Оценка за работу на уроке: |
6.
Работа с учебником: № 17.1, 17.15, 17.28.Доп. Задание: 1)Магический квадрат.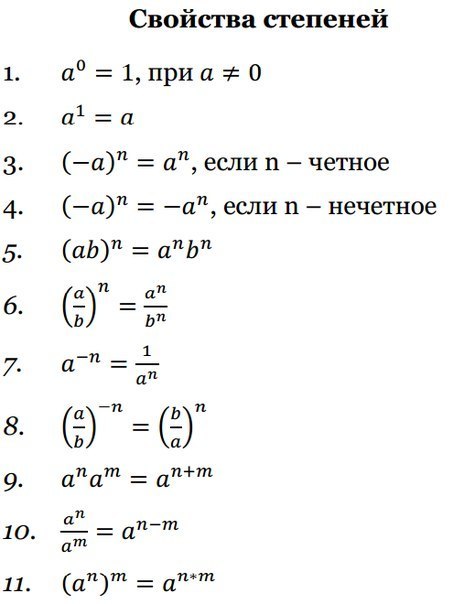
Задание на
скорость.
2) Узнайте, какое число изображает круг, если заштрихованная часть изображает указанное число. Ответ запишите в виде степени.
7
. Подведение итогов урока.Постановка домашнего задания.
На “3”: №17.3, 17.18, 17.31.
На “4”: №17.3, 17.18, 17.31, 17. 35.
На “5”: №17.3, 17.18, 17.31, 17. 35, доказательство свойств степеней.
Список использованной литературы:
- А.Г.Мордкович и др. Алгебра 7 класс, Задачник, М.: Мнемозина, 2007;
- А.Г.Мордкович и др. Алгебра 7 класс, Учебник, М.: Мнемозина, 2007;
- Лебединцева Е.А., Беленкова Е.Ю. Алгебра 7 класс. Задание для обучения и развития учащихся. – М.:Интеллект-центр, 2005.
- Мордкович А.Г., Тульчинская Е.Е. Алгебра: Тесты для 7-9 класса общеобразовательных учреждений. – М.:Мнемозина, 2002.
Презентация
абстрактная алгебра — Индуцированное $\frak{g}$-действие на внешнюю мощность и симметричную мощность?
Я бы сформулировал это так: данные $\mathfrak{g}$-представления на $V$ — это в точности данные гомоморфизма алгебр Ли $\rho : \mathfrak{g} \to \operatorname {Конец}(V)$.
r V\right)$. 9р В$. Наконец, нам нужно проверить, что отображение, переводящее каждый $x \in \mathfrak{g}$ в каждое такое сопоставленное отображение, является гомоморфизмом алгебры Ли, но я утверждаю, что это следует непосредственно из того же факта для тензорная алгебра (например, пример 1) .
Заменив $r$-ю внешнюю степень на $r$-ю симметричную степень и «чередуя» на «симметричную», вы должны получить конструкцию структуры $\mathfrak{g}$-представления на симметричных степенях также $V$. 9r V / I$ $\mathfrak{g}$-представлений. Совершенно аналогичны симметричные степени — дело в том, что интересующие вас конструкции являются лишь частными случаями понятия частного $\mathfrak{g}$-представлений.
Соглашения по алгебре: совместные действия для достижения справедливости и достижений в математике средних классов
Автор: Дэн Уитакер
В прошлом году школьные команды, участвующие в Сети средних классов, Сети совместных действий (CAN), поддерживаемой SEI, выявили различия в успеваемость по математике в средних классах и доступ к продвинутым курсам по математике в 8-м классе в качестве приоритетной задачи.
Чтобы решить эту проблему, SEI созвал в прошлом году первую встречу по соглашению по алгебре, чтобы подготовить данные для заинтересованных сторон по всему округу и начать работу, необходимую для преобразования преподавания математики и обучения для всех учащихся. На этой встрече был достигнут широкий консенсус в отношении того, что: доступ к продвинутым курсам по математике является вопросом справедливости, который оказывает значительное влияние на успех в будущем; необходимо выявить и устранить коренные причины различий в математических результатах в средних классах и связанные с ними будущие пути.
В настоящее время Algebra Accords работает как группа совместных действий (CAT), целью которой является повышение готовности к математике и успеваемости к концу 8-го класса. Были сформированы три подкомитета, чтобы начать обсуждения, чтобы перейти от разговоров к трансформации в следующих областях:
- Образ мышления : убеждения, связанные с математикой, включая природу математики, природу математических способностей и ценность или важность выхода за рамки минимальных математических стандартов. Комитет по установкам стремится понять, как заинтересованные стороны, включая учащихся, семьи и учителей, думают об этой проблеме, и лучше формировать образ мышления.
- Учебный план : как, что, когда и с кем изучать математику от Pre-K до алгебры 1. Учебный комитет стремится понять условия и ожидания, которые существуют до алгебры 1, чтобы лучше подготовить учащихся к успеху в алгебре 1; и
- Навыки и способности: компетенции и способности учащихся, семей и преподавателей в области преподавания и обучения математике.
