Математика. Координатная плоскость. 7 класс
Пройдите тест, узнайте свой уровень и посмотрите правильные ответы!
Категория:
Математика
Уровень:
7 класс
Автор теста: Boris Evdokimov
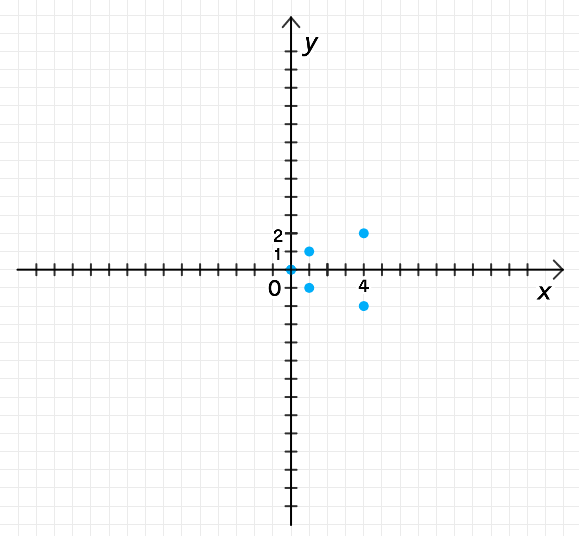
Через точку С(-2;-3) проведена прямая, параллельная оси абсцисс. Какая из точек лежит на этой прямой?
В(-6;3)
А(6;-3)
К(-2;5)
М(5;-2)
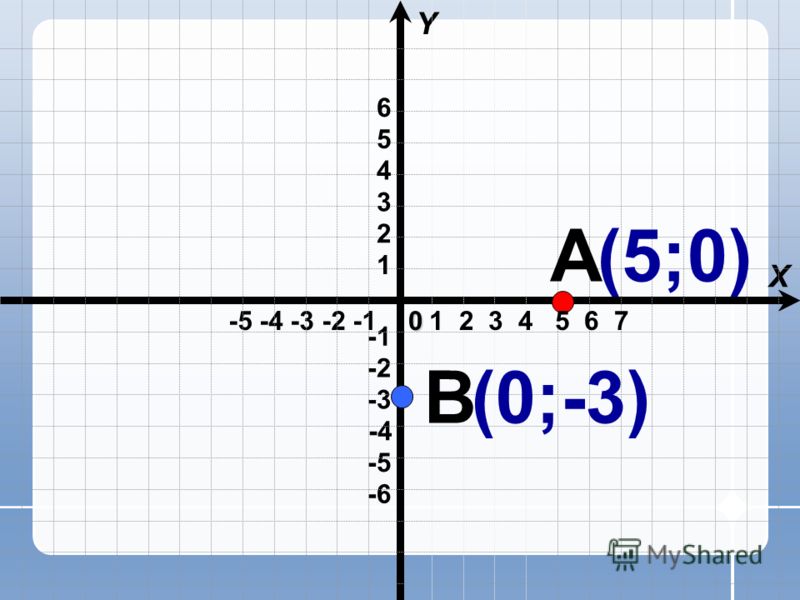
На координатной плоскости даны точки А(5;0), В(0;0), С(-6;5).
 Определите тип угла АВС.
Определите тип угла АВС. развернутый
острый
прямой
Через точку А(3;-5) проведена прямая, параллельная оси абсцисс. Укажите координаты точки пересечения этой прямой с осью ординат.
(-5;0)
(0;-5)
В какой координатной четверти находится точка Е(-4;103)?
в IV четверти
в III четверти
во II четверти
в I четверти
Где на координатной плоскости расположены точки, абсцисса которых равна 7?
в I и IV четвертях
в III и в IV четвертях
во II и в III четвертях
в I и во II четвертях
Какой координатной четверти принадлежит точка М(-18;-311)?
Укажите точку, которая лежит на оси ординат.
Е(7;-1)
С(-1;7)
В(-7;0)
А(0;-7)
Укажите точку, которая лежит на оси абсцисс.
Е(7;-1)
С(-1;7)
В(-7;0)
А(0;-7)
Мы занимаемся обработкой ваших ответов
Проверь себя, пройди другие тесты онлайн
- Животные.
 Многоклеточные. Тест 2. 7 класс Пищеварение в теле губок осуществляется… Тело многоклеточных животных снаружи покрывает… Выберите три верных утвержд…
Многоклеточные. Тест 2. 7 класс Пищеварение в теле губок осуществляется… Тело многоклеточных животных снаружи покрывает… Выберите три верных утвержд… - Test 10. Talking about countries and nationalities Match the words to the right translation. (Установите соответствие между словом и его переводом.) 1) hospitable 2) t…
- История. 7 класс. Итоговый тест по курсу «История. Государство и народы России.» Что способствовало укреплению центральной власти в России в XVI в.? О первых днях чьего царствования идет речь в отрывке…
- ЕГЭ 2017. Математика. Вариант 46 Какое число из промежутка (0,4; 1,8) не входит в область определения функции y = ctg(πx)? Укажите наибольшее целое значе…
- Test 1. The World Teenagers’ Competition Tick the odd one out. (Отметьте лишнее слово.) Choose the necessary verb.
 (Выберите нужный глагол.)
I will … my chanc…
(Выберите нужный глагол.)
I will … my chanc… - Народы и страны Евразии. 7 класс. Какая страна Евразии самая многонациональная? Какая страна зарубежной Европы самая большая по численности населения?
- Животные. Насекомые. Тест 2. 7 класс Органы выделения насекомых соединены с… Выберите последовательность стадий цикла развития кузнечика, начиная с яйца. В…
- Степень и ее свойства. 7 класс. Представьте в виде произведения степень (-3)4у2: Вычислите -2 × 32 + 4 × 53: Вычислите (-2)3 — (-1)6 + 42 — …
- ЕГЭ 2017. Математика. Вариант 73 К 40%-ному раствору соляной кислоты добавили 50 г чистой кислоты, после чего концентрация раствора стала равной 60%. Най…
- Математика. Тест 11. Для поступающих. При каком q один корень уравнения х²−9х+q=0 вдвое больше другого? Через точки (0; −2), (3; 0) проходит .
 ..
.. - Test 6. Speaking about famous people Find the wrong sentence. (Найдите неправильное предложение.) Mark the word with the sound [w]. (Отметьте слово со звуком…
- ЕГЭ 2017. Математика. Вариант 38 Найдите значение выражения 3 · 102 + 5 · 10–1 + 9 · 10–2. Площадь поверхности прямоугольного параллелепипеда с рёбрами а…
что это такое? Как отмечать точки и строить фигуры на координатной плоскости?
Видео: Алгебра 7 класс. 22 сентября. Координаты точек на координатной плоскости
Съдържание
- Видео: Алгебра 7 класс. 22 сентября. Координаты точек на координатной плоскости
- Определение понятия
- Историческая справка
- Примеры координатной плоскости
- Оси координат
- Четверти
- Работа с координатной плоскостью
- Правила построения плоскости
- Отмечаем точку
- Видео: Координатная плоскость — mirurokov.ru — Видеоурок по математике
- Видео: Постройте на координатной плоскости ах график уравнения
- Размещаем фигуру
- Видео: ЕГЭ по математике 2014.
 Задача С2. Построение сечений
Задача С2. Построение сечений - Выводы
- Видео: Построение графика линейной функции
Математика – наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.
Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат – строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь великого математика «декартовой».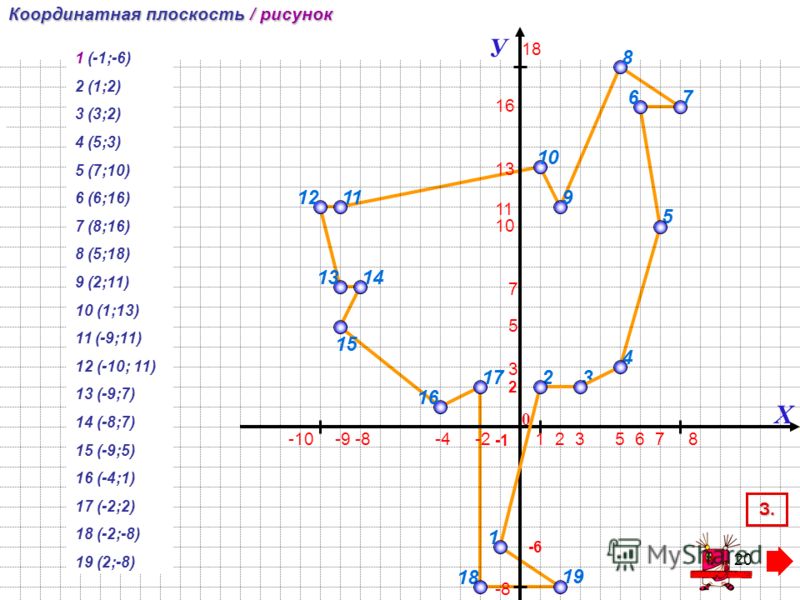
После опубликования труда «Геометрия» система координат Рене Декарта завоевала признание в научных кругах.
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты – одну координату буквенную, вторую – цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой». Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0. Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти
Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Далее мы поговорим подробнее о построении системы и непосредственно нанесении точек и фигур.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее. Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Далее на каждой оси указывают направление и подписывают их с помощью общепринятых обозначений x и y. Также отмечается точка пересечения осей и подписывается цифрой 0.
Также отмечается точка пересечения осей и подписывается цифрой 0.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.
Отмечаем точку
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.
Видео: Координатная плоскость — MirUrokov.ru — Видеоурок по математике
При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
Видео: Постройте на координатной плоскости ах график уравнения
com/embed/FEsFYoBPxu4″ frameborder=»0″ allowfullscreen=»»/>Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy. Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
Видео: ЕГЭ по математике 2014. Задача С2. Построение сечений
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.
Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.
Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость – это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.
Видео: Построение графика линейной функции
Основной навык, который следует выработать при работе с координатной плоскостью, – умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
Споделяне в социалните мрежи:
сроден
- Как нарисовать человека в полный рост? Как поэтапно нарисовать человека?
- Срисовать картинки: поэтапная инструкция для начинающих.
 Как срисовать рисунок карандашом?
Как срисовать рисунок карандашом? - Параллельность плоскостей: условие и свойства
- Что такое окружность как геометрическая фигура: основные свойства и характеристики
- Что такое натуральное число? История, область применения, свойства
- Изучаем колебания – фаза колебаний
- Какие точки земли называют географическими полюсами? Основные точки и окружности на земном шаре
- Какая линза какое изображение дает: примеры
- Перпендикулярные прямые и их свойства
- Что такое меридианы и параллели? Как определить меридианы и параллели? Меридианы и параллели…
- Что такое квадрат? Как найти вершины, сечение, плоскость, уравнение, объем, площадь основания и…
- Тупоугольный треугольник: длина сторон, сумма углов. Описанный тупоугольный треугольник
- Выпуклые многоугольники. Определение выпуклого многоугольника. Диагонали выпуклого многоугольника
- Простые механизмы. Подъемный механизм. Простые механизмы в быту
- Оси симметрии.
 Фигуры, имеющие ось симметрии. Что такое вертикальная ось симметрии
Фигуры, имеющие ось симметрии. Что такое вертикальная ось симметрии - Что такое касательная к окружности? Свойства касательной к окружности. Общая касательная к двум…
- Что такое прямоугольник? Частные случаи прямоугольника
- Что такое прямая и какой она бывает?
- Основное свойство дроби. Правила. Основное свойство алгебраической дроби
- Пример деления числа на число. Таблица деления
- Уравнение плоскости: как составить? Виды уравнений плоскости
Урок математики в 6-м классе по теме «Координатная плоскость»
Цель урока: введение понятия координатная плоскость, координаты точки на плоскости.
Задачи урока:
- изучить определение координатной плоскости, координат точки на плоскости;
- научиться строить координатную плоскость;
- научиться определять координаты точек на плоскости;
- научиться строить точки с заданными координатами в координатной плоскости.

Ход урока
1. ОргмоментПрозвенел сейчас звонок,
Начинаем наш урок.
Вы за парты тихо сели
На меня вы посмотрели.
Предлагаю подружиться
И всем вместе потрудиться.
(Приложение 1, слайд 1)
Я надеюсь, что на сегодняшний урок вы пришли в добром здравии и хорошем настроении, ведь от каждого из вас зависит, как этот урок пройдет. Поэтому наш урок мы так и назовем «Все в твоих руках». (Приложение 1, слайд 2).
Помните правила работы на уроке (Приложение 1, слайд 3).
II. ПовторениеI этап нашего урока – повторение.
1)
Что за линия такая? (Приложение 1, слайд 4)
И от края и до края
Точка, стрелка, буквы тутКак скажи её зовут?
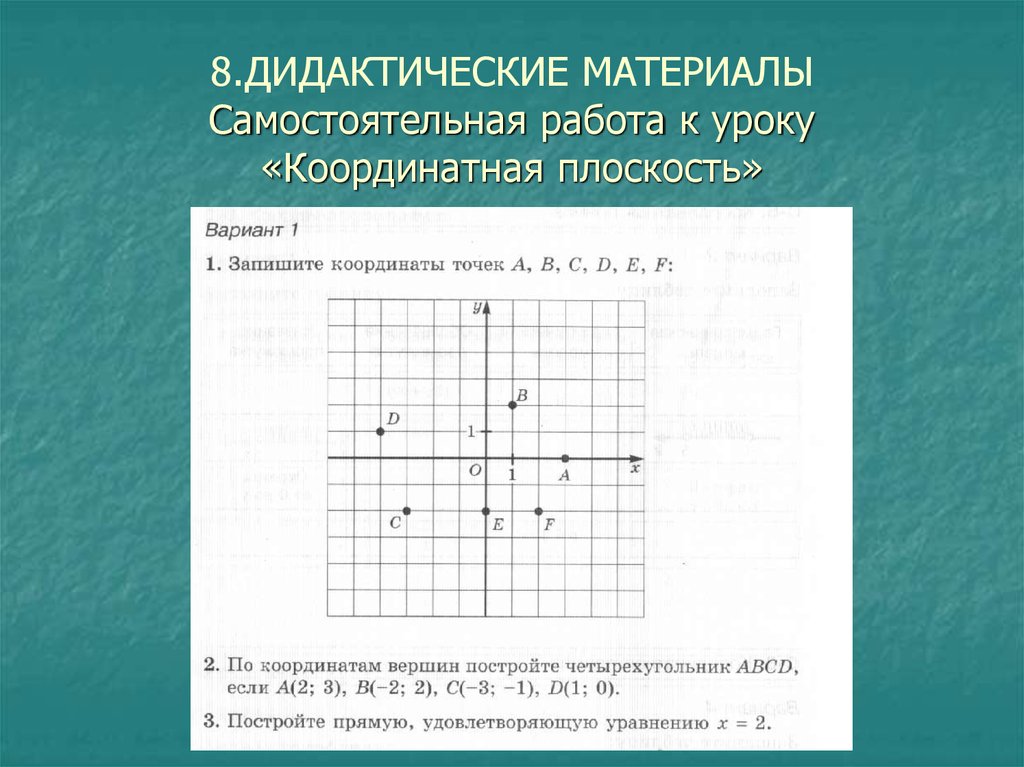
— Назовите координаты точек: Р, О, А, М.
— Появляется вертикальная прямая: С, В, К.
— А можете назвать координаты точки Е?
III. Сообщение темы и задач урокаКоординаты каких точек мы умеем определять? (на координатной прямой)
Лежит ли точка Е на координатной прямой? (нет)
А где она лежит? (в плоскости)
Вывод: 1) если точка лежит в плоскости её координаты не умеем определять.
Для определения координат точек, лежащих на прямой мы использовали координатную прямую.
Что же нужно для определения координат точек, лежащих на плоскости? (координатная плоскость).
Это и будет темой нашего урока (Приложение 1, слайд 5), которую вы запишите в свои рабочие листы. (Приложение 2).
Какие учебные задачи мы можем поставить перед собой на уроке (ученики сами определяют по четырем словам, которые учитель вывешивает на доске):
1) изучить определение координатной плоскости, координат точки на плоскости;
2) научиться строить координатную плоскости;
3) научиться строить точки в координатной плоскости;
4) научиться определять координаты точек, лежащих на плоскости.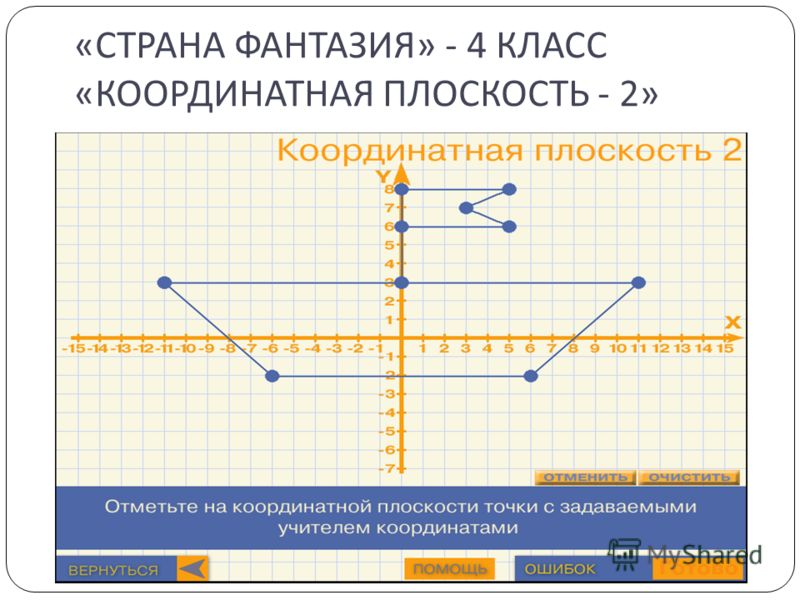
Перейдём к решению наших учебных задач.
Но у меня вопрос: «А зачем нам нужно определять координаты точек на плоскости?
(Ответ: Потому, что в нашей жизни есть такие объекты, координаты которых нужно уметь определять)
Например: (Приложение 1, слайд 6)
Вы купили билет в кино. Что в них указано? (номер ряда и место)
Сколько чисел будут определять ваше положение в зале кинотеатра?
(2) Сначала мы находим ряд, а затем нужное место в этом ряду.
Вывод:
2) Сколько чисел определяют положение точки на плоскости? (2)
Сколько нужно координатных прямых, чтобы определить положение точки на плоскости? (2)
Как вы считаете, какими они должны быть по отношению друг к другу? (перпендикулярными)
IV. Объяснение нового материалаРассмотрим две перпендикулярные координатные прямые (Приложение 1, слайды 7-10), которые пересекаются в точке О – начале отсчёта.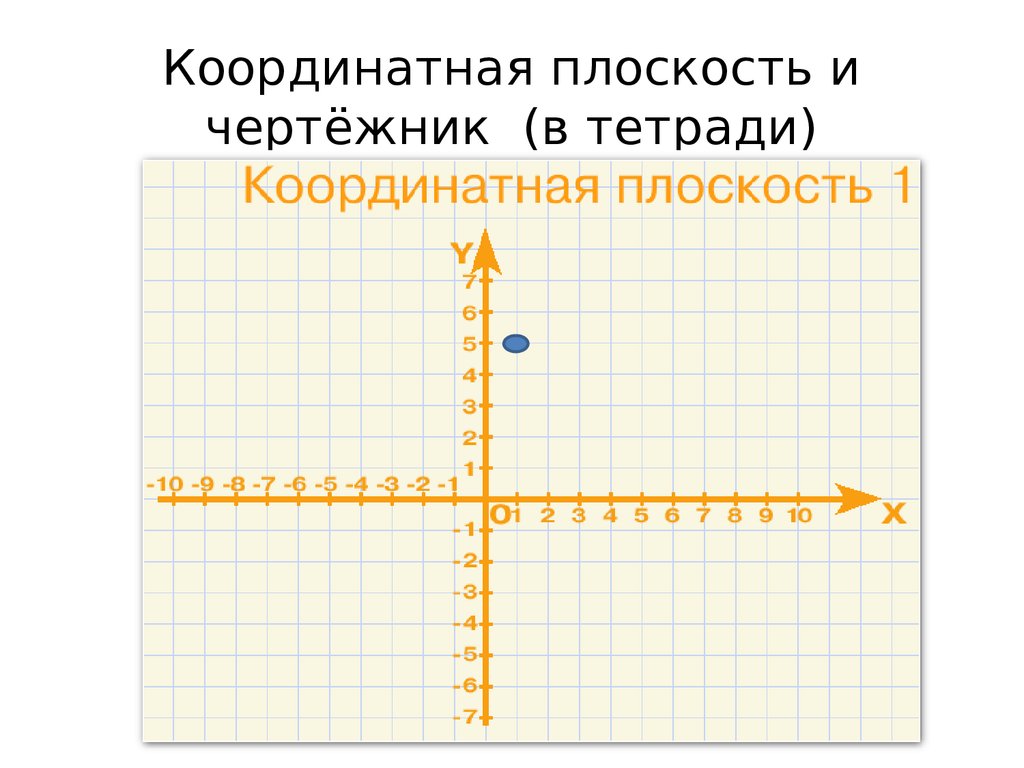 Их называют системой координат на плоскости (щелчок)
Их называют системой координат на плоскости (щелчок)
Их обозначают (щелчок) x и y b называют осями координат (повторите)
При этом
- горизонтальная ось х называется ось абсцисс.
- вертикальная ось y называется ось ординат.
- точка О называется начало координат .
Плоскость, на которой выбрана система координат, называется координатной плоскостью.
Для чего нужна координатная плоскость? (чтобы определять координаты точек на плоскости)
Пару чисел, определяющих положение точки на координатной плоскости, называют координатами точки.
Записывают M(x;y)
- x называется первая координата или абсцисса точки.
- y называется вторая координата или ордината точки.
Какую учебную задачу выполнили?
V. Закрепление1) Фронтальная устная работа: определяем координаты точек на слайде (Приложение 1, слайд 11)
2) Работа в парах:
Возьмите карточку №1 жёлтого цвета (Приложение 3)
- I в – «отвечающий» – определяет координаты точек и записывает их на карточке
- II в – «проверяющий» – проверяет.

Теперь берём карточку №2 салатового цвета и меняемся ролями (Приложение 4)
- I в – «проверяющий»,
- II в – «отвечающий».
А теперь поднимите руку, кто сделал правильно?
3) Физминутка «Где сидишь?» (Приложение 1, слайд 12)
Во время урока дети меняют свое положение в классе. Для этого каждому выдается карточка, на которой написаны координаты. Первая означает номер ряда в классе, а вторая координата — номер парты. Взяв карточку, ученик проверяет по слайду свои координаты и сравнивает их с теми, которые написаны на карточке.
а) встаньте те, кто сидит на своём месте
б) встаньте те, кто сидит неправильно и займите правильно свои места (дети меняются местами)
4) Работа в парах сменного состава
Как вы считаете где может пригодится определение координат точек? в смежных дисциплинах?
Наряду с математическими координатами, есть и другие – географические. (Приложение 1, слайд 13). У вас на столах лежит карта Калужской области. Работая в парах, определите координаты выделенных городов. Та пара, которая готова поднимает руку и говорит найденные координаты. После проверки правильности ответа учителем, им выдается герб города, который прикрепляется к большой карте Калужской области.
Работая в парах, определите координаты выделенных городов. Та пара, которая готова поднимает руку и говорит найденные координаты. После проверки правильности ответа учителем, им выдается герб города, который прикрепляется к большой карте Калужской области.
| 1) Мосальск (-4;1) | 8) Козельск (1;-4) |
2) Сухиничи (-3;-3) | 9) Малоярославец (6;6) |
3) Боровск (5;7) | 10) Обнинск (7;7) |
4) Барятино (-7;-1) | 11) Киров (-8;-3) |
5) Спас – Деменск (-10;1) | 12) Медынь (2;6) |
6) Юхнов (-2;5) | 13) Людиново (-7;-5) |
7) Калуга (4;1) | 14) Мещовск (-3;-1) |
А теперь можно сесть на свои места. Вы хорошо справились с этими заданиями.
Вы хорошо справились с этими заданиями.
Какую учебную задачу выполнили?
5) А теперь давайте научимся строить координатную плоскость. (Приложение 1, слайд 14) (Учитель на доске, дети в тетрадях)
6) Как отметить точки с заданными координатами? (Приложение 5)
А(2;3), В(-4;-6) – 2 человека у доски
7) Индивидуальная работа. (Приложение 1, слайд 15)
У вас на столах лежат белые листы с координатной плоскостью. Сейчас вы будете работать на них.
В годы Великой Отечественной войны вашим сверстники, нужно было уметь определять координаты точек на местности. Об этом говорится в стихотворении Константина Симонова « Сын артиллериста». Я читаю стихотворение Константина Симонова «Сын артиллериста», а вы отмечаете в координатной плоскости точки с теми координатами, которые услышите в стихотворении. Называть точки можете по своему желанию, если хотите. (музыка, Приложение 6).
Всю ночь, шагая как маятник,
Глаз майор не смыкал,
Пока по радио утром
Донёсся первый сигнал:
Всё в порядке, добрался,
Немцы левее меня,
Координаты (-2;-8)
Скорее давайте огня!
Орудия зарядили,
Майор рассчитал всё сам.
И с рёвом первые залпы
Ударили по горам.
И снова сигнал по радио:
Немцы правей меня,
Координаты (6;-4)
Скорее ещё огня!
Летели земля и скалы,
Столбом поднимался дым.
Казалось, теперь оттуда
Никто не уйдёт живым.
Третий сигнал по радио:
Немцы вокруг меня,
Координаты (2;4)
Не жалейте огня.
Майор побледнел, услышав:
(2;4) – как раз
То место, где его Лёнька
Должен сидеть сейчас.
А теперь снимите верхний лист и копирку и проверьте, если точки совпали, то вы выполнили задание верно. Если у вас есть ошибки, то сейчас есть возможность понять, в чём ошибка. Будем работать в группах.
8) Групповая работа:
Наряду с математическими есть и другие, не только географические, но и координаты на карте звёздного неба. (Приложение 1, слайд 16)
Я предлагаю каждому на уроке зажечь свою звезду. Помогайте друг другу, работайте вместе и сообща.
Учащиеся разбиваются на 4 группы. Каждая группа на раскрашенном плакате, символизирующем звездное небо, составляет созвездия: Большая Медведица, Малая Медведица, Персей, Андромеда. Группы получают конверты, внутри которых находятся вырезанные из блестящей клейкой бумаги звезды. На обороте каждой написаны координаты точек, по 1-2 на каждого ученика. Так как модель звездного неба представляет из себя также координатную плоскость, то дети прикрепляют свои звезды согласно координатам. Один прикрепляет — другие проверяют его. Итог — правильно собранное звездное скопление.
Группы получают конверты, внутри которых находятся вырезанные из блестящей клейкой бумаги звезды. На обороте каждой написаны координаты точек, по 1-2 на каждого ученика. Так как модель звездного неба представляет из себя также координатную плоскость, то дети прикрепляют свои звезды согласно координатам. Один прикрепляет — другие проверяют его. Итог — правильно собранное звездное скопление.
Какую учебную задачу выполнили?
VI. Итоги урокаА теперь проверим насколько хорошо вы усвоили новый материал и действительно ли все задачи урока выполнены.
1) Перед вами лежат конверты. В них находятся карточки с координатами точек. Я буду вам показывать на слайдах точки, а вы поднимать карточку, на которой написана координата точки.
| А (3;2) – голубая | А (-2;-3) – зелёная |
А (-3;-2) – жёлтая | А (2;-3) – розовая |
А (-3;2) — красная | А (2;3) – оранжевая |
Выкладывайте карточки перед собой.
1) А (2;3) – оранжевая (Приложение 1, слайд 17)
2) А (-3;2) – красная (Приложение 1, слайд 18)
3) А (-2;-3) – зелёная (Приложение 1, слайд 19)
А теперь переверните их, какую фразу получили? («Всё в твоих руках») (Приложение 1, слайд 20)
2) Как вы ее понимаете?
VII. Домашнее задание(Приложение 1, слайд 21)
1) заполнить пропуски в рабочих листах (Приложение 2): если хорошо усвоили тему, то самостоятельно; если нет – то по учебнику п.45.
2) построить по точкам попугая (этот вариант сложнее) или рыбку (этот вариант легче) (точки необходимо соединять отрезками по порядку) (Приложение 7)
IX. Рефлексия собственной деятельностиА теперь каждый оцените свою работу на уроке, возьмите одну из карточек на вашем столе и поднимите ее вверх. (Я все понял, я был активным….)
(Приложение 1, слайд 22)
X. Заключительное слово учителя(Приложение 1, слайд 23)
Звенит звонок
Уверенно, настойчиво, размеренно.
Час расставанья близится.
Урок закончен класс.
Спасибо за внимание,
Терпение, старание.
И будьте в вечном здравии.
Благодарю всех вас.
Конспект урока по математике в 7 классе на тему «Координатная плоскость»
МБОУ «Светлинская средняя общеобразовательная школа»
Сакмарского района Оренбургской области
Конспект урока алгебры по теме
«Координатная плоскость»
проведенного в 7 классе
учителем математики
Харахориной Ольгой Александровной
с использованием интерактивной доски
Урок 15. Тема: Координатная плоскость.
Цели урока:
Образовательная:
систематизировать и обобщить знания учащихся по данной теме, закрепить умение находить точки по заданным координатам на координатной плоскости. Развивать умение находить координаты точек, отмеченных координатной плоскости.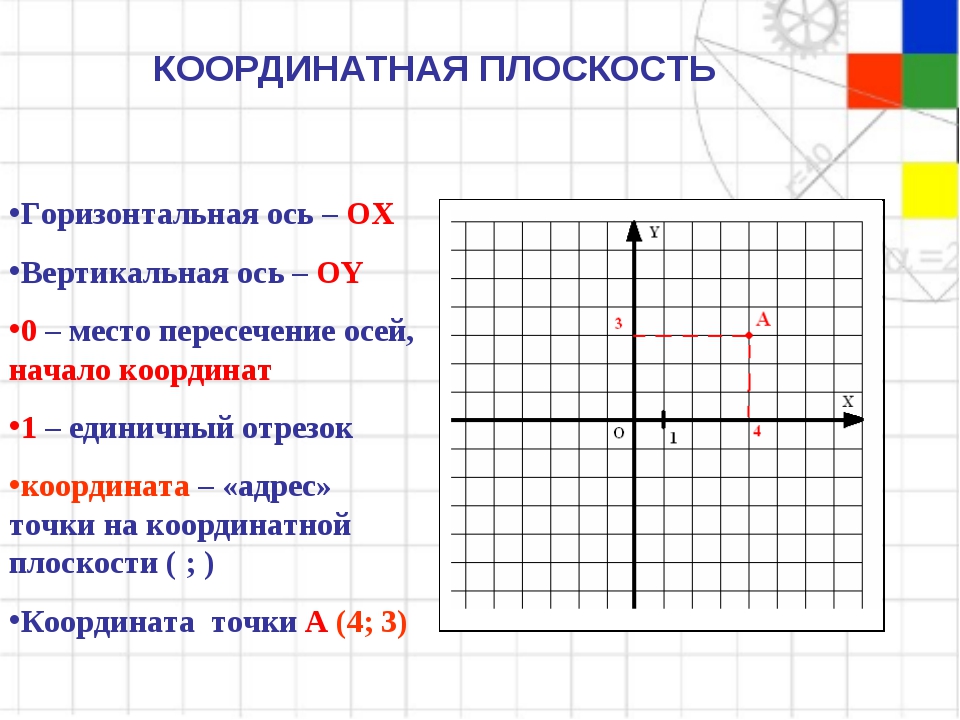
2. Развивать:
логическое мышление, память, математическую речь, познавательный интерес к изучаемому предмету
3. Воспитывать:
точность, последовательность, внимательность учащихся, аккуратность в построении координатой плоскости.
Ход урока:
Организационный момент.
Актуализация знаний.
Провести фронтальный опрос:
Что называют прямоугольной системой координат?
Под каким углом пересекаются оси координат?
Как называется ось ?
Как называется ось Оу?
Что такое координата точки?
Определите координату точки А.
Назовите ординату точки А.
Как называется координата 4?
Алгоритм построения точки А(х;у) в прямоугольной системе координат
Проверочная работа
Вариант I
Вариант II
1.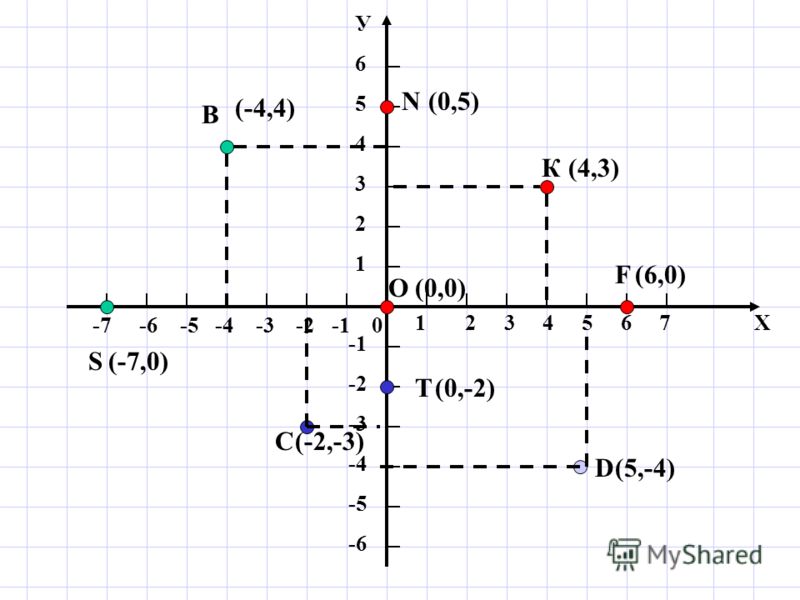 Как называется первое из чисел, задающих положение точки на координатной плоскости?
Как называется первое из чисел, задающих положение точки на координатной плоскости?
1. Как называется второе из чисел, задающих положение точки на координатной плоскости?
2. Запишите обозначение точки A, если ее абсцисса равна 1, а ордината 7.
2. Запишите обозначение точки K, если ее ордината равна — 6, а абсцисса равна 0.
3. Чему равна ордината точки ?
3. Чему равна абсцисса точки ?
4. В какой четверти находится точка ?
4. В какой четверти находится точка ?
5. На какой координатной оси находится точка ?
5. На какой координатной оси находится точка ?
Ответы:
№
1
2
3
4
5
I
абсцисса
— 3
III
II
ордината
— 1
II
Изучение нового материала.

«Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.»
Гиппа́рхНике́йский (годы жизни около190 — ) — , и , часто называемый величайшим . Главной заслугой Гиппарха считается то, что он привнёс в греческие геометрические модели движения небесных тел.
«Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался долготой и широтой в качестве географических координат. Но эти понятия впервыебыли систематизированы в 17 веке Рене Декартом.» Греческий геометр, астроном и физик Клавдий Птолемей провёл большую часть жизни в Александрии, где в 127 -151 гг. производил астрономические наблюдения; никаких сведений о его биографии и даже о месте рождения не сохранилось. Птолемей разработал так называемую геоцентрическую систему мира, согласно которой все видимые движения небесных светил объяснялись их движением (часто очень сложным) вокруг неподвижной Земли.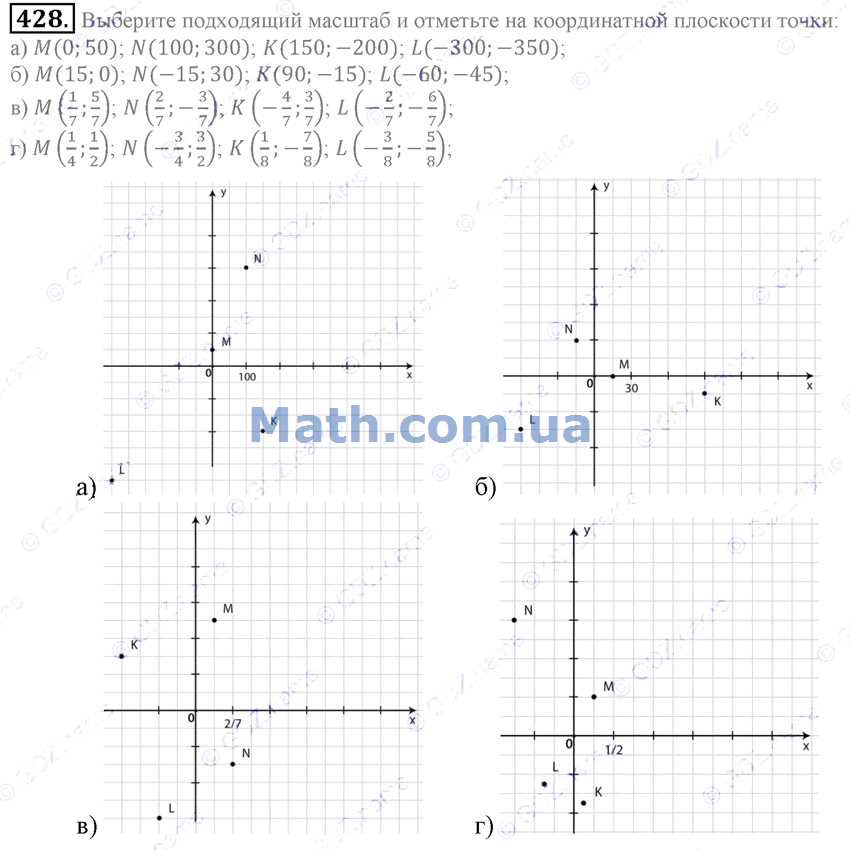 Основное сочинение Птолемея по астрономии — «Великое математическое построение астрономии в 13 книгах», известное под названием «Альмагест».
Основное сочинение Птолемея по астрономии — «Великое математическое построение астрономии в 13 книгах», известное под названием «Альмагест».
«Рене Декарт (1596-1650) — французский философ, естествоиспытатель, математик. Целью Декарта было описание природы при помощи математических законов. Автор прямоугольной координатной плоскости, поэтому ее часто называют декартовой системой координат.»Декарт происходил из старинного, но обедневшего дворянского рода и был младшим (третьим) сыном в семье. Он родился в городе . Им единолично сделаны и сформулированы законы инерции, преломления и отражения лучей, сохранения и измерения движения, алгебры переменных величин, условных рефлексов у животных, относительности движения, ввел использование в математике и физике оси координат X, Y, Z. Он автор теории, объясняющей образование и движение небесных тел вихревым движением частиц материи (вихри Декарта). Ввел представление о рефлексе (дуга Декарта).
5. Отработка навыков. Решение задач.
Найдем координаты точки при помощи тренажера рыбка
Построить по координатам рисунок: отметь точки и соедини их последовательно отрезками
1) Работа у доски : 6.11, 6.23
2) Устно 6.10
Итог урока.
Домашнее задание: № 6.37, 6.32.
АЛГЕБРА 7 класс — Технологические карты уроков по учебнику А. Г. Мордковича
Глава 1. МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Урок 1. ЧИСЛОВЫЕ И АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Урок 2. ЧИСЛОВЫЕ И АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Урок 3. ЧИСЛОВЫЕ И АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Урок 4. ЧТО ТАКОЕ МАТЕМАТИЧЕСКИЙ ЯЗЫК
Урок 5. ЧТО ТАКОЕ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Урок 6. ЧТО ТАКОЕ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Урок 7. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ
Урок 8. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ
Урок 9. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ
Урок 10. КООРДИНАТНАЯ ПРЯМАЯ
Урок 11. КООРДИНАТНАЯ ПРЯМАЯ
Урок 12. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 13. КОНТРОЛЬНАЯ РАБОТА № 1
Уроки 14-15. ПОДГОТОВКА К ГИА
Глава 2. ЛИНЕЙНАЯ ФУНКЦИЯ
Урок 16. КООРДИНАТНАЯ ПЛОСКОСТЬ
Урок 17. КООРДИНАТНАЯ ПЛОСКОСТЬ
Урок 18. ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК
Урок 19. ЛИНЕЙНОЕ УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК
Урок 20. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
Урок 21. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
Урок 22. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
Урок 23. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
Урок 24. ЛИНЕЙНАЯ ФУНКЦИЯ у = kх
Урок 25. ЛИНЕЙНАЯ ФУНКЦИЯ у = kх
Урок 26. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГРАФИКОВ ЛИНЕЙНЫХ ФУНКЦИЙ
Урок 27. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГРАФИКОВ ЛИНЕЙНЫХ ФУНКЦИЙ
Урок 28. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 29. КОНТРОЛЬНАЯ РАБОТА № 2
Уроки 30-31. ПОДГОТОВКА К ГИА
Глава 3. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
Урок 32. ОСНОВНЫЕ ПОНЯТИЯ
Урок 33. ОСНОВНЫЕ ПОНЯТИЯ
Урок 34. МЕТОД ПОДСТАНОВКИ
МЕТОД ПОДСТАНОВКИ
Урок 35. МЕТОД ПОДСТАНОВКИ
Урок 36. МЕТОД ПОДСТАНОВКИ
Урок 37. МЕТОД ПОДСТАНОВКИ
Урок 38. САМОСТОЯТЕЛЬНАЯ РАБОТА № 1
Урок 39. МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ
Урок 40. МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ
Урок 41. МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ
Урок 42. САМОСТОЯТЕЛЬНАЯ РАБОТА № 2
Урок 43. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЕАЛЬНЫХ СИТУАЦИЙ
Урок 44. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЕАЛЬНЫХ СИТУАЦИЙ
Урок 45. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЕАЛЬНЫХ СИТУАЦИЙ
Урок 46. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ РЕАЛЬНЫХ СИТУАЦИЙ
Урок 47. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 48. КОНТРОЛЬНАЯ РАБОТА № 3
Уроки 49-50. ПОДГОТОВКА К ГИА
Глава 4. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА
Урок 51. ЧТО ТАКОЕ СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Урок 52. ЧТО ТАКОЕ СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
ЧТО ТАКОЕ СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Урок 53. ТАБЛИЦА ОСНОВНЫХ СТЕПЕНЕЙ
Урок 54. СВОЙСТВО СТЕПЕНЕЙ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Урок 55. СВОЙСТВО СТЕПЕНЕЙ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Урок 56. САМОСТОЯТЕЛЬНАЯ РАБОТА № 3
Урок 57. УМНОЖЕНИЕ И ДЕЛЕНИЕ СТЕПЕНЕЙ С ОДИНАКОВЫМИ ПОКАЗАТЕЛЯМИ
Урок 58. УМНОЖЕНИЕ И ДЕЛЕНИЕ СТЕПЕНЕЙ С ОДИНАКОВЫМИ ПОКАЗАТЕЛЯМИ
Урок 59. СТЕПЕНЬ С НУЛЕВЫМ ПОКАЗАТЕЛЕМ
Урок 60. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 61. КОНТРОЛЬНАЯ РАБОТА № 4
Уроки 62-63. ПОДГОТОВКА К ГИА
Глава 5. ОДНОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ
Урок 64. ПОНЯТИЕ ОДНОЧЛЕНА. СТАНДАРТНЫЙ ВИД ОДНОЧЛЕНА
Урок 65. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОДНОЧЛЕНОВ
Урок 66. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОДНОЧЛЕНОВ
Урок 67. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОДНОЧЛЕНОВ
Урок 68. УМНОЖЕНИЕ ОДНОЧЛЕНОВ. ВОЗВЕДЕНИЕ ОДНОЧЛЕНА В НАТУРАЛЬНУЮ СТЕПЕНЬ
Урок 69. УМНОЖЕНИЕ ОДНОЧЛЕНОВ. ВОЗВЕДЕНИЕ ОДНОЧЛЕНА В НАТУРАЛЬНУЮ СТЕПЕНЬ
Урок 70.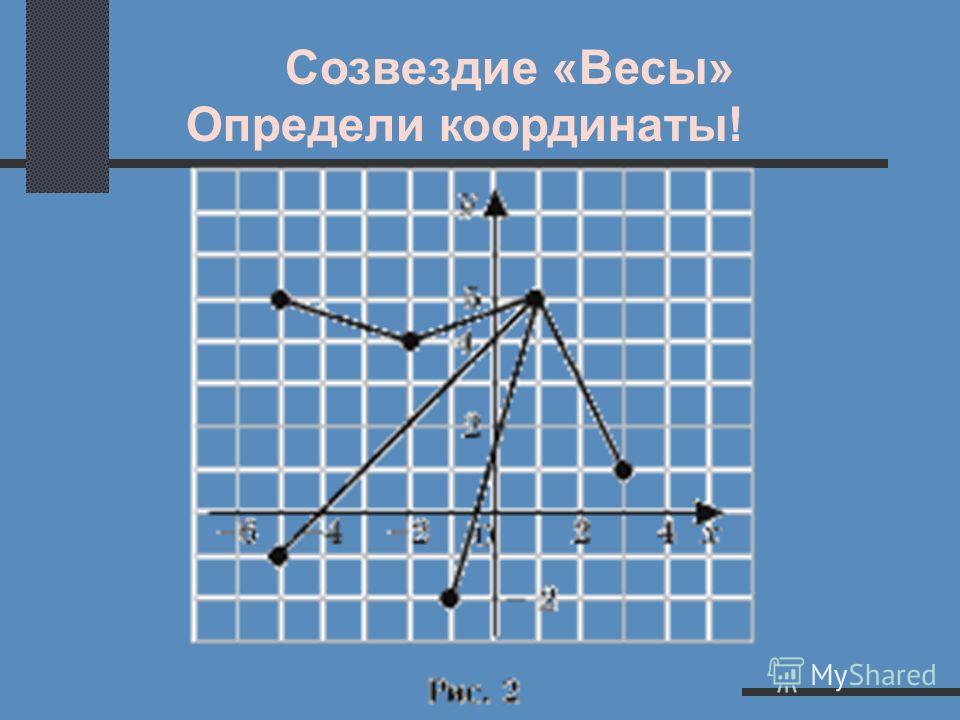 ДЕЛЕНИЕ ОДНОЧЛЕНА НА ОДНОЧЛЕН
ДЕЛЕНИЕ ОДНОЧЛЕНА НА ОДНОЧЛЕН
Урок 71. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 72. КОНТРОЛЬНАЯ РАБОТА № 5
Уроки 73-74. ПОДГОТОВКА К ГИА
Глава 6. МНОГОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
Урок 75. ОСНОВНЫЕ ПОНЯТИЯ
Урок 76. ОСНОВНЫЕ ПОНЯТИЯ
Урок 77. СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЧЛЕНОВ
Урок 78. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН
Урок 79. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН
Урок 80. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН
Урок 81. САМОСТОЯТЕЛЬНАЯ РАБОТА № 4
Урок 82. УМНОЖЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН
Урок 83. УМНОЖЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН
Урок 84. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 85. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 86. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 87. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 88. САМОСТОЯТЕЛЬНАЯ РАБОТА № 5
Урок 89. ДЕЛЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН
Урок 90. ДЕЛЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН
Урок 91. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 92. КОНТРОЛЬНАЯ РАБОТА № 6
КОНТРОЛЬНАЯ РАБОТА № 6
Уроки 93-94. ПОДГОТОВКА К ГИА
Глава 7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ
Урок 95. ЧТО ТАКОЕ РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ И ЗАЧЕМ ОНО НУЖНО
Урок 96. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
Урок 97. ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
Урок 98. СПОСОБ ГРУППИРОВКИ
Урок 99. СПОСОБ ГРУППИРОВКИ
Урок 100. СПОСОБ ГРУППИРОВКИ
Урок 101. САМОСТОЯТЕЛЬНАЯ РАБОТА № 6
Урок 102. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ С ПОМОЩЬЮ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 103. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ С ПОМОЩЬЮ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 104. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ С ПОМОЩЬЮ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 105. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ С ПОМОЩЬЮ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
Урок 106. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ С ПОМОЩЬЮ КОМБИНАЦИИ РАЗЛИЧНЫХ ПРИЕМОВ
Урок 107. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ С ПОМОЩЬЮ КОМБИНАЦИИ РАЗЛИЧНЫХ ПРИЕМОВ
Урок 108. САМОСТОЯТЕЛЬНАЯ РАБОТА № 7
САМОСТОЯТЕЛЬНАЯ РАБОТА № 7
Урок 109. СОКРАЩЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
Урок 110. СОКРАЩЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
Урок 111. СОКРАЩЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
Урок 112. СОКРАЩЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
Урок 113. ТОЖДЕСТВА
Урок 114. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 115. КОНТРОЛЬНАЯ РАБОТА № 7
Уроки 116-117. ПОДГОТОВКА К ГИА
Глава 8. ФУНКЦИЯ у = х2
Урок 118. ФУНКЦИЯ у = х2 И ЕЕ ГРАФИК
Урок 119. ФУНКЦИЯ у = х2 И ЕЕ ГРАФИК
Урок 120. ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ
Урок 121. ГРАФИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ
Урок 122. ЧТО ОЗНАЧАЕТ В МАТЕМАТИКЕ ЗАПИСЬ y = f(x)
Урок 123. ЧТО ОЗНАЧАЕТ В МАТЕМАТИКЕ ЗАПИСЬ y = f(x)
Урок 124. ЧТО ОЗНАЧАЕТ В МАТЕМАТИКЕ ЗАПИСЬ y = f(x)
Урок 125. ЧТО ОЗНАЧАЕТ В МАТЕМАТИКЕ ЗАПИСЬ y = f(x)
Урок 126. ПОВТОРЕНИЕ И СИСТЕМАТИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА
Урок 127. КОНТРОЛЬНАЯ РАБОТА № 8
Уроки 128-132. ИТОГОВОЕ ПОВТОРЕНИЕ
Уроки 133-134.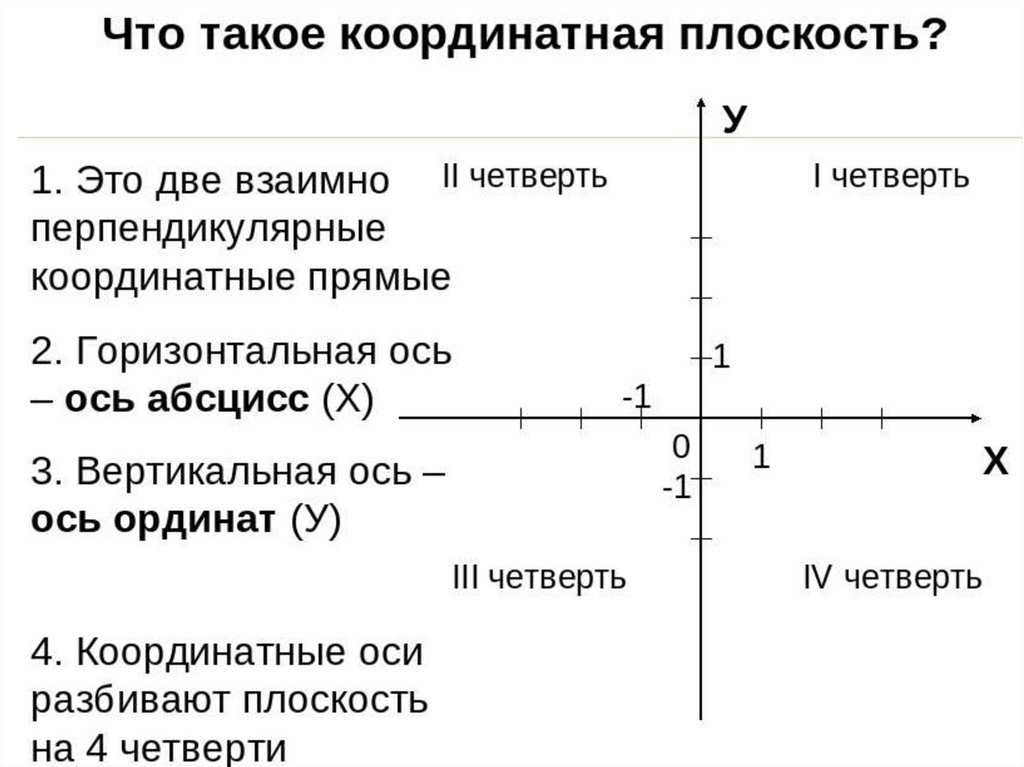 ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
Уроки 135-136. ПОДГОТОВКА К ГИА
Внеклассное мероприятие по Алгебре «Координатная плоскость» 6 класс
Автор: Широбокова Любовь Ивановна, учитель математики МБОУ Большеошворцинская СОШ имени Ф.А. Пушиной, Якшур — Бодьинского района, Удмуртской Республики.
Урок-путешествие в 6 классе по теме «Координатная плоскость»
Многие тысячи лет на Земле живет человек, и, по крайней мере, ему были даны два чуда природы: день, освещенный Солнцем, и ночь с ее манящими и загадочными россыпями звезд. Те, кто более пристально изучал перемещение небесных светил и звездных узоров, давно обнаружили строгую ритмичность суточных и сезонных движений. Эти явления были положены в основу различных способов счета времени и ведения календаря – двух необходимых атрибутов любой цивилизации. Занятия астрономией были всегда уважаемы. Математика и позже физика вышли из астрономии, математика – как аппарат для точных расчетов положений звезд, физика – для объяснения неизвестных явлений, обнаруженных при их наблюдении.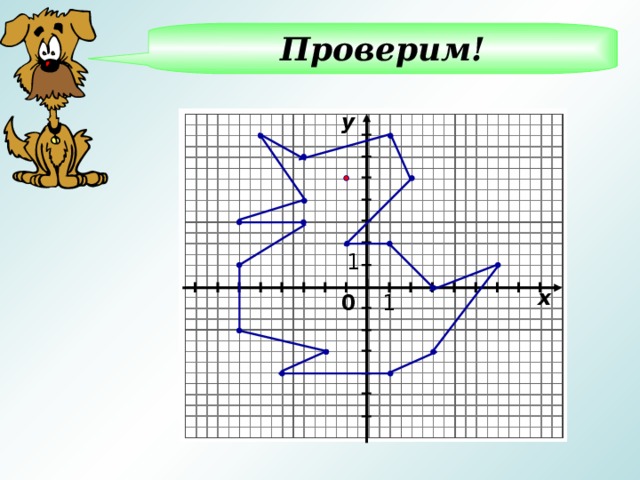 Так почему бы не вернуться к астрономии хотя бы на одном уроке математики, например, при изучении темы «Координатная плоскость»?
Так почему бы не вернуться к астрономии хотя бы на одном уроке математики, например, при изучении темы «Координатная плоскость»?
Задание: На координатной плоскости отмечаем точки, заданные своими координатами, в порядке их следования. А затем соединяем каждую точку с предыдущим отрезком. В результате получаем рисунки созвездий.
Варианты созвездий
1) Созвездие Дракон
(6; 6,5), (5, 5), (4,5; 1), (2,5; -2,5), (0,5; -3), (-2,5; -0,5), (-3; 2), (-4; 2,5),
(-5; 3,5), (-6,5; 3,5), (-6; 2), (-5; -3), (-4; -4), (-4; -5), (-6; -5), (-5; -3).
2) Созвездие Орёл
(1,5; -0,5), (3,5; 4,5), (-1; 3), (-4; -2), (-1,5; -1,5), (1,5; -0,5), (3; -4),
(4; -4,5).
3) Созвездие Лира
(1; 2), (2; 1,5), (1; 0,5), (-0,5; 0), (-1; -2,5), (0,5; -2), (1; 0,5).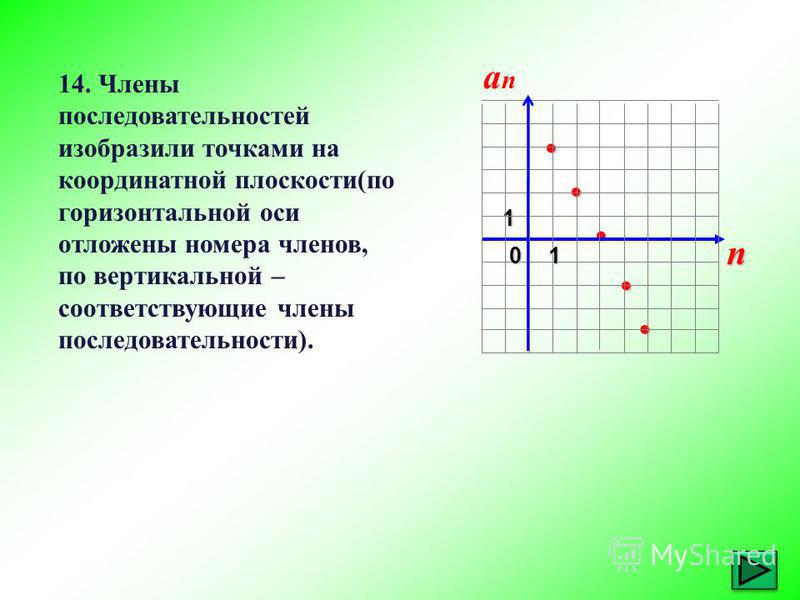
4) Созвездие Дельфин
(1; 0,5), (0,5; 1,5), (-1; 2), (-0,5; 1), (1; 0,5).
5) Созвездие Рыбы
(4; -0,5), (5; 0), (6; -1), (5; -2), (3.5; -2), (4; -0,5), (2; 0), (-2; 0), (-3,5; 0),
(-5,5; -0,5), (-7; -0,5), (-8,5; -1), (-7; 1), (-5,5; 3), (-4; 6), (-4,5; 7), (-4; 8).
6) Созвездие Треугольник
(-1; 0), (0; 1), (1; 0), (3; -3), (-1; 0).
7) Созвездие Скульптор
(-5; 0), (-1,5; 0,5), (1,5; 0,5), (4; -1,5), (2,5; -4)
8) Созвездие Ворон, Чаша и Гидра
Ворон: (-3; -2), (-3,5; -1,5), (-3,5; 0), (-5; 0), (-5; -2), (-3,5; -1,5).
Чаша: (-2,5; 0), (-1,5; -0,5), (-0,5; 0), (0; 0,5), (0; 2), (-1; 2), (-0,5; 0),
(0.5; -1,5), (1; -0,5), (0; 0,5).
Гидра: (-10,5; -4), (-8; -2), (-2; -5), (0; -4), (2; 0), (0; 0), (5; 1), (6; 0), (8; 2), (7; 4), (10; 5), (11; 5,5), (11,5; 5,5), (12; 5), (12; 4,5), (11,5; 4,5), (11; 5,5).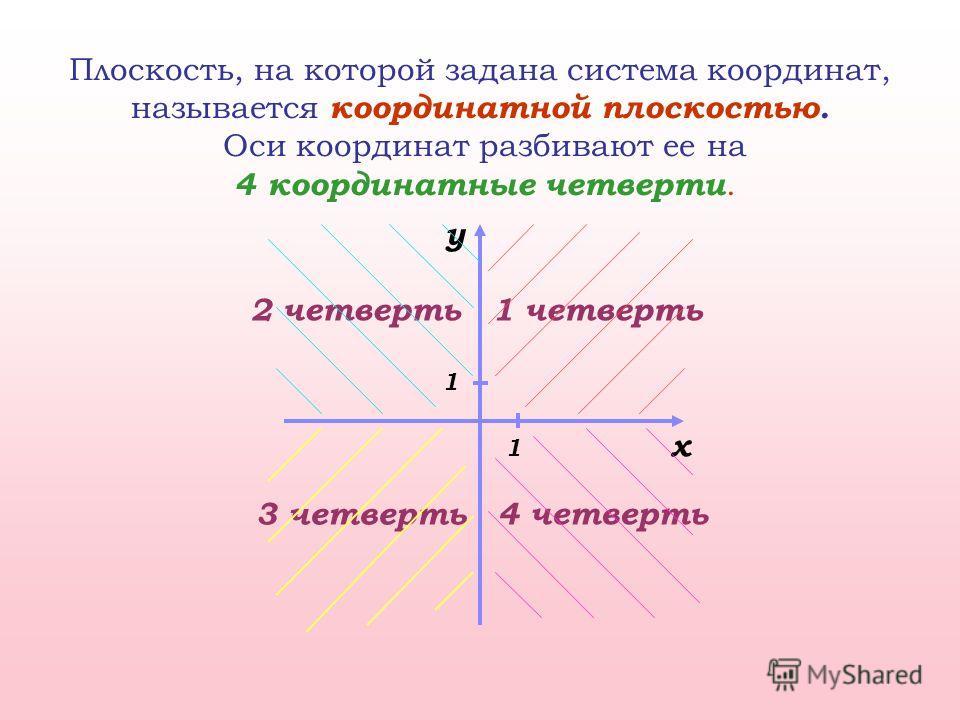
9) Созвездие Козерог
(5; 4), (4,5; 3), (1,5; -2), (1; -3), (-1; -2), (-3; -1), (-4; 0,5), (-5; 2), (-4; 2),
(-2,5; 2), (-0,5; 1,5), (4,5; 3).
10) Созвездие Малая Медведица
(0; -1,5), (1,5; -3), (0,5; -4), (-1; -2), (0; -1,5), (-0,5; 0,5), (0; 2,5), (1; 4).
11) Созвездие Волопас
(3; -2), (1.5; -2), (0; 2), (0; 4,5), (-2; 5,5), (-3; 3), (-1; 0,5), (1,5; -2),
(-0,5; -4).
12) Созвездие Кассиопея
(2; 0), (0,5; -1,5), (0; 0,5), (-2; 0), (-3; 2).
13) Созвездие Кит
(-7; 4,5), (-5,5; 6,5), (-7; 7), (-8; 6,5), (-8,5; 5), (-7; 4,5), (-6,5; 3,5), (-5; 2),
(-2,5; -0,5), (-2; -2,5), (3; -3), (5; 0), (1; -0,5), (0; 0,5), (-2,5; -0,5).
14) Созвездие Киль
(-4; -2), (-2; -3,5), (4; -4), (-6; -2,5), (-6; -1,5), (-5,5; -1), (-3; 0,5), (0,5; 0,5),
(1; 3), (6; 1,5).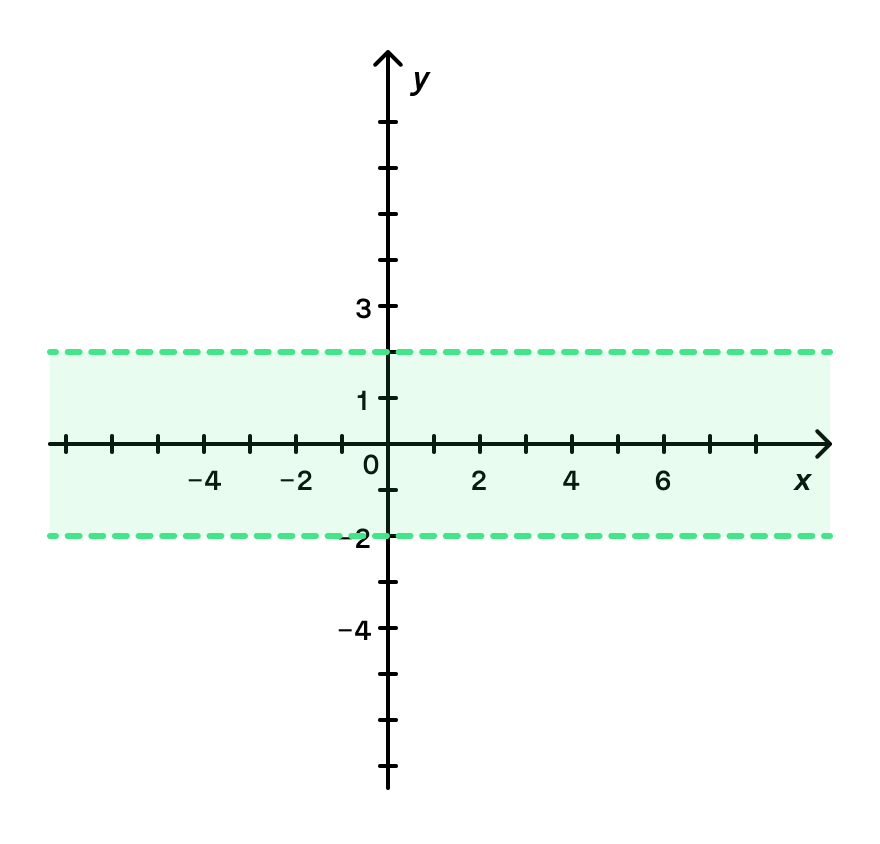
15) Созвездие Лев
(4,5; 2,5), (4; 3), (2; 2), (2; 1), (-1; 1), (-2; 1), (-5,5; -1), (-2,5; -0,5), (3; -2),
(3; 0), (2; 1).
16) Созвездие Ящерица
(0,5; 2,5), (0; 2), (0,5; 1,5), (0; 1), (0,5; 0,5), (0; -0,5), (1; -2), (1; -2,5).
17) Созвездие Рысь
(4; 4,5), (3; 4), (2,5; 1,5), (0; 0), (-2; 0), (-3; -1), (-3,5; -2)
18) Созвездие Северная Корона
(2; 2), (-1,5; 0), (0,5; -1), (1; -0,5), (2; -0,5), (3; 1,5), (2; 3).
19) Созвездие Тукан
(3; -1), (3,5; 1), (0; 2), (-3; -1), (-2,5; -1,5), (-1,5; -1,5), (0; 2).
20) Созвездие Журавль
а) (4; 4), (2,5; 3), (0,5; 1,5), (0, 0), (-0,5; -2), (-1; -2,5).
б) (2; 0), (0; 0), (-2; 0,5), (-2; 1).
21) Созвездие Лебедь
а) (-2; 2), (-0,5; 0), (2; -2), (4,5; -5).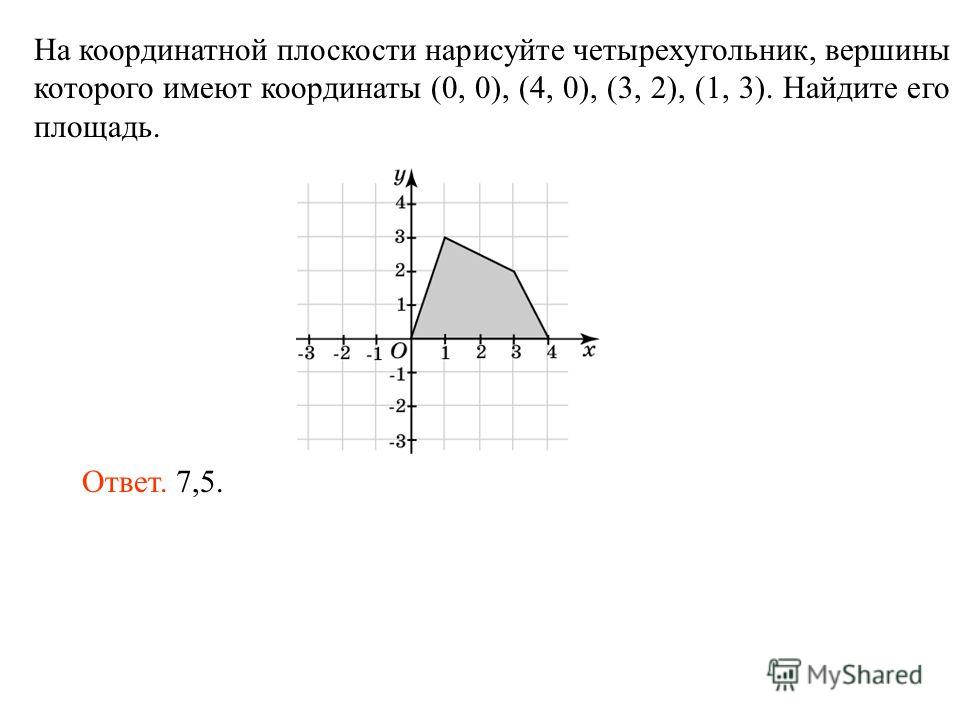
б) (-5; -4,5), (-2,5; -3), (-0,5; 0), (2; 2), (2,5; 5), (3,6).
22) Созвездие Телец
а) (6,5; -3,5), (6; -3), (2,5; -2), (0,5; -0,5), (0; 0,5), (-1,5; 2,5), (-4; 4), (-6; 5).
б) (-7; 2), (-1,5; 0), (-0,5; -0,5), (0,5; -0,5).
23) Созвездие Скорпион
а) (-3,5; -2,5), (-4; -3), (-4,5; -4), (-3,5; -5), (-1,5; -5), (-0,5; -4,5), (0; -2,5),
(0; -1), (1; 1,5), (2; 2,5), (3; 3), (5; 4).
б) (5; 1), (5; 2,5), (5; 4), (4; 5), (3,5; 5,5).
24) Созвездие Весы
а) (-4; 1,5), (-3,5; 0,5), (-2,5; 1), (-2; 1,5), (0; 4), (2,5; 1), (1,5; -3), (-1,5; -4),
(-2; -5).
б) (0; 4), (1,5; -3).
25) Созвездие Водолей
а) (7,5; -0,5), (4; 1), (1; 3), (-0,5; 2,5), (-1; 3), (-2; 2,5), (-5; 1), (-3; 0,5),
(-3; -1,5), (-3,5; -2,5), (-4,5; -4).
б) (1,-2), (0; 0), (1; 3).
26) Созвездие Геркулес
а) (4; -4), (2,5; -3), (1,5; 0,5), (1; 3,5), (-1,5; 2,5), (0; 0), (-1; -2), (-4; -1),
(-5; -0,5), (-5,5; -0,5).
б) (-1; -6), (2,5; -3).
в) (-3; 6), (-4; 3), (-1,5; 2,5).
г) (4; 5), (2; 6), (1; 3,5).
27) Созвездие Персей
а) (7; 3,5), (2; 5), (1,5; 4), (0; 2), (-1,5; 1), (-3; -2,5), (-3,5; -4,5), (-3; -6),
(-2,5; -6).
б) (3; -3,5), (2; -3,5), (1,5; -3), (1; -2), (1; -0,5), (0; 2).
Литература
1. Дубкова С. И. Прогулки по небу – легенды и мифы о созвездиях: детская энциклопедия.- М: Белый город, 2001.
Урок 2 | узоры и координатная плоскость | 5-й класс Математика
Задача
Построить координатную плоскость и нанести точки по заданным координатам.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89505.Г.А.1 — Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии, и заданной точкой на плоскости, расположенной с помощью упорядоченной пары. чисел, называемых его координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствуют (например, ось x и координата x, ось y и координата y).
Основополагающие стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89502.
 MD.B.6
MD.B.6
Критерии успеха
Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Имея координаты точки, нанесите ее на координатную плоскость с интервалами в 1 единицу.
- Поймите, что есть два разных способа интерпретации точки, например, (2, 3): (1) как инструкции (справа 2, вверх 3) и (2) как точки, определяемой расстоянием 2 от y -ось и расстояние 3 от x -оси.
- Получив инструкции из другой точки на координатной плоскости, начертите точку на координатной плоскости с интервалом в 1 единицу.
Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Якорные задачи
Задания, разработанные для обучения критериям успеха урока, и рекомендации, помогающие ученикам понять
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Проблема 1
Часть A:
Нанесите точку на координатную сетку ниже (2, 6).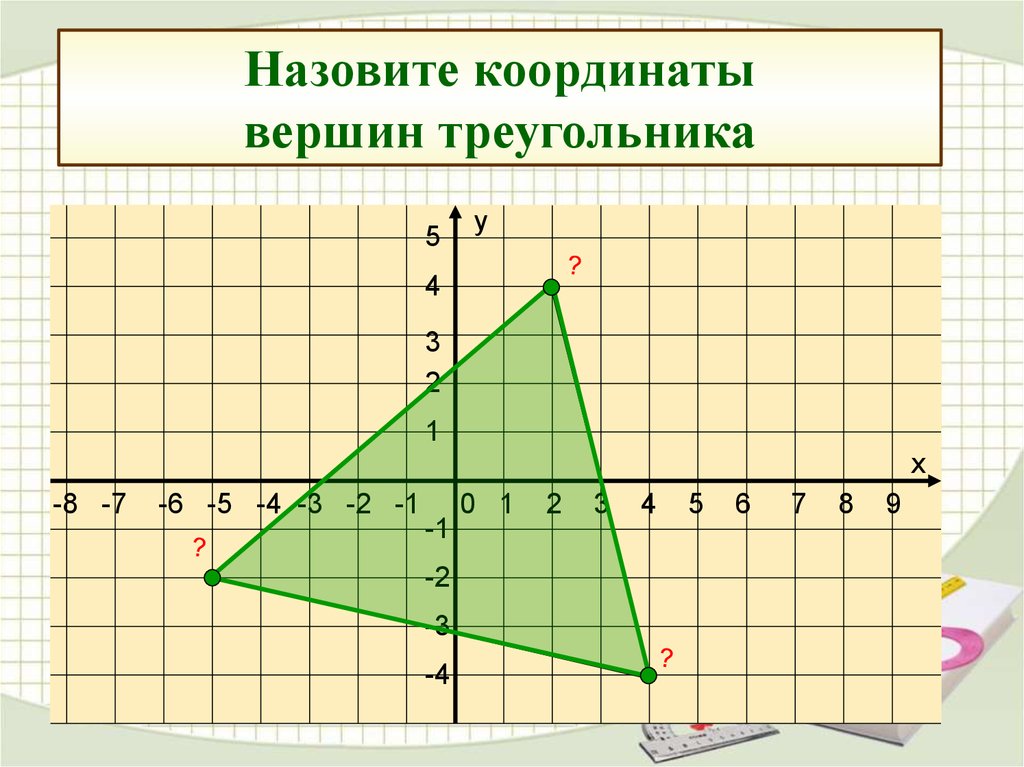
Часть B:
Алекс говорит, что упорядоченная пара (2, 6) – это 2 единицы по оси x и 6 единиц по оси 9.0046 и -ось. Ты согласен или несогласен?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Каталожные номера
Достижение Первое 5 класс, раздел 9, урок 2 (2017-2018) — «Подумай об этом!»
Класс 5, Раздел 9, Урок 2 (2017–2018) предоставляется компанией Achievement First как часть их веб-портала с открытым исходным кодом по лицензии CC BY 4.0. Copyright © 1999-2017 Достижение прежде всего. Проверено 25 мая 2018 г., 3:09вечера..
Изменено Fishtank Learning, Inc.
Проблема 2
- Нанесите следующие точки на координатную сетку ниже:
- Точка А : (3, 8)
- Точка B : (7, 2)
- Точка C : (6, 0)
- Точка D : (0, 4)
- Точка E : 3 единицы влево и 4 единицы вверх от точки B
- Точка F : 5 единиц вправо и 2 единицы вниз от точки Д
- Каковы координаты точки E ? Пункт F ?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.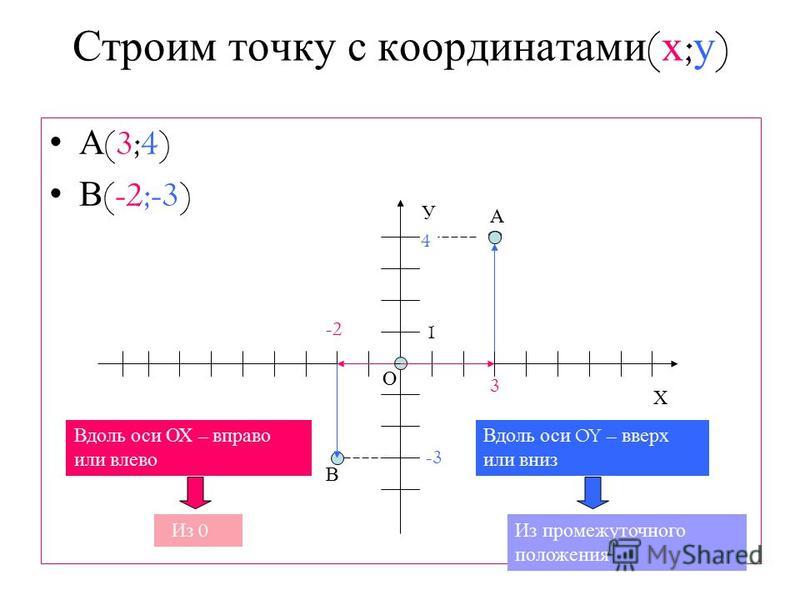
Набор задач и домашнее задание
Набор проблем
Домашнее задание
Ключи ответов
Ключи ответов для наборов задач и домашних заданий доступны при наличии подписки Fishtank Plus.
Обсуждение набора задач
- См. #2(b). Какая фигура находится на расстоянии 2 единиц от оси и ? Соответствует ли это координате x или координате y ?
- Если точка A лежит на расстоянии 3 единиц от оси x-, какую координату вы знаете?
- Где остановилась Эми в #5? Если кто-то выбрал точку A , какую ошибку он мог совершить? Как насчет точки C ? Пункт Д ?
Целевая задача
Задание, которое представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950 Координаты баллов приведены в таблице.
| Точка | Координата |
| Ш | (2, 3) |
| Х | (4, 0) |
| Д | (5, 2) |
| З | (0, 1) |
Отобразите все точки из таблицы в координатной сетке. Обозначьте их соответствующими буквами.
Ответ студента
Пример ответа на Целевое задание с ожидаемым от учащихся уровнем детализации.
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Создайте бесплатную учетную запись или войдите, чтобы просмотреть ответ учащегося
Дополнительная практика
Fishtank Plus Content
Словесные задачи и упражнения на беглость речи
Доступ к ежедневным задачам со словами и нашим упражнениям на беглость речи, разработанным для того, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.
Предварительный просмотр
Узнать больше
значок/стрелка/вправо/крупная копияУрок 1
значок/стрелка/вправо/большойУрок 3
Координатная плоскость | Математика средней школы | Целые числа и координатная плоскость
Популярные учебники
в координатной плоскостиКак наносить точки на координатную плоскость?
Знание того, как строить упорядоченные пары, является важной частью графических функций.
 В этом уроке вы увидите, как взять упорядоченную пару и нанести ее на координатную плоскость. Взглянем!
В этом уроке вы увидите, как взять упорядоченную пару и нанести ее на координатную плоскость. Взглянем!Что такое упорядоченная пара?
Упорядоченные пары являются фундаментальной частью построения графиков. Упорядоченные пары составляют функции на графике, и очень часто вам нужно построить упорядоченные пары, чтобы увидеть, как выглядит график функции. Этот урок познакомит вас с упорядоченными парами!
Каково происхождение?
Координатная плоскость имеет две оси: горизонтальную и вертикальную. Эти две оси пересекаются друг с другом в точке, называемой началом координат. Узнайте об упорядоченной паре, которая указывает начало координат и ее положение в координатной плоскости, посмотрев этот урок!
Что такое координатная плоскость?
Вы не можете изобразить функцию или построить упорядоченные пары без координатной плоскости! Узнайте о координатной плоскости, посмотрев этот урок.

Что такое квадранты на координатной плоскости?
Знаете ли вы, что координатную плоскость составляют четыре квадранта? Узнайте об этих квадрантах и о том, какие упорядоченные пары расположены в каждом из них, посмотрев этот урок!
Что такое координата X?
Упорядоченные пары являются важной частью построения графика, но вам нужно знать, как определить координаты в упорядоченной паре, если вы собираетесь нанести ее на координатную плоскость. В этом уроке вы увидите, как определить координату x в упорядоченной паре!
Что такое координата Y?
Упорядоченные пары являются важной частью построения графика, но вам нужно знать, как определить координаты в упорядоченной паре, если вы собираетесь нанести ее на координатную плоскость. В этом уроке вы увидите, как определить координату Y в упорядоченной паре!
Что такое ось X?
Чтобы построить график функции или построить упорядоченную пару, вам нужно использовать координатную плоскость, так что вы должны знать все об этом! В этом уроке вы узнаете об оси x и увидите, где она расположена в координатной плоскости.

Что такое ось Y?
Чтобы построить график функции или построить упорядоченную пару, вам нужно использовать координатную плоскость, так что вы должны знать все об этом! В этом уроке вы узнаете об оси Y и увидите, где она расположена в координатной плоскости.
Как найти периметр прямоугольника на координатной плоскости?
Найти периметр прямоугольника в координатной плоскости проще, чем вы думаете! В этом руководстве показано, как использовать координатную плоскость для нахождения периметра прямоугольника.
Как нарисовать прямоугольник на координатной плоскости?
Если вы хотите нарисовать прямоугольник на координатной плоскости, просто нарисуйте вершины, а затем соедините их! Этот учебник шаг за шагом проведет вас через весь этот процесс.
Как найти площадь прямоугольника на координатной плоскости?
Если вам нужно найти площадь прямоугольника на координатной плоскости, все, что вам нужно, это длина и ширина этого прямоугольника! В этом учебном пособии показано, что нужно сделать, чтобы найти площадь прямоугольника, начерченного на координатной плоскости.

Как найти площадь неправильной фигуры на координатной плоскости?
Найти площадь составной фигуры в координатной плоскости проще, чем вы думаете! Следуйте этому руководству, чтобы увидеть процесс шаг за шагом.
Как определить точки на графике?
Нанесение точек на координатную плоскость — основа графических уравнений! Но прежде чем вы сможете построить графики уравнений, вы должны быть хорошо знакомы с координатной плоскостью. В этом уроке вы увидите, как идентифицировать упорядоченную пару точек на координатной плоскости. Кроме того, посмотрите, как определить, в каком квадранте находится точка!
Как построить график упорядоченных пар в каждом квадранте?
Нанесение точек на координатную плоскость — основа построения графиков уравнений! Ознакомьтесь с этим учебным пособием, чтобы попрактиковаться в построении точек и определении того, в каком квадранте находится каждая точка.

10 Занятия на координатной плоскости для экономии времени на планирование
«Класс, что вы знаете о построении графиков положительных и отрицательных целых чисел на координатной плоскости?» Возможно, это не лучший способ представить эту тему классу, полному шестиклассников. С этой темой ваши ученики будут изучать новый словарный запас и математические понятия, но я думаю, что они также получат массу удовольствия, используя все четыре квадранта координатной плоскости.
Отображение координатных точек в первом квадранте входит в курс математики 5-го класса, но в связи с COVID-19 есть вероятность, что у ваших учеников нет никаких предварительных знаний. Даже если ваши ученики не знают, что такое упорядоченная пара, все они могут стать мастерами в этом году!
Мне очень нравится преподавать построение графиков на координатной плоскости, особенно когда используются все четыре квадранта! В Интернете так много фантастических ресурсов, и у нас есть список из 10 отличных вариантов, которые вы можете изучить сегодня!
Занятия :
- Идентификация точки Цифровая квест-комната
- Графическое изображение точки Цифровая квест-комната
- Координатная плоскость Карточки задач
- Координатные точки Лабиринт #1 Plane2 90 Пары на графике по порядку
- График точек для поиска сокровищ #1
- Зоопарк для вас: рабочий лист координат
- Nearpod: координатная плоскость
- Нанесение точек на координатную сетку: 4 квадранта
- Запаситесь полками
Не волнуйтесь, если вы новичок в цифровых квестах, их очень легко настроить и объяснить учащимся. Эта квест-комната — отличный способ помочь повторить предыдущие знания и убедиться, что ваши ученики понимают, как определить точку. Первая задача состоит в том, чтобы дать заказанную пару для шести определенных букв. Затем учащиеся должны заполнить пропуск, используя правильное словарное слово. Наконец, учащиеся записывают значение x или y для шести точек и располагают их в порядке от наименьшего к наибольшему.
Эта квест-комната — отличный способ помочь повторить предыдущие знания и убедиться, что ваши ученики понимают, как определить точку. Первая задача состоит в том, чтобы дать заказанную пару для шести определенных букв. Затем учащиеся должны заполнить пропуск, используя правильное словарное слово. Наконец, учащиеся записывают значение x или y для шести точек и располагают их в порядке от наименьшего к наибольшему.
Учитывая, насколько сумасшедшим был прошлый учебный год, я бы порекомендовал пройтись по лексике и отметить баллы в первом квадранте. Затем вы можете использовать эту квест-комнату, чтобы бросить вызов своим ученикам, чтобы увидеть, смогут ли они узнать, как строить планы, используя все четыре квадранта. Это делает отличную партнерскую деятельность и действительно заставляет студентов говорить. Мне всегда нравится группировать своих учеников и быть доступным для любых пар, которым может понадобиться дополнительная поддержка.
Удивительно, есть ДВЕ комнаты квеста, которые вы можете использовать с этими стандартами! Цифровая квест-комната Graphing a Point — это именно то, на что это похоже: студенты рисуют точки. Студенты должны определить упорядоченную пару для символа на координатной плоскости. Затем они сопоставляют заказанную пару с буквой, отмеченной на плоскости. Чтобы найти последний фрагмент головоломки, учащиеся перемещают точки на сетку и используют прямую линию, чтобы расположить их по порядку.
Студенты должны определить упорядоченную пару для символа на координатной плоскости. Затем они сопоставляют заказанную пару с буквой, отмеченной на плоскости. Чтобы найти последний фрагмент головоломки, учащиеся перемещают точки на сетку и используют прямую линию, чтобы расположить их по порядку.
Мне нравится использовать эту квест-комнату в качестве обзора перед тестом или быстрой формирующей оценки. Вы легко увидите, понимают ли ученики, как построить заданную точку. Преимущество всех четырех квадрантов в том, что очень легко определить, где студент делает ошибку.
Вы уже пробовали цифровой математический квест? Учителя и ученики в восторге от них! Чтобы узнать, о чем идет речь, нажмите на ссылку ниже, оставьте свой адрес электронной почты, и мы вышлем вам БЕСПЛАТНУЮ цифровую математическую квест-комнату!
Этот квест построен в Google Slides и имеет 3 головоломки: одну для комбинирования одинаковых терминов, одну для распределения свойств и последнюю для решения двухшаговых уравнений. Хватай сегодня!
Хватай сегодня!
ДА! Пришлите мне БЕСПЛАТНУЮ математическую квест-комнату!
Карточки заданий всегда полезны, но этот набор мне нравится больше, чем обычно. Создание собственной активности с координатной плоскостью может занять много времени и усилий. В этих карточках с заданиями на координатную плоскость есть множество вопросов, и все ответы на них предоставлены, что всегда является победой в моей книге.
В этом наборе карточек вы найдете: словарные вопросы, определение точек, определение квадрантов и запись координатных точек. Всего 24 карточки с заданиями и лист ответов ученика. Я сразу вижу в этом отличное занятие для обзора SCOOT перед тестом. Если вы хотите что-то изменить, вы можете вытаскивать пару карточек каждый день для быстрой викторины или работы со звонком.
Это еще один пример отличного ресурса, который сэкономит вам столько времени и усилий! В нашем лабиринте координатных точек есть три отдельных лабиринта, в которых ваши ученики могут практиковаться. К каждому лабиринту прилагается ключ для ответа, который можно использовать в цифровом виде или распечатать.
К каждому лабиринту прилагается ключ для ответа, который можно использовать в цифровом виде или распечатать.
В каждом лабиринте есть вопросы о конкретных координатных плоскостях, которые указаны на бумаге. Студенты доберутся до финиша, правильно определяя координаты и упорядоченные пары. В первом лабиринте задаются вопросы о первом и третьем квадранте, что означает, что одна ось Y отрицательна. Второй лабиринт показывает второй и четвертый квадранты, что означает, что обе оси X отрицательны, а одна ось Y. Последний лабиринт показывает координатную плоскость со всеми четырьмя квадрантами вместе.
Есть множество способов использовать это задание в классе. Мне нравится использовать первые два лабиринта для студентов, которые не готовы отвечать на вопросы обо всех четырех квадрантах сразу. Я могу работать со студентами в небольших группах и помогать им разбираться в самолетах. Я бы отдал последний лабиринт ученикам, которые усвоили концепцию и готовы к испытаниям.
What’s the Point — это задание, которое было разработано для ознакомления с графическим отображением координатных точек.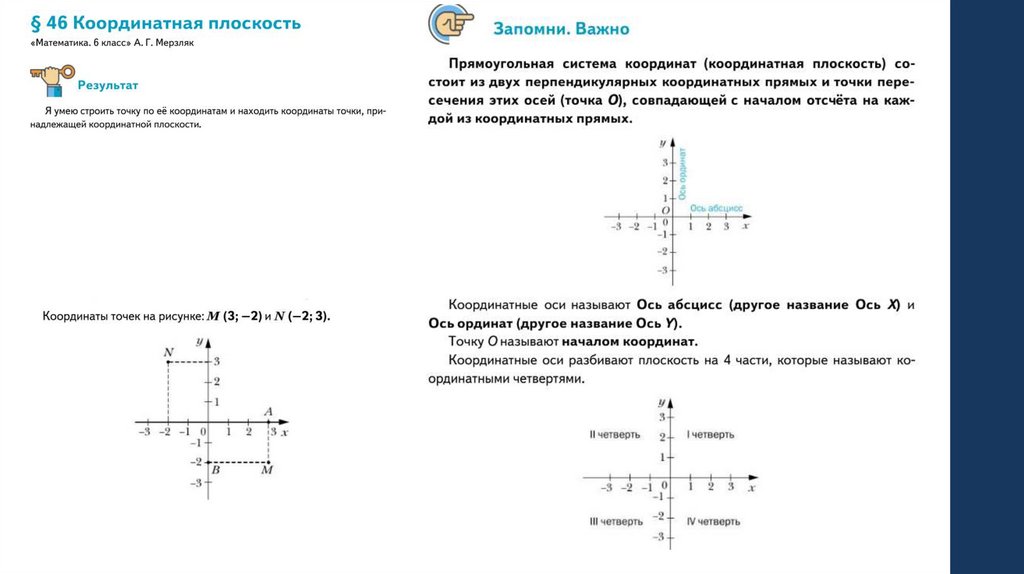 Всегда полезно иметь «я делаю, мы делаем» во время занятий по математике, и это позволяет именно это. Есть три разных координатных плоскости с крышками от бутылок с буквами. Студенты должны идентифицировать букву в правильной упорядоченной паре.
Всегда полезно иметь «я делаю, мы делаем» во время занятий по математике, и это позволяет именно это. Есть три разных координатных плоскости с крышками от бутылок с буквами. Студенты должны идентифицировать букву в правильной упорядоченной паре.
Вы можете сделать это на проекторе, а учащиеся ответят на листе бумаги или белой доске. Это также отличный способ разбудить умы учащихся в качестве звонка или может быть быстрым выходным билетом. Кроме того, они представлены в цифровой версии в Google Slides 9.0506 ТМ . Есть два отдельных занятия, которые предоставляют вам больше возможностей помочь учащимся освоить координатные точки.
Одна из основных причин, по которой я люблю преподавать координатные плоскости, заключается в том, что существует так много доступных игр с зарытыми сокровищами! Эта онлайн-игра на сайте education.com — увлекательный способ для учащихся попрактиковаться в определении точек на координатной плоскости. На острове есть несколько разных ориентиров, и они должны правильно писать точки x и y.
Эта игра будет отличным вариантом для тех, кто рано финиширует. Студенты по-прежнему будут практиковать важные навыки, которые им необходимо знать, но они будут использовать другую среду. Программа также хороша тем, что ученики продолжают попытки, если они вводят неправильную координату.
Этот рабочий лист очень похож на игру с сокровищами, которую я только что упомянул, но это отличный вариант, если вы не можете использовать технологии в своем классе каждый день. На координатной сетке есть 12 изображений, и учащиеся должны определить точки, а также квадранты, в которых они находятся.
Вы можете легко использовать это как средство досрочного завершения, домашнее задание или попросить весь класс работать над ним вместе на доске. В рабочем листе есть отличные вопросы, на которые учащиеся должны ответить, чтобы увидеть свое понимание координатной плоскости. Дополнительное задание, которое вы можете выполнить, — это предложить учащимся написать вопрос, на который должен ответить партнер или весь класс. Бросьте им вызов, чтобы поставить в тупик класс или даже учителя!
Бросьте им вызов, чтобы поставить в тупик класс или даже учителя!
Это видео Nearpod — фантастическое введение в координатную плоскость. Вы можете показать видео своему классу, как и любой клип на YouTube. Он также имеет «интерактивный режим», в котором видео автоматически останавливается и задает вопрос. Вы можете позволить учащимся войти в Nearpod для ответа или использовать другие средства для ответов учащихся.
Мне нравится идея показать это видео в первый день работы с координатными плоскостями, а затем использовать упражнение «В чем суть» для практики. В ролике задаются вопросы «Как много вы уже знаете о координатной плоскости: много, мало или совсем ничего?» и «Где вы могли бы увидеть координатную плоскость в реальной жизни?» Вы можете попросить учащихся ответить на эти вопросы еще раз в качестве выходного билета в конце урока. Или предложите им задать своим сверстникам вопрос о координатной плоскости, на который они знают ответ.
Видео мистера Джея всегда пользуются успехом в моем классе, потому что он так хорошо объясняет с помощью анимации. Этот клип длится почти шесть минут, но он отлично справляется с созданием лесов и показывает, как строить точки. Есть несколько способов использовать это видео, поэтому я дам вам несколько простых идей.
Этот клип длится почти шесть минут, но он отлично справляется с созданием лесов и показывает, как строить точки. Есть несколько способов использовать это видео, поэтому я дам вам несколько простых идей.
Предложите учащимся делать заметки во время просмотра видео. Распечатайте координатную плоскость, похожую на ту, что у г-на J на экране. Когда ваш класс будет смотреть видео, попросите их аннотировать свой график, как это делает он. Это даст вашим ученикам лист для заметок, к которому они могут вернуться, который они помогли создать.
Еще один вариант — учащиеся отвечают на вопросы во время просмотра видео, чтобы привлечь внимание всех.
- В каком направлении идет ось Y?
- Опишите происхождение.
- Как прочитать упорядоченную пару?
- Опишите, как нанести (-9,8) на координатную плоскость.
- Что нового вы узнали из этого видео?
Я бы порекомендовал распечатать их, чтобы учащиеся могли ответить или заранее записать их на доске. Нет неправильного способа использования вопросов, и вы всегда можете добавить или убрать что-то в зависимости от потребностей ваших учеников.
Нет неправильного способа использования вопросов, и вы всегда можете добавить или убрать что-то в зависимости от потребностей ваших учеников.
У мистера Нуссбаума есть огромное количество ресурсов по всем предметам, и мои ученики всегда с удовольствием посещают этот сайт. Stock the Shelves — это двухминутная игра на время, в которой учащиеся должны помочь Сэмми поставить напитки на координатную плоскость в правильном месте. У него есть две минуты, чтобы правильно разместить 20 напитков, чтобы вовремя открыть магазин.
Мне нравится использовать игры на время в классе, потому что ученики становятся очень конкурентоспособными, а это значит, что они стараются изо всех сил. Эту игру можно использовать как станцию, вариант раннего финиша или разминку в течение дня. Моим ученикам всегда нравится, когда мы делаем брекет-систему с такими видами деятельности. Они хотят увидеть, кто самый быстрый!
Планирование координатных планов
Надеюсь, вы готовы использовать некоторые увлекательные занятия для координатных планов в своем будущем! Иногда есть так много отличных вариантов, что может быть трудно выбрать, что использовать для ваших студентов. Подумайте, какие ресурсы лучше всего подходят для ВАС, и попробуйте один или два из них. Сохраните любые другие действия, которые выскочили на вас, вы никогда не знаете, когда они могут вам понадобиться!
Подумайте, какие ресурсы лучше всего подходят для ВАС, и попробуйте один или два из них. Сохраните любые другие действия, которые выскочили на вас, вы никогда не знаете, когда они могут вам понадобиться!
20 Удивительных заданий на координатной плоскости для математики в средней школе
Математика в средней школе является критическим моментом для развития основных навыков. Это время, когда студенты могут научиться любить математику или ненавидеть ее. Координатная плоскость важна для алгебры и геометрии. Используйте эти веселые и увлекательные занятия, чтобы помочь учащимся с координатными плоскостями, чтобы они полюбили свое математическое путешествие!
1. Не потопи мой боевой корабль Эта классическая игра — замечательное увлекательное занятие для учащихся, помогающих понять, как строить и определять упорядоченные пары на координатной плоскости. Вы можете использовать настоящую игру «Морской бой» или создать геймифицированные рабочие листы, такие как .
Узнайте больше: Бриттани Кисер (TPT)
2. Пробудите внутреннего художникаУченикам понравится практиковаться в построении упорядоченных пар и создании уникальных рисунков путем графического изображения, когда все линии соединяются в формы. Вы можете использовать это великое загадочное изображение координирует деятельность самолета или даже позволяет учащимся создавать свои собственные загадочные графические изображения! Графические точки никогда не было так весело!
Подробнее: Kraus Math
3. Устройте заказную охоту за паройВы можете заставить учеников взаимодействовать друг с другом, пытаясь найти разные упорядоченные пары, которые могут быть у их одноклассников. Вы можете сделать это задание «У меня есть, у кого есть» или использовать это замечательное задание «Найти кого-то, кто…»! Как это здорово для введения в графику!
Подробнее: Математика в середине
4. Откройте приложения
Откройте приложения Посмотрим правде в глаза, подростки любят игры в приложениях! Используйте то, что они любят, чтобы помочь им полюбить математику с помощью этого бесплатного приложения, полного онлайн-задач цифровой математики. Это занятие с цифровой координатной сеткой обязательно понравится в средних классах.
Узнать больше: Элементарный математический маньяк
5. Иди по-крупному или иди домойОбъедините учащихся в группы или сделайте это партнерским занятием. Пусть они нарисуют и построят одно большое или группу маленьких зданий! Каждая группа может работать над созданием различных типов зданий на сетке, пока весь класс не закончит, а затем работать над созданием города, полностью основанного на графических изображениях на координатной плоскости!
Подробнее: Digital: Разделяй и властвуй
6. Вытащите внутренний Пикассо Учащиеся могут продемонстрировать, что они узнали о наклоне, точках пересечения, линейных уравнениях и многом другом, с помощью этого задания на координатную сетку, которое включает в себя создание в классе красивого абстрактного витража.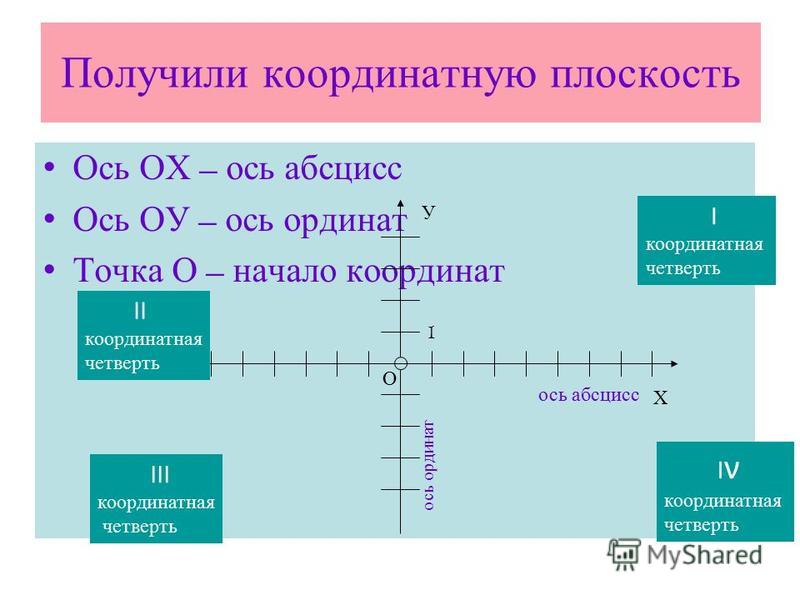
Подробнее: Hello Learning Resources
7. БИНГОИспользуйте забавную игру БИНГО, подобную этой, чтобы просмотреть квадранты на координатной плоскости. Сделайте его более продвинутым, заказав парные места, где учащиеся должны найти определенную картинку или предмет на своем плане, а не только в определенных квадрантах.
Подробнее: Out of the Mill
8. Займитесь физкультурой: пройдите линиюПостройте гигантскую координатную плоскость и попросите учащихся пройтись по сетке. Студенты получают набор упорядоченных пар, затем идут к этой точке на сетке, чтобы разместить свою точку. Каждому понравится это активное изучение графических навыков.
Узнайте больше: Apples and Bananas Education
9. Четыре в ряд Еще одно увлекательное занятие, основанное на популярных настольных играх, — соединение в ряд. Здесь вы также используете координатную плоскость для печати, пару игральных костей, две цветные ручки и партнеров. Каждый партнер бросает кости, чтобы получить свои координаты, а затем рисует их, используя свой цвет. Первый до четырех побед подряд!
Каждый партнер бросает кости, чтобы получить свои координаты, а затем рисует их, используя свой цвет. Первый до четырех побед подряд!
Узнать больше: Учитель в панике
10. Координаты городовПредложите учащимся работать с координатной сеткой на большом листе бумаги или координатной сеткой плаката. Затем учащиеся спроектируют и создадут город, названный в их честь, в котором будут здания, демонстрирующие их интересы и деятельность с помощью графических изображений. Учащиеся должны будут изобразить линии и фигуры на сетке, чтобы создать карту города. Какая забавная деятельность по расширению или обзору!
Подробнее: Математик средней школы
11. Делайте заметки интересными с помощью MatchingИнтерактивные заметки отлично сказываются на обучении учащихся, поэтому используйте симпатичные пазлы в качестве упражнения на координатной плоскости, чтобы идентифицировать и связывать понятия в студенческих тетрадях, а не просто писать заметки!
Подробнее: Kraus Math
12. Сделайте практику интерактивной
Сделайте практику интерактивной Сделайте занятия по плану координат суперинтерактивными для студентов-математиков с помощью этих удивительных координатных планок! Вы можете использовать его, чтобы задать вопросы ученикам, устроить из этого игру или гонку или просто использовать его, чтобы повеселиться с графической практикой!
Подробнее: Education Orchard
13. Играйте!Используйте веб-сайты цифровых математических игр для старшеклассников, такие как Math Nook, веб-сайт с множеством игр с координатной сеткой для всех классов! Этот веб-сайт онлайн-игр делает математику увлекательной для студентов, изучающих геометрию!
Узнать больше: Математический уголок
14. Получить Geogebra У этого замечательного веб-сайта с простыми в использовании цифровыми математическими инструментами есть и цифровое приложение! Вы можете использовать его для создания цифровых действий или использовать готовые цифровые действия, найденные на ресурсах веб-сайта. Так много всего можно сделать в этом одном цифровом месте.
Так много всего можно сделать в этом одном цифровом месте.
Узнайте больше: Geogebra
15. Создайте математический квестКвесты сейчас в моде, так почему бы не использовать их, чтобы привлечь подростков к математике! Действия и навыки координатной сетки могут быть легко перенесены в этот вид деятельности.
Узнайте больше: Индивидуальные классные комнаты и идеи для обучения
16. Создайте математическую загадку Вы можете использовать Powtoon, Canva или даже PowerPoint, чтобы настроить вводное видео, а затем дать учащимся ряд действий с координатной плоскостью, которые нужно решить, чтобы получить от вас следующую серию подсказок и разгадать тайну. Они отлично подходят для дифференциации, поскольку для каждого навыка могут быть назначены разные уровни сложности в зависимости от готовности ученика! Математические загадки — это веселые занятия с партнером, которые могут служить дополнительными занятиями или упражнениями для повторения.
Подробнее: Ресурсные создания миссис Джей
17. Используйте ДесмосЕще один замечательный математический веб-сайт с цифровыми математическими онлайн-инструментами — Desmos! Некоторые удивительные художественные творения стали результатом использования бесплатных инструментов Desmos.
Подробнее: Desmos
18. БУМ!Создайте несколько карт Boom! Ученикам среднего школьного возраста понравится это цифровое занятие! Это может быть обзор или введение в зависимости от того, как вы создаете карты. Если вы не хотите создавать свои собственные, вы можете посмотреть, что другие создали на Boom для покупки здесь.
Узнайте больше: что такое Boom Cards и как это работает для учителей?
19. Используйте пошаговые заметки Создавайте раздаточные материалы с пошаговыми заметками, чтобы помочь учащимся средних классов в интерактивном режиме соединиться с понятиями, которые они изучают! В управляемых заметках учитель заказывает и подготавливает справочную информацию и стандартные подсказки в раздаточном материале, но оставляет пробелы для учащихся и пробелы, которые учащиеся могут заполнить, нарисовать, установить связи и т. д. по мере того, как концепции рассматриваются в классе. Такой подход делает ведение заметок более увлекательным, а также не дает учащимся перегружаться в процессе ведения заметок!
д. по мере того, как концепции рассматриваются в классе. Такой подход делает ведение заметок более увлекательным, а также не дает учащимся перегружаться в процессе ведения заметок!
Узнайте больше: Разберитесь в математике
20. Играйте в настольную игру!В увлекательной настольной игре Cross Town Coordinates учащиеся могут изучать и практиковать различные математические навыки в координатной плоскости в контексте реального мира. Эту интересную и интересную игру можно купить здесь!
Узнать больше: Board Game Geek
Рабочие листы координатной плоскости, математика для 7-го класса pdf
для 7-го класса, Таблицы / by math5childrenplus Графики находятся в таблице x-y для детей 7-го класса по математике. Это математический PDF-лист с несколькими упражнениями, который можно распечатать. На второй странице прикреплен ключ ответа. Этот рабочий лист является дополнительным ресурсом для седьмого класса, который поможет учителям, родителям и детям дома и в школе.
Печать рабочего листа
Узнайте, как найти координаты In X, Y с помощью этого рабочего листа. Рабочие листы координатной плоскости могут быть подготовлены на миллиметровой или плоской бумаге, если игроки хотят правильно расставить точки. Помните, что вертикальная ось также называется осью «y», а ось «x» — горизонтальной осью. Изучение того, как находить точки на графиках, дает детям гибкость понимания положения объектов в пространстве. Графики координат — важная тема в 7 9Математика 0506-го класса , которая также присутствует в начальной алгебре, поэтому детям необходимо овладеть такими навыками. Этот рабочий лист представляет концепцию с красочной графикой, которую легко различить детям. Под осью «x» детям разрешается записывать свои пары координат в предусмотренных для этого местах. Считайте это печатным тестом по математике для преподавания в школе или дополнительным материалом для домашнего задания для родителей дома. Получите рабочие листы координатной плоскости и продолжайте совершенствовать свои навыки.
Этот рабочий лист для печати для детей 7-го класса содержит график, представляющий некоторую информацию о местоположении водных организмов. Дети находят свое место на графике, отвечают на вопросы и пишут в соответствующем поле. Это привьет детям наблюдательность и математические способности. Дети научатся находить ось x-y на данном рабочем листе.
Родственные рабочие листы
Теорема Пифагора о сторонах треугольника. 1 рабочий лист по математике для детей 7-го класса – PDF для печати
https://math5childrenplus.com/wp-content/uploads/2013/11/percents-and-ratios-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:28:382015-05-31 11:16:39Проценты и отношения по математике для детей 7-го класса – PDF для печати
Координатная геометрия по математике для детей 7-го класса – PDF для печати
https://math5childrenplus.com/wp-content/uploads/2013/11/coordinate-geometry-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:26:162015-05-31 11:08:53Тест по геометрии координат для детей 7-го класса – для печати в формате PDF классные дети. Это математика… https://math5childrenplus.com/wp-content/uploads/2013/11/coordinates-3-002.png 237 168 математика5детиплюс https://math5childrenplus.
 com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:24:592015-05-31 11:03:25Координаты 3. Лист по математике для 7-го класса – PDF для печати
com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:24:592015-05-31 11:03:25Координаты 3. Лист по математике для 7-го класса – PDF для печатиКоординаты 2 по математике для детей 7-го класса – PDF для печати
Координаты 2 для 7-го класса классные дети. Это математика…
https://math5childrenplus.com/wp-content/uploads/2013/11/coordinates-2-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:23:482015-05-31 10:59:57Координаты 2 лист по математике для детей 7-го класса – для печати в формате PDFКоординаты 1 лист по математике для детей 7-го класса – для печати в формате PDF дети. Это математика…
https://math5childrenplus.com/wp-content/uploads/2013/11/coordinates-1-002.png 237 168 математика5детиплюс https://math5childrenplus.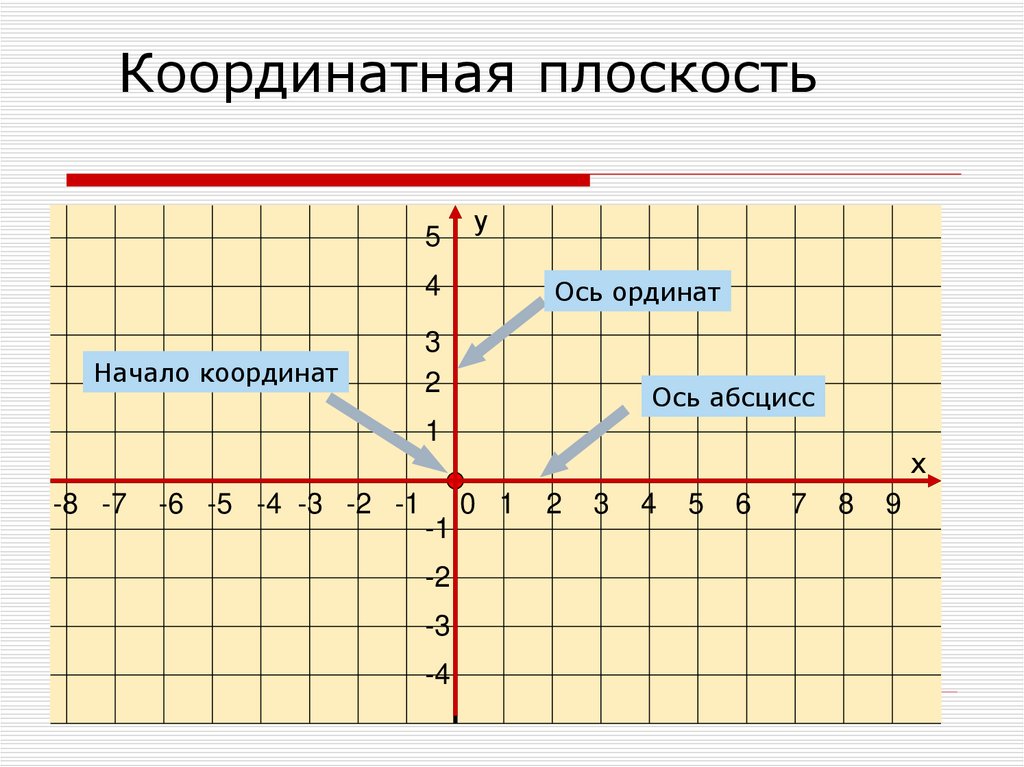 com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:22:242015-05-31 10:55:33Координаты 1 лист по математике для детей 7-го класса – PDF для печати
com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:22:242015-05-31 10:55:33Координаты 1 лист по математике для детей 7-го класса – PDF для печатиРасширения факторизации лист по математике для детей 7-го класса – PDF для печати
Расширения для факторизации 7-го класса классные дети. Это…
https://math5childrenplus.com/wp-content/uploads/2013/11/expansions-factorisations-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:16:052014-06-19 07:09:29Расширения факторизации математический лист для детей 7-го класса – PDF для печатиЛинейный математический лист для детей 7-го класса – PDF для печати
Линейный лист для 7-го класса классные дети. Это…
Это…
Рабочий лист Logs по математике для детей 7-го класса – PDF для печати
Рабочий лист Logs для детей 7-го класса . Это математический PDF для печати…
https://math5childrenplus.com/wp-content/uploads/2013/11/logs-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:14:252014-06-19 07:09:04Листок по математике для 7-х классов – для печати в формате PDFРабочие листы по математике для 7-х классов – для печати в формате PDF дети 7 класса.
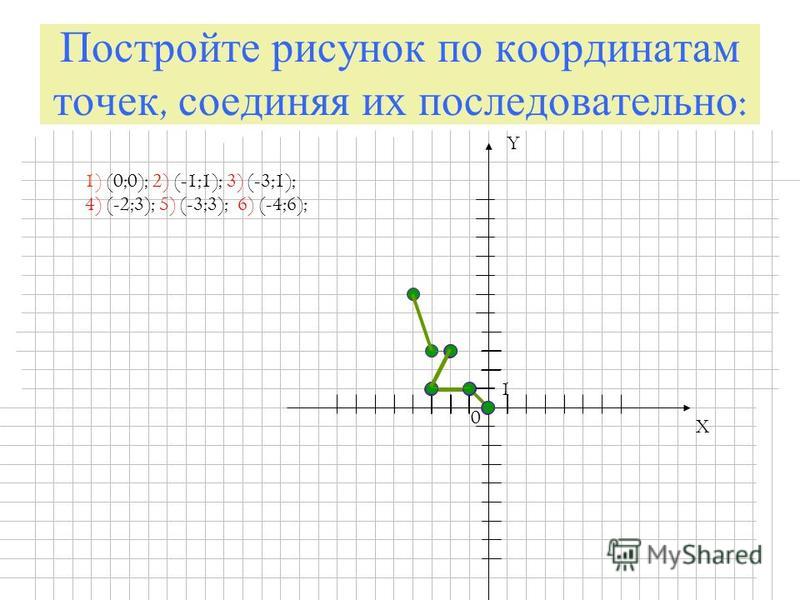 Это… https://math5childrenplus.com/wp-content/uploads/2013/11/порядок-операций-002.png
237
168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:13:382014-06-19 07:08:55Порядок выполнения математических заданий для детей 7-го класса – PDF для печати https://math5childrenplus.com/wp-content/uploads/2013/11/graphs-locate-in-x-y-0021.png
237
168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 11:51:532015-05-31 10:15:26Графики расположены на листе xy по математике для детей 7-го класса – PDF для печати
Это… https://math5childrenplus.com/wp-content/uploads/2013/11/порядок-операций-002.png
237
168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 19:13:382014-06-19 07:08:55Порядок выполнения математических заданий для детей 7-го класса – PDF для печати https://math5childrenplus.com/wp-content/uploads/2013/11/graphs-locate-in-x-y-0021.png
237
168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-28 11:51:532015-05-31 10:15:26Графики расположены на листе xy по математике для детей 7-го класса – PDF для печати© Copyright — Math 4 Children Plus
Математическая таблица с линейными уравнениями для детей 7-го класса – PDF pr… Математическая таблица с графиками для детей 7-го класса – PDF для печати
Kullabs
регистр Логин
Найдите свой запрос
Обзор
Координатная геометрия — это раздел математики, который занимается комбинацией алгебры и геометрии.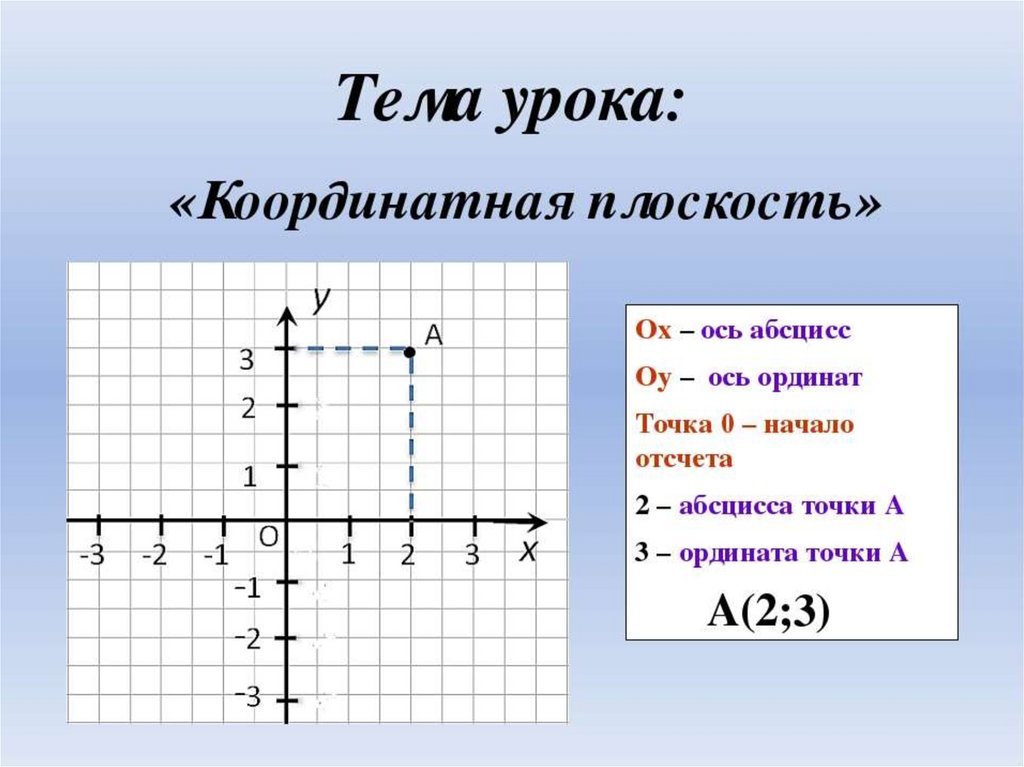 В этом примечании содержится информация о координатной геометрии и описании декартовой координатной плоскости.
В этом примечании содержится информация о координатной геометрии и описании декартовой координатной плоскости.- Примечание
- То, что нужно запомнить
- Видео
- Упражнение
- Контрольный опрос
Координатная геометрия
Введение:
Рене Декарт — известный математик, который изобрел концепцию координатной геометрии в 17 9 г.0506-й -й век. Алгебра и геометрия — это перекрывающаяся часть, которую мы теперь называем координатной геометрией. Координатная геометрия — это раздел математики, который занимается комбинацией алгебры и геометрии. Обратите внимание, что он имеет дело с точным расположением точки, линии и поверхности.
Координатная геометрия — это раздел математики, который занимается комбинацией алгебры и геометрии. Обратите внимание, что он имеет дело с точным расположением точки, линии и поверхности.
Что нужно знать; нам нужно знать, как найти точку на числовой прямой, которая будет удобной для плоскости. строка ниже — это числовая линия. Здесь мы стоим на 0, и правая часть 0 является положительной, а левая сторона 0 — отрицательной.
Описание декартовой координатной плоскости.
Здесь декартова плоскость координат также известна как прямоугольная система координат. Который состоит из двух числовых линий и образует оси.
- Горизонтальная числовая линия является осью X. Ее также называют абсциссой.
- Вертикальные числовые линии — это ось Y. Он также известен как ордината.
- Часть, пересекающаяся двумя линиями, называется Origin . В этот момент обе числовые линии равны нулю.
Оси разделены на четыре квадранта, которые отмечены на графике римскими цифрами.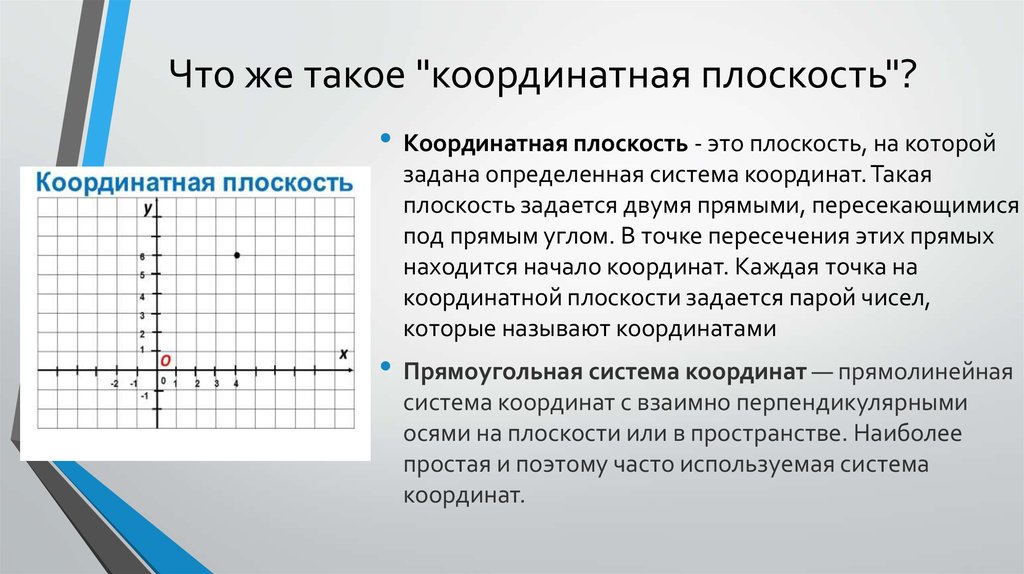
Каждая точка на графике связана с упорядоченной парой. На простом рисунке точка может быть описана ее координатами X и Y. Здесь координаты записываются в виде пары: ( X , Y ). При работе с ( x , y ) координаты x и y всегда являются первыми и вторыми соответственно. В упорядоченной паре есть два значения, поэтому мы должны быть осторожны, чтобы оно ассоциировалось только с одной точкой на графике. На графике у нас есть точка A, и чтобы узнать точку A, давайте посмотрим на начало координат. Итак, чтобы добраться до Awe, сделайте четыре (4) шага вправо и остановитесь. Снова нам нужно переместиться на два (2) шага вверх, чтобы получить точную точку A. Следовательно, координата точки A в ( 4 , 2 ). Поскольку нам потребовалось 4 шага вправо и 2 шага выше, чтобы достичь точки. Здесь ось x удлинилась в обе стороны. Таким образом, мы можем представить ее как XX ‘; где X представляет положительную сторону, а X’ представляет отрицательную сторону. Таким же образом ось Y вытянута вверх и вниз, образуя YY’, где Y представляет собой положительную сторону, а Y’ представляет отрицательную сторону.
Обобщение четырех квадрантов.
Как мы знаем из теории и примеров, что четыре квадранта с помощью двух осей квадрант I, квадрант II, квадрант III, квадрант IV, соответственно. Эвен может обобщить природу X и Y и изучить их природа, как показано ниже.
| Квадрант | X-координата | Y-координата | Природа | |
| I | положительныйположительный | 0214 ( a, b ) | ||
| II | positive | positive | (-a,b ) | |
| III | positive | positive | (-a,-b) | |
| IV | положительный | положительный | (a,- b ) |
Аналогично,
Все точки на оси x будут иметь природу ( a, 0 ), если они находятся справа от начала координат и (-a, 0), если он находится слева от начала координат. С другой стороны, все точки на оси Y будут иметь природу (0, b), если они выше начала координат, и (0, -b), если они ниже начала координат.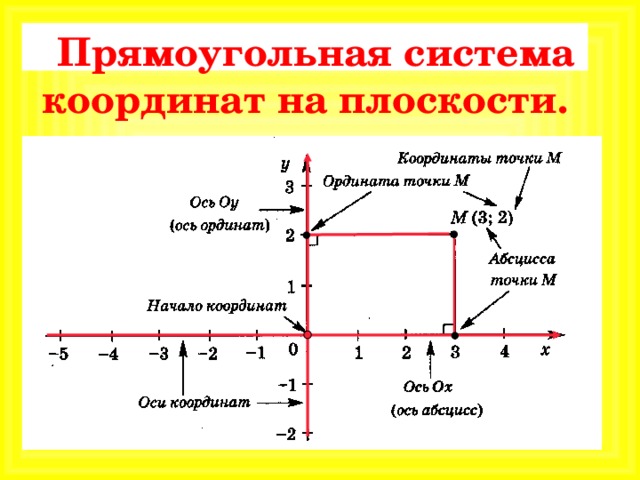
Расстояние между двумя точками:
Расстояние между двумя точками можно определить по тому, насколько мы их переместили. Если точки находятся на осях, нам становится легко, но если мы движемся произвольно, нам нужно думать. Следующий пример иллюстрирует это: ( Рисунок )
Что нужно помнить
- Прямоугольная координата состоит из двух числовых линий.
- Горизонтальная числовая линия — это ось x, а вертикальная числовая линия — ось y.
- оси x и оси y, также известные как абцисса и ордината соответственно.
- Включает в себя все отношения, установившиеся между людьми.
- В обществе может быть более одного сообщества. Сообщество меньше, чем общество.
- Это сеть социальных отношений, которую нельзя увидеть или потрогать.
- общие интересы и общие цели обществу не нужны.

Видео по координатной геометрии
Вопросы и ответы
Рене Декратес — основатель координатной геометрии.
Вертикальная линия называется осью x.
Горизонтальная линия известна как ось Y.
Точка пересечения осей X и Y называется исходной точкой.
Координатная геометрия — это раздел математики, который занимается комбинацией алгебры и геометрии.
Solution
X(-3, 2), Y(-1, 2) и Y(4,2) представляют треугольник. При измерении с помощью весов две стороны XY и YZ равны, поэтому треугольник представляет собой равнобедренный.
Решение
В соответствии с вопросом,
O(0,0), Q(4,0) и R(0,5) представляет треугольник, так как он имеет 3 стороны, и это прямоугольный треугольник как ∠ROQ составляет 90º, как измерено с протектором.
Решение:
A(1,-1), B(7,3), C(4,6) и D(-2, 2) представляет собой четырехугольник, так как он имеет четыре стороны. Так как противоположные стороны равны, он представляет собой прямоугольник.
Решение:
Поскольку точка P соответствует 2 по оси x и -3 по оси y, то упорядоченная пара координат P равна (2, -3).
Решение:
P(0,0) и Q(6, 0)
Здесь пусть P(0, 0) будет (x 1 , y 1 ) и Q(6, 0) будет ( х 2 , Y 2 )
Теперь, x- компонент = x 2 — x 1
= 6 — 0
= 6
Y- Компонент = Y 2 — Y 1
66.
= 0 — 0
= 0
Здесь, PQ = 6 единиц (по мере его прохождения — только одна ось)
Решение:
P(-5,0) и Q(2, 0)
Здесь пусть P(-5, 0) будет (x 1 , y 1 ) и Q(2, 0) BE (x 2 , Y 2 )
Теперь, x- компонент = x 2 — x 1
= 2 — ( — 5)
= 2 + 5
= 7
0006
Y- Компонент = Y 2 — Y 1
= 0 — 0
= 0
Здесь, PQ = 7 единиц (по мере его прохождения — это только одна ось)
Решение:
P(0,5) и Q(0, -2)
Здесь пусть P(0, 5) будет (x 1 , y 1 ) и Q(0, -2) быть (х 2 , Y 2 )
Теперь, x- компонент = x 2 — x 1
= 0- 0
= 0
Y- Компонент = y 2 — Y 1
= -2 -5
= -7
здесь, поскольку PQ перемещается только вдоль оси y PQ = 7 единиц (расстояние никогда не бывает отрицательным)
Решение:
P(1,2) и Q(5, 4)
Здесь пусть P(1, 2) будет (x 1 , y 1 ) и Q(5, 4) будет ( x 2 , Y 2 )
Теперь, x- компонент = x 2 — x 1
= 5 — 1
= 4
Y- Компонент = Y 2 — Y 1
= 4- 2
= 2
Теперь расстояние между PQ определяется как
(PQ) 2 = (x компонент) 2 + (Y Component) 2
= (4) 2 + (2) 2
= 16 +4
= 20
(PQ) = \ (\ SQRT {20} \)
(PQ) = \ (\ SQRT {20} \)
(PQ) = \ (\ SQRT {20} \)0006∴ PQ = \(\sqrt{20}\) единиц
Решение:
Здесь для ОА
O(0,0) быть (x 1 , y 1 )
A(2, 2) быть (x 2 , y 2 )
5
Теперь x- компонент = x 1 — x 2
= 2 — 0
= 2
Y- Компонент = Y 2 — Y 1
= 2- 0
= 2
(OA) 2 = (x-компонент) 2 + (Y-компонент) 2
= (2) 2 + (2) 2
= 4 + 4
= 8
OA = \ (\ SQRT {8} \) Единицы.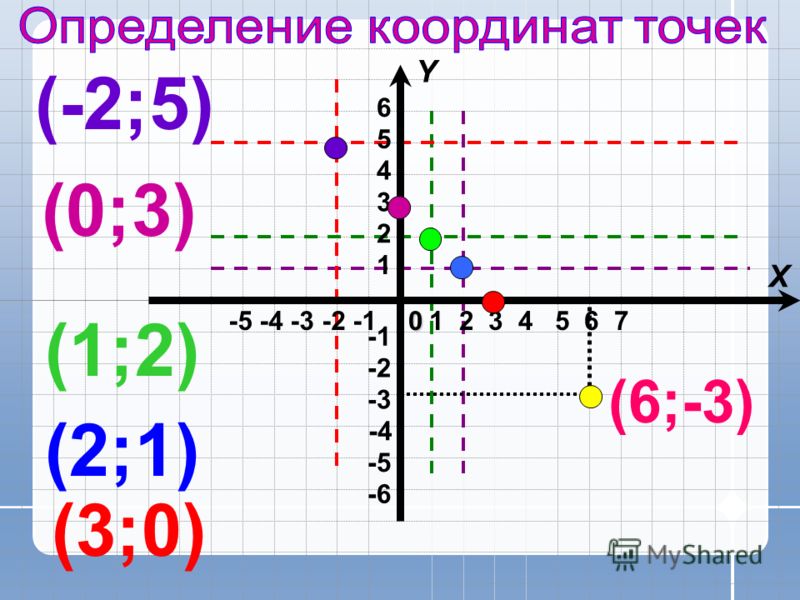

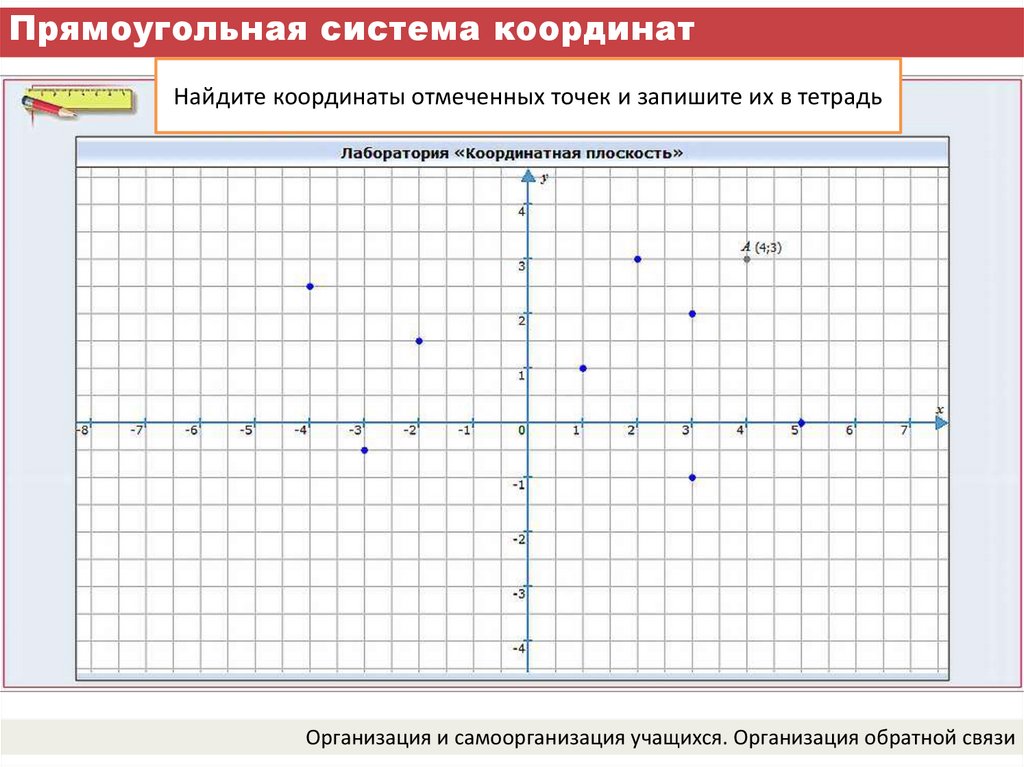 Многоклеточные. Тест 2. 7 класс Пищеварение в теле губок осуществляется… Тело многоклеточных животных снаружи покрывает… Выберите три верных утвержд…
Многоклеточные. Тест 2. 7 класс Пищеварение в теле губок осуществляется… Тело многоклеточных животных снаружи покрывает… Выберите три верных утвержд…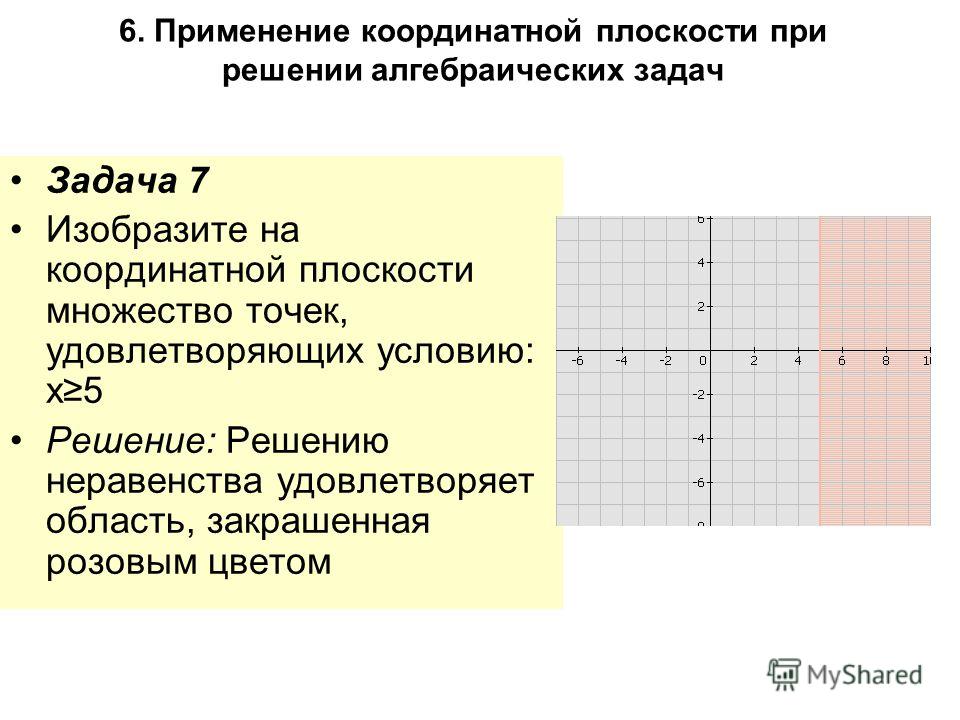 (Выберите нужный глагол.)
I will … my chanc…
(Выберите нужный глагол.)
I will … my chanc…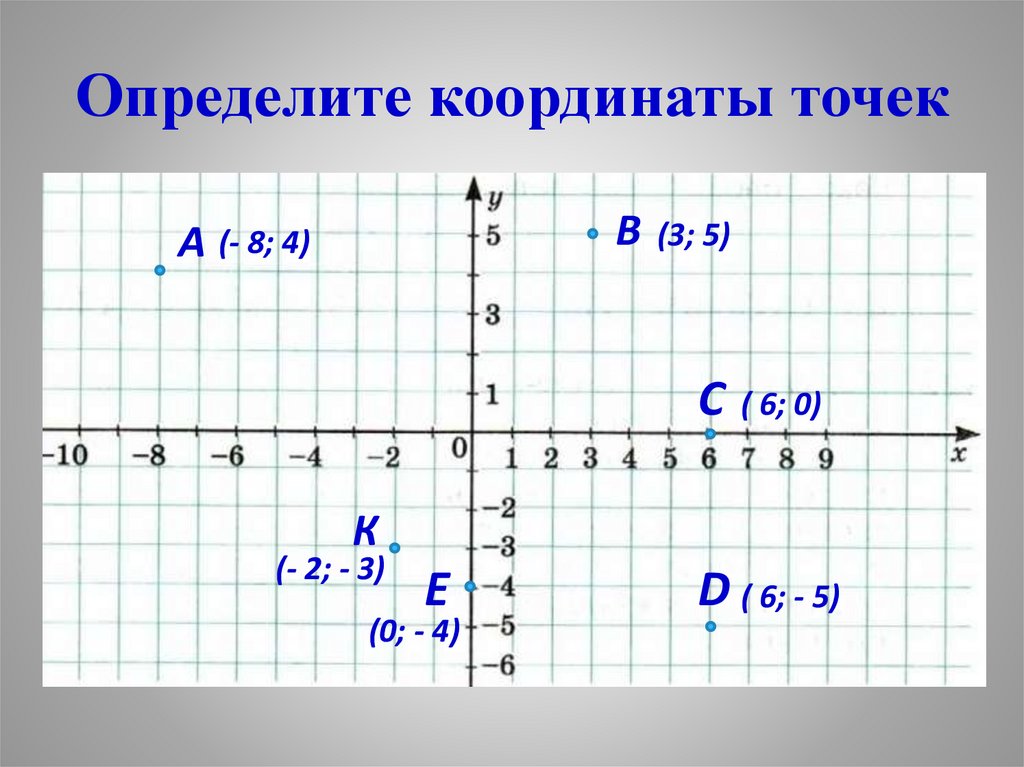
 Задача С2. Построение сечений
Задача С2. Построение сечений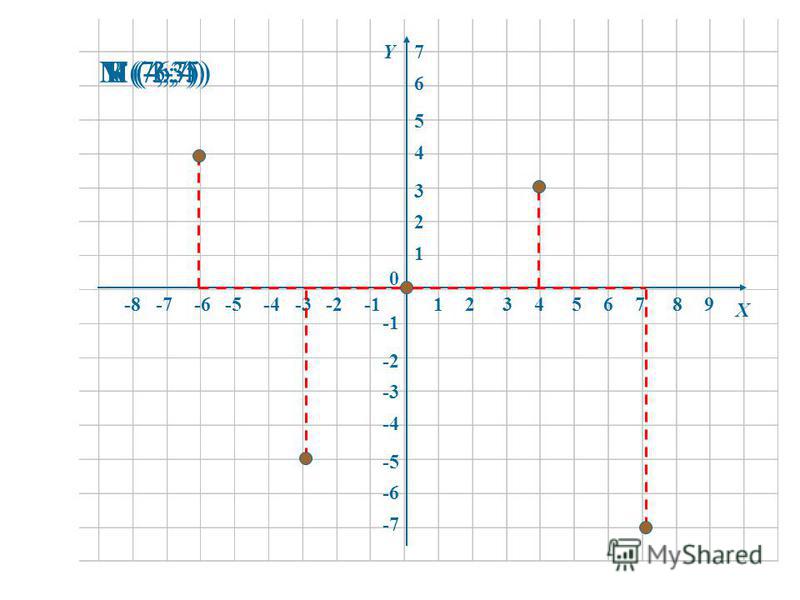 Как срисовать рисунок карандашом?
Как срисовать рисунок карандашом? Фигуры, имеющие ось симметрии. Что такое вертикальная ось симметрии
Фигуры, имеющие ось симметрии. Что такое вертикальная ось симметрии
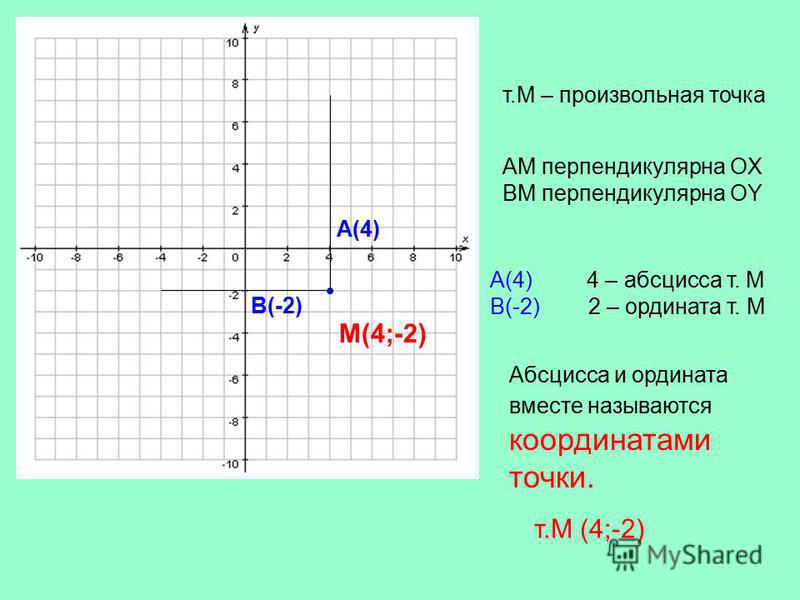



 MD.B.6
MD.B.6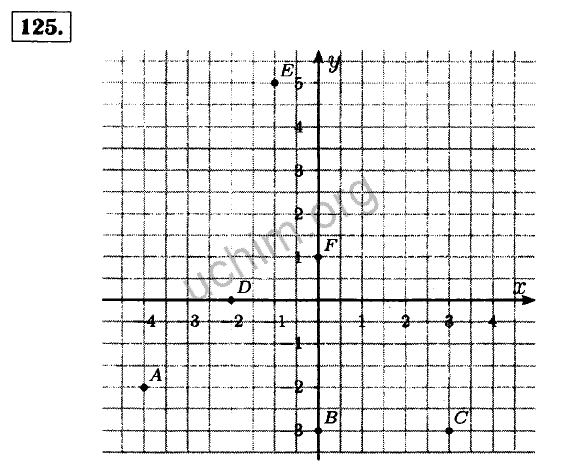 В этом уроке вы увидите, как взять упорядоченную пару и нанести ее на координатную плоскость. Взглянем!
В этом уроке вы увидите, как взять упорядоченную пару и нанести ее на координатную плоскость. Взглянем!