Алгебра парабола: Квадратичная функция — урок. Алгебра, 8 класс.

Алгебра Примеры | Conic Sections

Этап 1

Запишем в виде уравнения.

Этап 2

Перепишем уравнение в форме с выделенной вершиной.

Нажмите для увеличения количества этапов…

Этап 2.1

Составим полный квадрат для .

Нажмите для увеличения количества этапов…

Этап 2.1.1

Применим форму , чтобы найти значения , и .

Этап 2.1.2

Рассмотрим параболу в форме с выделенной вершиной.

Этап 2.1.3

Найдем значение по формуле .

Нажмите для увеличения количества этапов…

Этап 2.1.3.1

Подставим значения и в формулу .

Этап 2.1.3.2

Сократим общий множитель и .

Нажмите для увеличения количества этапов…

Этап 2.1.3.2.1

Вынесем множитель из .

Этап 2.1.3.2.2

Сократим общие множители.

Нажмите для увеличения количества этапов. ..

Этап 2.1.3.2.2.1

Вынесем множитель из .

Этап 2.1.3.2.2.2

Сократим общий множитель.

Этап 2.1.3.2.2.3

Перепишем это выражение.

Этап 2.1.3.2.2.4

Разделим на .

Этап 2.1.4

Найдем значение по формуле .

Нажмите для увеличения количества этапов…

Этап 2.1.4.1

Подставим значения , и в формулу .

Этап 2.1.4.2

Упростим правую часть.

Нажмите для увеличения количества этапов…

Этап 2.1.4.2.1

Упростим каждый член.

Нажмите для увеличения количества этапов…

Этап 2.1.4.2.1.1

Возведем в степень .

Этап 2.1.4.2.1.2

Умножим на .

Этап 2.1.4.2.1.3

Разделим на .

Этап 2.1.4.2.1.4

Умножим на .

Этап 2.1.4.2.2

Вычтем из .

Этап 2.1.5

Подставим значения , и в уравнение с заданной вершиной .

Этап 2.2

Приравняем к новой правой части.

Этап 3

Воспользуемся формой с выделенной вершиной , чтобы определить значения , и .

Этап 4

Поскольку имеет положительное значение, ветви параболы направлены вверх.

вверх

Этап 5

Найдем вершину .

Этап 6

Найдем , расстояние от вершины до фокуса.

Нажмите для увеличения количества этапов…

Этап 6.1

Найдем расстояние от вершины до фокуса параболы, используя следующую формулу.

Этап 6.2

Подставим значение в формулу.

Этап 6.3

Сократим общий множитель .

Нажмите для увеличения количества этапов…

Этап 6.3.1

Сократим общий множитель.

Этап 6.3.2

Перепишем это выражение.

Этап 7

Найдем фокус.

Нажмите для увеличения количества этапов…

Этап 7.1

Фокус параболы можно найти, добавив к координате y , если ветви параболы направлены вверх или вниз.

Этап 7. 2

Подставим известные значения , и в формулу и упростим.

Этап 8

Найдем ось симметрии, то есть линию, которая проходит через вершину и фокус.

Этап 9

Найдем направляющую.

Нажмите для увеличения количества этапов…

Этап 9.1

Директриса параболы ― это горизонтальная прямая, которую можно найти вычитанием из y-координаты вершины , если ветви параболы направлены вверх или вниз.

Этап 9.2

Подставим известные значения и в формулу и упростим.

Этап 10

Используем свойства параболы для анализа и построения ее графика.

Направление ветвей: вверх

Вершина:

Фокус:

Ось симметрии:

Директриса:

Этап 11

Введите СВОЮ задачу

parabola

Вы искали parabola? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра парабола, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «parabola».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как parabola,алгебра парабола,виды парабол,виды парабола,все о параболе,геометрия парабола,директриса параболы,директриса параболы это,как выглядит парабола,как найти фокус параболы,координаты фокуса параболы,обратная парабола,определение парабола,определение параболы,парабала,парабол,парабола,парабола в математике,парабола виды,парабола геометрия,парабола и ее свойства,парабола картинки,парабола обратная,парабола определение,парабола перевернутая,парабола примеры,парабола рисунок,парабола свойства,парабола стандартная,парабола уравнение,парабола формула,парабола формулы,парабола что это,парабола это,парабола это что,параболе,параболы,параболы определение,параболы примеры,параболы уравнения,перевернутая парабола,половина параболы,порабола,примеры парабола,примеры параболы,свойства парабола,стандартная парабола,уравнение директрисы параболы,уравнение парабола,уравнение параболы,уравнение параболы формула,уравнения параболы,фокус параболы,фокус параболы как найти,фокус параболы формула,формула для параболы,формула параболы,формулы парабола,формулы параболы,функция кривизны параболы по параметру ее длины,что есть у параболы,что такое в алгебре парабола,что такое вершина параболы,что такое директриса параболы,что такое парабола,что такое парабола в алгебре,что такое парабола в математике.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и parabola. Просто введите задачу в окошко и нажмите «решить» здесь (например, виды парабол).

Решить задачу parabola вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Графические параболы — Алгебра II

Все ресурсы по Алгебре II

10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept

Алгебра II Помощь » Функции и графики » Квадратичные функции » Параболические функции » Графики парабол

Все нижеприведенные уравнения являются уравнениями направленных вниз парабол, КРОМЕ:

Возможные ответы:

Правильный ответ:

Объяснение:

Парабола, которая открывается вниз, имеет общую формулу

,

, так как знак минус перед членом заставляет переворачивать параболу вокруг горизонтальной оси.

Напротив, парабола формы вращается вокруг вертикальной оси, а не горизонтальной оси.

Следовательно, это не уравнение для параболы, которая открывается вниз.

Сообщить об ошибке

Рассмотрим уравнение:

Вершина этой параболической функции будет находиться в точке:

 

Возможные ответы:

Правильный ответ:5

Объяснение:

Для любой параболы общее уравнение имеет вид

, а координата x ее вершины равна

.

Для данной задачи координата x равна

.

Чтобы найти координату Y, подставьте в исходное уравнение:

Следовательно, вершина находится в точке .

Сообщить об ошибке

В каком направлении открывается график параболы, описываемой приведенным выше уравнением?

Возможные ответы:

вниз

влево

вверх

вправо

Правильный ответ:

вправо

5 Объяснение:

Параболы могут быть в форме

для вертикальных парабол или в форме

для горизонтальных парабол. Поскольку уравнение, которое дает нам задача, имеет член в квадрате у, но не член в квадрате х, мы знаем, что это горизонтальная парабола. Правила для горизонтальной параболы следующие:

• Если   , то горизонтальная парабола открывается вправо.
• Если , то горизонтальная парабола открывается влево.

В этом случае коэффициент перед членом, возведенным в квадрат y, будет положительным, как только мы изолируем x. Получается горизонтальная парабола, открывающаяся вправо.

Сообщить об ошибке

Найдите вершинную форму следующего квадратного уравнения:

Возможные ответы:

Правильный ответ:

5 9 Объяснение:

Фактор 2 как GCF из первых двух членов дает нам:

Теперь мы завершаем квадрат, добавляя 4 к выражению в скобках и вычитая 8 (потому что ), что приводит к следующему уравнению:

, что равно

Следовательно, вершина расположена по адресу

Сообщить об ошибке

На основании рисунка ниже, какая линия изображает квадратичную функцию?

Возможные ответы:

Зеленая линия

Blue Line

Purple Line

Ни один из них

Red Line

Правильный ответ:

Red Line

Объяснение:

Парабола является одним из примеров квадратичной функции, независимо от того, указывает ли она вверх или вниз.

Красная линия представляет квадратичную функцию и будет иметь формулу, подобную .

Синяя линия представляет собой линейную функцию и будет иметь формулу, аналогичную .

Зеленая линия представляет экспоненциальную функцию и будет иметь формулу, аналогичную .

Фиолетовая линия представляет функцию абсолютного значения и будет иметь формулу, аналогичную .

Сообщить об ошибке

Какая из следующих парабол направлена ​​вниз?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем определить, направлена ​​ли парабола вверх или вниз, по коэффициенту члена. Он будет направлен вниз тогда и только тогда, когда этот коэффициент отрицательный. Будьте осторожны с выбором ответа . Напомним, что это означает, что все значение в скобках будет возведено в квадрат. И отрицательное умножение на отрицательное дает положительный результат.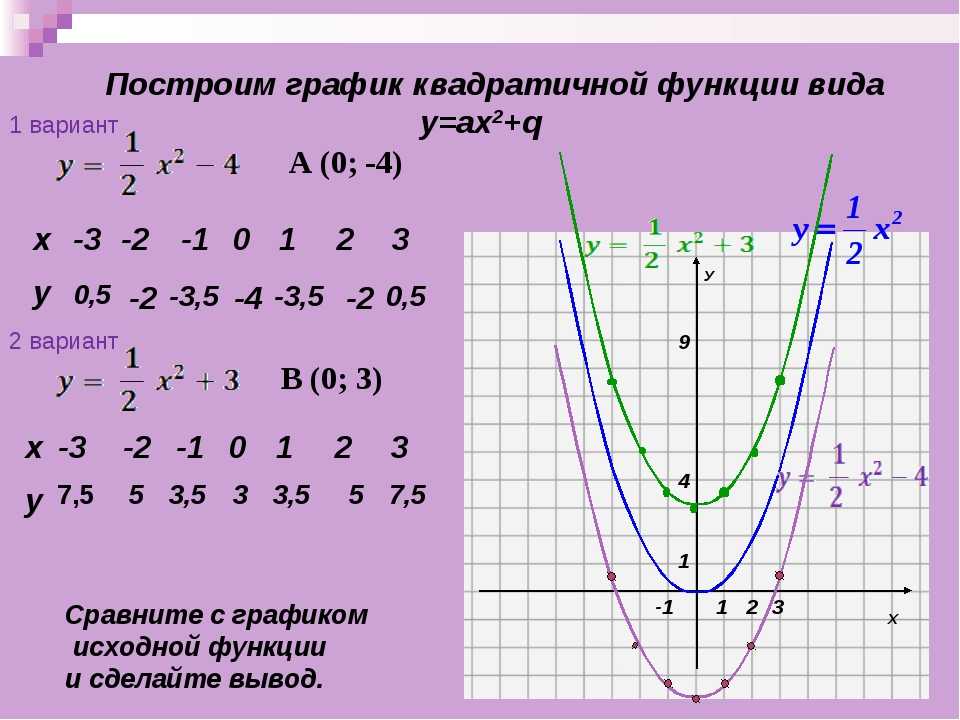 Таким образом, это эквивалентно . Поэтому наш ответ должен быть .

Сообщить об ошибке

Что является вершиной функции? Это максимум или минимум?

Возможные ответы:

; максимум

; минимум

; минимум

; максимум

Правильный ответ:

; минимум

Пояснение:

Уравнение параболы можно записать в вершинной форме: .

Точка в этом формате является вершиной. Если — положительное число, вершина является минимумом, а если — отрицательным числом, вершина — максимум.

В этом примере . Положительное значение означает, что вершина является минимальной.

Сообщить об ошибке

Сколько -перехватов имеет график функции

?

Возможные ответы:

Ни один из этих

Один

Ноль

Два

Четыре

Правильный ответ:

Объяснение:

График квадратичной функции имеет -перехват в любой точке, в которой , поэтому, сначала приравняем квадратное выражение к 0:

Количество -перехватов графика равно количеству действительных нулей приведенное выше уравнение, которое можно определить, вычислив дискриминант уравнения, .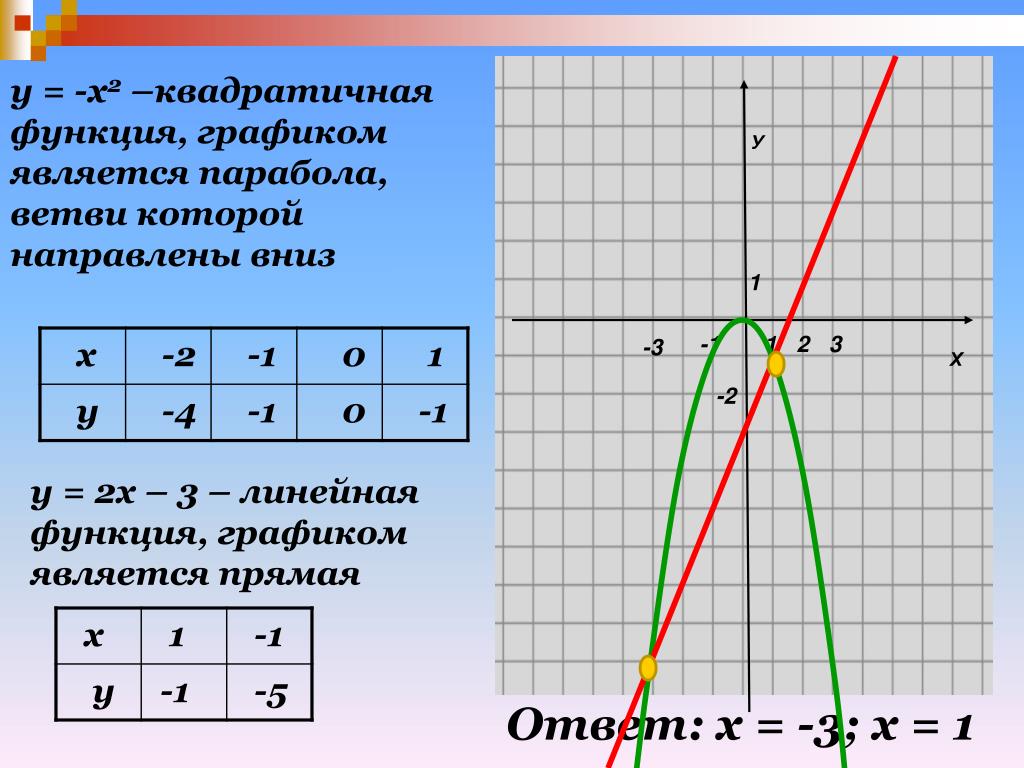 Установите и оцените:

Дискриминант отрицательный, поэтому уравнение имеет два решения, ни одно из которых не является действительным. Следовательно, график функции не имеет -перехватов.

Сообщить об ошибке

Какой из следующих графиков соответствует функции ?

Возможные ответы:

Правильный ответ:

Объяснение:

Начните с визуализации графика, связанного с функцией :

Члены в круглых скобках, связанные с квадратом переменной x, сместят параболу по горизонтали, а члены за пределами круглых скобок сдвинут параболу по вертикали. В приведенном уравнении 2 находится вне скобок и вычитается из членов, находящихся в скобках; следовательно, парабола на графике сместится вниз на 2 единицы. Упрощенный график  выглядит так:

Помните, что в скобках также есть термин. В скобках из переменной x вычитается 1; таким образом, парабола на графике сдвинется вправо на 1 единицу. В результате заданной функции соответствует следующий граф:

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы Algebra II

10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Учитесь по концепции

Фокус и Директриса Параболы: Алгебра 2

Хорошей среды, друзья математики! В сегодняшней статье мы поговорим о том, что такое фокус и директриса параболы и как их найти. Мы также рассмотрим, как найти уравнение параболы, зная фокус и директрису. Возможно, вы уже знакомы с параболами и квадратными уравнениями, но в этом посте мы углубимся в определение параболы и поймем ее на совершенно новом уровне! Не забудьте посмотреть видео и практические вопросы ниже. Спасибо, что заглянули и удачных расчетов! 🙂

Парабола? Вершина? Фокус? Директриса? Что все это значит?!

Парабола: Набор всех точек на плоскости, которые равноудалены от данной точки (фокуса) и заданной линии (директрисы). Уравнение параболы относительно фокуса и директрисы:

Вершина: Максимальная или минимальная точка на параболе. Эта координатная точка всегда попадает на саму параболу. Принимает координатную форму (a,(.5(b+k))) из приведенного выше уравнения параболы.

Фокус: Координатная точка, которая находится «внутри» параболы и имеет такое же расстояние от вершины, как и расстояние между вершиной и директрисой. Обычно обозначается как (a, b) в приведенном выше уравнении параболы.

Директриса: Горизонтальная линия, обозначенная как «y= » или «k=  », равная расстоянию от вершины по сравнению с расстоянием между вершиной и фокусом.

Приведенные выше определения объясняют, что каждая точка параболы равноудалена от вершины до фокуса, как и до директрисы. На картинке ниже мы видим, что вершина находится в 2 единицах от фокуса и в 2 единицах от директрисы. Они равноудалены:

Это явление действует не только на вершину, но и на каждую точку параболы!

Ниже мы можем видеть равноудаленность между несколькими точками на параболе, которые сравнивают расстояние между вершиной до директрисы и расстояние от вершины до фокуса. Обратите внимание, что они все одинаковые!

Готовы проверить наши новые знания со следующим Примером ?

Шаг 1: Сначала нарисуем нашу параболу с заданной информацией. Мы знаем, что вершина находится в точке (2,-1), которая лежит на самой параболе, поэтому давайте нанесем ее на карту. Мы также знаем, что направляющая k=3 и представлена ​​линией как y=-3.

Шаг 2: Далее измерим расстояние между директрисой и вершиной. Расстояние между вершиной и директрисой равно 2 единицам. Это означает, что мы также должны измерить 2 единицы на противоположной стороне вершины, чтобы найти значение фокуса. Это приводит нас к пункту (2,1).

Теперь ко второй части нашего вопроса, как найти уравнение параболы теперь, когда у нас есть значение фокуса и заданная директриса. Для этого нам нужно будет использовать причудливо выглядящее уравнение для параболы, упомянутое ранее в этом посте.

Шаг 1: Сначала нам нужно собрать всю нашу информацию, формулу уравнения параболы, заданную направляющую, k=-3 и фокус, который мы нашли в предыдущем примере (2,1), который соответствует формуле как a=2 и b=1.

Шаг 2: Теперь давайте подставим все в нашу формулу, где a=2, b=1 и k=-3, чтобы найти уравнение для нашей параболы:

Практические вопросы:

Решения:

Остались вопросы? Без проблем! Не стесняйтесь комментировать любые вопросы ниже.

No related posts.