Как решить пример с дробями 5 класс: Сложение и вычитание дробей с разными знаменателями — урок. Математика, 5 класс.

5 класс уравнения с дробями

Вы искали 5 класс уравнения с дробями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 6 класс уравнения с дробями примеры, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «5 класс уравнения с дробями».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 5 класс уравнения с дробями,6 класс уравнения с дробями примеры,7 класс как решать уравнения с дробями,дроби с х как решать,дробное уравнение,дробное уравнение как решать,дробные уравнения,дробные уравнения как решать,дробные уравнения как решить,как в уравнении избавиться от дроби,как в уравнении избавиться от знаменателя дроби,как избавиться от дроби в уравнении,как избавиться от знаменателя в уравнении,как найти корень дробного уравнения,как найти корень уравнения с дробями,как находить корень уравнения с дробями,как решать дроби с х,как решать дробное уравнение,как решать дробные уравнения,как решать уравнение дробное,как решать уравнение с дробью,как решать уравнение с дробями,как решать уравнения 7 класс по алгебре с дробями,как решать уравнения с дробью,как решать уравнения с дробями 5 класс,как решать уравнения с дробями 9 класс,как решать уравнения с дробями десятичными,как решаются дробные уравнения,как решаются уравнения с дробями,как решить дробное уравнение,как решить уравнение 7 класс по алгебре с дробями,как решить уравнение с дробями десятичными,найти корень уравнения с дробями,примеры уравнение с дробями 5 класс,решение дробного уравнения,решение дробных уравнений,решение уравнений с дробями алгебра 7 класс,решения дробных уравнений,решить дробное уравнение,решить уравнение с дробями 7 класс по алгебре,уравнение как решать с дробью,уравнение с дробью как решать,уравнение с дробями 5 класс примеры,уравнение с дробями десятичными,уравнения 5 класс с дробями,уравнения с дробью как решать,уравнения с дробями 5 класс,уравнения с дробями примеры 6 класс.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 5 класс уравнения с дробями. Просто введите задачу в окошко и нажмите «решить» здесь (например, 7 класс как решать уравнения с дробями).

Решить задачу 5 класс уравнения с дробями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Умножение и деление десятичных дробей 5 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Что такое запись числа в десятичной системе счисления? Например, запись числа 2536?

 

Это краткая запись суммы:

Десятичная дробь – это тоже краткая запись суммы:

С помощью запятой отделяется целая часть от дробной. Умножение или деление на 10, 100, 0,1, 0,01 и так далее не меняет цифры в записи, а лишь сдвигает запятую.

Напоминание:

 

Кроме того, стоит помнить, что любую десятичную дробь можно представить в виде произведения:

 

 

Умножение десятичной дроби на целое число или другую десятичную дробь

 

 

В предыдущем разделе были повторены все необходимые правила для того, чтобы умножать десятичную дробь на целое число или на другую десятичную дробь.

 

Пример: а) ; б)

а)

б)

Каждый раз запятая была убрана, но информация о ней сохранялась с помощью множителя 0,1, 0,01 и так далее. Потом было выполнено умножение целых чисел. И снова запятая возвращалась на место, учитывая множитель.

 

 

Правило умножения дробного числа на целое число

 

 

Чтобы умножить дробь на целое число, нужно умножать, не обращая внимания на запятую, затем в ответе вернуть запятую на место, то есть отделить ею столько же цифр в дробной части, сколько было в исходном числе.

 

Пример:

Выполняя умножение, не стоит обращать внимания на запятую.

Затем необходимо поставить запятую так, чтобы в дробной части получилось, как и раньше, 3 цифры.

 

 

Умножение двух десятичных дробей. Правило

 

 

Для умножения двух десятичных дробей принцип абсолютно такой же.

 

Правило

Чтобы перемножить две десятичные дроби, нужно их перемножить, не обращая внимания на запятые, затем в ответе отделить запятой столько цифр, сколько их было у обоих чисел вместе.

 

Пример 1

Сначала необходимо переписать каждую дробь в виде целого числа и вспомогательного множителя. Таким образом, каждая дробь будет представлена в виде произведения.

Затем нужно выполнить умножение целых чисел отдельно, вспомогательных множителей отдельно. Полученный результат нужно умножить на 0,001, то есть выполняется отделение запятой дробной части длиной в 3 цифры.

 

Пример 2

Нужно выполнить умножение, не обращая внимания на запятые. Количество цифр после запятой – 3, поэтому запятая ставится, отделяя 3 цифры. Последний ноль можно убрать из записи.

 

Пример 3

Выполняется умножение в столбик, при этом не обращая внимания на запятые, но помня, что в конце надо будет также отделить запятой 4 цифры.

 

 

Пример 4

В ходе урока мы уже выяснили, что умножать десятичные дроби технически означает просто умножать целые числа. Далее в ответе нужно отделить запятой знаков столько, сколько их было у всех чисел вместе.

Конечно, это правило распространяется и на случай нескольких множителей:

 

 

Деление десятичных дробей

 

 

Ситуация с делением десятичных дробей такая же: если уметь делить целые числа одно на другое, то тогда получится и десятичную дробь делить на другую десятичную дробь.

 

Пример

Когда заканчивается целое число, которое надо разделить, то ставится запятая и продолжается выполнение вычислений:

 

Пример

Здесь ситуация ровно такая же: как только кончается целая часть – ставится запятая:

То есть технически не важно, что делить на целое число – дробь или другое целое число. Алгоритм одинаковый.

 

 

Общий алгоритм деления

 

 

Пусть надо число  поделить на число . Это можно записать так:

 

 или 

Стоит помнить, что  и  можно умножить на одно и то же число, от этого результат не изменится.

В самом деле, можно делить , а можно , а можно . Можно все переписать в виде дробей. Результат все равно один – это равно 2.

 

 

Решение примеров

 

 

Пример. Одну десятичную дробь разделить на другую десятичную дробь:

 

Можно умножить обе части на одно и то же число. В данном случае это 10. Умножение на 10 означает сдвиг запятой вправо на одну позицию. Тогда второе число станет целым. А деление на целое число уже было изучено на этом уроке:

Задание: 1. ; 2.

1.     

2.     

 

Вывод

На этом уроке были изучены правила деления и умножения десятичных дробей. Кроме того, были также рассмотрены и решены различные примеры на данную тему.

 

Список литературы

1. Виленкин Н.Я.. Математика: учеб. для 5 кл. общеобр. учр. 17-е изд. – М.: Мнемозина, 2005.

2. Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011.

3. Ершова А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006.

4. Хлевнюк Н.Н., Иванова М.В.. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011.          

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Портал «Школьный помощник» (Источник)

2. Портал «Школьная математика» (Источник)

3. Портал «МетаШкола» (Источник)

4. Портал Matematika-na.ru (Источник)

 

Домашнее задание

1. Вычислите:

а) ; б)

2. Вычислите:

а) ; б)

 

Учебная программа по математике для 5 класса: примеры и шаблоны

• Домашняя страница
• Математика
• Учебная программа по математике для 5 класса

Это ресурсная страница для родителей, которые хотят научить своего ребенка математике в шестом классе. Он охватывает содержание средней учебной программы 6 класса. Прочитайте разделы и загрузите предоставленные рабочие тетради. Не забывайте, что тренировки должны быть веселыми и сложными, и ваш ребенок будет процветать!

Соскучились по математике в 4 классе? Посетите нашу страницу ресурсов по математике для 4 класса. Мы также любим писать веселые и находчивые блоги об обучении. Посмотрите наш блог о 6 бесплатных занятиях по математике в школе, чтобы перейти на следующий уровень.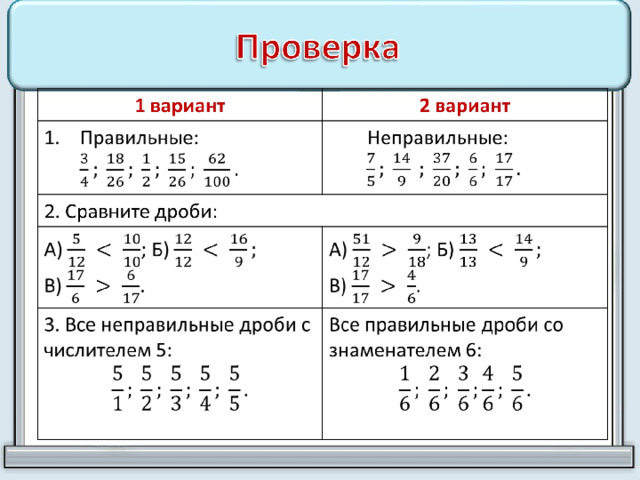

Добавьте заголовок, чтобы начать создание оглавления

Введение в математическое образование

Как и в строительстве здания, в изучении математики нет коротких путей. Вся новая математика основана на существующих математических концепциях. Сэр Исаак Ньютон, знаменитый ученый и математик, однажды написал: «Если я и видел дальше, то потому, что стоял на плечах гигантов». Это означает, что мы открываем истину, опираясь на предыдущие открытия. Поэтому важно, чтобы мы изучили основу как можно лучше. Это откроет математику, которую нам еще предстоит изучить. Без прочного фундамента нам будет трудно следовать за классом в последующие годы. Подобно строительству дома, мы должны стремиться к максимально полному фундаменту. Трещины должны быть устранены, прежде чем строительство может быть продолжено.

Эти 2 пирамиды представляют собой образовательное обучение, в основе которого лежит математика в начальной школе. Pinnacle является pHD.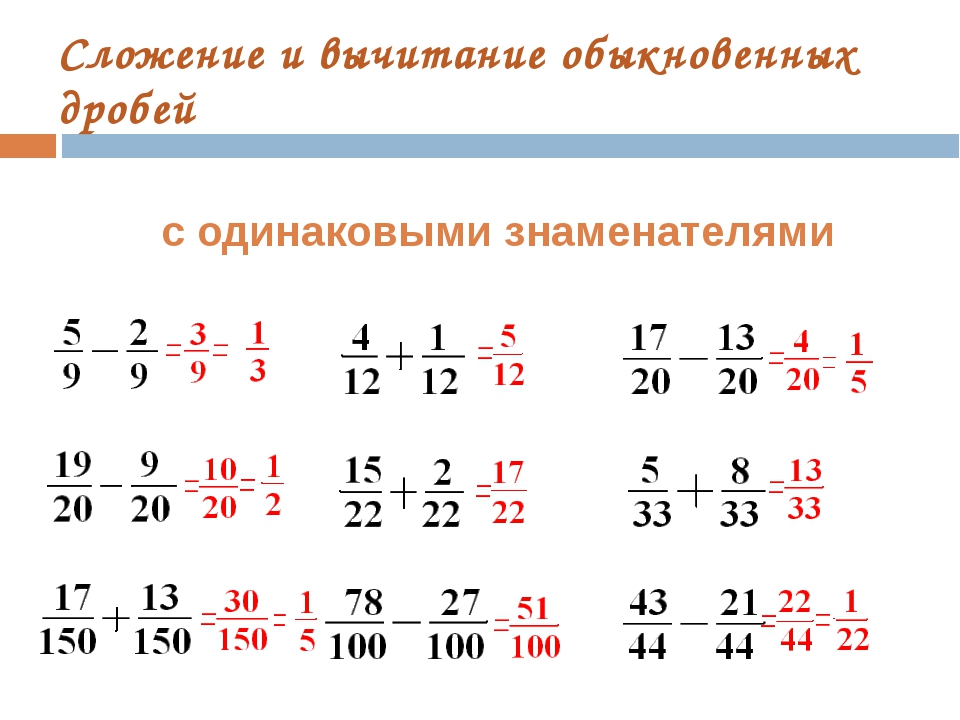

Пробел в знаниях в основе прорывается к вершине.

Учебный план по математике для 5 класса

Для родителей очень важно знать, что их ребенок изучает в школе. Ваша школа получает указания от руководящего органа. Школьный совет издает учебную программу (или математический стандарт), которой должны следовать школы. Учебная программа варьируется по всему миру. Например. в России таблица умножения начинается с 1 класса, а в Онтарио — с 3 класса. Это означает, что учебная программа вашей школы отличается от той, которую вы можете найти в Интернете. В этой статье мы рассмотрим оценку того, что вы можете ожидать от учебной программы вашей школы.

• Десятичный разряд: 5 класс
• Добавить десятичные знаки: 5-й класс
• Вычитание десятичных дробей: 5 класс
• Сложение и вычитание дробей: 5 класс
• Многозначное умножение и деление: 5 класс
• Умножить дроби: 5 класс
• Разделить дроби: 5 класс
• Умножение десятичных дробей: 5 класс
• Разделить десятичные дроби: 5 класс
• Степени десяти: 5-й класс
• Том: 5 класс
• Координатная плоскость: 5 класс
• Алгебраическое мышление: 5 класс
• Преобразование единиц измерения: 5 класс
• Линейные участки: 5 класс
• Свойства форм: 5 класс

Найдите репетитора по математике онлайн уже сегодня!

Бесплатный поиск репетиторов!

Примеры учебных программ по математике для 5 класса

Десятичный разряд

Мы используем «арабские цифры». Числа работают так, что каждая цифра имеет позицию. Есть 1 позиция. Есть 10-е место. Есть позиция 100. Это полезно, потому что позволяет числу представлять что-то очень большое. Подумайте о числе 973. 9 представляет 9 сотен, 7 представляет 7 десятков, а 3 представляет 3 единицы. Сложите все это вместе, и вы получите (9 х 100) + (7 х 10) + (3 х 1) = 973. Вот как вы представляете большие вещи. На самом деле вы можете продолжать подниматься вверх вечно! Точно так же число позволяет представлять что-то очень маленькое. Посмотрим, как.

 

Когда вы пишете число, вы можете думать о том, что каждая цифра умножается на коэффициент разрядности для каждой позиции. Что, если этот коэффициент ценности места был равен 0,1? Так можно записать 1 десятую часть числа. Например, 1,1 = (1 х 1) + (1 х 0,1). 2,2 = (2 х 1) + (2 х 0,1). Видите, как это работает так же, как когда число большое? Подумайте о числе 0,973. 9 представляет 9 десятых, 7 представляет 7 сотых, 3 представляет 3 тысячи. Сложите все это вместе, и вы получите (9 x 0,1) + (7 x 0,01) + (3 x 0,001). Вот как вы можете представлять маленькие вещи. На самом деле вы можете продолжать снижаться в значении места навсегда!

Обыкновенные дроби в десятичной форме

В математике есть много форм одних и тех же вещей. В большинстве случаев вы можете переписать дробь в десятичной форме. Выполнение вычисления одним способом может быть настолько сложным, что было бы проще преобразовать это число во что-то другое, чтобы упростить вычисление.

Дроби можно преобразовать в десятичную форму, если вы найдете правильный коэффициент для их умножения. Например, дробь 1/5 можно преобразовать в 0,2, умножив числитель и знаменатель на 2. Тогда, когда дробь будет записана как 2/10, вы можете понять, что это то же самое, что иметь 2 на десятых местах в десятичная форма. Таким образом, вы можете написать 2/10 = 0,2.

Другой пример — переписать дробь 1/4 как 0,25. Сначала попробуйте придумать число, которое при умножении превратит 4 в 100. Число 25 сделает это. Умножьте числитель и знаменатель на 25, чтобы получить 25/100.

Теперь поймите, что это то же самое, что иметь 2 в десятых и 5 в сотых, поэтому 25/100 = 0,25

 

Сложение десятичных знаков

Сложение десятичных знаков почти такое же, как сложение целых чисел. Ключ состоит в том, чтобы добавить одно и то же значение, удерживая цифры вместе. При сложении чисел 8 и 2 оба числа имеют одинаковую разрядность 1. Таким образом, можно сказать, что 8 + 2 = 10. При сложении чисел 0,8 и 0,2 оба числа имеют одинаковую разрядность 0,1. Таким образом, вы можете сказать 0,8 + 0,2 = 1,0. Перенос всегда происходит, когда вы достигаете 10 от этой стоимости места. Вот как это работает для сложения однозначных чисел.

Для добавления нескольких цифр повторите тот же процесс, что и для добавления одной цифры. Начните с наименьшего разряда и продвигайтесь вверх. Например, добавляя 8,8 и 2,2, начните с добавления 0,8 и 0,2, что равно 1,0. Теперь перенесите 1 на следующее разрядное значение. Таким образом, у вас будет 8 и 3. 8 + 3 = 11. Итак, вы знаете, что 8,8 + 2,2 = 13. Практика делает совершенным!

Сложение по вертикали

Одним из способов добавления номера является использование вертикального метода. Вы ставите два числа друг на друга. Затем, начиная с самых маленьких цифр, складывайте их. Переносите 1 каждый раз, когда две цифры больше 10. Это отлично работает для десятичных чисел или целых чисел. Этот метод требует много шагов, но добавляет только два 0-9цифры. Тем не менее, требуется много часов практики, чтобы научиться делать это быстро. Лучший способ учиться — это делать.

Вертикальный метод вычитания с десятичными дробями

Вертикальный метод, показанный ранее, можно использовать для вычитания двух чисел. Разница лишь в том, что перенос происходит в обратном порядке. Когда цифра, из которой вы вычитаете, меньше, перенесите 1 из следующего по величине разряда и «разбейте» ее на 10. Это сделает число, из которого вы вычитаете, достаточно большим. Разница будет положительной. Десятичные числа работают так же, как и числа, мы просто помним, что они намного меньше разрядного значения.

Многозначное умножение

Самое удивительное в умножении то, что порядок, в котором вы это делаете, не имеет значения. Точно так же, как результат чистки зубов, а затем чистки зубной нитью такой же, как и результат чистки зубной нитью, а затем чистки: вы получаете чистые зубы! То же самое и с цифрами. Таким образом, 2 x 3 равно 3 x 2. Это означает, что вы можете упростить расчеты, изменив порядок! Когда нам нужно умножить много цифр, таких как 234 x 321, это сложно. Как всегда есть подвох. Признайте, что 234 = 2 x 100 + 3 x 10 + 4 и что 321 = 3 x 100 + 2 x 20 + 1. Таким образом, 234 x 321 равно ((2 x 100) + (3 x 10) + 4) x (3). х 100 + 2 х 10 + 1). Переставляя, мы имеем 2 х 3 х 100 + 3 х 2 х 10 + 4 + 1. Мы знаем, что 2 х 3 = 6 и, следовательно, 3 х 2. Тогда мы имеем 6 х 100 + 6 х 10 + 14, что равно 600 + 60. + 14. Упростите, и ваш ответ будет 674. 

Мы также можем сделать вертикальный метод!

Многозначный раздел

При делении двух больших чисел мы можем использовать вертикальный метод, но вместо того, чтобы начинать с наименьшего разрядного значения, мы начинаем с наибольшего разрядного значения. Мы разбиваем задачу на более простые задачи, спрашивая, сколько раз делитель может содержаться в цифре. Затем мы вычитаем общее количество, чтобы получить остаток. Мы делим этот остаток на следующую наименьшую цифру-заполнитель. Мы повторяем этот процесс до тех пор, пока у нас не останется цифр для деления.

Умножение дробей

При умножении двух или более дробей просто перемножайте числители (верхние числа) и знаменатели (нижние числа). Вы также должны поставить дробь в самых низких условиях общего пользования. Например, если числитель и знаменатель являются четными числами, разделите их оба на 2, чтобы разделить их пополам. Продолжайте, пока дробь не примет простейшую форму.

Деление дробей

Вы должны понять, что дроби и деление — это одно и то же. Это означает, что деление дроби равносильно умножению на дробь. Предположим, мы хотим разделить 5/3 на 3. Затем мы умножим 5/3 x 1/3. Используя технику умножения дробей, мы имеем 5/3 х 1/3 = 5/9. Это означает, что 5/3 делится на три равные части 5/9. В этом видео показано, как делить дроби и чем это похоже на умножение обратной.

Рабочие листы с задачами по математике для пятого класса

Вы ищете что-нибудь, что можно передать своему второкласснику, чтобы он начал учиться? Ознакомьтесь с нашими бесплатными загружаемыми таблицами по математике для 5-го класса или попробуйте наш генератор математических задач, чтобы учиться онлайн. Вы можете сделать копию, скачать и распечатать эти задачи. Сделайте это увлекательной игрой и начните изучать математику для 6 класса уже сегодня! Если у вас нет принтера, откройте его с помощью iPad и играйте онлайн.

Ссылки на избранные сайты

• Академия Хана
• Учебная программа по математике Онтарио

Откройте для себя торговую площадку TutorOcean с потрясающими и доступными онлайн-репетиторами по математике

Найдите онлайн-репетитора по математике

Урок 5 | Умножение и деление дробей | Математика 5-го класса

Цель

---

Умножить дробь на целое число, где произведение представляет собой целое число или дробь.

Общие базовые стандарты

---

Основные стандарты

Основные стандарты, рассмотренные в этом уроке

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• 5.NF.B.4.A — интерпретировать произведение (a/b) × q как части разбиения q на b равных частей; эквивалентно, в результате последовательности операций a × q ÷ b. Например, используйте модель визуальной дроби, чтобы показать (2/3) × 4 = 8/3, и создайте контекст истории для этого уравнения. Сделайте то же самое с (2/3) × (4/5) = 8/15. (В общем, (a/b) × (c/d) = ac/bd.)

• 5.NF.B.6 — Решайте реальные задачи, связанные с умножением дробей и смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи.

Основополагающие стандарты

Основные стандарты, рассмотренные в этом уроке

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• 4. NF.B.4

Критерии успеха

Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

---

1. Решить контекстуальные задачи на нахождение некоторой дробной части величины, ответом на которую является целое число или дробь (MP.4).
2. Свяжите понятие поиска дробной группы набора с поиском любого количества групп набора и соедините это с умножением (MP.2).
3. Интерпретируйте $$\frac{a}{b} \times q$$ как части $$a$$, разделив $$q$$ на $$b$$ равные части.
4. Найти значение выражений в виде $$\frac{a}{b} \times q$$.
5. Поймите, что нахождение единичной дроби целого числа равносильно делению целого числа на знаменатель единичной дроби, и используйте это для нахождения любой дроби целого числа.
    

Fishtank Plus

Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.

Якорные задачи

Задания, предназначенные для обучения критериям успеха урока, и рекомендации, помогающие ученикам понять

А628D5C3-5B97-4E03-B1EC-5AD5C66D8950

---

Проблема 1

1. У Рози 15 ярдов ткани. Она использует $${{2\over3 }}$$ на платье. Сколько ткани в ярдах уходит на платье?
2. Рози также купила 11 футов ленты. Она использует $${{1\over2}}$$ из них, чтобы сделать бант для своего платья. Сколько ленты в футах она использует для изготовления банта?

Наводящие вопросы

Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.

Каталожные номера

EngageNY Mathematics Grade 5 Mathematics > Модуль 4 > Тема C > Урок 7 — Развитие концепции

Математика для 5 класса > Модуль 4 > Тема C > Урок 7 общеобразовательной учебной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3.0. По состоянию на 2 декабря 2016 г., 17:15.

Изменено Fishtank Learning, Inc.

Проблема 2

1. Как бы вы написали «5 групп по 12» в виде математического выражения? Как это говорит о том, как написать «$${{1\over4}}$$ group of 12» в виде математического выражения?
2. Используйте свое наблюдение из части (а), чтобы решить следующее:
   1. $${1\over5} \умножить на 20$$
   2. $${{3\over8}\times 16}$$
   3. $${1\over6} \times19$$
   4. $${{3\over4} \times 26}$$

Наводящие вопросы

Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной проблемы.

Проблема 3

а. Фредерик говорит, что $$\frac16 \times 18 = 18 \div 6$$. Ты согласен или несогласен? Обоснуйте свое мышление.

б. Как бы вы изменили уравнение Фредерика, чтобы представить $$\frac56 \times 18$$?

Наводящие вопросы

Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.

Набор задач и домашнее задание

---

• Набор проблем

• Домашнее задание

Ключи ответов

Ключи ответов для наборов задач и домашних заданий доступны при наличии подписки Fishtank Plus.

Обсуждение набора задач

• Посмотрите на #1(a) и 1(b). Что вы заметили в своих решениях?
• Посмотрите на № 1 (c) и 1 (d). Что вы заметили в своих решениях?
• Посмотрите на № 1 (д) и 1 (е). Мы знаем, что 4 пятых и 1 седьмая не равны, так как же мы получили одинаковый ответ?
• Посмотрите на № 3 (b). Как вы решили? Сколько градусов прямой угол? (Это связано с содержанием 4 класса 4.MD.5—7.) 
• Посмотрите на № 3 (с). Что сделало эту проблему немного сложной? Как вы решили? Было ли более одного правильного способа решения? (Студенты могли найти долю учащихся, которые составляют мальчики, а затем умножить на 48, или они могли найти четверть от 48, а затем вычесть это произведение из 48.)
• Посмотрите на #3(d). Что сделало эту задачу еще более сложной, чем № 3 (с)? Как вы решили? Было ли более одного правильного способа решения?
• Посмотрите на #4. Почему мысли Алисии имеют смысл?

Целевая задача

Задание, которое представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

---

Проблема 1

Решить. Покажите или объясните свою работу.

а. $${{3\over4} \times 32}$$

б. $${{2\over5} \times 8}$$

Ответ учащегося

Создайте бесплатную учетную запись или войдите, чтобы просмотреть ответ учащегося

Проблема 2

В понедельник миссис Джонсон отправилась на прогулку длиной в $4$$ мили.

No related posts.