Записать число z в алгебраической. Модуль и аргумент комплексного числа. Тригонометрическая. Алгебраическая форма комплексного числа
Записать число z в алгебраической. Модуль и аргумент комплексного числа. Тригонометрическая. Алгебраическая форма комплексного числа
Комплексные числа — это минимальное расширение множества привычных нам действительных чисел. Их принципиальное отличие в том, что появляется элемент, который в квадрате дает -1, т.е. i, или .
Любое комплексное число состоит из двух частей: вещественной и мнимой :
Таким образом видно, что множество действительных чисел совпадает с множеством комплексных чисел с нулевой мнимой частью.
Самая популярная модель множества комплексных чисел — это обычная плоскость. Первая координата каждой точки будет её вещественной частью, а вторая -мнимой. Тогда в роли самих комплексных чисел бдут выступать вектора с началом в точке (0,0).
Операции над комплексными числами.
На самом деле, если брать в расчет модель множества комплексных чисел, интуитивно понятно, что сложение (вычитание) и умножение двух комплексных числе производятся так же как соответственные операции над векторами.
Причем имеется в виду векторное произведение векторов, потому что результатом этой операции является опять же вектор.
1.1 Сложение.
(Как видно, данная операции в точности соответствует )
1.2 Вычитание , аналогично, производится по следующему правилу:
2. Умножение.
3. Деление.
Определяется просто как обратная операция к умножению.
Тригонометрическая форма.
Модулем комплексного числа z называется следующая величина:
,
очевидно, что это, опять же, просто модуль (длина) вектора {a,b}.
Чаще всего модуль комплексного числа обозначается как ρ.
Оказывается, что
z = ρ(cosφ+isinφ) .Непосредственно из тригонометрической формы записи комплексного числа вытекают следующие формулы :
Последнюю формулу называют Формулой Муавра . Непосредственно из нее выводится формула корня n-ной степени из комплексного числа
:таким образом, существует n корней n-ной степени из комплексного числа z.
План урока.
1. Организационный момент.
2. Изложение материала.
3. Домашнее задание.
4. Подведение итогов урока.
Ход урока
I. Организационный момент .
II. Изложение материала .
Мотивация.
Расширение множества вещественных чисел состоит в том, что к действительным числам присоединяются новые числа (мнимые). Введение этих чисел связано с невозможностью во множестве действительных чисел извлечения корня из отрицательного числа.
Введение понятия комплексного числа.
Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi , где i – мнимая единица, причем i 2 = — 1 .
Исходя из этого, получим следующее определение комплексного числа.
Определение . Комплексным числом называется выражение вида a + bi , где a и b — действительные числа. При этом выполняются условия:
а) Два комплексных числа a 1 + b 1 i и a 2 + b 2 i равны тогда и только тогда, когда a 1 =a 2 , b 1 =b 2 .
б) Сложение комплексных чисел определяется правилом:
(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i .
в) Умножение комплексных чисел определяется правилом:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 — b 1 b 2) + (a 1 b 2 — a 2 b 1) i .
Алгебраическая форма комплексного числа.
Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.
Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0
Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a : a + 0i = a .
Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi : 0 + bi = bi .
Два комплексных числа z = a + bi и = a – bi , отличающиеся лишь знаком мнимой части, называются сопряженными.
Действия над комплексными числами в алгебраической форме.
Над комплексными числами в алгебраической форме можно выполнять следующие действия.
1) Сложение.
Определение . Суммой комплексных чисел z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i называется комплексное число z , действительная часть которого равна сумме действительных частей
Числа z 1 и z 2 называются слагаемыми.
Сложение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z 1 + z 2 = z 2 + z 1 .
2º. Ассоциативность: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Комплексное число –a –bi называется противоположным комплексному числу z = a + bi . Комплексное число, противоположное комплексному числу z , обозначается -z . Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0
Пример 1.
Выполните сложение (3 – i) + (-1 + 2i) .
(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i .
2) Вычитание.
Определение. Вычесть из комплексного числа z 1 комплексное число z 2 z, что z + z 2 = z 1 .
Теорема . Разность комплексных чисел существует и притом единственна.
Пример 2. Выполните вычитание (4 – 2i) — (-3 + 2i) .
(4 – 2i) — (-3 + 2i) = (4 — (-3)) + (-2 — 2) i = 7 – 4i .
3) Умножение.
Определение . Произведением комплексных чисел z 1 =a 1 +b 1 i и z 2 =a 2 +b 2 i называется комплексное число z , определяемое равенством: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i .
Числа z 1 и z 2 называются сомножителями.
Умножение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z 1 z 2 = z 2 z 1 .
2º. Ассоциативность: (z 1 z 2)z 3 = z 1 (z 2 z 3)
3º.
(z 1 + z 2) z 3 = z 1 z 3 + z 2 z 3 .
4º. z · = (a + bi)(a – bi) = a 2 + b 2 — действительное число.
На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.
В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.
Пример 3. Выполните умножение (2 + 3i) (5 – 7i) .
1 способ. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i .
2 способ. (2 + 3i) (5 – 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 – 14i + 15i + 21 = 31 + i .
4) Деление.
Определение . Разделить комплексное число z 1 на комплексное число z 2 , значит найти такое комплексное число z , что z · z 2 = z 1 .
Теорема. Частное комплексных чисел существует и единственно, если z 2 ≠ 0 + 0i .
На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.
Пусть z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i , тогда
.
В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.
Пример 4. Найти частное .
5) Возведение в целую положительную степень.
а) Степени мнимой единицы.
Пользуясь равенством i 2 = -1 , легко определить любую целую положительную степень мнимой единицы. Имеем:
i 3 = i 2 i = -i,
i 4 = i 2 i 2 = 1,
i 5 = i 4 i = i,
i 6 = i 4 i 2 = -1,
i 7 = i 5 i 2 = -i,
i 8 = i 6 i 2 = 1 и т. д.
Это показывает, что значения степени i n , где n – целое положительное число, периодически повторяется при увеличении показателя на
Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.
Пример 5. Вычислите: (i 36 + i 17) · i 23 .
i 36 = (i 4) 9 = 1 9 = 1,
i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 · i = i.
i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 · i 3 = — i.
(i 36 + i 17) · i 23 = (1 + i) (- i) = — i + 1= 1 – i.
б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.
Пример 6. Вычислите: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
Комплексные числа
Мнимые и комплексные числа. Абсцисса и ордината
комплексного числа. Сопряжённые комплексные числа.
Операции с комплексными числами. Геометрическое
представление комплексных чисел. Комплексная плоскость.
форма комплексного числа.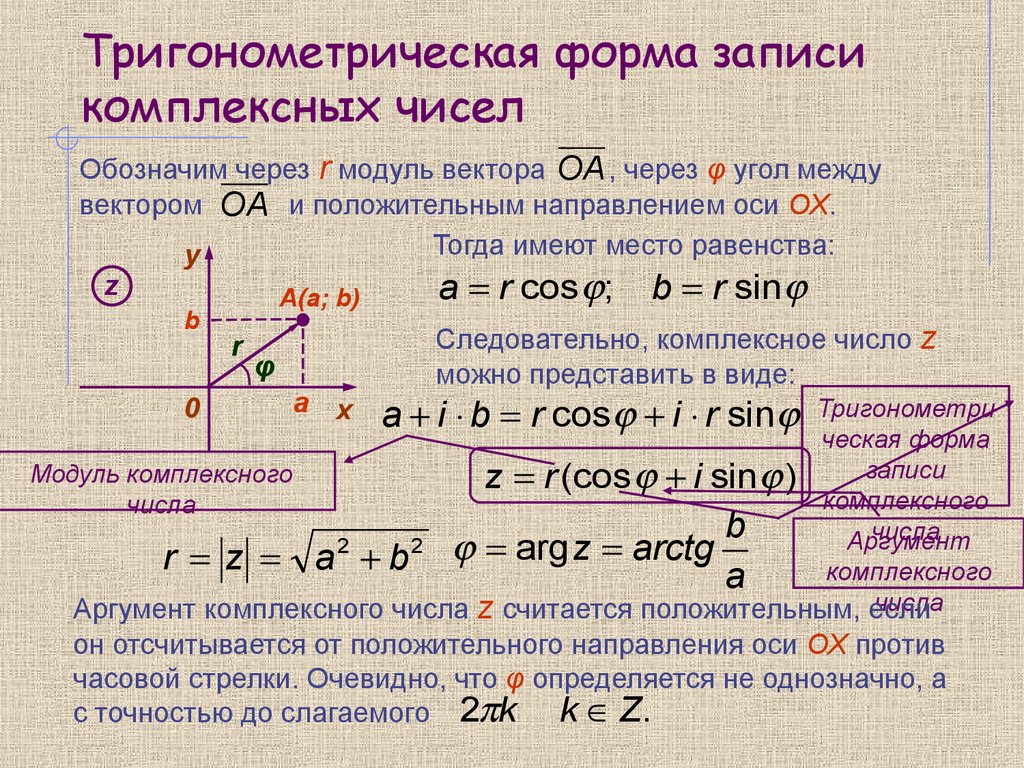
Операции
с комплексными
числами в тригонометрической форме. Формула Муавра.
Начальные сведения о мнимых и комплексных числах приведены в разделе «Мнимые и комплексные числа». Необходимость в этих числах нового типа появилась при решении квадратных уравнений для случая D D – дискриминант квадратного уравнения). Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики
и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.
Комплексные числа записываются в виде: a
+
bi .
Здесь a и b – действительные числа ,
а i – мнимая единица, т.
e
.
i 2 = –1. Число a называется абсциссой ,
a b
–
ординатой комплексного числа a
+
bi
. Два комплексных числа a
+
bi и a
–
bi называются сопряжёнными комплексными числами.
Основные договорённости:
1. Действительное число а может быть также записано в форме комплексного числа: a + 0 i или a – 0 i . Например, записи 5 + 0 i и 5 – 0 i означают одно и то же число 5 .
2. Комплексное число 0+ bi называется чисто мнимым числом . Запись bi означает то же самое, что и 0+ bi .
3. Два комплексных числа a + bi и c + di считаются равными, если a = c и b = d . В противном случае комплексные числа не равны.
Сложение. Суммой комплексных чисел a + bi и c + di называется комплексное число (a + c ) + (b + d ) i . Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.
Это определение соответствует правилам действий с обычными многочленами.
Вычитание.
Разностью двух комплексных чисел a
+
bi (уменьшаемое) и c
+
di (вычитаемое) называется комплексное число ( a
–
c ) + (b
–
d ) i
.
Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a + bi и c + di называется комплексное число:
( ac – bd ) + (ad + bc ) i . Это определение вытекает из двух требований:
1) числа a + bi и c + di должны перемножаться, как алгебраические двучлены,
2) число i обладает основным свойством: i 2 = – 1.
П р и м е р . (a+ bi )( a – bi ) = a 2 + b 2 . Следовательно, произведение
двух сопряжённых комплексных чисел равно действительному
положительному числу.
Деление. Разделить комплексное число a
+
bi (делимое) на другое c
+
di (делитель) — значит найти третье
число e
+
f i (чатное), которое будучи умноженным на делитель c
+
di ,
даёт в результате делимое a
+
bi
.
Если делитель не равен нулю, деление всегда возможно.
П р и м е р. Найти (8 + i ) : (2 – 3 i ) .
Р е ш е н и е. Перепишем это отношение в виде дроби:
Умножив её числитель и знаменатель на 2 + 3 i
И выполнив все преобразования, получим:
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a + bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью .
Модулем комплексного числа называется длина вектора OP ,
изображающего комплексное число на координатной (комплексной ) плоскости.
Модуль комплексного числа a
+
bi обозначается | a
+
bi | или буквой r
Комплексные числа — Математика — Уроки
Комплексные числа.
Тема: Мнимая единица, множество комплексных чисел, алгебраическая форма комплексного числа, действия над комплексными числами в алгебраической формуле. Геометрическая интерпретация комплексных чисел.
Определение: Мнимой единицей называется число j, квадрат которого равен «-1»
Пример:
Определение: Объединение множества действительных чисел с мнимой единицей называется множеством комплексных чисел и обозначается «С».
Определение: Выражение вида: a+bj, где а и b – действительные числа, j – мнимая единица, называется алгебраической формой комплексного числа.
а – действительная часть комплексного числа.
b – мнимая часть комплексного числа.
Если а=0, то bj – чисто мнимое комплексное число.
Задача:
Ответ: Корнями уравнения являются два сопряженных комплексных числа.
z=a+bj ему сопряженное , а противоположное -z = —a—bj
Два комплексных числа равны, если равны их действительные и мнимые части.
Комплексные числа в смысле «», «
Комплексное число z=a+bj геометрически изображается точкой М(a,b) на координатной плоскости и наоборот: каждая точка координатной плоскости
изображает какое либо комплексное число.
Комплексное число z=a+bj геометрически изображается радиусом вектора ОМ с координатными (а;b).
Определение: длина радиуса вектора изображающего комплексное число z=a+bj, называется модулем комплексного числа и обозначается «r»,
Определение: Аргументом комплексного числа называется величина угла, образованного радиус – вектором, изображающим комплексное число с положительным направлением действительной оси.
Действия над комплексными числами:
Пусть даны два комплексных числа: и
сложение:
вычитание:
умножение:
Произведением двух комплексных чисел, заданных в алгебраической форме, является комплексное число в алгебраической форме, которое получается по правилу умножения двучлена на двучлен:
4. деление:
Частным двух комплексных чисел, заданных в алгебраической форме, является комплексное число в алгебраической форме, которое получается после умножения числителя и знаменателя дроби на число, сопряженное знаменателю.
Задача:
Тема: Тригонометрическая форма комплексного числа. Переход от алгебраической формы к тригонометрической и наоборот. Действия над комплексными числами, заданными в тригонометрической форме.
Рассмотрим прямоугольный ОАМ
Определение: Выражение вида , где r— модуль, φ – аргумент комплексного числа, j – мнимая единица, называется тригонометрической формой комплексного числа.
; — формулы перехода
от тригонометрической к алгебраической форме.
Пример: 2,6(
Переход из тригонометрической формы к алгебраической производится с помощью калькулятора. r(cosφ+sinφj)=a+bj
Формулы перехода от алгебраической к тригонометрической форме комплексного числа: ; ;
Пример:
Переход от алгебраической формы комплексного числа
к тригонометрической осуществляется с помощью калькулятора. a+bj=r(cosφ+sinφj)
Действия над комплексными числами
в тригонометрической форме.
Сложение и вычитание выполняется только в алгебраической форме.
1) Умножение:
Пример:
2) Деление:
Пример:
3) Возведение комплексных чисел в n степень(формула Муавра) n – натуральное:
Пример:
4) Извлечение корня n-й степени.
Корень n-й степени из комплексного числа имеет ровно n-значений, которые получаются при к=0,1…(n-1)
, где k=0,1…(n-1)
Пример:
Тема: Показательная форма комплексного числа. Переход от показательной формы комплексного числа. Действия над комплексными числами показательной формы.
Формула Эйлера:
Определение: Выражение вида , где r-модуль, φ-аргумент, j-мнимая единица, называется показательной формой комплексного числа.
Т.к. комплексное число в показательной форме задается модулем r и аргументом φ, то формулой перехода от алгебраической формы к показательной и наоборот, такие же, как от тригонометрической к показательной и наоборот.
Пример:
Пусть даны комплексные числа: ;
умножение:
деление:
возведение в натуральную степень: z=(
извлечение корня n-й степени: к=0,1,…,(n -1)
Справочник по всем алгебраическим уравнениям комплексных чисел
При выполнении математических вычислений действительные числа — это числа, которые обычно используются в качестве основы для нашей работы.
Однако мнимые числа используются только для математических расчетов при работе с комплексными числами.
В большинстве случаев это не так.
Число называется комплексным, если оно может быть записано в виде a + bi, где a и b — действительные числа, а i — мнимая единица измерения, и число должно также удовлетворять уравнению i2 = 1, чтобы считать комплексным числом.
Простым примером комплексного числа может быть сумма 5 и 6i, где 5 — действительное число, а 6i — мнимое число.
Из-за этого сумма действительного числа и мнимого числа называется комплексным числом.
В следующей таблице подробно описаны четыре различных типа алгебраических операций, которые можно выполнять над комплексными числами.
Следующие четыре операции можно выполнять над комплексными числами:
Сложение
Вычитание
Умножение
Сложение комплексного числа
Чтобы сложить два комплексных числа, просто сложите действительную и мнимую составляющие, соответствующие каждому целому числу.
(a + bi) + (c + di) = (a + c) + (b + d)i
Вычитание с использованием комплексных чисел
Чтобы вычесть два комплексных числа, нужно просто вычесть действительную и мнимую составляющие которые соответствуют каждому из чисел.
(a + bi) − (c + di) = (a − c) + (b − d)i
Вычисление произведения двух комплексных чисел
Умножение двух двучленов эквивалентно умножению двух комплексных числа.
Предположим, нам нужно выполнить операцию умножения a + bi на c + di.
Мы будем умножать их почленно.
(a + bi) ∗ (c + di) = (a + bi) ∗ c + (a + bi) ∗ di
= (a ∗ c + (b ∗ c)i)+((a ∗ d )i + b ∗ d ∗ −1)
= (a ∗ c − b ∗ d + i(b ∗ c + a ∗ d))
Дискриминант
В математике дискриминант полинома – это величина, которая зависит от коэффициентов и влияет на различные особенности корней.
Другими словами, дискриминант многочлена является математически важным корнем.
Наиболее распространенным определением для него является полиномиальная функция, где переменными служат коэффициенты исходного полинома.
Дискриминант широко используется в процессе факторизации полиномов, теории чисел и алгебраической геометрии.
Обычно обозначается тильдой ∆.
Если рассматриваемый многочлен имеет двойной корень, и только тогда этот дискриминант будет равен нулю.
В случае вещественных коэффициентов положительно, если многочлен имеет два различных действительных корня, и отрицательно, если он имеет два различных комплексно-сопряженных корня.
Если многочлен имеет два разных действительных корня, он имеет положительное значение.
Аналогичным образом, для кубического многочлена существует дискриминант, равный 0 тогда и только тогда, когда многочлен имеет кратный корень.
Это единственное обстоятельство, при котором дискриминант может быть равен нулю.
В случае куба с действительными коэффициентами дискриминант считается положительным, если рассматриваемый многочлен имеет три отдельных действительных корня,
и отрицательным, если рассматриваемый многочлен имеет только один действительный корень, но два уникальных комплексно-сопряженных корня.
Алгебраические уравнения
Выражение, в котором два других выражения равны друг другу, называется алгебраическим уравнением.
Алгебраическое уравнение может быть описано как математическое выражение.
Переменная, некоторые коэффициенты и некоторые константы составляют типичные компоненты алгебраического уравнения.
Уравнения или знак равенства — это символ, который при буквальном переводе означает равенство.
Приравнивание одной величины к другой является фундаментальной концепцией, лежащей в основе всех математических уравнений.
Уравнение в форме является примером алгебраического уравнения.
P = 0
В этом случае P будет многочленом.
Например, алгебраическое уравнение будет выглядеть так: x + 8 = 0, где x + 8 — многочлен.
В связи с этим мы также называем его полиномиальным уравнением.
Уравнение в алгебре всегда записывается как сбалансированное уравнение, и оно должно иметь переменные, коэффициенты и константы.
Различные виды уравнений в алгебре
В алгебре существует множество различных типов уравнений. Ниже приводится подборка алгебраических уравнений:
Полиномиальные уравнения
Все полиномиальные уравнения, как и линейные уравнения, принадлежат к более широкой категории алгебраических уравнений.
Напомним, что полиномиальное уравнение — это уравнение, в структуру которого входят переменные, показатели степени и коэффициенты.
Уравнения в линейной форме: ax + b = c (a не равно 0)
Квадратные уравнения
Квадратное уравнение представляет собой полиномиальное уравнение с одной переменной, имеющее вид
f(x) = ax 2 + bx + c и имеет степень 2 в переменной.
Квадратные уравнения: ax 2 + bx + c = 0 (a не равно 0)
Кубические уравнения
Кубические многочлены — это просто другое название многочленов степени 3.
Каждый из кубических многочленов можно записать как уравнение в алгебре.
Кубические многочлены
ax 3 + bx 2 + cx + d = 0
Уравнения рациональных многочленов вида P(x)/Q(x)=0
Тригонометрические уравнения
Каждое из тригонометрических уравнений рассматривается как отдельная алгебраическая функция.
В уравнении, включающем тригонометрию, выражение включает тригонометрические операции, выполняемые над переменной.
Заключение
Итак, в заключение Комплексные числа — это числа, состоящие из двух частей: действительного числа и мнимого числа. Действительное число и мнимое число составляют комплексное число. Комплексные числа служат фундаментальными строительными блоками для более сложных математических областей, таких как алгебра.
Они имеют широкий спектр потенциальных применений в реальной жизни, особенно в области электроники и электромагнетизма.
Видео-вопрос: Преобразование комплексных чисел из алгебраической формы в полярную
Стенограмма видео
Выразите корень числа три 𝑖 в тригонометрической форме.
Нам дано комплексное число в прямоугольной или алгебраической форме. В общем, можно сказать, что комплексное число в прямоугольной форме равно 𝑎 плюс 𝑏𝑖. 𝑎 реальная часть. А 𝑏 — мнимая составляющая нашего комплексного числа.
Мы хотим записать это число в тригонометрической форме. Это 𝑟 cos 𝜃 плюс 𝑖 sin 𝜃, где 𝑟 — модуль нашего комплексного числа, а 𝜃 — его аргумент. И есть несколько формул преобразования, которые мы можем использовать, чтобы сэкономить время. Но давайте посмотрим на диаграмму Аргана, чтобы понять, откуда они взялись.
На этой диаграмме Аргана горизонтальная ось представляет действительную составляющую. А вертикальная ось представляет собой мнимую составляющую нашего комплексного числа.
Мы видим, что корень три 𝑖 будет лежать где-то на этой вертикальной оси, тогда как общее комплексное число в нашей алгебраической форме с положительными значениями 𝑎 и 𝑏 будет лежать где-то в этом первом квадранте.
Мы можем добавить прямоугольный треугольник. И мы также можем добавить высоту по вертикали 𝑏 и ширину по горизонтали 𝑎 единиц. Модуль — это гипотенуза этого треугольника. Иногда его называют величиной комплексного числа. И мы можем использовать теорему Пифагора, чтобы найти уравнение для 𝑟. Его можно найти, найдя квадратный корень из 𝑎 в квадрате плюс 𝑏 в квадрате.
Далее рассмотрим аргумент. Он измеряется против часовой стрелки от горизонтальной оси, как показано на рисунке. Мы можем обозначить треугольник относительно этого включенного угла. Обозначив противоположную соседнюю и гипотенузу относительно прилежащего угла, мы видим, что можем составить уравнение для 𝜃, используя коэффициент тангенса.
Tan 𝜃 равен противоположному больше соседнего. В данном случае это 𝑏 больше 𝑎.
И мы можем решить это уравнение для 𝜃, найдя обратный тангенс или 𝑟 арктангенс обеих сторон. Таким образом, 𝜃 равно арктангенсу 𝑏 над 𝑎. И теперь у нас есть две формулы преобразования, которые мы можем использовать для выражения комплексного числа в прямоугольной форме в тригонометрической форме.
𝑎 — константа. В данном случае это ноль. А 𝑏 — это коэффициент 𝑖. Это корень три. Таким образом, модуль нашего комплексного числа равен квадратному корню из нуля плюс корень из трех в квадрате, что равно просто корню из трех. А 𝜃 мы можем вычислить, рассмотрев положение на диаграмме Аргана. Но воспользуемся формулой. Это арктан корня три больше нуля.
И, конечно же, корень три, разделенный на ноль, не определен. И мы знаем, что функция тангенса не определена в точке, где 𝜃 равно 𝜋 на два. Теперь это имеет большой смысл, поскольку мы сказали, что 𝜃 измеряется в направлении против часовой стрелки от горизонтальной оси. В качестве альтернативы мы могли бы измерить его в градусах.