Алгоритм исследования функции: Схема исследования функции и построения графика. Алгоритм полного исследования функции

Схема исследования функции и построения графика. Алгоритм полного исследования функции

Исследование функции (с помощью производных) — широко распространенное задание, как в курсе школьной, так и университетской математики, которое позволяет проверить знания и навыки по нескольким разделам математики (общие сведения о функциях, преобразования функций, пределы, производная и ее приложения).

Целью исследования функции является изучение важных свойств функции и построение по результатам графика функции (поэтому иногда задание формулируют как «исследование графика функции»). Чтобы правильно построить график, нужно последовательно выполнять шаги исследования.

Ниже приведена полная схема исследования функции (или алгоритм исследования функции) по пунктам. Часть из этих шагов обычно опускается при исследовании функции, в зависимости от вида функции и требований к решению (например, для многочлена можно не проверять наличие асимптот или точек разрыва и т. п.).

Ключевые пункты (основная схема исследования) выделены черным, пункты, которые включаются в исследование опционально, выделены серым.

• Найти область определения функции.
• Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы.
• Исследовать непрерывность функции, выделить особые точки (точки разрыва).
• Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
• Найти точки пересечения с осями координат.
• Найти нули функции. Найти интервалы знакопостоянства функции.
• Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.
• Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается.
• Найти первую производную. Найти точки экстремума (локального минимума и максимума) и интервалы монотонности (возрастания и убывания) функции.
• Найти вторую производную. Найти точки перегиба и интервалы выпуклости-вогнутости.
• Найти наклонные/горизонтальные асимптоты функции.
• Исследовать поведение функции на бесконечности.
• Построить график функции. Построить асимптоты.
• Отметить важные точки на графике.

Используйте этот алгоритм для решения своих заданий на исследование функций, и вы добьтесь успеха. Нужны еще примеры, чтобы разобраться «на пальцах»? На сайте вы найдете примеры исследования функций самых разных типов, которые можно скачать бесплатно для изучения.

Смотрите также:

• Примеры подробного исследования графика функций разных типов
• Готовые задачи на исследование функции
• Можно ли сделать исследование графика функции онлайн?

Графики: исследование, построение, алгоритм OTUS

Если нужно построить график некой заданной функции, не обойтись без предварительного исследования этой функции, причем полного. И только потом, применяя полученные данные, можно построить правильный график. На практике построение бывает как отдельной задачей, так и задачей, связанной с графикой (вспомогательной задачей), то есть в последнем случае речь идет о решении уравнений графическим методом. Именно поэтому надо понимать, как происходит исследование и построение.

Вся работа по исследованию функции и построению выполняется поэтапно, то есть существует алгоритм построения графика функции. Если следовать этому алгоритму, вероятность ошибки будет сведена к минимуму.

Для исследования возьмем функцию y = f(x). Пошаговая реализация алгоритма выглядит следующим образом:

1. Нахождение области определения функции D(f). Речь идет об определении интервалов, на которых эта function существует.
2. Определение четности или нечетности. Когда область определения симметрична относительно нуля (для любого значения x из D(f) значение -x тоже принадлежит области определения), надо выполнить проверку на четность. К примеру, когда f(-x) является равной f(x), функция четная (классическая функция вида y = x ² является четной). Важное значение имеет факт того, что график четной функции является симметричным относительно оси OY. А вот если f(-x) равняется -f(x), следует говорит о нечетности (для примера нечетности можно вспомнить y = x³). В этом случае график симметричен относительно начала координат. Когда функцию считают четной либо нечетной, есть возможность построить часть ее графика для x ⩾ 0, а потом отразить ее соответствующим образом.
3. Нахождение точек пересечения с осями координат. Речь идет о точках пересечения графика функции y = f(x) с OX — осью абсцисс. Чтобы это сделать, надо решить уравнение f(x) = 0. Корни данного уравнения будут абсциссами точек пересечения графика с осью ОХ. Чтобы найти точку пересечения графика с OY (осью ординат) надо найти значение функции при x = 0.
4. Нахождение промежутков знакопостоянства. Следующий важный шаг. Здесь надо найти промежутки, на которых наша ф-я сохраняет знак. Это потребуется в дальнейшем в целях контроля правильности построения нашего графика. Для обнаружения промежутков знакопостоянства надо решить такие неравенства, как f(x) > 0 и f(x) < 0.
5. Поиск асимптот. Асимптота — прямая, к которой приближается график функции, делая это бесконечно близко. Бывают горизонтальные асимптоты, вертикальные асимптоты, наклонные асимптоты. Подробнее на эту тему читайте здесь.
6. Нахождение периода функции (утверждение справедливо для периодических функций). Также стоит добавить, что если ф-я тригонометрическая, то надо сначала определить, является ли она периодической либо нет.
7. Исследование с помощью производной. Исследование заключается в поиске промежутков убывания и возрастания и поиске точек экстремума (точек минимума и максимума). Это делается следующим образом:

а) ищем производную функции f(x);

б) второй этап — приравнивание производной к нулю с нахождением корней уравнения f(x) = 0 — в данном случае это стационарные точки;

в) третий шаг — найти промежутки знакопостоянства производной.

Промежутки, где производная является положительной, — это промежутки возрастания, где она отрицательна — убывания.

Точки, где производная меняет знак с «+» на «-» — точки максимума, если же с минуса на плюс — это точки минимума.

8. Последний шаг алгоритма — поиск точек перегиба и промежутков вогнутости и выпуклости. Эта тема неплохо рассмотрена вот в этой статье.

Надеемся, что материал был полезен, и у вас не возникнет проблем с построением графиков. И не забывайте, что математика может быть очень полезна в IT-сфере, особенно в Data Science.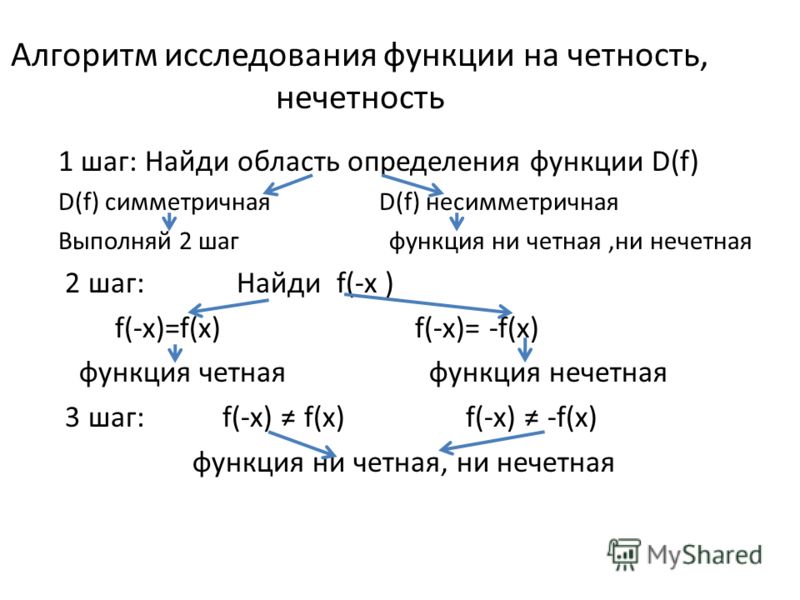 Если же вы чувствуете, что нужно повторить свои знания по математике, обратите внимание на соответствующий курс в OTUS:

Источники:

• https://ege-ok.ru/2013/11/12/issledovanie-funktsii-i-postroenie-grafika;
• https://www.matburo.ru/ex_ma.php?p1=maissl;
• http://matecos.ru/mat/matematika/issledovanie-funktsii-i-postroenie-grafika-funktsii.html.

Ученые-компьютерщики находят ограничения ключевого алгоритма исследования

Многие аспекты современных прикладных исследований опираются на решающий алгоритм, называемый градиентным спуском. Это процедура, обычно используемая для нахождения наибольшего или наименьшего значения конкретной математической функции — процесс, известный как оптимизация функции. Его можно использовать для расчета чего угодно, от наиболее прибыльного способа производства продукта до наилучшего способа распределения рабочих по сменам.

Тем не менее, несмотря на эту широко распространенную полезность, исследователи так и не поняли, в каких ситуациях алгоритм борется чаще всего. Теперь новая работа объясняет это, устанавливая, что градиентный спуск, по сути, решает фундаментально сложную вычислительную проблему. Новый результат накладывает ограничения на производительность, которую исследователи могут ожидать от этой техники в конкретных приложениях.

«Есть своего рода наихудшая жесткость, о которой стоит знать», — сказал Пол Голдберг из Оксфордского университета, соавтор работы вместе с Джоном Фернли и Рахулом Савани из Ливерпульского университета и Александросом Холлендером из Оксфорд. Результат получил награду за лучшую статью в июне на ежегодном симпозиуме по теории вычислений.

Вы можете представить функцию как ландшафт, где высота земли равна значению функции («прибыли») в данном конкретном месте. Градиентный спуск ищет локальный минимум функции, ища направление наибольшего подъема в заданном месте и ища вниз по склону от него. Наклон ландшафта называется градиентом, отсюда и название градиентного спуска.

Градиентный спуск — важный инструмент современных прикладных исследований, но есть много общих задач, для решения которых он не работает. Но до этого исследования не было всестороннего понимания того, что именно затрудняет градиентный спуск и когда — вопросы, на которые помогла ответить другая область компьютерных наук, известная как теория вычислительной сложности.

«Большая часть работ по градиентному спуску не касалась теории сложности», — сказал Костис Даскалакис из Массачусетского технологического института.

Сложность вычислений — это изучение ресурсов, часто времени вычислений, необходимых для решения или проверки решений различных вычислительных задач. Исследователи сортируют задачи по разным классам, при этом все задачи одного класса имеют некоторые общие вычислительные характеристики.

В качестве примера, относящегося к новой газете, представьте себе город, в котором людей больше, чем домов, и все живут в доме. Вам дают телефонную книгу с именами и адресами всех жителей города, и вас просят найти двух человек, которые живут в одном доме. Вы знаете, что можете найти ответ, потому что людей больше, чем домов, но это может занять некоторое время (особенно если у них нет одной фамилии).

Этот вопрос относится к классу сложности под названием TFNP, сокращенно от «недетерминированный полином полной функции». Это набор всех вычислительных задач, которые гарантированно имеют решения и решения которых можно быстро проверить на правильность. Исследователи сосредоточились на пересечении двух подмножеств проблем в рамках TFNP.

 Первое подмножество называется PLS (полиномиальный локальный поиск). Это набор задач, связанных с нахождением минимального или максимального значения функции в определенной области. Эти проблемы гарантированно имеют ответы, которые можно найти с помощью относительно простых рассуждений.

Одной из задач, подпадающих под категорию PLS, является задача планирования маршрута, который позволит вам посетить определенное количество городов с кратчайшим возможным расстоянием, учитывая, что вы можете изменить маршрут, только поменяв порядок любой пары последовательные города в туре. Длину любого предложенного маршрута легко рассчитать, а с учетом ограничений на то, как вы можете изменить маршрут, легко увидеть, какие изменения сокращают поездку. Вы гарантированно в конце концов найдете маршрут, который не сможете улучшить с помощью приемлемого хода — локального минимума.

PRAXIS: Алгоритм Брента для минимизации функции

PRAXIS: Алгоритм Брента для минимизации функции

Скачать PDF

Скачать PDF

• Рефераты программ/алгоритмы
• Опубликовано: Декабрь 1992 г.

• Карл Р. Гегенфуртнер ¹  

Методы исследования поведения, инструменты и компьютеры

том 24 , страницы 560–564 (1992 г. )Процитировать эту статью

• 1220 доступов

• 55 цитирований

• Сведения о показателях

Abstract

Представлены реализации алгоритма Brent (1973) PRincipal AXIS (PRAXIS) на широко используемых языках программирования C и PASCAL. Алгоритм минимизирует многомерную функцию без использования производных. Пример компьютерной программы, которая вычисляет оценку максимального правдоподобия параметров психометрической функции, иллюстрирует использование подпрограммы. Другой алгоритм, Localmin, также принадлежит Бренту (1973), эффективно находит минимум одномерной функции.

Пример программы использует этот алгоритм для оценки полихорического коэффициента корреляции из таблицы наблюдаемых частот pxq.

Скачайте, чтобы прочитать полный текст статьи

Ссылки

• Бок, Р. Д., и Джонс, Л. В. (1968). Измерение и предсказание суждения и выбора . Сан-Франциско: Холден-Дэй.

  Google Scholar

• Брент, Р. П. (1973). Алгоритмы минимизации функций без производных . Энглвуд Клиффс, штат Нью-Джерси: Прентис-Холл.

  Google Scholar

• Бройден, К.Г. (1967). Квазиньютоновские методы и их применение для минимизации функций. Математика вычислений , 21 , 368–381.

  Артикул Google Scholar

• Чендлер, Дж. П. (1969). ШАГ; Находит локальные минимумы гладкой функции нескольких параметров. Наука о поведении , 14 , 81–82.

  Google Scholar

• Драсгоу, Ф. (1986). Полихорические и полисериальные корреляции. В S. Kotz, NI Johnson, & CB Read (Eds.), Энциклопедия статистических наук: Vol. 7 (стр. 68–74). Нью-Йорк: Уайли.

  Google Scholar

• Флетчер, Р., и Пауэлл, М.Дж.Д. (1963). Метод быстрого сходящегося спуска для минимизации.

  Компьютерный журнал , 6 , 163–168.

  Google Scholar

• Левенберг, К. А. (1944). Метод решения некоторых нелинейных задач методом наименьших квадратов. Ежеквартальный журнал прикладной математики , 2 , 164–168.

  Google Scholar

• Пауэлл, MJD (1964). Эффективный метод нахождения минимума функции нескольких переменных без вычисления производных. Компьютерный журнал , 7 , 155–162.

  No related posts.