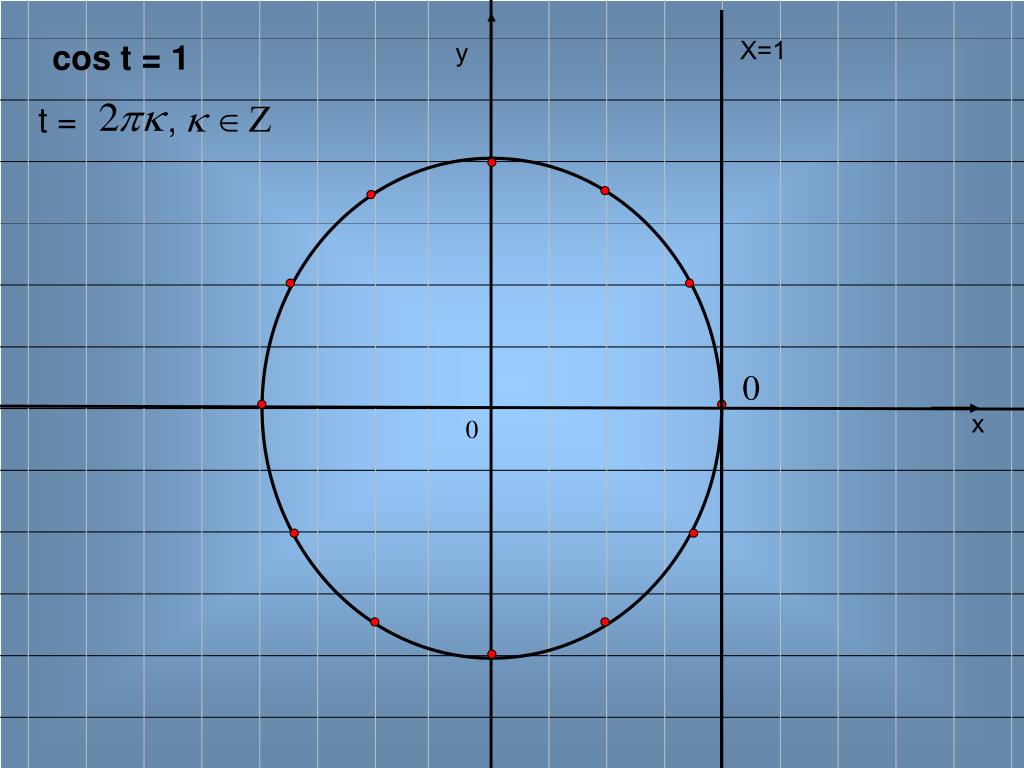
Чему равен arccos? – Обзоры Вики
Определение Arccos
Арккосинус x определяется как функция арккосинуса x, когда -1≤x≤1. Когда косинус y равен x: cos y = x. Тогда арккосинус x равен функции арккосинуса x, которая равна y: arccos x = cos–1 х = у.
Аналогично, что является производным от arccos? Что такое производное от Arccos? Производная arccos x определяется выражением -1/√(1-х2) где -1 < х < 1. Ее также называют производной от косинуса, обратного х, то есть производной функции арккосинуса.
Как мне узнать, есть ли у меня SOH CAH TOA? SOHCAHTOA — это мнемоническое устройство, помогающее запомнить, какое соотношение соответствует какой функции.
- SOH = Синус противоположен гипотенузе.
- CAH = косинус смежен с гипотенузой.
- TOA = Касательная противоположна соседнему.
Во-вторых, как вы пишете arccos в Matlab? Y = acos( X ) возвращает арккосинус (cos–1) элементов X в радианах.
Функция принимает как вещественные, так и комплексные входные данные. Для реальных значений X в интервале [-1, 1] acos(X) возвращает значения в интервале [0, π].
Что эквивалентно arcsec?
Основные ценности
| функция | полученный из | ассортимент |
|---|---|---|
| Арктан | функция, обратная касательной | Q IV, I: (−π / 2, + π / 2) |
| Арккот | Арккот x = π / 2 — Арктангекс x | IQ, II: (0, π) |
| угл.сек | Arcsec x = Arccos (1 / x) | QI, II: [0, π] |
| Arccsc | Arccsc x = Arcsin(1/x) | Q IV, I: [−π/2, +π/2] |
• 30 октября 2016 г.
тогда является ли arccos таким же, как SEC? Функция секанса является мультипликативной, обратной функции косинуса, которая определяется нулями функции косинуса. Один из них, арккос, функция, обратная cos.
Это обратная операция. Другой, sec, равен 1cos, поэтому он возводит результаты операции в степень −1.
Как найти производную от arctan? Как доказать производную формулы арктана? Чтобы получить производную arctan, предположим, что y = arctan x, тогда tan y = x. Дифференцируя обе части по y, тогда sec2у = dx / dy. Принимая обратное с обеих сторон, dy / dx = 1 / (сек2у) = 1/(1+загар2у) = 1 / (1 + х2).
Как найти недостающую сторону Сохкахтоа?
Как решить КАН?
Что такое решение arccos 0.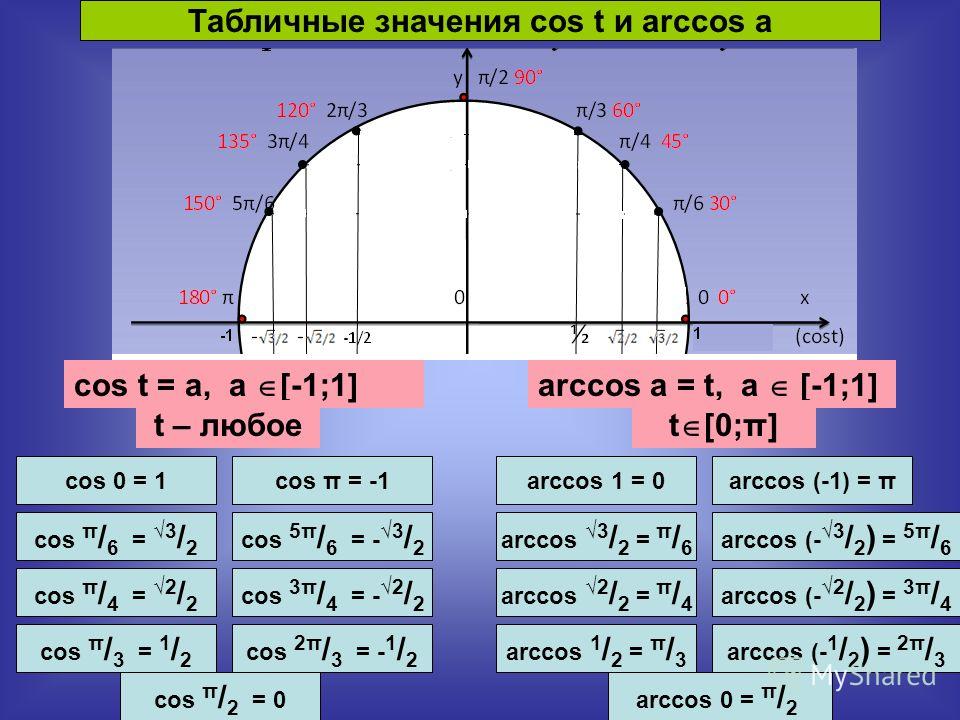
5? арккосинус (0.5) = 60°
Как найти арктан вручную?
Арктан и загар 1 — это одно и то же?
Арктангенс обозначается арктангенсом. или на калькуляторе будет отображаться как атан или загар–1. … Синус, косинус, секанс, тангенс, косеканс и котангенс — все это функции, однако обратные значения являются функцией только в ограниченной области.
Что такое решение Arccos 0.5? арккосинус (0.5) = 60°
Как найти экспоненту в MATLAB? В MATLAB функция exp(x) дает значение экспоненциальной функции ex. Найдите значение е. е = е1 = ехр(1). MATLAB не использует символ e для математической константы e = 2.718281828459046.
Что такое Acos MATLAB?
акос( X ) возвращает функцию арккосинуса (функция арккосинуса) X . Все углы в радианах.
Для реальных значений X в интервале [-1,1] acos(x) возвращает значения в интервале [0,pi].
Является ли кроватка инверсией загара? Котангенс не совпадает с арктангенсом. Функция котангенса равна обратной величине функции тангенса.
Как вы делаете arcsec на калькуляторе?
Является ли arcsec таким же, как грех? Функции обычно обозначаются аббревиатурой: арксинус (arcsin), арккосинус (arccos), арктангенс (arctan), арккосеканс (arccsc), арксеканс (arcsec) и арккотангенс (arccot).
…
Математические таблицы Math3.org:
| грех (д) = ОПП / гип | csc (q) = 1 / sin (q) |
|---|---|
| загар (д) = грех (д) / соз (д) | кроватка (q) = 1 / tan (q) |
Является ли Arccsc тем же, что и грех?
Обычно функции сокращаются: арксинус (arcsin), арккосинус (arccos), арктангенс (arctan), арккосеканс (arccsc), арксеканс (arcsec) и арккотангенс (arccot).
…
Математические таблицы Math3.org:
| грех (д) = ОПП / гип | csc (q) = 1 / sin (q) |
|---|---|
| загар (д) = грех (д) / соз (д) | кроватка (q) = 1 / tan (q) |
Какая производная от кроватка? Мы знаем, что производная от ctg x равна -csc2x. Кроме того, csc x = 1/(sin x). Итак, d/dx (cot x) = -1/sin2x.
Арктан — это то же самое, что детская кроватка?
Оказывается, арктан и детская кроватка — это действительно разные вещи: кроватка (x) = 1 / tan (x) , поэтому котангенс — это величина, обратная касательной, или, другими словами, мультипликативная обратная величина. arctan (x) — угол, тангенс которого равен x.
Арктан и Тан-1 это одно и то же? Арктангенс обозначается арктангенсом. или на калькуляторе будет отображаться как атан или загар–1. … Синус, косинус, секанс, тангенс, косеканс и котангенс — все это функции, однако обратные значения являются функцией только в ограниченной области.
ARCCOS — ПМК вики
ARCCOS (арккосинус) — традиционное слово Каллисто. Вычисление Арккосинуса.
ARCCOS ( x −− x1 ) Вычисление Арккосинуса. x1 := arccos x
x1 — главный угол, чей косинус равен x. Модуль x должен быть меньше либо равен 1. Единица измерения угла (градусы или радианы) задаётся словами DEGREES и RADIANS.
Содержание
- 1 Ввод слова ARCCOS
- 2 FACOS в стандарте ANS Forth
- 3 История
- 4 Реализация
- 5 Ссылки
Ввод слова ARCCOS[править]
В режиме ЛАТ последовательно нажмите клавиши ШГ← × С/П С/П 5 1
FACOS в стандарте ANS Forth[править]
12.6.2.1476 FACOS "f-a-cos" FLOATING EXT
( F: r1 -- r2 ) or ( r1 -- r2 )
r2 - главный угол в радианах, чей косинус - r1. Неопределенная
ситуация существует, если |r1| больше единицы.
В Форте FSP88M это слово известно под именем ACS
В Форте FSP88 было два слова ACSD и ACSR для вычисления арккосинуса в градусах и радианах.
В Каллисто имя ARCCOS восходит к надписи на клавиатуре советского ПМК «Электроника Б3-34», выпущенного в 1980 году.
В Каллисто 1.0 слово ARCCOS является «обёрткой» вокруг команды ЭКВМ F arccos. Размерность результата задаётся R9045:
1689 ;#ARCCOS 1690 ; ARCCOS ( x −− x1 ) Арккосинус. x1 := arccos x 1691 LACOS: .DB 6 1692 .TEXT "ARCCOS" ; ( x −− arccos x ) 1693 .DW LASIN 1694 ACOS: .DW JACOS 1695 JACOS: PKRM03 FARCCOS PKM03 KGOTO9 ; Обёртка вокруг FARCCOS.
Арккосинус не определён для аргументов, превышающих по модулю 1. Обработка этой ошибки производится встроенной программой. Например, последовательность слов 2 ARCCOS вызывает аварийный останов Каллисто с сообщением «Неверный аргумент» в строке комментариев.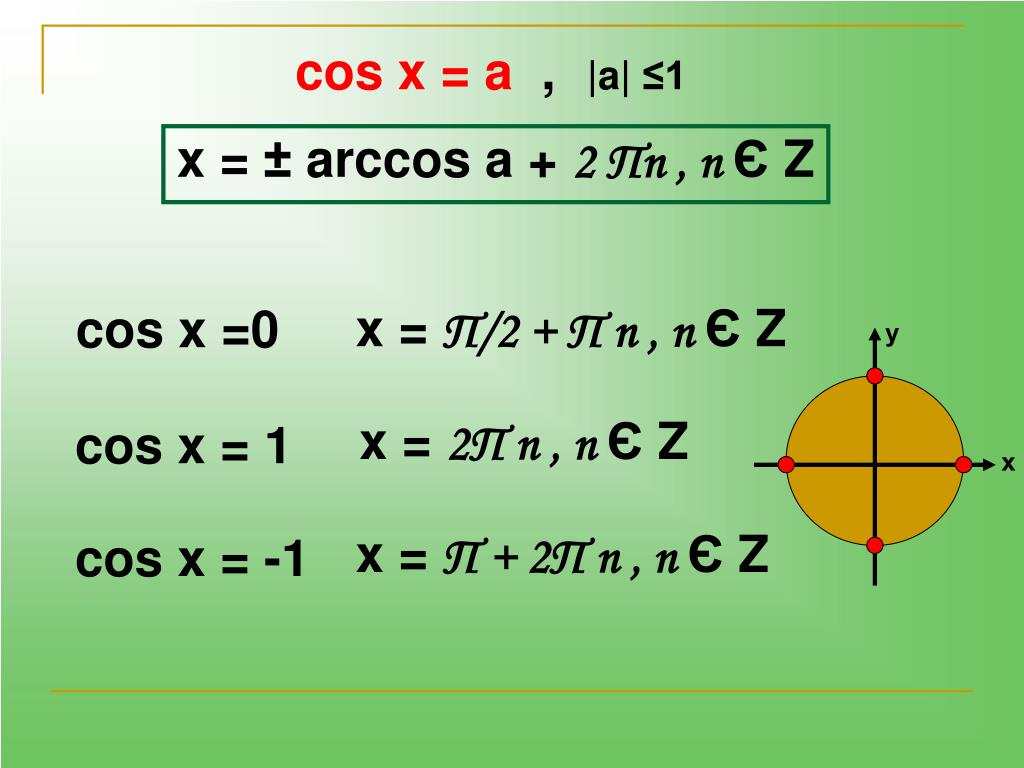
В случае аварийного останова рекомендуется произвести «холодную перезагрузку» Каллисто с удалением всех введённых слов, нажав последовательно клавиши В/О С/П .
Реализация из SP-Forth 4.20:
CODE FACOS \ *
FLD1
FLD ST(1)
FMUL ST, ST
FSUBP ST(1), ST
FSQRT
FXCH
FPATAN
RET
END-CODE
- Исходный текст слова ARCCOS в Каллисто Классик 1.0
- См. слова ARCSIN, ARCTG и COS
- Слово FACOS (f-a-cos) в стандарте ANS Forth (англ.)
- Слово FACOS (f-a-cos) в черновике Forth 200x (англ.)
- Функция Arccos на Википедии
| У этой статьи нет иллюстраций. Вы можете помочь проекту, добавив их. |
Это заготовка статьи. Вы можете помочь проекту, дополнив её. |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | арктан(-1) | ||
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| Найти точное значение | csc(60 градусов) | ||
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
функции — В чем разница между arccos(x) и sec(x)
Проблема с обозначениями и, возможно, отсутствием определений.
Мы определяем $\sec x$ как мультипликативную обратную величину $\cos x$, другими словами, фиксированное $a \in \mathbb{R}$, $\sec a$ — это число такое, что $\sec a \cos а = 1$. Теперь $\arccos x$ — это немного другое: это обратная функция $\cos x$.
Не знаю, усвоили ли вы это, но формальное определение функции — это набор упорядоченных пар. Другими словами, поскольку функция из множества $A$ в множество $B$ должна быть правилом, устанавливающим для каждого $a \in A$ некоторое $b \in B$, мы можем просто определите функцию как набор всех упорядоченных пар элементов в $a$ вместе со связанными элементами в $b$. Однако нам потребуется дополнительное свойство, состоящее в том, что если $(a,b) \in f$ и если $(a,c)\in f$, то $b = c$, и это всего лишь формальный способ формулировки «вертикальной линии правило». Поскольку второй элемент в каждой паре уникален, мы даем ему имя: если $(a,b) \in f$, то $b = f(a)$. Также для определения начального и конечного множеств мы записываем функции от $A$ до $B$ как $f: A \to B$.