Разложение в ряд Тейлора. Разложение в ряд Маклорена элементарных функций. Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
Если функция допускает в некоторой окрестности точки разложение в степенной ряд по степеням , то этот ряд (ряд Тейлора) имеет вид
При ряд Тейлора называют также рядом Маклорена. Последнее равенство справедливо, если при остаточный член ряда Тейлора
при
Для оценки остаточного члена можно пользоваться формулой (форма Лагранжа)
Разложение основных функций в степенной ряд Маклорена
Пользуясь основными разложениями, а также формулой для
геометрической прогрессии, можно во многих случаях просто получать разложение
данной функции в степенной ряд, причем отпадает необходимость исследования
остаточного члена.
Иногда при разложении полезно использовать почленное дифференцирование или интегрирование. При
разложении в степенные ряды рациональных функций рекомендуется разлагать эти
функции на простейшие дроби.
I. Бесконечная убывающая геометрическая прогрессия со знаменателем .
II. Разложение экспоненты в ряд Маклорена
III. Разложение синуса в ряд Маклорена
IV. Разложение косинуса в ряд Маклорена
V. Биномиальный ряд
VI. Разложение в ряд Макклорена функции ln(1+x)
VII. Разложение арктангенса в ряд Маклорена
Пример решения задачи
Задача
Разложить функцию в ряд по степеням .
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач.
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Находим производные данной функции:
….
Вообще , если – четное, и , если – нечетное
Полагая получаем:
….
Вообще , если – четное, и , если – нечетное
На основании формулы разложения в ряд Тейлора имеем:
Для определения интервала сходимости ряда применим признак Даламбера.
при любом
.
Следовательно, ряд сходится в интервале
.
Остаточный член имеет вид:
Так как , то
Поэтому:
Ряд с общим членом сходится при любом (в этом можно убедиться с помощью признака Даламбера), поэтому в соответствии с необходимым признаком сходимости:
а следовательно, при любом .
Это значит, что сумма ряда для любого действительно равна .
математика — Разложение в ряд Тейлора функции(Python). Приближённое значение функции
Вроде бы ввожу правильное значение разложения в ряд Тейлора функции, а выдаёт не правильное значение. Подскажите, в чём проблема.
import math
from math import factorial
a=3.0
b=4.0
lich = 0
krok=(b-a)/10
lich=0
def f(x):
return 1/(1+((math.e)**(1+x)))
def f_tochne(x, n):
result=0
for i in range(n):
result += ((factorial(n))/((1+x)**n))
return result
while a<=b:
print(round(a,2), end=' ')
print(round(f(a),5),end=' ')
print(round(f_tochne(a,lich),5))
lich+=1
a+=krok[![введите сюда описание изображения][1]][1]
- python
- математика
- ряды
1
Можно и без всяких импортов математики и факториалов.
..
def f(x):
return 2.718281828459045**(1+x)
def tailor(x, eps):
x = 1+x
sum = 1+x
term = x;
n = 2;
while term*term > eps*eps:
term *= x/n
n += 1
sum += term
return sum
a=3.0
b=4.0
krok=(b-a)/10
while a<=b:
print(round(a,2), end=' ')
print(round(f(a),5),end=' ')
print(round(tailor(a,1e-6),5))
a+=krok
Как там таблицу выводить красиво — это я не очень знаю, Python — не мое, смотрите сами. Но вот так считать, не по количеству членов, а по заданной точности — оно как-то надежнее 🙂 Кстати, пятью членами в этом диапазоне значений никак не отделаться — нужно штук 20…
3
from math import factorial
def taylor(x, n):
return sum((1+x) ** i / factorial(i) for i in range(n + 1))
2
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
{-x}$Задавать вопрос
спросил
Изменено 8 лет, 5 месяцев назад
Просмотрено 2к раз
$\begingroup$
кто-нибудь может показать мне разложение в ряд Тейлора для $e^{-x}$.
Я пытался выяснить, как 9{-i\theta} = \cos(\theta) — i\sin(\theta).$$
$\endgroup$
6
Math Tutor — Series — Theory
Math Tutor — Series — Theory — Function seriesЗдесь мы отвечаем на главный вопрос. У нас есть функция f и номер a , и мы хотели бы выразить эту функцию как сумму степени серия с центром и . Мы начните с некоторой теории, а затем посмотрите на расширение, используя характеристики. В конце мы обращаемся к обратному процесс, к заданному ряду мы пытаемся найти его сумма.
Как мы изложили в общих чертах в разделе Системы функций, есть необходимо ответить на два вопроса: какие функции могут быть выражены в этом путь и как мы находим серию для них. И действительно, первый вопрос трудно, мы просто дадим частичный ответ позже. Начнем с определения.
Определение.
Пусть f — функция, а — некоторая точка внутри его домен.
Мы говорим, что мы расширили функцию f в степени ряд (at a ), если мы найдем такой степенной ряд, чтов каком-то районе и .
Затем этот ряд мощности называется расширением из f .
По результатам в предыдущий раздел следует что каждая функция, которая может быть разложена таким образом, должна иметь производные от все заказы в и . Это говорит нам о том, что нет смысла пытаться расширить другие функции. В нем также говорится, что когда мы говорим о расширении, мы имеем все эти производные доступны.
Отправной точкой нашего исследования является следствие в конце
предыдущий раздел. Предположим, что
у нас есть функция, которая может быть выражена серией от до . Если мы
подставляем этот центр а в формулу для n -й
производной, сразу получаем следующее.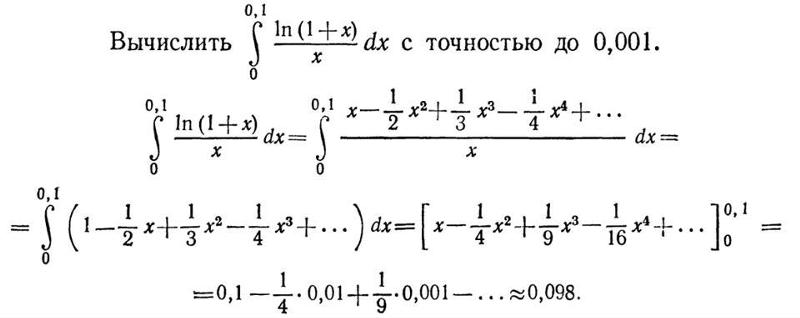
Теорема (единственность разложения).
Пусть f — функция, которую можно разложить в степенной рядв каком-то районе и . Тогда для каждых k коэффициенты a k обязательно выполнить
Другими словами, есть только один способ разложить функцию в степень. серии (если это вообще возможно). Эта уникальная силовая серия заслуживает названия.
Определение.
Пусть f — функция, а — некоторая точка внутри его домен. Предположим, что f имеет производные всех порядков от до . Затем мы определяем его ряда Тейлора в точках a по формуле
Формула для коэффициентов та же, что и в случае
Полином Тейлора,
так что это действительно что-то вроде «бесконечного многочлена Тейлора».
Обратите внимание, что приведенная выше теорема была импликацией. Это означает, что как только мы
функция, разложенная в степенной ряд, то этот ряд обязательно является
Серия Тейлор. Однако, если мы возьмем функцию со всеми производными в точках a и постройте ряд Тейлора по приведенной выше формуле,
то нет гарантии, что и этот ряд будет сходящимся
где-то еще, чем на , и даже если он сходится, нет
гарантировать, что она действительно сходится к исходной функции ф .
Например, в
этой заметке мы показываем пример
функция, которая является «хорошей» по большинству стандартов (имеет производные всех порядков
всюду), ее ряд Тейлора сходится к ее сумме равномерно на всем
реальная линия, однако сумма этого ряда Тейлора равна исходной
функционировать только в одной точке, в центре ряда (где он фактически имеет
работать для любой функции и серии, поэтому у него нет выбора). Эта ситуация
где у нас есть проблемы с тем, чтобы серия попала в нужное место
часто возникает, когда мы работаем с системами функций, и вдохновляет
следующие обозначения.
Тильда означает, что серия справа получена из f используя приведенные выше формулы (это ряд Тейлора для f ), но это также означает, что процесс создания этой серии Тейлора является чисто формально, так как на данный момент у нас нет информации, является ли сумма этого серия на самом деле не имеет ничего общего с f .
Очевидно, наша цель — заменить эту тильду на равенство, т. е. хотелось бы видеть, что ряд Тейлора справа на самом деле сходится к ф хоть где-то (кроме а , где сходимость есть автоматический). Как мы это узнаем? По определению следует взять частичные суммы T N из T и проверить, сходятся к f .
Точно так же мы хотели бы выяснить, как разница
| f − T N |
ведет себя, надеясь, что он пойдет к нулю как N уходит в бесконечность.
Однако на самом деле это то, что мы уже видели раньше, поскольку T N точно
Полиномы Тейлора
(см.
Производные — Теория — Приложения),
поэтому мы довольно много знаем об этой разнице. В частности, у нас есть
Лагранж
оценка его. Таким образом, мы можем переформулировать вопрос следующим образом:
Предположим, что f имеет производные всех порядков в некоторой окрестности U из и . Пусть х таково, что замкнутый интервал I с конечными точками a и x лежит в U . Мы хотим знать, когда правда, что
Обратите внимание, что в этой формуле x фиксировано и, следовательно, x — a является константой. Когда мы вспоминаем что c Н / Н ! стремится к нулю в бесконечности, мы видим, что все зависит от того, насколько быстро растет максимум с Н . Если она совсем не растет или растет очень медленно, то лагранжева оценка ошибки стремится к нулю. Таким образом, мы получаем следующее.
Теорема.
Пусть f — функция такая, что она имеет производные всех порядков на некоторая окрестность U точки a . Пусть T будет его Тейлором серии и .
Если есть константа M такой, что | f ( k ) ( t )| ≤ М к для всех натуральных чисел k и всех t из U , затем T сходится (равномерно) к f на U .
Таким образом, мы получаем одну группу функций, ряд Тейлора которых фактически равен их, а именно функции с равномерно ограниченными производными. Однако, это условие является слишком ограничительным, есть и другие функции, Ряды Тейлора сходятся там, где должны. Поиск правильного характеристика — сложная задача, определенно выходящая за рамки Math Tutor, и мы оставляем это профессиональным математикам.
Есть некоторые функции, для которых мы можем легко найти их разложения.
x 2 = [( x − 1) + 1] 2 = ( x — 1) 2 + 2( x 9001,
Последний является степенным рядом с центром 1 (его коэффициенты равны нулю при k > 2), поэтому это искомый Тейлор ряд. (Мы получили бы тот же ряд, если бы воспользовались формулой из определения, конечно.) Попытка применить этот прием к бесконечному ряду не будь милым больше.
Теперь мы рассмотрим шесть известных расширений, которые являются основой большинства
другие расширения.
Теорема.
Следующие расширения верны для указанных наборов.
Как следует из этих формул, выбор и = 0 для центра очень популярен. На самом деле, он настолько популярен, что некоторые люди используют традиционное имя Серия McLaurin для серии Taylor с этим центром. Однако он не универсален, и вы найдете его особенно в старых текстах.
Во всех шести случаях мы легко находим формулу для полиномов Тейлора из определение. Как насчет их сходимости? Вторая и третья формула ясны, сходимость следует из предыдущей теоремы (синус и косинус имеют все производные, ограниченные единицей всюду).
Для экспоненты мы также можем использовать эту теорему, но мы не можем этого сделать.
глобально, поскольку экспонента ограничена только на ограниченных множествах.
Однако это не проблема. Если мы возьмем любое действительное число х , мы можем
всегда рассматривайте, например, открытое соседство У 2| х | (0).
Это ограниченное множество и
поэтому все производные от e x равномерно
ограничены на нем, поэтому по приведенной выше теореме ряд Тейлора сходится к
экспоненциальный там; в частности, он сходится к экспоненциальному на x ,
поскольку x принадлежит этому району. Для полноты мы
включить прямое доказательство с использованием оценки Лагранжа, см.
это примечание.
Разложение для логарифма может быть фактически получено несколькими способами, мы вернемся к нему и ниже; относительно его сходимости интервал, который мы заявленное явно самое большое, на что можно надеяться, поскольку в предыдущем разделе мы доказали, что этот интервал является в точности областью сходимости этого ряда Тейлора. Таким образом, остается показать, что сумма ряда в этой области в точности равна ln(
это примечание.Пятая формула как раз геометрический ряд, поэтому в этом нет ничего нового.
Вероятно, наиболее интересной из шести является последняя формула, также называемая биномиальный ряд или биномиальное расширение . Это верно для всех c и A , что, в частности, показывает, что биномиальные числа также может быть определен для общего номера A . Это делается вторым формула с пониманием того, что когда k = 0, получаем 1. В качестве примера покажем, как выглядит ряд, когда c = 1, которая является часто используемой формой. Мы также показываем специальную формулу для «минус А «, иногда бывает полезно при работе с обратными. Работают оба для | х | < 1,
Заметим также, что если A — натуральное число, то по определению для k > A все коэффициенты равны нулю.
Таким образом, сумма конечна, она всегда сходится и фактически является известной
биномиальная формула, которую мы знаем из средней школы.
Одна из причин, по которой эти формулы важны, заключается в следующем: мы редко расширяем функции по определению, как мы сделали это выше. В большинстве случаев мы используем различные уловки, чтобы хоть как-то получить новые расширения из тех, что мы уже знать. Приведенные выше шесть являются отправной точкой для большинства таких расчетов. трюки появляются только сейчас.
Расширение и операции
Чтобы получить разложения новых функций из известных разложений, мы используем свойства, которые, как известно, работают для степенных рядов. Теорема о алгебраические операции из предыдущий раздел дает этот удобный факт.
Теорема.
Предположим, что у нас есть эти разложения в некоторой окрестности и .Тогда и в этом районе
Как насчет деления f / g ? Очевидно, это
достаточно знать, как расширить функцию 1/ f (при условии
что f ( a ) ≠ 0).
Теорема.
Предположим, что функция f может быть разложена в ряд Тейлора при и что f ( a ) ≠ 0. Тогда также функция 1/ f могут быть расширены в серию Taylor с по и этот ряд имеет положительный радиус сходимости.
Эта теорема не предлагает никакой формулы для нового ряда — и с хорошей причина, нет никакого разумного способа указать это. На практике мы используем метод неопределенных коэффициентов . Мы действительно можем применить это напрямую к f / g и возьмем 1/ f как частный случай. Предположим, что оба f и g расширяются до серии Taylor с номерами и и что г ( a ) ≠ 0. По приведенной выше теореме также их отношение может быть разложить в ряд Тейлора с неизвестными коэффициентами к к . Мы можем написать
Получившаяся система бесконечного числа линейных уравнений с бесконечно
много неизвестных к к обычно невозможно решить в явном виде, но позволяет вычислить как
много коэффициентов к к как мы хотим, что очень полезно, когда мы хотим аппроксимировать ж / г используя только конечную часть ряда Тейлора. Для примера мы ссылаемся на Решенные проблемы, а именно
эта проблема (это необычно
красиво, но хорошо иллюстрирует идею) и
Эта проблема
(это более характерно).
Мы также часто связываем функции с другими функциями, используя производную или интеграл. Тогда мы можем использовать эта теорема из предыдущей раздел.
Теорема.
Предположим, что у нас есть следующее разложение в некоторой окрестности и .Тогда и в этом районе
Во второй постановке можно использовать и неопределенный интеграл, но тогда необходимо найти правильную константу. Мы покажем пример ниже. Наконец, есть и другие операции, которые могут помочь в расширении новых функций.
Теорема (подстановка в ряд).
Предположим, что у нас есть следующее разложение в некоторой окрестности и .Тогда также
Первое утверждение верно для любых A и радиуса сходимости новый ряд такой же, как и исходный, но его центр (и регион сходимости) соответственно сдвигаются.
Второе утверждение верно для всех ненулевых A и радиуса сходимость нового ряда есть R f /| А |.
Третье утверждение немного шатко, так как результатом является мощность серия только для особых г . Тогда область сходимости должна быть исследованы индивидуально.
На самом деле, в первых двух утверждениях мы фактически знаем даже область сходимость нового ряда. В первом утверждении новый регион просто оригинал, но сдвинутый. Область сходимости во втором случае можно получить, уменьшив оригинал на A отрицательный также должен перевернуть его вокруг . То есть, если исходный ряд сходится в правом конце, то новый также сходится в правая конечная точка для A > 0 и сходится в левой конечной точке для A < 0. Это все на самом деле просто здравый смысл и хорошее понимание замены.
Пример: Выведем расширение для ф ( x ) = ln(1 − x ) в a = 0,
Ключом к этому расширению является наблюдение, что f ′′( x ) = −1/(1 − x )
и это именно сумма
принадлежащий
геометрический ряд, который
все знают.
Итак, начнем с формулы геометрического ряда (мы
используйте переменную t ), а затем мы интегрируем обе стороны от 0 до х
Этот ряд часто используется для логарифмирования. Исходный ряд сходится для t удовлетворяющих −1 < t < 1, поэтому новый также сходится по крайней мере на этом множестве, и его радиус сходимости должен остаются прежними (то есть 1). Тем не менее, мы, возможно, добились сходимости в какой-то момент. конечные точки. Когда мы вставляем x = −1 и x = 1 и используя подходящие тесты, мы находим, что область сходимости этого серия [−1,1). Откуда мы знаем, что сумма этого ряда при x = −1 равно лн(2)? Одним из возможных аргументов является использование непрерывности, см. Теорема Абеля о сходимости в предыдущем разделе. Таким образом, мы имеем справедливое расширение на [−1,1).
Если мы запишем этот результат, используя y , а затем воспользуемся заменой y = − x , мы получаем
Исходный ряд сходится для и , удовлетворяющих
−1 ≤ г < 1,
поэтому, когда мы заменяем
- х для y получаем область сходимости
(−1,1] для новой серии.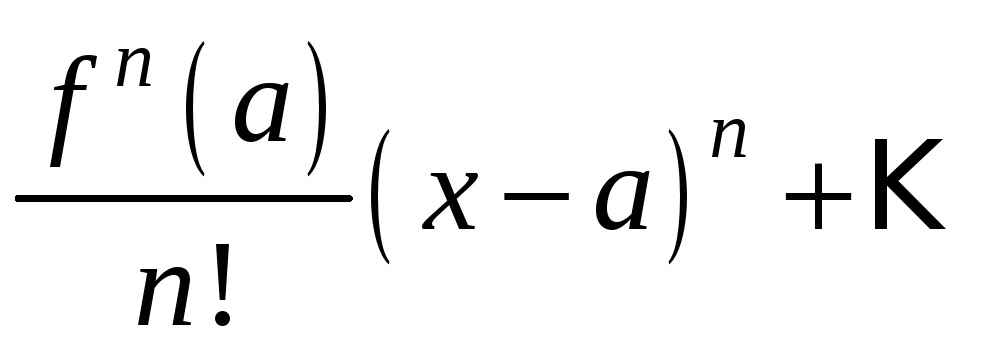
С другой стороны, если мы заменим y = 1 − x , то мы получим именно тот ряд для лн ( х ) что у нас было выше Теорема.
Возможно, это удивительно, учитывая трудности, с которыми мы столкнулись при поиске серий. для 1/ ф что на самом деле существует явный способ расширить обратную функцию.
Теорема (формула обращения Лагранжа).
Предположим, что функцию f можно разложить в ряд на некоторых окрестности точки a . Предположим далее, что е ′′( а ) не равен нулю. Обозначать b = f ( a ).
Тогда есть окрестности a , на которых функция f обратимой и окрестностью b , на которой эта обратная ф −1 можно разложить в степенной ряд. Более того, эту серию можно найти как
Завершим эту часть еще одним полезным утверждением.
Теорема.
Предположим, что у нас есть следующее разложение в некоторой окрестности и .Тогда в этой окрестности мы также имеем следующие разложения.
(i) Для любого положительного целого числа n ,
(ii) Если f имеет корень кратности n при a , то
Второе утверждение имеет смысл по следующей причине. Если является корень из кратности n вместо f , затем первый n − 1 производные от f и a являются нуль (см. это примечание). Поэтому и первый п — 1 коэффициенты ряда Тейлора равны нулю, а это означает, что фактически в серии для f индексация начинается с n , а не с 0. Это объясняет почему после сдвига индекса получается вторая формула.
Дополнительные примеры использования вышеуказанных свойств для расширения функций см.
Обзор методов
и
Решенные проблемы — серия
функции.
Мы завершаем эту часть о свойствах рядов Тейлора тем, что можно уже догадались из шести расширений выше.
Факт.
Пусть f — функция, имеющая ряд Тейлора с центром в a = 0, пусть a k — его коэффициенты.
Если f нечетно, то а k = 0 для всех четных k .
Если f четно, то a k = 0 для всех нечетных k .
Подведение итогов серии
Мы несколько раз упоминали, что подведение итогов может быть довольно сложным.
Приведенные выше приемы расширения функции можно также использовать для суммирования мощности.
серии (при условии, что нам повезет). Основная идея состоит в том, чтобы изменить данное
ряд в тот, который мы уже знаем, применяя преобразования из
приведенные выше теоремы к нему, отслеживая, что он делает со своей суммой.
Это
лучше всего объяснить на примере.
Пример: Найдите сумму
Есть сериал похожий на этот? Есть ряд, в котором есть термины г к / к , мы можем почти добраться туда, обозначив y = x + 1. Осталось зафиксировать мощность так, чтобы она совпадала с числом в знаменатель, но это не проблема. Вот так.
А как насчет значения x = −1? Это просто, мы просто поместите его в данную серию и найдите, что f (−1) = 0,
Мы также можем попробовать другой подход. Часто нам нужно избавиться от лишних к в серии. В нашей серии есть доп. к + 1
в знаменателе, поэтому мы были бы признательны, если бы к + 1
появилось также в числителе. Есть способ получить к в
числитель, а именно взяв производную от ряда. Нам нужно к + 1,
поэтому перед дифференцированием нам нужно создать
( x + 1) к + 1 там.
Раз нет деления на к + 1,
мы используем
геометрический ряд.
Осталось закрепить правый C . Самый простой способ это просто положить некоторые хороший x в последнее равенство. Так как слева подставляем в f , то есть в данную серию у нас особого выбора нет. Единственная ценность, которую мы действительно можем вложить в эту серию, это x = −1, но, к сожалению, это единственное значение, которое нам не разрешено в последней строке. Что мы можем сделать?
Казалось бы, мы могли бы решить эту проблему, используя предпоследнюю строку.
Приглядевшись, мы видим, что это неправда. Обратите внимание, что если x = −1, то во второй строке умножаем на
ноль, что недопустимо в уравнении. Таким образом, для этого значения все
последующие равенства сомнительны. К счастью для нас, мы можем смотреть еще
ближе. Что у нас есть на предпоследней строке? У нас есть одна функция на
слева и справа, и мы точно знаем, что они равны
для всех x от определенного интервала кроме одной точки в его середине.