Сложение и вычитание обыкновенных и десятичных дробей. смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.
12+
5 месяцев назад
Математика от Баканчиковой241 подписчик
Математика 5 класс. Продолжая тему «Десятичные дроби», сегодня мы расскажем Вам о том, как обращать обыкновенную дробь в десятичную. А начнём мы с объяснения для чего обращают обыкновенную дробь в десятичную. Оказывается это нужно для того, чтобы выполнить сложение или вычитание обыкновенной дроби и десятичной, т.к. не существует правил сложения и вычитания таких дробей. Мы дадим Вам и на конкретных примерах пошагово разберём правило обращения обыкновенной дроби в десятичную дробь. Затем поспорим с авторами современных учебников математики 5 класса о том, что при делении одного натурального числа на другое натуральное число получается обыкновенная дробь. А для обращения обыкновенной дроби в десятичную, числитель необходимо представить сначала в виде десятичной дроби, а затем уже десятичную дробь разделить на знаменатель, потому что при делении десятичной дроби на натуральное число получается десятичная дробь.
Равные десятичные дроби. Правило нулей. Математика 5 класс. https://rutube.ru/video/73e724f37977aeb256ba64ecb7932f54/
Округление десятичных дробей. Разряды и классы десятичной дроби. Математика 5 класс.
https://rutube.ru/video/27b315e7f6947dcede06cf447ae5e949/
Сложение и вычитание десятичных дробей. Математика 5 класс. https://rutube.ru/video/fde1d5a21516a66460a9744103adeb91/
Решение уравнений на сложение и вычитание десятичных дробей в 5 классе. Примеры решения уравнений. https://rutube.ru/video/14bfaafb1c6047388e14c264284db257/
Умножение десятичных дробей. Математика 5 класс. https://rutube.ru/video/d10e83ffbc0994bff4cc8c131e834c81/
#ДесятичныеДроби #ОбыкновеннуюДробьВДесятичную #СложениеДесятичнойДробиИОбыкновеннойДроби #МатематикаОтБаканчиковой
математика 5 класс, десятичные дроби, как обратить обыкновенную дробь в десятичную, обыкновенную дробь в десятичную, сложение и вычитание обыкновенной и десятичной дроби, сложение и вычитание десятичной и обыкновенной дроби, правило обращения обыкновенной дробь в десятичнуюДесятичные дроби.
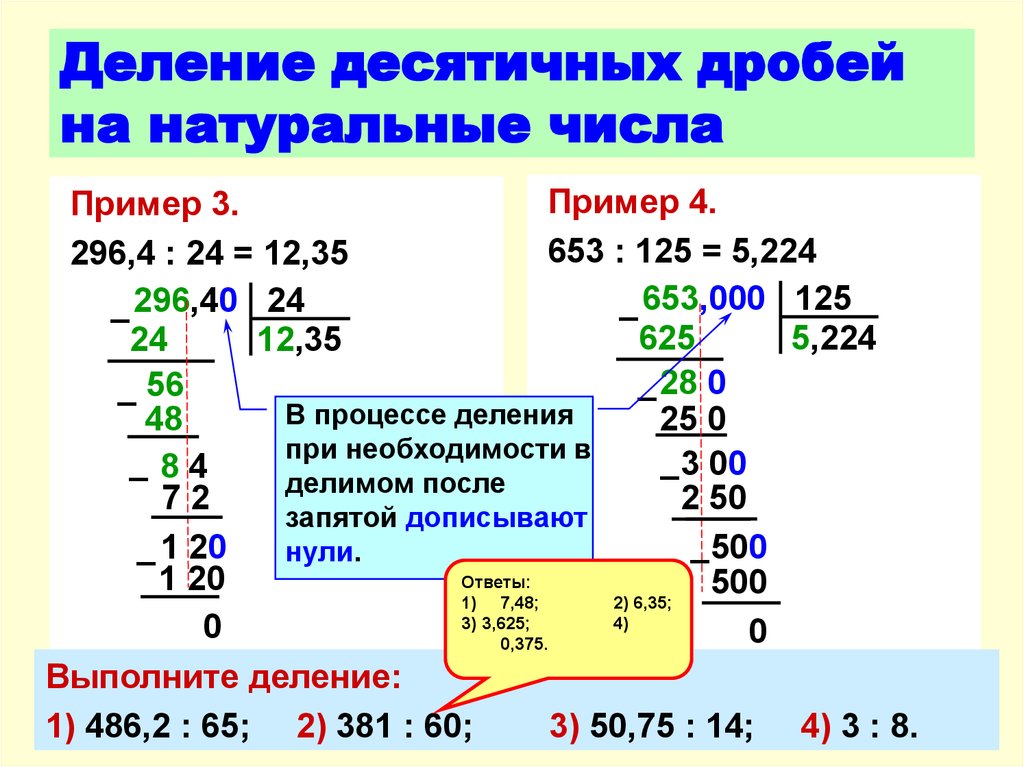Разряды и классы десятичных дробей.Home » 5 класс » Десятичные дроби. Разряды и классы десятичных дробей.
Posted on Author admin 0
Рассмотрим урок на тему десятичные дроби. Научимся записывать и читать десятичные дроби. А также разберем разряды и классы десятичных дробей.
Вы уже знаете, что такое обыкновенные дроби и что такое отрицательные дроби? Возникает вопрос, зачем нужны десятичные дроби? Ответ очень прост, десятичные дроби вошли во все сферы нашей жизни, например, в строительную, в экономическую и многие другие. В строительной сфере десятичными дробями показывают сколько нужно материалов для ремонта квартиры. Или покупая в магазине конфеты вы всегда видите цену товара, она записана в виде десятичной дроби. Десятичная дробь показывает сколько целых частей имеется и сколько части единицы от целого числа. Подробно мы рассмотрим ниже.
Десятичная дробь понятие и смысл.
Определение:
Десятичная дробь – это дробь с упрощенной записью, где целая и дробная части разделены запятой и у которой в знаменателе стоит 10, 100, 1000 и т.д. Пример: ; ; ; . Считается, что дроби имеют целую часть равную 0.
Разряды десятичных дробей.
В записи десятичной дроби добавили запятую, как мы знаем у каждой цифры есть своя позиция. Эту позицию или место в записи называют разрядом цифры или разрядом числа. У десятичной дроби каждый разряд отличается от предыдущего в 10 раз.
Разряды и классы натуральных чисел вы изучали ранее в курсе математике. Сейчас мы разберем разряды десятичной дроби. До запятой разряды и классы десятичной дроби ничем не отличаются от разрядов и классов натуральных чисел (единицы, десятки, сотни, тысячи и т.д.). После запятой названия разрядов десятичной дроби (десятые, сотые, тысячные, десятитысячные, стотысячные, миллионные и т.д.).
Рассмотрим таблицу разрядов для десятичной дроби.
Как читается десятичная дробь?
Десятичная дробь 5,3 читается: “Пять целых три десятых”.
Десятичная дробь 52,03 читается: “Пятьдесят две целых три сотых”.
Десятичная дробь 4,017 читается: “Четыре целых семнадцать тысячных”.
Десятичная дробь 0,0017 читается: “Нуль целых семнадцать десятитысячных”.
Если внимательно посмотреть, то мы видим, что сколько нулей содержит знаменатель столько же цифр после запятой
Рассмотрим пример:
Запишите обыкновенные и смешанные дроби в виде десятичной дроби и прочитайте их: а) б) в) г) .
Решение:
а) =0,7 читается: “Нуль целых семь десятых”.
б) =2,17 читается: “Две целых семнадцать сотых”.
в) =13,003 читается: “Тринадцать целых три тысячных”.
г) =0,0011 читается: “Нуль целых одиннадцать десятитысячных”.
Следующий пример:
Прочитайте дроби и запишите их в виде обыкновенных или смешанных дробей: а) 0,1 б)15,09 в)3,013.
Решение:
а) 0,1= читается: “Нуль целых одна десятая”.
б)15,09= читается: “Пятнадцать целых девять сотых”.
в)3,013=3 читается: “Три целых тринадцать тысячных”.
Класс 5 Десятичные дроби – основы, задачи и примеры решения
- Десятичная дробь – это дробь, знаменатель которой представляет собой степень числа десять, а числитель выражается цифрами, расположенными справа от десятичной точки.
Например, 123,45 — десятичное число. Цифры слева от точки представляют собой целую часть или часть целого числа, а цифры справа от точки представляют собой десятичную или дробную часть.
- Ниже показано, как мы записываем десятичное число на диаграмме разрядности:
ШАГ 1: Рассмотрим дробь и
ШАГ 2: Теперь запишем 3 в десятых () разряде для . И напишите 4 в сотых для .
РЕШЕНИЕ: Последняя цифра в числителе (2) будет записана в десятых, так как число 12 делится на 10.
В таблице разрядов числа записываются справа налево . Из-за этого число 1 будет записано слева от десятичной точки.
РЕШЕНИЕ: Последняя цифра в числителе, 3, будет записана в сотых, так как число 123 делится на 100.
Направление записи числа в таблице разрядности справа налево. левый. Из-за этого 2 будет написано на десятом месте, а 1 будет написано на своем месте.
ПРИМЕР 1: Преобразуйте 1,03 в дробь.
РЕШЕНИЕ: Количество цифр в десятичной части равно 2. [ Считать 0 значащей цифрой, если она
— наименьшим разрядным значением.]
Напишите эквивалент дроби и десятичного числа для заштрихованной части.
ПРИМЕР 2: Преобразуйте 012,340 в дробь.
РЕШЕНИЕ:
Не считать 0 значащей цифрой:
i) Если он расположен слева от старшего разряда.
ii) Если он расположен справа от наименьшего разряда после запятой.
- Десятичные числа, имеющие одинаковое количество знаков после запятой, называются одинаковыми десятичными.
Например,
23, 2.34, 3.45
имеют по 2 десятичных знака
. Следовательно, это
, как десятичные числа. - Десятичные числа, не имеющие одинакового количества знаков после запятой, называются, в отличие от
. Например,
1,2, 2,34, 3,456
имеют десятичные
Десятичные разряды не совпадают. Следовательно,
не похожи на десятичные числа.
ПРИМЕР 1: Преобразование 6,7, 7,89, 8,901 в одинаковые десятичные дроби.РЕШЕНИЕ: 6.7 имеет 1 десятичный знак.
7,89 имеет 2 десятичных знака.
8.901 имеет 3 десятичных знака.
Наибольшее число десятичных знаков равно 3.
Следовательно, мы должны поставить два 0 в 6.7, чтобы получить 3 десятичных знака. И
один 0 в 7,89, чтобы получить три десятичных знака. Теперь числа 6,700, 7,890 и 8,901, и эти 3 подобны десятичным дробям.
- Десятичные числа можно расположить в порядке возрастания и убывания. В порядке возрастания наименьшее число ставится первым, а наибольшее — последним. В порядке убывания наибольшее число ставится первым, а наименьшее — последним.
ПРИМЕР 1: Расположите три десятичных числа 1,203, 1,23 и 0,5 в порядке возрастания.
РЕШЕНИЕ: В таблице они выглядят следующим образом:
Сравните, используя первый столбец (Единицы)
Два из них равны 1, а последний равен 0. В порядке возрастания нужно сначала наименьшее. Отсюда и вычитается 0,5.
- Теперь таблица выглядит так:
- Значение десятых долей, 2, одинаково для обоих чисел. Итак, переместимся на сотое место. В одном числе 0 в сотых, а в другом 6. 0
- Следовательно, числа в порядке возрастания: 5, 1.203, 1.23. [ОТВЕТ]
ПРИМЕР 2: Расположите числа 1,24, 0,35, 67,891 в порядке убывания.
РЕШЕНИЕ: В диаграмме стоимостей числа выглядят следующим образом:
- Сравните следующий столбец (Единицы).
1>0. Следовательно, следующее по величине число равно 1,240. - Таким образом, числа в порядке убывания 67,891>1,24>0,35>. [ОТВЕТ]
ПРИМЕР 1: Добавить 1,2 + 34,56 + 789,012
Ответ: 23,26
0,123 х 1 = | 0,123 |
0,123 х 10 = | 1,23 |
0,123 х 100 = | 12,3 |
- Сумма десятичных цифр в множимом и множителе должна быть равна десятичной цифре в произведении.
Например,
2 X 2 = 2,4 (1 десятичная цифра)
1
десятичная
цифра)
ПРИМЕР 1: Электрик зарабатывает 12,34 рупий в час.
Если в этом месяце он отработал 256 часов, то сколько он заработал?
РЕШЕНИЕ:
Деньги, заработанные электриком = рупий. (12,34 X 256)
Следовательно, электрики заработали 3130,88 рупий за 256 часов работы. [ОТВЕТ]
ПРИМЕР 2: Что больше: 12,3 х 40 или 123 х 4?
РЕШЕНИЕ: 12,3 х 40 = 12,3 х (10 х 4) = (12,3 х 10) х 4 = 123 х 4 Следовательно, 12,3 х 40 и 123 х 4 равны.
- Обычный способ деления десятичных дробей на степени десяти состоит в том, чтобы переместить десятичную точку влево на столько шагов, сколько нулей в числе 10, 100, 1000 и т. д.
Следовательно, 6,78 X 9,01 = 61,0878 [ANS]
ПРИМЕР 1: Разделите десятичное число 23,45 на целое число 5.
РЕШЕНИЕ:
Полученное частное равно 469. Следовательно, поставьте запятую через 2 знака от самого низкого разряда.
[0 дважды, так что 2 десятичных знака
знаков]
Таким образом, частное равно 4,69. [ANS]
ПРИМЕР 2: Разделите десятичное число 67,85 на другое десятичное число 2,5.
Решение:
-1750
350 [Путь 0]
-250
1000 [Точка 0]
-1000
[Точка 0]
-1000
[Точка 0]
-1000
[Точка 0]
-1000
0 дважды. Из-за этого мы должны поставить десятичную точку
на 2 знака слева от самого низкого разряда. Следовательно, ответ 27,14.
ШАГ 3: Запишите 4 с десятичной точкой через 1 пробел справа. (потому что 10 имеет 1 ноль)
Ответ= 0,4
ПРИМЕР 2: Преобразуйте 16/3 в десятичное число.
РЕШЕНИЕ:
ШАГ 1: Невозможно сделать 3 кратным 10, 100 или любой единице, за которой следует любое число. нулей.
ШАГ 3: Теперь 999 почти равно 1000, поэтому давайте запишем 5333 с запятой через 3 пробела справа. (Поскольку 1000 имеет 3 нуля)
Ответ: 5,333 [Приблизительно]
Q1) Преобразуйте следующие десятичные числа в смешанные дроби:
i)1.2 ii)23.45 iii)678.901
Q2) Расположите десятичные числа в порядке возрастания: ,3.46,2.32,1.23,7.78,2.34
Q3) Расположите десятичные числа в порядке убывания:
i)2.31,2.42,67.6,5.6,2
ii)2.08,7.89,7.98,9.87,2.34,3.42
iii )1,23,5,43,8,76,2,32,7,76
Q4) Сложите следующие числа:
i)1,2+3,4 ii)56,78+90,12 iii)345,678+901,234
Q5) Вычтите следующие числа:
I) 5,6-3,4 II) 78,901- 23,456 III) 234,567-56,789
Q6) Умножьте следующие числа:
I) II) 45,67 x 89,01 III) 234,567 x 890,123
Q8). от одиннадцати до восьмидесяти одной сотой.
В9) Если вы пробежали 1 км в понедельник, 23,45 часа во вторник, 678,901 метра в среду, сколько километров вы пробежали в общей сложности за три дня?
В10) Если разделить 2345,6785 рупий между 5 детьми, сколько получит каждый ребенок?
- Десятичные числа, имеющие одинаковое количество знаков после запятой, называются десятичными.
- Десятичные числа с неравным количеством знаков после запятой называются в отличие от
- В XX.YY целая часть — XX, а десятичная часть — YY
- При выполнении сложения или вычитания всегда выравнивайте десятичную точку.
- При умножении десятичных чисел количество знаков после запятой в произведении должно быть равно общему количеству знаков после запятой в множимом и множителе.
- При делении десятичных чисел общее количество нулей, добавляемых после наименьшего разряда, должно равняться десятичным разрядам в частном.
Десятичная дробь – определение, операции и примеры решения
Напомним, что дробь состоит из двух частей – числителя и знаменателя.
И выражается как — Числитель/Знаменатель.
Дробь или смешанное число, в котором знаменатель представляет собой степень 10, например 10, 100, 1000 и т. д., обычно выражаемая с использованием десятичной точки, называется математикой десятичных дробей.
Запись дроби в виде десятичной дроби упрощает выполнение с ней математических операций. Например, любая дробь, имеющая знаменатель в степени 10, например 53/100, может быть записана в десятичном виде как 0,53.
Примеры десятичных дробей
4/100 = 0,04
57/10 = 5,7
53/100 = 0,53
Правильный способ изучения десятичных дробей
. «, а затем прочитайте дробный компонент так же, как и целые числа, но со значением разряда последней цифры. Отдельные цифры всегда читаются как десятичное число. Десятичное число 145,367, например, может быть интерпретировано как сто сорок пять целых три десятых шесть семь.
Что такое десятичная дробь?
Дробь, в которой знаменатель, т.е. нижнее число, представляет собой степень числа 10, например 10, 100, 1000 и т. д., называется десятичной дробью. Вы можете писать десятичные дроби с десятичной точкой и без знаменателя, что упрощает выполнение вычислений, таких как сложение, вычитание, деление и умножение дробей.
Некоторые примеры десятичных дробей:
1/10 = читается как одна десятая = записывается как 0,1 в десятичных дробях.
6/1000 = читается как шеститысячные = записывается как 0,006 в десятичных дробях
Операции с десятичными дробями:
Данные числа располагаются так друг под другом, что десятичные точки лежат в одном столбце друг под другом. Числа теперь добавляются или вычитаются обычным способом.
Например: добавить 0,007 и 3,002
0. 0 0 0 7
+ 3. 0 0 0 2
____________________________
3. 0 0 0
, когда десятичная фракция умножается на полномочия 10
. , сдвиньте запятую вправо на столько знаков, сколько составляет степень числа 10.
Например, 5,9632 x 1000 = 5963,2;
0,073 x 1000 = 730.
Умножьте данные числа без десятичной точки.
Теперь в произведении Десятичная точка отмечена таким количеством знаков после запятой, как сумма количества знаков после запятой в заданных числах.
Например: нам нужно найти произведение 0,2 x 0,02 x 0,0002
Рассмотрим число без десятичной точки
Теперь 2 x 2 x 2 = 8.
Сумма десятичных разрядов = (1 + 2 + 4) = 7,
Таким образом, отметьте десятичную запятую на 7 знаков влево, что будет равно 0,0000008
0,2 x 0,02 x 0,002 = 0,0000008
Разделите заданное число без десятичной точки на заданное число. Теперь в частном отметьте запятой столько десятичных знаков, сколько есть в делимом.
Например, мы должны найти частное для 0,0204 ÷ 17
Теперь 204 ÷ 17 = 12.
Дивиденд содержит 4 знака после запятой.
Итак, 0,0204 ÷ 17 = 0,0012
Умножьте делимое и делитель на подходящую степень 10, чтобы делитель получился целым числом.
Теперь действуйте, как описано выше.
Thus, | 0.00066 | = | 0.00066 x 100 | = | 0.066 | = . 006 |
0,11 | 0,11 x 100 | 11 |
Как преобразовать десятичную дробь в дробную
Вы можете преобразовать десятичную дробь, выполнив следующие три шага.
Преобразуем 0,25 в дроби
Шаг 1: Перепишем десятичное число над единицей в виде дроби, где десятичное число — это числитель, а знаменатель — единица.
0,25/1
Шаг 2: Умножьте числитель и знаменатель на 10 в степени числа знаков после запятой.
Если после запятой одно значение, умножьте на 10, если после запятой два значения, умножьте на 100, если после запятой три значения, умножьте на 1000 и так далее.
Для преобразования 0,25 в дробь после запятой идут две цифры. Поскольку 10 во 2-й степени равно 100, мы должны умножить и числитель, и знаменатель на 100 на втором шаге.
0,25/1 x 100/100 = 25/100
Шаг 3. Выразите дробь в виде десятичной дроби и в простейшей форме.
25/100 = ¼
Выполнив приведенные выше шаги в вопросах о десятичной дроби, вы можете сделать вывод, что десятичная дробь 0,25 при преобразовании в дробь равна 1/4.
Давайте решим десятичные вопросы.
Решенные примеры
Десятичные фракции Вопросы
Преобразовать заданные фракции в десятичные фракции:
½
Раствор: ½ x 5
9 .
10 =
Решение: 10 =
= 10 1/4 x 25/25
= 10 (25/100)
= 9 02 38 90 30368 1. Джим купил 100 яблок у местного торговца фруктами и обнаружил, что пять из них гниют. Можете ли вы рассчитать дробь и десятичные дроби гнилых яблок по отношению к общему количеству яблок, купленных Джимом?
Ответ: Из 100 яблок у нас 5 гнилых. В результате Процент гнилых апельсинов составляет 5/100. Теперь мы должны преобразовать эту дробь в десятичную. Для этого мы должны разделить числитель 5 на знаменатель 100. В результате, добавив два десятичных знака к дроби 5/100, ее можно преобразовать в десятичную дробь. 0,05 — это десятичный ответ. В результате гнилые яблоки имеют десятичные дроби 0,05.
2. В классе из 80 учеников 48 учеников выбрали мороженое в качестве перекуса, а остальные ученики предпочли безалкогольные напитки. Подсчитайте процент учащихся, выбравших безалкогольный напиток, и укажите результат в десятичных дробях.