4 arccos
Вы искали 4 arccos? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 arccos 0, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «4 arccos».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 4 arccos,4 arccos 0,4 arccos 1,arccos 0 75,arccos 0 8,arccos 1 5,arccos 1 6,arccos 4,arccos 4 3,arccos 5 1,arccos 5 3,arccos калькулятор,arccos калькулятор онлайн,arccos калькулятор онлайн в градусах,arccos онлайн калькулятор,arccos онлайн калькулятор в градусах,арккосинус вычислить,арккосинус калькулятор,арккосинус калькулятор онлайн,арккосинус калькулятор онлайн в градусах,арккосинус онлайн,арккосинус онлайн калькулятор,арккосинус онлайн калькулятор в градусах,арккосинус посчитать,арккосинус посчитать онлайн,вычислите arccos cos 10,вычислить arccos,вычислить арккосинус,калькулятор arccos,калькулятор arccos онлайн,калькулятор арккосинус,калькулятор арккосинус онлайн,калькулятор арккосинуса,найти арккосинус,найти арккосинус онлайн,посчитать арккосинус.
Где можно решить любую задачу по математике, а так же 4 arccos Онлайн?
Решить задачу 4 arccos вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Урок 50. тригонометрические неравенства — Алгебра и начала математического анализа — 10 класс
Урок Конспект Дополнительные материалыТригонометрические неравенства
Решите неравенство $2sinx\leq\sqrt2$
ПодсказкаИзобразите тригонометрическую окружность, выделите дугу, соответствующую неравенству, и запишите решение
Тригонометрические неравенства
Решите неравенство
$2cosx\leq−\sqrt2$
ПодсказкаИзобразите тригонометрическую окружность, выделите дугу, соответствующую неравенству, и запишите решение
Тригонометрические неравенства
Решите неравенство $2tanx\leq−\sqrt{3}$
Изобразите тригонометрическую окружность, линию тангенсов, выделите дуги, соответствующие неравенству, и запишите решение
Тригонометрические неравенства
Заполните кроссворд
ПодсказкаВспомните основные термины темы
Тригонометрические неравентва
Соотнесите неравенства с их изображениями на окружности.
1)
2)
3)
A) $sinx\lt 1$
B) $2sinx\gt \sqrt 2$
C) $−2cosx\lt 1$
ПодсказкаИзобразите для каждого неравенства соответствующую ему дугу
Тригонометрические неравенства
Решите неравенство. Заполните пропуски
ПодсказкаВведите новую переменную, решите вспомогательное неравенство
Тригонометрические неравенства
Подставьте значение переменных в ответ, решив неравенство.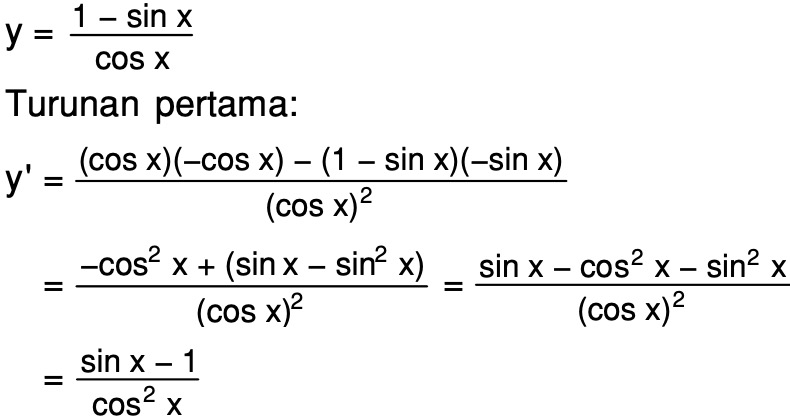 2 2 x \le 1$
2 2 x \le 1$
$\frac{\alpha\pi}{b}+\pi k;\frac{c\pi}{b}+\pi k$
ПодсказкаВыразите $\tan 2x$, затем решите простейшие неравенства
Тригонометрические неравенства
Собери решение
$\frac{1+\cos 2x}{2\cos x+1}>0$
ПодсказкаОбратите внимание, что числитель дроби всегда неотрицательный
$\lgroup\frac{-2\pi}{3}+2\pi k;\frac{-\pi}{2}+2\pi k\rgroup$
$\lgroup\frac{-\pi}{4}+2\pi k;\frac{-\pi}{2}+2\pi k\rgroup$
$\lgroup\frac{-\pi}{2}+2\pi k;\frac{\pi}{2}+2\pi k\rgroup$
$\lgroup\frac{-\pi}{2}+2\pi k;\frac{2\pi}{3}+2\pi k\rgroup$
$\lgroup\frac{\pi}{2}+2\pi k;\frac{2\pi}{3}+2\pi k\rgroup$
$\lgroup\frac{-\pi}{3}+2\pi k;\frac{\pi}{2}+2\pi k\rgroup$
Тригонометрические неравенства
Решите неравенство $\frac{1}{\cos}\ge\frac{6}{\pi}$ и выберите правильный ответ
ПодсказкаРассмотрите разность левой и правой частей, приведите к общему знаменателю и решите методом интервалов
Тригонометрические неравенства
Решите неравенство $\frac{1}{\sin x}\ge\frac{4}{\pi}$ и введите пропуски в ответ
ПодсказкаРассмотрите разность левой и правой частей, приведите к общему знаменателю и решите методом интервалов
Тригонометрические неравенства
Сопоставьте неравенства с их решениями
A) $\sqrt{2\cos 8x+3}\le 3-\sqrt{5-\sin 4x}$
B) $\sqrt{-1-2\cos 10x}\ge 2-\sqrt{3\sin 5x-2}$
C) $\sqrt{\cos 6x+2}\le 2-\sqrt{4-3\sin 3x}$
1) $x=\frac{\pi}{10}+\frac{2\pi k}{5}, k\in Z$
2) $x=\frac{\pi}{8}+\frac{\pi k}{2}, k\in Z$
3) $x=\frac{\pi}{6}+\frac{2\pi k}{3}, k\in Z$
ПодсказкаУчитывайте свойства подкоренных выражений и область возможных значений $\sin x$ и $\cos x$
Тригонометрические неравенства
Подставьте значение переменных в ответ, решив неравенство.
$0,5\cos 2x\le\sin x\cos x$
Ответ: $\lbrack\frac{\alpha\pi}{b}+2\pi k;\frac{c\pi}{b}+2\pi k\rbrack$
1) a=____
1) b=____
1) c=____
ПодсказкаИспользуйте формулу синуса двойного аргумента
Тригонометрические неравенства
Подставьте значение переменных в ответ, решив неравенство.
$\cos 2x<\sin x$
Ответ: $(\frac{\alpha\pi}{b}+2\pi k;\frac{c\pi}{b}+2\pi k)$
1) a=____
1) b=____
3) c=____
ПодсказкаВведите новую переменную и решите вспомогательное неравенство
Тригонометрические неравенства
Подставьте значение переменных в ответ, решив неравенство.
$\cos (\frac{2\pi}{3}-4x)+\cos(\frac{2\pi}{3}+4x)-\frac{1}{2}<0 x$
Ответ: $(\frac{\alpha\pi}{b}+2\pi k;\frac{c\pi}{b}+2\pi k)$
1) a=___
2) b=___
3) c=___
ПодсказкаПреобразуйте сумму косинусов в произведение
Шпаргалка: Вопросы по алгебре — 5rik.ru
основные тригонометрические тождества;
доказательство формул;
мнемоническое правило.
Свойства тригонометрических функций:
sin x, y= cos x, y= tg x, y= ctg x.
Их графики.
Определения синуса, косинуса, тангенса и котангенса через тригонометрический
круг.
Простейшие тригонометрические уравнения.
Определения и свойства обратных тригонометрических функций: y= arcsin x, y= arccos x, y= arctg x, y= arcctg x.
Их графики.
Простейшие тригонометрические неравенства (sin x < a).
Любая производная из листа, таблицы.
Правила вычисления производной (Лагранж).
Геометрический смысл производной:
производная в данной точке;
уравнение касательной;
угол между прямыми.
Физический смысл производной.
Экстремумы функций. Правила нахождения их с помощью производной.
Возрастание и убывание функции. Правило Лагранжа.
Наибольшее и наименьшее значение функции. Правила. На эту тему.
Многочлены. Теорема Безу, ее доказательство.
Правила нахождения рациональных корней, доказательство.
Четность, периодичность.
Вычислить cos 22,5° sin(arcsin11/12)-cos(arccos1/6) tg(arcsin21/29) tg(arccos1/4) tg(arcctg7) sin(arccos1/3)-cos(arcsin(-1/3)) sin(arctg12)+cos(arcctg(-2)) cos(arctg(-5))-sin(arctg3) cos(p /2+arcsin3/4) cos(p -arctg17) cos(3p /2+arcctg(-4)) cos(2p -2arccos(-Ö 3/2)) sin(p /2-arccos1/10) sin(p +arctgÖ 3/7) sin(3p /2-arcctg81) sin(2p -3arcsinÖ 2/2) tg(p /2-arccos(-1/3)) tg(3p /2+4arctgÖ 3/3) tg(p +arcsin(-2/17)) tg(2p -arcctg(-5)) arcsin(-Ö 3/2) arcsin1 arcsin(-1) arccos(-Ö 3/2) arccos0 arccos(-1) arctg(-1/Ö 3) arctg(-1) arctg1 arcctg(-1/Ö 3) arcctg(-1) arcctg0 cos(arctg2) sin(arctg(-3/4)) tg(arcctg(-3)) sin(arcctg p) tg(arcsin p), -1 cosÖ 3 sin2× sin4× sin6 cos5× cos7× cos8 tg(-1)× tg3× tg6× tg(-3) ctg1× ctg(-2)× ctg9× ctg(-12) sin(-3)× cos4× tg(-5) / ctg6 sin7× cos(-8) / tg6× ctg(-5) (sin6+cos(-4)) / (tg(-2)+ctg(-10)) (sin(-8)+cos9) / cos11tg(-9) (cos10× sin7-tg10) / cos(-Ö 2)× ctg(-4) arcsin(tg(-1/2))+arctg(cos(-4)) sin(-212° ) sin3p /7× cos9p /8× tg2,3p sin1× cos3× ctg5 sin1,3p × cos7p /9× tg2,9 sin8× cos0,7× tg6,4 sin7p /6× cos3p /4 sin5p /3× cos2p /5× cos7p /4 sin1,3× cos(-1,5)× sin(-1,9) sin23° -sin36° cos37° -cos18° cosp /9-cos2p /9 cos212° -cos213° sin310° -sin347° cos5p /6-cos5p /7 sinp /12-sinp /18 cos3p /7-cos3p /11 cosp /11-sinp /11 sin2p /3-cos3p /4 sin16° -cos375° ctg153° -ctg154° tg319° -tg327° tg(33p /8)-tg(37p /9) ctg(101p /14)-ctg(251p /27) tgp /6-ctgp /4 tgp /6-ctgp /6 Решить уравнения: sin(x2 + x) =1/2; 4 — сos2 x = 4sinx 5 — 2cosx = 5Ö 2sin(x/2) cos4x = cos2x sin4x + cos4x = sin2x-1/2 sin2x + 3sin2x — 2сos2x = 2 cos(x/2) + 3/2sinx + 5sin2(x/2) = 3 sinx — 2cosx = 1 cos6x + sin6x — cos22x = 1/16 cos2x — sin3x× cosx + 1 = sin2x + sinx× cos3x tgx — tg2x = sinx 2sin3x — cos2x — sinx = 0 2cos2x = Ö 6(cosx — sinx) 1 — sinx = cosx — sin2x 2Ö 3sin2(x/2) + 2 = 2sin2x + Ö 3 1 + cos(x2 + 1) = sin2(x2 + 1) 2sinx× cos2x + cos4x = 2sinx + cos2x + cos2x tg2x + ctg2x + 3tgx + 3ctgx +4 = 0 1 + cos(x/2) + cosx = 0 1 — sin(x/2) = cosx 2sin2x + cos4x = 0 sin4x + 2cos2x = 1 5sinx — 4ctgx = 0 3cosx + 2tgx = 0 1 + 4cosx = cos2x 2cos2x + 5sinx + 1 = 0 cos2x + 3Ö 2sinx — 3 = 0 2cos2x + 4cosx =sin2x 2cos2x + sin3x = 2 cos4x + 4sin2x = 1 + 2sin22x 4 — 6cosx = 3 sin2x — sin2(x/2) 5 + 2sin2x — 5cosx = 5sinx cos4x + 8sin2x — 2 = 6cos2x — 8 cos4x 4 — 3cos4x = 10sinx× cosx sin4x = (1 +Ö 2)(sin2x + cos2x — 1) cos(10x + 12) + 4Ö 2sin(5x + 6) = 4 sin3x + cos3x = 1 — 1/2sin2x ctg2x — tg2x = 16cos2x 1 + sinx + cosx + sin2x + cos2x = 0 1/2(cos2x + cos22x) — 1 = 2sin2x — 2sinx — sinx — sin2x tg(p /2× cosx) = ctg(p /2× sinx) sin3x — sinx + cos2x = 1 2cos2x + 3sinx = 0 2sin2x + 1/cos2x = 3 2sin2x + Ö 3cosx = 0 Ö 1 + sinx¢ + cosx = 0 sin4x + cos4x = sin2x 4cos4x + 6sin22x + 5cos2x = 0 cos2x + 4sin3x = 1 1 — sin2x = -(sinx + cosx) 4sin22x — 2cos22x = cos8x 8sin4x + 13cos2x = 7 2sinx + 3sin2x = 0 cos(x/2) = 1 + cosx sin2x = 1 + Ö 2cosx + cos2x sin2x = Ö 3sinx 2cos23x — cos3x = 0 Ö 3sin2x = 2cos2x 3sin2x — cos2x — 1 = 0 Ö 3sin2x — cos2x = Ö 3 Доказать:tg208° <sin492°
Что больше:sin1 или cos1
tg1 или tg2
Калькулятор
— cos (10) — Solumaths
Резюме:
Тригонометрическая функция cos вычисляет косинус угла в радианах,
градусы или градианы.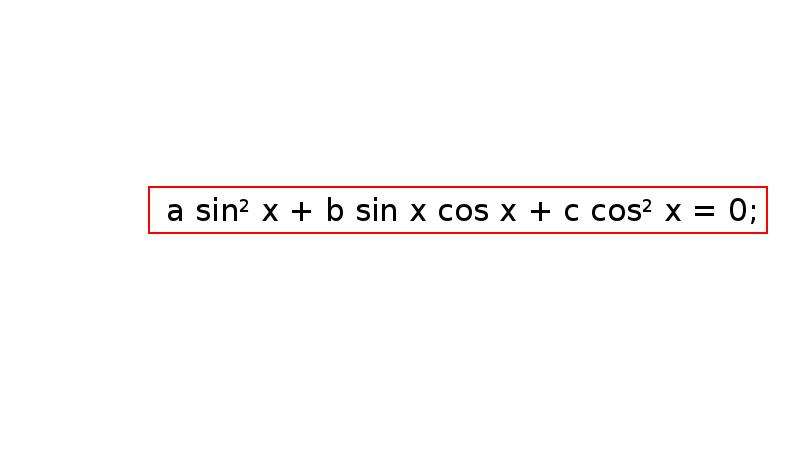
Описание:
Калькулятор позволяет использовать большинство тригонометрических функций , можно вычислить косинус , синус и касательная угла через одноименные функции..
Тригонометрическая функция косинус отмечена cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, градианы и радианы, которые являются угловыми единицами по умолчанию.
- Расчет косинуса
- Специальные значения косинуса
Косинус для вычисления угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, сначала необходимо
выберите желаемую единицу измерения, нажав кнопку параметров модуля расчета. После этого можно приступать к расчетам.
После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн числа «пи / 6», введите cos (`pi / 6`), после вычисления результат sqrt (3) / 2 возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу щелкнув по кнопке опций модуля расчета.После этого вы можете приступить к расчету.
Чтобы вычислить косинус 90, введите cos (90), после вычисления restults 0 возвращается.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать желаемую единицу измерения. щелкнув по кнопке опций модуля расчета. После этого вы можете приступить к расчету.
щелкнув по кнопке опций модуля расчета. После этого вы можете приступить к расчету.
Чтобы вычислить косинус 50, введите cos (50), после вычисления возвращается результат sqrt (2) / 2.
Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и выполнять исчисление со специальными связанными точными значениями.
Косинус допускает некоторые особые значения, которые калькулятор может определять в точной форме. Вот список специальные значения косинуса :
Производная косинуса равна -sin (x).
Первообразная косинуса равна sin (x).
Функция косинуса является четной функцией для каждого действительного x: `cos (-x) = cos (x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
В калькуляторе есть решающая программа, позволяющая решать уравнение с косинусом имеет вид cos (x) = a .Расчеты для получения результата детализированы, поэтому можно будет решить такие уравнения, как `cos (x) = 1 / 2` или же `2 * cos (x) = sqrt (2)` с шагами расчета.
Тригонометрическая функция cos вычисляет косинус угла в радианах, градусы или градианы.
Синтаксис:
cos (x), где x — мера угла в градусах, радианах или градианах.Примеры:
cos (`0`), возвращает 1Производный косинус:
Чтобы дифференцировать функцию косинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса
Производная от cos (x) — это производная_вычислителя (`cos (x)`) = `-sin (x)`
Первоначальный косинус:
Калькулятор первообразной функции косинуса позволяет вычислить первообразную.
Первообразная от cos (x) — это первообразная_вычислителя (`cos (x)`) = `sin (x)`
Предельный косинус:
Калькулятор пределов позволяет вычислить пределы функции косинуса.
Предел для cos (x) равен limit_calculator (`cos (x)`)
Косинус обратной функции:
Функция, обратная косинусу , — это функция арккосинуса, отмеченная как arccos.
Графический косинус:
Графический калькулятор может строить функцию косинуса в интервале ее определения.
Свойство функции косинус:
Функция косинуса является четной функцией.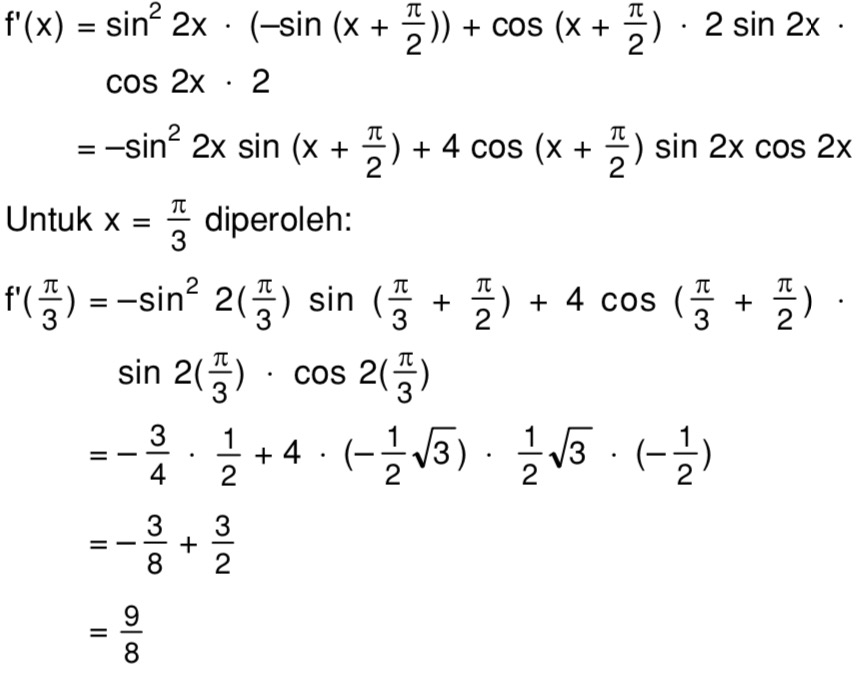
Рассчитать онлайн с cos (косинусом)
Распространенных математических ошибок
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Ошибки триггера
Это довольно короткий раздел, но он содержит некоторые ошибки, которые, как я вижу, постоянно делают мои студенты, изучающие математику, поэтому я подумал, что включу их здесь как отдельный раздел.
градусов по сравнению с радианами
Большинство курсов по триггерингу, которые я видел, имеют тенденцию концентрироваться на выполнении задач в градусах. Я полагаю, это потому, что ученикам легче визуализировать, но в действительности почти все вычисления выполняются в радианах, и студенты слишком часто выходят из класса триггеров, плохо подготовленных к работе со всеми радианами в классе исчисления.
Вы просто должны привыкнуть делать все в радианах в классе исчисления.Если вас попросят оценить \ (\ cos \ left (x \ right) \) в \ (x = 10 \), мы просим вас использовать 10 радиан, а не 10 градусов! Ответы очень и очень разные! Рассмотрим следующее:
\ [\ begin {array} {lcl} \ cos \ left ({10} \ right) = — 0,8329076 & \ hspace {0,5in} & {\ mbox {в радианах}} \\ \ cos \ left ({10} \ right) = 0,984807753012 & \ hspace {0,5 дюйма} & {\ mbox {в градусах}} \ end {array} \]
Вы заметите, что это даже не один и тот же знак!
Итак, будьте осторожны и убедитесь, что вы всегда используете радианы при работе с функциями триггера в классе триггеров. Убедитесь, что ваш калькулятор настроен на вычисления в радианах.
Убедитесь, что ваш калькулятор настроен на вычисления в радианах.
\ (\ cos \ left (x \ right) \) НЕ является умножением
Я вижу, как студенты постоянно пытаются выполнить оба следующих действия.
\ [\ begin {eqnarray *} \ cos \ left ({x + y} \ right) & \ ne & \ cos \ left (x \ right) + \ cos \ left (y \ right) \\ \ cos \ left ({3x} \ right) & \ ne & 3 \ cos \ left (x \ right) \ end {eqnarray *} \]Это просто неправда. Единственная причина, которую я могу придумать для этих ошибок, заключается в том, что ученики должны думать о \ (\ cos \ left (x \ right) \) как об умножении чего-то, что называется \ (\ cos \) и \ (x \).Это далеко от истины! Косинус — это функция, а \ (\ cos \) используется для обозначения того, что мы имеем дело с функцией косинуса!
Если вы не уверены, что это неправда, просто выберите пару значений для \ (x \) и \ (y \) и подключитесь к первому примеру.
\ [\ begin {eqnarray *} \ cos \ left ({\ pi + 2 \ pi} \ right) & \ ne & \ cos \ left (\ pi \ right) + \ cos \ left ({2 \ pi} \ right) \\ \ cos \ left ({3 \ pi} \ right) & \ ne & — 1 + 1 \\ — 1 & \ ne & 0 \ end {eqnarray *} \] Итак, ясно, что первое неверно, и мы могли бы провести аналогичный тест для второго примера.
Я полагаю, что проблема в том, что иногда для них есть истинные значения. Например, вы можете использовать \ (x = \ frac {\ pi} {2} \) во втором примере, и обе стороны будут равны нулю, поэтому это будет работать для этого значения \ (x \). В целом, однако, для подавляющего большинства ценностей в мире это просто неправда!
О более общем примечании.{- 1}} x = \ arccos x \]
sin40 cos10 cos40 sin10 qqqq As cos (xy sin y cos xcos … · As cos (x- y) = sin y cos xcos y +
Pearson Education Ltd 2017. Копирование разрешено только для закупочной организации. Этот материал не авторское право свободно.1
Смешанное упражнение по тригонометрии и моделированию
1 ai sin40 cos10 cos40 sin10
1
sin (40 10) sin 302
ii 1 1
cos15 sin152 2
cos 45 cos15 sin15 sin15
1cos (45 15) cos60
2
iii 1 tan15 tan 45 tan15
1 tan15 1 tan 45 tan15
3tan (45 15) tan30
3
2
3 a
b
1 5
3 351
33
tan tan Использование tan ()
1 tan tan
2 1
1 2
45
A BA B
AB
AB
As cos (x — y ) = грех у
cos xcos y + sin xsin y = sin y (1)
Нарисуйте прямоугольный треугольник,
, где sin x = 1
5
Используя теорему Пифагора,
a2 = 5 () 2
— 1 = 4 a = 2
Итак, cos x = 2
5
Подставляем в (1):
2
5cos y +
1
5sin y = sin y
2cos y + sin y = 5sin y
2cos y = sin y 5-1 ()
2
5-1 = tan y tan y =
sin y
cos y
tan y = 2 5 +1 ()
5 -1 () 5 +1 ()
= 2 5 +1 ()
4 =
5 +1
2
tan A = 2, tan B =
1
3, поскольку y =
1
3x —
1
3
Требуемый угол составляет (A- B).
Pearson Education Ltd 2017. Копирование разрешено только для закупающих организаций. Этот материал не защищен авторскими правами. 2
4
sin (30) sin (30)
4 5
5sin (30) 4sin (30)
5 (sin cos30 cos sin 30)
4 (sin cos30 cos sin 30)
sin cos30 9cos sin 30
sin sin 30 9 9 tan 30
cos cos30
3 tan 9 3 3
3
5
арифметической прогрессии,
sin (30) 3 cos sin sin (30 )
2sin (30) sin 3 cos
2 (sin cos30 cos sin 30)
sin 3 cos
3 sin cos sin 3 cos
sin 3 1 cos 3 1
3 1 tan
3 1
Калькулятор va
1 3 1 blue is tan 753 1
Никаких других значений, кроме значительных.
6 a
3 54125 5 13 13
sin, cos sin, cos AABB
i
ii
55612
2 119514412
2
1
5144 120
b
7 a
2
2 8 31 2 1
5 55
b
2
3 9 42 1 2 1
10 510
Использование
sin B
sin B
sinC
c
Поскольку три значения являются последовательными членами
sin (A + B) = sin Acos B + cos Asin B
=
3
5
12
13+
4
5
5
13 =
56
65
tan2B =
2tan B
1- tan2 B
cosC = cos 180- (A + B) ()
= -cos (A + B )
= — (cos Acos B — sin Asin B)
= -4 90 005
5
12
13-
3
5
5
13
= -33
65
cos2x 1- 2sin2 x
cos2y 2cos2 2017 -1 год4 . Копирование разрешено только для закупочной организации. Этот материал не защищен авторскими правами. 3
Копирование разрешено только для закупочной организации. Этот материал не защищен авторскими правами. 3
7 c
i
71
3 3
2 13 3
27
1
ii
Как и острые, и,
острые
5So
не может быть
4 4
xyxy
xy
xy
8 a
1 1 5
2 3 6
5sin () 5 (sin cos cos sin)
1 1 1 1 55 5
2 3 6 6
xyxyxy
b
tan 3
tan 2
3tan 3so tan
2 2
x
y
y kx
c
2
000 4k
9 a 23sin2 2sin 1
23 sin 2 1 2sin cos 2
sin 2 1 1 tan 2
cos 2 3 3
b 1
tan 2, for 0 2 23
7 7
2« 6 6 12 12
10 а cos2 5sin
2
2
cos 2 5sin 0
1 2sin 5sin 0
2sin 5sin 1 0
a = 2, b = 5 и c = 1
b 22sin 5sin 1 0
Использование квадрокоптера формула
25 5 4 (2) (1) sin
2 (2)
5 33
4
sin 0. 1861, для
1861, для
sin положительно, поэтому решения в первом и втором квадрантах
1 1sin 0,1861, sin 0,1861
0,187, 2,954 (3 dp)
11 a cos (60) cos cos60 sin sin 60x xx
1 3
cos sin2 2
xx
So 1 3
2sin cos sin2 2
xxx
12
32
3 1 2 sin cos
2 2 2
1 2 1 tan
3 4 3xx
x
b 1
tan 0.44 (2 dp) 4 3
x
, в интервале
0 360
tan положителен, поэтому решения в первом и третьем квадрантах
23,8, 203,8 (1 dp) x
tan (x + y ) = tan x + tan y
1- tan x tan y
tan (x — y) = tan x — tan y
1+ tan x tan y =
53
53
= 1
sin (x + y) sin xcos y + cosxsin y
sin xcos y
cos xsin y =
12
13
= 3
2
tan2x = 2tan x
1- tan2 x =
3k
1- 94k 2
Pearson Education Ltd 2017. Копирование разрешено только для закупочной организации. Этот материал не защищен авторскими правами. 4
Копирование разрешено только для закупочной организации. Этот материал не защищен авторскими правами. 4
12 a cos (20) sin (90 20) xx
sin (70) x
sin70 cos cos70 sinx x (1)
4sin (70) 4sin 70 cosx x
4cos70 sin x (2)
As (1) = (2)
4sin70 cos 4cos70 sinx x
sin70 cos cos70 sinx x
5sin cos70 3sin 70 cos
3tan tan 70
5
xx
x
b
tan tan 705
x, для 0180
tan отрицательный, поэтому решение находится во втором квадранте
13
180 tan tan 705
x
1180 tan (1.648)
180 (58,8) 121,2 (1 d.p.)
x
x
13 a Нарисуйте прямоугольный треугольник и найдите
sin и cos.
3 4 sin, cos
5 5
3sin () 4cos ()
3 (sin cos cos sin)
4 (cos cos sin sin)
4 3 3 sin cos
5 5
4 3 4 cos sin
5 5
12 9 16 12 sin cos cos sin
5 5 5 5
25 cos 5
5
cos
b cos (270) x
cos cos 270 sin грех 270
(0. 8) (0) (0,6) (1)
8) (0) (0,6) (1)
0 0,6 0,6
xx
cos (540) x
cos cos540 sin sin 540
(0,8) (1) (0,6) (0)
0,8 0 0,8
xx
14 a Одного примера достаточно, чтобы опровергнуть
утверждение. Пусть 60, 0
сек () сек (60 0)
1 сек 60 2
cos 60
1 сек сек 60 2
cos 60
1 сек сек0 1
cos 0
So сек сек 2 1 3
So sec (60 0) sec60 sec0
sin () sec sec неверно
AB
AB
A
B
AB
ABAB
для всех значений,.AB
b LHS загар
2 2
12
sin cos
cos sin
sin cos
sin cos
1
sin 2
2 2 Использование sin cos 1 и
2sin cos
So 2
LHS sin 2
2cosec 2
RHS
Pearson Education Ltd 2017. Копирование разрешено только для закупочной организации. Этот материал не защищен авторскими правами. 5
15 a 2
2 tan Использование tan 2 с
1 tan 8
8
2
8
2
2
2
2 tan tan
4 1 tan
2So 1
1
1 2
2 1 0
2 8 2 2 2
2 2
1 2
Как острый, tan 8 8
положительный, поэтому tan 2 18
t
t
t
tt
tt
t
b 4 8
4 8
tan tan3tan tan
8 4 8 1 tan tan
1 2 1 2 9000 2
12 2 2
2 2 2 2
22 2 2 1
2
16 a Пусть sin 3cos sin () xx x R
2
2 2
sin cos cos sin
0 , 0 90
Сравнить sin: cos 1 (1)
Сравнить cos: sin 3 (2)
90 004 Разделить (2) на (1): tan 360
3 1 4 2
So sin 3 cos 2sin (60)
R x R x
R
x R
x R
RR
xxx
b Нарисуйте 2sin (60), сначала переведя sin на 60 на
вправо, а затем растягивая результат
в направлении с коэффициентом масштабирования 2.
yx
y
График соответствует оси -ax, когда 0,
ie 2sin (60) 3, at 0, 3
График соответствует оси -axis, когда 0,
ie (300, 0), (120, 0 ),
(60, 0), 240, 0)
yx
y
xy
17 a Let 7cos 2 24sin 2 cos (2) R
2 2 2
cos 2 cos sin 2 sin
0, 02
Сравнить cos 2: cos 7 (1)
Сравнить sin 2: sin 24 (2)
24 Разделить (2) на (1): tan
7
1.29 (2 dp)
24 7 25
So 7 cos 2 24sin 2 25cos (2 1,29)
RR
R
R
R
RR
b 14cos2 48sin cos
1 cos 21 (2sin cos)
2
7 (1 cos 2) 24sin 2
7 7cos 2 24sin 2
Максимальное значение
7cos 2 24sin 2 равно 25
с использованием (a) с cos (2 1,29) 1
Таким образом, максимальное значение
7 7cos 2 24sin 2 7 25 32
Pearson Education Ltd 2017.Копирование разрешено только для закупочной организации.
