Arcsin 1 sin: Is arcsin(x)=1/sin? | Wyzant Ask An Expert

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )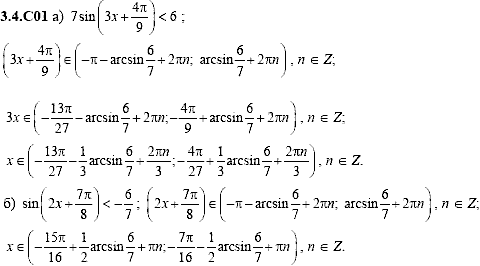
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

определение, формула, таблица, график, свойства

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Обратная тригонометрическая функция: Арксинус (arcsin)

• Определение
• График арксинуса
• Свойства арксинуса
• Таблица арксинусов

Определение

Арксинус (arcsin) – это обратная тригонометрическая функция.

Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.

Если синус угла у равен х (sin y = x), значит арксинус x равняется y:

arcsin x = sin^-1 x = y

Примечание: sin^-1x означает обратный синус, а не синус в степени -1.

Например:

arcsin 1 = sin^-1 1 = 90° (π/2 рад)

График арксинуса

Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):

Свойства арксинуса

Ниже в табличном виде представлены основные свойства арксинуса с формулами.

Свойство	Формула
Синус арксинуса	sin (arcsin x) = x
Арксинус синуса	arcsin (sin x) = x + 2kπ, где k∈ℤ (k — целое число)
Арксинус отрицательного числа	arcsin (-x) = -arcsin x
Дополнительные углы	arcsin x = π/2 — arccos x = 90° — arccos x
Сумма арксинусов	ru/wp-content/uploads/2020/02/arcsin-summa-exc.png" class="stbSkipLazy aligncenter size-full" width="590" height="1318" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsin-summa-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arcsin-summa-exc.png" class="stbSkipLazy aligncenter size-full" width="590" height="1318" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsin-summa-exc.png" />»>
Разность арксинусов	ru/wp-content/uploads/2020/02/arcsin-raznost-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arcsin-raznost-exc.png" class="stbSkipLazy aligncenter size-full" width="590" height="1344" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsin-raznost-exc.png" />»>
Косинус арксинуса	ru/wp-content/uploads/2020/02/arcsinus-formula-exc-3.png" class="stbSkipLazy aligncenter size-full" width="300" height="598" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arcsinus-formula-exc-3.png" />»>
Тангенс арксинуса	ru/wp-content/uploads/2020/02/arcsinus-formula-exc-5.png" />»>
Производная арксинуса	png" />»>
Неопределенный интеграл арксинуса

microexcel. ru

Таблица арксинусов

x	arcsin x (рад)	arcsin x (°)
-1	-π/2	-90°
-√3/2	-π/3	-60°
-√2/2	-π/4	-45°
-1/2	-π/6	-30°
0	0	0°
1/2	π/6	30°
√2/2	π/4	45°
√3/2	π/3	60°
1	π/2	90°

microexcel. ru

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Решение уравнений sinx=a.

Понятие арксинуса числа

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Решение уравнений sinx=a. Понятие арксинуса числа.

Понятие арксинуса числа а
Число называют арксинусом
6
1
2
и записывают
1
arcsin
6
2
1
arcsin
6
2
Арксинусом числа a 1;1 называется такое число
; , синус которого равен а
2 2
arcsin a = α, если sinα = a и
2
2
arcsin a = α, если sinα = a и
2
2
например
2
arcsin
2
4
и
2
так как sin
4
2
2
4
2
arcsin(-a)=-arcsina

4.

АРКСИНУС ЧИСЛА• Например
2
arcsin
;
2
4
arcsin 0 0;
3
arcsin
;
3
2
т.к.
т.к.
т.к.
2
; sin
.
2 4 2
4
2
2
0
2
; sin 0 0.
3
; sin
.
2 3 2
3 2

5. АРКСИНУС ЧИСЛА ОСНОВНЫЕ ФОРМУЛЫ

• Например
2
2
1
1
2 arcsin 3 arcsin
2 arcsin
2
2
2
2
3
13
3 2
4
6
4
3
12
1
3
2.
2 arcsin 1 5 arcsin 0
arcsin
2
2
1. 3 arcsin
1
3
arcsin
2 5 0
2
2
2
1
7
2 3
6
6
вычислить
3
3
arcsin
arcsin
2
2
3
arcsin(-a)=- arcsina
arcsin1-arcsin(-1)=arcsin1+arcsin(1)= 2 2
Определим, имеют ли смысл выражения:
Выражение имеет смысл, если удовлетворяет условию
1 sin x 1
1) arcsin (√5) — выражение не имеет смысла, так как √5 > 1;
2) arcsin (√2/3) — выражение имеет смысл, так как – 1
√2/3
1;
3) arcsin (-π/5) — выражение имеет смысл, так как – 1
— π /5
1;
4) arcsin (-√3) — выражение не имеет смысла, так как -√3 < -1.

8. При каких значениях х имеет смысл выражение:

1. arcsin(x²-1)
-1≤ х²-1 ≤ 1
0 ≤ х² ≤2
Ответ:
2.arcsin(5-2x)
—
1≤ 5-2х ≤1
-6≤ -2х ≤ -4
2≤ х ≤3
Ответ: [2;3]
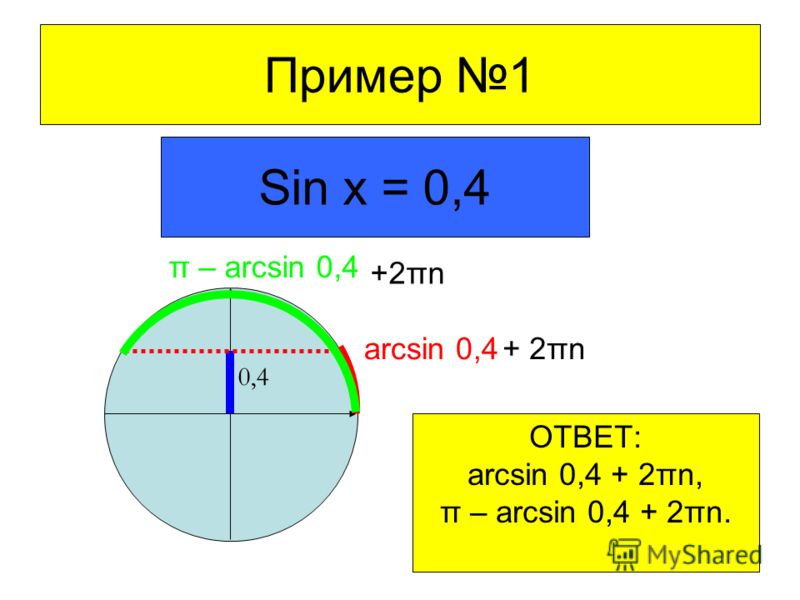
Решить уравнение sin x=a
По определению:
синусом углаα называется ордината точки
-1
0
1
И значит определения синуса
следует, что 1 sin x 1
Поэтому, если sinx = 2,5, то уравнение
не имеет корней т.к 2,5>1
уравнение sinx= -1,5 тоже не имеет корней
т.к -1,5<-1
Решить уравнение
M1
x2
5
6
1
Ординату, равную 2 имеют
две точки окружности М и М1, т.к
1
1
2
0
1
sin x
2
M
1
sin
2
6
6
-1
То точка М1 получена
поворотом точки Р(0;1)
5
на угол равный x2 6
а также на углы x 5 2 k ,
5
6
6
6
То точка М получена
поворотом точки Р(0;1)
на угол равный x1
а также на углы
где k=±1,±2….
x
6
6
2 k ,
Получили , что решением уравнения являются
х1
6
2 k
x2
6
где k=±1,±2….
2 k
Эти 2 корня можно объединить в одну формулу
x ( 1)
n
6
n, n Z
1
sin x
2
значит x1 6 2 k
5
6
1
2
6
5
x2
2 k
6
k Z
Объединим в одну формулу
x ( 1) n n,
6
n Z
n 1
x
(
1
)
n,
Преобразуем ее по свойствам
6
степени в вид
n Z

13. Уравнение sinx=a

1
sin 2 x
2
1
2 x 1 arcsin n
2
n
2 x 1
n
x 1
n
Ответ:
1 n
12
n
2
12
6
, n Z.
n
n
2
, n Z.
вывод
Корни уравнения sin x=a
Выражаются общей формулой
Если а > 0, то
x ( 1) n n,
6
n Z
Если а< 0,то
x ( 1) n n,
6
n Z

15. Солнышко, запомни

sin x 5
3
sin x
2
2
sin x
2
Корней нет
x 1 k , k Z
6
k
x 1
k 1
4
k , k Z
Решить уравнение
2
sin x
3
2
x ( 1) arcsin
n,
3
n Z
n
Решить уравнение
x
2 sin 1
3
x
1
sin
3
2
х
1
n
( 1) arcsin
n, n Z
3
2
arcsin( a) arcsin a
х
1
( 1) n arcsin
n, n Z
3
2
х
1
n 1
( 1)
arcsin
n, n Z
3
2
х
1
( 1) n 1 arcsin
n, n Z
3
2
x ( 1) n 1
ответ
( 1)
n 1
3
3 n, n Z
4
3
3 n, n Z
4
1
2
2
2

19.

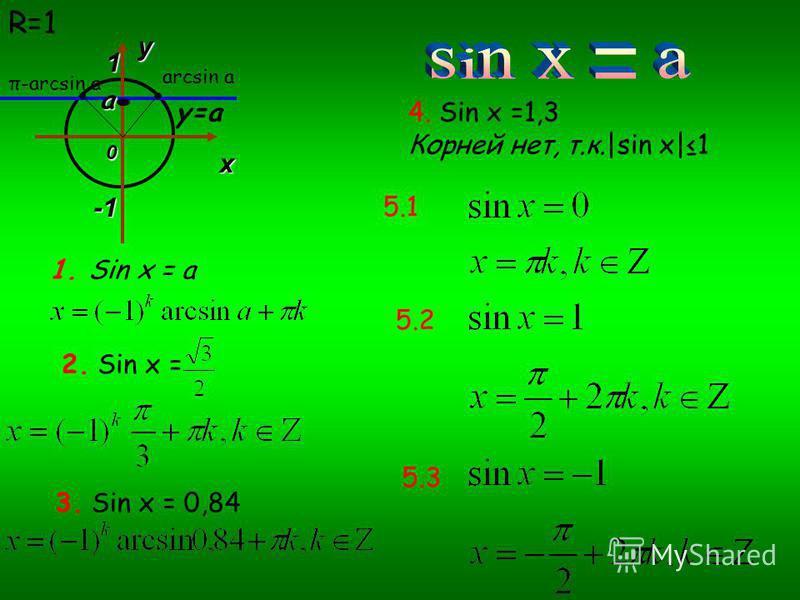Уравнение sinx=a3sin x 1 2 sin x 1 0
3sin x 1 0;
2sin x 1 0;
1
sin x ;
3
1
sin x ;
2
1
x 1 arcsin n, n Z .
3
n
x ( 1)
n 1
n,
6
n Z
1
Ответ: 1 arcsin 3 n, n Z .
n
( 1)
n 1
n, n Z
6

20. Обратите внимание, никаких х в ответе нет, тем более с индексами

Частные случаи
sin x = 1
sin x = -1
у
у
x
2
2 k, k Z
у
х
х
sin x = 0
x
2
2 k, k Z
х
x πk, k Z

22. Тренируемся решать:

1. Sin 5x = 1
5x
2
2 k, k Z
2
k, k Z
x
10 5
2
k, k Z
Ответ :
10 5

23. Тренируемся решать:

sin x
0
4
x
4
x
4
n, n
n, n
Ответ :
4
n, n

English     Русский Правила

Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом, сумма арксинуса и арккосинуса числа, арктангенс от тангенса

Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg

Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.

Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.

Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса

Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.

для α∈-1, 1  sin(arccis α)=α,   cos(arccos α)=α,для α∈(-∞, ∞)  tg(arctg α)=α, ctg(arcctg α)=α

Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.

Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса

для -π2≤α≤π2  arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α

Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.

Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел

В этом блоке мы сформулируем важное утверждение:

Определение 1

Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.

для α∈-1, 1  arccis (-α)=-arcsin α,   arccos (-α)=π-arccos α,для α∈(-∞, ∞)  arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α

Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.

Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс

Они выглядят следующим образом:

для α∈-1, 1  arccis α+arccos α=π2,для α∈(-∞, ∞)  arctg α+arcctg α=π2

Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.

Формулы связи между прямыми и обратными тригонометрическими функциями

Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.

-1≤α≤1,sin (arcsin α)=α	-1≤α≤1,sin (arccos α)=1-α2	-∞≤α≤+∞,sin (arctg α)=α1+α2	-∞≤α≤+∞, sin (arcctg α)=11+α2
-1≤α≤1,cos (arcsin α)=1-α2	-1≤α≤1,cos (arccos α)=α	-∞≤α≤+∞,cos (arctg α)=11+α2	-∞≤α≤+∞, cos (arcctg α)=11+α2
-1<α<1,tg (arcsin α) =α1-α2	α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α	-∞≤α≤+∞,tg (arctg α)=α	α≠0 ,tg (arcctg α)=1α
α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α	-1<α<1,ctg (arccos α)=α1-α2	α≠0,ctg (arctg α)=1α	-∞≤α≤+∞, ctg (arcctg α)=α

Теперь разберем примеры, как они применяются в задачах.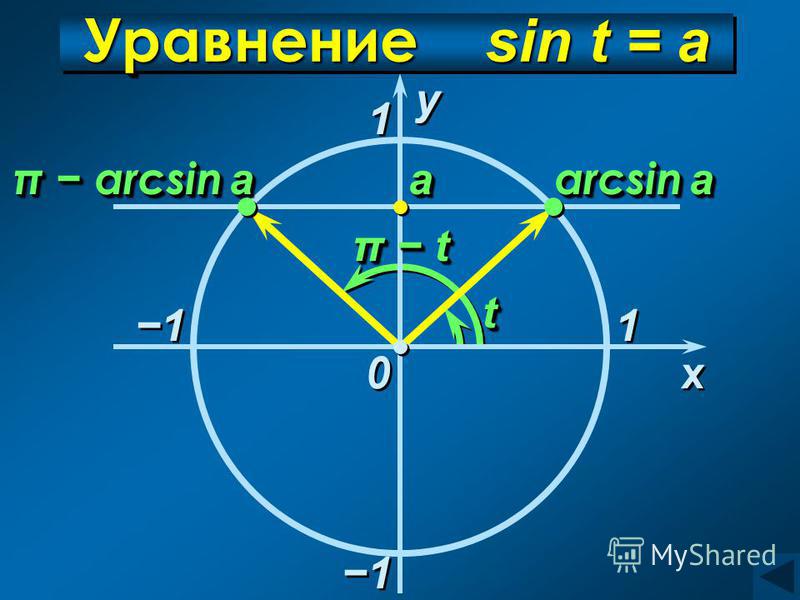

Пример 1

Вычислите косинус арктангенса из 5.

Решение

У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2

Подставляем нужное значение: cos(arctg5)=11+(5)2=26

Пример 2

Вычислить синус арккосинуса 12.

Решение

Для этого нам понадобится формула: sin (arccos α)=1-a2

Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32

Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32

Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.

Доказательства формул синусов арккосинуса, арккотангенса и арктангенса

Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:

sin2α+cos2α=11+ctg2α=1sin2α

Вспомним, что tgα·ctgα=1. Из этого можно получить:

sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π

У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.

Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.

Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.

Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.

Все наши расчеты можно сформулировать более емко:

1. sinα=1-cos2α, 0≤α≤π

Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2

2. sinα=tgα1+tgα, -π2<α<π2,

Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2

3. sinα=11+ctg2α, 0<α<π

Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2

Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.

Их мы выведем по имеющемуся шаблону:

1. Из cosα=1-sin2α, -π2≤α≤π2 следует, что

cos(arcsin α)=1-sin2(arcsin α)=1-a2

2. Из cosα=11+tg2α, -π2<α<π2 следует, что
3. Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2

следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2

Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса

1. Исходим из tgα=sin α1-sin2α, -π2<α<π2. Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.
2. Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем

tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).

3. Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.

Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:

ctgα=1tgα

Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса.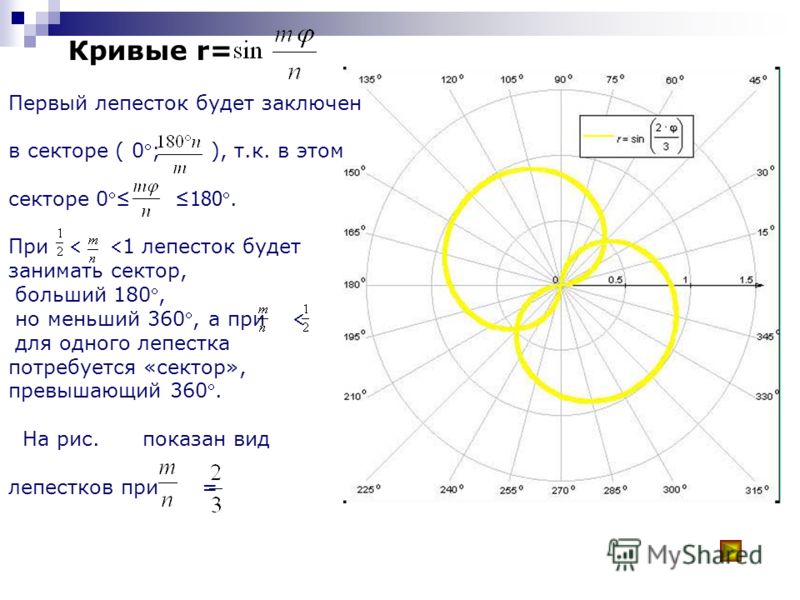 Для этого понадобится поменять в них местами числитель и знаменатель.

Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее

Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.

Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:

arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0

А так мы выразим арккосинус через остальные обратные функции:

arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1

Формула выражения арктангенса:

arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0

Последняя часть – выражение арккотангенса через другие обратные функции:

arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0

Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.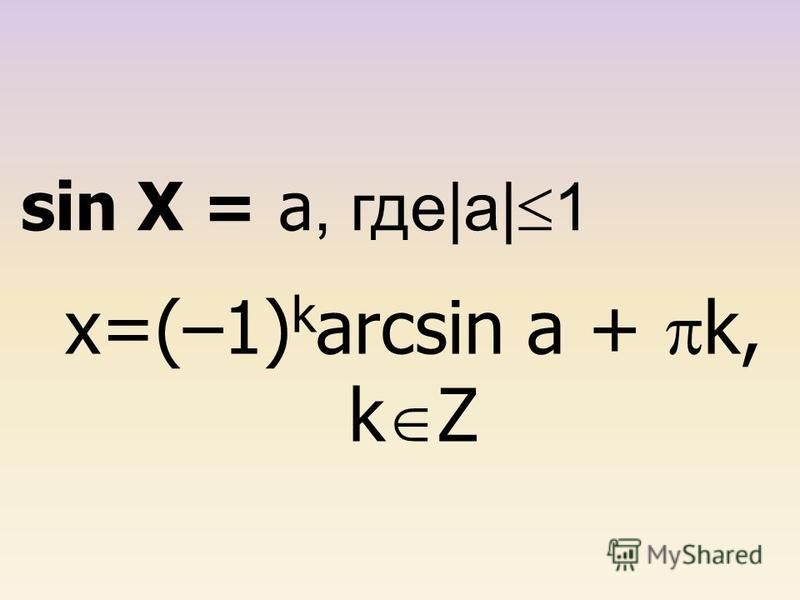

Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.

Мы знаем, что arctgα1-α2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:

sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α

Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.

Вывод: arcsina=arctga1-a2, -1<a<1

Прочие формулы доказываются по аналогии.

В завершение разберем один пример применения формул на практике.

Пример 3

Условие Вычислить синус арккотангенса минус корня из 3.

Решение

Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0
Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π

В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12

Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2  sin(arcctg(-3))=11+(-3)2=12

Прочие формулы с обратными функциями

Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.

Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:

sin2α2=1-cosα2

Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:

sinα2=1-cosα2

Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:

sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2

Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:

arccosα2=arcsin1-α2

Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.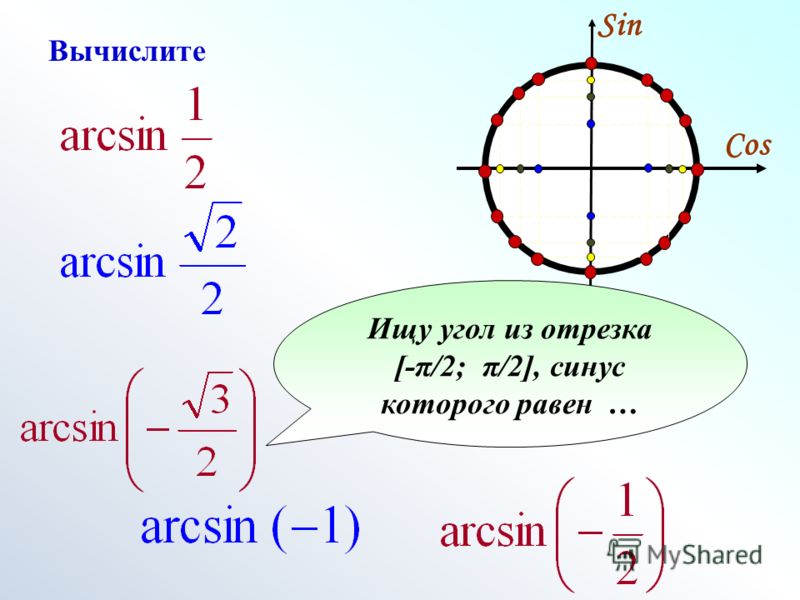

В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Арксинус. Решение простейших уравнений с синусом. Часть 2

Арксинусом числа \(a\) (\(a∈[-1;1]\)) называют число \(x∈[-\frac{π}{2};\frac{π}{2}]\) синус которого равен \(a\) т.е.

\(\arcsin ⁡a=x\)     \(<=>\)     \(\sin ⁡x=a\)

Примеры:

\(\arcsin⁡{\frac{\sqrt{2}}{2}}=\frac{π}{4}\) потому что \(\sin ⁡\frac{π}{4}=\frac{\sqrt{2}}{2}\) и \(\frac{π}{4}∈[-\frac{π}{2}; \frac{π}{2}]\)
\(\arcsin ⁡1=\frac{π}{2}\) потому что \(\sin⁡\frac{π}{2}=1\) и \(\frac{π}{2}∈[-\frac{π}{2};\frac{π}{2}]\)
\(\arcsin ⁡0=0\) потому что \(\sin ⁡0=0\) и \(0∈[-\frac{π}{2};\frac{π}{2}] \)
\(\arcsin⁡\sqrt{3}\) – не определен, потому что \(\sqrt{3}>1\)

Проще говоря, арксинус обратен синусу.

На круге это выглядит так:

     

Как вычислить арксинус?

Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от \(-\frac{π}{2}\) до \(\frac{π}{2}\) ) равен аргументу арксинуса?

Например, вычислите значение арксинуса:

а) \(\arcsin⁡(-\frac{1}{2})\)
б) \(\arcsin⁡(\frac{\sqrt{3}}{2})\)
в) \(\arcsin(-1)\)

а) Синус какого числа равен \(-\frac{1}{2}\)? Или в более точной формулировке можно спросить так: если \(\sin ⁡x=-\frac{1}{2}\), то чему равен \(x\)? Причем, обратите внимание, нам нужно такое значение, которое лежит между \(-\frac{π}{2}\) и \(\frac{π}{2}\). Ответ очевиден:

\(\arcsin⁡(-\frac{1}{2})=-\frac{π}{6}\)

б) Синус какого числа равен \(\frac{\sqrt{3}}{2}\)? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ \(\frac{π}{3}\).

\(\arcsin⁡(-\frac{\sqrt{3}}{2})=-\frac{π}{3}\)

в) Синус от чего равен \(-1\)?
Иначе говоря, \(\sin ⁡x=-1\), \(x=\) ?

\(\arcsin⁡(-1)=-\frac{π}{2}\)

Тригонометрический круг со всеми стандартными арксинусами:

Зачем нужен арксинус? Решение уравнения \(\sin x=a\)

Чтобы понять зачем придумали арксинус, давайте решим уравнение: \(\sin ⁡x=\frac{1}{2}\).

Это не вызывает затруднений:

\( \left[ \begin{gathered}x=\frac{π}{6}+2πn, n∈Z\\ x=\frac{5π}{6}+2πl, l∈Z\end{gathered}\right.\)

Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.

А теперь решите уравнение: \(\sin ⁡x=\frac{1}{3}\).

Что тут будет ответом? Не \(\frac{π}{6}\), не \(\frac{π}{4}\), даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?

Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin⁡\frac{1}{3}\), потому что известно, что синус равен \(\frac{1}{3}\). Длина дуги от \(0\) до правой точки тогда тоже будет равна \(\arcsin⁡\frac{1}{3}\). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному \(\arcsin⁡\frac{1}{3}\) от \(π\), то её значение составляет \(π- \arcsin⁡\frac{1}{3}\).

Ок, значение этих двух точек нашли. Теперь запишем полный ответ: \( \left[ \begin{gathered}x=\arcsin \frac{1}{3}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{3}+2πl, l∈Z\end{gathered}\right. \) Без арксинусов решить уравнение \(\sin ⁡x=\frac{1}{3}\) не получилось бы. Как и уравнение \(\sin ⁡x=0,125\), \(\sin ⁡x=-\frac{1}{9}\), \(\sin⁡ x=\frac{1}{\sqrt{3}}\) и многие другие. Фактически без арксинуса мы можем решать только \(9\) простейших уравнений с синусом:

С арксинусом – бесконечное количество.

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac{1}{\sqrt{3}}\).
Решение:

Ответ:   \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac{1}{\sqrt{2}}\).

Решение:
Кто поторопился написать ответ \( \left[ \begin{gathered}x=\arcsin \frac{1}{\sqrt{2}}+2πn, n∈Z\\ x=π-\arcsin \frac{1}{\sqrt{2}}+2πl, l∈Z\end{gathered}\right.\), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров \(\arcsin⁡ \frac{1}{\sqrt{2}}\) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}= \frac{\sqrt{2}}{2}\). Таким образом, получаем:

\(\arcsin⁡ \frac{1}{\sqrt{2}} = \arcsin \frac{\sqrt{2}}{2}=\frac{π}{4}\)

Значит в ответе вместо арксинусов нужно написать \(\frac{π}{4}\).

Ответ:   \( \left[ \begin{gathered}x=\frac{π}{4}+2πn, n∈Z\\ x=\frac{3π}{4}+2πl, l∈Z\end{gathered}\right.\)

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=\frac{7}{6}\).

Решение:
И вновь тот, кто поторопился написать \( \left[ \begin{gathered}x= \arcsin \frac{7}{6}+2πn, n∈Z\\ x=π- \arcsin\frac{7}{6}+2πl, l∈Z\end{gathered}\right. \) на ЕГЭ потеряет \(2\) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать \(\arcsin⁡\frac{7}{6}\)? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен \(1\) и больше или равен \(-1\). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.

Ответ:   решений нет.

Думаю, вы уловили закономерность.

Если \(\sin ⁡x\) равен не табличному значению между \(1\) и \(-1\), то решения будут выглядеть как: \( \left[ \begin{gathered}x= \arcsin a +2πn, n∈Z\\ x=π- \arcsin a +2πl, l∈Z\end{gathered}\right.\)

Арксинус отрицательного числа

Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:

\(\arcsin⁡({-a})=-\arcsin ⁡a\)

Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:

Примеры:

\(\arcsin⁡(-0,7)=-\arcsin⁡ 0,7\)
\(\arcsin⁡(-\frac{\sqrt{3}}{2})=-\arcsin⁡\frac{\sqrt{3}}{2}=-\frac{π}{6}\)
\(\arcsin⁡(-\frac{\sqrt{7}}{2}) \neq -\arcsin⁡\frac{\sqrt{7}}{2}\)

Удивил последний пример? Почему в нем формула не работает? Потому что запись \(\arcsin⁡(-\frac{\sqrt{7}}{2})\) в принципе неверна, ведь \(-\frac{\sqrt{7}}{2}<-1\), а значит арксинус от \(-\frac{\sqrt{7}}{2}\) взять нельзя – он не вычислим, не существует, точно также как \(\sqrt{-5}\) или \(\frac{3}{0}\).

Пример. Решите тригонометрическое уравнение: \(\sin ⁡x=-\frac{1}{\sqrt{3}}\).

Решение:
Можно воспользоваться готовой формулой и написать:

\( \left[ \begin{gathered}x=\arcsin (-\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π-\arcsin (-\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)

\( \left[ \begin{gathered}x=-\arcsin (\frac{1}{\sqrt{3}})+2πn, n∈Z\\ x=π+\arcsin (\frac{1}{\sqrt{3}})+2πl, l∈Z\end{gathered}\right.\)

Но я фанатка круга, поэтому:

Ответ:   \( \left[ \begin{gathered}x=-\arcsin \frac{1}{\sqrt{3}}+2πn, n∈Z\\ x=π+\arcsin \frac{1}{\sqrt{3}}+2πl, l∈Z\end{gathered}\right.\)

На всякий случай, уточню, что при решении уравнений написанное синим писать не обязательно – это скорее пояснения, как надо рассуждать.

Смотрите также:
Синус
Тригонометрические уравнения

Мэтуэй | Популярные задачи

92

1	Найти точное значение	грех(30)
2	Найти точное значение	грех(45)
3	Найти точное значение	грех(30 градусов)
4	Найти точное значение	грех(60 градусов)
5	Найти точное значение	загар (30 градусов)
6	Найти точное значение	угловой синус(-1)
7	Найти точное значение	грех(пи/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	грех(45 градусов)
10	Найти точное значение	грех(пи/3)
11	Найти точное значение	арктан(-1)
12	Найти точное значение	cos(45 градусов)
13	Найти точное значение	cos(30 градусов)
14	Найти точное значение	желтовато-коричневый(60)
15	Найти точное значение	csc(45 градусов)
16	Найти точное значение	загар (60 градусов)
17	Найти точное значение	сек(30 градусов)
18	Найти точное значение	cos(60 градусов)
19	Найти точное значение	cos(150)
20	Найти точное значение	грех(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	загар (45 градусов)
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 градусов)
25	Найти точное значение	сек(45 градусов)
26	Найти точное значение	csc(30 градусов)
27	Найти точное значение	грех(0)
28	Найти точное значение	грех(120)
29	Найти точное значение	соз(90)
30	Преобразовать из радианов в градусы	пи/3
31	Найти точное значение	желтовато-коричневый(30)
32
35	Преобразовать из радианов в градусы	пи/6
36	Найти точное значение	детская кроватка(30 градусов)
37	Найти точное значение	арккос(-1)
38	Найти точное значение	арктан(0)
39	Найти точное значение	детская кроватка(60 градусов)
40	Преобразование градусов в радианы	30
41	Преобразовать из радианов в градусы	(2 шт. )/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	тан(пи/2)
45	Найти точное значение	грех(300)
46	Найти точное значение	соз(30)
47	Найти точное значение	соз(60)
48	Найти точное значение	соз(0)
49	Найти точное значение	соз(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	сек(60 градусов)
53	Найти точное значение	грех(300 градусов)
54	Преобразование градусов в радианы	135
55	Преобразование градусов в радианы	150
56	Преобразовать из радианов в градусы	(5 дюймов)/6
57	Преобразовать из радианов в градусы	(5 дюймов)/3
58	Преобразование градусов в радианы	89 градусов
59	Преобразование градусов в радианы	60
60	Найти точное значение	грех(135 градусов)
61	Найти точное значение	грех(150)
62	Найти точное значение	грех(240 градусов)
63	Найти точное значение	детская кроватка(45 градусов)
64	Преобразовать из радианов в градусы	(5 дюймов)/4
65	Найти точное значение	грех(225)
66	Найти точное значение	грех(240)
67	Найти точное значение	cos(150 градусов)
68	Найти точное значение	желтовато-коричневый(45)
69	Оценить	грех(30 градусов)
70	Найти точное значение	сек(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	КСК(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	загар((5pi)/3)
75	Найти точное значение	желтовато-коричневый(0)
76	Оценить	грех(60 градусов)
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3 пи)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	угловой синус(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	КСК(45)
83	Упростить	арктан(квадратный корень из 3)
84	Найти точное значение	грех(135)
85	Найти точное значение	грех(105)
86	Найти точное значение	грех(150 градусов)
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	загар((2pi)/3)
89	Преобразовать из радианов в градусы	пи/4
90	Найти точное значение	грех(пи/2)
91	Найти точное значение	сек(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	угловой синус(0)
95	Найти точное значение	грех(120 градусов)
96	Найти точное значение	желтовато-коричневый ((7pi)/6)
97	Найти точное значение	соз(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразование градусов в радианы	88 градусов

тригонометрия — Разница между арксинусом и арксинусом.

Спросил 3 года, 9 месяцев назад

Изменено 17 дней назад

Просмотрено 26 тысяч раз

$\begingroup$

Впервые я узнал, что арксинус и арксинус — это два способа сказать одно и то же.

Но потом я подумал о том, что функция обратного синуса является функцией, поэтому она должна быть ограничена в диапазоне от -1 до +1.

Как бы вы назвали синусоидальную функцию, отраженную через линию y=x, диапазон которой не ограничен? 9{-1}(0,5)=\frac{\pi}{6}$ ?

Если нет и они оба имеют только одно решение, то как бы вы представили граф с бесконечными решениями?

Я нашел это:

https://www.dummies.com/education/math/trigonometry/how-to-distinguish-between-trigonometry-functions-and-relations/

буквы используются для различения функций и отношений.

• тригонометрия
• обратная функция

$\endgroup$ 9{-1}(x)$) является уникальной функцией, так что:

$$\arcsin(\sin(x)) = \sin(\arcsin(x)) = x $$

Теперь обратимся к другим вашим вопрос. $\arcsin(x)$ ЕСТЬ функция. Если вы хотите узнать ее область определения и диапазон, сначала рассмотрите область определения и диапазон $\sin(x)$

Это ограниченная периодическая функция, областью определения которой являются все действительные числа, а диапазоном значений является от -1 до 1 включительно. . Напомним, что домен и диапазон инверсий переключаются. Следовательно, область определения $\arcsin$ лежит в диапазоне от -1 до 1 с вертикальными асимптотами в точках -1 и 1, а диапазоном являются все действительные числа:

$\endgroup$

1

$\begingroup$

Если я правильно понял ваш вопрос, вы хотите задать следующее:

• У меня есть неинъективная функция; это означает, что существуют два значения $x_1$ и $x_2$ с $x_1\neq x_2$ и $f(x_1)=f(x_2)$

  В вашем случае: $f(x)=\sin(x)$

• Теперь я рисую график $x=f(y)$

  Поскольку функция не является инъективной, граф содержит несколько точек с одной и той же координатой $x$.

• Существует ли для таких графов определенный термин (слово, название)?
• Существует ли специальный термин для какой-либо функции $g(y)=\{x:f(x)=y\}=\{x_1,x_2,…\}$?

Сомневаюсь что существует определенный термин (слово, имя) для таких графиков и/или функций вообще.

Особенно в случае «обратной функции» вы должны помнить, что функция имеет ровно одно функциональное значение для заданного аргумента функции. 9*(0)=\{0,\pm\pi,\pm 2\pi,\pm 3\pi…\}$.

Однако я сомневаюсь, что имя такой функции существует.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 9{-1}$?

Спросил 6 лет, 3 месяца назад

Изменено 1 год, 5 месяцев назад

Просмотрено 7к раз

$\begingroup$

У меня домашняя проблема. {-1}(x)= \theta,$$ где $\theta$ — единственный угол между $-\pi/2$ и $\pi/2$ (включительно), такой, что $\sin\theta = x$, который часто называют главным значением. 9{-1}\, $ — всего лишь две разные записи для одного и того же отображения.

Определение : Арксинус $x$, обозначаемый как $\operatorname{Arcsin}(x)$, определяется как «множество всех углов, синус которых равен $x$». Его можно интерпретировать как отношение «один ко многим».

Определение : арксинус от x, обозначаемый $\arcsin(x)$, определяется как «(единственный) угол из замкнутого интервала $[-\pi/2, +\pi/2]$ синус которого равен $x$». Его можно интерпретировать как отношение один к одному. 9{-1}}\left(\frac1 2\right) = \left.\left\{\frac{\pi}{6} + 2k\pi, \frac{5\pi}{6} + 2k\pi \\право| \ k \in \mathbb Z\right\} $$

См. также определения и иллюстрации этих функций/отображений в электронной книге The Algebra Help на сайте MathOnWeb. com.

---

Редактировать:

Кажется, что определения имен с заглавными и строчными буквами поменяны местами . Несколько других источников — см. ответ jgon — определяют их противоположным образом.

$\endgroup$ 9-1(x) в Desmos или графический калькулятор, настроенный на радианы, вы можете увидеть график функции арксинуса (обратная функция $\sin x$). Вы также увидите, что линия резко обрывается в точках $x=-1$ и $x=1$, а также $y=-\pi/2$ и $y=\pi/2$. Так как для любого одного значения $x$ не может быть двух значений $y$, график останавливается. Обозначим этот отрезок как «арксинус». Но если бы график продолжался как отношение, он выглядел бы как синусоида, простирающаяся от $y=-\infty$ до $y=\infty$. Мы обозначаем это как «арксинус».

Надеюсь, кому-то это будет полезно.

$\endgroup$

1

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. 2 + 1}}$$ 92 + 1}} = \sin(\arctan(x)) \blacksquare$$

$\endgroup$

$\begingroup$

Положим $\arctan 2 = x$, тогда $\tan x= 2$, поэтому $\sin x = {2\over \sqrt{5}}$ и $\cos x = {1\over \sqrt{5 }}$.

Пусть $\arcsin {1\over \sqrt{10}}= y$, поэтому $\sin y = {1\over \sqrt{10}}$, поэтому $\cos y = {3\over \sqrt{ 10}}$.

Сейчас:

$$\sin{(\arctan{2}-\arcsin{\frac{1}{\sqrt{10}}})} = \sin (xy) = \sin x \cos y- \cos x \sin y= {\sqrt{2}\over 2} $$

92 u}} = \tan u \cos u = \sin u = \sin( \arctan x).$$

$\endgroup$

2

$\begingroup$

$$\sin{(\arctan{2}-\arcsin{\frac{1}{\sqrt{10}}})} = \\\sin (xy) =\\ \sin x \cos y- \cos x \sin y= \frac{2}{\sqrt 5}.\frac{3}{{\sqrt {10}}}-\frac{1}{\sqrt 5}.\frac{1}{ {\ sqrt {10}}} \\ = \\\ frac {6-1} {\ sqrt {50}} = \ frac {1} {\ sqrt2} \ to xy = \ frac {\ pi} {4} $$

$\endgroup$

$\begingroup$

Если $t=\arcsin\dfrac1{\sqrt{10}},0

$\имплицит t=\arctan\dfrac13$

Теперь $\arctan2-\arctan\dfrac13=\arctan\dfrac{2-\dfrac13}{1+\dfrac23}=\dfrac \pi4$

$\endgroup$

1

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Arcsin 1 — значение, градусы, радианы, примеры

Значение arcsin 1 равно 90 градусам или π/2 радианам. Прежде чем мы научимся вычислять значение sin, обратное 1, давайте сначала вспомним значение обратной тригонометрической функции arcsin. Arcsin или Sin inverse — это обратная функция тригонометрической функции синуса, обозначаемая как arcsin x или sin ^-1 x. Arcsin 1 или sin, обратный 1 дает значение угла, соответствующее значению, когда функция синуса равна 1. Мы можем найти значение sin, обратное 1, используя единичный круг и его координаты, которые задаются (cos x, sin x).

Далее в этой статье мы определим значение arcsin 1 с помощью единичного круга и таблицы тригонометрии в градусах и радианах (две единицы измерения угла). Мы также выразим значение sin, обратное 1, через число пи (π). Мы решим несколько примеров и оценим значение функции arcsin для разных значений, чтобы лучше понять концепцию.

1.	Что такое Arcsin 1?
2.	Значение Sin, обратное 1, с использованием единичного круга
3.	Arcsin 1 в градусах
4.	Синус, обратный 1, в радианах
5.	Arcsin 1 в терминах Пи
6.	Часто задаваемые вопросы по Arcsin 1

Что такое Arcsin 1?

Арксинус 1 дает меру угла, для которого значение синусоидальной функции равно 1. Синус и арксинус обратны друг другу и определяются как, sin: [–π/2, π/2] → [-1 , 1] и arcsin: [-1, 1] → [–π/2, π/2] такие, что если sin x = y, то x = sin ^-1 y. Используя таблицу тригонометрии, мы знаем, что sin (π/2) = 1 или sin 90° = 1. Таким образом, используя обратное определение sin, мы получаем значение arcsin 1 как sin 9.1381 -1 (1) = π/2 рад или 90°.

Значение Sin, обратное 1, с использованием единичного круга

Мы знаем, что координаты точек на единичной окружности задаются как (cos θ, sin θ), где θ — угол, образованный положительной осью x, координата x — это cos θ, а координата y — это sin θ. Чтобы найти значение sin, обратное 1, нам нужно найти угол, образуемый с положительной осью x, когда координата y, sin θ равна 1. Ниже приведено изображение единичного круга (круг с радиусом равен 1 единице). Как мы видим на изображении, когда угол, образованный с положительной осью x (в направлении против часовой стрелки), равен π/2 радианам, тогда координаты точки на окружности равны (0, 1).

Итак, мы имеем (cos θ, sin θ) = (0, 1), когда угол с положительной осью x в направлении против часовой стрелки равен π/2 радианам или 90 градусам. Следовательно, значение sin θ равно 1, когда угол равен π/2 радиан. Другими словами, мы можем сказать, что θ равно π/2 радианам, когда sin θ равен 1, что означает, что значение sin, обратное 1, равно π/2 рад или 90 градусам.

Arcsin 1 в градусах

Теперь, когда мы знаем значение arcsin 1, давайте выразим его в градусах. Как обсуждалось ранее, функция arcsin определяется как arcsin: [-1, 1] → [-90°, 90°], то есть его домен и диапазон равны [-1, 1] и [-90°, 90°] соответственно. Кроме того, поскольку мы знаем, что синусоидальная функция является периодической, мы знаем, что sin θ = 1 для бесконечного множества значений θ = 90°, 450°, 810° и так далее. Но так как мы ограничили область определения синусоидальной функции до [–90°, 90°], мы имеем, что синусоидальная функция равна 1 только тогда, когда угол равен 90°, который лежит в интервале главных значений [–90°, 90° ]. Итак, значение arcsin 1 в градусах равно 90 градусам, то есть arcsin 1 = 90°.

Инверсия Sin 1 в радианах

Поскольку мы знаем, что главная ветвь arcsin определяется как arcsin: [-1, 1] → [–π/2, π/2], где [–π/2, π/2] — диапазон sin обратная функция. Итак, используя таблицу тригонометрии, мы имеем

arcsin 1 = θ

⇒ sin θ = 1

⇒ sin θ = sin π/2 — [Поскольку sin π/2 = 1]

⇒ θ = π /2, где π/2 лежит в диапазоне главной ветви [–π/2, π/2]

Следовательно, значение sin, обратное 1, равно π/2 радианам. Это также можно интерпретировать как arcsin 1 в радианах, равном 1,57079. 633 рад.

Arcsin 1 в терминах Pi

Поскольку мы знаем, что arcsin 1 равен 90 градусам, мы преобразуем это значение sin, обратное 1, в радианы, чтобы выразить его в пи, используя формулу преобразования градусов в радианы. Формула для преобразования градусов в радианы:

Угол в радианах = Угол в градусах × π / 180° — [Умножение угла в градусах на π/180]

⇒ Арксинус 1 в пересчете на π = 90 ° × π / 180°

= π/2 радиан

Следовательно, arcsin 1 в терминах числа пи определяется как π/2 рад.

Важные замечания по арксинусу 1

• Арксинус 1 равен 90° или π/2 радианам.
• Функция арксинуса определяется арксинусом от [-1, 1] → [–90°, 90°].
• Синус, обратный 1 в радианах, равен 1,57079633 рад.

☛ Связанные темы:

• Производная от Arcsin
• Интеграл от Sin, обратный
• Арккосинус

Часто задаваемые вопросы по Arcsin 1

Что такое Arcsin 1?

Arcsin 1 дает меру угла, для которого значение функции синуса равно 1. Значение arcsin 1 равно 90 градусам или π/2 радианам.

Как найти значение Sin, обратное 1?

Мы можем определить значение arcsin 1, используя единичный круг и таблицу тригонометрии в градусах и радианах. Мы знаем, что координаты точек на единичной окружности задаются как (cos θ, sin θ). Чтобы найти значение sin, обратное 1, нам нужно найти угол, образуемый с положительной осью x, когда координата y sin θ равна 1,9.0909

Что такое Sin, обратный 1, в градусах?

Значение sin, обратное 1, в градусах равно 90 градусам, то есть arcsin 1 = 90°.

Что такое арксинус 1 в радианах?

Значение sin, обратное 1, равно π/2 радианам. Это также можно интерпретировать как arcsin 1 в радианах, равном 1,57079633 рад.

Как записать значение Arcssin 1 в терминах числа Пи?

Синус, обратный 1 в терминах числа пи, равен π/2 рад. У нас есть

sin θ = sin π/2 — [Поскольку sin π/2 = 1]

⇒ θ = π/2

Каково значение арксинуса 1 по корню 2?

Значение arcsin 1 для корня 2 равно 45 градусам, поскольку sin 45° = 1/√2.

Что такое Sin, обратный 1 на 2?

Значение sin, обратное 1 на 2, равно π/6 радиан, поскольку sin (π/6) = 1/2, а π/6 лежит в интервале [–π/2, π/2].

Каково значение арксинуса (-1)?

Значение arcsin (-1) равно -π/2 рад, поскольку arcsin (-1) = — arcsin 1 = — π/2 рад.

Калькулятор арксинуса. Нахождение обратной функции синуса.

Создано Ханной Памула, кандидатом наук

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 30 августа 2022 г.

Содержание:

• Что такое арксинус?
• График арксинуса x
• Обратный синус, тригонометрические функции и другие соотношения
• Пример использования калькулятора арксинуса твоя проблема. Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно помнить, это ограниченный домен арксинуса (-1 ≤ синуса ≤ 1). Если вам интересно что такое арксинус или как выглядит график арксинуса x , не ждите больше — прокрутите вниз и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинуса, таких как отношение между интегралом арксинуса и производной. Так чего же ты ждешь?

  Что такое арксинус?

  Арксинус является обратной функцией синуса. Другими словами, это помогает найти угол треугольника, для которого известно значение синуса. Поскольку домен синуса для действительных чисел равен [−1, 1] , мы можем вычислить арксинус только для чисел в этом интервале.

  Синус — это периодическая функция, поэтому существует несколько чисел, имеющих одинаковое значение синуса. Например, sin(0) = 0, но также sin(π) = 0, sin(2π) = 0, sin(-π) = 0 и sin(-326π) = 0. Следовательно, если кто-то хочет вычислить arcsin( 0), ответ может быть 0, 2π (360°) или -π (-180°), чтобы назвать несколько вариантов! Все они верны, но обычно мы даем только одно число, называемое главным значением .

  Сокращение	Определение	Домен arcsin x для реального результата	Диапазон обычных основных значений
  arcsin(x) sin -1 x, asin	х = грех(у)	-1 ≤ х ≤ 1	-π/2 ≤ y ≤ π/2 -90° ≤ y ≤ 90°

  Arcsin(x) является наиболее распространенным обозначением, так как sin ^-1 x может привести к путанице (поскольку sin ^-1 x ≠ 1/sin(x) ). Аббревиатура asin обычно используется в языках компьютерного программирования.

  График арксинуса x

  Поскольку базовая функция синуса не является взаимно однозначной, ее область определения должна быть ограничена, чтобы арксинус также был функцией. Обычно выбирается область -π/2 ≤ y ≤ π/2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции арксинуса составляет [−π/2,π/2], а область арксинуса находится между [−1,1]. Ниже вы можете найти график арксинуса (x), а также некоторые часто используемые значения арксинуса:

  х	угловой синус(х)		График
  	°	рад
  -1	-90°	-π/2	Geek3, CC BY-SA 4. 0 через Wikimedia Commons
  -√3 / 2	-60°	-π/3
  -√2 / 2	-45°	-π/4
  -1/2	-30°	-π/6
  0	0°	0
  1/2	30°	π/6
  √2 / 2	45°	№/4
  √3 / 2	60°	п/3
  1	90°	п/2

  Хотите знать, откуда взялся этот график арксинуса x? Его можно найти, отразив график sin(x) между диапазоном [-π/2 π/2] через линию y = x:

  Jaro. p CC BY-SA 3.0, через Wikimedia Commons

  Обратный синус, тригонометрические функции и другие отношения

  Связь между тригонометрическими функциями и арксинусом может помочь вам лучше понять тему. Хорошей отправной точкой является прямоугольный треугольник с гипотенузой длиной 1.

  Небольшое напоминание: для прямоугольного треугольника функция синуса принимает угол θ и возвращает отношение противоположности к гипотенузе, которое равно x в нашем примерном треугольнике. Функция обратного синуса, арксинус, принимает отношение противоположности к гипотенузе (x) и возвращает угол θ. Итак, зная, что для нашего треугольника arcsin(x) = θ, мы также можем написать, что:

  • Синус: sin(arcsin(x)) = x
  • Косинус: cos(arcsin(x)) = √(1-x²)
  • Тангенс: tan(arcsin(x)) = x / √(1-x²)

  Другие полезные соотношения с арксинусом:

  • arcsin(x) = π/2 - arccos(x)
  • арксинус(-х) = -арксинус(х)

  Иногда также необходимы интеграл и производная от arcsin:

  • интеграл от arcsin: ∫arcsin(x) dx = x arcsin(x) + √(1 - x²) + C
  • производная от arcsin: d/dx arcsin(x) = 1 / √(1 - x²) , где х ≠ -1, 1

  Пример использования калькулятора арксинуса

  Арксинус — полезная функция, например, при нахождении угла прямоугольного треугольника. Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, известная теорема Пифагора не будет столь полезной. Нахождение углов прямоугольного треугольника требует применения арксинуса:

  • для α: sin(α) = a/c, поэтому α = arcsin(a/c)
  • для β: sin(β) = b/c, поэтому β = arcsin(b/c)

  Итак, давайте предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α:

  1. Введите значение, которое вы хотите найти арксинус . В нашем случае это 6/10. Итак, вы можете ввести значение как 0,6, но подойдет и форма 6/10 . Просто помните, что значение должно быть между −1 и 1.
  2. И… все! Калькулятор арксинуса сделал свое дело и вы нашли арксинус вашего значения . Теперь вы знаете, что арксинус (6/10) = 36,87 °
  .

  Отлично! Теперь, когда вы понимаете, что такое арксинус, возможно, вы хотели бы проверить более сложные приложения тригонометрии? Например, закон синусов (тесно связанный с законом косинусов) является обязательным при решении задач на треугольники.

  No related posts.