Найти производную по направлению вектора в точке онлайн: Градиент функции онлайн

Содержание

Как по заданным функции, точке и вектору вычислить градиент в точке и производную функции в точке по направлению вектора

Альфашкола
Статьи
Как по заданным функции, точке и вектору вычислить градиент в точке и производную функции в точке по направлению вектора

Даны функция

Вычислить:

б) производную функции z в точке А по направлению вектора а.

Решение

а) Находим частные производные функции z в общем виде:

Значения этих величин в точке А:

Градиент определяем по формуле:

б) Определяем модуль этого вектора:

Отсюда получаем значения направляющих косинусов вектора а:

Значение производной заданной функции по направлению вектора а определяем по формуле:

Окончательно получаем:

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Любовь Александровна Илюшина

Репетитор по математике

Стаж (лет)

Образование:

Самарский национальный исследовательский университет имени академика С.П. Королева

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по химии 7-11 классы. Химия — наука очень систематизированная, но в тоже время очень творческая и интересная различными фактами из разных областей жизни.

Наталья Николаевна Шарапова

Репетитор по математике

Стаж (лет)

Образование:

Челябинский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике с 1 по 11 класс. Подготовка к ОГЭ/ЕГЭ, профиль до 70 баллов. Репетитор по информатике для 7-9 классов. Люблю математику и информатику, потому что просто люблю. Если бывает трудно, то предлагаю идти вместе. Когда человек не один, то всегда легче и интереснее. Заодно и вспомним, что забыл и выясним, что не знал. До встречи!

Галина Михайловна Кондакова

Репетитор по математике

Стаж (лет)

Образование:

Ленинградский государственный университет им. А.А.Жданова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Здравствуйте! Я преподаю русский язык 6-11 классам. В процессе обучения стремлюсь пробуждать интерес к изучению тем и выполнению заданий, активно используя вопросы «почему?», «для чего?», «что изменится, если. ..?» и т.п. Особое внимание — учащимся с уровнем оценок по предмету «средний» и «ниже среднего» с отработкой наиболее трудных случаев по освоению орфографии и синтаксиса.

Градиент

Производная по направлению. Градиент

Пусть в некоторой области задана функция и точка . Проведем из точки вектор , направляющие косинусы которого . На векторе , на расстоянии от его начала рассмотрим точку , т.е. .

Будем предполагать, что функция и ее частные производные первого порядка непрерывны в области .

Предел отношения при называется производной от функции в точке по направлению вектора и обозначается , т.е. .

Для нахождения производной от функции в заданной точке по направлению вектора используют формулу: ,
где – направляющие косинусы вектора , которые вычисляются по формулам:

Пусть в каждой точке некоторой области задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции и обозначается или (читается «набла у»): .

При этом говорят, что в области определено векторное поле градиентов.

Для нахождения градиента функции в заданной точке используют формулу:
.

Свойства градиента

1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента. Это наибольшее значение производной равно .

2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю.

Примеры решения задач

Пример 1. Найти производную от функции в точке по направлению вектора .

Решение.

Для решения задачи воспользуемся формулой для нахождения производной от функции в заданной точке по направлению вектора :
,
где – направляющие косинусы вектора , которые вычисляются по формулам:
.

По условию задачи вектор имеет координаты . Тогда его длина равна:
.

Следовательно, для направляющих косинусов вектора получим следующие значения:
.

Далее для решения задачи необходимо найти все частные производные первого порядка от функции :

Вычислим значения этих частных производных первого порядка в точке :

В заключении подставим полученные значения для направляющих косинусов вектора и значения частных производных первого порядка от функции в точке в формулу для нахождения производной по направлению в заданной точке:

Ответ: производная от функции в точке по направлению вектора равна .

Пример 2. Найти градиент функции в точке .

Решение.

Поскольку градиентом функции называется вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, то для решения задачи сначала найдем все частные производные первого порядка от заданной функции:

Далее вычислим значения этих частных производных первого порядка в точке :

Подставим полученные значения в формулу градиента функции в заданной точке :
.

Ответ: градиент функции в точке равен .

Пример 3. Найти производную функции в точке по направлению градиента функции в той же точке.

Решение.

Для нахождения производной от функции в заданной точке по направлению вектора используют формулу:
,
где – направляющие косинусы вектора , которые вычисляются по формулам:
.

В данном случае вектор совпадает с градиентом функции в точке : .

Следовательно, для решения задачи необходимо найти значения всех частных производных первого порядка от функции в точке , а также координаты и длину градиента функции в той же точке.

Вычислим значения частных производных первого порядка от функции в точке :

Для нахождения координат вектора , равного градиенту функции в заданной точке , вычислим значения частных производных первого порядка от функции в этой точке:

Длина вектора равна: .

Найдем направляющие косинусы вектор по формулам:
.

Подставим полученные значения в формулу для нахождения производной от функции в заданной точке по направлению вектора :

Ответ: производная функции в точке по направлению градиента функции в той же точке равна 1.

Задания для самостоятельной работы

1. Найти производную функции в точке по направлению вектора .
Ответ: .

2. Найти производную функции в точке по направлению вектора .
Ответ: .

3. Найти производную функции в точке по направлению вектора .
Ответ: .

4. Найти градиент функции в точке .
Ответ: .

5. Найти градиент функции в точке .
Ответ: .

6. Найти градиент функции в точке .
Ответ: .

Производная по направлению и градиент — КиберПедия

Навигация:

Главная Случайная страница Обратная связь ТОП Интересно знать Избранные

Топ:

Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении…

Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение…

Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования…

Интересное:

Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений. ..

Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны…

Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является…

Дисциплины:

Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

⇐ ПредыдущаяСтр 4 из 6Следующая ⇒

Пусть функция определена на открытом множестве и . Рассмотрим прямую : , где . Здесь – направляющий вектор прямой (рис.1). В координатном виде уравнения кривой записать следующим образом:

…. .

Рис.1

Здесь вектор единичный вектор, проходящий через точку .

Определение 18. Производной по направлению вектора(прямой ) в точке называют предел по множеству .

(18)

Если , то совпадает с направлением оси и производная по направлению совпадает с частной производной .

Запишем (18) подробнее. Так как , , то

По теореме о дифференцировании сложной функции имеем

(19)

В частном случае, в пространстве , формула (19) для функции в точке по направлению , формула имеет вид

. (20)

Определение 19. Градиентом дифференцируемой в точке функции называется n – мерный вектор

. (21)

В пространстве формула (21) имеет вид :

На плоскости Oxy :

С помощью символического оператора , который называется оператором Гамильтона, градиент в R³ также обозначают

Используя понятие градиента можно в векторной форме записать формулу полного приращения функции в точке :

а также дифференциал функции

и производную функции по направлению

, (22)

где – вектор приращений аргумента, — вектор бесконечно малых.

Свойства градиента:

1. Если вектор градиент функции тождественно равен нулю для любого , то функция постоянна на множестве Х.

2. Если и – дифференцируемые функции в , то справедливы следующие соотношения

а) ;

б) ;

в) ,

где дифференцируемая функция одной переменной .

Справедливость этих свойств следует из определения градиента и свойств векторов.

3. Производная функции по направлению вектора (рис.2) принимает наибольшее значение в направлении и равна модулю , т.е.

Из (22) следует .

Так как , то . <

Таким образом, есть вектор, указывающий направление наибольшего возрастания функции в данной точке и имеющий модуль, равный скорости этого возрастания.

4. Пусть дифференцируемая функция, и

( )

параметрические уравнения некоторой гладкой кривой Г, удовлетворяющие условию

. (23)

Такая кривая называется линией уровня функции .

Вектор (рис 7.3) является касательным вектором к кривой Г, а – радиусом-вектором точки М .

Продифференцируем (23) по t как сложную функцию:

Рис.3

Обозначим . Тогда в векторном виде будем иметь

т.е. скалярное произведение двух векторов рано нулю. Это означает, что в каждой точке линии уровня векторы и , т.е. вектор градиент и касательный вектор к кривой ортогональны, или вектор градиент в каждой точке ортогонален линии уровня.

Примеры. 1) Найти наибольшее значение в точке , если .

Решение. Найдем в точке М:

; .

Тогда

2) Найти производную функции в точке по направлению внешней нормали к окружности в точке .

Решение.Производная по направлению вычисляется, как скалярное произведение и вектора направления (внешняя нормаль)

Вычислим в точке М:

Вычислим вектор в точке М. Для этого в уравнении окружности определим зависимость х и у от параметра : , . Так как точка М принадлежит окружности, получаем

и .

Отсюда . .

Поскольку векторы и ортогональны, то координаты вектора нормали находятся из соотношения

Отсюда получаем, , . Нормируем вектор :

Производная по направлению нормали к окружности в точке М равна

⇐ Предыдущая123456Следующая ⇒

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства…

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого…

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим…

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни…

Физика. Механика

Мы уже говорили, что законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмерного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство изотропно, в нем нет выделенных направлений. С этой симметрией связан закон сохранения момента импульса. Эта связь проявится в том, что момент количества движения, как мы увидим в дальнейшем, является одной из основных величин, описывающих вращательное движение.

Момент импульса L отдельной частицы равен векторному произведению радиус-вектора r частицы на ее импульс р :

Направление вектора L определяется по правилу буравчика (штопора), а его величина равна

где — угол между векторами r и р. Величина l = r равна расстоянию от начала координат 0 до прямой, вдоль которой направлен импульс частицы. Эта величина называется плечом импульса (рис. 4.22). Вектор L зависит от выбора начала координат, поэтому говоря о нем, обычно указывают: «момент импульса относительно точки 0».

Рис. 4.22. Момент импульса L частицы массой m

Рассмотрим производную по времени от момента импульса:

Первое слагаемое равно нулю, так как и очевидным образом параллельны

Во втором слагаемом, согласно второму закону Ньютона, производную импульса можно заменить на силу, действующую на частицу.

Векторное произведение радиус-вектора на силу называется моментом силы относительно точки 0 :

Направление момента силы определяется тем же правилом буравчика. Его величина

где — угол между радиус-вектором и силой. Аналогично тому, как это было сделано выше, определяется и плечо силы l = r — расстояние от точки 0 до линии действия силы. В итоге из полученного в результате дифференцирования соотношения находим уравнение движения для момента импульса частицы:

По форме уравнение аналогично второму закону Ньютона: вместо импульса частицы стоит момент импульса, а вместо силы — момент силы.

Если M = 0, то L = const, то есть

Момент импульса частицы постоянен в отсутствие моментов сил, действующих на нее.

Для центральных сил

и момент силы относительно силового центра равен нулю:

Таким образом, для центральных сил

то есть L = const.

Другими словами,

При движении в поле центральных сил момент импульса частицы сохраняется.

Отсюда вытекает важное следствие. Поскольку момент импульса ортогонален плоскости, задаваемой импульсом тела и радиус-вектором, проведенным из центра сил, эта плоскость не меняет своего положения со временем. Иными словами, орбита каждого тела в поле центральных сил лежит в одной плоскости, проходящей через центр сил (хотя для разных тел эти плоскости могут различаться). Таким образом, в поле центральных сил невозможны, например, винтовые траектории.

Рассмотрим теперь систему, состоящую из двух взаимодействующих частиц (рис. 4.23).

Рис. 4.23. Система, состоящая из двух взаимодействующих частиц

Уравнения движения этих частиц имеют вид:

где F₁ и F₂ — внешние силы, a f₁₂=-f₂₁ — внутренние силы взаимодействия между частицами, направленные вдоль линии, их соединяющей

Умножим первое уравнение векторно слева на радиус-вектор первой частицы r₁, а второе — векторно слева на радиус-вектор второй частицы r₂

Учтем, что

поскольку

Используя третий закон Ньютона f₁₂ = –f₂₁, перепишем систему уравнений движения частиц в виде:

Сложим полученные соотношения:

Имеет место соотношение между векторами

Поэтому их векторное произведение равно нулю.

Таким образом, мы получаем

В левой части равенства стоит производная от суммы моментов импульса частиц (ее называют полным моментом импульса L системы), а в правой — сумма моментов внешних сил — полный момент М внешних сил, действующих на тела системы.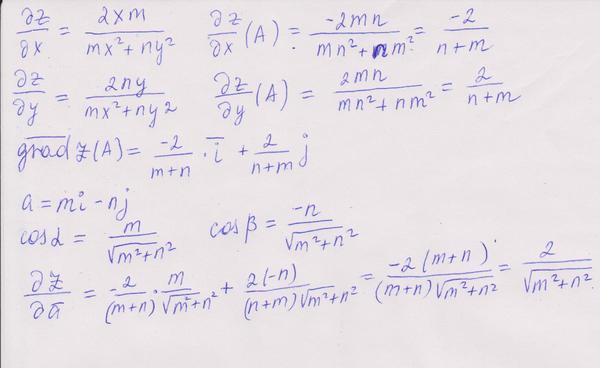 Обобщение на случай системы из многих частиц (или твердого тела) очевидно.

Момент импульса системы N частиц равен

Полный момент внешних сил будет

Уравнение, определяющее изменение во времени момента импульса системы частиц имеет вид:

Отсюда следует, что при М = 0 и, соответственно, L = const следует закон сохранения момента импульса системы:

Если система замкнута или суммарный момент внешних сил, действующих на нее, равен нулю, то суммарный момент импульса системы сохраняется.

Видео 4.12. Демонстрация закона сохранений момента импульса: стрельба из пушки, установленной на вращающейся платформе по касательной, по диаметру и «кривым» снарядом.

Пример. Выясним, при каких условиях момент импульса системы не зависит от выбора начала координат 0.

Найдем сначала, как изменяется момент импульса при смене начала координат. Возьмем некую точку 0′, положение которой относительно точки 0 задается радиус-вектором r₀. Радиус-векторы r_i‘, проведенные из 0′, связаны с радиус-векторами r_i соотношениями

Подставим это выражение в формулу для момента импульса L относительно точки 0 :

В первом члене мы введем полный импульс системы

а второй член есть не что иное, как момент импульса L’ относительно точки 0′.

Имеем

Мы ищем условие, когда

для произвольного вектора r₀. Это возможно только при равенстве нулю полного импульса системы р = 0. Иными словами, момент импульса не зависит от выбора начала координат в системе отсчета, связанной с центром масс системы.

Алгоритмы выделения контуров изображений / Хабр

В свете недавних статей об обработке изображений я хотел бы немного рассказать об алгоритмах выделения контуров: методы Робертса, Превитта и Собеля (эти методы взяты для рассмотрения как самые известные и часто используемые).

Не буду докучать объемной теорией, а ограничусь лишь минимальными сведениями, необходимыми для понимания сути алгоритмов.
Все указанные методы основываются на одном из базовых свойств сигнала яркости – разрывности. Наиболее общим способом поиска разрывов является обработка изображения с помощью скользящей маски, называемой также фильтром, ядром, окном или шаблоном, которая представляет собой некую квадратную матрицу, соответствующую указанной группе пикселей исходного изображения. Элементы матрицы принято называть коэффициентами. Оперирование такой матрицей в каких-либо локальных преобразованиях называется фильтрацией или пространственной фильтрацией.

Схема пространственной фильтрации иллюстрируется на рисунке ниже (см. рисунок 1).

Рисунок 1. Схема пространственной фильтрации

Процесс основан на простом перемещении маски фильтра от точки к точке изображения; в каждой точке (x,y) отклик фильтра вычисляется с использованием предварительно заданных связей. В случае линейной пространственной фильтрации отклик задается суммой произведения коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра. Для маски 3х3 элемента, показанной на рисунке 1, результат (отклик) R линейной фильтрации в точке (x,y) изображения составит:

(1.1)

что, как видно, есть сумма произведений коэффициентов маски на значения пикселей непосредственно под маской. В частности заметим, что коэффициент w(0,0) стоит при значении f(x,y), указывая тем самым, что маска центрирована в точке (x,y).

При обнаружении перепадов яркости используются дискретные аналоги производных первого и второго порядка. Для простоты изложения будут рассмотрены одномерные производные.

Первая производная одномерной функции f(x) определяется как разность значений соседних элементов:

(1.2)

Здесь использована запись в виде частной производной для того, чтобы сохранить те же обозначения в случае двух переменных f(x,y), где придется иметь дело с частными производными по двум пространственным осям. Использование частной производной не меняет существа рассмотрения.

Аналогично, вторая производная определяется как разность соседних значений первой производной:

(1.3)

Вычисление первой производной цифрового изображения основано на различных дискретных приближениях двумерного градиента. По определению, градиент изображения f(x,y) в точке (x,y) — это вектор [2]:

(1.4)

Как известно из курса математического анализа, направление вектора градиента совпадает с направлением максимальной скорости изменения функции f в точке (x,y) [2].
Важную роль при обнаружении контуров играет модуль этого вектора, который обозначается ∇f и равен

(1.5)

Эта величина равна значению максимальной скорости изменения функции f в точке (x,y), причем максимум достигается в направлении вектора ∇f. Величину ∇f также часто называют градиентом.

Направление вектора градиента также является важной характеристикой. Обозначим α(x,y) угол между направлением вектора ∇f в точке (x,y) и осью x. Как известно из математического анализа [2],

(1.6)

Отсюда легко найти направление контура в точке (x,y), которое перпендикулярно направлению вектора градиента в этой точке. А вычислить градиент изображения можно, вычислив величины частных производных ∂f/∂x и ∂f/∂y для каждой точки.

Оператор Робертса

Пусть область 3х3, показанная на рисунке ниже (см. рис. 2), представляет собой значения яркости в окрестности некоторого элемента изображения.

Рисунок 2. Окрестность 3х3 внутри изображения

Один из простейших способов нахождения первых частных производных в точке состоит в применении следующего перекрестного градиентного оператора Робертса [1]:

(1.7)
и
(1. 8)

Эти производные могут быть реализованы путем обработки всего изображения с помощью оператора, описываемого масками на рисунке 3, используя процедуру фильтрации, описанную ранее.

Рисунок 3. Маски оператора Робертса

Реализация масок размерами 2х2 не очень удобна, т.к. у них нет четко выраженного центрального элемента, что существенно отражается на результате выполнения фильтрации. Но этот «минус» порождает очень полезное свойство данного алгоритма – высокую скорость обработки изображения.

Оператор Превитта

Оператор Превитта, так же как и оператор Робертса, оперирует с областью изображения 3х3, представленной на рисунке 2, только использование такой маски задается другими выражениями:

(1.9)
и
(1.10)

В этих формулах разность между суммами по верхней и нижней строкам окрестности 3х3 является приближенным значением производной по оси x, а разность между суммами по первому и последнему столбцам этой окрестности – производной по оси y. Для реализации этих формул используется оператор, описываемый масками на рисунке 4, который называется оператором Превитта.

Рисунок 4. Маски оператора Превитта

Оператор Собеля

Оператор Собеля тоже использует область изображения 3х3, отображенную на рисунке 2. Он довольно похож на оператор Превитта, а видоизменение заключается в использовании весового коэффициента 2 для средних элементов:

(1.11)
и
(1.12)

Это увеличенное значение используется для уменьшения эффекта сглаживания за счет придания большего веса средним точкам.

Маски, используемые оператором Собеля, отображены на рисунке ниже (см. рис. 5).

Рисунок 5. Маски оператора Собеля

Рассмотренные выше маски применяются для получения составляющих градиента . Для вычисления величины градиента эти составляющие необходимо использовать совместно:

(1.14)
или
(1.15)

Ну и в завершении продемонстрирую результаты обработки изображений (см. рисунки 6-8) описанными методами.

Рисунок 6. Исходное изображение №1

Рисунок 7. Исходное изображение №2

Рисунок 8. Исходное изображение №3

Результаты обработки методами Робертса, Превитта и Собеля продемонстрированы ниже:

Рисунок 9. Исходные изображения после обработки методом Робертса

Рисунок 10. Исходные изображения после обработки методом Превитта

Рисунок 11. Исходные изображения после обработки методом Собеля

Список литературы

Р. Гонсалес, Р. Вудс Цифровая обработка изображений — М: Техносфера, 2005 – 1007с
Кудрявцев Л.В. Краткий курс математического анализа – M.: Наука, 1989 – 736с
Анисимов Б.В. Распознавание и цифровая обработка изображений – М.: Высш. школа, 1983 – 295с

Математика. Материалы курса — Тестирование

Дифференциал тест математика

Эта лекция посвящена понятию дифференциала функции. У вас, думаю, возникал вопрос о том, что изучаем дифференциальное исчисление, но однокоренных слов для прилагательного «дифференциальное» не встречали. Оказывается, есть и такое слово – дифференциал. Сегодня мы раскроем это понятие, а также рассмотрим производные и дифференциалы высших порядков.

Итак, начнем с очень важной теоремы, необходимое и достаточное условие дифференцируемости. Помним, под дифференцируемостью мы понимаем существование конечной производной в точке, равной числу. Это условие эквивалентно теореме: функция дифференцируема в точке x 0 тогда и только тогда, когда приращение функции в этой точке, представимо в следующем виде: Δ f ( x 0)= A *Δ x 0+ o (Δ x ), где А – это некоторое действительные число, o (Δ x ) — бесконечно малая величина более высокого порядка, чем Δ x (предел отношения этих величин равен нулю при Δ x стремящемся к 0, слагаемое o (Δ x ) стремится к нулю гораздо быстрее, чем величина Δ x ).

Проведем доказательство, оно несложное. Итак, в одну сторону: пусть f дифференцируема в точке x 0. Значит, что в точке x 0 существует конечная производная, равная пределу дроби Δ f ( x 0)/Δ x. Из сказанного легко получаем следующую запись: предел разности Δ f ( x 0)/Δ x – f ’( x 0) при Δ x → 0 равен 0. Если предел некоторой функции равен нулю, значит, эта функция называется бесконечно малой при Δ x → 0. Так, α(Δ x )=Δ f ( x 0)/ Δ x – f ’( x 0) — бесконечно малая величина. Выразим приращение функции: Δ f ( x 0)= f ’( x 0)Δ x + α (Δ x )Δ x. Проанализируем полученную формулу: перед Δ x стоит число равное f ’( x 0), скажем, что это А, а второе слагаемое как раз и есть бесконечно малая более высокого порядка, чем Δ x ( o (Δ x )= α (Δ x )Δ x ). Итак, на самом деле, приращение функции представимо в виде, о котором мы говорили.

Проведем доказательства в другую сторону. Пусть приращение функции представимо в виде Δ f ( x 0)= A *Δ x 0+ o (Δ x ). Нам нужно доказать, что функция дифференцируема, то есть существует конечная производная. Начнем вычислять производную по определению (предел Δ f ( x 0)/Δ x при Δ x → 0), вместо приращения подставим значение, которое нам дано по условию, и почленно разделим числитель на знаменатель. Имеем предел A *Δ x 0/Δ x + o (Δ x )/Δ x при Δ x → 0. Простые вычисления приводят нас к результату: f ’( x 0)=А. Мы получили, что из представимости приращения функции в точке следует дифференцируемость функции. Два пункта доказательства нам говорят, что эти два утверждения равносильны. Дифференцируемость функций в точке означает, что приращение функции имеет указанный вид.

Давайте проанализируем еще раз это равенство Δ f ( x 0)= A *Δ x 0+ o (Δ x ). Первое слагаемое A *Δ x 0 — главная линейная часть, потому что вторым слагаемом можно пренебречь, оно очень мало. A *Δ x 0 — это главная, существенная часть приращения функции, именно она и называется дифференциалом функции f в точке x 0, будем обозначать её df( x 0). Получили, дифференциал функции f ( x 0), если функция дифференцируема, имеет вид df( x 0)= f ’( x 0)Δ x. Мы будем использовать немного другой вид дифференциала. Давайте рассмотрим функцию h(х)=х. Вычисляя ее дифференциал dx = x ’Δ x =1Δ x (производная этой функции в любой точке равна единице), мы видим, что dx и Δ x это одно и то же. 2). Если мы букву d заменим на штрих, то мы получим в точности правила дифференцирования.

Доказательства обосновываются довольно быстро. Рассмотрим доказательства для произведения, со всем остальным доказательствами вы справитесь самостоятельно.

Итак, дифференциал произведений находим по формуле d ( UV )=( UV )’ d, раскрываем по правилу дифференцирования произведения ( U ’ V + V ’ U ) d x, затем объединяем множители и получаем требуемый результат: U ’ d x V + V ’ d x U = dU * V + dV * U = UdV + VdU.

Важнейший факт, который мы используем дальше, не только в дифференциальном, но и в интегральном исчислении, поэтому на него следует обратить особое внимание. Инвариантность формулы дифференциала первого порядка. Инвариантность — это неизменность, сохранение чего-то. Формула дифференциала df( x )= f ’( x ) dx не зависит от того, зависимой или независимой является переменная х. Свойство инвариантности говорит, что формула остается одинаковой. Давайте проведем рассуждения.

Формула дифференциала у нас было изначально получена df( x )= f ’( x ) dx, когда х – независимая переменная. Давайте будем считать, что х сама является функцией переменной t, x = f ( t ), то есть независимая переменная уже не x, а t. Тогда, находя дифференциал функции, мы понимаем, что df( x )=df( x ( t ))=(f( x ( t )))’ dt. Вычисляем производную сложной функции и заменяем x(t) на x и x’(t)dt на dx: f ’( x ( t ))* x ’( t ) dt = f ’( x ) dx. Получаем ту же самую формулу, здесь x – это уже сама функция переменной t, зависимая переменная, a формула осталась прежней. Итак, свойство инвариантности работает.

Где же находится дифференциал? Что ж это такое? Давайте запишем определение и построим картинку, которую мы строили, когда рассматривали геометрический смысл производной (см. видео). Введем буквенные обозначения вершин треугольников, появились точки N, T. Рассмотрим треугольник М0 NT : tgα = f ’( x 0). Катеты этого треугольника связаны с помощью тангенса следующей формулой: | NT |=| M 0 N |* tgα = f ’( x 0)Δ x = df ( x 0). Остаётся сделать замену, и мы понимаем, что по формуле дифференциала катет NT в этом треугольнике, это и есть дифференциал функции. Посмотрите, дифференциал функции – это длина отрезка NT, это главная линейная часть приращения функции. Если Δ x →0, то другой отрезок, дающий в сумме приращение функции MT практически исчезает. Итак, точка Т находиться на касательной, чтобы найти дифференциал нужно из ординаты точки Т вычесть ординату точки N или M 0. Итак, дифференциал функции в точке x0 – это превращение ординаты по касательной, длина отрезка NT.

Дифференциал применяется, например, для вычисления приближенного значения функции. Давайте посмотрим, мы сказали, что приращение функции примерно равно дифференциалу функции, если Δ x достаточно мало, то есть f ’( x 0)Δ x. Заменяя приращение функции на разность значений функций в точках x 0, x 0+Δ x, получаем приближённое равенство: f ( x 0+Δ x )≈ f ( x 0)+ f ’( x 0)Δ x. Значит, в точке x 0+Δ x значение может быть найдено по указанной формуле.

Давайте посмотрим, как этим можно воспользоваться.

Допустим нужно вычислить приближёно √3,99. Мы не пользуемся калькулятором, понимаем, что это число довольно близко к 4, из которого корень извлекается без проблем. Мы рассмотрим функцию f ( x )=√ x, изначальная точка x 0=4, новая точка x 0+Δ x =3,99 (она получилась в результате изменения точки х0 на -0,01), Δ x =0,01. Осталось воспользоваться формулой, для этого нам нужно знать значение функции в точке x0 и значение производной в точке x0. Значение в точке f ( x 0)=2, значение производной в точке x 0 это f ’( x 0)=1/4. Подставляя в формулу, мы получаем приближённый ответ: √3,99 приближенно равен 1,9975.

А сейчас рассмотрим производные, а потом и дифференциалы высших порядков. Мы уже заметили, в общем-то и пользовались этим фактом, если мы в каждой точке x 0 вычислим значение производной (допустим функция дифференцируема на каком-то интервале), то мы получим новую функцию, которую мы обозначаем f ’. Эта функция в свою очередь тоже может быть дифференцируемой, ее производная называется производной функции второго порядка. По индукции, таким же образом, мы можем вычислить значение производной любого порядка: f n +1 ( x )=( f n +1 ( x ))’.

Ну и чтобы нам пользоваться производными высших порядков, посмотрим, какие применяются обозначения. Мы можем использовать римские цифры, особенно это касается первых пяти производных, штрихи мы воспринимаем как римские единицы. А вот 10 порядок, мы можем написать римской цифрой f Х ( x 0). Если мы используем арабские цифры, то чтобы не путать со степенью, мы их заключаем в скобки f (10) ( x 0).

Также как мы знали, что производную десятого порядка, тоже можно обозначить в виде частного d 10 f / dx 10 ( x 0).

У нас было обобщение формулы производной произведения UV, когда количество сомножитель увеличивалось. Можно рассмотреть обобщение этой формулы и по порядку производной. Производную произведения функции UV n — го порядка, можно вычислить по формуле Лейбница (см. видео).

Давайте посмотрим на примере производной третьего порядка произведения sin ( x )* e x : ( sin ( x ) e x )’’’=( sin ( x ))’’’ e x +3( sin ( x ))’’( e x )’+3( sin ( x ))’( e x )’’+ sin ( x )( e x )’’’. Коэффициенты как в формуле ( a + b ) 3 , коэффициенты перед четырьмя слагаемыми 1, 3, 3, 1. Вот это и есть те самые числа, которые мы написали перед нашими слагаемыми. Дальше осталось только найти производные 3, 2, 1 порядка для данных функций. Ну и ответ довольно быстро получается: 2 e x ( cos ( x )- sin ( x )). Имейте в виду полезную формулу, которую можно использовать при решении задач.

Что же такое дифференциал высших порядков? Дифференциал второго порядка находится как дифференциал от дифференциала первого порядка d 2 f ( x )= d ( df ( x ))= f ’’( x ) dx 2 . Тут, конечно, возникает вопрос: в формуле дифференциала два сомножителя и получается, что он зависит и от x, и от dx (dx это Δx). Дифференциал второго порядка находятся из предположения, что dx остается тем же самым, постоянной. В результате мы получаем следующую формулу (см. видео). По индукции находятся дифференциалы любого более высокого порядка. В результате мы получаем формулу дифференциала n — го порядка функции f: d n f ( x )= f ( n ) ( x ) dx n. Отсюда мы видим, откуда взялось обозначение производной n — го порядка: f ( n ) ( x )= d n f ( x )/ dx n. Дифференциал второго порядка, а значит, и более высокого порядка, не обладает свойством инвариантности. Нужно помнить, что дифференциал первого порядка является инвариантным, формула является инвариантной, а вот дифференциал второго и более высокого порядка формула свойством инвариантности не обладает. Вы можете проверить, также как мы это делали для дифференциала первого порядка, и сравнить формулы дифференциала второго порядка, когда х – независимая переменная или зависимая. Вы увидите, что результаты отличаются.

Формула дифференциала у нас было изначально получена df x f x dx, когда х независимая переменная.

E. vyatsu. ru

27.07.2018 19:20:22

2017-12-03 20:46:07

Источники:

Https://e. vyatsu. ru/mod/page/view. php? id=324119

Дифференциал (математика) | Математика | Fandom » /> » /> .keyword { color: red; }

Дифференциал тест математика

Дифференциа́л в математике — линейная часть приращения функции или отображения. Это понятие тесно связанное с понятием производной по направлению.

Обычно дифференциал » width=»» height=»» /> обозначается » width=»» height=»» />, а его значение в точке » width=»» height=»» /> обозначается f>» width=»» height=»» />.

Содержание

Неформальное описание

Рассмотрим гладкую функцию » width=»» height=»» />. Проведем касательную к ней в точке » width=»» height=»» />, и отложим на ней отрезок, такой длины, чтобы его проекция на ось » width=»» height=»» /> была равна » width=»» height=»» />. Проекция этого отрезка на ось » width=»» height=»» /> называется Дифференциалом функции » width=»» height=»» /> в точке » width=»» height=»» /> от » width=»» height=»» />. Таким образом, дифференциал может пониматься как функция двух переменных » width=»» height=»» /> и » width=»» height=»» />,

F(\Delta x)>» width=»» height=»» />

F(\Delta x)=f'(x)\cdot \Delta x,>» width=»» height=»» />

F(\Delta x)+o(\Delta x).>» width=»» height=»» />

Определения

Для функций

Дифференциал гладкой вещественнозначной функции » width=»» height=»» /> определённой на » width=»» height=»» /> (» width=»» height=»» /> — область в ^>» width=»» height=»» /> или гладкое многообразие) представляет собой 1-форму и обычно обозначается » width=»» height=»» /> и определяется соотношением

» width=»» height=»» />

Где » width=»» height=»» /> обозначает производную » width=»» height=»» /> по направлению вектора » width=»» height=»» /> в.

Для отображений

Дифференциал гладкого отображения из гладком многообразия в многообразие » width=»» height=»» /> есть отображение между их, такое что для любой гладкой функции >» width=»» height=»» /> имеем

» width=»» height=»» />

Где » width=»» height=»» /> обозначает производную » width=»» height=»» /> по направлению » width=»» height=»» />. (В левой части равенства берётся производная в » width=»» height=»» /> функции » width=»» height=»» /> по » width=»» height=»» /> в правой — в » width=»» height=»» /> функции » width=»» height=»» /> по » width=»» height=»» />).

Это понятие естественно обобщает дифференциал функции.

Примеры

История

Термин Дифференциал (от differentia — разность, различие) введен применялось для обозначение «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался не удобным в большинстве разделов математики (за исключением См. также

Содержание

F(\Delta x)>» width=»» height=»» />

F(\Delta x)=f'(x)\cdot \Delta x,>» width=»» height=»» />

F(\Delta x)+o(\Delta x).>» width=»» height=»» />

f(\Delta x)>» width=»» height=»» />

Где width height обозначает производную width height по направлению вектора width height в.

Math. fandom. com

07.10.2019 23:14:55

2019-10-07 23:14:55