Arctg 1 3 в градусах: Арктангенс — калькулятор онлайн

Найпростіші тригонометричні рівняння — Free Tutor

Поняття про arcsin (арксинус), arccos (арккосинус), arctg (арктангенс) і arcctg (арккотангенс) числа.

Відразу варто зауважити головний сенс у «arc… х». Ця функція перетворює число у радіальну (градусну міру). Вона просто запитує при яких радіанах (градусах) дана функція (тригонометрична функція) буде рівна числу «х».

Розглянемо все детально, але не варто це сильно завчати. В кінці виділимо необхідне. Також варто прочитати, що таке тригонометричні функції.

arcsin (арксинус) числа «а», де «|a| ≤ 1», називають таке число (кут) з проміжку, [-/π/2; /π/2] синус якого дорівнює «а».

Позначають арксинус числа «а» так: «arcsin> Отже будемо мати:

arcsin a = φ, тоді коли: 1) sin⁡ φ = a; 2) φ ∈ [-/π/2; /π/2]

Наприклад:

1. «arcsin⁡ /1/2 = /π/6» бо «sin⁡ /π/6 = /1/2» і «/π/6 ∈ [-/π/2; /π/2]»

2. «arcsin⁡ /√3/2 = /π/3» бо «sin⁡ /π/3 = /√3/2» і «/π/3 ∈ [-/π/2; /π/2]»

У випадках, коли є від’ємний кут, тоді будемо мати:

arcsin⁡ (-α) = — arcsin ⁡α

Наприклад:

«arcsin⁡ (-/√2/2) = -arcsin⁡/√2/2 = -/π/4» бо «- arcsin⁡/√2/2 = -/π/4» і «-/π/4 ∈ [-/π/2;/π/2]»

arccos (арккосинус) числа «а», де «|a| ≤ 1», називають таке число (кут) з проміжку, [0; π] косинус якого дорівнює «а».

Позначають арккосинус числа «а» так: «arccos a». Отже будемо мати:

arccos a = φ, тоді коли: 1) cos⁡ φ = a; 2) φ ∈ [0; π]

Наприклад:

1. «arccos⁡/1/2 = /π/3» бо «cos⁡/π/3 = /1/2» і «/π/3 ∈ [0; π]»

2. «arccos⁡ /√3/2 = /π/6» бо «cos⁡/π/6 = /√3/2» і «/π/6 ∈ [0; π]»

У випадках, коли є від’ємний кут, тоді будемо мати:

arccos⁡ (-α) = π — arccos ⁡α

Наприклад:

«arccos⁡ (-/√2/2) = π — arccos⁡√2/2 = π — /π/4 = /3π/4» бо «π — arccos⁡/√2/2 = /3π/4» і «/3π/4 ∈[0; π]»

Якщо є сума арксинуса та арккосинуса однакового кута то їх результат буде «/π/2».

arcsin x + arccos x = /π/2

arctg (арктангенс) числа «а», називають таке число (кут) з проміжку, (-/π/2; /π/2) тангенс якого дорівнює «а».

Позначають арктангенс числа «а» так: «arctg a». Отже будемо мати:

arctg a = φ, тоді коли: 1) tg⁡ φ = a; 2) φ ∈ (-/π/2; /π/2)

Наприклад:

1. «arctg⁡ 1 = /π/3» бо «tg⁡ /π/3 = 1» і «/π/3 ∈ (-/π/2; /π/2)»

2. «arctg ⁡√3 = /π/3» бо «tg⁡ /π/3 = √3» і «/π/3 ∈ (-/π/2; /π/2)»

У випадках, коли є від’ємний кут, тоді будемо мати:

arctg (-α) = — arctg ⁡α

Наприклад:

«arctg⁡ (-/√3/3) = -arctg⁡ /√3/3 = -/π/6» бо «- arctg⁡ /√3/3 = -/π/6» і «-/π/6 ∈ (-/π/2; /π/2)»

arcctg (арккотангенс) числа «а», називають таке число (кут) з проміжку, (0; π) арккотангенс якого дорівнює «а».

Позначають арккотангенсом числа «а» так: «arcctg a». Отже будемо мати:

arcctg a = φ, тоді коли: 1) arcctg⁡ φ = a; 2) φ ∈ (0; π)

Наприклад:

1. «arcctg⁡ 0 = /π/2» бо «ctg⁡ /π/2 = 0» і «/π/2 ∈ (0; π)»

2. «arcctg⁡ √3 = /π/6» бо «ctg⁡ /π/6 = √3» і «/π/6 ∈ (0; π)»

У випадках, коли є від’ємний кут, тоді будемо мати:

arcctg⁡ (-α) = π — arcctg ⁡α

Наприклад:

«arcctg⁡ (-1) = π — arcctg ⁡1 = π — /π/4 = /3π/4» бо «π — arcctg⁡1 = /3π/4» і «/3π/4 ∈ (0; π)»

Якщо є сума арктангенса та арккотангенса однакового кута то їх результат буде «/π/2».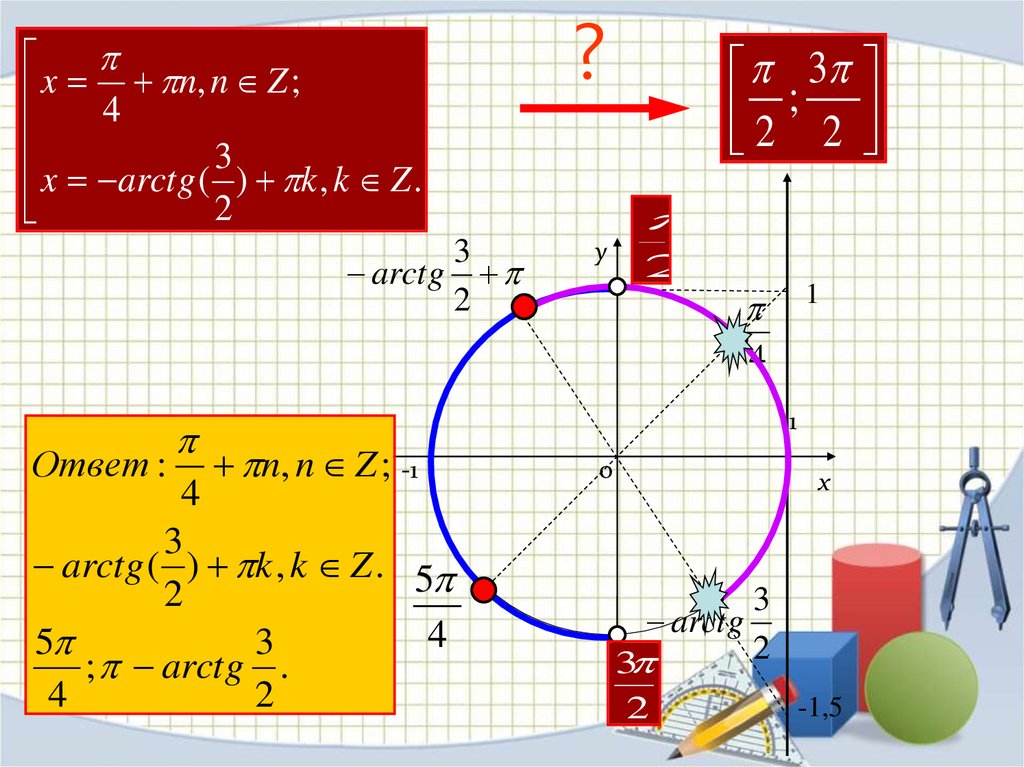

arctg x + arcctg x = /π/2

Отже. Після того як ми розібралися з «arc…» тригонометричних функцій залишилося зрозуміти навіщо він нам необхідний.

Для цього розглянемо графіки тригонометричних функцій.

sin x (зауважте, ця функція не виходить за межі [-1; 1]):

cos x (зауважте, ця функція не виходить за межі [-1; 1]):

tg x:

ctg x:

Коли ми маємо тригонометричне рівняння вигляду: «sin⁡ x = a», «cos ⁡x = a», «tg x = a», «ctg x = a». То це означає, що ми маємо горизонтальну пряму (вона є паралельною до осі «х») яка проходить через точку «а».

Наприклад, тригонометричне рівняння «sin x = a».

Отже, коли у нас є тригонометрична функція яка рівна якомусь числу, то такий запис називається «тригонометричним рівнянням».

Наприклад:

«sin x = 0», «cos x = /1/2», «tg x = 3», «ctg x = /√3/3 »

Розв’язати тригонометричне рівняння, означає «знайти усі точки перетину прямої та графіку тригонометричної функції».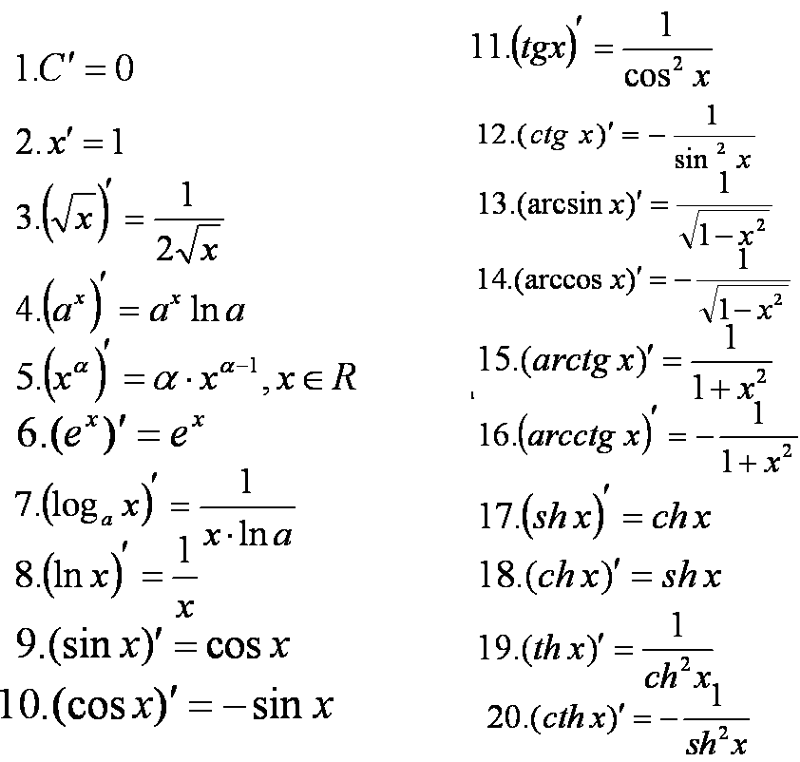

На прикладі точки перетину функції «sin x» та прямої «a» виділені червоним кольором.

Оскільки, кожна з функцій є безмежна та періодична та пряма «а» є безмежною, то таких точок буде безліч. Щоб не перераховувати кожну з цих точок є виведені спеціальні формули де застосовується «arc…».

Тригонометричне рівняння, типу «sin x = a».

Відразу зауважимо, що у випадках, коли «a або «a > 1», то рівняння розв’язків не має.

Є три варіанти стандартного розв’язання такого рівняння.

Якщо, «sin x = -1» (а = -1), то розв’язок буде таким:

x = -/π/2 + 2πn, n ∈ Z

Якщо, «sin x = 0» (а = 0), то розв’язок буде таким:

x = πn, n ∈ Z

Якщо, «sin x = 1» (а = 1), то розв’язок буде таким:

x = /π/2 + 2πn, n ∈ Z

У випадках, коли «0 будемо мати такий розв’язок:

x = (-1)ⁿ arcsin ⁡a + πn, n ∈ Z

У випадках, коли «-1 будемо мати такий розв’язок:

x = (-1)^{n + 1} arcsin |⁡a| + πn, n ∈ Z

Наприклад:

1. sin ⁡x = /√2/2

В першу чергу перевіряємо чи підходить значення якому рівний синус по обмеженню: «-1 Все добре. Оскільки це значення не є стандартним, то ми використовуємо загальну формулу:

x = (-1)ⁿ arcsin⁡/√2/2 + πn, n ∈ Z

Тепер необхідно знайти arcsin. Будемо мати: «sin⁡ /π/4 = /√2/2». Отримаємо остаточну відповідь:

x = (-1)ⁿ/π/4+ πn, n ∈ Z

2. 2sin ⁡x + 1 = 0

Тут в першу чергу необхідно звести рівняння до правильного вигляду: «sin x = a». Для цього перенесемо «1» в протилежну частину. Та поділимо на «2», що стоїть з синусом.

2sin ⁡x = -1

sin⁡ x = -/1/2

Виконаємо перевірку: «-1 Все добре. Але через те, що ми маємо від’ємне число, то нам необхідно скористатися другою стандартною формулою (для запису від’ємних чисел).

x = (-1)^{n + 1} arcsin⁡/1/2 + πn, n ∈ Z

Тепер необхідно знайти arcsin. Будемо мати: «sin⁡/π/6 = /1/2». Отримаємо остаточну відповідь:

x = (-1)^{n + 1} /π/6 + πn, n ∈ Z

Тригонометричне рівняння, типу «

cos x = a».

Відразу зауважимо, що у випадках, коли «a або «a > 1», то рівняння розв’язків не має.

Є три варіанти стандартного розв’язання такого рівняння.

Якщо, «cos x = -1» (а = -1), то розв’язок буде таким:

x = π + 2πn, n ∈ Z

Якщо, «cos x = 0» (а = 0), то розв’язок буде таким:

x = /π/2 + πn, n ∈ Z

Якщо, «cos x = 1» (а = 1), то розв’язок буде таким:

x = 2πn, n ∈ Z

У випадках, коли «0 будемо мати такий розв’язок:

x = ±arccos a + 2πn, n ∈ Z

У випадках, коли «-1 будемо мати такий розв’язок:

x = ±(π — arccos⁡ |a|) + 2πn, n ∈ Z

Наприклад:

1. cos⁡ x = /√2/2

Перевіряємо чи дане рівняння має розв’язки. «-1 отже рівняння має розв’язки. Скористаємося загальною формулою:

x = ±arccos⁡/√2/2 + 2πn, n ∈ Z

Знайдемо arccos: «cos⁡ /π/4 = /√2/2».

x = ±/π/4 + 2πn, n ∈ Z

2. 2cos ⁡x + √3 = 0

У цьому випадку як і у випадку з синусом необхідно звести рівняння до стандартного вигляду: «cos x = a». Для цього перенесемо в іншу сторону «√3» та поділимо на «2».

2cos ⁡x = -√3

cos ⁡x = -/√3/2

Тепер необхідно перевірити чи рівняння має розв’язки: «-1 Розв’язки є, але оскільки число є від’ємним, то варто скористатися другою стандартною формулою:

x = ±(π — arccos⁡ /√3/2) + 2πn, n ∈ Z

З’ясуємо значення арккосинуса: «cos⁡/π/6 = /√3/2».

x = ±(π — /π/6) + 2πn, n ∈ Z

Тепер залишається лише порахувати вираз у дужках. Оскільки там є дріб скористаємося правилом віднімання дробів (дробу та числа). Детальніше читайте у розділі «Алгебраїчний дріб».

Будемо мати: «π — /π/6 = /6π — π/6 = /5π/6»

x = ±/5π/6 + 2πn, n ∈ Z

Тригонометричне рівняння, типу «

tg x = a».

Якщо, «tg x = 0» (а = 0), то розв’язок буде таким:

x = πn, n ∈ Z

У випадках, коли «a > 0» будемо мати:

x = arctg a + πn, n ∈ Z

У випадках, коли «a будемо мати:

x = -arctg |a| + πn, n ∈ Z

Наприклад:

1. tg x = √3

Тангенс та котангенс обмежень не мають.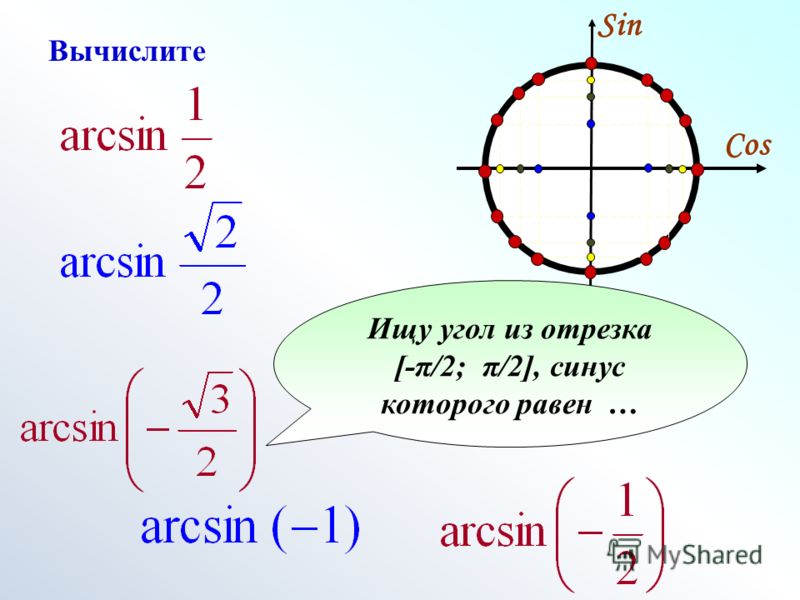 Тому не потрібно робити перевірок.

x = arctg √3 + πn, n ∈ Z

x = /π/3 + πn, n ∈ Z

2. 4√3 ∙ tg x + 4 = 0

Необхідно звести рівняння до стандартного вигляду «tg x = a». Для цього перенесемо «4» в протилежну сторону та поділимо на «4√3», що знаходяться біля тангенсу. Будемо мати:

4√3 ∙ tg x = -4

tg x = -/4/4√3

tg x = -/1/√3

x = -arctg /1/√3 + πn, n ∈ Z

x = -/π/6 + πn, n ∈ Z

Тригонометричне рівняння, типу «ctg x = a».

Якщо, «ctg x = 0» (а = 0), то розв’язок буде таким:

x = /π/2 + πn, n ∈ Z

У випадках, коли «a > 0» будемо мати:

x = arcctg a + πn, n ∈ Z

У випадках, коли «a будемо мати:

x = π — arcctg |a| + πn, n ∈ Z

1. ctg x = √3

Тангенс та котангенс обмежень не мають. Тому не потрібно робити перевірок.

x = arcctg √3 + πn, n ∈ Z

x = /π/6 + πn, n ∈ Z

2. 2ctg x + 2√3 = 0

Необхідно звести рівняння до стандартного вигляду «ctg x = a». Для цього перенесемо «2√3» в протилежну сторону та поділимо на «2», що знаходяться біля котангенсу.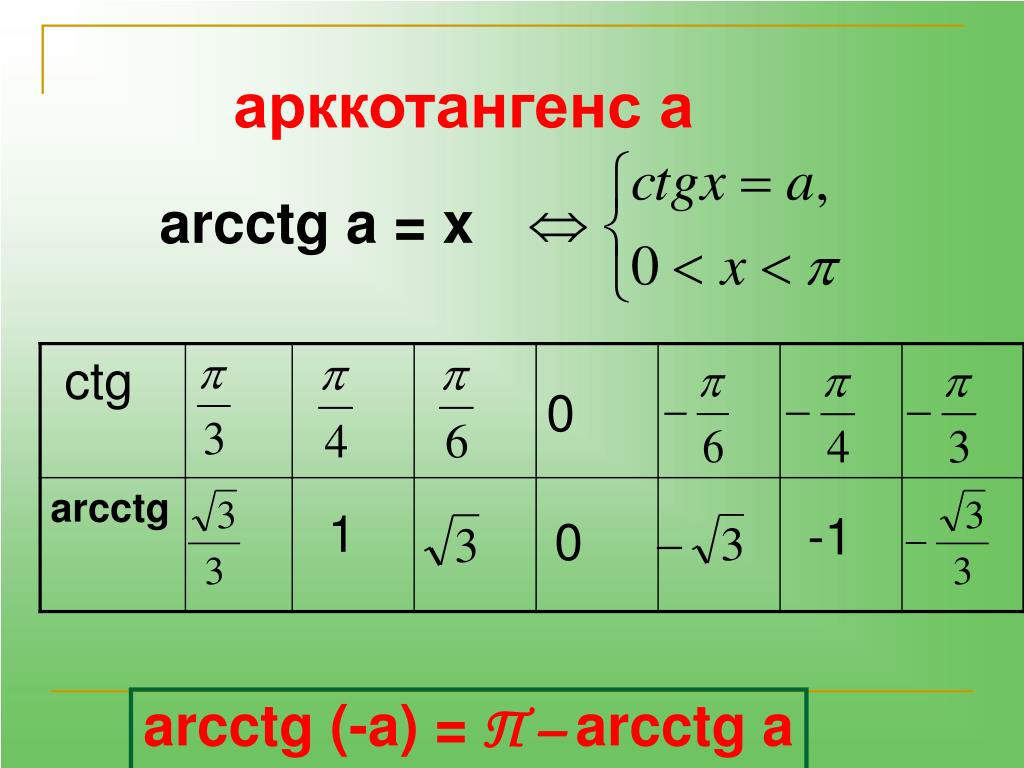 Будемо мати:

2ctg x = -2√3

ctg x = -/2√3/2

ctg x = -√3

x = π — arcctg √3 + πn, n ∈ Z

x = π — /π/6 + πn, n ∈ Z

x = /5π/6 + πn, n ∈ Z

Часто доводиться зустрічати приклади, коли «х» є не сам. Тобто може бути такий вигляд: «sin(ax + b)», «cos(ax + b)», «tg(ax + b)», «ctg(ax + b)». В таких випадках «ax + b» вважають одним цілим і просто записують замість «х» як в попередніх прикладах. Після чого необхідно знайти «х».

Варто зауважити. У випадках коли до «х» щось додається або віднімається, то при перенесені в протилежну сторону (коли шукаємо «х») не потрібно нічого додавати/віднімати.

Наприклад: 2sin⁡(/x/4 — /π/3) — √3 = 0

Як ми вже знаємо в першу чергу необхідно звести приклад до стандартного вигляду «sin x = a».

2sin⁡(/x/4 — /π/3) = √3

sin⁡(/x/4 — /π/3) = /√3/2

Хоча в дужках є «/x/4 — /π/3», але ми все одно вважаємо його як одне ціле яке будемо писати замість «х». Отже будемо мати:

/x/4 — /π/3 = (-1)ⁿ arcsin⁡ /√3/2 + πn, n ∈ Z

/x/4 — /π/3 = (-1)ⁿ arcsin⁡ /π/3 + πn, n ∈ Z

Тепер необхідно забрати «-/π/3» у протилежну сторону від «х». Не забуваємо, що при перенесені у протилежну сторону знак змінюється на протилежний. Будемо мати:

/x/4 = (-1)ⁿ/π/3 + /π/3 + πn, n ∈ Z

Варто зауважити, що у випадках коли ви маєте щось біля «arc…» (наприклад: «±», «(-1)ⁿ»), то не потрібно нічого додавати/віднімати. Тобто все залишиться як є.

Тепер необхідно позбутися «4» у знаменнику. Для цього помножимо весь вираз на «4». Будемо мати:

x = (-1)ⁿ/4π/3 + /4π/3 + 4πn, n ∈ Z

Це вже і є розв’язок.

Часто бувають ситуації, коли «х» є не першим в дужках.

Наприклад: «sin⁡(π — x)».

В таких прикладах варто зробити змінну («х») першою.

Тобто: «sin⁡(-x + π)».

Після чого, варто позбутися мінуса («-») біля «х».

Для цього його необхідно винести за дужки: «sin⁡(-(x — π))».

Тепер варто скористатися правилами винесення «-» з під тригонометричної функції (властивості парних та не парних функцій).

Нагадаємо:

sin⁡(-x) = — sin ⁡x

cos⁡(-x) = cos⁡ x

tg(-x) = — tg x

ctg(-x) = — ctg x

Детальніше читайте тут.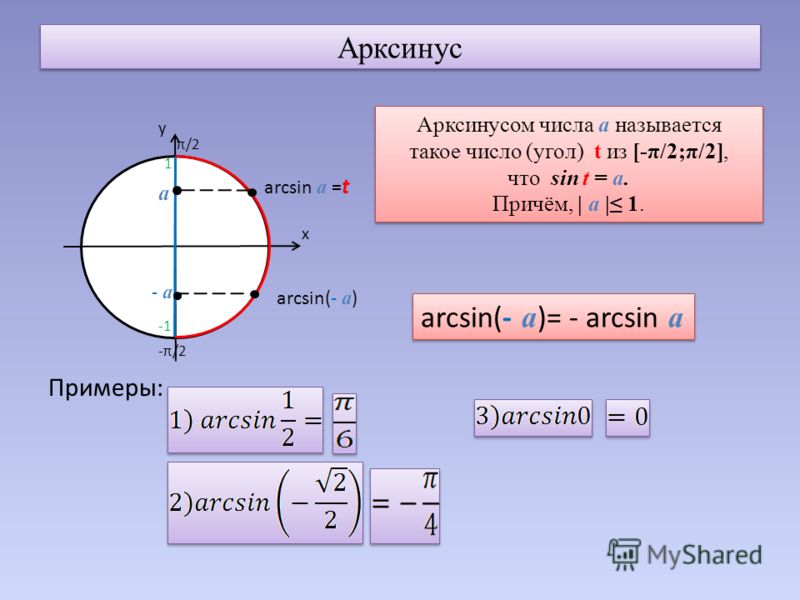

В нашому випадку будемо мати:

sin⁡(-(x — π)) = — sin⁡(x — π)

Після чого розв’язуємо як попередній приклад.

Приклад: tg (/π/4 — /x/2) = -1

Як видно «х» стоїть другим ще й зі знаком «-». Тому ми відразу винесемо «-» за дужки:

tg(-(/x/2 — /π/4)) = -1

«tg» це не парна функція, тому «-» від аргументу виноситься на перед:

— tg(/x/2 — /π/4) = -1

Залишилося звести до стандартного вигляду: «tg x = a». Для цього варто позбутися «-». Просто змінимо знаки у нашому рівнянні (помножимо все рівняння на «-1»).

tg(/x/2 — /π/4) = 1

/x/2 — /π/4 = arctg 1 + πn, n ∈ Z

/x/2 — /π/4 = /π/4 + πn, n ∈ Z

/x/2 = /π/4 + /π/4 + πn, n ∈ Z

/x/2 = /π/2 + πn, n ∈ Z

Помножимо на «2» для того щоб позбутися знаменника біля «х».

x = π + 2πn, n ∈ Z

arctan | NumPy

numpy.arctan(x, *ufunc_args) = <ufunc 'arctan'>

Функция arctan() вычисляет тригонометрический арктангенс (обратный тангенс), если y = tan(x), то x = arctan(y).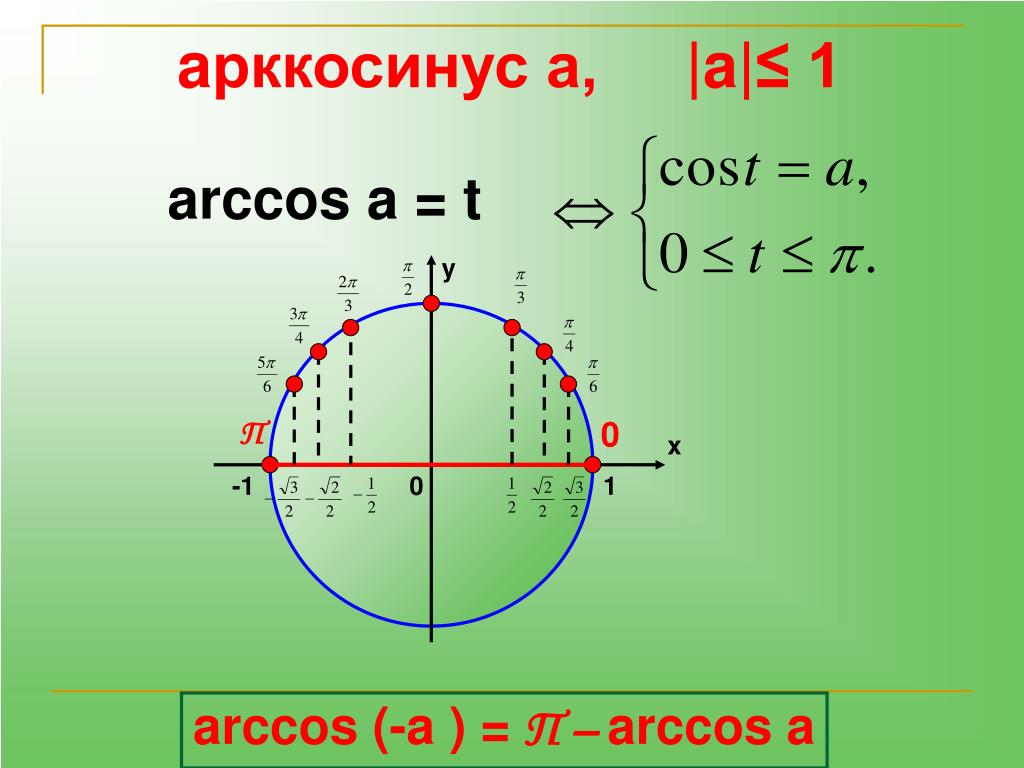

Параметры:

x — подобный массиву объект

y — координата или массив y-координат единичной окружности.

*ufunc_args — аргументы универсальной функции

Аргументы, позволяющие настроить и оптимизировать работу функции (подробнее см. универсальные функции).

Возвращает:

результат — массив NumPy или его подкласс

Арктангенс элементов x в интервале [-pi/2, pi/2] (arctan(-inf) = -pi/2 и arctan(inf) = pi/2).

Замечание

arctan(x) — многозначная функция, т. е. для каждого x существует бесконечное количество значений углов α при которых tan(α) = x, поэтому принято соглашение о том, что функция numpy.arctan(x) возвращает значение угла в интервале [0, pi].

Для комплексных входных значений arctan так же представляет собой бесконечнозначную функцию, которая, по соглашению находится на листе D₀ с разрезами [1j, infj] и [-1j, -infj].

Иногда арккосинус обозначается как atan или tan^-1

Смотрите так же:tan, tanh, arcsin, arccos

---

Примеры

>>> import numpy as np
>>> 
>>> np.arctan(0.77)
0.6561787179913949
>>> 
>>> x = np. array([-np.inf, -1, -0.5, 0, 0.5, 1, np.inf])
>>> 
>>> np.arctan(x)     #  Значение углов в радианах
array([-1.57079633, -0.78539816, -0.46364761,  0.        ,  0.46364761,
        0.78539816,  1.57079633])
>>> 
>>> np.arctan(x)*180/np.pi     #  Значение углов в градусах
array([-90.        , -45.        , -26.56505118,   0.        ,
        26.56505118,  45.        ,  90.        ])

---

---

→ hypot()
← arccos()

---

---

---

Как atan(1) * 4 равно PI?

Задавать вопрос

спросил 7 лет, 8 месяцев назад

Изменено 1 год, 11 месяцев назад

Просмотрено 33 тысячи раз

$\begingroup$

Мне нужна была константа PI в C++, и я получил ответ, что:

 константа PI = atan(1) * 4
 

Обратите внимание, что, несмотря на использование кода, я спрашиваю это с точки зрения математики.

У меня есть 2 вопроса по этому поводу:

• Это оценка PI, или она должна дать мне большую степень точности?
• Как это дает PI?

По второму пункту, если я правильно понимаю atan , он берет отношение двух сторон и возвращает соответствующий угол.

Это означает, что atan(1) относится к ситуации с двумя сторонами одинаковой длины.

Думаю, я что-то неправильно понимаю, поскольку atan(1) дает мне 0.7853981633974483 , что кажется очень маленьким углом.

Если кто-то может заполнить пробелы, мы будем очень благодарны.

$\endgroup$

6

$\begingroup$

Я включаю эту маленькую гифку из Википедии как отличный способ понять радианы.

$\endgroup$

$\begingroup$

Функция $\arctan\colon \mathbb{R}\to (-\frac{\pi}{2},\frac{\pi}{2})$ является обратной к $\tan$. (для правой области определения). Поскольку $\tan \frac{\pi}{4} = 1$, это означает, что $\arctan 1=\frac{\pi}{4}$.

Относительно вашего вопроса об углах: углы (в математике) измеряются в радианах (в $[0,2\pi)$ или $[-\pi,\pi)$), а не в градусах: вы должны ожидать значение или закажите $\pi$ или около того, 9{-1}{1}$

$\endgroup$

$\begingroup$

Математическое объяснение от человека, не имеющего отношения к математике:

В прямоугольном треугольнике, если две короткие стороны равны, угол равен 45 градусам.

45 градусов в радианах равно π/4. (Полная окружность равна 2πr, 180 градусов — это π, а 45 градусов — это π/4)

sin π/4 = cos π/4, потому что две стороны равны.

тангенс π/4 = тангенс 45 = 1.

Арктан(1) — это градус (или радиан), который возвращает значение 1. Таким образом, арктангенс 1 равен либо 45 градусам, либо π/4.

π = 4*арктан(1)

$\endgroup$

$\begingroup$

Это показывает геометрическое объяснение взаимосвязи между тан, атан и Пи.

Поскольку горизонтальный отрезок AB = 1 и вертикальный отрезок BD = 1, угол альфа = 45°. Отсюда вы можете использовать atan( BD ), чтобы определить 45° в радианте и умножить это на 4, чтобы получить Пи.

$\endgroup$

$\begingroup$

Вы правы во всех языках программирования, таких как fortran, c, c++ и многих других, для обобщенной строки ввода программы, которая выглядит примерно так:

 print, numeric, %pi , acos(-1), 4*atan (1)
 

все возвращают одно и то же числовое значение. Здесь системное сохраненное значение %pi может быть быстрее, чем оценка триггера.

 3.141592653589793, 3.141592653589793, 3.141592653589793
 

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.