Программа элективного курса для учащихся 11-го класса «Обратные тригонометрические функции»
Пояснительная записка
Предлагаемый элективный курс для учащихся 11-го класса посвящен одному из важнейших понятий математики. Понятия арксинуса, арккосинуса, арктангенса и арккотангенса вводятся в курс алгебры и начал анализа во время изучения учащимися простейших тригонометрических уравнений. При этом следует заметить, что практически все старшеклассники плохо знают, а тем более понимают, эти определения. Что же тогда говорить об обратных тригонометрических функциях?
В последнее время в материалах ЕГЭ и вступительных экзаменов в высшие учебные заведения, часто предлагаются задания по данной теме. Такие задачи вызывают затруднения у учащихся, так как практических заданий по этой теме в школьных учебниках мало.
Цель данного элективного курса –
повысить математическую культуру учащихся в
рамках школьной программы по математике,
прояснить и дополнить школьный материал,
связанный с обратными тригонометрическими
функциями, представить его систематизацию и
помочь старшеклассникам успешно сдать ЕГЭ по
математике.
В курсе заложена возможность дифференцированного обучения, как путем использования задач различного уровня сложности, так и на основе различной степени самостоятельности осваивания нового материала. Следовательно, программа применима для самых различных групп школьников, в том числе не имеющих хорошей подготовки.
На изучение всего курса отводится 11 часов, по окончании предусмотрено зачетное мероприятие на 2 часа, а также возможны и другие формы комбинированной диагностики.
Учебно-тематический план
№ п/п |
Тема |
Количество часов |
Форма контроля |
1. |
Определения арксинуса, арккосинуса, арктангенса и арккотангенса |
1 |
Математический диктант |
2. |
Функции у=arcsin x, y=arccos x их графики и свойства. |
1 |
Работа с таблицами с последующей взаимопроверкой |
3. |
Функции у=arcsin x, y=arccos x их графики и свойства. |
1 |
Самостоятельная работа обучающего характера |
4. |
Функции у=arcsin x, y=arccos x, их графики и свойства. |
1 |
Тест (различные уровни сложности) |
5. |
Функции у=arctg x, y=arcctg x, их графики и свойства. |
1 |
Самостоятельная работа обучающего характера |
6. |
Функции у=arctg x, y=arcctg x, их графики и свойства. |
1 |
Урок взаимопроверки |
7. |
Функции у=arctg x, y=arcctg x, их
графики и свойства. |
1 |
Тест (различные уровни сложности) |
8. |
Обобщающий урок по теме: “Обратные тригонометрические функции, их графики и свойства” |
2 |
Практикум, работа в группах. Домашняя контрольная работа. |
9. |
Итоговый контроль |
2 |
Зачет (тест) |
Содержание
Тема 1. Определения арксинуса,
арккосинуса, арктангенса и арккотангенса.
На первом занятии учащимся сообщается цель и значение данного курса. Определения арксинуса, арккосинуса, арктангенса и арккотангенса. Основное внимание здесь нужно уделить на идеально точное воспроизведение определений, так как даже самое маленькое отличие от “идеала” влечет за собой большие ошибки.
Темы 2-4. Функции у=arcsin x, y=arccos x их графики и свойства.
Свойства функций: область определения, область значений, непрерывность, четность и нечетность, возрастание и убывание, экстремумы, наибольшие и наименьшие значения, сохранение знака. Графики функций и их преобразование.
Темы 5-7. Функции у=arctg x, y=arcctg x, их графики и свойства.
Свойства функций: область определения,
область значений, непрерывность, четность и
нечетность, возрастание и убывание, экстремумы,
наибольшие и наименьшие значения, сохранение
знака.
Тема 8. Обратные тригонометрические функции, их свойства и графики.
Решение различных заданий, связанных с понятием обратных тригонометрических функций, из вариантов ЕГЭ (группа В и С).
Тема 9. Итоговый контроль.
Итоговая диагностика может быть проведена в виде зачета, виде тестовых заданий, но обязательно дифференцированного характера.
Занятие 1. Определения арксинуса, арккосинуса, арктангенса и арккотангенса.
При решении тригонометрических
уравнений простейших (кроме частных случаев) или
более сложных неизменно приходишь к формулам
корней, в которых есть несколько “магических”
слов: арксинус, арккосинус, арктангенс или
арккотангенс. Эти четыре слова почти для всех
старшеклассников становятся “камнем
преткновения”, большинство школьников (в том
числе и те, кто потом блестяще сдают математику)
не могут точно определить эти функции.
Итак, попробуем разобраться в этих запутанных определениях.
у=arcsin x: у – это число (а не угол!), причем у, такое, что sin у = х. Здесь нужно констатировать еще один факт: х [-1;1].
Продемонстрируем на задачах, как применяется это определение.
№1.
а) arcsin 1/2 =?
Решение: 1/2= х. Значит, мы должны найти такое число у, из отрезка , синус которого равен
arcsin 1/2 = .
б) arcsin=?
Решение: Рассуждаем аналогично.
= х. Значит,
мы должны найти такое число у, из отрезка , синус
которого равен . Можно сделать вывод, что у= .
arcsin= .
в) arcsin (-)=?
Решение: К этому моменту, почти все старшеклассники (особенно те, которые чуть слабее в знаниях), понимают, что ответ гораздо быстрее найти в учебнике, на первых страницах (есть там такие “замечательные” таблицы). И тут начинаются ошибки. Их надо сразу пресечь, четко повторяя, что у – число из отрезка .
Для того чтобы найти это число у, можно воспользоваться такой формулой arcsin(-х)= — arcsin х.Теперь, решение будет гораздо проще.
arcsin (-)= — arcsin = — .
y=arccos x: у – это число (а не угол!), причем у, такое, что cos у = х. Здесь нужно констатировать еще один факт: х [-1; 1].
у=arctg x: у – это число (а не угол!),
причем у, такое, что tg у= х.
Причем для
х здесь ограничений нет.
y=arcctg x: у – это число (а не угол!), причем у , такое, что ctg у= х. Причем для х здесь ограничений нет.
№2.
а) arccos 1/2=?
Решение: 1/2=х. Значит, мы должны найти такое число
arccos 1/2= .
б) ) arccos=?
Решение: Рассуждаем аналогично. = х. Значит, мы должны найти такое число у, из отрезка, косинус которого равен . Можно сделать вывод, что у= .
arccos= .
в) arccos(-)=?
Решение: Для того чтобы школьники
опять не воспользовались таблицами, следует
сразу им дать формулу: arсcos(-х) = – arсcos х.
Для вычисления отрицательных значений арктангенса и арккотангенса применимы формулы: arctg(- x) = — arctg x
№ 3.
Вычислить:
а) arctg0
б) arсcos(-1/2)
в) arсctg(-1)
г) arcsin 1
д)
е) arcsin (-0,5)
ж)
№ 4.
Найти область допустимых значений переменной для выражений:
а) arcsin(1-х)
б) arсcos(2-х/2)
в) arcsin(2х+х2)
г) arctg (1-х2)
д)
№5.
Вычислить:
а) sin (arсcos (-1/4))
б) cos (arcctg(-2))
в) sin (2 arcsin 1/3)
г) tg (2 arcsin 1/3).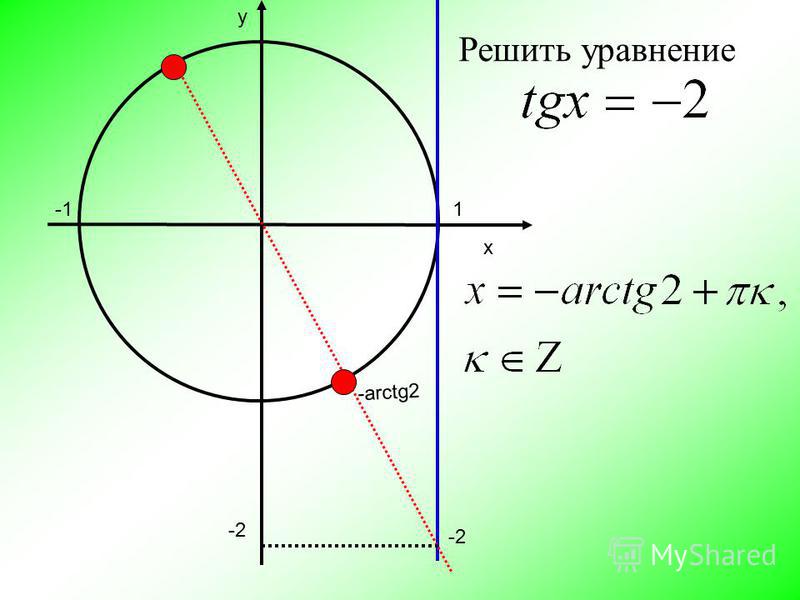
Решение: а) sin (arсcos (-1/4))=?
Пусть у= arсcos (-1/4). Значит, мы должны найти sin y.
По определению арккосинуса у – это число, из отрезка , косинус которого равен -1/4.
Итак, у= arсcos (-1/4), у, т.е. у может принадлежать I и II четвертям. При этом cos у = -1/4.
Теперь можно уточнить, у принадлежит II четверти, т.к. cos у<0. Используем формулу
sin2y + cos2y =1.
sin2y= 1 — cos2y
siny = ±, т.к. у II ч., то siny>0.
Значит, siny= .
Ответ: siny=.
№6.
Произведите указанные действия:
а) arcsin 3/5 + arcsin 12/13
б) arсcos 7/25 + arсcos 3/5
в) arсctg 5 — arсctg 4
г) arctg4 + arctg 5.
Решение:
Пусть arcsin 3/5 + arcsin 12/13= у, тогда cos у=cos(arcsin 3/5 + arcsin 12/13). Применим формулу косинус суммы и получим:
cos у= cos (arcsin 3/5) cos(arcsin 12/13) – sin(arcsin 3/5) sin(arcsin 12/13)
Вычисляя каждое выражение в отдельности, получим cos у= -16/65, значит у=arсcos(-16/65)
Ответы:
3. а) 0 б) в) г) д) е) ж) 0.
4. а) [ 0;2] б) [ 2;6] в) г) ж)
5.
б) в) г)
.
6. а) arсcos(-16/65) б) arсcos(-3/5) в) – arctg1/21 г) arсctg(-19/9)
Итогом этого занятия должен быть математический диктант с последующей проверкой. Проверка может осуществляться через проецирование с помощью оверхеда, ответы могут быть заранее готовы на дополнительных досках, а также к проверке можно привлечь и учащихся.
Занятия 2-4. Функции у=arcsin x, y=arccos x, их графики и свойства.
Данные занятия следует начинать с понятия обратная функция.
Определение. Пусть каждому значению у
Е(f) соответствует
только одно значение х D(f), для которого у= f (х).
Указанное соответствие у>х задает функцию с
областью определения Е(f) и областью значений D(f).
Эту функцию называют обратной к функции f (х).
Обозначив обратную функцию через g, имеем: если у=
f (х), то х = g(у).
Примерами обратных функций могут служить показательная и логарифмическая функции. Для каждой из этих функций всегда можно найти обратную функцию. А вот для функции у=х2 есть обратная функция только при определенных условиях. При каких? (Монотонность функции. y=х2 имеет обратную ей только для х ). Каким свойством обладают графики взаимообратных функций? (Графики взаимно обратных функций симметричны относительно прямой у=х).
Используя эти определения и свойства, построим графики функций у=arcsin x, y=arccos x. Объяснение лучше проводить с помощью ИКТ.
Слайд 1.
С помощью средств анимации построение
графика функции у= arcsin х будет
выполнено пошагово и наглядно.
Аналогично поступаем и с функцией у= arccos x.
Слайд 2.
Далее необходимо напомнить учащимся о возможных преобразованиях графиков функций и выполнить с классом устную работу.
Устная работа.
- Установить соответствие между графиком и формулами.
- Для каждой из предложенных функций указать область определения и область значений.
- При каком значении а уравнения не имеют решений:
Слайд 3.
2. Указать для каждой из данных функции область определения и область значений.
3. Решить уравнения:
а) arccos x= 3х+ 3,15
б) arcsin х= (1/2)х + 1,58
№1.
Построить графики функций:
а) у=2 arccos (х+2) – 2
б) у= -0.
5 arcsin (x-1) +1
в) y= | 3 arccos (х+1,5)- 5 |
Это задание может быть выполнено школьниками с помощью таблиц Эльконина–Давыдова с последующей взаимопроверкой. Таблица выглядит следующим образом.
№2.
Укажите все точки на оси Ох, являющиеся проекциями точек графика функции:
Текст задания поставит в тупик многих школьников. Смысл этого задания состоит в том, что процесс нахождения области определения функции совпадает с заданием в этом номере.
№3.
Решить уравнение:
Текст этого задания можно
варьировать: найти нули функции, найти абсциссы
точек пересечения графиков функций, определить
значения х, при которых точки одного графика
лежат на графике другой функции.
№4.
Найти область определения функции:
№5.
Найти область значений функции:
Текст этого задания можно сформулировать иначе: найти сумму наибольшего и наименьшего значений функции, указать число целых значений функции.
Ответы:
2.а) (0;1] б) в) (0;1]
3.а) 1 б) -1 в) 2
4. а) б) [0;1/2] в) [2;3)U(3;4]
5. а) [1;2] б) в) [0;25]
Задания для самостоятельной работы
1. Вычислить:
2. Найти область определения функции:
3.
Найти сумму наибольшего и
наименьшего значений функции:
4. Решить уравнение:
Занятия 5-7. Функции у=arctg x, y=arcctg x, их графики и свойства.
Объяснение материала рекомендую вести с помощью ИКТ, проводя сравнительный анализ между функциями у=tg x и у=arctg x, y=ctg x и y=arcctg x. С помощью средств анимации построение графиков функций будет выполнено пошагово и наглядно.
Слайд 4.
Слайд 5.
Далее необходимо напомнить учащимся о возможных преобразованиях графиков функций и выполнить с классом устную работу.
Устная работа.
1.
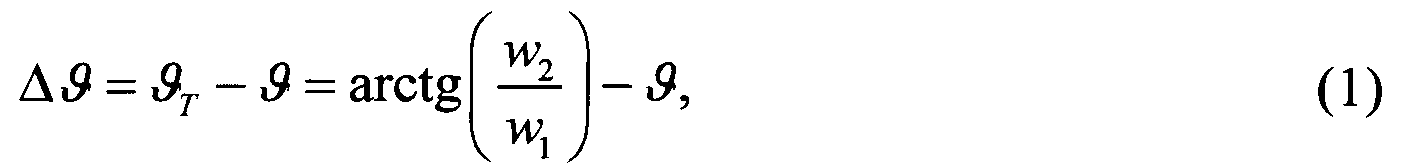Установить соответствие между
графиком и формулами:
Слайд 6.
а) arctg x=cos x+ a
б) arcctg x — а = х.
№1.
Построить графики функций:
Это задание может быть выполнено школьниками с помощью таблиц Эльконина–Давыдова с последующей взаимопроверкой. Таблица выглядит следующим образом.
№ 2.
Решить уравнения:
Опыт показывает, что нередко ученик,
“берясь” за решение уравнения (впрочем, как и
неравенства), концентрирует свое внимание только
на поиске преобразований, сводящих исходное
уравнение к более простому, забывая при этом, что
не каждое преобразование безобидно.
Нужно
помнить и о свойствах функций, их области
определения и области значений. При решении
приведенных выше уравнений необходимо
обязательно найти ОДЗ.
№ 3.
Найти множество значений функции:
№ 4.
Решить неравенство:
Решение:
в)
Решение данного неравенства опирается на свойства функций y=sin x и y=arctg x . Введем функции y1=sin x-1999 и y2=2arctg x +.
Е(sin x) = [-1; 1], E(y1) =[-2000; -1998]. Это значит, что выражение sin x-1999 < 0 при любых значениях аргумента. Поэтому, выражение 2arctg x +должно принимать неотрицательные значения, т.е. 2arctg x +0.
2arctg x — .
arctg x — .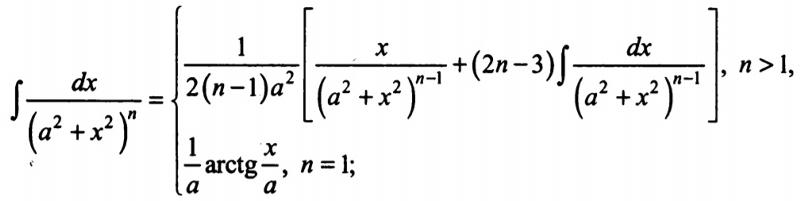
Так как функция y2=2arctg x + возрастающая, то знак неравенства при дальнейшем решении сохраняется. То есть
Ответ: х.
№ 5.
При каких значениях а уравнение имеет единственный корень:
Ответы:
2. а) 1 б) 0; 2 в) 2; 3
3. а) [0; 2] б) [-1; 0] в) [-3; 0]
4. а) б)
5. а) б) в)
Задания для самостоятельной работы
№ 1.
Вычислить:
№ 2.
Найти множество значений функции:
№ 3.
Решить уравнение или неравенство:
Занятия 8-9.
Обратные
тригонометрические функции, их свойства и
графики.
Эти два занятия я рекомендую провести как практикум, заранее разделив класс на группы. В каждой группе должны быть учащиеся с разной математической подготовкой, тогда работа класса будет более плодотворной и результативной.
Приведу примерный вариант карточек для проведения этого практикума.
Карточка 1.
- Построить графики функций:
- Вычислить:
- Вычислить значения следующих выражений:
Карточка 2.
1.Найти область определения функции:
2. Найти множество значений функции:
3.Найти наименьшее значение функции:
Карточка 3.
- Решить уравнения:
- Найти сумму х0+у0, если (х0;у0) – решение системы
- Решить неравенства:
Карточка 4.
1.Сколько получится числовых промежутков, если из отрезка, определяемого множество значений функции , удалить все целые числа?
2. Для каждого значения параметра а решить неравенство .
Занятие 10-11. Зачет (тест)
В качестве зачетных заданий предлагаются задания из разделов “Задания для самостоятельной работы”. Школьникам заранее дать текст этих заданий, провести консультацию по возникшим вопросам.
См. презентацию.
Тригонометрические уравнения и неравенства
Тригонометрия
Тригонометрические
уравнения и неравенства
Попкова Т.
Г. МОУ СОШ № 2 Горячий Ключ
Повторим значения синуса косинуса
у π/2 90°
120° 2π/3 1 π/3 60°
135° 3π/4 π/4 45°
150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
— — — 1/2 ½ 2π 360 (cost)
210° 7π/6 — 1/2 11π/6 330° [-π/6]
—
225° 5π/4 — 7π/4 315° [-π/4]
240° 4π/3 -1 5π/3 300° [-π/3]
270° 3π/2 [-π/2]
(sint)
Арксинус
Примеры:
Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2] ,
что sin t = а .
Причём, | а |≤ 1 .
у
π/2
1
arcsin а = t
а
х
— а
arcsin( — а )
arcsin( — а )= — arcsin а
-1
-π/2
Арккосинус
у
Арккосинусом числа а называется
такое число (угол) t из [0;π], что
cos t = а .
Причём, | а |≤ 1 .
π/2
arccos а = t
arccos( — а )
х
π
0
arccos( — а ) = π- arccos а
-1
1
а
-а
Примеры:
= π
1)arccos(-1)
2)arccos
При каких значениях х имеет смысл выражение:
1.arcsin(2x+1)
2.arccos(5-2x)
2) -1≤ 5-2х ≤1
1) -1≤ 2х-1 ≤1
-2≤ 2х ≤0
-6≤ -2х ≤ -4
-1≤ х ≤0
2≤ х ≤3
Ответ: [2;3]
Ответ: [-1;0]
4.arcsin(4x²-3x)
3.arccos(x²-1)
-1≤4х²-3х≤1
4х²-3х ≥ -1
4х²-3х ≤ 1
4х²-3х-1 ≤ 0
Ответ:
-1≤ х²-1 ≤ 1
0 ≤ х² ≤2
Ответ:
Повторим значения тангенса и котангенса
Линия тангенсов tg t ЄR , но t ‡ + π k , kЄZ
у π/2
2π/3 π/3 1
5π/6 π/4
π/6 ctg t ЄR, но t ‡ 0 + πk , kЄZ
0 х Линия котангенсов
у
4π/3
-π/2
π 0 х
Арктангенс
а
у
Арктангенсом числа а называется
такое число (угол) t из (-π/2;π/2),
что tg t = а .
Причём, а Є R.
π/2
arctg а = t
х
0
arctg( — а ) = — arctg а
arctg( — а )
-π/2
— а
Примеры:
1) arctg√3/3 =
2) arctg(-1) =
-π/4
π/6
Арккотангенс
у
Арккотангенсом числа а называется
такое число (угол) t из (0;π),
что c tg t = а .
Причём, а ЄR .
— а
а
arcctg а = t
arcctg( — а )
π
0
х
arcctg( — а ) = π – arcctg а
Примеры:
1) arcctg(-1) =
3π/4
2) arcctg√3 =
π/6
Формулы корней простых тригонометрических уравнений
1.
cost = а , где | а| ≤ 1
2.sint = а, где | а |≤ 1
3. tgt = а, а ЄR
t = arctg а + πk‚ kЄZ
или
или
Частные случаи
Частные случаи
4. ctgt = а, а ЄR
1) cost=0
1) sint=0
t = 0+πk‚ kЄZ
t = π/2+πk‚ kЄZ
t = arcctg а + πk‚ kЄZ
2) cost=1
t = 0+2πk‚ kЄZ
2) sint=1
t = π/2+2πk‚ kЄZ
3) cost = -1
t = π+2πk‚ kЄZ
3) sint = — 1
t = — π/2+2πk‚ kЄZ
Примеры:
1) cost= — ½;
2) sint = 0;
Частный случай:
t= ±arccos(-1/2)+2πk, kЄZ
t= ±2π/3+2πk, kЄZ
t = 0+πk, kЄZ
4) ctgt = —
3) tgt = 1;
t = arctg1+πk, kЄZ
t = arcctg( )+πk, kЄZ
t = π/4+πk, kЄZ.
t = 5π/6+πk, kЄZ.
Решение простейших уравнений
2) cos(x+π/3) = ½
- tg2x = -1
2x = arctg (-1) + πk, kЄZ
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/8 + πk/2, kЄZ.
Ответ: -π/3 ± π/3 + 2πk, kЄZ
3) sin(π – x/3) = 0
упростим по формулам приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.
Другие тригонометрические уравнения
1.Сводимые к квадратным
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и
решить простые уравнения.
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = m
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
Ответ: (-arctg а +πk; π/2+πk), kЄZ «
Простые тригонометрические неравенства
y
y
arccos а
2) sint а
1) cost а
а
arcsin а
-(π+arcsin а )
x
x
а
-arccos а
Ответ: (-(π+arcsin а )+2πk; arcsin а +2πk), kЄZ
Ответ: (-arccos а +2πk; arccos а+ 2πk), kЄZ
а
y
π/2
y
4) ctgt а
3) tgt — а
arcctg а
0
x
x
-arctg а
— а
Ответ: (0+πk; arcctg а +πk), kЄZ.
Ответ: (-arctg а +πk; π/2+πk), kЄZ
Калькулятор — arctan(1) — Солуматы
Арктан, расчет онлайн
Резюме:
Функция арктангенса позволяет вычислить арктангенс числа.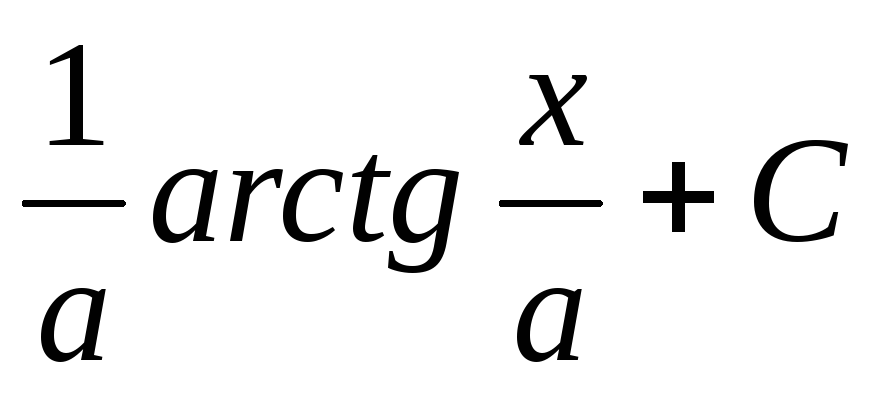
Функция арктангенса является обратной функцией функции тангенса.
arctan онлайн
Описание:
Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .
- Расчет арктангенса
- Пределы арктангенса Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция.
Например, чтобы вычислить арктангенс следующего числа 10, введите arctan(`10`), или сразу 10, если кнопка arctan уже появляется, возвращается результат 1.4711276743. 92)`.
- Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
- Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
- `lim_(x->-oo)arctan(x)=pi/2`
- `lim_(x->+oo)arctan(x)=-pi/2`
| arctan(`-1`) | `3*pi/4` | |
| arctan(`-sqrt(3)/3`) | `5*pi/6` | `2*pi/3` |
| arctan(`0`) | `0` | |
| arctan(`sqrt(3)`) | `/3` | |
| arctan(`1`) | `pi/4` | |
| arctan(`sqrt(3)/3`) | `pi/6` |
Syntax :
arctan(x) , x — число. 92)`
Предельный арктангенс :
Калькулятор пределов позволяет вычислить пределы функции арктангенса.
предел арктангенса(x) is limit(`»arctan»(x)`)
Обратная функция арктангенса :
обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.
Графический арктангенс :
Графический калькулятор может строить график функции арктангенса в интервале ее определения.
Свойство функции арктангенс :
Функция арктангенса является нечетной функцией.
Расчет онлайн с арктангенсом (арктангенсом)
См. также
Список связанных калькуляторов:
- Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
- Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
- Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Калькулятор позволяет получить тригонометрическое разложение выражения.Прочие ресурсы
- Исправленные упражнения по числовым функциям
- Бесплатные онлайн математические игры про функции — производная — примитив — f(x)=0
- Научитесь считать с помощью обычных математических функций
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | 902:30|
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | кос(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | 902:30|
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | 902:30|
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. |