Arctg что это такое: определение, формула, таблица, график, свойства

Содержание

определение, формула, таблица, график, свойства

Определение

Арктангенс (arctg или arctan) – это обратная тригонометрическая функция.

Арктангенс x определяется как функция, обратная к тангенсу x, где x – любое число (x∈ℝ).

Если тангенс угла у равен х (tg y = x), значит арктангенс x равняется y:

arctg x = tg^-1 x = y, причем -π/2<y<π/2

Примечание: tg^-1x означает обратный тангенс, а не тангенс в степени -1.

Например:

arctg 1 = tg^-1 1 = 45° = π/4 рад

График арктангенса

Функция арктангенса пишется как y = arctg (x). График в общем виде выглядит следующим образом:

Свойства арктангенса

Ниже в табличном виде представлены основные свойства арктангенса с формулами.

Таблица арктангенсов


x (°)	x (рад)	arctg x
-90°	-π/2	-∞
-71.565°	-1.2490	-3
-63.435°	-1.1071	-2
-60°	-π/3	-√3
-45°	-π/4	-1
-30°	-π/6	-1/√3
-26.565°	-0.4636	-0.5
0°	0	0
26.565°	0.4636	0.5
30°	π/6	1/√3
45°	π/4	1
60°	π/3	√3
63.435°	1.1071	2
71.565°	1.2490	3
90°	π/2	∞

microexcel.ru

Арктангенс, арккотангенс — свойства, графики, формулы

Арктангенс, arctg

Определение и обозначения

Арктангенс ( y = arctg x ): – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .
tg(arctg x) = x ;
arctg(tg x) = x .

Арктангенс обозначается так:
.

График функции арктангенс

График функции y = arctg x

График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.

Арккотангенс, arcctg

Определение и обозначения

Арккотангенс ( y = arcctg x ): – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений .
ctg(arcctg x) = x ;
arcctg(ctg x) = x .

Арккотангенс обозначается так:
.

График функции арккотангенс

График функции y = arcctg x

График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.

Четность

Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x

Функция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x ≠ ± arcctg x.

Свойства – экстремумы, возрастание, убывание

Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x. (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.

	y = arctg x	y = arcctg x
Область определения и непрерывность	– ∞ < x < + ∞	– ∞ < x < + ∞
Множество значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы, минимумы	нет	нет
Нули, y = 0	x = 0	нет
Точки пересечения с осью ординат, x = 0	y = 0	y = π/2
	–	π
		0

Таблица арктангенсов и арккотангенсов

В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.

x	arctg x		arcctg x
	град.	рад.	град.	рад.
– ∞	– 90°	–	180°	π
–	– 60°	–	150°
– 1	– 45°	–	135°
–	– 30°	–	120°
0	0°	0	90°
	30°		60°
1	45°		45°
	60°		30°
+ ∞	90°		0°	0

≈ 0,5773502691896258
≈ 1,7320508075688772

Формулы

См. также: Вывод формул обратных тригонометрических функций

Формулы суммы и разности

     при

     при

     при

Выражения через логарифм, комплексные числа

См. также: Вывод формул

,
.

Выражения через гиперболические функции

Производные

См. Вывод производных арктангенса и арккотангенса > > >

Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.

См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.

Аналогично для арккотангенса. Пусть . Тогда
;
.

Интегралы

Делаем подстановку x = tg t и интегрируем по частям:
;
;
;

Выразим арккотангенс через арктангенс:
.

Разложение в степенной ряд

При |x| ≤ 1 имеет место следующее разложение:
;
.

Обратные функции

Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.

Следующие формулы справедливы на всей области определения:
tg(arctg x) = x
ctg(arcctg x) = x .

Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x) = x при
arcctg(ctg x) = x при .

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 14-07-2014 Изменено: 23-12-2018

Обратные тригонометрические функции — это… Что такое Обратные тригонометрические функции?

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

аркси́нус (обозначение: arcsin)
аркко́синус (обозначение: arccos)
аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
арксе́канс (обозначение: arcsec)
арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin⁻¹ для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.

Основное соотношение

Функция arcsin

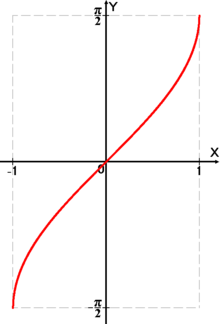$\operatorname {arctg}\, x + \operatorname {arcctg}\, x = \frac{\pi}{2}$ График функции .

Арксинусом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Свойства функции arcsin

Получение функции arcsin

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — . Так как для функции на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция график которой симметричен графику функции на отрезке относительно прямой

Функция arccos

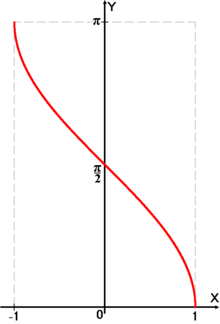График функции .

Арккосинусом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

Свойства функции arccos

Получение функции arccos

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — На этом отрезке строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция график которой симметричен графику на отрезке относительно прямой

Функция arctg

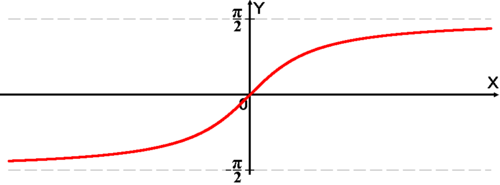График функции .

Арктангенсом числа m называется такое значение угла , для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Свойства функции arctg

, при x > 0.

Получение функции arctg

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная , график которой симметричен графику на отрезке относительно прямой

Функция arcctg

График функции y=arcctg x

Арккотангенсом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

Свойства функции arcctg

Получение функции arcctg

Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — . На этом отрезке строго убывает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой График симметричен к арктангенсу

Функция arcsec

Функция arccosec

Производные от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных и комплексных x:

Для действительных x ≥ 1:

См. также Список интегралов от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных и комплексных x:

Для действительных x ≥ 1:

См. также Список интегралов от обратных тригонометрических функций

Использование в геометрии

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:

α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)

Связь с натуральным логарифмом

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

См. также

Ссылки

Арктангенс ℹ️ определение, свойства и функции, формулы расчета производной, график функции, таблица значений, онлайн-калькулятор

Чётность и возрастание

Чтобы получить график арктангенса, используется кривая тангенса путём замены местами осей ординат и абсцисс. Для устранения многозначности используется интервал, на котором функция монотонна. Это определение считается основным значением арктангенса. Если показатель отрицательный, значит функция нечётная.

Главное свойство arctg — бесконечность на его области определения (для числа х). Так как y = arctg x, где y равен нулю, тогда x = 0, значит и arctg 0. При выполнении расчётов используется таблица арктангенсов.

В ней указаны значения в градусах и радианах, при определённых данных аргумента. Если вычисления выполняются на математическом веб-ресурсе, пользователю предоставляется возможность бесплатно использовать онлайн-калькулятор и таблицу Брадиса. Можно вычислить синус, косинус, производную арктангенса в экселе либо с помощью языка программирования Паскаль.

Чтобы посчитать величину правильно, используются свойства функций. При помощи определения арксинуса выполняется уравнение sin (arcsin a)=a. Свойства других величин:

косинус: cos (arccos a)=a;
тангенс: tg (arctg a)=a;
катангенс: ctg (arcctg a)=a.

В первых двух свойствах соблюдается условие −1≤a≤1. Если значение а выходит за указанные пределы, тогда функции нет смысла определять. Учитывая свойства синуса арксинуса, нельзя записать sin (arcsin8)=8, так как выражение sin (arcsin8) не имеет смысла. Аналогичный ответ получается, если необходимо определить разность арккосинуса sqrt (квадратный корень) из пяти.

Противоположные числа

Формулы, с помощью которых производится расчёт связи между производными: arcsin (-a)=-arcsina, arccos (-a)=пи-arccosa, arctg (-a)=-arctga, arcctg (-a)=пи-arcctga. Должно соблюдаться условие −1≤a≤1. Если а принадлежит промежутку −∞ до +∞, тогда arctg (−a), и arcctg (−a).

Чтобы доказать первое отношение с противоположными числами, рассматривается определение arcsin (−a). Число либо угол находится в пределах −π/2-π/2 и синус, равный −a. Учитывая определение арксинуса, можно записать следующее равенство: −π/2≤arcsin a≤π/2.

На основе свойств неравенств, выполняется умножение составных частей на -а. Заменив знаки неравенств на противоположные, можно произвести умножение на -1: −π/2≤−arcsin a≤π/2.

Необходимо доказать, что sin (−arcsin a)=−a. Для этого рекомендуется придерживаться свойств противоположных углов. Из рассмотренных примеров можно сделать вывод: sin (−arcsin a)=−sin (arcsin a)=−a.

Аналогичным способом можно доказать, что arccos (−a)=π−arccos a. Используя определение производной функции, подтверждается, что π−arccos a — угол либо число, значение которого колеблется в пределах 0-π, а cos (π−arccos a)=−a. Придерживаясь определения арккосинуса числа, выполняется неравенство 0≤arccos a≤π.

Используя свойства неравенств, перемножаются поочерёдно его части на -1, сменяются знаки. Решается неравенство из сумм частей и числа пи, при этом сохраняются знаки: −π+π≤−arccosa+π≤0+π. Получается двойное выражение вида 0≤π−arccos a≤π.

Если средняя часть уравнения равняется −a, тогда, придерживаясь формулы приведения, записывается следующее равенство cos (π−arccos a)=−cos (arcos a). С помощью свойства производной косинуса завершается доказательство cos (π−arccos a)=−cos (arcos a)=−a. Аналогичной схемы рекомендуется придерживаться при рассмотрении свойств арккотангенсов и арктангенсов противоположных знаков. Плюс утверждения — возможность избавиться от вычисления производных функций отрицательных чисел.

Сложение величин

Свойство, согласно которому устанавливается связь между arccos arcsin числа а, и между arctg и arcctg переменной, записывается следующим образом: arcsina+arccosa=пи/2, arctga+arcctga=пи/2. Чтобы доказать первую часть равенства, где расписана сумма производных синуса и косинуса числа а, делённая на два, необходимо рассмотреть следующую запись: arcsin a=π/2−arccos a.

Основываясь на определение арксинуса, можно доказать, что выражение верно, когда π/2−arccos a — угол (цифровое значение), лежащий на промежутке −π/2 до π/2, а синус угла равен а. Чтобы показать такую действительность, используется определение арккосинуса и равенство 0≤arccos a≤π. Последнее выражение считается справедливым.

С учётом свойств неравенств, умножаются части на минус один, изменяются знаки. Полученные значения суммируются с числом π/2. Выполнив перечисленные действия, получается неравенство −π/2≤π/2−arccosa≤π/2. Чтобы показать, что sin (π/2−arccos a)=a, используется формула приведения, свойство производной функции косинус.

Доказано, что сумма arccos и arccos a равна π/2. Аналогично понадобится доказать, что сумма арккотангенса числа a и арктангенса равняется π/2. Главное предназначение таких свойств заключается в том, что они выражают арксинус через акрккосинус одного числа, а также арккотангенс через арктангенс и наоборот.

Примеры и задачи

Задания на свойства функций и их производных от числа либо угла можно решить с помощью разных программ: excel, pascal. Действия будут зависеть от условий задачи. Решение должно основываться на основные признаки, доказанные либо утверждённые равенства. Свойствам производных отвечают следующие выражения:

arcsin (sinx)=x;
arccos (cosx)=x;
arctg (tgx)=x;
arcctg (ctgx)=x.

Равенства при определённых условий следуют из определений функций числа. Чтобы понять утверждения, необходимо доказать: arcsin (sin α)=α, при этом должно выполняться требование −π/2≤α≤π/2. Аналогичным образом доказываются оставшиеся свойства. Если обозначить sin α=а, которое находится на отрезке [−1, 1], тогда получится выражение arcsin (sin α)=α, то есть arcsin a=α. Известно из условий задач, что −π/2≤α≤π/2. При решении через а обозначили sin α.

Поэтому можно записать, что arcsin a=α, что эквивалентно определению производной функции синуса. Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.

Известно, аrcsin sin (-15)= -15 град., arccos (cos (2π/3))=2π/3, arctg (tg (0,2))=0,2. Нужно отметить, что выражение arcsin (sin α) справедливо на отрезке −π/2≤α≤π/2. Но равенство arcsin (sin α)=α имеет смысл только при соблюдении этого условия. Нельзя утверждать, что arcsin (sin (7π/4))=7π/4, так как 7π/4 не принадлежит указанному интервалу (−π/2-π/2).

Запись arccos (cos α) правдивая, не только при условии, что 0≤α≤π. Выражение arccos (cos α)=α считается справедливым только при таком условии. Поэтому arccos (cos (−3π))=−3π не верно, так как −3π не принадлежит указанному отрезку. Схожие утверждения логичны и для arcctg (ctg α), arctg (tg α).

Используя определение всех функций, их признаки, тригонометрические формула можно получить другие равенства и уравнения, в которых отображается связь между arcsin, arcctg, arctg и arccos. Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.

определение, формула, таблица, график, свойства

Определение

Арккотангенс (arcctg или arccot) – это обратная тригонометрическая функция.

Арккотангенс x определяется как функция, обратная к котангенсу x.

Если котангенс угла у равен х (ctg y = x), значит арккотангенс x равняется y:

arcctg x = ctg^-1 x = y

Примечание: ctg^-1x означает обратный котангенс, а не котангенс в степени -1.

Например:

arctg 1 = ctg^-1 1 = 45° = π/4 рад

График арккотангенса

Функция арккотангенса пишется как y = arcctg (x). График в общем виде выглядит следующим образом (0 < y < π, –∞ < x < +∞):

Свойства арккотангенса

Ниже в табличном виде представлены основные свойства арккотангенса с формулами.

Таблица арккотангенсов


x (°)	x (рад)	arcctg x
180°	π	-∞
150°	5π/6	-√3
135°	3π/4	-1
120°	2π/3	-1/√3
90	π/2	0
60	π/3	1/√3
45	π/4	1
30	π/6	√3
0	0	∞

microexcel.ru

определение, формула, таблица, график, свойства

Определение

Арксинус (arcsin) – это обратная тригонометрическая функция.

Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.

Если синус угла у равен х (sin y = x), значит арксинус x равняется y:

arcsin x = sin^-1 x = y

Примечание: sin^-1x означает обратный синус, а не синус в степени -1.

Например:

arcsin 1 = sin^-1 1 = 90° (π/2 рад)

График арксинуса

Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):

Свойства арксинуса

Ниже в табличном виде представлены основные свойства арксинуса с формулами.

Таблица арксинусов


x	arcsin x (рад)	arcsin x (°)
-1	-π/2	-90°
-√3/2	-π/3	-60°
-√2/2	-π/4	-45°
-1/2	-π/6	-30°
0	0	0°
1/2	π/6	30°
√2/2	π/4	45°
√3/2	π/3	60°
1	π/2	90°

microexcel.ru

Что такое арктангенс?

Категории

Добавлено: 12.07.2016 18:52 Добавил: Авету

Тригонометрия – важный раздел математики, в переводе с греческого значит – «измерение треугольников». Она включает в себя такие понятия как арксинус, арккосинус, арктангенс, арккотангенс. Возникновение тригонометрии неразрывно связно со строительным делом, астрономией и землемерием. В школе знакомство с тригонометрическими функциями происходит, когда мы берем в руки транспортир. Позднее знание арктангенса, арксинуса и других обратных функций помогает в решении уравнений тригонометрии.

Существует несколько областей применения тригонометрии и свойств функций тригонометрии на практике. Ярким примером служит метод триангуляции в астрономии, он помогает определять расстояние до звезд в Космосе. Используют тригонометрию и в географии. Знание формул, свойств, особенностей тригонометрических функций помогает определить расстояние между объектами. Применяется этот раздел Алгебры и в спутниковой, морской, воздушной навигации, а также в акустике, оптике, в электронике, теории вероятностей, сейсмологии, океанографии, экономике, метеорологии, других науках и сферах жизни.

Как определяется арктангенс?

Арктангенс в алгебре – это обратная тригонометрическая функция к tg (тангенсу), его еще называют аркфункцией. Область ее определения от — ∞ +∞. Обозначается он в математике как arctg x. Во многих учебниках и методической литературе зарубежных стран можно встретить другое обозначение: arctang x.
Из особенностей этой обратной функции выделяют то, что она является возрастающей. Функция y=arctg x ограничена и непрерывна на всей протяженности своей числовой прямой.
История происхождения названия обратных функций тоже имеет свою историю. Оно образовано при помощи приставки «арк», которая происходит от латинского слова arcus и переводится как дуга. Это объясняется тем, что значение обратной функции неразрывно связано с длиной дуги единичной окружности.

Обозначение обратных функций в тригонометрии при помощи приставки «arc» в математику привнес австрийский ученый Крал Шерфер, который жил в XVIII веке. Распространению этой приставки «arc» к обратным функциям мир математики обязан Лагранжу (он жил во Франции в это же время, Жозеф Луи Лагранж также известен известен, как и крупнейший математик XVIII Эйлер).

Позднее в XIX веке немецкие и английские математические школы использовали другие обозначения обратных функций: tg-1, 1/tg. Такие же обозначения как tg-1 встречаются в разных научных изданиях. С одной стороны это имеет место быть, а с другой – некорректно, возникает путаница с возведением функции в минусовую степень.

Понятие арктангенса в тригонометрии

В учебнике по алгебре школьного курса понятие арктангенса звучит следующим образом:
Арктангенсом числа m принято называть такое значение угла x с градусной мерой в радианах, тангенс которого равен m на отрезке -π/2 до π/2. Говоря математическим языком, это звучит так:
arctg m=x, следовательно, tg x =m. При условии, что x больше -π/2 , но меньше π/2, (числовое выражение: -π/2π/2).
График функции arctg выводят из графического отображения прямой функции тангенс. Для этого всего лишь меняют местами ось ординат и ось абсцисс. Для устранения многозначности необходимо ограничить интервалом множество значений: минус π/2 π/2. На этом отрезке функция монотонна. Это определение считают главным значением arctg.

Во всех математических справочниках и учебниках школьного курса вы найдете определение тангенса и котангенса, их графическое определение, формулы, свойства, графики. Также для решения тригонометрических уравнений вам понадобятся таблицы котангенсов, интегралы, производные и разложения в ряды, знание связи с гиперболическими функциями и умение выражать через комплексные переменные.

Остались вопросы?

Получить подробные ответы на свои вопросы в области обратных тригонометрических функций, узнать их особенности и свойства, изучить график арктангенса и грамотно подготовиться к ЕГЭ вы можете в режиме онлайн вы можете на сайте http://interneturok.ru/На этом портале найдете уроки как по алгебре, так и по другим предметам школьной программы.

Понравилось? Поделитесь с друзьями!

Среди множества онлайн — казино… PM casino – это онлайн… Гладиаторские бои, спортивные состязания, игры… Большое разнообразие игровых автоматов Эльдорадо… Раньше наземные казино были в… Сегодня большое число людей предпочитает… Всемирная сеть интернета достигла самых… В Эльдорадо можно открыть страну-мечту,… Большое число людей сегодня предпочитают… Теннис — это самый популярный…

Статья об Arctg от Free Dictionary

функция, которая является решением проблемы нахождения дуги (числа) по заданному значению ее тригонометрической функции. Шесть обратных тригонометрических функций соответствуют шести тригонометрическим функциям: (1) Arc sin x , обратный синус x ; (2) Arc cos x , обратный косинус x ; (3) Arc tan x , арктангенс x ; (4) арка x , обратный котангенс x ; (5) Arc sec x , обратная секущая x ; и (6) Arc csc x , обратный косеканс x .

В качестве примера, согласно этим определениям, x = Arc sin a — любое решение уравнения sin x = a ; то есть sin Arc sin a = a . Функции Arc sin x и Arc cos x определены в реальной области для ǀ x ǀ ≤ 1, функции Arc tan x и Arc cot x определены для всех реальных x , а функции Arc sec x и Arc csc x определены для ǀ x ǀ ≥ 1.Две последние функции используются редко.

Поскольку тригонометрические функции периодичны, обратные к ним функции многозначны. Некоторые однозначные ветви (главные ветви) этих функций обозначаются как arc sin x , arc cos x ,…, arc csc x . В частности, arc sin x : ветвь функции Arc sin x , для которой –π / 2 ≤ arc sin x ≤ π / 2. Аналогичным образом, функции arc cos x , arc tan x и arc cot x определяются соответственно из условий 0 x ≤ π, –π / 2 x <π / 2, и 0 x <π.Обратные тригонометрические функции Arc sin x ,… могут быть легко выражены через arc sin x ,…; например,

Arc sin x = (-1) ⁿ arc sin x + π n

Arc cos x = ± arc cos x + 2π n

Загар дуги x = загар дуги x + π n

Загар x = загар x + π n

, где n = 0, ± 1, ± 2, ….

Хорошо известные соотношения между тригонометрическими функциями дают соотношения между обратными тригонометрическими функциями, например, формула

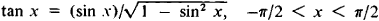
означает, что

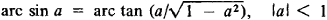
Производные обратных тригонометрических функций имеют вид

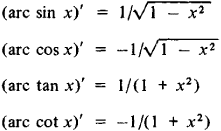
Обратные тригонометрические функции могут быть представлены в виде степенного ряда, например,

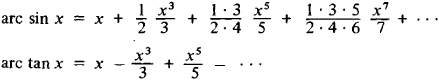
Эти ряды сходятся для — 1 ≤ x ≤ 1.

Обратные тригонометрические функции могут быть определены для произвольных комплексных значений независимой переменной, но значения этих функций будут действительными только для значений независимой переменной, указанных выше. Обратные тригонометрические функции комплексной независимой переменной могут быть выражены с помощью логарифмической функции, например,

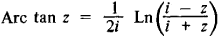
СПРАВОЧНИК

Новоселов С.И. Обратные тригонометрические функции , 3-е изд.Москва, 1950.

Тригонометрическая функция arctan () — арктангенс — математическое определение слова

Функция тригонометрии arctan () — арктангенс — определение слова в математике — справочник по математике

Функция arctan является обратной по отношению к функции касательной.
Возвращает угол, тангенс которого является заданным числом.

Попробуй это Перетащите любой вершине треугольника и посмотрите, как вычисляется угол C с помощью функции arctan ().

Для каждой тригонометрической функции существует обратная функция, которая работает наоборот.Эти обратные функции имеют то же имя, но с дугой впереди. (На некоторых калькуляторах кнопка arctan может быть помечена как атан, а иногда загар ^-1.) Таким образом, тангенс, обратный tan, равен arctan и т. Д. Когда мы видим «arctan x», мы понимаем его как «угол, тангенс которого равен x».

загар 30 = 0,577	Означает: тангенс 30 градусов равен 0,577
арктан 0,577 = 30	означает: угол, тангенс которого равен 0,577, равен 30 градусам.

Используйте arctan, если вы знаете тангенс угла и хотите узнать фактический угол.
См. Также Обратные функции — тригонометрия

Пример — использование arctan для нахождения угла

На рисунке выше нажмите «сбросить». Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что поэтому нам нужно знать угол, тангенс которого равен 0,577, или формально: С помощью калькулятора находим arctan 0,577 равным 30 °.

Большие и отрицательные углы

Напомним, что мы можем применить триггерные функции на любой угол, включая большие и отрицательные углы.Но когда мы Рассмотрим обратную функцию, и мы столкнемся с проблемой, потому что существует бесконечное количество углов, имеющих одинаковую касательную. Например, 45 ° и 360 + 45 ° будут иметь одинаковую касательную. Подробнее об этом см. Обратные тригонометрические функции.

Чтобы решить эту проблему, ассортимент обратных триггерных функций ограничены таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.

Диапазон и владение arctan

Напомним, что область действия функции — это набор допустимых входных данных для нее.Диапазон — это набор возможных выходов.

Для y = arctan x:

Диапазон
Домен	Все реальные числа

Условно диапазон arctan ограничен от -90 ° до + 90 ° * .

Итак, если вы используете калькулятор для вычисления, скажем, arctan 0,55, из бесконечного числа возможностей он вернет 28,81 °, тот, который находится в диапазоне функции.

* На самом деле, -90 ° и + 90 ° сами по себе не входят в диапазон. Это потому, что функция tan имеет значение бесконечность при этих значениях. Но значения чуть ниже них находятся в диапазоне, например +89.9999999. Но для простоты объяснения мы говорим, что диапазон составляет ± 90 °.

Что попробовать

На рисунке выше нажмите «сбросить» и «скрыть детали».
Отрегулируйте треугольник до нового размера
Используя функцию arctan, вычислите значение угла C из длин сторон
Нажмите «Показать подробности», чтобы проверить ответ.

Другие темы по тригонометрии

Уголки

Тригонометрические функции

Решение задач тригонометрии

Исчисление

Arcotangente arctan (x)

L ‘ arcotangente è una funzione goniometrica inversa, indicata con arctan (x), con arctg (x) o talvolta con atan (x), che viene Definita come inversa della chengzione tangente e come valori gli angoli tra -∏ / 2 e + ∏ / 2 espressi in radianti.

Cerchi un rapido formulario in cui leggere le proprietà della funzione arcotangente y = arctan (x) e vederne il grafico? Sei finito nel posto giusto! Qui trovi tutto quello che serve sapere sull’arcotangente, ma andiamo conordine…

Definizione di arcotangente : fissato, si Definisce l’angolo in 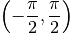$\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ la cui tangente è.

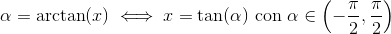
$\alpha=\arctan(x)\iff x=\tan(\alpha)\mbox{ con }\alpha\in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$

Da qui si capiscemediate che l’arcotangente è la funzione inversa della funzione tangente sull’intervallo 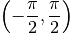$\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ .

Per calcolare l’arcotangente di un valore dobbiamo needariamente appellarci alla Definizione. Nello specifico, si deve individualuare l’angolo 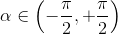$\alpha\in\left(-\frac{\pi}{2},+\frac{\pi}{2}\right)$ la cui tangente vale.

A titolo di esempio

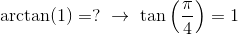
$\arctan(1)=?\ \to\ \tan\left(\frac{\pi}{4}\right)=1$

e di consguenza

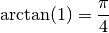
$\arctan(1)=\frac{\pi}{4}$

Eventualmente potete aiutarheori con la tabllei de la valzée

Grafico della funzione arcotangente

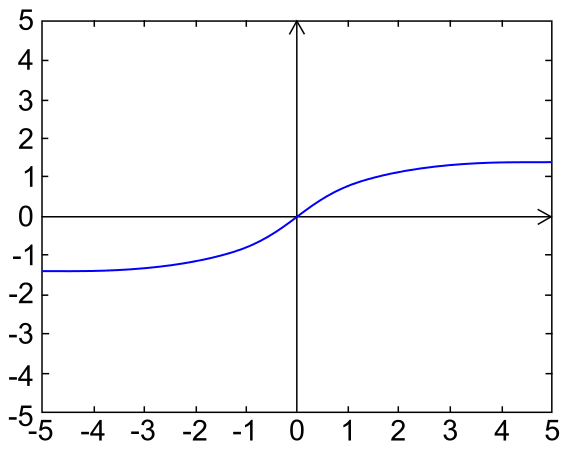
Identità dell’arcotangente

Prima di cominciare, vale la pena di segnazione arcotangente degli esercizi.Ad ogni modo non preoccupatevi, non vanno ricordate a memoria. 😉

$\arctan(\tan(x))=x\ \ \ \mbox{per }-\frac{\pi}{2}< x< \frac{\pi}{2}$

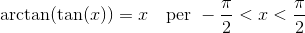
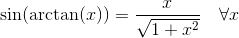$\sin(\arctan(x))=\frac{x}{\sqrt{1+x^2}}\ \ \ \forall x$ (Dimostrazione sin (arctan (x)))

$\cos(\arctan(x))=\frac{1}{\sqrt{1+x^2}}\ \ \ \forall x$

000
000
000
000
000
000
000
000
000
000
000
000
000
$\arctan(x)+\mbox{arccot}(x)=\frac{\pi}{2}\ \ \ \forall x$
$\arctan(x)+\arctan\left(\frac{1}{x}\right)=\begin{cases}-\frac{\pi}{2}\mbox{ se }x<0\\ +\frac{\pi}{2}\mbox{ se }x>0\end{cases}$
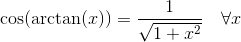
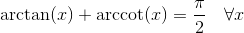
Per approfondire potete consultare la lezione con всех основных тригонометрических формулах.
Собственность, выполняющая функции аркотанги x
1) Dominio:.
2) È una funzione dispari.
3) Funzione limitata con immagine 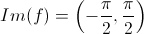$Im(f)=\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ .
4) Funzione monotona strettamente crescente su tutto il dominio.
5) Concava sull’intervallo, convssa sul.
6) Непрерывно на всех, производных на всех.
7) Limiti agli estremi del dominio:
$\\ \lim_{x\to -\infty}\arctan(x)=-\frac{\pi}{2}\\ \\ \lim_{x\to +\infty}\arctan(x)=+\frac{\pi}{2}$
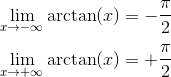
8) Limite notevole associato:
$\lim_{x\to 0}\frac{\arctan(x)}{x}=1$
ata
)
)
$\frac{d}{dx}\arctan(x)=\frac{1}{1+x^2}$
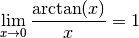
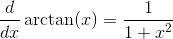
10) Integrale dell’arcotangente:
$\int\arctan(x)dx=x\arctan(x)-\frac{1}{2}\log(x^2+1)+c$
11) Per studenti Universitari:
000
000
000
Se siete in cerca di esercizi svolti e non, o in caso di dubbi, non esitate e usate la barra di ricerca interna: lo staff di YM ha risposto a migliaia di domande e risolto altrettanti esercizi.;)
…..
Теги: lezione di riepilogo con la Definizione, il grafico e all le proprietà della funzione arcotangente di x arctan (x) dominio, tracui: il , la monotonia, la conssità, i limiti agli estremi, il limite notevole associato, la производные и l’integrale dell’arcotangente.
.
Что такое интеграл от arctan (x)?
Исчисление
Наука
Анатомия и физиология
Астрономия
Астрофизика
Биология
Химия
наука о планете Земля
Наука об окружающей среде
Органическая химия
Физика
Математика
Алгебра
Исчисление
Геометрия
Предалгебра
Precalculus
Статистика
Тригоно
.
No related posts.