Обратные тригонометрические функции, их свойства и графики. — Студопедия
Поделись
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
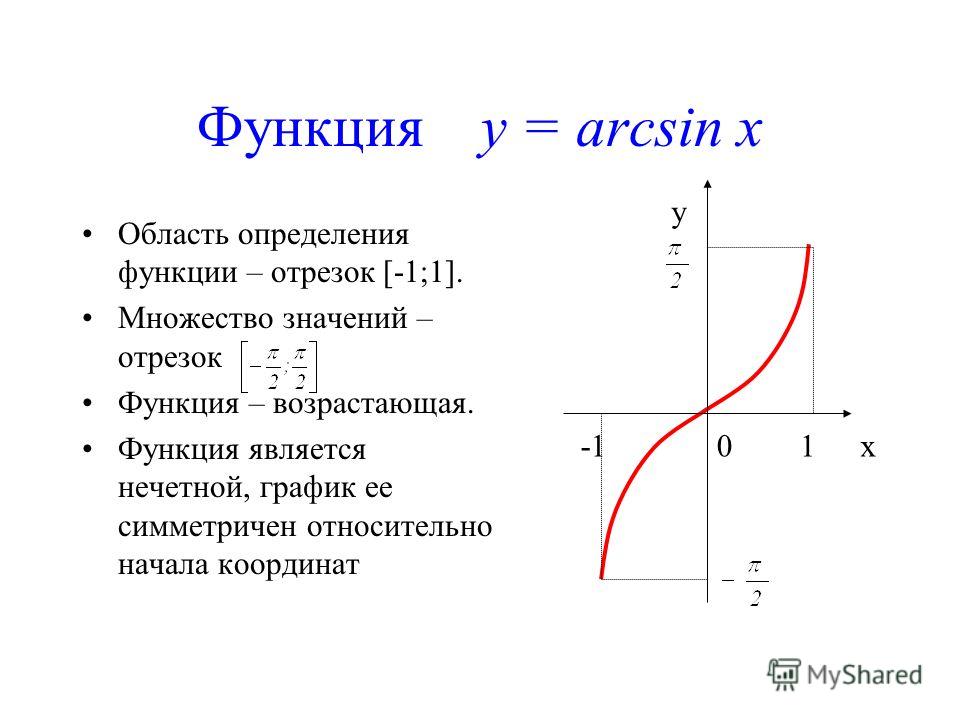
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
Свойства функции арксинус y = arcsin(x).
· Областью определения функции арксинус является интервал от минус единицы до единицы включительно: .
· Область значений функции y = arcsin(x): .
· Функция арксинус — нечетная, так как .
· Функция y = arcsin(x) возрастает на всей области определения, то есть, при .
· Функция вогнутая при , выпуклая при .
· Точка перегиба (0; 0), она же ноль функции.
· Асимптот нет.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
Свойства функции арккосинус y = arccos(x).
· Область определения функции арккосинус: .
· Область значений функции y = arccos(x): .
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция арккосинус убывает на всей области определения, то есть, при .
· Функция вогнутая при , выпуклая при .
· Точка перегиба .
· Асимптот нет.
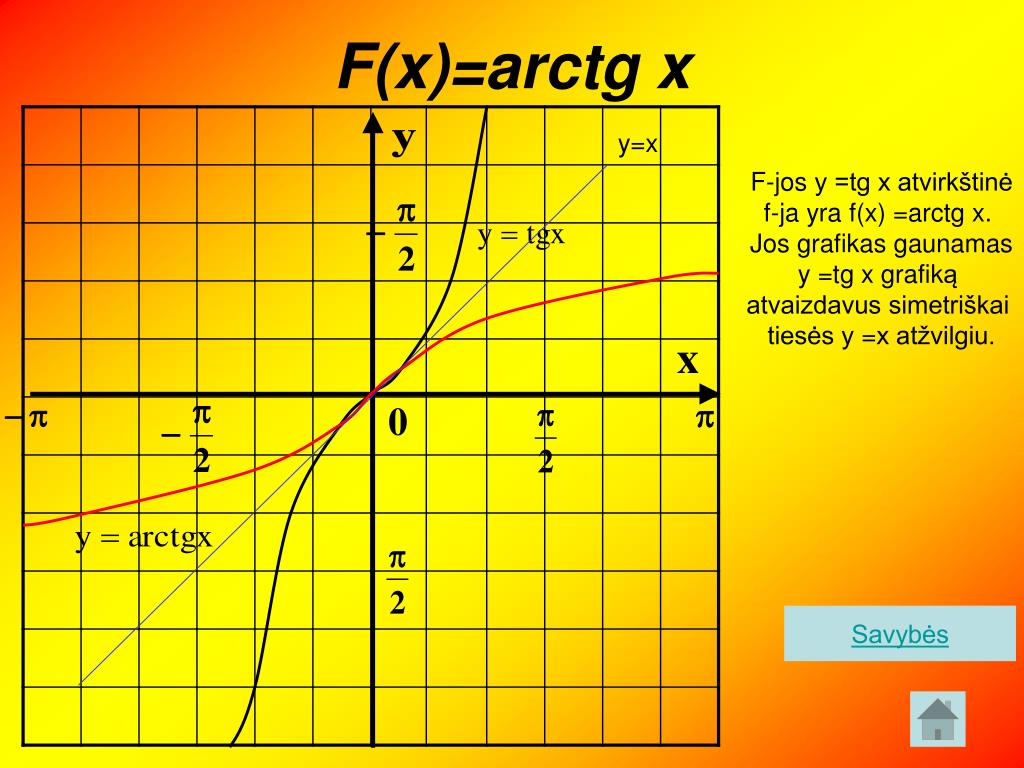
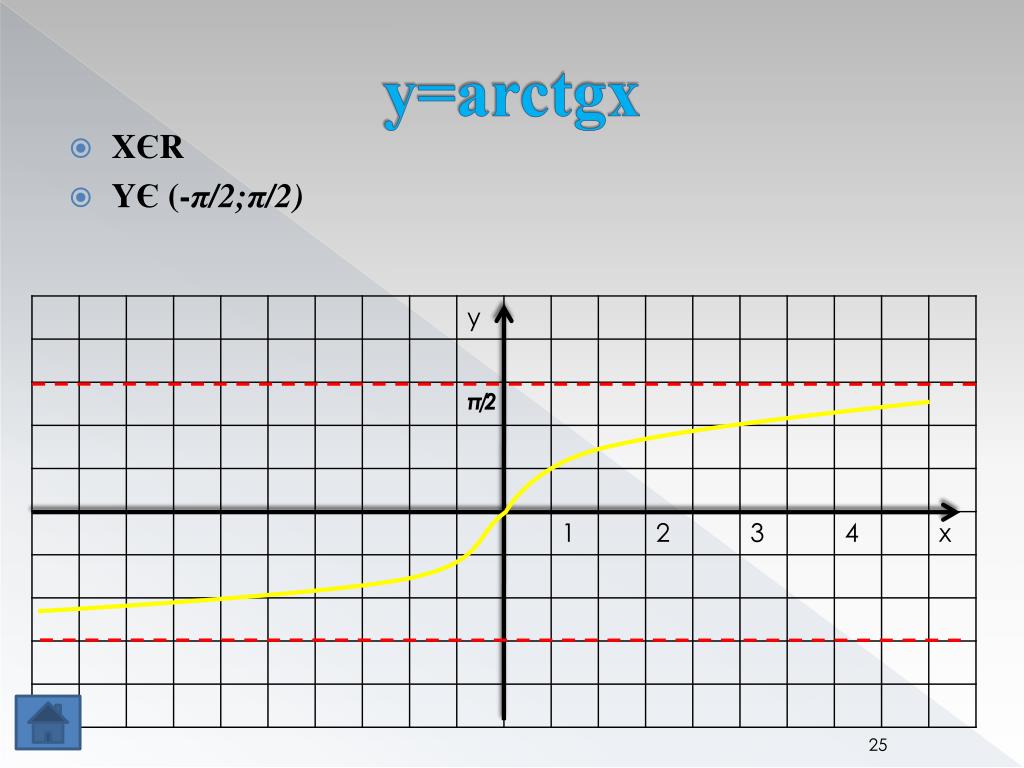
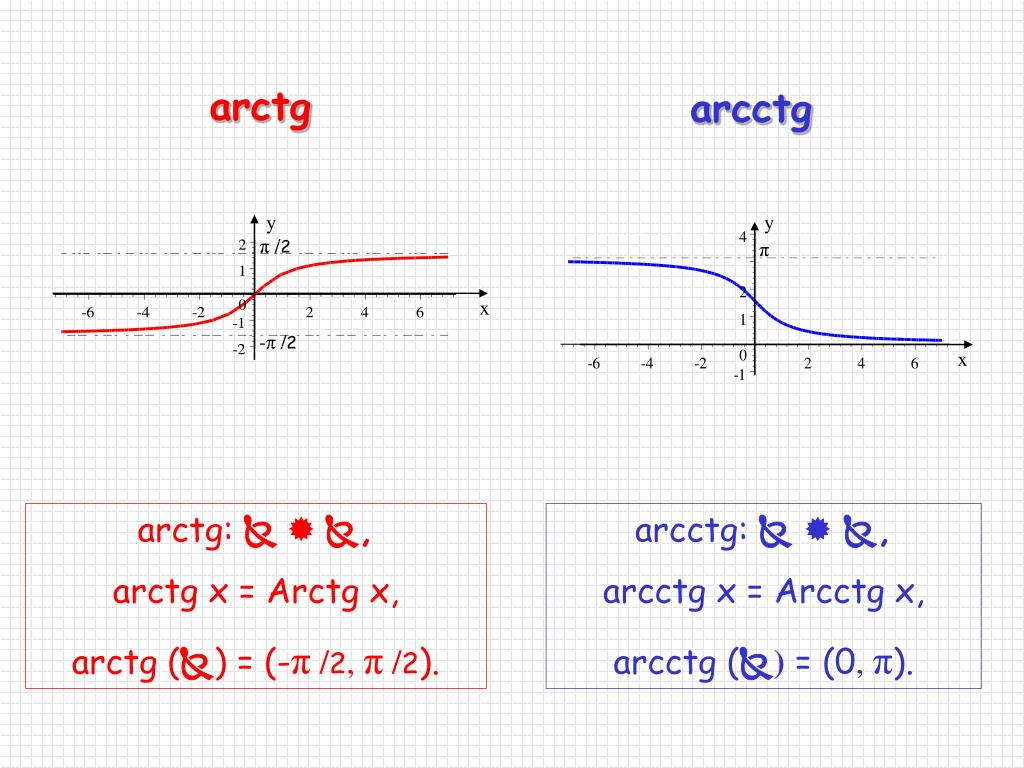
Функция арктангенс y = arctg(x).
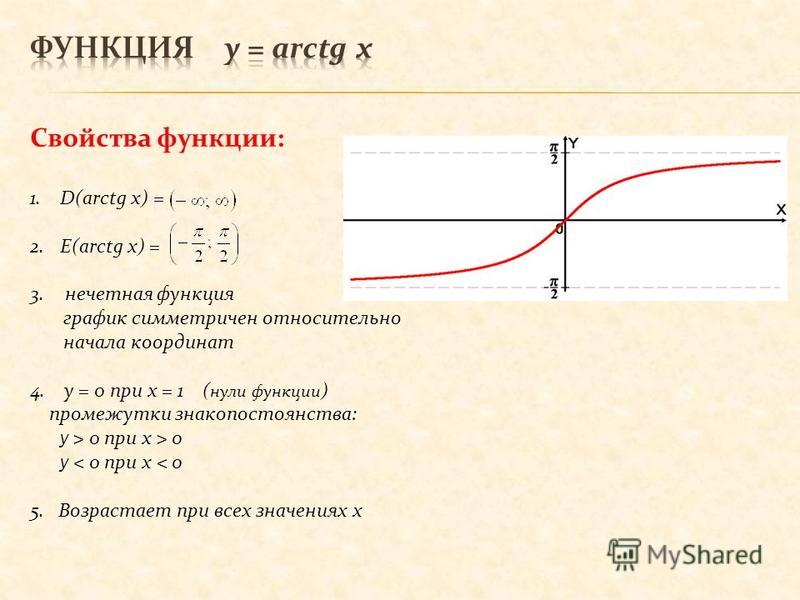
График функции арктангенс имеет вид:
Свойства функции арктангенс y = arctg(x).
· Область определения функции y = arctg(x): .
· Область значений функции арктангенс: .
· Функция арктангенс — нечетная, так как .
· Функция возрастает на всей области определения, то есть, при .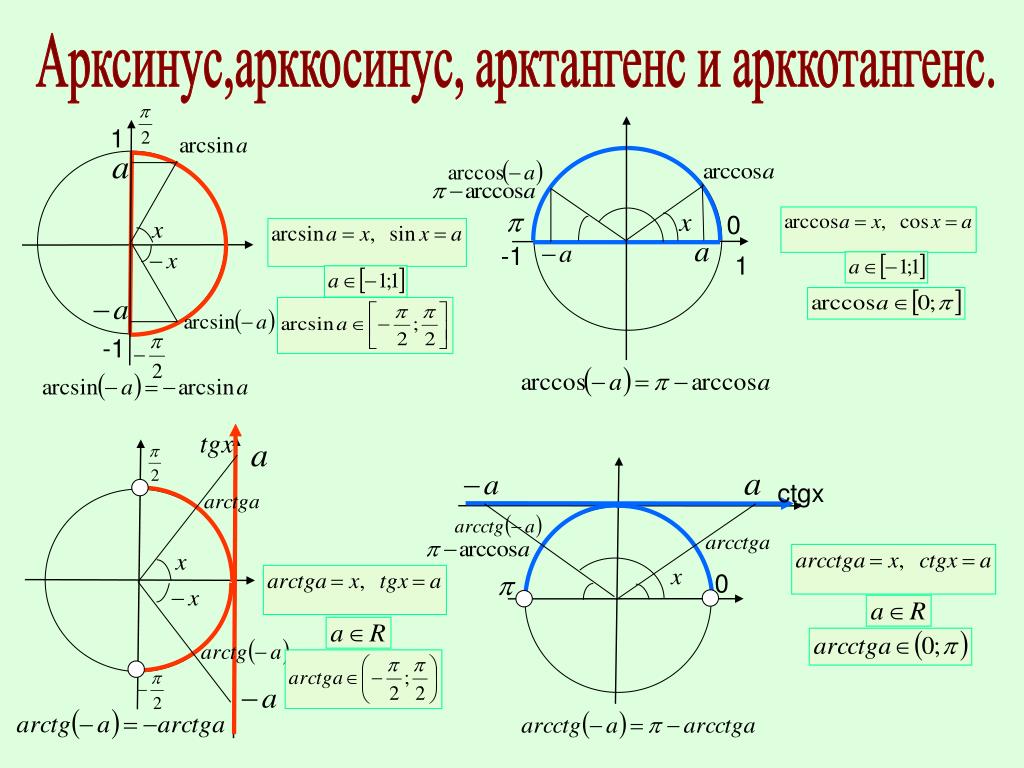
· Функция арктангенс вогнутая при , выпуклая при .
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые при и при . На чертеже они показаны зеленым цветом.
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
Свойства функции арккотангенс y = arcctg(x).
· Областью определения функции арккотангенс является все множество действительных чисел: .
· Область значений функции y = arcctg(x): .
· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при .
· Функция вогнутая при , выпуклая при .
· Точка перегиба .
· Горизонтальными асимптотами являются прямые при (на чертеже показана зеленым цветом) и
графическое представление функции arctan(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
это онлайн-график , который позволяет отображать функции в режиме онлайн.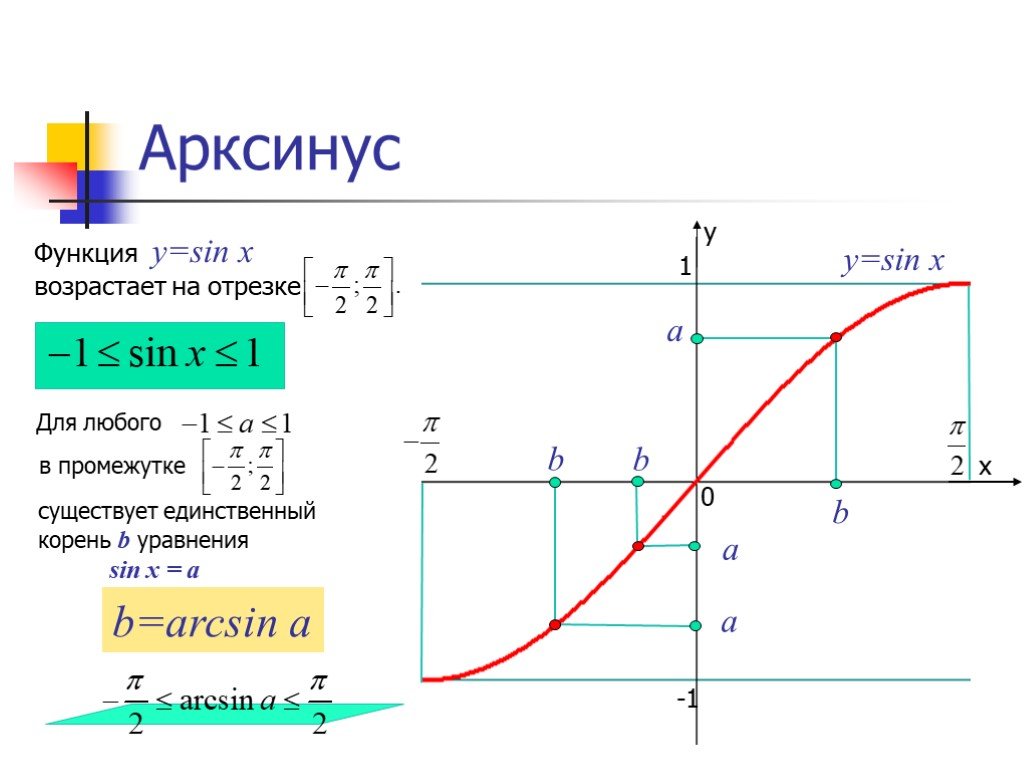 Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для питания
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно , просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн
.
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.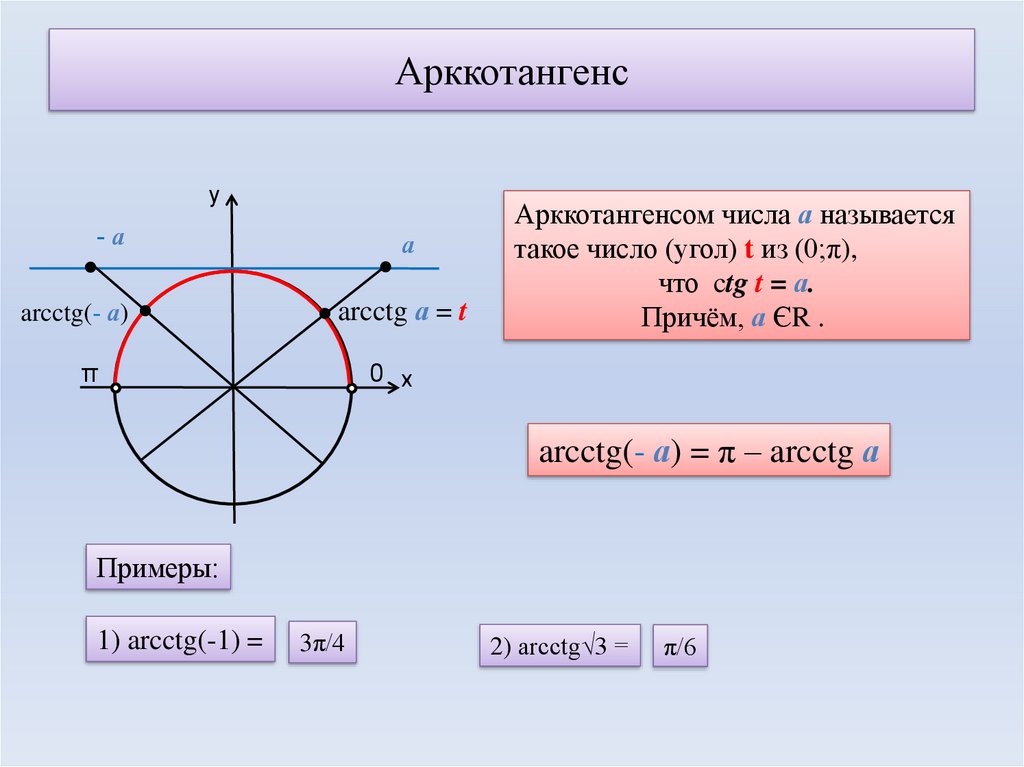
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.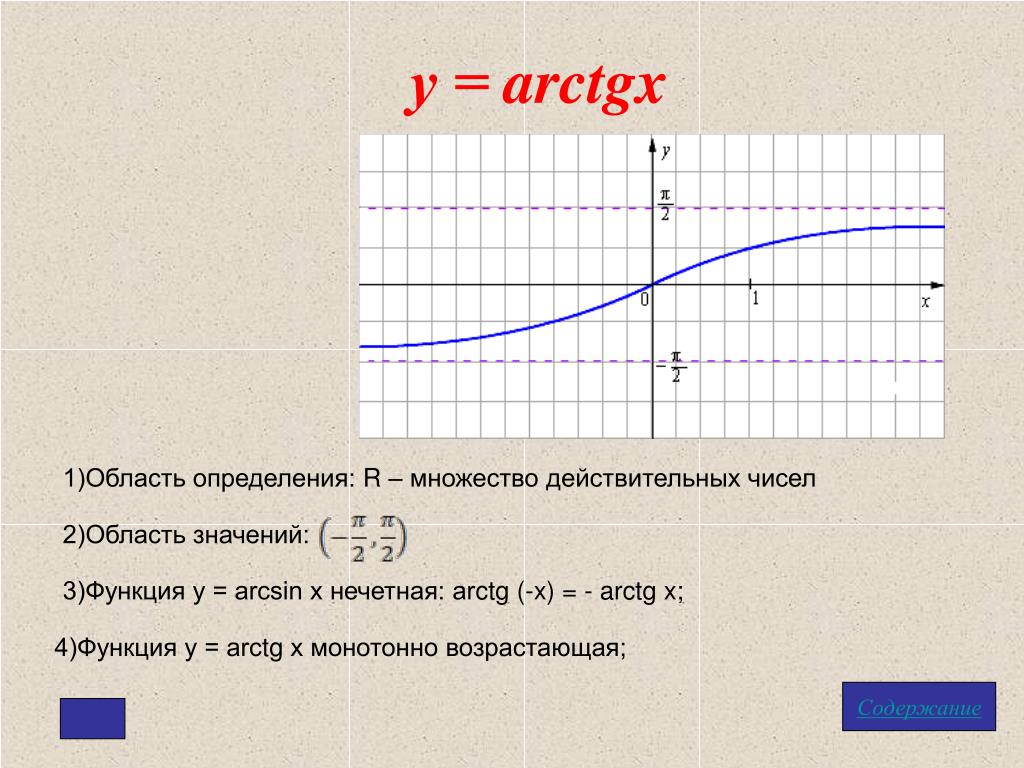
9Построитель кривых 0003 также можно использовать для вычисления производной функции и к участок он для этого, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.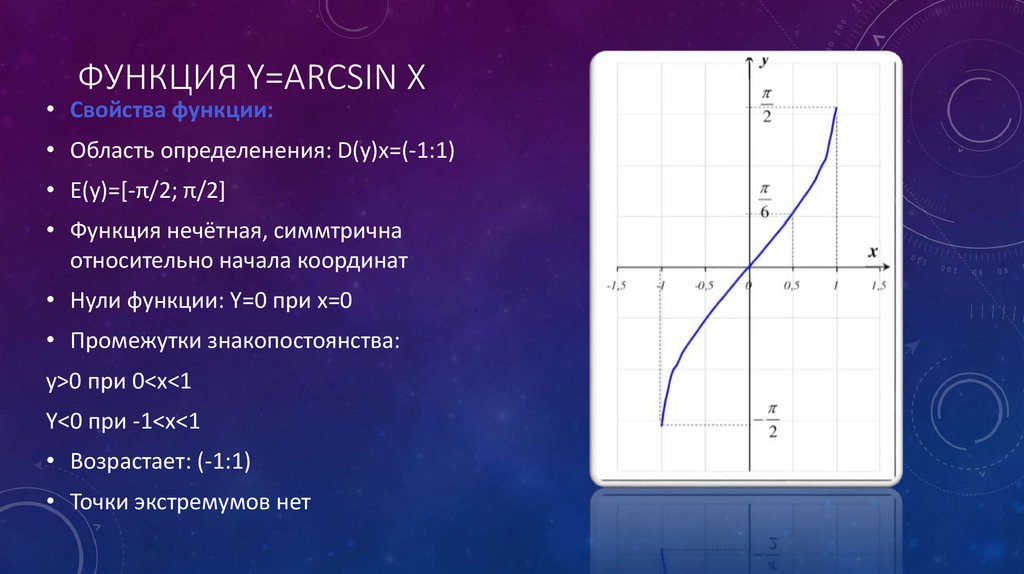
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.
4.3: Обратные тригонометрические функции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 89301
- Мэтью Болкинс, Дэвид Остин и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Мотивирующие вопросы
- Может ли периодическая функция, не прошедшая тест горизонтальной линии, иметь обратную функцию?
- Для ограниченных функций косинуса, синуса и тангенса, как определить соответствующие функции арккосинуса, арксинуса и арктангенса?
- Каковы основные свойства функций арккосинуса, арксинуса и арктангенса?
9{-1}(y)\)» говорят одно и то же, но с двух разных точек зрения.

Тригонометрические функции \(f(t) = \sin(t)\text{,}\) \(g(t) = \cos(t)\text{,}\) и \(h(t) = \tan(t)\) являются периодическими, поэтому каждая из них не проходит проверку горизонтальной прямой, и, таким образом, эти функции в своих полных областях определения не имеют обратных функций. В то же время разумно думать об изменении перспективы и углов обзора как о результатах в определенных ограниченных настройках. Например, мы можем сказать, что оба 9{-1}\left(\frac{\sqrt{3}}{2}\right) \nonumber \]
в зависимости от контекста, в котором мы рассматриваем соотношение между углом и длиной стороны.
Важно также понять, почему важен вопрос нахождения угла по известному значению тригонометрической функции. Предположим, что мы знаем следующую информацию о прямоугольном треугольнике: один катет имеет длину \(2,5\text{,}\), а гипотенуза имеет длину \(4\text{.}\). Если мы допустим \(\theta\) равным угол, противоположный стороне длины \(2,5\text{,}\), отсюда следует, что \(\sin(\theta) = \frac{2,5}{4}\text{. }\) Естественно, мы хотим использовать обратная функция синуса для решения самого последнего уравнения для \(\theta\text{.}\) Но функция синуса не имеет обратной функции, так как же мы можем решить эту ситуацию?
}\) Естественно, мы хотим использовать обратная функция синуса для решения самого последнего уравнения для \(\theta\text{.}\) Но функция синуса не имеет обратной функции, так как же мы можем решить эту ситуацию?
В то время как исходные тригонометрические функции \(f(t) = \sin(t)\text{,}\) \(g(t) = \cos(t)\text{,}\) и \(h(t ) = \tan(t)\) не имеют обратных функций, оказывается, что мы можем рассматривать их ограниченные версии, у которых есть соответствующие обратные функции. Таким образом, мы исследуем, как мы можем иначе думать о тригонометрических функциях, чтобы мы могли осмысленно обсуждать обратные функции.
Preview Activity \(\PageIndex{1}\)
Рассмотрим график функции стандартного косинуса в Рисунок \(\PageIndex{1}\) вместе с выделенной частью графика на \([0,\pi]\text{.}\)
Рисунок \(\PageIndex{1}\) Функция косинуса на \([-\frac{5\pi}{2},\frac{5\pi}{2}]\) с частью на \([0 ,\pi]\) подчеркнуто. Пусть \(g\) будет функцией, область определения которой равна \(0 \le t \le \pi\) и чьи выходы определяются правилом \(g(t) = \cos(t)\text{.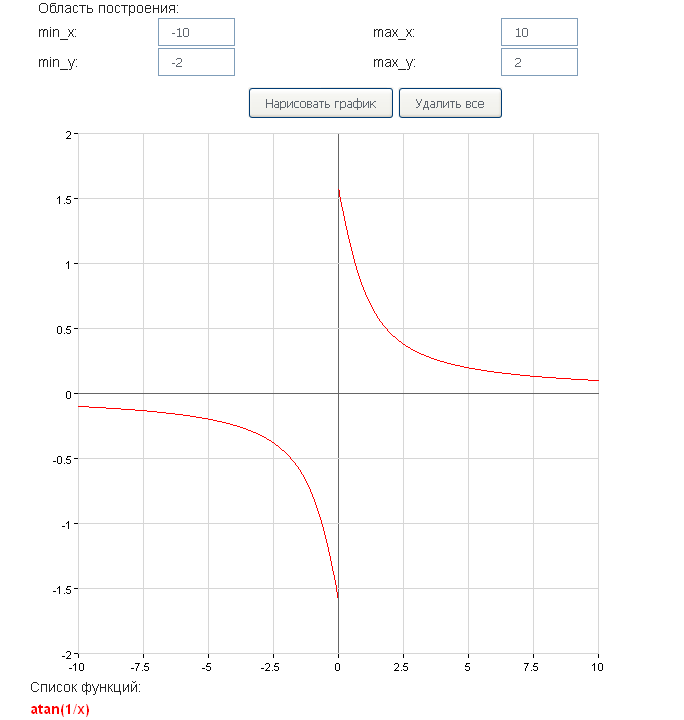 } \) Обратите внимание : \(g\) определяется в терминах функции косинуса, но, поскольку она имеет другую область определения, она равна 9{-1}(-1)\text{.}\) Используйте правильные обозначения для маркировки результатов.
} \) Обратите внимание : \(g\) определяется в терминах функции косинуса, но, поскольку она имеет другую область определения, она равна 9{-1}(-1)\text{.}\) Используйте правильные обозначения для маркировки результатов.
Функция арккосинуса
Для функции косинуса, ограниченной областью определения \([0,\pi]\), которую мы рассматривали в Предварительном задании 4.3.1 , функция строго убывает в своей области определения и, таким образом, пересекает горизонтальную линию Тест. Следовательно, эта ограниченная версия функции косинуса имеет обратную функцию; мы будем называть эту обратную функцию функцией арккосинуса .
Определение \(\PageIndex{2}\)
Пусть \(y = g(t) = \cos(t)\) определено в домене \([0,\pi]\text{,}\) и обратите внимание на \(g : [0,\pi] \to [-1,1]\text{.}\) Для любого действительного числа \(y\), которое удовлетворяет \(-1 \le y \le 1\text {,}\) арккосинус \(y\) , обозначаемый
\[ \arccos(y) \nonumber \]
, является углом \(t\), удовлетворяющим \(0 \le t \le \ pi\) такой, что \(\cos(t) = y\text{. {-1}(y)\) говорят одно и то же для функции и ее обратной в общем случае 9t\) и \(t = \ln(y)\) говорят об одном и том же), функция арккосинуса позволяет нам делать то же самое для определенных углов и выходных значений косинуса. Например, сказать \(\cos(\frac{\pi}{2}) = 0\) — это то же самое, что написать \(\frac{\pi}{2} = \arccos(0)\text{,} \), который гласит: «\(\frac{\pi}{2}\) — это угол, косинус которого равен \(0\)». Действительно, эти отношения отражены на графике выше, где мы видим, что любая точка \((a,b)\), лежащая на графике \(y = \cos(t)\), соответствует точке \(( b,a)\), лежащий на графике \(y = \arccos(t)\text{.}\)
{-1}(y)\) говорят одно и то же для функции и ее обратной в общем случае 9t\) и \(t = \ln(y)\) говорят об одном и том же), функция арккосинуса позволяет нам делать то же самое для определенных углов и выходных значений косинуса. Например, сказать \(\cos(\frac{\pi}{2}) = 0\) — это то же самое, что написать \(\frac{\pi}{2} = \arccos(0)\text{,} \), который гласит: «\(\frac{\pi}{2}\) — это угол, косинус которого равен \(0\)». Действительно, эти отношения отражены на графике выше, где мы видим, что любая точка \((a,b)\), лежащая на графике \(y = \cos(t)\), соответствует точке \(( b,a)\), лежащий на графике \(y = \arccos(t)\text{.}\)
Activity \(\PageIndex{2}\)
Используйте специальные точки на единичной окружности (см., например, рис. 2.3.1) для определения точных значений каждого из следующих числовых выражений. Сделайте это без использования вычислительного устройства.
- \(\displaystyle \arccos(\frac{1}{2})\)
- \(\displaystyle \arccos(\frac{\sqrt{2}}{2})\)
- \(\displaystyle \arccos(\frac{\sqrt{3}}{2})\)
- \(\displaystyle \arccos(-\frac{1}{2})\)
- \(\ displaystyle \ arccos (- \ frac {\ sqrt {2}} {2}) \)
- \(\displaystyle \arccos(-\frac{\sqrt{3}}{2})\)
- \(\displaystyle \arccos(-1)\)
- \(\displaystyle \arccos(0)\)
- \(\displaystyle \cos(\arccos(-\frac{1}{2}))\)
- \(\displaystyle \arccos(\cos(\frac{7\pi}{6}))\)
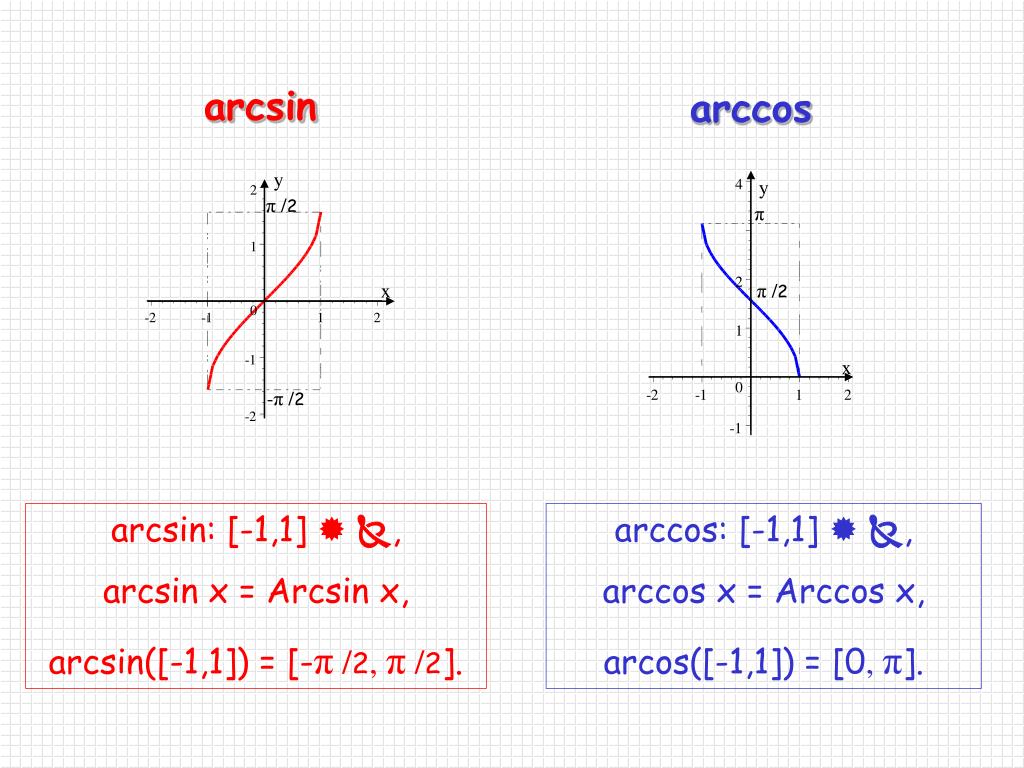
Функция арксинуса
Аналогичным образом мы можем построить обратную функцию для ограниченной версии функции синуса.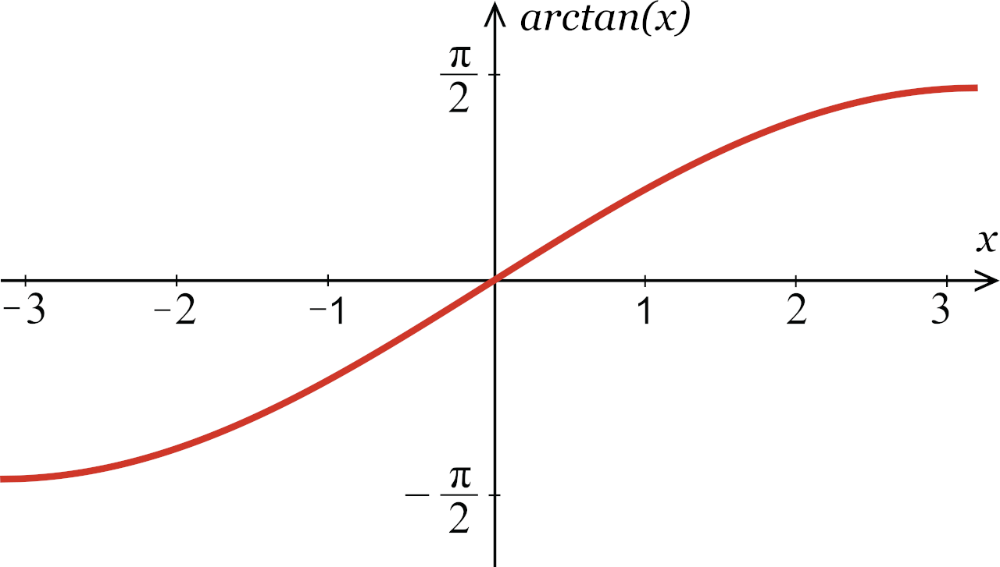 Как и в случае с функцией косинуса, нам нужно выбрать интервал, на котором функция синуса всегда увеличивается или всегда уменьшается, чтобы функция прошла тест горизонтальной линии. Стандартным выбором является область \([-\frac{\pi}{2}, \frac{\pi}{2}]\), в которой \(f(t) = \sin(t)\) возрастает и достигает всех значений в диапазоне функции синуса. Таким образом, мы рассматриваем \(f(t) = \sin(t)\), так что \(f : [-\frac{\pi}{2}, \frac{\pi}{2}] \to [- 1,1]\) и, следовательно, определить соответствующую функцию арксинуса.
Как и в случае с функцией косинуса, нам нужно выбрать интервал, на котором функция синуса всегда увеличивается или всегда уменьшается, чтобы функция прошла тест горизонтальной линии. Стандартным выбором является область \([-\frac{\pi}{2}, \frac{\pi}{2}]\), в которой \(f(t) = \sin(t)\) возрастает и достигает всех значений в диапазоне функции синуса. Таким образом, мы рассматриваем \(f(t) = \sin(t)\), так что \(f : [-\frac{\pi}{2}, \frac{\pi}{2}] \to [- 1,1]\) и, следовательно, определить соответствующую функцию арксинуса.
Определение \(\PageIndex{3}\)
Пусть \(y = f(t) = \sin(t)\) определено в области \([-\frac{\pi}{2},\ frac{\pi}{2}]\text{,}\) и наблюдаем \(f : [-\frac{\pi}{2},\frac{\pi}{2}] \to [-1, 1]\text{.}\) Для любого действительного числа \(y\), которое удовлетворяет \(-1 \le y \le 1\text{,}\) арксинусу \(y\), обозначенному
\ [ \arcsin(y) \nonumber \]
— это угол \(t\), удовлетворяющий \(-\frac{\pi}{2} \le t \le \frac{\pi}{2}\) такой, что \(\sin(t) = у\текст{. }\)
}\)
Активность \(\PageIndex{3}\)
Целью этого упражнения является понимание основных свойств функции арксинуса способом, аналогичным нашему обсуждению функции арккосинуса в подразделе 4.3.1 .
- Использование Определение 4.3.3 , каковы область определения и диапазон функции арксинуса?
- Точно определить следующие значения: \(\arcsin(-1)\text{,}\) \(\arcsin(-\frac{\sqrt{2}}{2})\text{,}\) \( \ arcsin (0) \ text {,} \) \ (\ arcsin (\ frac {1} {2}) \ text {,} \) и \ (\ arcsin (\ frac {\ sqrt {3}} {2 })\текст{.}\)
- На осях, указанных в Рисунок \(\PageIndex{4}\) , нарисуйте аккуратный график ограниченной синусоидальной функции на интервале \([-\frac{\pi}{2},\frac{\pi }{2}]\) вместе с соответствующей обратной функцией арксинуса. Отметьте не менее трех точек на каждой кривой так, чтобы каждая точка на графике синусоиды соответствовала точке на графике арксинуса. Кроме того, нарисуйте линию \(y = t\), чтобы продемонстрировать, как графики являются отражением друг друга через эту линию.

4. Верно или неверно: \(\arcsin(\sin(5\pi)) = 5\pi\text{.}\) Напишите полное предложение, объясняющее ваши рассуждения.
Функция арктангенса
Наконец, мы разрабатываем обратную функцию для ограниченной версии функции тангенса. Выберем область \((-\frac{\pi}{2}, \frac{\pi}{2})\), на которой \(h(t) = \tan(t)\) возрастает и достигает все значения в диапазоне функции тангенса.
Определение \(\PageIndex{5}\)
Пусть \(y = h(t) = \tan(t)\) определено в области \((-\frac{\pi}{2},\ frac{\pi}{2})\text{,}\) и наблюдаем \(h : (-\frac{\pi}{2},\frac{\pi}{2}) \to (-\infty ,\infty)\text{.}\) Для любого действительного числа \(y\text{,}\) арктангенс \(y\) , обозначаемый
\[ \arctan(y) \nonumber \]
— это угол \(t\), удовлетворяющий условию \(-\frac{\pi}{2} \lt t \lt \lt \frac{\pi}{2}\), такой, что \(\tan(t) = y \текст{. }\)
}\)
Активность \(\PageIndex{4}\)
Целью этого упражнения является понимание основных свойств функции арктангенса.
- Использование Определение 4.3.5 , каковы область определения и диапазон функции арктангенса?
- Точно определить следующие значения: \(\arctan(-\sqrt{3})\text{,}\) \(\arctan(-1)\text{,}\) \(\arctan(0)\text {,}\) и \(\ arctan(\frac{1}{\sqrt{3}})\text{.}\)
- График ограниченной функции тангенса на интервале \((-\frac{\pi}{2},\frac{\pi}{2})\) представлен в Рисунок \(\PageIndex{6}\) Нарисуйте соответствующую обратную функцию, функцию арктангенса, на тех же осях. Отметьте не менее трех точек на каждой кривой так, чтобы каждая точка на графике касательной соответствовала точке на графике арктангенса. Кроме того, нарисуйте линию \(y = t\), чтобы продемонстрировать, как графики являются отражением друг друга через эту линию.
4. Закончите следующее предложение: «при неограниченном увеличении \(t\) \(\arctan(t)\) \(\ldots\)».
Резюме
- Любая функция, не прошедшая проверку горизонтальной линии, не может иметь обратную функцию. Однако для периодической функции, которая не проходит тест горизонтальной прямой, если мы ограничим область определения функции интервалом, равным длине одного периода функции, мы затем определим связанную функцию, которая на самом деле имеет обратная функция. Это позволяет нам развивать функции, обратные ограниченным функциям косинуса, синуса и тангенса.
- Мы решили определить ограниченные функции косинуса, синуса и тангенса в соответствующих областях \([0,\pi]\text{,}\) \([-\frac{\pi}{2}, \frac{ \pi}{2}]\text{,}\) и \((-\frac{\pi}{2}, \frac{\pi}{2})\text{.}\) на каждом таком интервале , ограниченная функция является строго убывающей (косинус) или строго возрастающей (синус и тангенс) и, следовательно, имеет обратную функцию. Каждая функция ограниченного синуса и косинуса имеет диапазон \([-1,1]\text{,}\), а диапазон ограниченного тангенса представляет собой набор всех действительных чисел.
 Таким образом, мы определяем обратную функцию каждого следующим образом:
Таким образом, мы определяем обратную функцию каждого следующим образом:- Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\) арккосинус \(y\) (обозначается \(\arccos(y)\)) равен угол \(t\) в интервале \([0,\pi]\) такой, что \(\cos(t) = y\text{.}\) То есть \(t\) — это угол, косинус которого это \(у\текст{.}\)
- Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\), арксинус \(y\) (обозначается \(\arcsin(y)\)) является углом \(t\) в интервале \([-\frac{\pi}{2}, \frac{\pi}{2}]\) такой, что \(\sin(t) = y\text{.} \) То есть \(t\) — это угол, синус которого равен \(y\text{.}\)
- Для любого действительного числа \(y\text{,}\) арктангенс \(y\) (обозначается \(\arctan(y)\)) представляет собой угол \(t\) в интервале \((- \frac{\pi}{2}, \frac{\pi}{2})\) такие, что \(\tan(t) = y\text{.}\) угол, тангенс которого равен \(y\text{.}\)
- Чтобы обсудить свойства трех обратных тригонометрических функций, мы разместим их на тех же осях, что и соответствующие им ограниченные тригонометрические функции.
 Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси.
9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).
Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси.
9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).Упражнения
5.
Используйте специальные точки на единичной окружности (см., например, рис. 2.3.1), чтобы определить точные значения каждого из следующих числовых выражений. Сделайте это без использования вычислительного устройства.
- \(\displaystyle \arcsin(\frac{1}{2})\)
- \(\displaystyle \arctan(-1)\)
- \(\ displaystyle \ arcsin (- \ frac {\ sqrt {3}} {2}) \)
- \(\displaystyle \arctan(-\frac{1}{\sqrt{3}})\)
- \(\displaystyle \arccos(\sin(\frac{\pi}{3}))\)
- \(\displaystyle \cos(\arcsin(-\frac{\sqrt{3}}{2}))\)
- \(\ displaystyle \ tan (\ arcsin (- \ frac {\ sqrt {2}} {2})) \)
- \(\displaystyle \arctan(\sin(\frac{\pi}{2}))\)
- \(\displaystyle \sin(\arcsin(-\frac{1}{2}))\)
- \(\displaystyle \arctan(\tan(\frac{7\pi}{4}))\)
6.

Для каждого из следующих утверждений определите, является ли оно истинным или ложным. Если это так, напишите одно предложение, чтобы обосновать свои рассуждения. Если ложно, приведите пример значения, показывающего, что утверждение не выполняется.
- Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\) \(\sin(\arcsin(y)) = y\text{.}\)
- Для любого действительного числа \(t\text{,}\) \(\arcsin(\sin(t)) = t\text{.}\)
- Для любого действительного числа \(t\text{,}\) \(\arccos(\cos(t)) = t\text{.}\)
- Для любого \(y\), такого что \(-1 \le y \le 1\text{,}\) \(\cos(\arccos(y)) = y\text{.}\)
- Для любого действительного числа \(y\text{,}\) \(\tan(\arctan(y)) = y\text{.}\)
- Для любого действительного числа \(t\text{,}\) \(\arctan(\tan(t)) = t\text{.}\)
7.
Рассмотрим составную функцию \(h(x) = \cos(\arcsin(x))\text{.}\) Эту функцию имеет смысл рассматривать, поскольку функция арксинуса дает угол, при котором затем можно вычислить функцию косинуса.
 В следующих вопросах мы исследуем, как выразить \(h\) вообще без использования тригонометрических функций.
В следующих вопросах мы исследуем, как выразить \(h\) вообще без использования тригонометрических функций.- Каков домен \(h\text{?}\) Диапазон \(h\text{?}\)
- Поскольку функция арксинуса дает угол, допустим, что \(\theta = \arcsin(x)\text{,}\), так что \(\theta\) — это угол, синус которого равен \(x\text{. }\) По определению, мы можем изобразить \(\theta\) как угол в прямоугольном треугольнике с гипотенузой \(1\) и вертикальным катетом длины \(x\text{,}\), как показано на рисунке 9.0003 Рисунок \(\PageIndex{10}\) Используйте теорему Пифагора, чтобы определить длину горизонтального участка как функцию \(x\text{.}\)
3. Каково значение \(\cos(\theta)\) как функции \(x\text{? }\) Что мы показали относительно \(h(x) = \cos(\arcsin(x))\text{?}\)
4.


 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения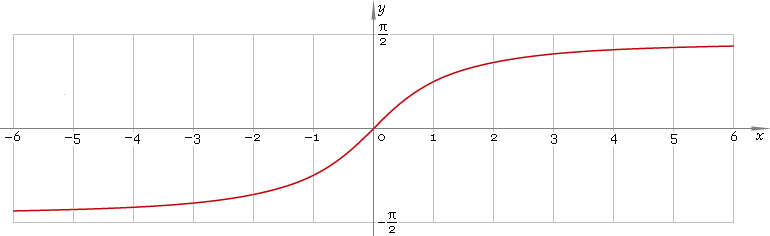
 Таким образом, мы определяем обратную функцию каждого следующим образом:
Таким образом, мы определяем обратную функцию каждого следующим образом: Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси.
9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).
Когда мы это делаем, мы используем \(t\) в качестве входной переменной для обеих функций одновременно, чтобы мы могли нанести их на одни и те же координатные оси.
9{-1}(t) = \arctan(t)\) (выделено темно-синим цветом).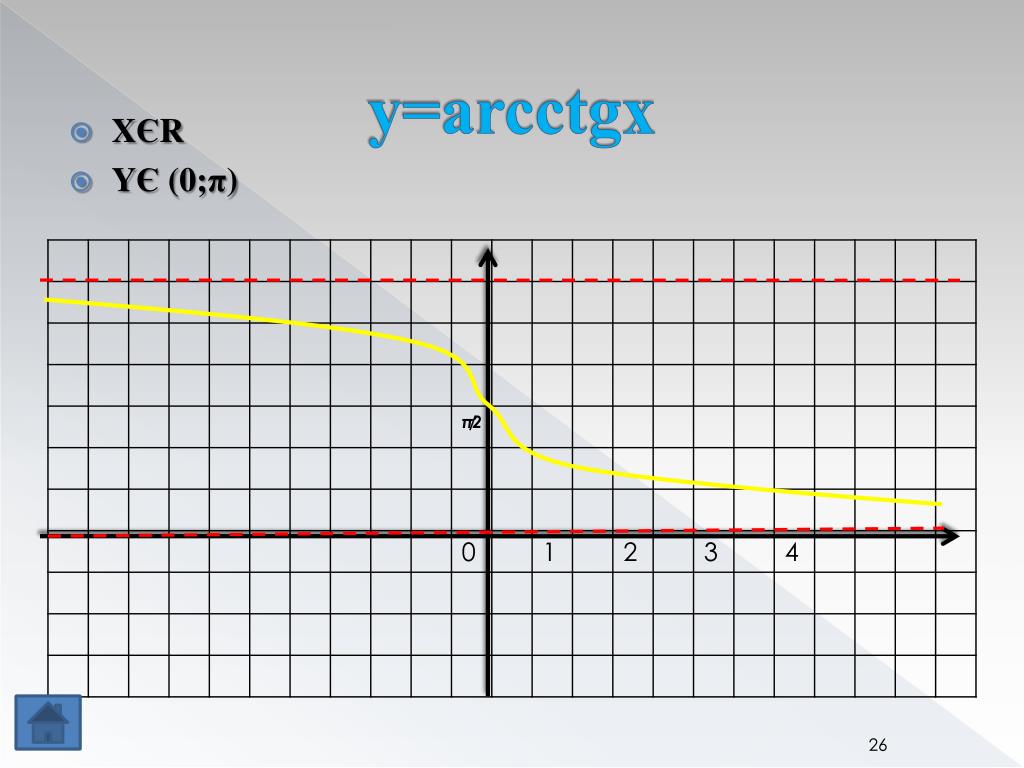
 В следующих вопросах мы исследуем, как выразить \(h\) вообще без использования тригонометрических функций.
В следующих вопросах мы исследуем, как выразить \(h\) вообще без использования тригонометрических функций.