sin(X), cos(X), tg(X), ctg(X), lg(X), arcsin(X), arcos(X), arctg(X), arcctg(X), ax, xn и гиперболических функций.
ln’ x=1/x
(ax)’= (ax)*ln a.
Производные гиперболических функций:
17. Производная функции заданной параметрически.
Пустьx=x(t), y=y(t), тогда какому-то x, будет соответствовать какое-то значение t (t=f(x)), поэтому t будет соответствовать y и можно говорить, что y является функцией x (y=(x)), можно говорить, что y’x. Заданная функция называется параметрически заданной функцией.
Теорема: Пусть y(x)
задана параметрически уравнением (выше)
предположим, что эти функции дифференцируемы
и функция x=x(t)
имеет обратную функцию t=f(x),
тогда y’x,
будет y’x=(y’(t))/(x’(t)).
Из системы следует, что y=y(f(x)),
y’x
18. Дифференциал функции, его геометрический смысл. Свойства дифференциала.
Рассмотрим функцию y = f(x), дифференцируемую в данной точке x. Приращение y ее представимо в виде
y = f’(x) x + ( x) x,
где первое слагаемое линейно относительно x, а второе является в точке x = 0 бесконечно малой функцией более высокого порядка, чем x. Если f'(x) 0, то первое слагаемое представляет собой главную часть приращения y. Эта главная часть приращения является линейной функцией аргумента x и называется дифференциалом функции y = f(x). Если f'(x) = 0, то дифференциал функции по определению считается равным нулю.
Определение: Дифференциалом
функции y = f(x) называется главная линейная
относительно
x часть приращения
y, равная произведению производной на
приращение независимой переменной dy
= f’(x ) x (4).
Заметим,
что дифференциал независимой переменной
равен приращению этой переменной dx =
x. Поэтому формулу для дифференциала
принято записывать в следующем виде: dy = f’(x)dx. Выясним каков геометрический
смысл дифференциала.
Возьмем на графике функции y = f(x)
произвольную точку M(x,y)
(рис21.). Проведем касательную к кривой
y = f(x) в точке M, которая образует угол
с положительным направлением оси OX, то есть f'(x) = tg .
Из прямоугольного треугольника MKN KN =
MNtg xtg = f’(x) x, то
есть dy = KN.
Таким образом, дифференциал функции
есть приращение ординаты касательной,
проведенной к графику функции y = f(x) в
данной точке, когда x получает приращение
x. Отметим
d c = 0; d(c u(x))
= c d u(x); d(u(x)
v(x))
= d
u(x)
d v(x); d(u(x) v(x))
= v(x)
d u(x)
+ u(x)d
v(x); d(u(x)
/ v(x))
= (v(x)
d u(x)
— u(x)
d v(x))
/ v2(x).
Укажем еще на одно свойство, которым
обладает дифференциал, но не обладает
производная. Рассмотрим функцию y = f(u),
где u =
(x), то есть рассмотрим сложную функцию
y = f((x)).
Если каждая из функций f и
являются дифференцируемыми, то производная
сложной функции согласно теореме
( функция y =
f((t))
дифференцируема в точке t, причем
справедлива формула (f((t)))‘
= f’(x)‘(t).)
равна y’ = f'(u)· u’. Тогда дифференциал
функции dy =
f’(x)dx
= f’(u)u’dx
= f’(u)du, так как u’dx =
du.
То есть dy
= f’(u)du (5). Последнее
равенство означает, что формула
дифференциала не изменяется, если вместо
функции от x рассматривать функцию от
переменной u. Это свойство дифференциала
получило название инвариантности
формы первого дифференциала. Замечание. Отметим, что
в формуле (4)
dx =
x, а в формуле (5)
du яляется лишь линейной частью приращения
функции u.Производная от обратной функции — основные понятия и определения с примерами решения и образцами выполнения
Содержание:
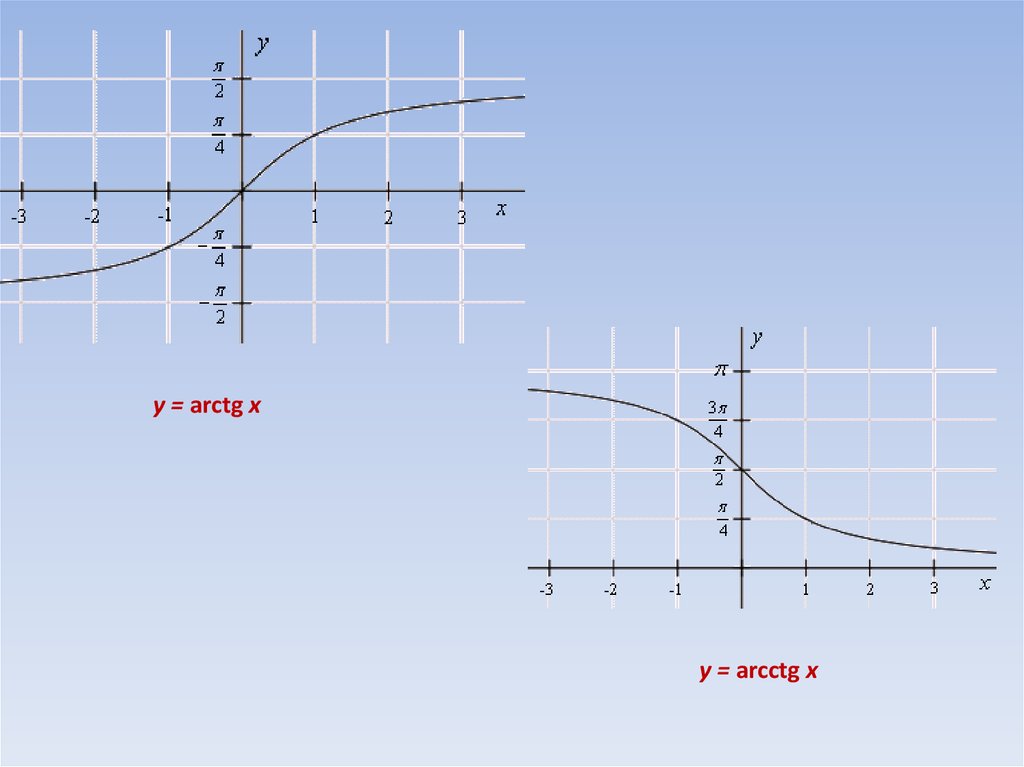
- Производные от обратных тригонометрических функций
Понятие обратной функции и ее производная:
Пусть y = f (x) — некоторая дифференцируемая функция от аргумента x. Если в этом уравнении y рассматривать как аргумент, а х — как функцию, то эта функция , где , называется обратной к данной функции.
Наша задача, зная производную , найти .
Теорема 1. Производная функции , обратной к данной функции y = f (x), равна величине, обратной к производной данной функции, если последняя не равна нулю.
То есть, или
Доказательство. Пусть дана функция y = f (x) и обратная ей функция . Тогда .
Итак, х можно рассматривать как сложную функцию. Дифференцируя это равенство по х, и учитывая, что применяя предыдущую теорему о дифференцировании сложной функции, имеем:
. Отсюда или Теорема доказана.
Следствие 1. Справедливы формулы
Доказательство. Если y = arcsin x, то обратная к ней x = sin y,
Поскольку, , а
Выразим cos y через х.
Имеем sin y = x.
Тогда Перед корнем берем знак «+», так как cos y для всех положительный. Итак, .
Аналогично доказывается .
Следствие 2. Производные функций
Доказательство. Обратной к функции y = arctg x есть функция x = tg y, .
Поскольку то
Выразим cos2 y через х. Имеем: tg y = x. Из школьного курса известно, что
Поэтому
Итак,
Аналогично доказывается .
Возможно вам будут полезны данные страницы:
| Построение прямой линии параллельно плоскости |
| Асимптотические методы решения дифференциальных уравнений |
Оператор Гамильтона. Оператор Лапласа. Понятие о криволинейных координатах |
| Ангидриды карбоновых кислот |
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная арктангенса – вывод, объяснение и пример
В этой статье мы сосредоточимся на понимании процесса определения производной арктангенса и используем его для упрощения производной других функций.