Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства
Арксинус, арккосинус, арктангенс и арккотангенс — обратные тригонометрические функции. Они обладают рядом свойств, которые мы рассмотрим в этой статье. Помимо словесных и математических формулировок основных свойств арксинуса, арккосинуса, арктангенса и арккотангенса, будут приведены доказательства этих свойств.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса
Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.
Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа- sinarcsin a=a, a∈1; -1;
- cosarccos a=a, a∈1; -1;
- tg(arctg a)=a, a∈-∞; +∞;
- ctg(arcctg a)=a, a∈-∞; +∞.
Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.
Рассмотрим доказательство на примере арксинуса. Согласно определению, арксинус числа — это такой угол или число, синус которого равен числу a. При этом число a лежит в пределах от -1 до +1 включительно. В виде формулы определение запишется так:
sin(arcsin a)=a
Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.
sin(arcsin(0,3)=0,3cosarccos-32=-32tg(arctg(8))=8ctg(arcctg(1589))=1589
Важно отметить, что для обратных функций синуса и косинуса имеет место ограничение для значений числа a. Так, при a, лежащем вне пределов отрезка -1, 1, арксинус и арккосинус не определены и записи arcsin a и arccos a попросту не имеют смысла. Это связано с тем, что область значений синуса и косинуса — от минус единицы до плюс единицы. Например, нельзя записать cos(arccos(9)), так как 9 больше 1 и данное выражение не имеет смысла. Делать подобные записи — ошибочно!
Делать подобные записи — ошибочно!
Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел
Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.
arcsin, arccos, arctg и arcctg противоположных чисел- arcsin-a=-arcsin a, a∈-1, 1;
- arccos-a=π-arccos a, a∈-1, 1;
- arctg-a=-arctg a, a∈-∞, +∞;
- arcctg-a=π-arcctg a, a∈-∞, +∞.
Докажем записанное. Начнем, как всегда, с доказательства для арксинусов. При -1≤a≤1 имеет место равенство arcsin-a=-arcsin a. Согласно дефиниции, arcsin(-a) — это угол (число) в пределах от -π2 до π2, синус которого равен -a. Для доказательства справедливости первого равенства необходимо доказать, что -arcsin a лежит в тех же пределах от -π2 до π2, что и arcsin(-a). Также необходимо обосновать, что sin(-arcsin a)=-a.
Для арксинуса, по определению, справедливо двойное неравенство -π2≤arcsin a≤π2. Умножим каждую часть неравенства на -1 и получим эквивалентное неравенство π2≥-arcsin a≥-π2.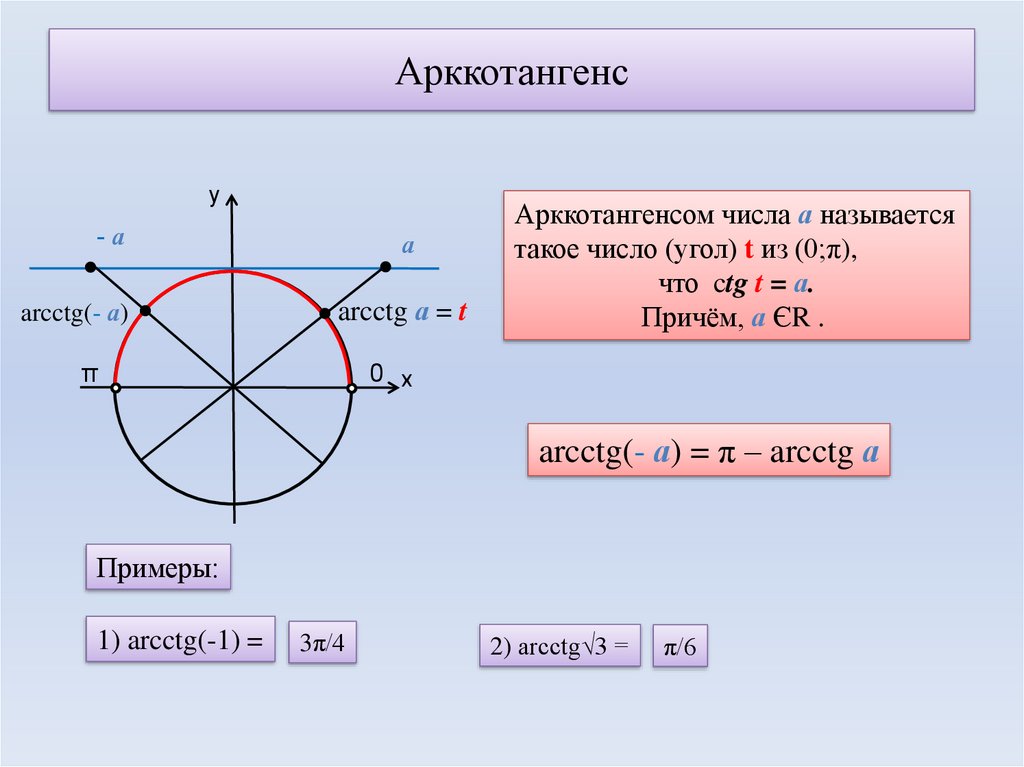 Переписав его, получим -π2≤-arcsin a≤π2.
Переписав его, получим -π2≤-arcsin a≤π2.
Переходим ко второй части доказательства. Теперь осталось показать, что sin(-arcsin a)=-a. Для этого воспользуемся свойством синусов противоположных углов и запишем: sin-arcsin a=-sinarcsin a. С учетом свойства арксинуса, рассмотренного в предыдущем пункте, закончим доказательство.
sin-arcsin a=-sinarcsin a=-a
Доказательство свойства арксинусов противоположных чисел завершено.
Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.
Для того, чтобы доказать, что arccos-a=π-arccos a при a∈-1, 1 необходимо во-первых показать, что число undefined.
Для арккосинуса, по определению, справедливо двойное неравенство 0≤arccos a≤π. Умножив каждую часть неравенства на — 1 и поменяв знаки, получим эквивалентное неравенство 0≥-arccos a≥-π. Перепишем его в другом виде. По свойствам неравенств, можно добавить к каждой части слагаемое, не меняя знаков. Добавим в каждую часть неравенства слагаемое π. Получим π≥π-arccos a≥0, или 0≤π-arccos a≤π.
Теперь покажем, что cosπ-arccos a=-a. Для этого воспользуемся формулами приведения, согласно которым можно записать cosπ-arccos a=-cos(arccos a). Обратившись к свойству арккосинуса, разобранному ранее (см. 1 пункт), заканчиваем доказательство.
cosπ-arccos a=-cos(arccos a)=-a.
Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.
Основная польза данного свойства — возможность избавиться от операций с отрицательными числами при работе с арксинусами, арккосинусами, арктангенсами и арккотангенсами. Например, справедливы записи:
arcsin-12=-arcsin12arccos-557=π-arccos557arctg-1=-arctg1arcctg(-3)=π-arcctg3
Сумма арксинуса и арккосинуса, арктангенса и арккотангенса
Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.
Сумма arcsin и arccosarcsin a+arccos a=π2, a∈-1, 1
Соответственно, для арктангенса и арккотангенса
arctg a+arcctg a=π2, a∈-∞, +∞
Приведем доказательство для арксинуса и арккосинуса. Формулу для суммы arcsin и arccos можно переписать в виде arcsin a=π2-arccos a. Теперь обратимся к определению, согласно которому арксинус — это число (угол), лежащее в пределах от -π2 до π2, синус которого равен a.
Формулу для суммы arcsin и arccos можно переписать в виде arcsin a=π2-arccos a. Теперь обратимся к определению, согласно которому арксинус — это число (угол), лежащее в пределах от -π2 до π2, синус которого равен a.
Запишем неравенство, вытекающее из определения арккосинуса: 0≤arccos a≤π. Умножим все его части на -1, а затем прибавим к каждой части π2. Получим:
0≤arccos a≤π0≥-arccos a≥-ππ2≥π2-arccos a≥-π2-π2≤π2-arccos a≤π2
Завершая доказательство, покажем, что sinπ2-arccos a=a. Для этого используем формулу приведения и свойство косинуса от арккосинуса.
sinπ2-arccos a=cosarccos a=a
Таким образом, доказано, что сумма арксинуса и арккосинуса равна π2. По такому же принципу проводится доказательство для суммы арктангенса и арккотангенса.
Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.
Пример 2. Сумма арксинуса и арккосинусаИзвестно, что arcsin6-22=π12. Найдем арккосинус этого числа.
Найдем арккосинус этого числа.
arcsin6-22+arccos6-22=π2arccos6-22=π2-arcsin6-22arccos6-22=π2-π12=5π12
Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса
Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса- arcsin(sin α)=α, -π2≤α≤π2;
- arccos(cos α)=α, 0≤α≤π;
- arctg(tg α)=α, -π2≤α≤π2;
- arcctg(ctg α)=α, 0≤α≤π.
Данные равенства и неравенства являются прямым следствием определений арксинуса, арккосинуса, арктангенса и арккотангенса. Покажем это, доказав, что arcsin(sin α)=α при -π2≤α≤π2.
Обозначим sinα через a. a — число, лежащее в интервале от -1 до +1. Тогда равенство arcsin(sin α)=α можно переписать в виде arcsin a=α. Данное равенство, при заданных условиях, аналогично определению синуса. Таким образом, мы доказали, что arcsin(sin α)=α при -π2≤α≤π2.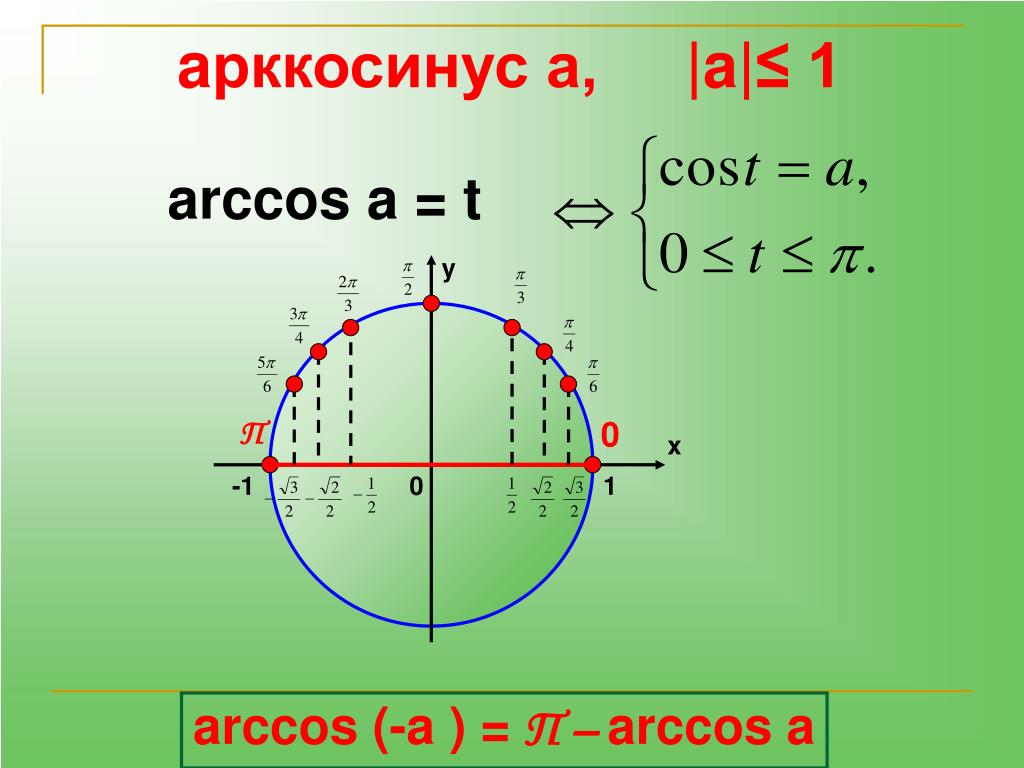
Выражение arcsin(sin α) имеет смысл не только при α, лежащем в пределах от -π2 до π2. Однако, равенство arcsin(sin α)=α выполняется только при соблюдении условия -π2≤α≤π2.
Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.
К примеру, запись arcsin(sin8π3)=8π3 будет ошибочной, так как число 8π3 не удовлетворяет условиям неравенства.
Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Как найти арксинус числа — Dudom
Арксинус — это обратная тригонометрическая функция, которая является исходным углом значения синуса и возвращает угол по значению его синуса.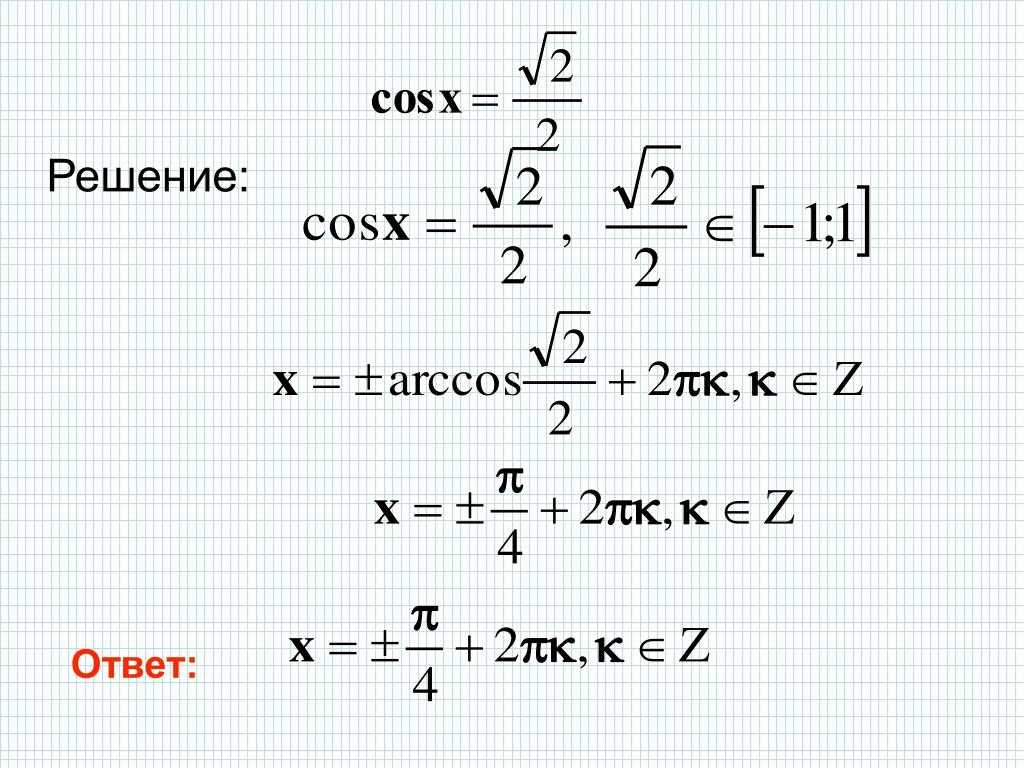
значение x должно быть от -1 до +1
Смотрите также калькулятор перевода градусов в радианы.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления арксинуса. С помощью этого калькулятора вы в один клик сможете найти arcsin(x).
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций.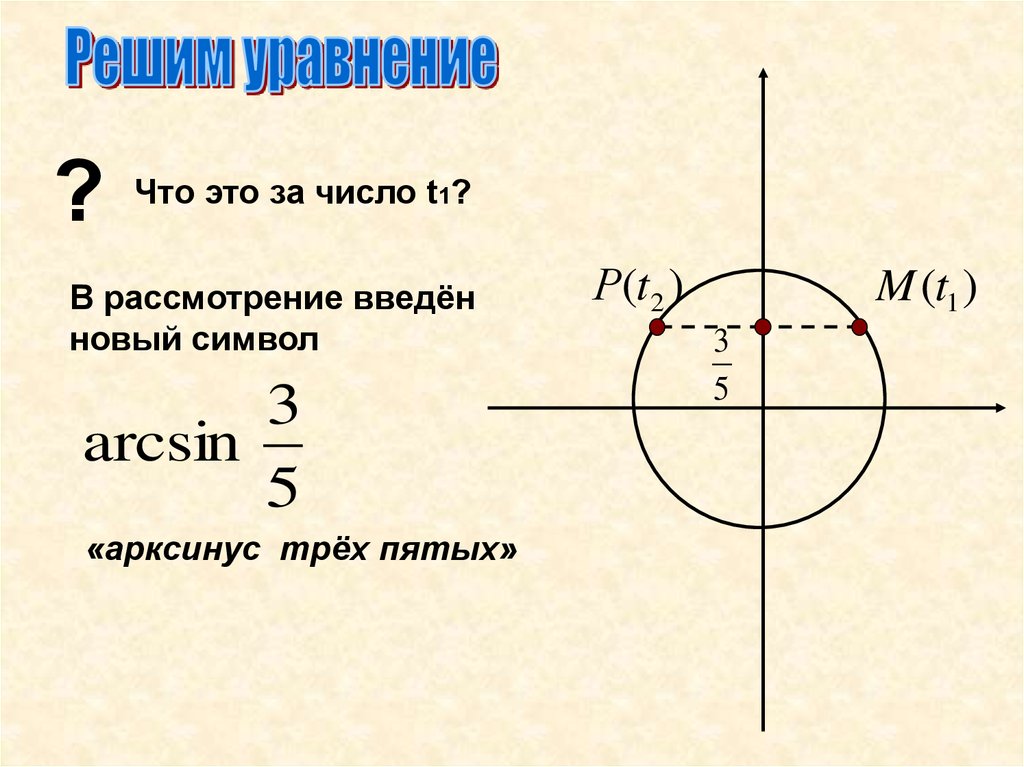 Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов.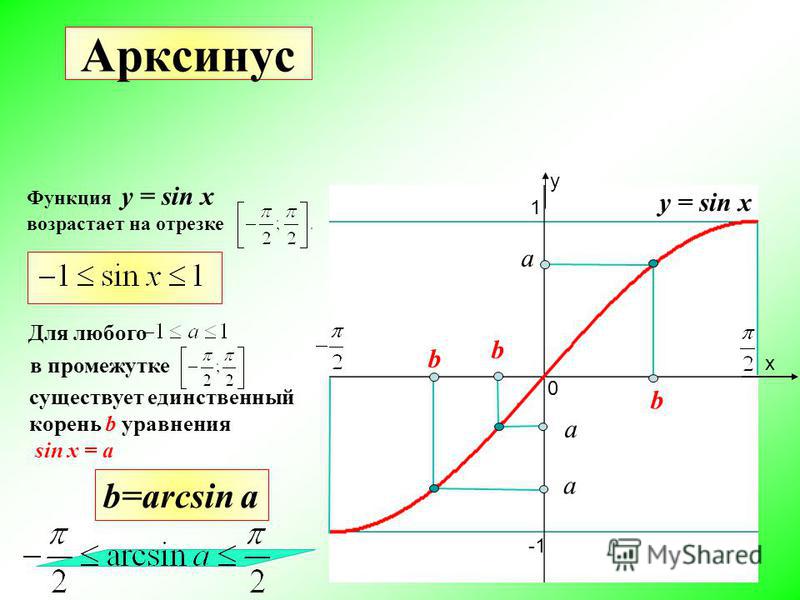 Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin ( — π 2 ) = — 1 , sin ( — π 3 ) = — 3 2 , sin ( — π 4 ) = — 2 2 , sin ( — π 6 ) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | |
| a r c sin α к а к у г о л | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 3 | ||
| в г р а д у с а х | — 90 ° | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c sin α к а к ч и с л о | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Тогда имеем:
cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1
Следуя из таблицы, находим значения арккосинуса:
a r c cos ( — 1 ) = π , arccos ( — 3 2 ) = 5 π 6 , arcocos ( — 2 2 ) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | 1 | |
| a r c cos α к а к у г о л | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 | |
| в г р а д у с а х | 180 ° | 150 ° | 135 ° | 120 ° | 90 ° | 60 ° | 45 ° | 30 ° | 0 ° | |
| a r c cos α к а к ч и с л о | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 | |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.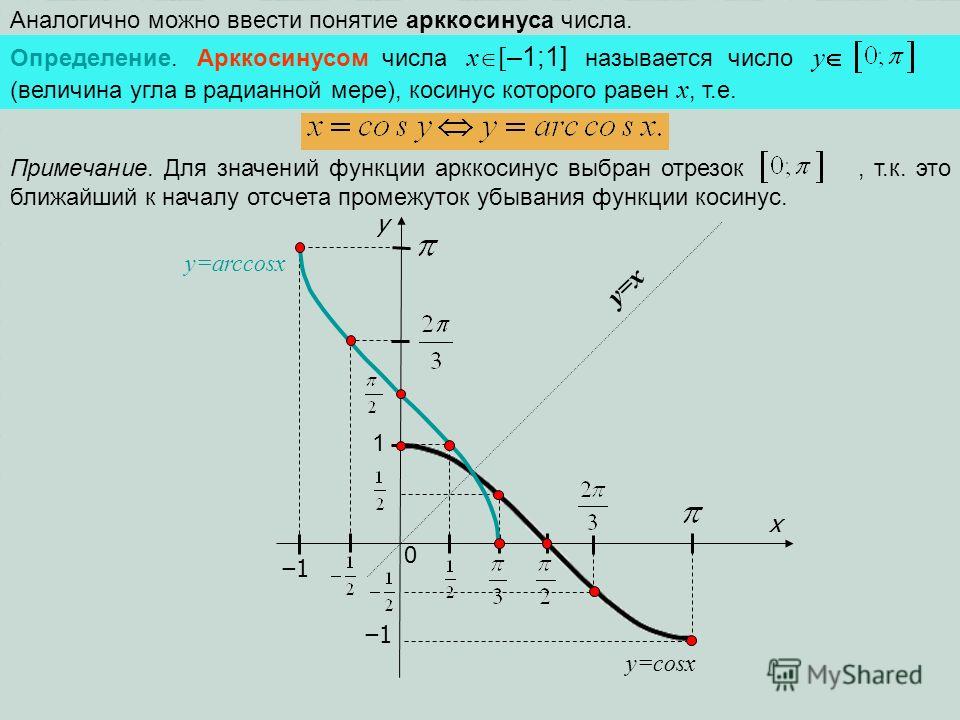
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:
a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Арксинус, arcsin
Определение и обозначения
Арксинус иногда обозначают так:
.
График функции арксинус
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
Арккосинус иногда обозначают так:
.
График функции арккосинус
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(– x ) = arcsin(–sin arcsin x ) = arcsin(sin(–arcsin x )) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(– x ) = arccos(–cos arccos x ) = arccos(cos(π–arccos x )) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 |
Формулы
Формулы суммы и разности
при или
при 0,,y>0 ;»> и 1″>
при и 1″>
при или
при 0,,y и 1″>
при 0 ;»> и 1″>
Арксинус, арккосинус, арктангенс числа.
 Корни тригонометрических уравнений. ⋆zagalina.ru
Корни тригонометрических уравнений. ⋆zagalina.ru←Тригонометрический круг
Тригонометрические уравнения→
Арксинус числа. Корни уравнения sin x = a
Арккосинус числа. Корни уравнения cos x = b
Арктангенс числа. Корни уравнения tg x = d
Итоговая таблица
Решим уравнение sin x = a. Здесь a — число. Решаем его графически, то есть решаем систему уравнений
Для этого рисуем графики у = sin x и у = a
Как видно из графика, решений у этого уравнения — бесконечное множество. Функция у = sin x — периодическая, в одном периоде — два решения, а потом они оба повторяются через 2π, то есть необходимо просто прибавить или отнять от предыдущего значения корня ±2π.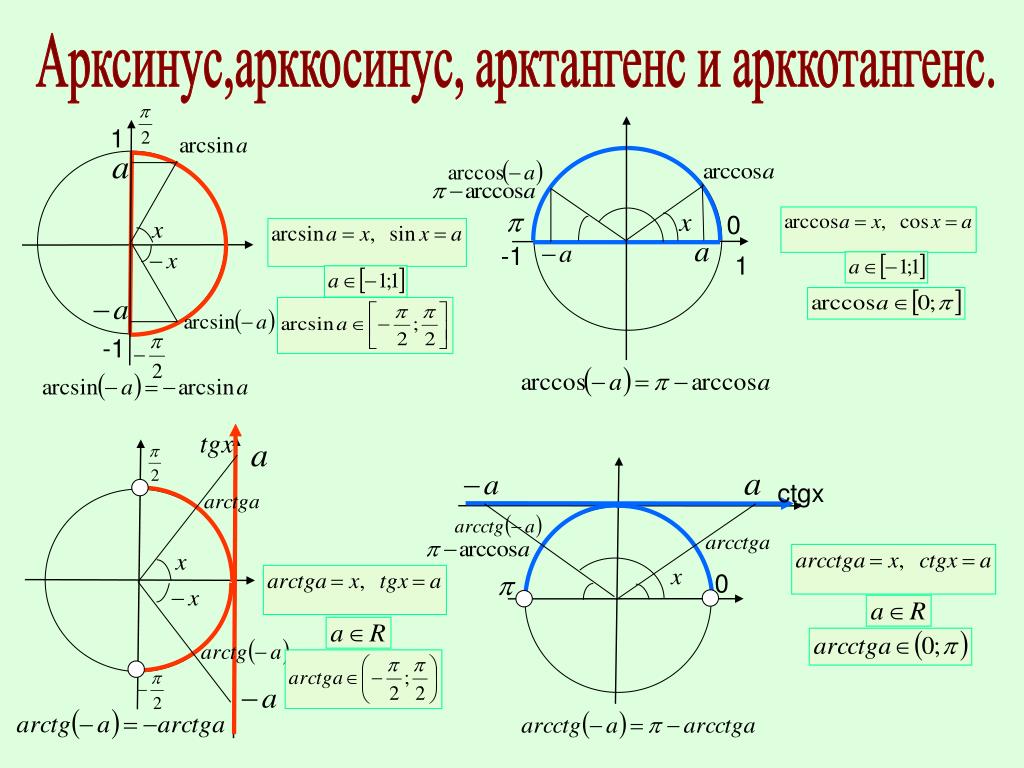
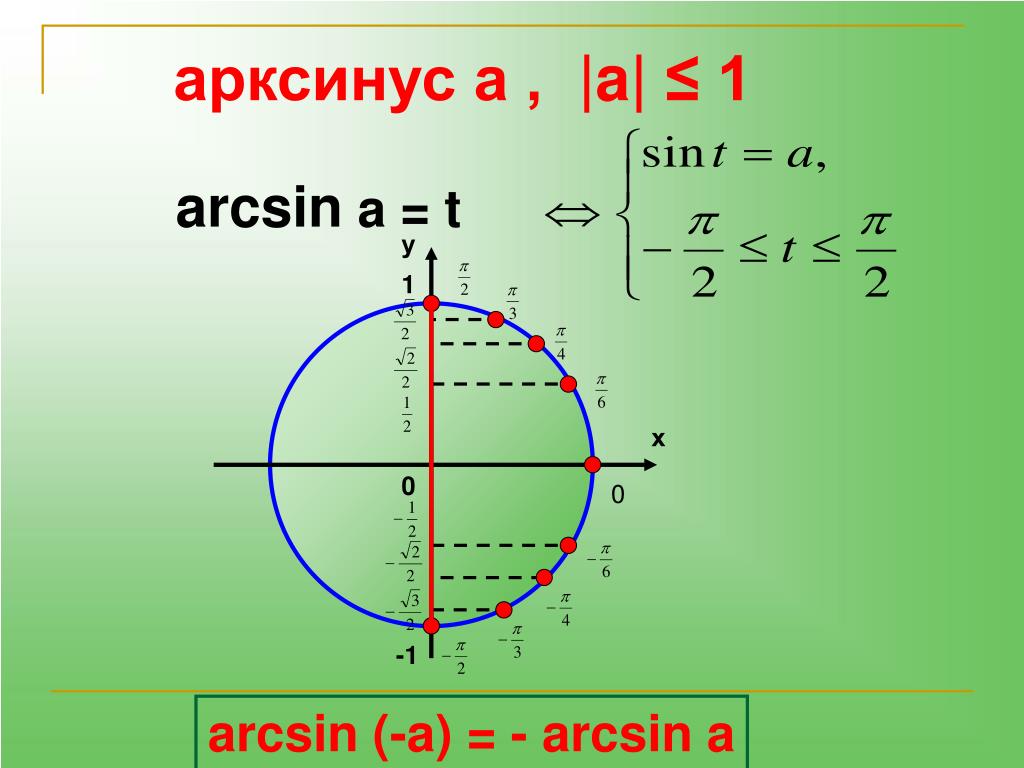
Строим те же графики на тригонометрическом круге. В этом случае мы график функции у = sin x заменяем на круг, а правая часть уравнения становится прямой, параллельной Ох. Смотрим на круге: Точки пересечения круга с прямой дают нам два решения: α1 и α2 . Причем, (смотрите на круге): α2 = π — α1 ! И тогда решениями уравнения будут точки
Еще из курса геометрии мы знаем некоторые значения синусов, косинусов, тангенсов и котангенсов для конкретных углов, а именно: для углов в 0°, 30°, 45°, 60°, 90°. А что же делать с остальными? И тут нам поможет арк(функция). Арк(функция) является обратной функцией для тригонометрических функций.
Рассмотрим конкретную функцию знакомого угла: sin 30° = 0,5. Тогда arcsin 0,5 = 30°. Собственно, эта формула и читается, как пишется. Угол (arc — это угол), синус которого равен 0,5, равен 30°. Все верно! То есть, если мы не знаем значения угла для какого-то синуса, мы его, этот угол, можем записать через арксинус.
Тогда arcsin 0,5 = 30°. Собственно, эта формула и читается, как пишется. Угол (arc — это угол), синус которого равен 0,5, равен 30°. Все верно! То есть, если мы не знаем значения угла для какого-то синуса, мы его, этот угол, можем записать через арксинус.
Решим простое уравнение для
x ∈ [0; 2π].
sin x = 0,35
Первый угол определить через геометрию мы не сможем, ну, и не надо! Решениями этого уравнения будут значения:
Теперь рассмотрим уравнение для
x ∈ [0; 2π]
с отрицательным значением:
sin x = — 0,35
Опить два корня, и первый по модулю (величине) будет таким же, как и в первом примере, но со знаком «минус». запишем результат:
Получается, что нам нет нужды рассматривать весь круг, все возможные значения для арксинуса укладываются в интервал [-π/2; π/2 ], все остальные значения находим уже по кругу. другими словами:
другими словами:
-π/2 ≤ arcsin a ≤ π/2
А модуль арксинусов вообще определяется первой четвертью круга, в четвертой просто появляется знак «минус».
Запишем теперь, как будет выглядеть полное решение уравнения sin x = a
⇒
Смотрите: Получется, что, если четное количество π (2πn), арксинус с плюсом, а если нечетное (π(2n+1)) — арксинус со знаком «плюс». Можно объединить запись коней!
x1,2 = arcsin a · (-1)n + πn, n ∈ Z
Здесь, если n — четное число, «минус» пропадает, и арксинус с «плюсом», если n — нечетное, то арксинус с «минусом».
Теперь по аналогии с арксинусом и помощью картинок определим остальные значения тригонометрических функций.
cos x = b
Так как косинус определяется координатой х, то и пересекать круг будем прямыми, проходящими через соответствующие точки на оси Ох.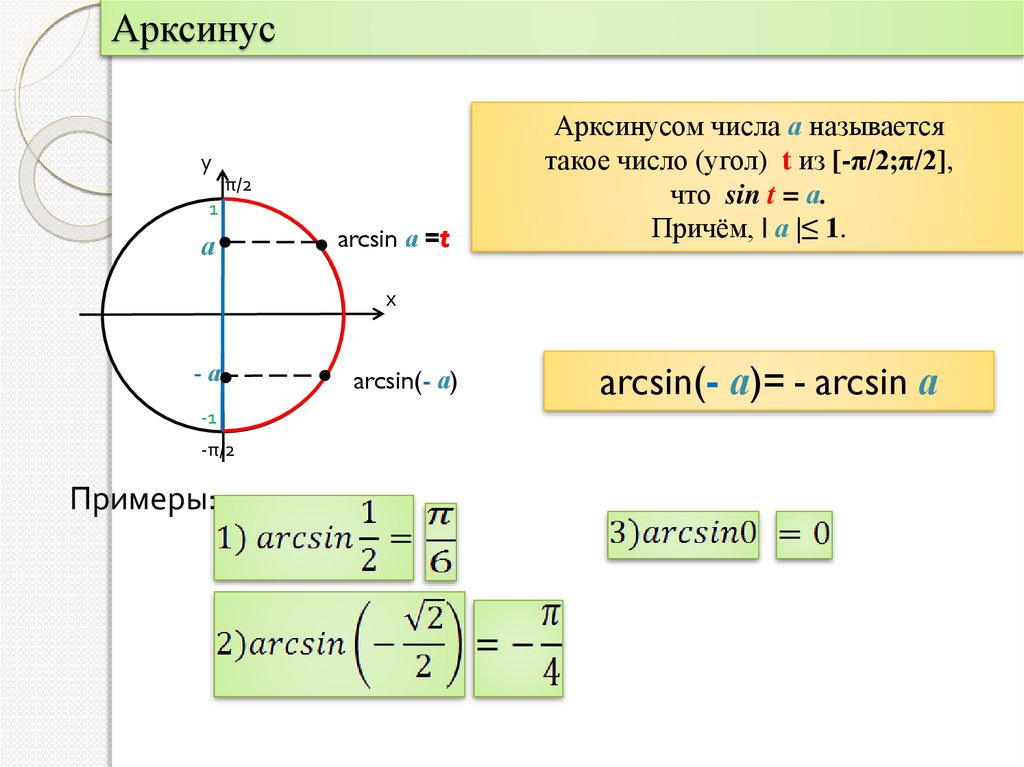 На этом круге решаем уравнение положительного значения арккосинуса. И в том случае можем смело утверждать, что = Получается:
На этом круге решаем уравнение положительного значения арккосинуса. И в том случае можем смело утверждать, что = Получается:
cos x = 0,4
Решение уравнения:
⇒
x = ± arccos 0,4 + 2πn, n ∈ Z
Теперь рассмотрим урвнение
cos x = — 0,6
Здесь тоже очевидно, что = .
Решение уравнения
⇒
x = ± arccos (-0,6) + 2πn, n ∈ Z
Общая формула для cos x = b будет:
x1,2 = ± arccos b + 2πn, n ∈ Z
Обратите внимание, что все значения арккосинуса находятся в первой и второй четвертях круга. То есть
0 ≤ arccos b ≤ π
Ну, и дополнительное напоминание — у тупых углов косинус отрицательный.
Тангес угла определяется, как
В отличие от синуса и косинуса, у тангенса углы повторяются не через 2π,а через π. Итак,
tg x = 1,5
Решение данного уравнения будет следующим:
x = arctg 1,5 + πn, n ∈ Z
Все значения для арктангенса, как видно из рисунка, укладываются в интервал
-π/2 < arctg d < π/2
Формула для определения корней уравнения
tg x = d
будет: x = arctg d + πn, n ∈ Z
Теперь про арккотангенс числа.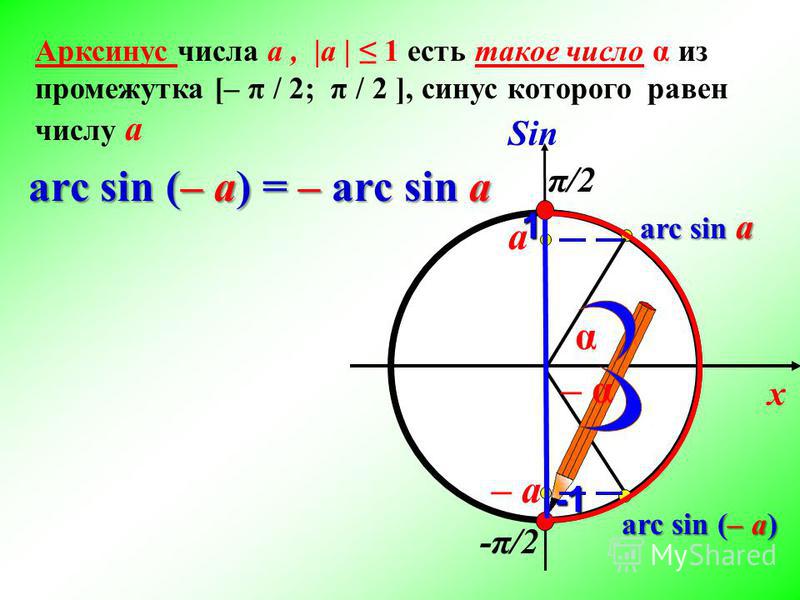 Конечно же он существует, и им можно пользоваться. Но зачем? Ведь любое уравнение с котангенсом легко превращается в уравнение тангенсом, поскольку .
Конечно же он существует, и им можно пользоваться. Но зачем? Ведь любое уравнение с котангенсом легко превращается в уравнение тангенсом, поскольку .
Подведем итоги:
| уравнение | корни уравнения | |
| sin x = a | x1,2 = arcsin a · (-1)n + πn, n ∈ Z | -π/2 ≤ arcsin a ≤ π/2 |
| cos x = b | x1,2 = ± arccos b + 2πn, n ∈ Z | 0 ≤ arccos b ≤ π |
| tg x = d | x = arctg d + πn, n ∈ Z | -π/2 < arctg d < π/2 |
Тест по теме Арксинус, арккосинус, арктангенс числа — Студопедия
Поделись
Практическая работа № 8
по теме: «Нахождение значений арксинуса, арккосинуса, арктангенса».
Пояснительная записка
Практическая работа предназначена для повторения теоретических и практических знаний по теме.
Цель работы – повторить понятия: тригонометрических функций, радианной меры углов, таблицы значений тригонометрических функций, формулы перевода градусов в радианы и наоборот, определения арксинуса, арккосинуса, арктангенса числа и подготовится к занятию по теме «Арксинус, арккосинус, арктангенс числа».
Данное пособие рекомендовано для студентов первого курса. Пособие содержит определения, свойства и формулы по теме: Арксинус, арккосинус, арктангенс числа, тест для самоконтроля.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Арксинус, арккосинус, арктангенс числа
Арксинус
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию.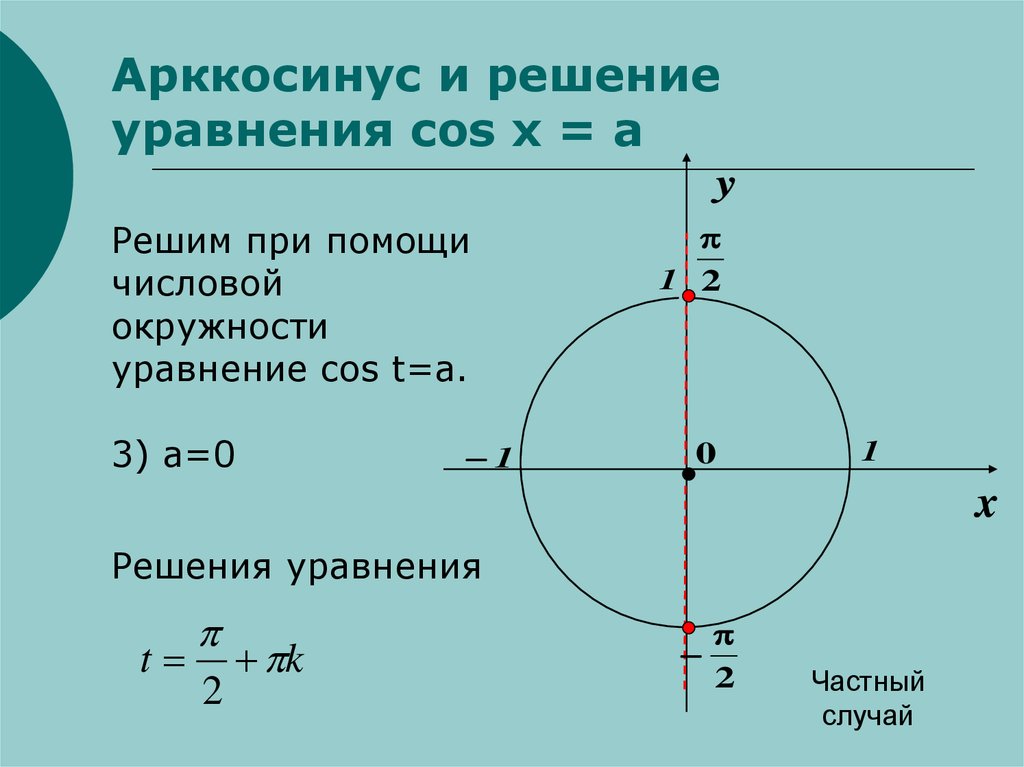 График y = arcsin x имеет вид асимметричной кривой, проходящей через центр координат.
График y = arcsin x имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
1.
2. Так как f(x) нечетная, то arcsin (- x) = — arcsin x.
3. Y = 0 при x = 0.
4. На всей своей протяженности график возрастает.
Если сопоставить графики sin и arcsin, у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
1. Функция определена на отрезке [-1; 1].
2. ОДЗ для arccos — [0, π].
3. График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
4. Y = 0 при x = 1.
5. Кривая убывает на всей своей протяженности.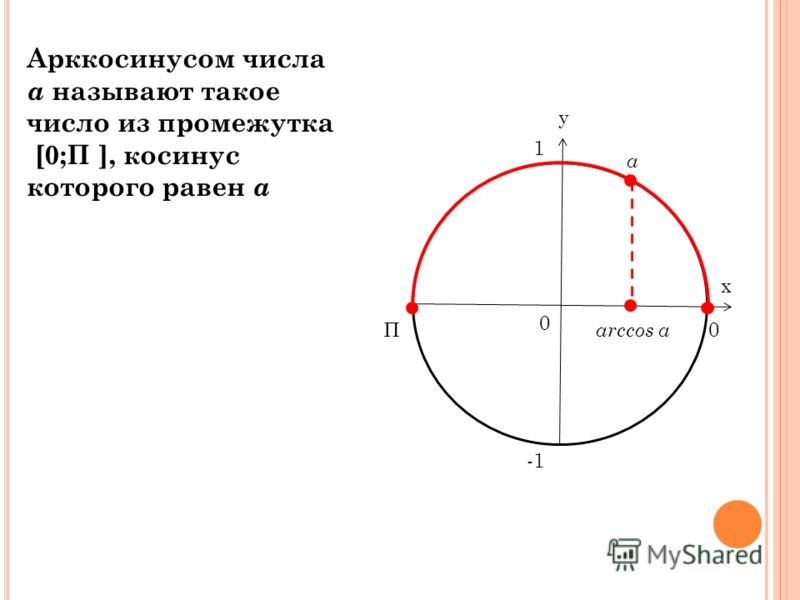 Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
1. График бесконечен и определен на промежутке (- ∞; + ∞).
2. Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
3. Y = 0 при x = 0.
4. Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
1. Интервал определения функции – бесконечность.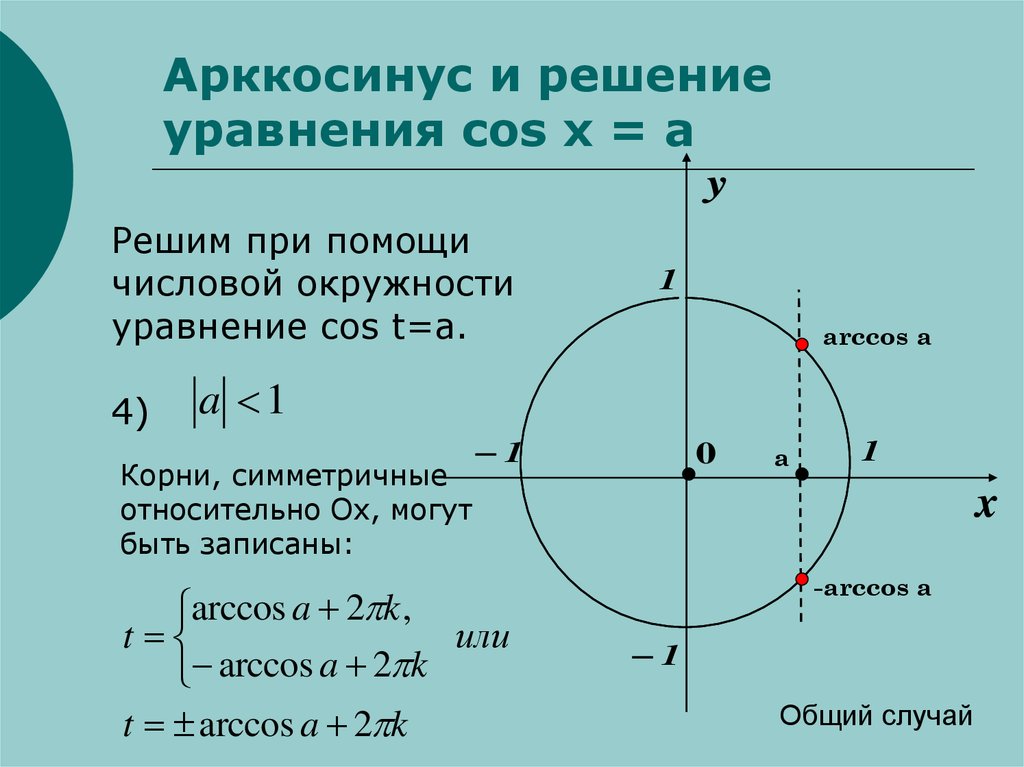
2. Область допустимых значений – промежуток (0; π).
3. F(x) не является ни четной, ни нечетной.
4. На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Пример 1. Вычислить значение .
Решение. Если обозначить , то . Из определения функции следует, что и . Так как , то и .
Однако , поэтому .
Ответ: .
Пример 2. Вычислить значение .
Решение. Если , то . Согласно определению функции , имеем и . Так как , то .
Поскольку и , то .
Ответ: .
Пример 3. Вычислить значение .
Решение. Пусть , тогда и , где . В таком случае и .
Поскольку , то .
Ответ: .
Пример 4. Вычислить значение . Решение.Так как , то или . Обозначим , тогда , . Поскольку , то .
Если , то , или . Однако , поэтому , и .
Ответ: .
Пример 5. Вычислить значение .
Решение. Если положить и , то или
, (1)
где из определения функции имеем и .
Однако и , поэтому и . В таком случае , и , .
Если , то , или . Поскольку , то .
С учетом того, что и , имеем и .
Если , то повторяя рассуждения, приведенные выше, получаем , и , .
Подставляя значения , , , в выражение (1) получаем .
Ответ: .
Примечание. Так как в примере 5 показано, что , где , и , то справедливо равенство
.
Отсюда также следует, что .
Пример 6. Вычислить значение .
Решение. Из определения функции следует, что . Из условия примера получаем .
Так как , то имеем уравнение или . Далее, принимая во внимание теорему 1, записываем две серии корней уравнения вида
и ,
где целые числа. Если положить , то из второй серии корней вытекает единственное значение , которое удовлетворяет двойному неравенству .
Ответ: .
Пример 7. Вычислить значение .
Решение. По определению функции имеем . Из условия следует, что , или
. (2)
Согласно теореме 2, здесь имеем две серии корней уравнения (2):
и , где целые числа.
Так как , то из первой серии корней при условии, что , получаем .
Ответ: .
Тест по теме Арксинус, арккосинус, арктангенс числа
Найдите значение выражения:
1.аrcsin ( — )
а) ; б) ; в) —
2. arcos (- )
arcos (- )
а) — ; б) ; в)
3.arctg
а) ; б) — ; в) 1
4.arctg 1 + arcos 1
а) ; б) 0; в)
5.аrcsin (- ) + arcos (- )
а) ; б) ; в) —
6.cos (arcos
а) ; б) — ; в) 1
7.arcos (cos )
а) ; б) ; в) —
Арксинус, арккосинус, арктангенс и арккотангенс числа с примерами решения
Содержание:
При изучении тригонометрических функций часто возникает вопрос о нахождении значения аргумента, при котором значение функции равно заданному числу.
Например, найдем все значения аргумента, при которых значение функции
На единичной окружности найдем точки ординаты которых равны Этим точкам соответствуют углы и и таких углов бесконечно много. Однако, если рассмотреть промежуток то на нем функция возрастает и принимает все значения от -1 до 1.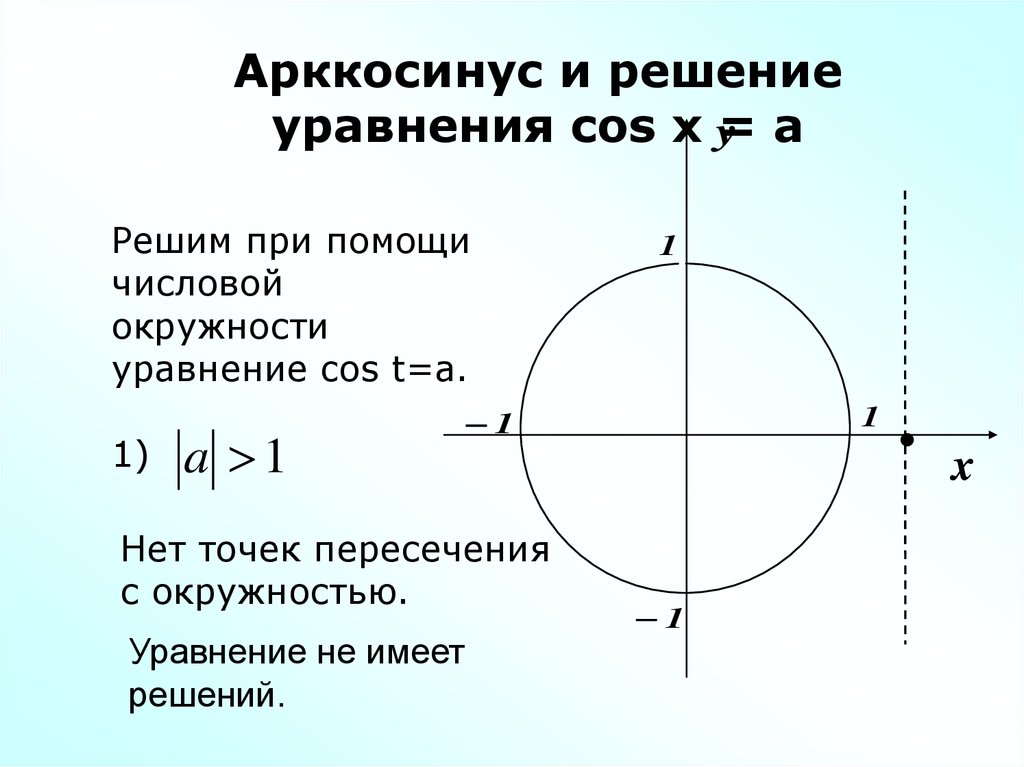 Поэтому для любого числа из промежутка существует единственное число такое что Так на промежутке существует единственное значение аргумента, при котором значение функции равно — это угол равный ( рис.93)
Поэтому для любого числа из промежутка существует единственное число такое что Так на промежутке существует единственное значение аргумента, при котором значение функции равно — это угол равный ( рис.93)
Определение Арксинуса
Определение:
Арксинусом числа называется угол, принадлежащий промежутку синус которого равен (рис. 94).
Этот угол обозначают Так, поскольку и
Пример №1Вычислите:
Решение:
так как
Пример №2Найдите значение выражения:
Решение:
так как
(рис. 95, б).
Заметим, что ( рис.95) Так как углы, соответствующие точкам и где с ординатами и отличаются только знаком, то для любого числа (рис. 96).
Пусть тогда
Так как точки имеют противоположные ординаты, то
Поскольку то по определению арксинуса Так как то для любого числа
Воспользуемся полученным равенством и найдем значение выражения
Так как
Отметим, что областью определения выражения является отрезок Если то выражение не имеет смысла.
Например, выражения не имеют смысла, так как
Выражение не имеет смысла, так как
Из определения арксинуса числа следует, что если
Например,
Рассмотрим промежуток на котором функция возрастает и принимает все значения от до 1. Для любого числа из промежутка существует единственное число такое, что
Определение Арккосинуса
Определение:
Арккосинусом числа называется угол, принадлежащий промежутку косинус которого равен (рис. 97).
Этот угол обозначают
Например: поскольку и
Вычислите:
Решение:
Пример №4
Найдите значение выражения:
Решение:
так как ( рис. 98.а)
( рис.98.б)
Заметим, что ( см.98)
Пусть Так как точки имеют противоположные абсциссы, то Поскольку то по определению арккосинуса Так как для любого числа (рис. 99).
99).
Воспользуемся полученным равенством и найдем значение выражения
Так как
Областью определения выражения является отрезок Если то выражение не имеет смысла.
Так, выражения не имеют смысла, поскольку
Выражение не имеет смысла, так как
Из определения арккосинуса числа следует, что если и
Например,
На промежутке монотонности функции существует единственный угол, тангенс которого равен некоторому данному числу
Определение Арктангенса
Определение:
Арктангенсом числа называется угол, принадлежащий промежутку тангенс которого равен (рис. 100).
Этот угол обозначают Так, поскольку и
Вычислите:
Решение:
так как и
и
Для любого числа верно равенство (рис. 101).
Пример №6
Найдите значение выражения
Решение:
Так как
Из определения арктангенса числа следует, что при
Например,
На промежутке монотонности функции существует единственный угол, котангенс которого равен некоторому данному числу
Определение Арккотангенса
Определение:
Арккотангенсом числа называется угол, принадлежащий промежутку котангенс которого равен (рис. 102).
102).
Этот угол обозначают Например, поскольку
- Заказать решение задач по высшей математике
Вычислите:
Решение:
так как
Для любого числа верно равенство (рис. 103).
Пример №8Найдите значение выражения
Решение:
Так как
Из определения арккотангенса числа следует, что если и
Например,
Примеры заданий и их решения
Пример №9Верно ли, что:
Решение:
а) Верно, так как
б) верно, так как
в) неверно, так как
г) неверно, так как
Пример №10Вычислите:
Решение:
Пример №11
Найдите значение выражения:
Решение:
Пример №12
Оцените значение выражения
Решение:
По определению арктангенса числа
Воспользуемся свойствами числовых неравенств и получим:
Пример №13Найдите область определения выражения:
Решение:
а) По определению арксинуса числа это угол, синус которого равен
б) По определению арккосинуса числа это угол, косинус которого равен
Пример №14Найдите значение выражения:
Решение:
Пример №15
Вычислите
Решение:
Пример №16
Найдите значение выражения
Решение:
Воспользуемся формулой при Поскольку то эту формулу сразу применить нельзя.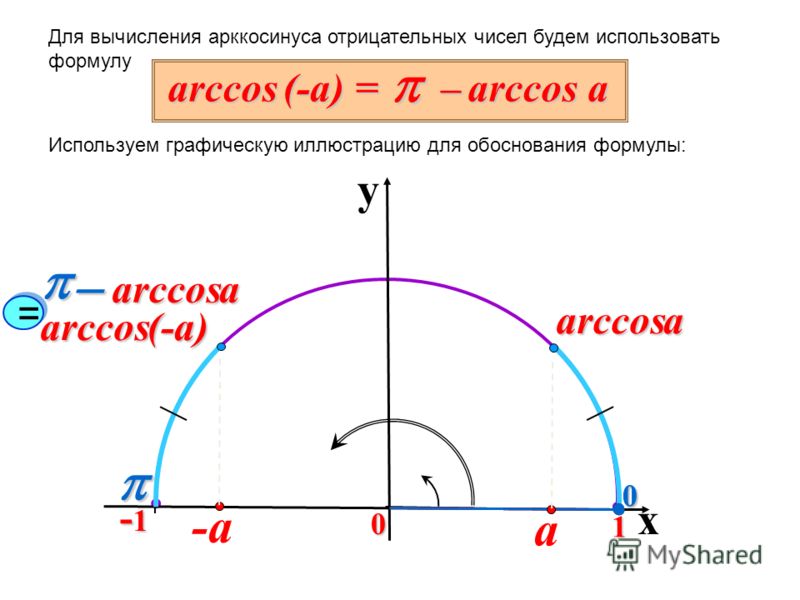
Так как
Пример №17Найдите значение выражения
Решение:
Так как при при
2) Понятие арксинуса и арккосинуса числа. Примеры. И 3 вопрос Арксинус, арккосинус, арктангенс и арккотангенс – основные сведения.
1)Понятие степени. Свойства степеней. Примеры.
Степенью называется выражение вида: , где:
Степень с натуральным показателем {1, 2, 3,…}
Определем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
Возвести число в натуральную степень — значит умножить число само на себяраз:
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
, n > 0
Возведение в нулевую степень:
, a ≠ 0
Если показателем степени является целое отрицательное число:
, a ≠ 0
Прим:
выражение не
определено, в случаеn
≤ 0.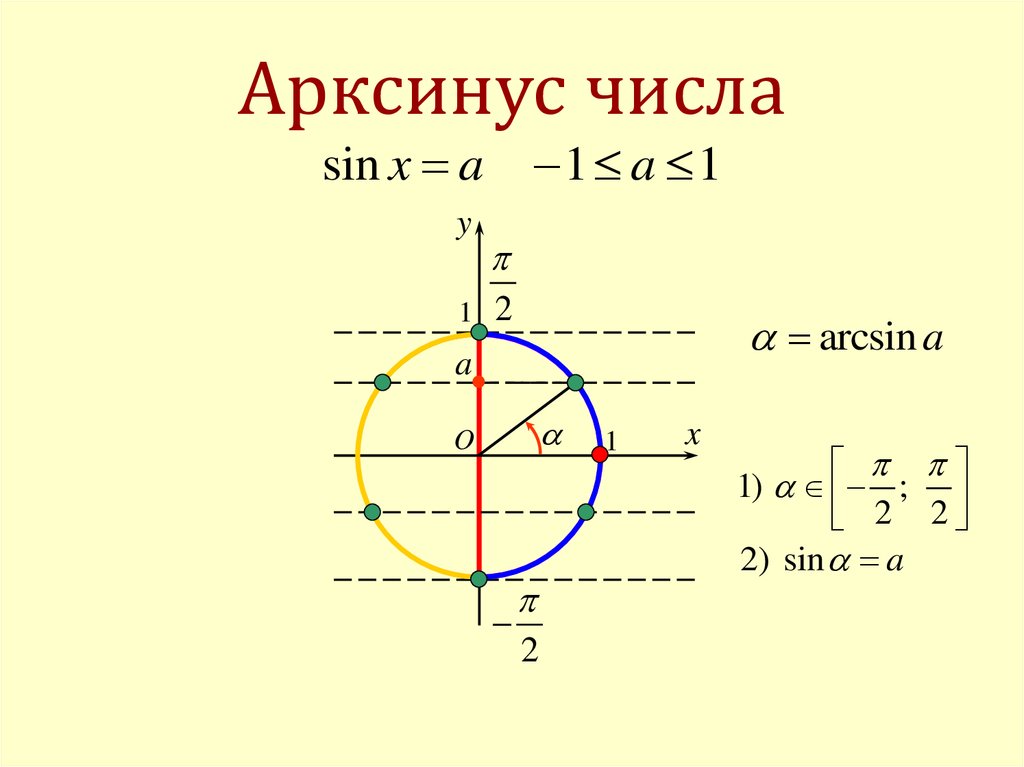 Если n
> 0,
то
Если n
> 0,
то
Пример 1.
Степень с рациональным показателем
Если:
Тогда:
Пример 2.
Свойства степеней
Произведение степеней | |
Деление степеней | |
Возведение степени в степень |
Пример 3.
Корень
Арифметический квадратный корень
Уравнение имеет
два решения:x=2 и
x=-2.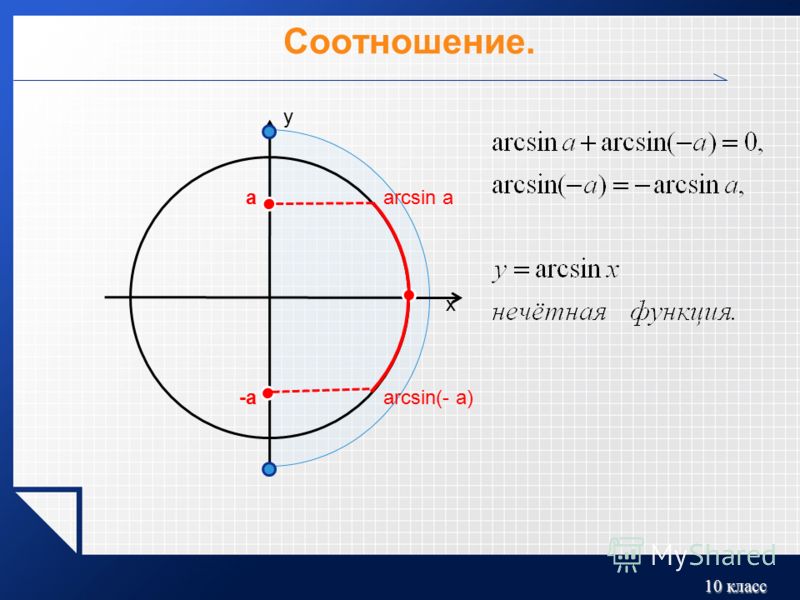 Это числа, квадрат которых равен 4.
Это числа, квадрат которых равен 4.
Рассмотрим уравнение . Нарисуем график функциии увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
Но в данному случае решения не являются целыми числами. Более того, они не являются рациональными. Для того, чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический квадратный корень — это неотрицательное число, квадрат которого равен,a ≥ 0. При a < 0 — выражение не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу.
Корень из квадрата
Например, . А решения уравнениясоответственнои
Кубический корень
Кубический
корень из числа —
это число, куб которого равен.
Кубический корень определен для всех.
Его можно извлечь из любого числа:.
Корень n-ой степени
Корень -й степени из числа— это число,-я степень которого равна.
Если — чётно.
Тогда, если a < 0 корень n-ой степени из a не определен.
Или если a ≥ 0, то неотрицательный корень уравнения называется арифметическим корнемn-ой степени из aи обозначается
Если — нечётно.
Пример 4.
Задача, обратная нахождению значений синуса, косинуса, тангенса и котангенса данного угла, подразумевает нахождение угла по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.
В
этой статье мы дадим определения
арксинуса, арккосинуса, арктангенса и
арккотангенса числа, введем принятые
обозначения, а также приведем примеры
арксинуса, арккосинуса, арктангенса и
арккотангенса. В заключение обговорим
некоторые тонкости, касающиеся этой
темы, и покажем, как арксинус, арккосинус,
арктангенс и арккотангенс связаны с
единичной окружностью.
В заключение обговорим
некоторые тонкости, касающиеся этой
темы, и покажем, как арксинус, арккосинус,
арктангенс и арккотангенс связаны с
единичной окружностью.
Навигация по странице.
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Обозначения arcsin, arccos, arctg и arcctg.
Примеры.
Арксинус, арккосинус, арктангенс и арккотангенс числа или угла?
Арксинус, арккосинус, арктангенс и арккотангенс на единичной окружности.
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа
Дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Определение.
Арксинус
числа a из
интервала от −1 до 1 включительно
– это такой угол, лежащий в пределах
от −π/2 до π/2 (от −90 до 90 градусов)
включительно, синус которого равен a.
Определение.
Арккосинусом числа a, −1≤a≤1, называется такой угол из отрезка [0, π] (от нуля до180 градусов включительно), косинус которого равен a.
Определение.
Арктангенсом числа a, a – любое действительное число, называется угол из интервала(−π/2, π/2) (от −90 до 90 градусов не включительно), тангенс которого равен a.
Определение.
Арккотангенс числа a, a – любое действительное число, — это такой угол из интервала(0, π) (от нуля до 90 градусов не включительно), котангенс которого равен a.
Из
приведенных определений видно, что
арксинус и арккосинус числа определены
для чисел, лежащих в интервале [−1,
1],
для остальных чисел арксинус и арккосинус
не определяются. Например, не
определены arcsin
2,
арксинус пяти, арксинус минус корня из
трех, арккосинус семи целых двух третьих
и арккосинус минус пи, так как
числа 2, 5, не
лежат в интервале от−1 до 1.
В свою очередь определения арктангенса и арккотангенса даются для любых действительных чисел a. То есть, имеют смысл и арктангенс нуля, и арктангенс −500,2, и арккотангенс миллиарда, и арккотангенс −π/3, как и арктангенс, и арккотангенс любого другого действительного числа.
Также стоит отметить, что при условиях, указанных для числа a в определениях, арксинус, арккосинус, арктангенс и арккотангенс существуют, причем они определены однозначно, то есть, для данного числа a имеют единственное значение.
К началу страницы
Обозначения arcsin, arccos, arctg и arcctg
Для
записи арксинуса, арккосинуса, арктангенса
и арккотангенса приняты
следующиеобозначения: arcsin, arccos, arctg и arcctg.
То есть, арксинус числа a можно
записать какarcsin
a,
арккосинус, арктангенс и арккотангенс
числа a запишутся
соответственно как arccos
a,arctg
a и arcctg
a.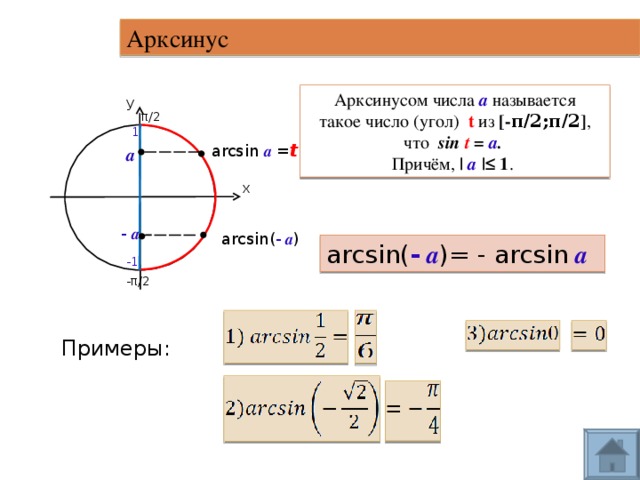
Также можно встретить обозначения arctan и arccot, они являются другой формой обозначения арктангенса и арккотангенса, принятой в англоязычной литературе. Мы же арктангенс и арккотангенс будем обозначать как arctg и arcctg.
В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа запишутся как:
arcsin a, где −1≤a≤1, есть угол α, если sinα=a и −π/2≤α≤π/2;
arccos a, где −1≤a≤1, есть угол α, если cosα=a и 0≤α≤π;
arctg a, где a – любое действительное число, есть угол α, если tgα=a и −π/2≤α≤π/2;
arcctg a, где a – любое действительное число, есть угол α, если ctgα=a и 0≤α≤π.
К началу страницы
Примеры
Самое
время привести примеры арксинуса,
арккосинуса, арктангенса и арккотангенса
числа.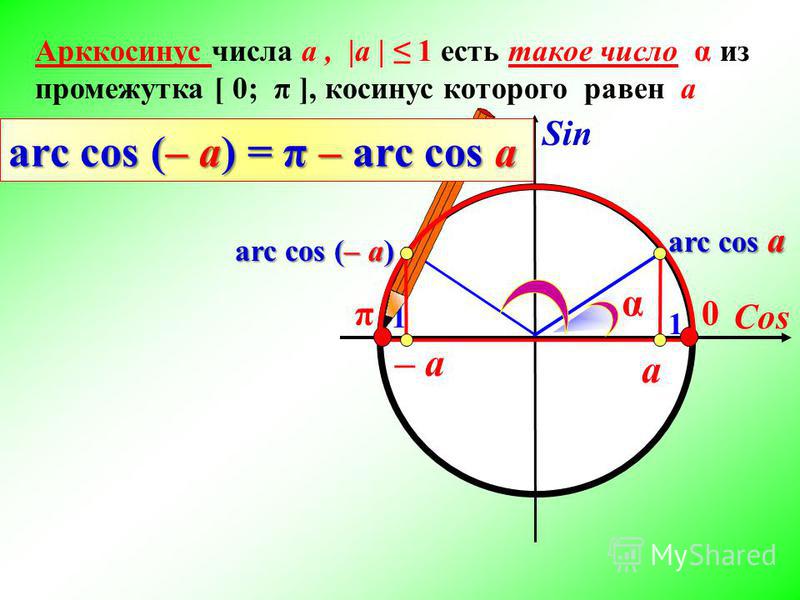
Начнем с примеров арксинуса. Угол π/3 является арксинусом числа , это действительно так, так как числопринадлежит интервалу от−1 до 1, угол π/3 лежит в пределах от −π/2до π/2 и . Приведем еще несколько примеров арксинуса числа:arcsin(−1)=−π/2,arcsin(0,5)=π/6, .
А вот π/10 не является арксинусом 1/2, так как sin(π/10)≠1/2. Еще пример: не смотря на то, что синус 270 градусов равен −1, угол 270 градусов не является арксинусом минус единицы, так как 270 градусов не является углом в пределах от −90 до 90 градусов. Более того, угол 270градусов вообще не может быть арксинусом какого-либо числа, так как арксинус числа должен лежать в пределах от −90 до 90 градусов.
Для
полноты картины осталось привести примеры
арккосинуса, арктангенса и арккотангенса
числа.
Например, угол 0 радиан
является арккосинусом единицы (так как
выполняются все условия из определения
арккосинуса: число 1 лежит
в отрезке от −1 до 1,
угол нуль радиан лежит в пределах от
нуля до пи включительно и cos0=1),
угол π/2 есть
арккосинус нуля.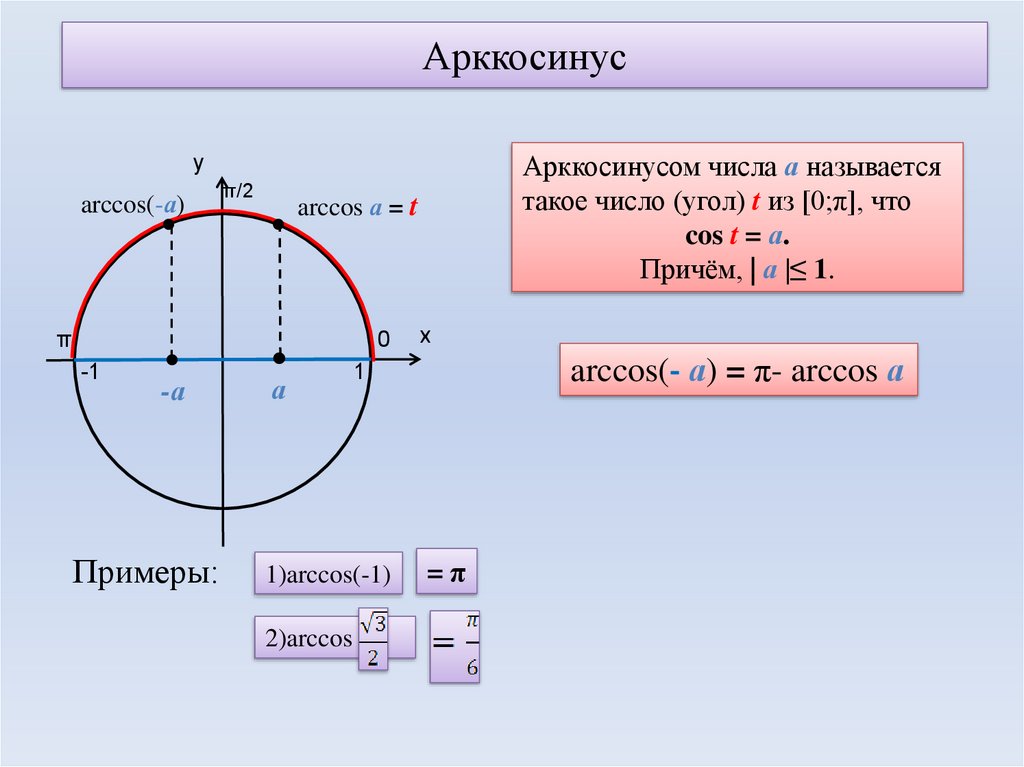 По определению
арктангенса числа arctg(−1)=−π/4 и
арктангенс корня из трех равен 60 градусам
(π/3 рад).
А из определения арккотангенса можно
заключить, чтоarcctg0=π/2,
так как π/2 лежит
в открытом интервале от 0 до
пи и ctg(π/2)=0.
По определению
арктангенса числа arctg(−1)=−π/4 и
арктангенс корня из трех равен 60 градусам
(π/3 рад).
А из определения арккотангенса можно
заключить, чтоarcctg0=π/2,
так как π/2 лежит
в открытом интервале от 0 до
пи и ctg(π/2)=0.
К началу страницы
Арксинус, арккосинус, арктангенс и арккотангенс числа или угла?
В первом пункте данной статьи мы дали определения арксинуса, арккосинуса, арктангенса и арккотангенса числа. Таким образом, мы говорим именно об арксинусе, арккосинусе, арктангенсе и арккотангенсе числа, а не угла.
Для себя нужно четко разграничить, что существует синус, косинус, тангенс и котангенс УГЛА, их значениями являются числа, и обратно: существует арксинус, арккосинус, арктангенс и арккотангенс ЧИСЛА, их значениями являются углы.
К началу страницы
Арксинус, арккосинус, арктангенс и арккотангенс на единичной окружности
Чтобы
получить наглядное представление об
арксинусе, арккосинусе, арктангенсе и
арккотангенсе числа a,
взглянем на них с позиций геометрии. Это несложно сделать, если знать про линии
синусов, косинусов, тангенсов и
котангенсов.
Это несложно сделать, если знать про линии
синусов, косинусов, тангенсов и
котангенсов.
arcsin a, arccos a, arctg a и arcctg a можно связать с дугами единичной окружности, стягивающими углы, соответствующие значениям арксинуса, арккосинуса, арктангенса и арккотангенса числа a.
Для примера получим дугу, соответствующую арксинусу числа a. Для этого на линии синусов отметим точку, отвечающую числу a, после чего из нее проведем луч, параллельно и в положительном направлении оси абсцисс. Этот луч будет пересекать единичную окружность в некоторой точке. Дуга единичной окружности от этой точки до начальной точки с координатами(1, 0) и будет отвечать арксинусу числа a.
По
схожим принципам можно получить дуги,
отвечающие арккосинусу, арктангенсу и
арккотангенсу числа a.
На рисунке ниже синими линиями показаны
дуги, отвечающие арккосинусу, арктангенсу
и арккотангенсу числа a.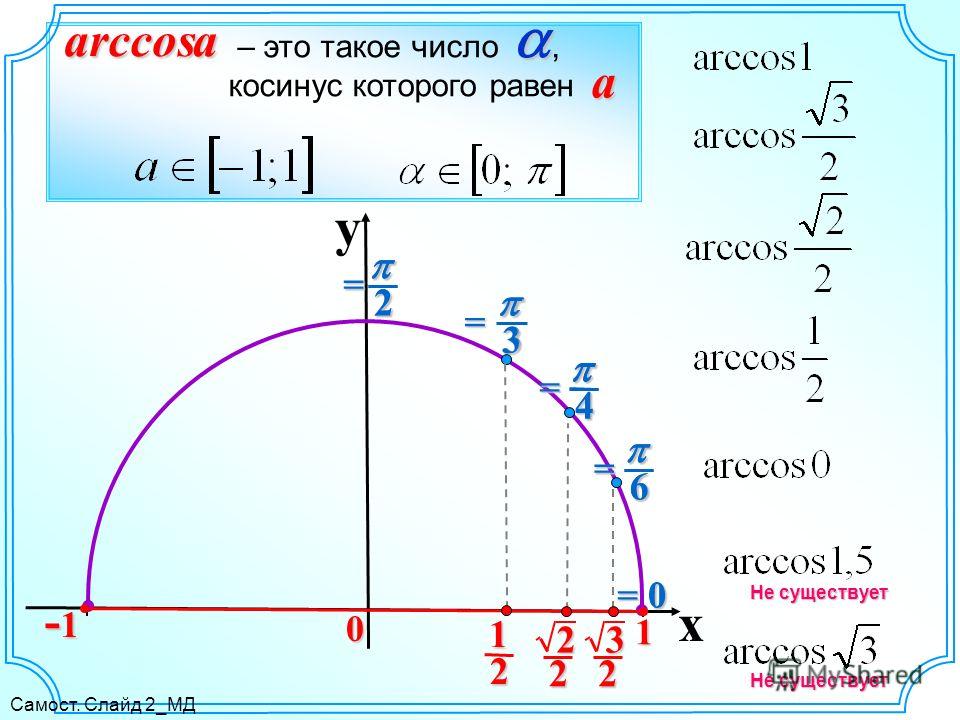
4) Показатели функции, ее свойства и график.
В практике часто используются функции y=2x,y=10x,y=(12)x,y=(0,1)x и т. д., т. е. функция вида y=ax, где a — заданное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Функция, заданная формулой y=ax(где a>0,a≠1), называется показательной функцией с основанием a.
Сформулируем основные свойства показательной функции:
1. Область определения — множество R действительных чисел.
2. Область значений — множество R+ всех положительных действительных чисел.
3.
При a>1 функция
возрастает на всей числовой прямой;
при 0<a<1 функция
убывает на множестве R.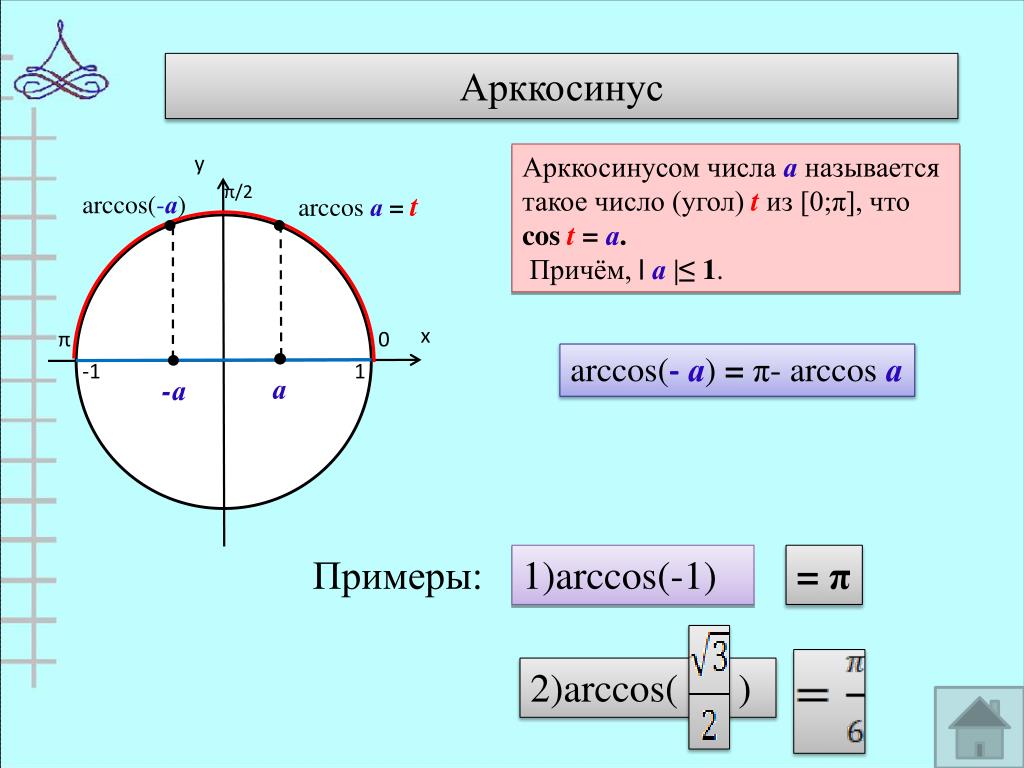
ax1<ax2, если x1<x2,(a>1),
ax1>ax2, если x1<x2,(0<a<1)
4. При любых действительных значениях x и y справедливы равенства
axay=ax+yaxay=ax−y(ab)x=axbx(ab)x=axbx(ax)y=axy
Графики показательных функций изображены на рисунках:
1) для случая a>1
2) для случая 0<a<1
Логарифм и его свойства. Примеры
Логарифмом числа по основанию() называется такое число, что, то есть записииравносильны. Логарифм имеет смысл, если.
Если немного перефразировать — Логарифм числа по основаниюопределяется как показатель степени, в которую надо возвести число, чтобы получить число(Логарифм существует только у положительных чисел).
Логарифм
в переводе с греческого буквально
означает «число, изменяющее отношение».
Специальные обозначения:
Свойства логарифмов:
1° —основное логарифмическое тождество.
2°
3°
Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.
4° —логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
5° —логарифм частного.
Логарифм частного (дроби) равен разности логарифмов сомножителей.
6° —логарифм степени.
Логарифм степени равен произведению показателя степени на логарифм ее основания.
7°
8°
9° —
переход к новому основанию.
Вычислить , если
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
Ответ.
Калькулятор — arccos(cos(2)) — Solumaths
Arccos, расчет онлайн
Резюме:
Функция arccos позволяет вычислить арккосинус числа. Функция arccos является обратной функцией функции косинуса.
arccos online
Описание:
Функция арккосинуса является обратной функцией функция косинуса, это вычисляет арккосинус числа онлайн .
Число, к которому вы хотите применить функцию арккосинуса, должно принадлежать диапазону [-1,1].
- Расчет арккосинуса
- Таблица замечательных значений
Чтобы вычислить арккосинус числа, просто введите число и примените функция arccos .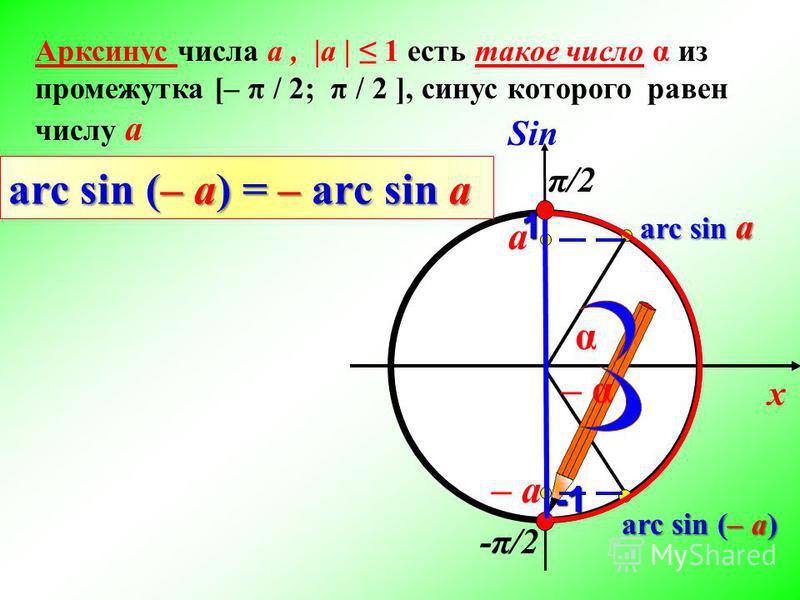 Таким образом, для вычисление арккосинуса числа, следующего за 0,4,
вы должны ввести
arccos(`0.4`) или сразу 0.4, если кнопка arccos уже есть,
результат 1.1592)`.
Таким образом, для вычисление арккосинуса числа, следующего за 0,4,
вы должны ввести
arccos(`0.4`) или сразу 0.4, если кнопка arccos уже есть,
результат 1.1592)`.
| arccos(`-1`) | `pi` | |
| arccos(`-sqrt(3)/2`) | `5*pi/6` | |
| `3*pi/4` | ||
| arccos(`-1/2`) | `2*pi/3` | |
| arccos(`0`) | ``2*pi/3` pi/2` | |
| arccos(`1/2`) | `pi/3` | |
| arccos(`sqrt(2)/2`) | `pi/4` | |
| arccos(`sqrt(3)/2`) | `pi/6` | |
| arccos(`1`) | `0` |
Syntax :
arccos(x), где x — число.
Иногда используются другие обозначения: acos
Примеры:
arccos(`1`) возвращает 0
Производная арккосинуса :
Чтобы дифференцировать функцию арккосинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арккосинуса 92)`
Предел арккосинуса :
Калькулятор предела позволяет вычислить пределы функции арккосинуса.
предел арккосинуса(x) is limit(`»arccos»(x)`)
Обратная функция арккосинуса :
обратная функция арккосинуса – это функция косинуса, отмеченная как cos.
Графический арккосинус :
Графический калькулятор может отображать функцию арккосинуса в заданном интервале.
Расчет онлайн с арккосинусом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус: арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции
Как использовать функцию ACOS
- Главная
- Функции
- Формулы
- Функции
Основы Excel Таблица Excel Расширенный фильтр Проверка данных Выпадающие списки Именованные диапазоны Решатель
- Карты
- Условное форматирование
- Сводная таблица
- VBA
Функции VBA Методы Характеристики Заявления Макросы Пользовательские функции Файлы и папки Флажки
- Архив
Все статьи отсортированы по дате Категории Товары Расширенный курс Excel
- Контакт
Обо мне Блоги я прочитал
Автор: Оскар Кронквист Последнее обновление статьи: 04 мая 2022 г.
Функция ACOS вычисляет арккосинус или арккосинус числа.
Формула в ячейке C3:
=ACOS(B3)
Синтаксис функций Excel
ACOS( число )
Аргументы
| Обязательно. Число, равное или большее -1 или равное или меньшее 1. -1 <= номер <= 1. |
Комментарии
Арккосинус — это угол, косинус которого равен числу . Возвращаемый угол задается в радианах в диапазоне от 0 (ноль) до пи.
Функции в этом изделии
ACOS
Функции в категории «Математика и тригонометрия»
Функция функции ACOS — одна из многих функций в категории «Математика и тригонометрия».
Функция ABS
Преобразует отрицательные числа в положительные числа.
Функция ACOS
Вычисляет арккосинус или арккосинус числа.
Функция ACOSH
Вычисляет гиперболический арккосинус числа.
Функция ACOT
Вычисляет арккотангенс числа.
Функция ACOTH
Вычисляет аркгиперболический котангенс числа.
Функция АГРЕГАТ
Выполнение различных конкретных функций для списка или базы данных.
Функция ASIN
Вычисляет арксинус числа.
Функция ASINH
Вычисляет арктический гиперболический синус числа.
Функция ATAN
Вычисляет арктангенс числа.
Функция ATAN2
Вычисляет арктангенс угла, используя определенные координаты x и y.
Функция ATANH
Вычисляет гиперболический арктангенс числа.
Функция ОСНОВА
Преобразует число в текстовое представление с заданной системой счисления (основанием).
Функция CEILING
Округляет число до ближайшего кратного.
Функция COMBIN
Возвращает количество комбинаций для определенного количества элементов из большей группы.
Функция COMBINA
Вычисляет количество комбинаций для заданного количества элементов из большей группы элементов.
Функция COS
Вычисляет косинус угла.
Функция COSH
Вычисляет гиперболический косинус числа.
Функция COT
Вычисляет котангенс угла, указанного в радианах.
Функция COTH
Вычисляет гиперболический котангенс гиперболического угла.
Функция CSC
Вычисляет косеканс угла (в радианах).
Функция DECIMAL
Преобразует текстовое представление числа в заданной системе счисления в десятичное число.
Функция ГРАДУСЫ
Вычисляет градусы в радианах.
ЧЕТНАЯ функция
Округляет число до ближайшего четного целого числа.
Функция EXP
Возвращает e, возведенное в степень числа, e равно 2,71828182845904.
Функция FACT
Возвращает факториал числа.
Функция FACTDOUBLE
Возвращает двойной факториал числа.
ИСПРАВЛЕННАЯ функция
Округляет число до указанного количества десятичных знаков, форматирует число в десятичном формате с использованием точки и запятых и возвращает результат в виде текста.
Функция FLOOR.MATH
Округляет число в меньшую сторону до ближайшего целого числа или до ближайшего кратного значения.
Функция FLOOR.PRECISE
Округляет число в меньшую сторону до ближайшего целого или ближайшего кратного значения.
Функция НОД
Вычисляет наибольший общий делитель, который делит все заданные аргументы без остатка.
Функция INT
Удаляет десятичную часть из положительных чисел и возвращает целое число (целое), за исключением того, что отрицательные значения округляются до ближайшего целого числа.
Функция LCM
Вычисляет наименьшее общее кратное. Наименьшее общее кратное — это наименьшее положительное целое число, кратное всем целым аргументам. Используйте функцию НОК, чтобы найти дроби с разными знаменателями.
Функция LET
Позволяет назвать результаты промежуточных вычислений, что может значительно сократить формулы и повысить производительность.
Функция LN
Вычисляет натуральный логарифм числа. Натуральные логарифмы основаны на константе e.
Натуральные логарифмы основаны на константе e.
Функция LOG
Вычисляет логарифм числа по определенному основанию.
Функция LOG10
Вычисляет логарифм числа по основанию 10.
Функция MINVERSE
Вычисляет обратную матрицу для заданного массива.
Функция МУМНОЖ
Вычисляет матричное произведение двух массивов, массива с тем же количеством строк, что и массив1, и столбцов, как массив2.
Функция MOD
Возвращает остаток после деления числа на делитель.
Функция ОКРУГЛ
Вычисляет число, округленное до заданного кратного.
МНОГОНОМНАЯ функция
Вычисляет отношение факториала суммы значений к произведению факториалов.
Функция MUNIT
Вычисляет единичную матрицу для заданного измерения
Функция PI
Возвращает число пи (¶).
Функция POWER
Вычисляет число, возведенное в степень.
Функция ПРОИЗВЕД
Возвращает произведение чисел, указанных в аргументе.
Функция ЧАСТНОЕ
Возвращает целую часть деления.
Функция RADIANS
Преобразует градусы в радианы.
Функция СЛУЧАЙ
Вычисляет случайное действительное число, большее или равное 0 и меньшее 1.
Функция СЛУЧАЙ
Создает массив случайных чисел .
Функция ОКРУГЛ
Округляет число на основе указанного вами количества цифр.
Функция ОКРУГЛВНИЗ
Округляет число в меньшую сторону на основе количества цифр, до которого вы хотите округлить число.
Функция ОКРУГЛВВЕРХ
Вычисляет число, округленное в большую сторону, на основе количества цифр, до которого вы хотите округлить число.
Функция SEC
Вычисляет секанс угла.
Функция SECH
Вычисляет гиперболический секанс угла.
Функция ПОСЛЕДОВАТЕЛЬНОСТЬ
Создает список последовательных чисел
Функция СЕРИЙСУММ
Вычисляет сумму степенного ряда на основе формулы.
Функция ЗНАК
Возвращает знак числа. 1 для положительного числа, 0 (ноль) для 0 (ноль) и -1 для отрицательного числа.
1 для положительного числа, 0 (ноль) для 0 (ноль) и -1 для отрицательного числа.
Функция SIN
Вычисляет синус угла.
Функция SINH
Вычисляет гиперболический синус числа.
Функция SQRT
Вычисляет положительный квадратный корень.
Функция ПРОМЕЖУТОЧНЫЙ ИТОГ
Возвращает промежуточный итог из списка или базы данных, вы можете выбрать один из множества аргументов, которые определяют, что вы хотите, чтобы функция делала.
Функция СУММ
Позволяет добавлять числовые значения, функция возвращает сумму в ячейке, в которую она введена. Функция СУММ умно разработана, чтобы игнорировать текст и логические значения, добавляя только числа.
Функция СУММЕСЛИ
Суммирует числовые значения на основе условия.
Функция СУММЕСЛИМН
Складывает числа на основе критериев.
Функция СУММПРОИЗВ
Вычисляет произведение соответствующих значений, а затем возвращает сумму каждого умножения.
Функция СУММСК
Вычисляет сумму квадратов аргументов.
Функция SUMX2MY2
Вычисляет сумму разности квадратов соответствующих значений в двух массивах.
Функция SUMX2PY2
Вычисляет сумму суммы квадратов соответствующих значений в двух массивах.
Функция SUMXMY2
Вычисляет сумму квадратов разностей соответствующих значений в двух массивах.
Функция TAN
Вычисляет тангенс угла.
Функция TANH
Вычисляет гиперболический тангенс числа.
Функция TRUNC
Удаляет дробную часть числа до целого числа.
Категории функций Excel
Работа с массивами
Функции Excel, позволяющие изменять размер, комбинировать и формировать массивы.
Совместимость
Функции обратной совместимости с более ранними версиями Excel. Функции совместимости заменены более новыми функциями с повышенной точностью. Используйте новые функции, если совместимость не требуется.
База данных
Выполнение основных операций со структурой, подобной базе данных.
Дата и время
Функции, позволяющие выполнять вычисления со значениями даты и времени в Excel.
Инженерное дело
Позволяет работать с двоичными числами, преобразовывать значения между различными системами счисления и вычислять мнимые числа.
Финансовый
Расчет приведенной стоимости, процентов, накопленных процентов, основной суммы, накопленной основной суммы, амортизации, платежа, цены, роста, доходности по ценным бумагам и других финансовых расчетов.
Информация
Функции, которые позволяют получить информацию из ячейки, форматирования, формулы, листа, книги, пути к файлу и других объектов.
Логические
Функции, позволяющие возвращать логические значения и управлять ими, а также управлять расчетами формул на основе логических выражений.
Поиск и ссылка
Эти функции позволяют сортировать, искать, получать внешние данные, такие как котировки акций, фильтровать значения на основе условий или критериев и получать относительное положение заданного значения в определенном диапазоне ячеек. Они также позволяют вычислять строки, столбцы и другие свойства ссылок на ячейки.
Они также позволяют вычислять строки, столбцы и другие свойства ссылок на ячейки.
Математика и тригонометрия
В этой категории вы найдете функции, которые вычисляют случайные значения, округляют числовые значения, создают последовательные числа, тригонометрию и многое другое.
Статистический
Расчет распределений, биномиальных распределений, экспоненциального распределения, вероятностей, дисперсии, ковариации, доверительного интервала, частоты, среднего геометрического, стандартного отклонения, среднего, медианы и других статистических показателей.
Текст
Функции, которые позволяют вам манипулировать текстовыми значениями, заменять строки, находить строку в значении, извлекать подстроку в строке, преобразовывать символы в код ANSI среди других функций.
Интернет
Получение данных из Интернета, извлечение данных из строки XML и многое другое.
Категории Excel
Домашняя страница
Последние обновленные статьи.
Функции Excel
Более 300 функций Excel с подробной информацией, включая синтаксис, аргументы, возвращаемые значения и примеры для большинства функций, используемых в формулах Excel.
Формулы Excel
Более 1300 формул, организованных в подкатегории.
Таблицы Excel
Таблицы Excel упрощают работу с данными, добавляя или удаляя данные, фильтруя, суммируя, сортируя, улучшая читаемость с помощью форматирования ячеек, ссылок на ячейки, формул и многого другого.
Расширенный фильтр
Позволяет фильтровать данные на основе выбранного значения, заданного текста или других критериев. Он также позволяет фильтровать существующие данные или перемещать отфильтрованные значения в новое место.
Проверка данных
Позволяет контролировать, что пользователь может вводить в ячейку. Это позволяет вам указать условия и показать собственное сообщение, если введенные данные недействительны.
Раскрывающийся список
Позволяет пользователю работать более эффективно, отображая список, из которого пользователь может выбрать значение. Это позволяет вам контролировать то, что отображается в списке, и это быстрее, чем ввод в ячейку.
Это позволяет вам контролировать то, что отображается в списке, и это быстрее, чем ввод в ячейку.
Именованные диапазоны
Позволяет назвать одну или несколько ячеек, это упрощает поиск ячеек с помощью поля Имя, чтение и понимание формул, содержащих имена вместо ссылок на ячейки.
Excel Solver
Excel Solver — это бесплатная надстройка, которая использует целевые ячейки, ограничения, основанные на формулах на листе, для выполнения анализа «что, если» и других задач принятия решений, таких как перестановки и комбинации.
Диаграммы
Функция Excel, позволяющая визуализировать данные в виде графика.
Условное форматирование
Форматирование ячеек или значений ячеек на основе условия или критериев. Существует несколько встроенных инструментов условного форматирования, которые можно использовать, или использовать пользовательскую формулу условного форматирования.
Сводные таблицы
Позволяет быстро суммировать большие объемы данных в очень удобной для пользователя форме.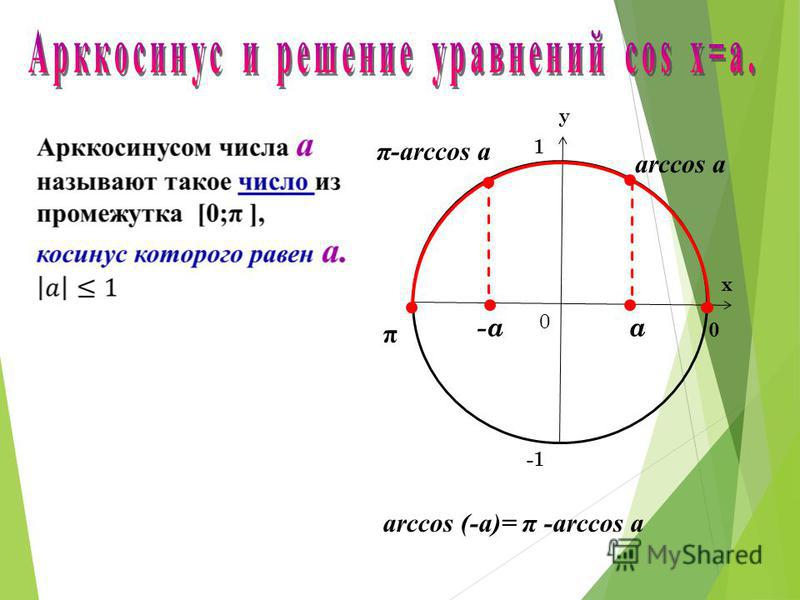 Эта мощная функция Excel позволяет эффективно анализировать, упорядочивать и классифицировать важные данные.
Эта мощная функция Excel позволяет эффективно анализировать, упорядочивать и классифицировать важные данные.
VBA
VBA означает Visual Basic для приложений и представляет собой язык программирования, разработанный Microsoft. Он позволяет автоматизировать трудоемкие задачи и создавать пользовательские функции.
Макросы
Программа или подпрограмма, встроенная в VBA, которую может создать любой. Используйте средство записи макросов, чтобы быстро создавать собственные макросы VBA.
UDF
UDF расшифровывается как User Defined Functions и представляет собой настраиваемые функции, которые может создать каждый.
Архив
Список всех опубликованных статей.
| 1 | Найти точное значение | грех(30) | 907:10|
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найдите точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc (45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | 907:10|
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | 907:10|
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек (60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | 907:10|
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценка | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | 907:10|
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | коричневый((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценка | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктангел (квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | грех((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | 907:10|
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найдите точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Полное руководство по вычислению производной Arccos
Производная от arccos в тригонометрии является обратной функцией, и вы можете использовать числа или символы, чтобы найти ответ на задачу.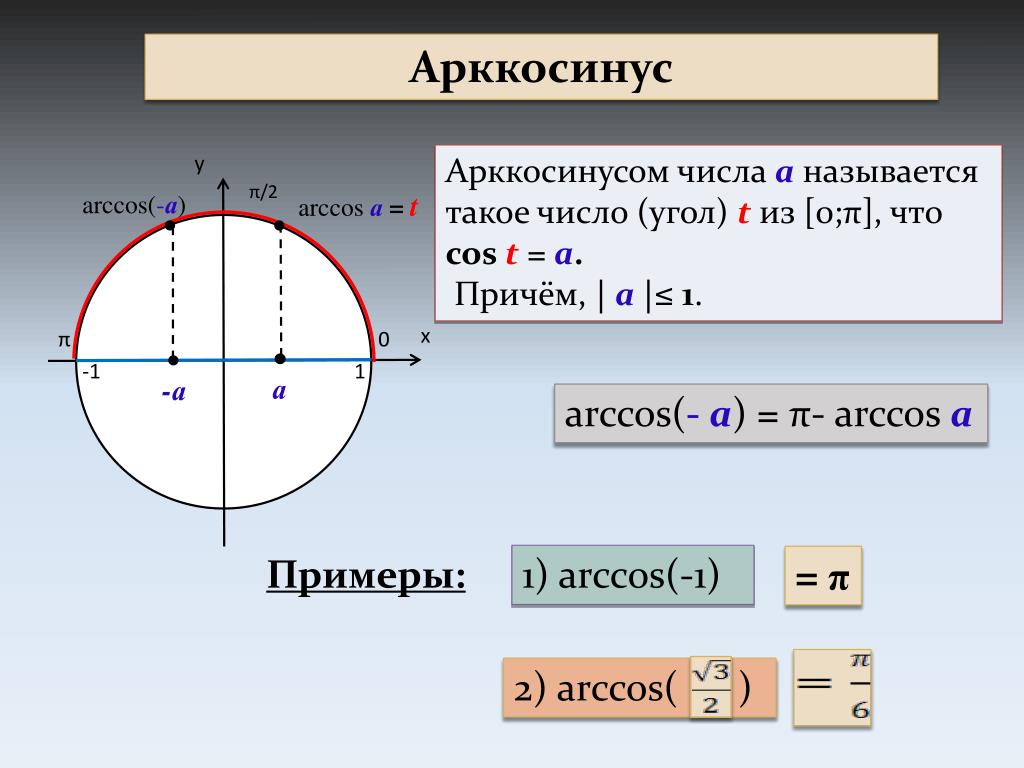 Он использует простую формулу, которая применяет косинус к каждой части уравнения. Некоторым людям проще найти решение с помощью рисунка треугольника, чем с помощью уравнений.
Он использует простую формулу, которая применяет косинус к каждой части уравнения. Некоторым людям проще найти решение с помощью рисунка треугольника, чем с помощью уравнений.
Производная Arccos используется в тригонометрии. Это обратная функция, и вы можете манипулировать ею с помощью чисел или символов. Есть несколько терминов, которые вам необходимо знать при работе с Arccos, включая радианы.
Arccos означает арккосинус. Вы также можете работать с арксинусом или арксинусом при работе с задачами тригонометрии.
Результаты для производной Arccos записываются в радианах. Решение проблемы, связанной с Arccos, в первую очередь требует знания радианов.
Обзор радиановИзображение от Pixabay
Радианы используются для измерения углов. Угол в один радиан стягивает или образует угол. В определенной точке конечности представляют собой прямые линии, которые соединяются в этой конкретной точке. Когда два луча проходят через конечные точки дуги, угол стягивается.
В определенной точке конечности представляют собой прямые линии, которые соединяются в этой конкретной точке. Когда два луча проходят через конечные точки дуги, угол стягивается.
Радиан имеет угол в один радиан, вытянутый из центра единичного круга. Радиан создает длину дуги, равную 1. Следовательно, мы можем определить, что полный угол измеряет 2pi радиан. Угол содержит 360 градусов на каждые 2 пи радиана, что эквивалентно 57,29577951 градусу на радиан или 180 градусам пи.
Прямой угол равен пи/2 радианам. Прямой угол измеряется в пи радианах. Радианы позволяют легко записывать интегралы и производные, например, d/(dx)six равно cosx, когда x измеряется в радианах.
Разница между геометрией и тригонометриейИзображение от Pixabay
Три раздела математики — это алгебра, арифметика и геометрия. Геометрия — это изучение размеров, свойств и форм пространств трехмерных и двумерных объектов. Евклида, отца геометрии, часто упоминают в связи с теоремами и постулатами о поле.
Евклида, отца геометрии, часто упоминают в связи с теоремами и постулатами о поле.
Геометрия представляет собой комбинацию греческих терминов Geo (земля) и Metron (мера). В своих исследованиях вы столкнетесь с твердотельной, сферической и плоской геометрией.
Сферическая геометрия — это изучение трехмерных объектов, таких как сферические многоугольники и сферические треугольники. Плоская геометрия содержит уроки о двухмерных объектах, таких как точки, кривые, линии и плоскости, включая многоугольники, окружности и треугольники. Объемная геометрия фокусируется на сферах, призмах, кубах, пирамидах и других трехмерных объектах.
Евклидова геометрия — это изучение плоских поверхностей, и это всего лишь один из разделов геометрии. Риманова геометрия, изучение криволинейных поверхностей, является еще одним важным разделом геометрии.
Тригонометрия — раздел геометрии.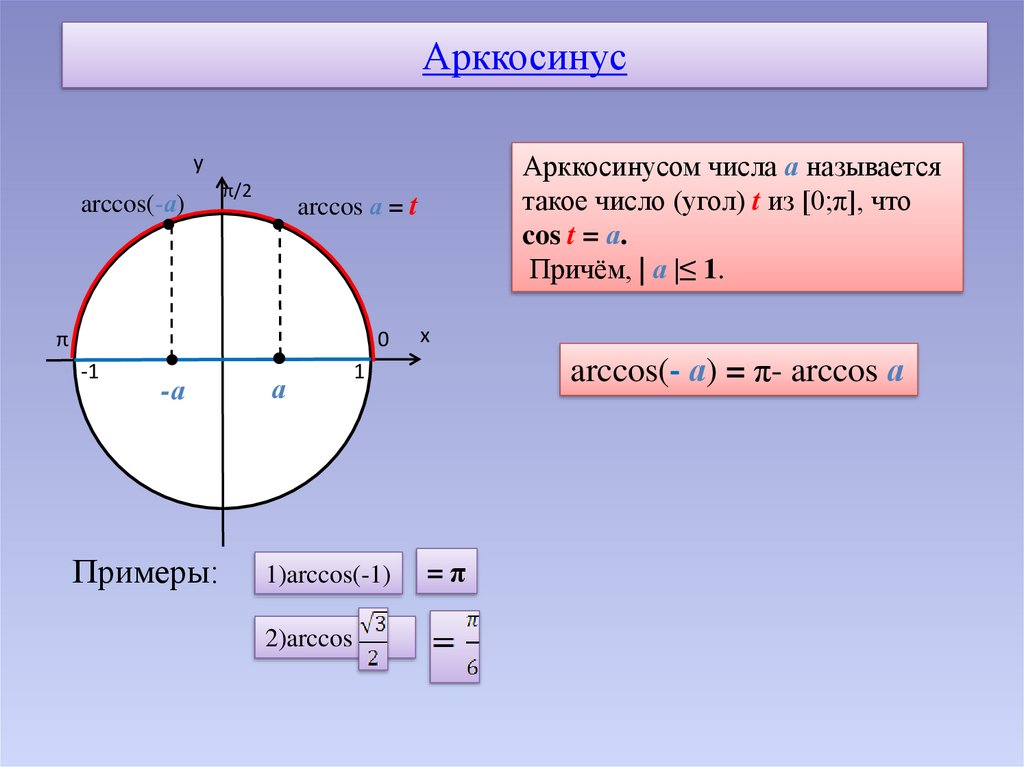 Поле возникло примерно в 150 г. до н.э. когда математик по имени Гиппарх использовал синус, чтобы составить таблицу триггеров.
Поле возникло примерно в 150 г. до н.э. когда математик по имени Гиппарх использовал синус, чтобы составить таблицу триггеров.
Тригонометрия имеет дело с треугольниками, их длинами и углами. Вы также можете использовать тригонометрию для изучения волн и колебаний. Вы узнаете, как длины сторон прямоугольных треугольников относятся друг к другу. Основные соотношения между треугольниками и их сторонами называются синусом, тангенсом и косинусом.
Если у вас прямоугольный треугольник, самое длинное основание называется гипотенузой. Сторона перед углом — это его противоположная сторона, а прилежащая сторона — это сторона за этим углом. Соотношение для прямоугольного треугольника тогда равно sin A, или противоположности гипотенузы, cos A, прилежащей стороне гипотенузы, и tan A, противоположной/прилежащей стороне.
Второстепенные соотношения в тригонометрии:
Секанс
Котангенс
Косеканс
Изображение от Pixabay
Эти измерения представляют собой соответствующие размеры синуса, косинуса и тангенса.
Сферическая тригонометрия, которая работает с треугольниками в трехмерных сценариях и используется в навигации и астрономии.
Тригонометрия помогала древним мореплавателям ориентироваться в морях. Сегодня тригонометрия имеет множество применений помимо уроков математики.
Океанографы используют тригонометрию для определения высоты океанских приливов или измерения морских животных. Тригонометрию можно использовать для постройки кораблей и помощи в навигации. Это математическое поле также помогает криминалистам определять траекторию пуль и других снарядов.
Археологи делят места раскопок для работы с помощью тригонометрии. Бортинженеры используют тригонометрию для определения наилучшего курса полета самолета. Тригонометрия помогает заполнить «третью сторону» уравнения ветра, скорости и направления полета, чтобы убедиться, что самолет движется в правильном направлении.
Изображение Pixabay
В тригонометрии Arccos означает косинус в отрицательной первой степени (z) или арккосинус комплексного числа, представленного (z). Вы будете считать, что в этой задаче используется обратная тригонометрическая функция, и запишите два тождества:
Cos (cos (cos в отрицательной степени 1 st (x)) равно x, тогда cos в отрицательной 1 st (степень (cos (х)) равно х.
Вам нужно решить, какую формулу использовать. Вы должны использовать первую формулу из-за цепного правила. Цепное правило позволяет найти производную для члена cos−1
(x) проще, чем с помощью первой формулы. Просто формула для cos (y) равна x. Теперь у вас есть неявная формула для решения задачи и определения y.
Используйте неявное дифференцирование, чтобы найти ответ для y’.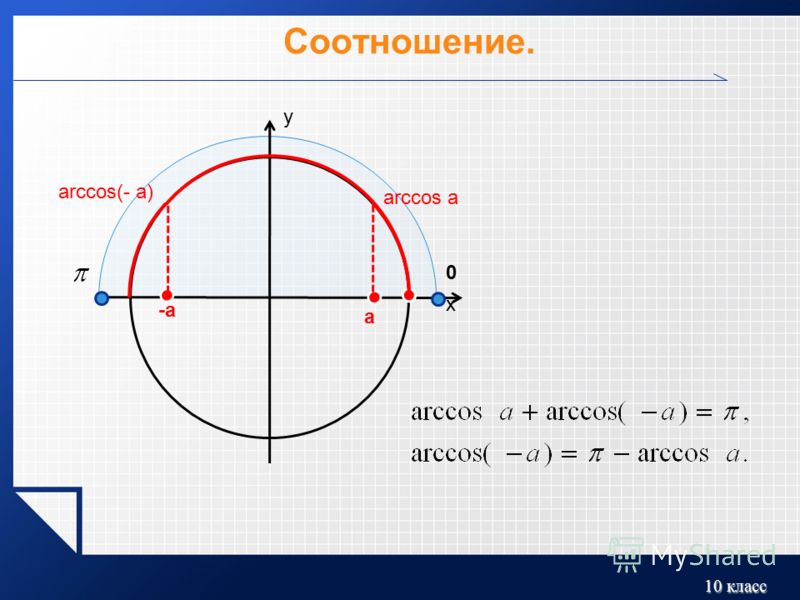
(cos(y))0 = (x), за которым следует y’ (− sin(y)) = 1 и y’ равно отрицательной 1 относительно sin(y), тогда y’ равно отрицательной 1 относительно sin(cos для минус 1 -я мощность (х)).
Формула, написанная выше, является отличным инструментом, но есть еще лучший способ записать ее, используя геометрию вместо алгебры. Кос имеет угол и число между отрицательными 1 и 1, косинус отрицательный также дает угол и имеет число между отрицательными 1 и 1.
Теперь определим θ равным косинусу минус 1(х), чтобы показать угол косинус отрицательный 1. Следовательно, x равно cos (θ) согласно обратной функции. Вы также можете использовать cos с обеими сторонами функции.
Рисование треугольника также может помочь вам найти ответ на эту проблему. Нарисуйте треугольник с точками ABC, и угол θ будет меньше угла C. Cos (θ) равен ACBC в геометрии, а cos (θ) также равен x.
Предположим, что BC равно 1, а AC равно x. Вы можете выбрать любую идентичность в приведенных выше значениях, но самые очевидные из них упрощают математику.
В примере с треугольником sin(θ) = AB над BC. Используйте теорему Пифагора, чтобы вычислить ответ для sin(cos−1(x)), который равен sin(θ).
Вот решение по теореме Пифагора:
BC в квадрате равно AB в квадрате плюс AC в квадрате, за которым следует AB в квадрате равно BC в квадрате минус AC в квадрате. Следовательно, AB в квадрате равен единице минус x в квадрате, а AB равен квадратному корню из 1 минус x в квадрате.
Вычисленное выше уравнение правильно отвечает на вопрос. Sin(cos отрицательное 1 (x)) равно sin(θ) равно AB над BC равно AB равно квадратному корню из 1 минус x в квадрате. Дополните ответ
Пример #2Изображение от Pixabay
Эта задача демонстрирует, как определить производную от Arccos x и Arcsin x.
Используемое вами уравнение: d относительно dx (arcsin x плюс arccos x) равно нулю. Обратите внимание, что arcsin x плюс arccos x равняется пи на 2. Это уравнение можно объяснить следующими вычислениями:
Если arcsin x равно нулю, то x равно sinθ равно cos(pi на 2 минус θ), тогда arccos x равно пи на 2 минус θ равно pi на 2 минус arcsin x; следовательно, arcsin x плюс arccos x равно pi на 2.
Пример #3Изображение от Pixabay
Производная, которую вы найдете для arccos x, будет отрицательной производной arcsin x. Этот статус производной выполняется для инверсии каждой пары кофункций.
Те же формулы применимы к аналогичным задачам тригонометрии. Производная Arccot x является отрицательной производной arctg x. Производная угловых секунд является отрицательной производной угловых секунд x.
Переменная y равна угловой секунде x, представьте, что тангенс y равен плюс-минус квадратному корню из x во второй степени минус один.
Начните решать задачу, используя y равно arcsec x, что показывает, что sec y равно x. Теперь используйте пифагорейское тождество b, чтобы определить следующий шаг.
Tan y равно плюс минус квадратный корень из секунды в квадрате y минус 1 равно плюс минус квадратный корень из x в квадрате минус 1. Производная Y равна arcsin x.
Тогда уравнение d над dx arcsin x равно единице на квадратный корень из единицы минус x в квадрате. Докажите это, посмотрев на y равно arcsin x, что означает sin y equals x. Нарисуйте производную x с помощью следующего уравнения:
Cos y, за которым следует dy над dx равно 1, затем dy над dx равно 1 больше cos y’, затем dy над dx равно 1 больше квадратного корня из 1 минус x в квадрате ‘.
Альтернативной теоремой для этого может быть d arcsin x над dx равно 1 над din sin y над dy равно 1 над cos y равно 1 над квадратным корнем из 1 минус x в квадрате.
Функции Arccos XАрккосинус x представляет собой функцию арккосинуса переменной x, когда отрицательная 1 меньше x, а x меньше 1. Если косинус y равен x, арккосинус переменной x равен функции арккосинуса x, которая равна y. Уравнение для этой функции читается как arccos x равно cos арккосинусу x равно y.
Источник изображения: Pixabay
Уравнение записывается как arccos 1 равно cos, за которым следует отрицательный символ 1, обозначающий функцию арккосинуса в этой задаче.
Следовательно, arccos 1 равен cos-отрицательной 1 (обратная функция), 1 равен нулю, а Rad равен нулю градусов.
->
Acos Python
Python — это продвинутый, но простой язык программирования, на котором даже новички могут легко программировать. Его стандартная математическая библиотека содержит несколько полезных встроенных функций, помогающих решать все математические задачи. Некоторые из встроенных функций математической библиотеки: cos(), sin(), log(), Degree(), asin(), acos() и т. д. В этом руководстве будет обсуждаться функция acos(). Функция acos в математике возвращает арккосинус заданного числа в радианах, который обычно называют арккосинусом числа.
Его стандартная математическая библиотека содержит несколько полезных встроенных функций, помогающих решать все математические задачи. Некоторые из встроенных функций математической библиотеки: cos(), sin(), log(), Degree(), asin(), acos() и т. д. В этом руководстве будет обсуждаться функция acos(). Функция acos в математике возвращает арккосинус заданного числа в радианах, который обычно называют арккосинусом числа.
Он принимает один номер параметра и возвращает его арккосинус в радианах. В общей математике acos = cos-1, что означает, что acos числа равен арккосинусу этого числа. Давайте изучим этот учебник, чтобы изучить функцию метода acos().
Функция Acos()
Функция acos() — это встроенная функция, предоставляемая стандартной математической библиотекой Python. Функция acos() принимает число, либо целое, либо число с плавающей запятой, в качестве параметра и возвращает значение арккосинуса в радианах. Домен функции acos находится в диапазоне от -1 до 1. Компилятор выдаст ошибку, если вы укажете число вне этого диапазона.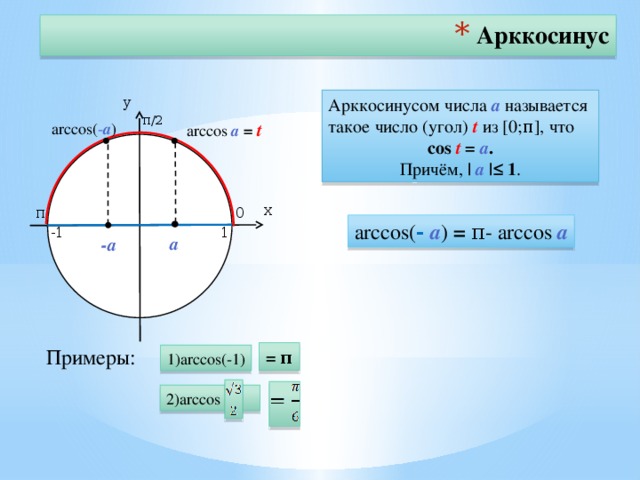 Вот синтаксис функции acos():
Вот синтаксис функции acos():
Параметр a, для которого необходимо найти значения acos(), является обязательным параметром, и если его пропустить, компилятор выдаст ошибку. Более того, это должно быть число от -1 до 1. Если вы укажете любой другой тип данных, например «строку», компилятор выдаст ошибку TypeError. Функция acos() вернет число с плавающей запятой, представляющее значение acos() вмененного параметра в радианах.
Обратите внимание, что acos() не является независимой функцией. Чтобы использовать функцию acos(), перед вызовом функции acos() необходимо убедиться, что математическая библиотека импортирована в программу. Теперь давайте рассмотрим несколько примеров, чтобы изучить использование функции acos() в программе Python.
Пример 1:
В этом примере мы рассмотрим использование функции acos(), предоставляемой стандартной математической библиотекой Python. Мы предоставим различные типы чисел функции acos() и посмотрим, какие результаты мы получим. Здесь мы просто задаем числа от -1 до 1 в качестве входного параметра, чтобы увидеть их значение арккосинуса. В дальнейших примерах мы проверим некоторые числа, выходящие за пределы допустимого диапазона, а также некоторые недопустимые входные данные. Итак, начнем с первого примера:
Здесь мы просто задаем числа от -1 до 1 в качестве входного параметра, чтобы увидеть их значение арккосинуса. В дальнейших примерах мы проверим некоторые числа, выходящие за пределы допустимого диапазона, а также некоторые недопустимые входные данные. Итак, начнем с первого примера:
import math
print(«Значение арккосинуса -0,45 = «, math.acos(-0,45))
print(«Значение арккосинуса 0 = «, math.acos(0))
print(«Значение арккосинуса 0,45 = «,math.acos(0,45))
Как видите, мы только что предоставили действительные числа в качестве входных параметров, а функция acos() вернула acos () значение для каждого числа. См. вывод ниже.
Пример 2:
В предыдущем примере мы просто задали допустимые числа в допустимом диапазоне функции acos(). Теперь мы собираемся протестировать функцию acos(), предоставив ей числа за пределами допустимого диапазона. См. код ниже:
import math
print(«Значение арккосинуса -5 равно = «, math. acos(-5))
acos(-5))
print(«Значение арккосинуса 9 равно = «, math.acos(9))
print(«Значение арккосинуса 45 равно = «,math.acos(45))
Как видите, все числа находятся за пределами допустимого диапазона функции acos(). Компилятор должен вызвать ValueError. Давайте посмотрим на вывод ниже:
Обратите внимание, что компилятор выдал ошибку ValueError для каждого предоставленного параметра, так как каждое число находится вне диапазона функции acos().
Пример 3:
Теперь давайте дадим неверный ввод в функцию acos(), чтобы посмотреть, какую ошибку она вызовет. См. приведенный ниже код:
import math
print(«Значение арккосинуса ‘2ab’ равно = «, math.acos(2ab))
Результат будет следующим:
Как вы Как видите, компилятор выдал ошибку SyntaxError, так как формат строки не поддерживается функцией acos(). Функция acos() работает только с числами с плавающей запятой и целыми числами, которые также находятся в диапазоне от -1 до 1.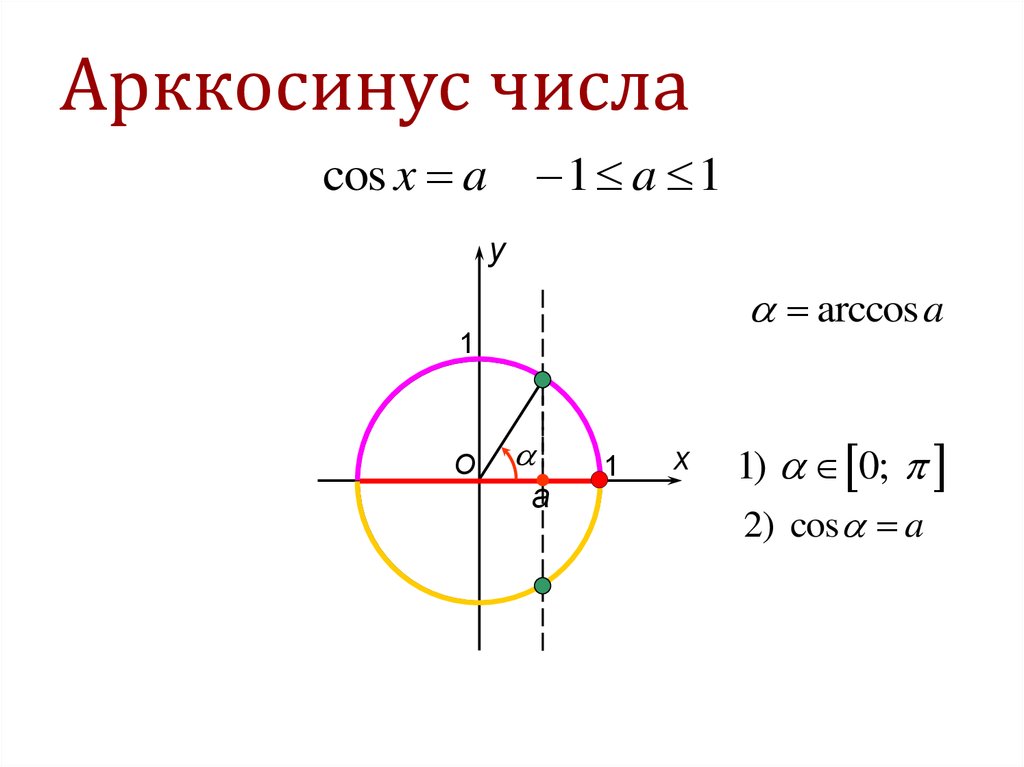 Любое другое число или другой тип данных, предоставленный в качестве входного параметра, приведет к синтаксической ошибке.
Любое другое число или другой тип данных, предоставленный в качестве входного параметра, приведет к синтаксической ошибке.
Пример 4:
Функция acos() возвращает значение заданного параметра acos() в радианном формате, которое отличается от того, которое мы видим в калькуляторе. Калькулятор возвращает значение в виде степени, однако python acos() возвращает значение в форме радиана, поэтому оба результата не совпадают друг с другом. Теперь давайте преобразуем значение радиана функции acos() Python в формат степени, используя встроенную функцию Degrees() стандартной библиотеки Python.
import math
print(«Значение арккосинуса -0,45 равно = «, math.степени(math.acos(-0,45)))
print(«Значение арккосинуса 0 равно = «, math. Degrees(math.acos(0)))
print(«Значение арккосинуса 0,45 = «,math.degrees(math.acos(0,45)))
См. вывод ниже:
Теперь, если вы сравните этот вывод с выводом первого примера, вы увидите разницу.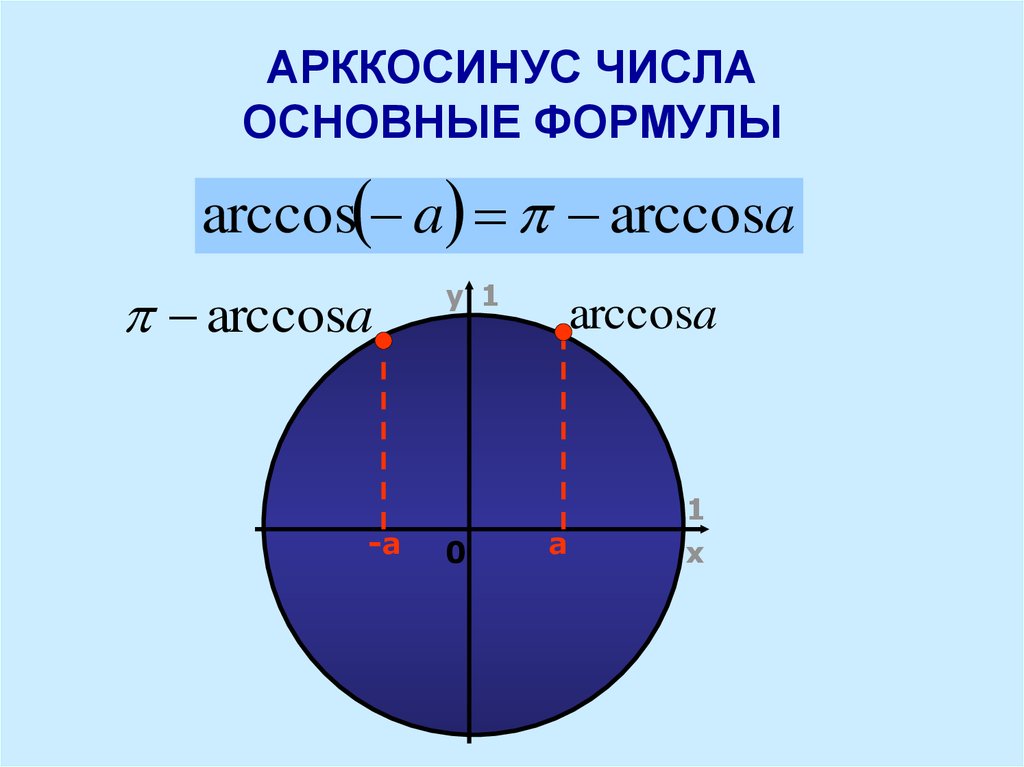 Если вы используете калькулятор для расчета acos(), вы получите тот же результат, что и в этом примере.
Если вы используете калькулятор для расчета acos(), вы получите тот же результат, что и в этом примере.
Пример 5:
Теперь, когда мы поняли, как работает acos(), давайте рассмотрим сложный практический пример, чтобы увидеть, как это работает в деталях. См. код ниже:
import math, numpy как np, matplotlib.pyplot как plt
input_array = np.linspace(-(1/4.5 * np.pi), 1/4.5 * np.pi, 10)
output_array = []
for i in range(len(input_array)):
input_array[i] = round(input_array[i],2)
output_array[input_array.append(round(math.acos) я]),2))
i = i + 1
print(«Входной массив: \n», input_array)
print(«\nВыходной массив : \n», output_array)
print(«\n Построенные площади: :\n»)
plt.plot(input_array, output_array, «go-«)
plt.title(«math.acos()»)
plt.xlabel(«X»)
plt.ylabel («Y»)
plt.show()
В этом примере мы автоматически сгенерировали массив из 10 элементов для создания строки.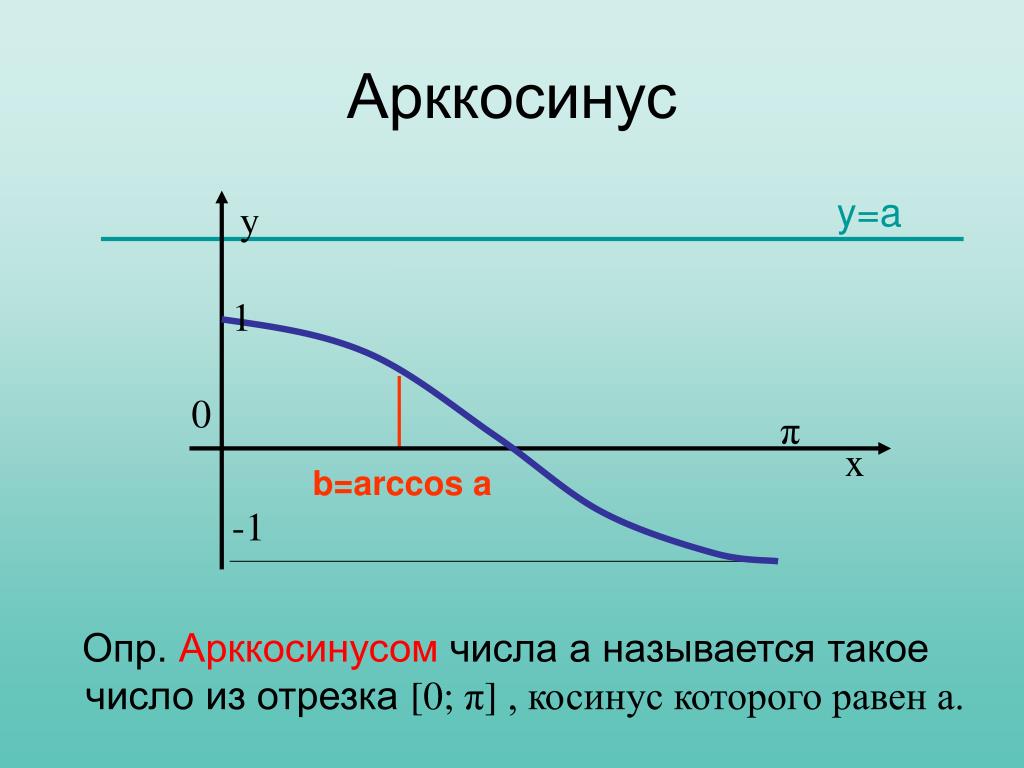 Для каждого элемента входного массива мы вычислили его значение acos() и сохранили его в другом массиве. После этого мы построили линию значений, хранящихся во втором массиве, с помощью функции plt стандартной библиотеки Python matplotlib.pyplot. См. ниже:
Для каждого элемента входного массива мы вычислили его значение acos() и сохранили его в другом массиве. После этого мы построили линию значений, хранящихся во втором массиве, с помощью функции plt стандартной библиотеки Python matplotlib.pyplot. См. ниже:
Обратите внимание, что мы усекли вывод до двух знаков после запятой, используя функцию округления. Элементы, хранящиеся как в input_array, так и в output_array, округляются до двух знаков после запятой с помощью функции round(array_name, no_of_decimal_places). После этого мы использовали функцию plt.plot, чтобы построить и нарисовать линию на графике.
Заключение
Функция acos(), предоставляемая стандартной математической библиотекой Python, принимает число от -1 до 1 в качестве допустимого ввода, вычисляет его значение acos() и возвращает результат в радианном формате. Функция acos() не является независимой функцией, поэтому для ее использования необходимо импортировать математическую библиотеку в программу python.
19.1: Функции arcsin, arccos и arctan
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49073
- Томас Тредлер и Холли Карли
- CUNY Нью-Йоркский технологический колледж через Нью-Йоркский городской технологический колледж в CUNY Academic Works
Обратные тригонометрические функции — это обратные функции функций \(y=\sin x\), \(y=\cos x\) и \(y=\tan x\), ограниченных соответствующими областями. В этом разделе мы даем точное определение этих функций.
Функция арктангенса
Начнем с обратной функции тангенса \(y=\tan(x)\). Напомним, что график \(y=\tan(x)\) следующий:
Имеет вертикальные асимптоты в точках \(x=\pm\dfrac{\pi}{2}, \pm\dfrac{3\pi}{2}, \pm\dfrac{5\pi}{2} , \точки\). Далее мы определяем функцию обратного синуса. Для этого снова сначала вспомним график функции \(y=\sin(x)\) и заметим, что это тоже , а не взаимно однозначно. Однако при ограничении синуса областью \(\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\) ограниченная функция равна один к одному. Кроме того, обратите внимание, что при ограничении домена до \(\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\) диапазон равен \([-1,1 ]\), и поэтому мы не можем распространить это на большую область таким образом, чтобы функция оставалась взаимно однозначной. Наконец, мы определяем арккосинус. Вспомните график \(y=\cos(x)\) и снова заметьте, что функция , а не однозначно. В этом случае способ ограничить косинус однозначной функцией не так ясен, как в предыдущих случаях для синуса и тангенса. По соглашению косинус ограничен областью определения \([0,\pi]\). Это обеспечивает функцию, которая является взаимно однозначной, которая используется для определения арккосинуса. Обратите внимание, что \(y=\tan(x)\) не является взаимно однозначной функцией в смысле определения [DEF:1-to-1] на стр. . (Например, горизонтальная линия \(y=1\) пересекает график в точках \(x=\dfrac{\pi}{4}\), \(x=\dfrac{\pi}{4}\pm\ pi\), \(x=\dfrac{\pi}{4}\pm2\pi\) и т. д.) Однако, когда мы ограничиваем функцию областью \(D=(\dfrac{-\pi}{ 2},\dfrac{\pi}{2})\) ограниченная функция равна 9{-1}(x)\)
Обратите внимание, что \(y=\tan(x)\) не является взаимно однозначной функцией в смысле определения [DEF:1-to-1] на стр. . (Например, горизонтальная линия \(y=1\) пересекает график в точках \(x=\dfrac{\pi}{4}\), \(x=\dfrac{\pi}{4}\pm\ pi\), \(x=\dfrac{\pi}{4}\pm2\pi\) и т. д.) Однако, когда мы ограничиваем функцию областью \(D=(\dfrac{-\pi}{ 2},\dfrac{\pi}{2})\) ограниченная функция равна 9{-1}(x)\) {-1}(x)} \номер\] 9{-1}(x)\)
{-1}(x)} \номер\] 9{-1}(x)\) Определение: арккосинус или арккосинус 9{-1}(17) \text{ is undefined} \nonumber \]
Другие входные значения можно получить с помощью калькулятора, нажав клавишу \(\boxed {\text{2nd}}\)\(\boxed {\ текст{cos}}\) ключи. Например, мы получаем следующие значения функции (здесь с использованием измерения в радианах).
Эта страница с заголовком 19.1: Функции arcsin, arccos и arctan используются совместно в соответствии с лицензией CC BY-NC-SA 4.0, авторами, ремикшированием и/или кураторами которой являются Томас Тредлер и Холли Карли (Нью-Йоркский городской колледж технологии в CUNY Academic Works) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.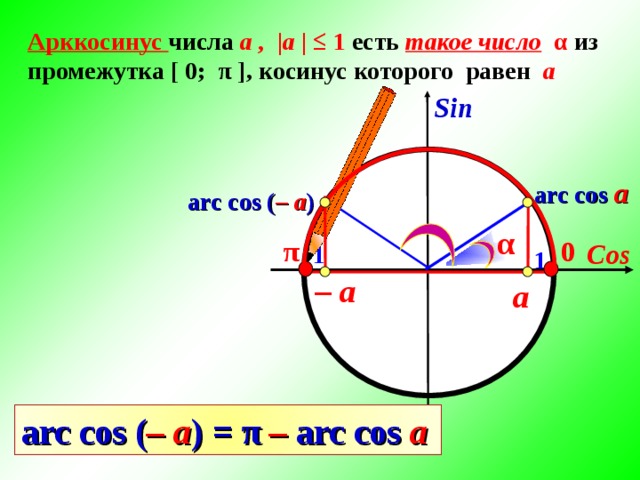

 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.