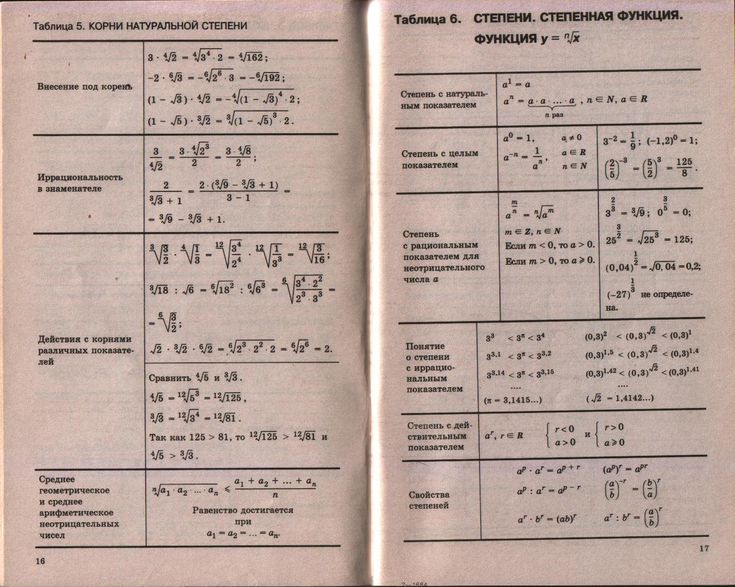
Как решать примеры со степенями и корнями. Квадратный корень
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень . Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней .
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат.
 То из них, квадрат которого равен исходному числу, и будет корнем.
То из них, квадрат которого равен исходному числу, и будет корнем.
Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
…
90 2 = 8100;
100 2 = 10 000.
Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]
То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:
[Подпись к рисунку]
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа .
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
2 2 = 4;
8 2 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
[Подпись к рисунку]
Для начала выясним, между какими числами лежит число 576:
400 20 2
Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
Осталось возвести каждое число в квадрат и сравнить с исходным:
24 2 = (20 + 4) 2 = 576
Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.
Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
900 30 2
Смотрим на последнюю цифру:
1369 → 9;
33; 37.
Возводим в квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
2500 50 2
Смотрим на последнюю цифру:
2704 → 4;
52; 58.
Возводим в квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]
Ограничиваем число:
3600 60 2
Смотрим на последнюю цифру:
4225 → 5;
65.
Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
Но давайте все-таки возведем его в квадрат и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются :
a m · a n = a m + n .
2. При делении степеней с
одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
( abc … ) n = a n · b n · c n …
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
( a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
(a m ) n = a m n .
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень
из отношения равен отношению корней делимого и делителя:
Корень
из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т
еперь
формула a
m : a
n = a
m
—
n может быть использована не
только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р . a 4 : a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а :
О выражениях, не имеющих смысла. Есть несколько таких выражений. любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно
определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
Случай 3.
0 0 — любое число.
Действительно,
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
(Почему?).
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
Нашем случае x > 0 , ответом является x > 0 ;
3) при x x / x = 1, т. e . –1 = 1, следовательно,
В этом случае нет решения.
Таким образом, x > 0.
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 9 2 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676 .
Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26 .
Еще пример: √6889 .
Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.
Проверяем: 83 2 = 6889.
Ответ: √6889 = 83 .
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025 .
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Еще пример: √20736 . Разложим число 20736 на множители:
Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах.
Вычислите √279841 .
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример . Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается .
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.
Правила сложения и вычитания квадратных корней
Определение 1
Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.
Пример 1
Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Действия с корнями: основы
Пример 2
6 50 — 2 8 + 5 12
Алгоритм действия:
- Упростить подкоренное выражение . Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
- Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
- После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
- У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня.
 Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Совет 1
Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.
Пример 3
Давайте попробуем решить данный пример:
6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .
2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .
5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
Результат упрощения: 30 2 — 4 2 + 10 3
30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
Пример 4
- Упрощаем (45) . Раскладываем 45 на множители: (45) = (9 × 5) ;
- Выносим 3 из-под корня (9 = 3) : 45 = 3 5 ;
- Складываем множители у корней: 3 5 + 4 5 = 7 5 .
Пример 5
6 40 — 3 10 + 5:
- Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 (4 × 10) ;
- Выносим 2 из-под корня (4 = 2) : 6 40 = 6 (4 × 10) = (6 × 2) 10 ;
- Перемножаем множители, которые стоят перед корнем: 12 10 ;
- Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12 — 3) 10 = 9 10 + 5 .
Пример 6
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т. д.) и записываем результат:
д.) и записываем результат:
(9 — 4) 5 — 2 3 = 5 5 — 2 3 .
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3 + (2 x) 1 / 2 .
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т. п.
п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?
Таблица квадратов целых чисел от 0
до 99
включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0
до 99
. Для примера выберем строку 8
десятков и столбец 3
единицы, этим мы зафиксировали число 83
. Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0
до 99
. На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
На пересечении выбранной нами строки 8
десятков и столбца 3
единицы находится ячейка с числом 6 889
, которое является квадратом числа 83
.
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683
. Находим число 19 683
в таблице кубов, из нее находим, что это число является кубом числа 27
, следовательно, .
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Пусть из натурального числа a
извлекается корень n
-ой степени, и его значение равно b
. В этом случае верно равенство a=b n
. Число b
как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m
в виде p 1 ·p 2 ·…·p m
, а подкоренное число a
в этом случае представляется как (p 1 ·p 2 ·…·p m) n
. Так как разложение числа на простые множители единственно, то разложение подкоренного числа a
на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n
, что дает возможность вычислить значение корня как .
Так как разложение числа на простые множители единственно, то разложение подкоренного числа a
на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n
, что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3
. На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2
. Следовательно, .
Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q
. Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169 .
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000
. Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13=
(2·3·13) 3 =78 3
и 1 000=10 3
, то и . Осталось лишь завершить вычисления .
Так как 474 552=2·2·2·3·3·3·13·13·13=
(2·3·13) 3 =78 3
и 1 000=10 3
, то и . Осталось лишь завершить вычисления .
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a и нечетного показателя корня 2·n−1 справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Приведем краткую запись решения: .
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n
числа 0, 10, 100, …
до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n
на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9
. При этом параллельно вычисляются n
-ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9
.
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100
и т.д. пока не получим число, превосходящее 2 151,186
. Имеем 0 3 =02 151,186
, таким образом, старшим разрядом является разряд десятков.
Для этого возводим в куб числа 0, 10, 100
и т.д. пока не получим число, превосходящее 2 151,186
. Имеем 0 3 =02 151,186
, таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.
 Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений. - Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Что сумма корней. Действие с корнями: сложение и вычитание
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.
Что такое математический корень?
Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х 2 =у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.
По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16 .
Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.
Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.

- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.
В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64. Учитывая это, выражение будет записано так:
√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=4 2 , 9=3 2 , 64=8 2 . Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. После вынесения множителей из-под знака корня имеем:
5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).
На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .
Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.
Шаг 1. Извлечение квадратных корней
Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа 2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.
Шаг 2. Вынесение множителя числа из-под корня
Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .
Для примера возьмём выражение √24 + √54 .
Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .
В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .
Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .
Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.
Шаг 3. Сокращение знаменателя
Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b) .
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .
Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .
Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .
Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .
Пример сложного сокращения знаменателя
Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.
Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .
Получаем:
12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.
Шаг 4. Вычисление приблизительного значения на калькуляторе
Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.
Пример вычисления приблизительного значения
Необходимо вычислить приблизительное значение данного выражения √7 + √5 .
В итоге получаем:
√7 + √5 ≈ 2,65 + 2,24 = 4,89 .
Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.
Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.
Формулы корней. Свойства квадратных корней.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Факт 1.
\(\bullet\)
Возьмем некоторое неотрицательное число \(a\)
(то есть \(a\geqslant 0\)
). Тогда (арифметическим) квадратным корнем из числа \(a\)
называется такое неотрицательное число \(b\)
, при возведении которого в квадрат мы получим число \(a\)
: \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\]
Из определения следует, что \(a\geqslant 0, b\geqslant 0\)
. 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\)
или \(\sqrt b\)
при сложении \(\sqrt
a+\sqrt b\)
найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\)
мы можем найти \(\sqrt{49}\)
– это \(7\)
, а вот \(\sqrt
2\)
никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\)
. Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\)
Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\]
(при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\)
;
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\)
;
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\)
. \(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\)
. Так как \(44100:100=441\)
, то \(44100=100\cdot 441\)
. По признаку делимости число \(441\)
делится на \(9\)
(так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\)
, то есть \(441=9\cdot 49\)
.
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\]
Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\)
Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\)
(сокращенная запись от выражения \(5\cdot
\sqrt2\)
). Так как \(5=\sqrt{25}\)
, то \
Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\)
,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\)
. 2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\)
и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\)
(число “пи”, приблизительно равное \(3,14\)
), \(e\)
(это число называют числом Эйлера, приблизительно оно равно \(2,7\)
) и т.д.
\(\bullet\)
Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\)
.
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой. 2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\)
.
2=168\cdot 168=28224\)
.
Следовательно, \(\sqrt{28224}=168\)
. Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.

- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Содержимое:
Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Шаги
Часть 1 Постигаем основы
- 1 (выражение под знаком корня). Для этого разложите подкоренное число на два множителя, один из которых является квадратным числом (число, из которого можно извлечь целый корень, например, 25 или 9).
 После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Здесь вы раскладываете 50 на множители 25 и 2; затем из 25 извлекаете корень, равный 5, и 5 выносите из-под корня. Затем 5 умножаете на 6 (множитель у корня) и получаете 30√2.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Здесь вы раскладываете 8 на множители 4 и 2; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 2 (множитель у корня) и получаете 4√2.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Здесь вы раскладываете 12 на множители 4 и 3; затем из 4 извлекаете корень, равный 2, и 2 выносите из-под корня. Затем 2 умножаете на 5 (множитель у корня) и получаете 10√3.

- 2 Подчеркните корни, подкоренные выражения которых одинаковы. В нашем примере упрощенное выражение имеет вид: 30√2 — 4√2 + 10√3. В нем вы должны подчеркнуть первый и второй члены (30√2 и 4√2 ), так как у них одинаковое подкоренное число 2. Только такие корни вы можете складывать и вычитать.
- 3 Если вам дано выражение с большим количеством членов, многие из которых имеют одинаковые подкоренные выражения, используйте одинарное, двойное, тройное подчеркивание для обозначения таких членов, чтобы облегчить решение этого выражения.
- 4
У корней, подкоренные выражения которых одинаковы, сложите или вычтите множители, стоящие перед знаком корня, а подкоренное выражение оставьте прежним (не складывайте и не вычитайте подкоренные числа!
). Идея в том, чтобы показать, сколько всего корней с определенным подкоренным выражением содержится в данном выражении.
- 30√2 — 4√2 + 10√3 =
- (30 — 4)√2 + 10√3 =
- 26√2 + 10√3
Часть 2 Практикуемся на примерах
- 1 Пример 1: √(45) + 4√5.

- Упростите √(45). Разложите 45 на множители: √(45) = √(9 x 5).
- Вынесите 3 из-под корня (√9 = 3): √(45) = 3√5.
- Теперь сложите множители у корней: 3√5 + 4√5 = 7√5
- 2 Пример 2: 6√(40) — 3√(10) + √5.
- Упростите 6√(40). Разложите 40 на множители: 6√(40) = 6√(4 x 10).
- Вынесите 2 из-под корня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
- Перемножьте множители перед корнем и получите 12√10.
- Теперь выражение можно записать в виде 12√10 — 3√(10) + √5. Так как у первых двух членов одинаковые подкоренные числа, вы можете вычесть второй член из первого, а первый оставить без изменений.
- Вы получите: (12-3)√10 + √5 = 9√10 + √5.
- 3 Пример 3. 9√5 -2√3 — 4√5. Здесь ни одно из подкоренных выражений нельзя разложить на множители, поэтому упростить это выражение не получится. Вы можете вычесть третий член из первого (так как у них одинаковые подкоренные числа), а второй член оставить без изменений.
 Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3. - 4 Пример 4. √9 + √4 — 3√2.
- √9 = √(3 х 3) = 3.
- √4 = √(2 х 2) = 2.
- Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
- Окончательный ответ: 5 — 3√2.
- 5 Пример 5. Решите выражение, содержащее корни и дроби. Вы можете складывать и вычислять только те дроби, у которых общий (одинаковый) знаменатель. Дано выражение (√2)/4 + (√2)/2.
- Найдите наименьший общий знаменатель этих дробей. Это число, которое делится нацело на каждый знаменатель. В нашем примере на 4 и на 2 делится число 4.
- Теперь вторую дробь умножьте на 2/2 (чтобы привести ее к общему знаменателю; первая дробь уже приведена к нему): (√2)/2 х 2/2 = (2√2)/4.
- Сложите числители дробей, а знаменатель оставьте прежним: (√2)/4 + (2√2)/4 = (3√2)/4 .
- Перед суммированием или вычитанием корней обязательно упростите (если возможно) подкоренные выражения.
Предупреждения
- Никогда не суммируйте и не вычитайте корни с разными подкоренными выражениями.
 {3} = -125\)
{3} = -125\) - \(\sqrt[2]{-9} = ?\)
- Если степень корня нечетная, а подкоренное выражение отрицательное, можно вынести минус перед корнем, тогда под корнем останется положительное число.
- Произведение чисел а и b в подкоренном выражении можно записать как произведение корней.
- Частное чисел а и b в подкоренном выражении можно записать как частное корней.
- Если в подкоренном выражении находится ещё один корень, от такой вложенности можно избавиться путём перемножения степеней.
- Степень подкоренного выражения можно выносить из под корня, тогда корень будет возводиться в эту степень.
- Если степень корня и степень подкоренного выражения имеют общий делитель k, тогда обе степени можно разделить на k, и значение выражения не изменится.
 {3*\frac{1}{3}} = -6\]
{3*\frac{1}{3}} = -6\]В этом варианте сначала воспользуемся свойством под номером 1, чтобы уйти от знака корня, далее число -216 представим в виде числа в степени 3, после чего перемножаем степени по свойству степеней и получаем -6.
Давайте рассмотрим другой пример.
Пример: \(\sqrt{9+16}\)
\[\large\sqrt{9+16} = \sqrt{25} = 5\]
В данном случае ни одно из свойств корней не подходит, поэтому складываем слагаемые подкоренного выражения и уже после находим результат.
Важно: Нельзя путать сумму в подкоренном выражении с произведением в подкоренном выражении, потому что свойство корней есть только для произведения, то есть \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\), аналогично и с разностью \(\sqrt{a — b} \neq \sqrt{a} — \sqrt{b}\).
Так же есть распространённая ситуация, когда нужно вынести множитель из-под знака корня.
Пример: \(\sqrt[4]{80}\)
\[\large\sqrt[4]{80} = \sqrt[4]{2 * 2 * 2 * 2 * 5} = \sqrt[4]{2^{4}} * \sqrt[4]{5} = 2\sqrt[4]{5}\]
Сначала 80 нужно разложить на множители.
 {2}}\) ?
{2}}\) ?- 144
- 4
- 12
- 8
Ответы: 1. — 2; 2. — 4; 3. — 1; 4. — 3; 5. — 3
Вычитание числа из корня
Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.
Правила сложения и вычитания квадратных корней
Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.
Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Действия с корнями: основы
6 50 — 2 8 + 5 12
- Упростить подкоренное выражение. Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).

- Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
- После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
- У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.
Давайте попробуем решить данный пример:
6 50 = 6 ( 25 × 2 ) = ( 6 × 5 ) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня.
 После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .
После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .2 8 = 2 ( 4 × 2 ) = ( 2 × 2 ) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .
5 12 = 5 ( 4 × 3 ) = ( 5 × 2 ) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
Результат упрощения: 30 2 — 4 2 + 10 3
30 2 — 4 2 + 10 3 = ( 30 — 4 ) 2 + 10 3 = 26 2 + 10 3 .
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
- Упрощаем ( 45 ) . Раскладываем 45 на множители: ( 45 ) = ( 9 × 5 ) ;
- Выносим 3 из-под корня ( 9 = 3 ) : 45 = 3 5 ;
- Складываем множители у корней: 3 5 + 4 5 = 7 5 .

- Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 ( 4 × 10 ) ;
- Выносим 2 из-под корня ( 4 = 2 ) : 6 40 = 6 ( 4 × 10 ) = ( 6 × 2 ) 10 ;
- Перемножаем множители, которые стоят перед корнем: 12 10 ;
- Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: ( 12 — 3 ) 10 = 9 10 + 5 .
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:
( 9 — 4 ) 5 — 2 3 = 5 5 — 2 3 .
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3 + ( 2 x ) 1 / 2 .

- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Складывать и вычитать квадратные корни можно только при условии, что у них одинаковое подкоренное выражение, то есть вы можете сложить или вычесть 2√3 и 4√3, но не 2√3 и 2√5. Вы можете упростить подкоренное выражение, чтобы привести их к корням с одинаковыми подкоренными выражениями (а затем сложить или вычесть их).
Необходимо произвести сложные расчеты, а электронного вычислительного устройства под рукой не оказалось? Воспользуйтесь онлайн программой — калькулятором корней. Она поможет:
- найти квадратные или кубические корни из заданных чисел;
- выполнить математическое действие с дробными степенями.
Число знаков после запятой: √ Что такое квадратный корень
Каждое математическое действие имеет противодействие: сложение→вычитание, умножение→деление, возведение в степень→извлечение корня.

Квадратным корнем из числа a будет число, квадрат которого равен a. Из этого следует ответ на вопрос, как вычислить корень из числа? Нужно подобрать число, которое во второй степени будет равно значению под корнем.
Обычно 2 не пишут над знаком корня. Поскольку это самая маленькая степень, а соответственно если нет числа, то подразумевается показатель 2. Решаем: чтобы вычислить корень квадратный из 16, нужно найти число, при возведении которого во вторую степень получиться 16.
Проводим расчеты вручную
Вычисления методом разложения на простые множители выполняется двумя способами, в зависимости от того, какое подкоренное число:
1.Целое, которое можно разложить на квадратные множители и получить точный ответ.
Квадратные числа — числа, из которых можно извлечь корень без остатка. А множители — числа, которые при перемножении дают исходное число.
8, 25, 36, 49 — квадратные числа, поскольку:
Получается, что квадратные множители — множители, которые являются квадратными числами.

Возьмем 784 и извлечем из него корень.
Раскладываем число на квадратные множители. Число 784 кратно 4, значит первый квадратный множитель — 4 x 4 = 16. Делим 784 на 16 получаем 49 — это тоже квадратное число 7 x 7 = 16. Применим правило Извлекаем корень из каждого квадратного множителя, умножаем результаты и получаем ответ.
Ответ.
2.Неделимое. Его нельзя разложить на квадратные множители.
Такие примеры встречаются чаще, чем с целыми числами. Их решение не будет точным, другими словами целым. Оно будет дробным и приблизительным. Упростить задачу поможет разложение подкоренного числа на квадратный множитель и число, из которого извлечь квадратный корень нельзя.
Раскладываем число 252 на квадратный и обычный множитель. Оцениваем значение корня.  Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки.
Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки.Подкоренное число — 7. Значит ближайшее большее квадратное число будет 8, а меньшее 4. между 2 и 4.
Оцениваем значение Вероятнее √7 ближе к 2. Подбираем таким образом, чтобы при умножении этого числа на само себя получилось 7. 2,7 x 2,7 = 7,2. Не подходит, так как 7,2>7, берем меньшее 2,6 x 2,6 = 6,76. Оставляем, ведь 6,76
7.
Вычисляем корень Как вычислить корень из сложного числа? Тоже методом оценивая значения корня.
При делении в столбик получается максимально точный ответ при извлечении корня.
Возьмите лист бумаги и расчертите его так, чтобы вертикальная линия находилась посередине, а горизонтальная была с ее правой стороны и ниже начала. Разбейте подкоренное число на пары чисел.  Десятичные дроби делят так:
Десятичные дроби делят так:— целую часть справа налево;
— число после запятой слева направо.
Пример: 3459842,825694 → 3 45 98 42, 82 56 94 Допускается, что вначале остается непарное число.
Для первого числа (или пары) подбираем наибольшее число n. Его квадрат должен быть меньше или равен значению первого числа (пары чисел). Извлеките из этого числа корень — √n. Запишите полученный результат сверху справа, а квадрат этого числа — снизу справа.
У нас первая 7. Ближайшее квадратное число — 4. Оно меньше 7, а 4 =
Вычтите найденный квадрат числа n из первого числа (пары). Результат запишите под 7. А верхнее число справа удвойте и запишите справа выражение 4_х_=_.
Примечание: числа должны быть одинаковыми.
Подбираем число для выражения с прочерками. Для этого найдите такое число, чтобы полученное произведение не было больше или равнялось текущему числу слева.  В нашем случае это 8.
В нашем случае это 8.Запишите найденное число в верхнем правом углу. Это второе число из искомого корня. Снесите следующую пару чисел и запишите возле полученной разницы слева.
Вычтите полученное справа произведение из числа слева. Удваиваем число, которое расположено справа вверху и записываем выражение с прочерками.
Сносим к получившейся разнице еще пару чисел. Если это числа дробной части, то есть расположены за запятой, то и в верхнем правом углу возле последней цифры искомого квадратного корня ставим запятую. Заполняем прочерки в выражении справа, подбирая число так, чтобы полученное произведение было меньше или равно разницы выражения слева.
Если необходимо большее количества знаков после запятой, то дописывайте возле текущей цифры слева и повторяйте действия: вычитание слева, удваиваем число в верхнем правом углу, записываем выражение прочерками, подбираем множители для него и так далее. 
Как думаете сколько времени вы потратите на такие расчеты? Сложно, долго, запутанно. Тогда почему бы не упростить себе задачу? Воспользуйтесь нашей программой, которая поможет произвести быстрые и точные расчеты.
1. Введите желаемое количество знаков после запятой.
2. Укажите степень корня (если он больше 2).
3. Введите число, из которого планируете извлечь корень.
Практическая работа №2 | Учебно-методическое пособие по теме:
ПРАКТИЧЕСКАЯ РАБОТА № 2
ОД.10 Математика
Тема: Преобразование алгебраических, рациональных, иррациональных, степенных выражений.
Вид занятия: Практическое занятие
Цель
занятия
учебная
Проверить знания и практические умения студентов по преобразованию алгебраических, рациональных, иррациональных, степенных выражений.
воспитательная и
развивающая
Способствовать овладению необходимыми навыками самостоятельной учебной деятельности; содействовать развитию умений применять полученные знания в типовых условиях
Межпредметные
связи
обеспечивающие
Математика (школьный курс)
обеспечиваемые
Физика, химия, техническая механика, экономика, курсовое и дипломное проектирование
Обеспечение урока:
Использование ИКТ (информационно – коммуникационных технологий)
(мультимедийные презентации, проекционное оборудование, интерактивная доска, персональный компьютер, компьютерное тестирование)
http://free.
 megacampus.ru/xbookM0001/index.html?go=part-006*page.htm
megacampus.ru/xbookM0001/index.html?go=part-006*page.htmНаглядные пособия и раздаточный материал: методические указания для практической работы №2, плакаты: «Свойства степени», «Свойства корня n-ой степени», «Формулы сокращенного умножения»
Литература: Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М.: Просвещение, 2012.
Цель работы:
Выполнить действия по преобразованию алгебраических, рациональных, иррациональных, степенных выражений.
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.
Корень n – степени: , n — показатель корня, а – подкоренное выражение
Если n – нечетное число, то выражение имеет смысл при а
Если n – четное число, то выражение имеет смысл при
Арифметический корень:
Корень нечетной степени из отрицательного числа:
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
- Правило извлечения корня из произведения:
- Правило извлечения корня из дроби:
- Правило извлечения корня из корня:
- Правило вынесения множителя из под знака корня:
- Внесение множителя под знак корня:
,
- Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.

- Правило возведения корня в степень.
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
=,a – основание степени, n – показатель степени
Свойства:
- При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
- При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
- При возведении степени в степень показатели перемножаются.
- При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.
- Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.
- Если
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
- По определению:
Свойства:
- Пусть r рациональное число , тогда
при r>0 > при r
7 .
 Для любого рациональных чисел r и s из неравенства > следует
Для любого рациональных чисел r и s из неравенства > следует> при a>1 при
Формулы сокращённого умножения.
Пример 1. Упростите выражение .
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием): .
Ответ: 9m7 .
Пример 2.Сократить дробь:
Решение. Так область определения дроби все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем .Сократив дробь, получим .Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби и равны при х ≠ 1 и х ≠ -2.
Пример 3.Сократить дробь:
Пример 4.Упростить:
Пример 5.Упростить:
Пример 6. Упростить:
Пример 7. Упростить:
Пример 8.Упростить:
Пример 9. Вычислить: .
Решение.
Пример 10.Упростить выражение:
Решение.
Пример 11.Сократить дробь , если
Решение..
Пример 12.
 Освободиться от иррациональности в знаменателе дроби
Освободиться от иррациональности в знаменателе дроби Решение.В знаменателе имеем иррациональность 2-й степени, поэтому помножим и числитель, и знаменатель дроби на сопряженное выражение, то есть сумму чисел и , тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
ВАРИАНТ — I
1. Упростите выражение:
2. Найдите значение выражения:
3. Представьте степень с дробным показателем в виде корня
4. Привести указанное выражение к виду , где а -рациональное число, b – натуральное число
,
5. Упростить:
;
6. Замените арифметические корни степенями с дробным показателем
, ,
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
10. Выполните действие:
8. Сократите дробь
9.
 Выполните действие
Выполните действиеВАРИАНТ — II
1. Упростите выражение:
2. Найдите значение выражения:
3. Представьте степень с дробным показателем в виде корня
4. Привести указанное выражение к виду , где а- рациональное число, b – натуральное число
,
5. Упростить:
;
6. Замените арифметические корни степенями с дробным показателем
, ,
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
10. Выполните действие:
8. Сократите дробь
9. Выполните действие
ВАРИАНТ — III
1. Выполните действие:
2. Найдите значение выражения:
3. Представьте степень с дробным показателем в виде корня
4. Привести указанное выражение к виду , где а -рациональное число, b – натуральное число
,
5.
 Упростить:
Упростить:;
6. Замените арифметические корни степенями с дробным показателем
, ,
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
10. Выполните действие:
8. Сократите дробь
9. Выполните действие
ВАРИАНТ — IV
1. Выполните действие:
2. Найдите значение выражения:
3. Представьте степень с дробным показателем в виде корня
,
4. Привести указанное выражение к виду , где а- рациональное число, b – натуральное число
,
5. Упростить:
;
6. Замените арифметические корни степенями с дробным показателем
, ,
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
10. Выполните действие:
8. Сократите дробь
9.
 Выполните действие
Выполните действиеВАРИАНТ — V
1. Упростите выражение:
2. Найдите значение выражения:
3. Представьте степень с дробным показателем в виде корня
,
4. Привести указанное выражение к виду , где а- рациональное число, b – натуральное число
,
5. Упростить:
;
6. Замените арифметические корни степенями с дробным показателем
, ,
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
10. Выполните действие:
8. Сократите дробь
9. Выполните действие
ВАРИАНТ — VI
1. Упростите выражение:
2. Найдите значение выражения:
3. Представьте степень с дробным показателем в виде корня
,
4. Привести указанное выражение к виду , где -а рациональное число, b – натуральное число
,
5.
 Упростить:
Упростить:;
6. Замените арифметические корни степенями с дробным показателем
, ,
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
10. Выполните действие
8. Сократите дробь
9. Выполните действие
Какие трудности ждут тех, кто взялся выполнять сложение корней? :: SYL.ru
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.

Что такое математический корень?
Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.
Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х2=у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица.
 А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.
По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16.
Во втором случае лучше ограничиться упрощением самих корней.
 А в ответе оставить их сумму.
А в ответе оставить их сумму.Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.
- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых.
 Если да, то снова выполнить второе действие.
Если да, то снова выполнить второе действие.
В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Рекомендация: после разложения на простые множители нужно сделать проверку. То есть умножить их друг на друга и проверить, получается ли исходное значение.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
Решение.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64.
 Учитывая это, выражение будет записано так:
Учитывая это, выражение будет записано так:√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=42, 9=32, 64=82. Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36.
 После вынесения множителей из-под знака корня имеем:
После вынесения множителей из-под знака корня имеем:5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).
На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
— 5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
Народная акция | Присоединяйтесь к нашему радостному бунту.
People’s Action с гордостью поддерживает более 100 местных, окружных, государственных и федеральных кандидатов на всеобщих выборах 2022 года.

Эти кандидаты присоединяются к сотням кандидатов, одобренных Народным действием, которые уже занимают должности на всех уровнях правительства.
В этом списке целый набор восходящих звезд! От Манделы Барнса (Висконсин) и Ильхана Омара (Миннесота) до Роберта Питерса (Иллинойс) и Деки Дхалака (Мэн). Все они необходимы для достижения реальных перемен в каждом уголке этой страны.
Скажите кандидатам и официальным лицам не брать корпоративные деньги!
Крупные финансовые, топливные и медицинские корпорации тратят миллионы на подкуп избранных должностных лиц и кандидатов.
Хотите, чтобы ваши представители работали на вас, а не за большие деньги?
Скажи им, чтобы они подписали Народное обещание ПРЯМО СЕЙЧАС!
СКАЖИТЕ ИМ СЕЙЧАС
Народное действие аплодирует сенаторам и организаторам, которые заблокировали грязную побочную сделку Manchin
27 сентября 2022 г.

ВАШИНГТОН, округ Колумбия — Сегодня сенаторы заблокировали «побочную сделку» сенатора от Западной Вирджинии Джо Мэнчина, чтобы позволить грязным и опасным проектам по добыче ископаемого топлива быть прикрепленным к государственному финансированию
Подробнее »
Народное действие объявляет народный список, поддерживая 113 кандидатов на 2022 год
19 сентября 2022 г.
ВАШИНГТОН, округ Колумбия — сегодня организация «Народное действие» объявила свой «Народный список» — список из 113 местных, окружных, государственных и федеральных кандидатов, одобренных организацией на всеобщем голосовании 2022 г.
Подробнее »
Народное действие и национальная коалиция запускают Lead Together, новый веб-сайт Американского плана спасения и ресурсный центр для местных органов власти и общественных организаций.
9 сентября 2022 г.
Нью-Йорк, штат Нью-Йорк — 8 сентября 2022 г.
 коалиция различных политических и членских организаций запустила Lead Together, новый веб-сайт и центр для
коалиция различных политических и членских организаций запустила Lead Together, новый веб-сайт и центр для. Подробнее »
People’s Action укрепляет власть бедных и работающих людей в городских, сельских и пригородных районах, чтобы добиваться перемен посредством споров и выборов. Мы представляем собой национальную сеть из 38 государственных и местных общественных организаций по строительству власти в 28 штатах, объединенных в работе по созданию большего «мы».
Сила сильнее ненависти
«Последние несколько недель мое сердце разрывалось… По нашей стране распространяется глубокая болезнь: болезнь расизма, ненависти и насилия. И мне больно быть свидетелем этого».
Прочтите специальное сообщение от исполнительного директора People’s Action Сульмы Ариас.
Lea un mensaje especial de Sulma Arias, Directora de People’s Action, sobre los ultimos sucesos en Buffalo, Nueva York and Uvalde, Texas.
People Action и специальные гости излагают наш план по завоеванию прогрессивной власти и созданию большего мы в 2022 году!
Мы свяжемся с лидерами нашей сети в Висконсине, Нью-Йорке, Иллинойсе и Пенсильвании, а также из Висконсина.
 Лейтенант-губернатор Мандела Барнс, член палаты представителей США Ро Ханна, член палаты представителей штата Иллинойс Делия Рамирес, Бриттани Рамос ДеБаррос и наш собственный исполнительный директор Сульма Ариас!
Лейтенант-губернатор Мандела Барнс, член палаты представителей США Ро Ханна, член палаты представителей штата Иллинойс Делия Рамирес, Бриттани Рамос ДеБаррос и наш собственный исполнительный директор Сульма Ариас! СМОТРИ
Сдать MAT Act
NOWЗакон о всестороннем лечении наркомании или Закон о МП поможет устранить барьеры, мешающие практикующим врачам назначать бупренорфин для лечения расстройств, связанных с употреблением опиоидов.
Белый дом должен обеспечить права арендаторов
Администрация Байдена, следуя указаниям людей, на которых повлияла десятилетия неудачной или отсутствующей жилищной политики, должна принять срочные меры для закрепления федеральных мер защиты арендаторов.
Учить больше
Народное действие приветствует Сульму Ариас, нового исполнительного директора
Народное действие и Институт народного действия приветствуют Сульму Ариас в качестве нашего нового исполнительного директора.
 Сульма является национальным лидером в борьбе за справедливость для иммигрантов и рабочих. Добро пожаловать, Сульма!
Сульма является национальным лидером в борьбе за справедливость для иммигрантов и рабочих. Добро пожаловать, Сульма!Народное действие, глубокий опрос, опубликованный в The Washington Post
«Максмин не просто разговаривала с избирателями, она стремилась их понять. People’s Action называет этот подход «глубокой агитацией» и обнаружила, что он помог уменьшить маржу Трампа, когда он был реализован в ключевых штатах на полях сражений».
Катрина ванден Хевел ТвитнутьВ новостях
Пресс-релизы
- Народное действие аплодирует сенаторам и организаторам, которые заблокировали грязную побочную сделку Manchin 27 сентября 2022 г.
- Директор по соблюдению программ и управлению рисками 27 сентября 2022 г.
- Контроллер 27 сентября 2022 г.
- Народное действие объявляет народный список, поддерживая 113 кандидатов на 2022 год
19 сентября 2022 г.

- Народное действие и национальная коалиция запускают Lead Together, новый веб-сайт Американского плана спасения и ресурсный центр для местных органов власти и общественных организаций. 9 сентября, 2022 г.
Радикальное видение расы Кларенса Томаса
Кларенс Томас является судьей Верховного суда дольше всех. Когда он присоединился к судье 19 октября 1991 года, Советский Союз был страной, Хиллари Клинтон была первой леди Арканзаса, а Дональд Трамп недавно объявил о банкротстве первого из шести своих предприятий. С тех пор Томас написал более семисот мнений, изложив противоречивые позиции по правам на оружие и финансированию избирательных кампаний, которые получили большинство в Верховном суде. «Взгляды Томаса, — сказал профессор права Йельского университета Акил Рид Амар, — теперь в каждом случае соблюдаются большинством членов суда». Это было в 2011 году. Сегодня к Томасу в суде присоединились Нил Горсач, который часто соглашается с мнением Томаса, и Бретт Кавано.
 Одиннадцать из его бывших клерков были назначены Трампом в федеральную скамью. Четверо из них заседают в Апелляционном суде, всего в одном шаге от Верховного суда.
Одиннадцать из его бывших клерков были назначены Трампом в федеральную скамью. Четверо из них заседают в Апелляционном суде, всего в одном шаге от Верховного суда.По общему мнению, Томас — самый консервативный член Двора. Поэтому удивительно, что центральной темой его юриспруденции является раса. Когда ему было почти сорок лет, всего за четыре года до своего назначения в суд, Томас изложил основы своего видения в профиле в The Atlantic . «Вы ничего не можете сделать, чтобы избавиться от черной кожи», — сказал он. «Мне все равно, насколько вы образованы, насколько хороши в своем деле — у вас никогда не будет таких же контактов или возможностей, вас никогда не будут считать равным белым». Это не было мгновенной неосмотрительностью; это была квинтэссенция всей жизни обучения, которое началось в обособленных районах Саванны в 1950-х и продолжалось в течение его студенческих лет, в 60-х. В Суде Томас продолжает верить — и спорит, мнение за мнением, — что раса имеет значение; что расизм — постоянная, неистребимая черта американской жизни; и что единственная надежда для чернокожих заключается в них самих, не как в личностях, а как в отдельном сообществе с отдельными институтами, помимо белых людей.

Это видение отличает Томаса от его коллег-консерваторов на скамейке запасных, которые верят, что расизм либо побежден, либо ослабевает. Это видение впервые появилось в ранние годы Томаса, когда он был левым и на глубоком уровне отождествлял себя с принципами черного национализма. Как и большинство идеологических обязательств, политика Томаса избирательна, но большая часть программы, которую он принял в юности, — прославление чернокожей самодостаточности, поддержка расового сепаратизма — остается жизненно важной для его убеждений и сегодня. Эти убеждения с каждым сроком становятся все ближе к тому, чтобы быть закрепленными в законе. Томас пишет в среднем тридцать четыре мнения в год — больше, чем любой другой судья. Несмотря на это, большинство американцев знают о нем только то, что однажды его обвинили в сексуальных домогательствах и что он почти никогда не говорит со скамьи подсудимых.
Томас родился в 1948 году в Пин-Пойнте, штат Джорджия, бедной общине чернокожих, основанной освобожденными рабами.
 В своих мемуарах «Сын моего дедушки» 2007 года воспоминания Томаса о Пин-Пойнте носят пасторальный характер: он катил велосипедные диски по песчаным дорогам, ловил пескарей в ручье. Переезд его семьи в Саванну, когда Томасу было шесть лет, положил конец этой идиллии. В Пин-Пойнте Томас питался прямо с суши и воды, питаясь «обильным и постоянным запасом свежей пищи: креветками, крабами, раковинами, устрицами, черепахами, цыплятами, свиными ножками, окороками и большим количеством свежих овощей. ». В Саванне, прежде чем он переехал к бабушке и дедушке, он ел ложкой «кукурузные хлопья, смоченные смесью воды и сгущенного молока с сахаром».
В своих мемуарах «Сын моего дедушки» 2007 года воспоминания Томаса о Пин-Пойнте носят пасторальный характер: он катил велосипедные диски по песчаным дорогам, ловил пескарей в ручье. Переезд его семьи в Саванну, когда Томасу было шесть лет, положил конец этой идиллии. В Пин-Пойнте Томас питался прямо с суши и воды, питаясь «обильным и постоянным запасом свежей пищи: креветками, крабами, раковинами, устрицами, черепахами, цыплятами, свиными ножками, окороками и большим количеством свежих овощей. ». В Саванне, прежде чем он переехал к бабушке и дедушке, он ел ложкой «кукурузные хлопья, смоченные смесью воды и сгущенного молока с сахаром».Саванна также была местом, где, по словам Томаса, он впервые столкнулся с расой — не от рук белых, а от черных. Хотя Томас пошел в начальную школу в 1954 году, через четыре месяца после того, как Верховный суд объявил сегрегацию неконституционной, он вырос, по его собственному отчету, в «полностью черной среде». Его прозвище на школьном дворе и на улицах было «ABC» — «Самый черный ребенок Америки».
 «Если бы он был чернее, — подшучивали его одноклассники, — он был бы синим». Цвет был кодом класса. Смуглая кожа Томаса — наряду с диалектом галла-гичи, который он унаследовал от Пин-Пойнта, — была признаком его низкого статуса и происхождения. «У Кларенса были большие губы, пушистые волосы, и он был буквально черным», — сказал одноклассник Джейн Майер и Джилл Абрамсон в их 19-летнем возрасте.94 книга «Странное правосудие: продажа Кларенса Томаса». «Эти люди были у основания полюса. Ты просто не хотел тусоваться с этими детьми».
«Если бы он был чернее, — подшучивали его одноклассники, — он был бы синим». Цвет был кодом класса. Смуглая кожа Томаса — наряду с диалектом галла-гичи, который он унаследовал от Пин-Пойнта, — была признаком его низкого статуса и происхождения. «У Кларенса были большие губы, пушистые волосы, и он был буквально черным», — сказал одноклассник Джейн Майер и Джилл Абрамсон в их 19-летнем возрасте.94 книга «Странное правосудие: продажа Кларенса Томаса». «Эти люди были у основания полюса. Ты просто не хотел тусоваться с этими детьми».Для Томаса эти жестокости — боль на всю жизнь. «Люди любят говорить о межрасовых конфликтах, — сказал он репортеру Кену Фоскетту, опубликовавшему биографию Томаса «Судя Томаса» в 2004 году. — Они никогда не говорят о конфликтах и напряженности внутри расы». С юных лет основное разделение, с которым пришлось столкнуться Томасу, происходило из-за привилегий, связанных с богатством чернокожих и светлой кожей. «У вас была черная элита, школьные учителя, светлокожие люди, дантисты, врачи», — сказал Томас.
 «Мой дедушка был внизу. Они будут смотреть на него свысока. Сейчас все пытаются это приукрасить, но так было на самом деле». Не было до 19В 64 года, когда он перешел в элитную католическую школу-интернат за пределами Саванны, Томас будет делить класс с белыми. Позже он назовет принудительную государством сегрегацию «настолько близкой к тоталитаризму, насколько мне хотелось бы».
«Мой дедушка был внизу. Они будут смотреть на него свысока. Сейчас все пытаются это приукрасить, но так было на самом деле». Не было до 19В 64 года, когда он перешел в элитную католическую школу-интернат за пределами Саванны, Томас будет делить класс с белыми. Позже он назовет принудительную государством сегрегацию «настолько близкой к тоталитаризму, насколько мне хотелось бы».Если переезд из Пин-Пойнта в Саванну познакомил Томаса с одной стороной цветной линии, то поездка на север, в колледж, познакомила его с другой. Томас провел один год в католической семинарии в Миссури, а затем в 1968 году поступил в Колледж Святого Креста, будучи одним из самых бедных из девятнадцати молодых чернокожих, завербованных Джоном Бруксом, либеральным иезуитом, который впоследствии стал президентом школы. Holy Cross находился в Вустере, маленьком городке недалеко от Бостона с двухпроцентным черным населением. В то время колледж был еще белее, чем его окрестности. За лето до приезда Томаса школа связалась с поступающими белыми учениками, чтобы узнать, не будут ли они возражать против темнокожего соседа по комнате.
 В ходе опроса от четверти до половины одноклассников Томаса согласились со следующими утверждениями: что у чернокожих «меньше амбиций», чем у белых; что у чернокожих «более свободные нравы», чем у белых; что черные люди «пахнут иначе», чем белые. В 19В письме Wall Street Journal Томас написал: «Новая причуда СМИ состоит в том, чтобы постоянно рассказывать о бедственном положении чернокожих студентов колледжей в кампусах, где преобладают белые. Хотите верьте, хотите нет, но проблемы те же, что и 20 лет назад. . . . Главное отличие в том, что СМИ тогда уделяли им мало внимания».
В ходе опроса от четверти до половины одноклассников Томаса согласились со следующими утверждениями: что у чернокожих «меньше амбиций», чем у белых; что у чернокожих «более свободные нравы», чем у белых; что черные люди «пахнут иначе», чем белые. В 19В письме Wall Street Journal Томас написал: «Новая причуда СМИ состоит в том, чтобы постоянно рассказывать о бедственном положении чернокожих студентов колледжей в кампусах, где преобладают белые. Хотите верьте, хотите нет, но проблемы те же, что и 20 лет назад. . . . Главное отличие в том, что СМИ тогда уделяли им мало внимания».Прежде чем отправиться на север, у Томаса была не история, а ситуация. Он знал Джима Кроу и, как и многие афроамериканцы, пережил жестокость его кончины. Он читал и любил Ричарда Райта: «Он сердитый черный писатель, а я был сердитым черным человеком», — сказал он в «Судящем Томасе». Но он еще не пришел к мировоззрению в отношении расы. На Севере, который он считал еще более враждебным, чем Юг, Томас нашел это мировоззрение в черном национализме, который вдохновлял многих афроамериканцев той эпохи.

Через несколько месяцев после прибытия в Холи-Кросс Томас и его друзья организовались в Союз черных студентов, где они умерили свои стремления к включению в свои ряды требованиями разделения. В учредительном заявлении БГУ содержится призыв к приему большего количества чернокожих студентов, найму чернокожих преподавателей, проведению курсов по черной литературе и истории, а также к мероприятиям в кампусе для демонстрации чернокожих художников. Они предваряли свои требования воодушевляющим утверждением черной идентичности: «Мы, черные студенты Колледжа Святого Креста, признавая необходимость укрепления чувства расовой идентичности и групповой солидарности, осознавая общее дело с другими угнетенными народов и желая разоблачить и искоренить социальное неравенство и несправедливость, настоящим учреждаем Союз черных студентов Святого Креста». Томас напечатал документ и был избран секретарем-казначеем.
Б.С.У. также опубликовал манифест из одиннадцати пунктов, который включал следующие правила:
Черный мужчина должен уважать черную женщину.
 Женщина черного мужчины — самая красивая из всех женщин.
Женщина черного мужчины — самая красивая из всех женщин.
. . .
Черный человек должен работать со своим черным братом.
. . .
Черный человек хочет. . . право увековечить свою расу.
. . .
Черный мужчина не хочет и не нуждается в белой женщине. История черного мужчины показывает, что белая женщина является причиной его неспособности быть настоящим черным мужчиной.Последнее правило вызвало небольшие трения в группе. После Б.С.У. Узнав, что участник встречается с белой женщиной, группа устроила инсценированный суд, признала его виновным и в наказание сломала его афро-гребешок. Томас отнесся к правилу более серьезно, особенно после встречи с Кэти Амбуш, чернокожей женщиной, на которой он женился в 1971 году и развелся в 1984 году. В стихотворении он назвал «Ты брат или нет?» он изложил обязанности чернокожих мужчин перед чернокожими женщинами. Даже в этой среде, как сообщают Кевин Мерида и Майкл Флетчер в своей биографии 2007 года «Высший дискомфорт», выделялось «резкое расовое сознание» Томаса.
 Когда он видел межрасовую пару, прогуливающуюся по кампусу, он громко спрашивал: «Я вижу черную женщину с белым мужчиной? Как это могло быть?» До 19В 86 году, когда Томас встретил Вирджинию Лэмп, белую девушку, которая станет его второй женой, он выступил против межрасового секса и брака.
Когда он видел межрасовую пару, прогуливающуюся по кампусу, он громко спрашивал: «Я вижу черную женщину с белым мужчиной? Как это могло быть?» До 19В 86 году, когда Томас встретил Вирджинию Лэмп, белую девушку, которая станет его второй женой, он выступил против межрасового секса и брака.Неудивительно, что Томас и его одноклассники подтвердили свою солидарность в гендерном плане. «Маскулинизм», как утверждал историк Стив Эстес, не был чем-то необычным в борьбе чернокожих за свободу — да и во многих движениях конца 1960-х годов. Боевики часто формулировали свои требования идиомой чести черных мужчин, которую можно было удовлетворить только за счет признания со стороны белых мужчин и уважения со стороны черных женщин. Для них это было мерилом черной свободы. «Черный мужчина никогда не заслужит чье-либо уважение, пока он не научится уважать своих собственных женщин», — писал Малкольм Икс в своей «Автобиографии», описывая систему верований, сложившуюся с первых лет его пребывания в «Нации ислама», согласно которой уважение к чернокожим женщинам кажутся средством для достижения более важной цели.

Томас прочитал «Автобиографию Малкольма Икса» на первом году обучения в Святом Кресте. Он повесил плакат с изображением Малькольма в своей комнате в общежитии и начал собирать записи речей Малькольма, которые он все еще мог декламировать по памяти два десятилетия спустя. «Я был очень неравнодушен к Малкольму Икс, — сказал Томас в 1987 году. — В том, что он говорит, много хорошего». Накануне своего назначения в Верховный суд Томас все еще вызывал Малькольма в качестве свидетеля обвинения против либерального истеблишмента. «Я не понимаю, как сегодня борцы за гражданские права могут называть Малкольма Икса своим», — сказал он. «Где, по его словам, чернокожие должны просить у Министерства труда работу? Он был адом для интеграторов. Где он говорит, что вы должны пожертвовать своими институтами, чтобы быть рядом с белыми людьми?»
В колледже Томас считал, что Черные Пантеры, одна из многих группировок, претендовавших на мантию Малкольма, предлагают «другой путь». Под их руководством он помог организовать программу бесплатных завтраков в Вустере, подавая ежедневные обеды из церкви примерно пятидесяти бедным детям.
 Он защищал лидера «Черных пантер» Кэтлин Кливер и члена Коммунистической партии Анджелу Дэвис, которые бежали от американского правительства из-за радикальных причастностей и обвинений в преступной деятельности. Когда на слушаниях по его утверждению его спросили, чем он занимается, Томас ответил: «Английская литература». Когда его спросили, в чем он пренебрегает, он ответил: «Протест». Его первая поездка в Вашингтон состояла в том, чтобы выступить против Пентагона и войны во Вьетнаме. Последний митинг, на котором он присутствовал, в Кембридже — один из самых жестоких в истории города, на котором две тысячи полицейских напали на три тысячи протестующих — состоял в том, чтобы потребовать освобождения соучредителя «Черной пантеры» Бобби Сила и лидера «Пантеры» Эрики Хаггинс. «Я никогда не был либералом, — сказал он на выступлении в 1919 году.96. «Я был радикалом». Даже в своих мемуарах Томас отказывается высмеивать причину. «Чем больше я читал о движении за власть черных, — пишет он, — тем больше я хотел быть его частью».
Он защищал лидера «Черных пантер» Кэтлин Кливер и члена Коммунистической партии Анджелу Дэвис, которые бежали от американского правительства из-за радикальных причастностей и обвинений в преступной деятельности. Когда на слушаниях по его утверждению его спросили, чем он занимается, Томас ответил: «Английская литература». Когда его спросили, в чем он пренебрегает, он ответил: «Протест». Его первая поездка в Вашингтон состояла в том, чтобы выступить против Пентагона и войны во Вьетнаме. Последний митинг, на котором он присутствовал, в Кембридже — один из самых жестоких в истории города, на котором две тысячи полицейских напали на три тысячи протестующих — состоял в том, чтобы потребовать освобождения соучредителя «Черной пантеры» Бобби Сила и лидера «Пантеры» Эрики Хаггинс. «Я никогда не был либералом, — сказал он на выступлении в 1919 году.96. «Я был радикалом». Даже в своих мемуарах Томас отказывается высмеивать причину. «Чем больше я читал о движении за власть черных, — пишет он, — тем больше я хотел быть его частью».
В 1971 году Томас поступил в Йельскую юридическую школу. Один из двенадцати чернокожих студентов, он был бенефициаром программы позитивных действий — Йельский университет постановил, что десять процентов поступающих в класс должны быть цветными студентами — таких, которых он позже стал поносить. У Томаса был долгий опыт самовыражения перед враждебно настроенной публикой, но теперь конкуренция была жестче, а ставки выше. Внимание исходило не только от сокурсников, но и от либеральных белых, которые выступали в качестве его покровителей. «Вы должны были доказывать свою состоятельность каждый день, потому что предполагалось, что вы глупы и не заслуживаете того, чтобы быть там», — сказал он Washington 9.0127 Пост . «Каждый раз, когда вы входили в юридический класс в Йельском университете, это было похоже на то, как обезьяна прыгает вам на спину с готических арок». На Юге, даже в Святом Кресте, Томас думал, что сможет пробиться к меритократии силой своего разума и воли. В Йельском университете его достижения казались лишенными авторства.
 «Как бы ни было больно слышать, что я хорошо учился [в старшей школе], несмотря на мою расу, — писал он позже, — гораздо хуже было чувствовать, что я теперь в Йельском университете из-за этого».
«Как бы ни было больно слышать, что я хорошо учился [в старшей школе], несмотря на мою расу, — писал он позже, — гораздо хуже было чувствовать, что я теперь в Йельском университете из-за этого».В Йельском университете Томас развил понимание расизма, от которого он никогда не избавится. Белые — южные и северные, либеральные и консервативные, сельские и городские — расисты. Расизм, как рассказывал Томас студентам из Университета Мерсера в 1993 году, «имеет сложные и, в определенной степени, необнаружимые корни». Не зная его начала, мы не можем знать и его конца. Максимум, на что можно надеяться, это на то, что белые будут честны в этом. Честность демонстрируется грубыми заявлениями о личной неприязни или интеллектуальными предположениями о расовом неравенстве. Нечестность демонстрируется через отрицание расизма и сочувственное предложение помощи. Нечестность усыпляет чернокожих ложным чувством безопасности, уверяя их, что они в безопасности, хотя на самом деле это не так. Одна из любимых песен Томаса — 1971 хит «Иногда улыбающиеся лица» от Undisputed Truth.
 Его классическая лирика — «Улыбающиеся лица, улыбающиеся лица лгут» — перекликается с его опытом общения с северными белыми либералами. По его словам, среди достоинств администрации Рейгана был тот факт, что никто не «улыбался вам в лицо».
Его классическая лирика — «Улыбающиеся лица, улыбающиеся лица лгут» — перекликается с его опытом общения с северными белыми либералами. По его словам, среди достоинств администрации Рейгана был тот факт, что никто не «улыбался вам в лицо».Сделав искренность лакмусовой бумажкой американского расизма, Томас взял нить черного национализма, которая повлияла на его раннее развитие, и вплел ее в целую философию расы. В 1920-х годах, в особенно острый момент расистской реакции в Соединенных Штатах, Маркус Гарви также находил утешение в обещании откровенности. «Они лучшие друзья моей расы, потому что рассказывают нам, кто они такие и что они означают, чем все лицемеры вместе взятые», — сказал Гарви из Ку-клукс-клана. «Я люблю честность и честную игру».
Для Томаса нечестность заключалась не только в расе; это было также о классе. Какими бы благими намерениями белые либералы ни занимались устранением расового неравенства, их элитарность оставалась непоколебимой. В Йельском университете некоторые одноклассники Томаса сомневались в отсутствии классных оценок и оценок.
 «Вы не отделяете сливки от сливок», — ответил профессор. «Ваша судьба, как студента юридического факультета Йельского университета, — стать одним из лидеров юридической профессии. Это произойдет не из-за вас лично, а из-за того, что вы здесь. Именно это происходит со студентами юридического факультета Йельского университета». Но чернокожие студенты Йельского университета были отделены от сливок; действительно, для осуществления этого разделения использовалось отсутствие ранжирования. Ближе к окончанию учебы Томас попытался устроиться в элитную юридическую фирму в Атланте, где не было чернокожих сотрудников. Одним из признаков против него было то, что у него не было оценок. Даже если он приехал из Йельского университета, как его потенциальные работодатели могли знать, насколько он хорош?
«Вы не отделяете сливки от сливок», — ответил профессор. «Ваша судьба, как студента юридического факультета Йельского университета, — стать одним из лидеров юридической профессии. Это произойдет не из-за вас лично, а из-за того, что вы здесь. Именно это происходит со студентами юридического факультета Йельского университета». Но чернокожие студенты Йельского университета были отделены от сливок; действительно, для осуществления этого разделения использовалось отсутствие ранжирования. Ближе к окончанию учебы Томас попытался устроиться в элитную юридическую фирму в Атланте, где не было чернокожих сотрудников. Одним из признаков против него было то, что у него не было оценок. Даже если он приехал из Йельского университета, как его потенциальные работодатели могли знать, насколько он хорош?Дерево декомпозиции — Power BI
- Статья
- 6 минут на чтение
ПРИМЕНЯЕТСЯ К: ✔️ Power BI Desktop ✔️ Служба Power BI
Визуальное представление дерева декомпозиции в Power BI позволяет визуализировать данные в нескольких измерениях. Он автоматически собирает данные и позволяет детализировать измерения в любом порядке. Это также визуализация искусственного интеллекта (ИИ), поэтому вы можете попросить его найти следующее измерение для детализации на основе определенных критериев. Этот инструмент полезен для специальных исследований и проведения анализа первопричин.
В этом учебном пособии используются два примера:
- Сценарий цепочки поставок, в котором анализируется процентная доля продуктов, находящихся в запасе (отсутствующих на складе).
- Сценарий продаж, в котором продажи видеоигр разбиваются по многочисленным факторам, таким как жанр игры и издатель.
Для Power BI Desktop можно загрузить набор данных сценария цепочки поставок.
 Если вы хотите использовать службу Power BI, загрузите Supply Chain Sample.pbix, а затем загрузите его в рабочую область в службе Power BI.
Если вы хотите использовать службу Power BI, загрузите Supply Chain Sample.pbix, а затем загрузите его в рабочую область в службе Power BI.Примечание
Чтобы поделиться своим отчетом с коллегой по Power BI, необходимо, чтобы у вас обоих были отдельные лицензии Power BI Pro или чтобы отчет был сохранен в емкости Premium.
Начало работы
Выберите значок дерева декомпозиции на панели Визуализации.
Визуализация требует ввода двух типов:
- Анализ — показатель, который вы хотите проанализировать. Это должна быть мера или совокупность.
- Объясни на — одно или несколько измерений, которые вы хотели бы детализировать.
После того, как вы перетащите меру в поле, визуальные элементы обновятся, чтобы продемонстрировать агрегированную меру. В приведенном ниже примере мы визуализируем средний процент товаров, находящихся в стадии ожидания (5,07%).
Следующим шагом является ввод одного или нескольких измерений, которые вы хотели бы детализировать.
 Добавьте эти поля в корзину «Объяснение по ». Обратите внимание, что рядом с вашим корневым узлом появился знак плюс. Нажав +, вы можете выбрать, какое поле вы хотите детализировать (вы можете детализировать поля в любом порядке).
Добавьте эти поля в корзину «Объяснение по ». Обратите внимание, что рядом с вашим корневым узлом появился знак плюс. Нажав +, вы можете выбрать, какое поле вы хотите детализировать (вы можете детализировать поля в любом порядке).Выбор Смещение прогноза приводит к расширению дерева и разбиению меры по значениям в столбце. Этот процесс можно повторить, выбрав другой узел для детализации.
При выборе узла на последнем уровне происходит перекрестная фильтрация данных. Выбор узла на более раннем уровне изменяет путь.
Взаимодействие с другими визуальными элементами перекрестно фильтрует дерево декомпозиции. В результате порядок узлов внутри уровней может измениться.
Чтобы продемонстрировать другой сценарий, в приведенном ниже примере рассматриваются продажи видеоигр по издателям.
Когда мы перекрестно фильтруем дерево по Ubisoft, путь обновляется, чтобы показать, что продажи Xbox перемещаются с первого на второе место, уступая PlayStation.

Если мы затем перекрестно отфильтруем дерево по Nintendo, продажи Xbox будут пустыми, поскольку Nintendo не разрабатывает игр для Xbox. Xbox вместе с его последующим путем отфильтровывается из представления.
Несмотря на исчезновение пути, существующие уровни (в данном случае жанр игры) остаются закрепленными на дереве. Таким образом, выбор узла Nintendo автоматически расширяет дерево до жанра игры.
AI Splits
Вы можете использовать «AI Splits», чтобы выяснить, где вы должны искать дальше в данных. Эти разделения появляются вверху списка и отмечены лампочкой. Разделения помогают автоматически находить высокие и низкие значения в данных.
Анализ может работать двумя способами в зависимости от ваших предпочтений. При повторном использовании примера цепочки поставок поведение по умолчанию выглядит следующим образом:
- Высокое значение : Рассматриваются все доступные поля и определяется, какое из них следует детализировать, чтобы получить наибольшее значение анализируемого показателя.

- Низкое значение : Рассматриваются все доступные поля и определяется, какое из них следует детализировать, чтобы получить наименьшее значение анализируемого показателя.
Выберите Высокое значение с помощью знака плюс рядом с Прерывистый . Появится новый столбец с пометкой Тип продукта .
Рядом с Тип продукта появляется лампочка, указывающая на то, что этот столбец был «разделен AI». Дерево также показывает пунктирную линию, рекомендующую Мониторинг пациентов узел, указывающий на наибольшее количество невыполненных заказов (9,2%).
Наведите указатель мыши на лампочку, чтобы увидеть всплывающую подсказку. В этом примере всплывающая подсказка: «% невыполненных заказов самый высокий, когда Тип продукта — Мониторинг пациента».
Вы можете настроить визуализацию для поиска относительных разделений AI, а не абсолютных .

Относительный режим ищет высокие значения, которые выделяются (по сравнению с остальными данными в столбце). В качестве примера снова обратимся к продажам видеоигр:
На скриншоте выше мы видим продажи видеоигр в Северной Америке. Сначала мы разделяем дерево по Имя издателя , а затем переходим к Nintendo. Выбор High Value приводит к расширению Платформа Nintendo . Поскольку Nintendo (издатель) разрабатывает только для консолей Nintendo, присутствует только одна ценность, и поэтому неудивительно, что это самая высокая ценность.
Тем не менее, было бы более интересно посмотреть, какое высокое значение выделяется по сравнению с другими значениями в том же столбце. Если мы изменим тип анализа с Абсолютный в Относительный , мы получаем следующий результат для Nintendo:
На этот раз рекомендуемое значение — Платформа в жанре игры .
 Платформа не дает более высокой абсолютной стоимости, чем Nintendo (19 950 000 долларов против 46 950 000 долларов). Тем не менее, это ценность, которая выделяется.
Платформа не дает более высокой абсолютной стоимости, чем Nintendo (19 950 000 долларов против 46 950 000 долларов). Тем не менее, это ценность, которая выделяется.Точнее, поскольку существует 10 значений жанра игры, ожидаемая стоимость для платформы составила бы 4,6 миллиона долларов, если их разделить поровну. Поскольку стоимость платформы составляет почти 20 миллионов долларов, это интересный результат, поскольку он в четыре раза превышает ожидаемый результат.
Расчет производится следующим образом:
Продажи в Северной Америке для платформ/Abs(Avg(Продажи в Северной Америке для игровых жанров))
vs.
Продажи в Северной Америке для Nintendo/Abs(Avg(Продажи в Северной Америке для платформ)), что переводится на:
19 550 000 / (19 550 000 + 11 140 000 + … + 470 000 + 60 000 /10) = 4,25x
против
46 950 000 / (46 950 000 /1) = 1x, если вы предпочитаете. расколы в дереве, у вас также есть возможность отключить их под Форматирование анализа опции:
Взаимодействия дерева с разделением ИИ
У вас может быть несколько последовательных уровней ИИ.
 Вы также можете смешивать различные виды уровней ИИ (переход от высокого значения к низкому значению и обратно к высокому значению):
Вы также можете смешивать различные виды уровней ИИ (переход от высокого значения к низкому значению и обратно к высокому значению):Если выбрать другой узел в дереве, AI Splits пересчитывается с нуля. В приведенном ниже примере мы изменили выбранный узел на уровне Forecast Bias . Последующие уровни меняются, чтобы получить правильные высокие и низкие значения.
Уровни ИИ также пересчитываются при перекрестной фильтрации дерева декомпозиции с помощью другого визуального элемента. В приведенном ниже примере мы видим, что наш процент невыполненных заказов является самым высоким для завода № 0477.
Но если мы выберем Апрель на гистограмме, самые высокие изменения в Тип продукта — Advanced Surgical . В этом случае не только узлы были переупорядочены, но и был выбран другой столбец.
Если мы хотим, чтобы уровни ИИ вели себя как уровни, отличные от ИИ, выберите лампочку, чтобы вернуть поведение по умолчанию.

Хотя несколько уровней ИИ могут быть соединены вместе, уровень без ИИ не может следовать за уровнем ИИ. Если мы делаем разделение вручную после разделения AI, лампочка на уровне AI исчезает, и уровень превращается в обычный уровень.
Блокировка
Создатель контента может блокировать уровни для потребителей отчетов. Когда уровень заблокирован, его нельзя удалить или изменить. Потребитель может исследовать различные пути на заблокированном уровне, но не может изменить сам уровень. Как создатель, вы можете навести указатель мыши на существующие уровни, чтобы увидеть значок замка. Вы можете заблокировать столько уровней, сколько хотите, но вы не можете иметь разблокированные уровни перед заблокированными уровнями.
В приведенном ниже примере заблокированы первые два уровня. Пользователи отчетов могут изменять уровни 3 и 4 и даже добавлять новые уровни впоследствии. Однако первые два уровня изменить нельзя:
Соображения и ограничения
Максимальное количество уровней дерева — 50.
 Максимальное количество точек данных, которые можно одновременно визуализировать в дереве, — 5000. Мы усекаем уровни, чтобы показать n первых. В настоящее время верхнее n на уровень установлено равным 10.
Максимальное количество точек данных, которые можно одновременно визуализировать в дереве, — 5000. Мы усекаем уровни, чтобы показать n первых. В настоящее время верхнее n на уровень установлено равным 10.Дерево декомпозиции не поддерживается в следующих сценариях:
- Локальные службы Analysis Services
Разделение AI не поддерживается в следующих сценариях:
- Azure Analysis Services
- Сервер отчетов Power BI
- Опубликовать в Интернете
- Комплексные меры и меры из схем расширений в «Анализе»
Другие ограничения:
- Поддержка внутри вопросов и ответов
Следующие шаги
Кольцевая диаграмма Power BI
Визуализации Power BI
10 доказанных полезных свойств куркумы и куркумина для здоровья
Крис Гуннарс, бакалавр наук — медицинский обзор Кэти Уорвик, доктора медицинских наук, CDE, Nutrition — обновлено 10 мая 2021 г.
Специя, известная как куркума, может быть наиболее эффективной пищевая добавка в наличии.

Многие высококачественные исследования показывают, что куркума очень полезна для тела и мозга. Многие из этих преимуществ связаны с его основным активным ингредиентом, куркумином.
Читайте дальше, чтобы узнать, что наука говорит о куркуме и куркумине, а также об их пользе.
Куркума — это специя, придающая карри желтый цвет.
На протяжении тысячелетий он использовался в Индии как пряность и лекарственное растение. В последнее время наука начала подтверждать традиционные утверждения о том, что куркума содержит соединения с лечебными свойствами (1).
Эти соединения называются куркуминоиды. Наиболее важным из них является куркумин.
Куркумин является основным активным ингредиентом куркумы. Обладает мощным противовоспалительным действием и является очень сильным антиоксидантом.
Вот 10 основных научно обоснованных преимуществ куркумы и куркумина для здоровья.
Однако содержание куркумина в куркуме не так велико. Это около 3% по весу (2).
 В большинстве исследований этой травы используются экстракты куркумы, которые содержат в основном сам куркумин, с дозировками, обычно превышающими 1 грамм в день.
В большинстве исследований этой травы используются экстракты куркумы, которые содержат в основном сам куркумин, с дозировками, обычно превышающими 1 грамм в день.Было бы очень трудно достичь этих уровней, просто используя куркуму в качестве приправы к пище.
Вот почему некоторые люди предпочитают использовать добавки.
Однако куркумин плохо всасывается в кровь. Чтобы испытать все эффекты куркумина, необходимо улучшить его биодоступность (скорость, с которой ваше тело поглощает вещество) (3).
Полезно употреблять с черным перцем, который содержит пиперин. Пиперин — это натуральное вещество, которое увеличивает усвоение куркумина на 2000% (4).
На самом деле лучшие добавки с куркумином содержат пиперин, что делает их значительно более эффективными.
Куркумин также является жирорастворимым, что означает, что он расщепляется и растворяется в жире или масле. Вот почему может быть хорошей идеей принимать добавки куркумина с пищей с высоким содержанием жира.

Резюме
Куркума содержит куркумин, вещество с мощными противовоспалительными и антиоксидантными свойствами. В большинстве исследований используются экстракты куркумы, которые стандартизированы и содержат большое количество куркумина.
Воспаление невероятно важно. Он помогает бороться с чужеродными захватчиками и играет роль в восстановлении повреждений в вашем теле.
Хотя острое кратковременное воспаление приносит пользу, оно может стать проблемой, если оно станет хроническим и поразит собственные ткани организма.
Теперь ученые считают, что хроническое слабовыраженное воспаление может играть роль в некоторых состояниях здоровья и заболеваниях. К ним относятся (5, 6, 7):
- болезни сердца
- рак
- метаболический синдром
- болезнь Альцгеймера
- различные дегенеративные состояния
лечить эти состояния.
Хотя тема воспаления многогранна и, вероятно, нет простого ответа, ключевой вывод о куркумине заключается в том, что это биоактивное вещество, которое может бороться с воспалением.
 Однако для получения лечебных результатов требуются очень высокие дозы (8, 9, 10).
Однако для получения лечебных результатов требуются очень высокие дозы (8, 9, 10).Резюме
Хроническое воспаление способствует развитию некоторых распространенных заболеваний. Куркумин может подавлять многие молекулы, которые, как известно, играют важную роль в воспалении, но его биодоступность необходимо повысить.
3. Куркума может увеличить антиоксидантную способность организма
Окислительное повреждение считается одним из механизмов старения и многих заболеваний.
В нем участвуют свободные радикалы, высокореакционноспособные молекулы с неспаренными электронами. Свободные радикалы склонны реагировать с важными органическими веществами, такими как жирные кислоты, белки или ДНК.
Основная причина, по которой антиоксиданты так полезны, заключается в том, что они защищают организм от свободных радикалов.
Куркумин является мощным антиоксидантом, который благодаря своей химической структуре может нейтрализовать свободные радикалы (11).

Кроме того, исследования на животных и клетках показывают, что куркумин может блокировать действие свободных радикалов и может стимулировать действие других антиоксидантов. Для подтверждения этих преимуществ необходимы дальнейшие клинические исследования на людях (12).
Резюме
Несмотря на то, что куркумин обладает антиоксидантным действием, необходимы дополнительные исследования, чтобы подтвердить его преимущества.
4. Куркумин может повышать нейротрофический фактор головного мозга
До того, как ученые лучше поняли нейроны, считалось, что они не могут делиться и размножаться после раннего детства. Однако теперь они знают, что это не так.
Нейроны способны образовывать новые связи, а в определенных областях мозга могут размножаться и увеличиваться в количестве.
Одним из основных драйверов этого процесса является мозговой нейротрофический фактор (BDNF). Это ген, который участвует в создании белка, ответственного за поддержание жизни нейронов.

Белок BDNF играет роль в памяти и обучении, и его можно найти в областях мозга, отвечающих за прием пищи, питье и массу тела (13, 14).
Многие распространенные заболевания головного мозга связаны со снижением уровня белка BDNF, включая депрессию и болезнь Альцгеймера (15, 16).
Интересно, что исследования на животных показали, что куркумин может повышать уровень BDNF в мозге (17, 18).
Таким образом, можно эффективно отсрочить или даже обратить вспять многие заболевания головного мозга и возрастное снижение функций мозга. Тем не менее, поскольку эти исследования проводились на животных, трудно сказать, что означают результаты для людей (19)., 20).
Он также может помочь улучшить память и внимание, что кажется логичным, учитывая его влияние на уровни BDNF. Однако для подтверждения этого необходимы дополнительные исследования (21).
Резюме
Куркумин повышает уровень гормона головного мозга BDNF, который увеличивает рост новых нейронов и может помочь бороться с различными дегенеративными процессами в вашем мозгу.

5. Куркумин может снизить риск сердечно-сосудистых заболеваний
Болезни сердца являются причиной смерти номер один в мире (22). Исследователи изучали его на протяжении многих десятилетий и многое узнали о том, почему это происходит. Неудивительно, что болезни сердца невероятно сложны, и этому способствуют различные факторы.
Куркумин может помочь обратить вспять многие этапы процесса сердечно-сосудистых заболеваний (23, 24).
Возможно, основным преимуществом куркумина при сердечных заболеваниях является улучшение функции эндотелия, выстилки ваших кровеносных сосудов (25).
Эндотелиальная дисфункция является основной причиной сердечно-сосудистых заболеваний. Это когда ваш эндотелий не может регулировать кровяное давление, свертываемость крови и различные другие факторы (26).
Несколько исследований показывают, что куркумин может привести к улучшению здоровья сердца (27, 28). Кроме того, одно исследование показало, что оно так же эффективно, как физические упражнения, у женщин в постменопаузе (29).
 ).
).Кроме того, куркумин может помочь уменьшить воспаление и окисление (как обсуждалось выше), которые могут играть роль в сердечных заболеваниях.
В ходе одного исследования 121 человека, перенесшего операцию коронарного шунтирования, исследователи назначали им либо плацебо, либо 4 грамма куркумина в день за несколько дней до и после операции.
В группе куркумина риск сердечного приступа в больнице снизился на 65% (30).
Резюме
Куркумин благотворно влияет на несколько факторов, которые, как известно, играют роль в сердечных заболеваниях. Кроме того, это противовоспалительное средство и антиоксидант.
6. Куркума может помочь предотвратить рак
Рак – это заболевание, характеризующееся неконтролируемым ростом клеток. Существует множество различных форм рака, на которые, по-видимому, влияют добавки куркумина (31).
Куркумин изучался как полезная трава для лечения рака, и было обнаружено, что он влияет на рост и развитие рака (32).

Исследования показали, что он может (33, 34):
- способствовать гибели раковых клеток
- уменьшают ангиогенез (рост новых кровеносных сосудов в опухолях)
- уменьшают метастазирование (распространение рака)
Может ли высокая доза куркумина — предпочтительно с усилителем абсорбции, таким как пиперин — помочь в лечении рака у людей, еще предстоит изучить правильно.
Однако есть доказательства того, что он может в первую очередь предотвращать возникновение рака, особенно рака пищеварительной системы, такого как колоректальный рак (35).
В ходе 30-дневного исследования с участием 44 мужчин с поражениями толстой кишки, которые иногда превращались в рак, 4 грамма куркумина в день уменьшали количество поражений на 40% (36).
Резюме
Куркумин приводит к ряду изменений на молекулярном уровне, которые могут помочь предотвратить и, возможно, даже лечить рак.
7. Куркумин может быть полезен при лечении болезни Альцгеймера
Болезнь Альцгеймера является наиболее распространенной формой деменции и может быть причиной до 70% случаев деменции (37).

В то время как лечение некоторых симптомов прекращается, лекарства от болезни Альцгеймера пока нет. Вот почему так важно предотвратить его появление в первую очередь.
На горизонте могут быть хорошие новости, поскольку было показано, что куркумин преодолевает гематоэнцефалический барьер (38).
Известно, что воспаление и окислительное повреждение играют роль в развитии болезни Альцгеймера, а куркумин благотворно влияет на оба этих состояния (39).
Кроме того, ключевым признаком болезни Альцгеймера является накопление белковых клубков, называемых амилоидными бляшками. Исследования показывают, что куркумин может помочь очистить эти бляшки (40).
Может ли куркумин замедлить или даже обратить вспять прогрессирование болезни Альцгеймера у людей, в настоящее время неизвестно и требует изучения.
Резюме
Куркумин может проникать через гематоэнцефалический барьер и, как было показано, приводит к различным улучшениям патологического процесса болезни Альцгеймера.

8. Пациенты с артритом хорошо реагируют на добавки куркумина
Артрит является распространенной проблемой в западных странах. Существует несколько различных типов артрита, большинство из которых связано с воспалением суставов.
Учитывая, что куркумин является мощным противовоспалительным соединением, можно предположить, что он может помочь при артрите. На самом деле, несколько исследований показывают, что связь существует.
В исследовании с участием людей с ревматоидным артритом куркумин оказался даже более эффективным, чем противовоспалительный препарат (41).
Некоторые другие исследования изучали влияние куркумина на артрит и отмечали улучшение различных симптомов (42).
Резюме
Артрит — распространенное заболевание, характеризующееся воспалением суставов. Многие исследования показывают, что куркумин может помочь в лечении симптомов артрита и в некоторых случаях более эффективен, чем противовоспалительные препараты.

9. Куркумин полезен при депрессии
Куркумин продемонстрировал некоторые перспективы в лечении депрессии.
В ходе контролируемого исследования 60 человек с депрессией были рандомизированы в три группы (43). Одна группа принимала прозак, другая группа принимала 1 грамм куркумина, а третья группа принимала и прозак, и куркумин.
Через 6 недель куркумин привел к улучшениям, сходным с таковыми при приеме прозака. Группа, принимавшая и прозак, и куркумин, показала лучшие результаты (44).
Согласно этому небольшому исследованию, куркумин так же эффективен, как антидепрессант.
Депрессия также связана со снижением уровня BDNF и сокращением гиппокампа, области мозга, играющей роль в обучении и памяти. Куркумин может помочь повысить уровень BDNF, потенциально обращая вспять некоторые из этих изменений (45).
Есть также некоторые доказательства того, что куркумин может повышать уровень нейротрансмиттеров серотонина и дофамина в мозге (46, 47).

Резюме
Исследование с участием 60 человек с депрессией показало, что куркумин столь же эффективен, как и прозак, в облегчении симптомов заболевания.
10. Куркумин может помочь замедлить старение и бороться с возрастными хроническими заболеваниями
Если куркумин действительно может помочь предотвратить сердечные заболевания, рак и болезнь Альцгеймера, он также может способствовать долголетию.
Это говорит о том, что куркумин может иметь потенциал в качестве добавки против старения (48).
Учитывая, что окисление и воспаление играют роль в старении, эффект куркумина может выходить далеко за рамки простого предотвращения болезней (49).
Резюме
Благодаря своим многочисленным положительным эффектам для здоровья, таким как способность предотвращать сердечные заболевания, болезнь Альцгеймера и рак, куркумин может способствовать долголетию.
Практический результат
Куркума, и особенно ее наиболее активное соединение, куркумин, обладают многими научно доказанными полезными свойствами для здоровья, такими как способность улучшать здоровье сердца и предотвращать болезнь Альцгеймера и рак.

Это мощное противовоспалительное и антиоксидантное средство. Это также может помочь улучшить симптомы депрессии и артрита.
Хотя эти преимущества возможны, в настоящее время они ограничены из-за недостаточной биодоступности куркумина, и необходимы дополнительные исследования.
Верна ли Песня о корнях Хитаэглира из Кольца Власти?
Автор Эндрю Андерсон
Делиться Твитнуть Делиться Делиться Делиться Электронная почта
Что открывает нам эта загадочная легенда о происхождении мифрила?
Изображение через Prime VideoПримечание редактора: ниже приведены спойлеры к эпизодам 1-5 «Кольца власти».
В пятом эпизоде Кольца Власти Элронд ( Роберт Арамайо ) был вынужден рассказать малоизвестную легенду об эльфе, сражающемся с Балрогом на вершине Туманных гор, под названием «Песнь корней Хитаэглира».
 Верховный король Гил-галад ( Бенджамин Уокер ), кажется, верит, что эта легенда верна, и принимает многие из своих недавних решений, основанных на этом убеждении. Из-за того, как был создан мифрил, король считает, что у металла есть какая-то божественная цель, которая будет спасением всех эльфов в Средиземье, поэтому он сосредоточился на том, чтобы Элронд восстановил свои отношения с Дурином ( Оуайн Артур ). Тем не менее, в теории короля Гил-галада есть много предположений, мотивирующих его действия, и может оказаться, что его желание получить мифрил для спасения эльфов может привести к катастрофе.
Верховный король Гил-галад ( Бенджамин Уокер ), кажется, верит, что эта легенда верна, и принимает многие из своих недавних решений, основанных на этом убеждении. Из-за того, как был создан мифрил, король считает, что у металла есть какая-то божественная цель, которая будет спасением всех эльфов в Средиземье, поэтому он сосредоточился на том, чтобы Элронд восстановил свои отношения с Дурином ( Оуайн Артур ). Тем не менее, в теории короля Гил-галада есть много предположений, мотивирующих его действия, и может оказаться, что его желание получить мифрил для спасения эльфов может привести к катастрофе.Что на самом деле происходит в «Песне о корнях Хитаэглира»? Изображение
через Prime Video«Песнь о корнях Хитаэглира» повествует об одиноком эльфе на вершине Туманных гор, пытающемся защитить дерево. Легенда гласит, что именно это дерево было укрытием для одного из потерянных сильмариллов. Сильмарил — один из трех невероятно мощных и красивых драгоценных камней, созданных до первой эпохи и содержащих свет Двух Древ Валинора.
 Чтобы защитить сильмариль от разрушения нападающим Балрогом, неизвестный эльф излил весь свой свет, который вы можете считать жизненной силой, в корни дерева. Одновременно огненный кнут Балрога хлестнул по дереву, и в дерево ударила огромная молния. Сочетание энергий чистого света эльфа, огня Балрога, света сильмарила и молнии отправило магию сильмарила глубоко в Туманную гору, создав тем самым минерал мифрил.
Чтобы защитить сильмариль от разрушения нападающим Балрогом, неизвестный эльф излил весь свой свет, который вы можете считать жизненной силой, в корни дерева. Одновременно огненный кнут Балрога хлестнул по дереву, и в дерево ударила огромная молния. Сочетание энергий чистого света эльфа, огня Балрога, света сильмарила и молнии отправило магию сильмарила глубоко в Туманную гору, создав тем самым минерал мифрил.Истоки Казад-дума в Туманных горах
Королевство Дурина — Казад-дум, величайший город гномов в истории Средиземья в самом сердце Туманных гор. В Tolkien lore Дурин I пробирался по восточной стороне Мглистых гор до того, как первая эпоха начала искать новый дом. Однажды ночью он наткнулся на озеро и, отдыхая, чтобы заглянуть в него, увидел себя в спокойной зеркальной глади воды с короной из семи звезд над головой. Он воспринял это как знак с небес, что он нашел свой дом, и начал работать с восточного берега горы, чтобы создать Кхазад-Дум, и назвал озеро у входа Зеркальной Топью.
 Во времена правления старого Дурина III в этих первых нескольких эпизодах Кольца Власти , гномы добывали гору и развивали свой город на протяжении тысячелетий. Зрители слышат, как Дурин IV упоминает Миррормир, когда Элронд подслушивает, чтобы узнать, что скрывал Дурин, и секретная шахта, где Дурин добывает мифрил, находится под этим озером.
Во времена правления старого Дурина III в этих первых нескольких эпизодах Кольца Власти , гномы добывали гору и развивали свой город на протяжении тысячелетий. Зрители слышат, как Дурин IV упоминает Миррормир, когда Элронд подслушивает, чтобы узнать, что скрывал Дурин, и секретная шахта, где Дурин добывает мифрил, находится под этим озером.СВЯЗАННО: «Кольца власти»: Назанин Бониади обсуждает путь Бронуин к лидерству
Мифрил — один из самых ценных материалов в Средиземье
Изображение через New Line CinemaМифрил желанен многими из самых могущественных существ Средиземья. Он гораздо чаще встречается в первые две эпохи и известен своим легким и почти неразрушимым составом, и, что важно, его можно найти только в Туманных горах. Поклонники Властелин колец и Хоббит узнают слово мифрил из-за рубашки, которую носят Бильбо ( Мартин Фриман ) и Фродо ( Элайджа Вуд ).
 Эта легкая броня бесчисленное количество раз спасала их в приключениях. Галадриэль ( Cate Blanchett ) кольцо в фильмах Неня, сделано из мифрила. Двери Дурина, которые Гэндальф ( Ян МакКеллен ) забывает, как открыть, когда Братство пыталось проникнуть в шахты Мории, облицованы Этильденом, новым сплавом, который Келебримбор ( Чарльз Эдвардс ) создал с использованием мифрила. . Из него делали лунные буквы, поэтому дверь можно было увидеть только при лунном или звездном свете. Войдя в третью эпоху, мифрил стал гораздо более редким и дорогим, чем раньше. Гэндальф рассказывает сообществу о богатствах и богатстве, которые они получили от добычи мифрила, и о том, как гномы «копались слишком жадно и слишком глубоко и потревожили то, от чего они бежали, проклятие Дурина». Гномы разбудили Балрога, который спал глубоко в горах, и он уничтожил большую часть Казад-дума, заставив гномов покинуть свой дом. Когда добыча мифрила была фактически прекращена, цена на металл стала неизмеримой.
Эта легкая броня бесчисленное количество раз спасала их в приключениях. Галадриэль ( Cate Blanchett ) кольцо в фильмах Неня, сделано из мифрила. Двери Дурина, которые Гэндальф ( Ян МакКеллен ) забывает, как открыть, когда Братство пыталось проникнуть в шахты Мории, облицованы Этильденом, новым сплавом, который Келебримбор ( Чарльз Эдвардс ) создал с использованием мифрила. . Из него делали лунные буквы, поэтому дверь можно было увидеть только при лунном или звездном свете. Войдя в третью эпоху, мифрил стал гораздо более редким и дорогим, чем раньше. Гэндальф рассказывает сообществу о богатствах и богатстве, которые они получили от добычи мифрила, и о том, как гномы «копались слишком жадно и слишком глубоко и потревожили то, от чего они бежали, проклятие Дурина». Гномы разбудили Балрога, который спал глубоко в горах, и он уничтожил большую часть Казад-дума, заставив гномов покинуть свой дом. Когда добыча мифрила была фактически прекращена, цена на металл стала неизмеримой.
Правдива ли легенда из «Песни о корнях Хитаэглира»?
Невероятная история происхождения мифрила, которую Кольца Власти представили зрителям в последнем эпизоде, представлена как легенда, в которую король, кажется, верит, но это не относится к большинству эльфов. Когда Элронда просят рассказать об этом, он говорит, что это «малоизвестная легенда, которую большинство считает недостоверной», историю, которую все знали, но, вероятно, считали легендой. Кажется странным, что Верховный Король так сильно верил в легенду, которую большинство представителей его рода назвали бы недостоверной, но когда вы слышите, как он описывает силу, созданную в той легендарной битве: «Такая же чистая и светлая, как хорошая, такая же сильная и непреклонный, как зло», становится очевидным, каковы его мотивы. Когда он показывает Элронду дерево и пожирающую его болезнь, он говорит, что это пророчество о гибели всего эльфийского рода. Он считает, что свет Валар — единственное, что спасет эльфов.
 Поскольку в Песне о корнях Хитаэглира рассказывается о сильмариле, содержащем свет Валар, магия которого распространилась на гору, он считает, что мифрил, созданный из него, буквально содержит свет Валар. Вот почему эльфам нужен мифрил, чтобы спасти свое существование в Средиземье. Независимо от того, есть ли за этой легендой какое-либо доверие, кажется, что она заставила Верховного Короля стать одержимым получением как можно большего количества этого, чтобы спасти свой народ.
Поскольку в Песне о корнях Хитаэглира рассказывается о сильмариле, содержащем свет Валар, магия которого распространилась на гору, он считает, что мифрил, созданный из него, буквально содержит свет Валар. Вот почему эльфам нужен мифрил, чтобы спасти свое существование в Средиземье. Независимо от того, есть ли за этой легендой какое-либо доверие, кажется, что она заставила Верховного Короля стать одержимым получением как можно большего количества этого, чтобы спасти свой народ.Кто мог быть Сауроном в этот момент в «Кольцах власти»?
Читать Далее
Делиться Твитнуть Делиться Делиться Делиться Эл. адрес
Связанные темы
- Функции телевизора
- Властелин колец: Кольца власти (2022)
Об авторе
Эндрю Андерсон (опубликовано 13 статей)
Еще от Эндрю Андерсона
Комментарий
Подпишитесь на нашу рассылку
Подпишитесь на информационный бюллетень Collider, чтобы получать эксклюзивные новости, функции, рекомендации по потоковой передаче и многое другое
Нажмите здесь, чтобы подписаться
12 Квадратные и кубические корни Эффективные занятия
Каждый год в начале учебного года я преподаю квадратные и кубические корни.
 Тема и простая, и веселая. Мне нравится, что мы делаем это в начале года, потому что это выигрыш для студентов. Они могут «получить это», и они начинают с некоторой уверенностью. Это закладывает основу для аппроксимации иррациональных чисел и позволяет нам с легкостью начать учебный год.
Тема и простая, и веселая. Мне нравится, что мы делаем это в начале года, потому что это выигрыш для студентов. Они могут «получить это», и они начинают с некоторой уверенностью. Это закладывает основу для аппроксимации иррациональных чисел и позволяет нам с легкостью начать учебный год.Я бы хотел, чтобы у меня было больше времени, чтобы проводить больше занятий с квадратным корнем и кубическим корнем со студентами, но первые несколько дней в школе заполнены знакомством с моими учениками и объяснением процедур. Таким образом, я могу сделать только несколько из них. Нам действительно весело, и студенты довольны своими достижениями. Каждый год я обязательно пробую хотя бы одну вещь, новинку для этого устройства. Мне нравится принимать вызов, и это не дает мне войти в рутину.
Когда я учился в колледже, я работал помощником учителя у нескольких учеников ELL в местной средней школе. Я помню одного учителя, у которого были диапозитивы, которые он показывал классу, и на одном из них было пятно.
 Было совершенно очевидно, что он использовал один и тот же слайд из года в год, и он не мог потрудиться исправить пятно. Этот опыт навсегда запечатлелся в моей памяти. Я никогда не хочу, чтобы мои ученики думали, что делать что-то особенное для них — слишком большая работа для меня. Эти действия могут быть легко реализованы, но они также могут сделать процесс обучения более особенным и не грязным для учащихся.
Было совершенно очевидно, что он использовал один и тот же слайд из года в год, и он не мог потрудиться исправить пятно. Этот опыт навсегда запечатлелся в моей памяти. Я никогда не хочу, чтобы мои ученики думали, что делать что-то особенное для них — слишком большая работа для меня. Эти действия могут быть легко реализованы, но они также могут сделать процесс обучения более особенным и не грязным для учащихся.Ниже приведен список упражнений, которые отлично подходят для демонстрации учащимся квадратных чисел, чисел в кубе, квадратных и кубических корней. Я надеюсь, что есть парочка, которую вы можете взять и использовать, чтобы сделать свой класс более крутым (я знаю, что это не то слово, но оно должно быть!)
- Лабиринт квадратных и кубических корней
- Крестики-нолики
- Эквивалентно ли…?
- Построить башню Упражнение
- Игра «Соответствие»
- Мнемонические устройства для идеальных кубических корней
- Квадратный номер Cheez-It Activity
- Сколько кубиков может поместиться?
- Шмуп Видео
- Большая головоломка с квадратными корнями
- Сделать часы или календарь из квадрата и кубиков
- Решение уравнений с квадратными и кубическими корнями KAHOOT
Вот небольшое описание того, как каждый из них выглядит в классе:
Что ж, если вы читали мои посты о математических занятиях, то уже знаете, что я люблю лабиринты! А еще лучше, мои дети любят проходить эти лабиринты.
 В течение первых двух дней в школе я просил учеников пройти эти 3 лабиринта на квадратных и кубических корнях, и я слышал от нескольких учеников, что они любовь лабиринты. Они настолько увлечены этой деятельностью, что почти кажется, что они даже не работают. Лабиринты для этой конкретной темы быстро и легко. Я использую их в начале урока как колокольчик. Когда я хожу по комнате, я даю ученикам обратную связь и штампую их бумагу, когда они точно завершают лабиринт.
В течение первых двух дней в школе я просил учеников пройти эти 3 лабиринта на квадратных и кубических корнях, и я слышал от нескольких учеников, что они любовь лабиринты. Они настолько увлечены этой деятельностью, что почти кажется, что они даже не работают. Лабиринты для этой конкретной темы быстро и легко. Я использую их в начале урока как колокольчик. Когда я хожу по комнате, я даю ученикам обратную связь и штампую их бумагу, когда они точно завершают лабиринт.Чтобы дать учащимся еще больше практики и развить беглость речи, я создал второй набор из трех лабиринтов с квадратными и кубическими корнями. Всего между этими 6 лабиринтами студенты получают много отличной практики.
Если вы любите лабиринты так же сильно, как и я, вам нужно вступить в клуб «Лабиринт месяца» (просто нажмите на эту ссылку). Когда вы регистрируетесь, вы получаете бесплатный эксклюзивный лабиринт для средней школы по математике, отправленный прямо на ваш почтовый ящик.
 Проверьте это!
Проверьте это!Это отличное совместное занятие для детей, которое вовлекает их и действительно рассказывает о математике. Мне нравится видеть, как они используют свою стратегию (или отсутствие стратегии) в играх в крестики-нолики, пока они практикуют квадратные и кубические корни. Это отличное занятие с губкой, потому что оно не занимает много времени, но предлагает немного дополнительной практики. Мне нравится иметь его под рукой в течение года в качестве дополнительного занятия для циклического обзора.
Вы когда-нибудь играли в игру «Угадай, кто»? Это настольная игра, которую я любил в детстве. Когда я впервые начал создавать свои собственные ресурсы, это был один из первых, которые я создал. Это особенно хорошо работает для студентов с особыми потребностями и детей, которые учатся говорить по-английски. Студенты тянут карту из колоды, а затем другой человек пытается выяснить, что это за карта. На карточках изображены квадратные и кубические числа в разной форме.
 Так же, как в «Угадай, кто?» вы можете исключить ответы, задавая друг другу вопросы «да» или «нет».
Так же, как в «Угадай, кто?» вы можете исключить ответы, задавая друг другу вопросы «да» или «нет».Я наткнулся на эту активность на Pinterest. Похоже, это не займет много времени, и студенты смогут увидеть взаимосвязь между различными квадратными числами. По сути, учащиеся делают небольшую башню из бумажных квадратов, чтобы увидеть визуальное представление квадратных чисел. Башни идеально подходят для того, чтобы записать их в интерактивный блокнот, чтобы учащиеся могли обращаться к ним позже. Это быстрая идея, к которой вы сможете направлять студентов на протяжении всего модуля и в течение года.
Эта игра на сопоставление подходит для работы с учащимися специального образования, ELL и любыми другими учащимися, у которых есть проблемы со словарным запасом. Иногда мы предполагаем, что все они знают терминологию, и правда в том, что многие студенты не знают словарный запас, связанный с квадратными корнями и кубическими корнями. Это задание на сопоставление дает им возможность произнести «кубический корень из 125» или «квадратный корень из 81» несколько раз.
 Я использовал его со своими учениками в моем классе математической лаборатории на протяжении многих лет, и он работает как отличная поддержка для них.
Я использовал его со своими учениками в моем классе математической лаборатории на протяжении многих лет, и он работает как отличная поддержка для них.Иногда в математике есть вещи, которые нелегко выучить математически. Не так-то просто запомнить, что кубический корень из 343 равен 7. Несколько лет назад меня сводило с ума вопрос, например, что такое куб из 343 в районном эталонном тесте, и только около 80 процентов дети поймут это правильно. Именно тогда я взял дело в свои руки и придумал несколько мнемонических приемов для запоминания кубических корней. Они не основаны на математике, а просто помогают легко запомнить кубические корни от 1 до 10.
Если вы хотите использовать их в своих классах, нажмите здесь и получите подарок. Он включает в себя мнемонические устройства и несколько различных способов, которыми вы можете практиковать их со своими учениками. С тех пор, как я начал использовать их и позволить детям придумывать свои собственные, я, честно говоря, получаю, что около 98 процентов учащихся получают ответы на вопросы о кубическом корне прямо на тесте.

Я не пробовал это задание в своем классе, но ученики любят использовать еду, когда занимаются математикой. У меня аллергия на глютен, поэтому Cheez-It не для меня, но мне нравится, как это занятие привлекает студентов. В этом упражнении у учащихся есть возможность построить несколько квадратных чисел с помощью Cheez-Its. Я уверен, что они запомнят это надолго.
Сколько кубиков поместится?
Иногда для урока просто необходим хороший упреждающий набор. Демонстрация отлично работает, чтобы заставить студентов задуматься и представить тему. Все, что вам нужно, это куб размером около 3-5 дюймов. Затем возьмите кубик размером один дюйм или один сантиметр и спросите учащихся, сколько кубиков размером один дюйм поместится в больший куб. Они делают прогноз, а затем объясняют, почему они так думают, на доске. Вы получите всевозможные предсказания. Прогнозов будет варьироваться от слишком мало до слишком много. Как только учащиеся увидят закономерность с числами в кубе, они станут намного лучше предсказывать.

Еще один способ создать предысторию в упреждающем наборе — просмотреть видео. Мне нравятся видео Shmoop, потому что они глупые. Обычно я даю студентам один или два вопроса, на которые они должны ответить во время просмотра видео. Часто я показываю видео два раза классу, а затем мы обсуждаем вопросы.
Возможный вопрос для этого видео:
Что обозначает символ квадратного корня?
Какова формула кубического корня?
Опишите что-то новое, что вы узнали из этого видео.
Мои продвинутые математические классы будут решать эту головоломку с партнером. Они должны решить головоломку и знать квадратные корни. Это немного усложняет практику. Им нужно немного больше времени, чтобы убедиться, что они делают это правильно. Некоторые из моих продвинутых учеников имеют тенденцию работать слишком быстро. Эта головоломка немного их замедляет. Они кажутся такими успешными, когда они закончили. Эта головоломка была создана MathCathy и доступна на сайте Teachers Pay Teachers.

Создание часов или календаря с помощью Radicals
У одного из моих коллег были часы с квадратным корнем для часов на часах. Недавно я видел похожий календарь. Это был бы классный проект, над которым работали бы быстрые финишеры в течение этого модуля. Они могут быть настолько умны, насколько захотят, чтобы создать такие часы или календарь. Они могут снять короткое видео, где объяснят свою работу. Я очень хочу попробовать это и посмотреть, как дети справятся с этим.
Наконец, отличный способ изучить квадратные и кубические корни — это игра Kahoot. Студенты с удовольствием демонстрируют свои знания о квадратном корне в дружеском соревновании, и Kahoot — отличный способ сделать это. Для игры ученикам просто необходимо собственное устройство. Затем они вводят код игры и идут. Эта игра — идеальный способ просмотреть и завершить эту тему.
Попробуй что-нибудь…
Надеюсь, ты выберешь одно занятие из этого списка и попробуешь его в своем классе. Со всеми этими идеями вы тот, кто знает, что работает для ваших учеников.

Допустим, ответ 3. Проверим: 3 * 3 = 9 – не подходит.
Пробуем -3. Проверяем: (-3) * (-3) = 9, так как минус на минус дает плюс.
Получается, что \(\sqrt[2]{-9}\) не имеет смысла, так как степень – четная, а подкоренное выражение – отрицательное. Любое число в квадрате будет больше или равно нулю.
| В поисках отличий или как не запутаться в корнях? При работе с четными и нечетными степенями корней важно помнить, что: — корень нечетной степени можно взять из любого числа |
Могут ли получиться разные результаты, если степень корня и подкоренное выражения одинаковые?
Да, такое возможно. Число, извлеченное из корня четной степени, может быть и положительным, и отрицательным, потому что любое число в четной степени будет больше или равно нулю. {1}\)), но нужно не забывать про четность степени.
{1}\)), но нужно не забывать про четность степени.
\[\Large\sqrt[n]{-a} = -\sqrt[n]{a}, n – нечетно\]
\[\Large\sqrt[n]{a * b} = \sqrt[n]{a} * \sqrt[n]{b}\]
\[\Large\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\]
\[\Large\sqrt[n]{\sqrt[m]{a}} = \sqrt[n * m]{a}\]
\[\Large\sqrt[n]{a^{m}} = (\sqrt[n]{a})^{m}\]

 То из них, квадрат которого равен исходному числу, и будет корнем.
То из них, квадрат которого равен исходному числу, и будет корнем.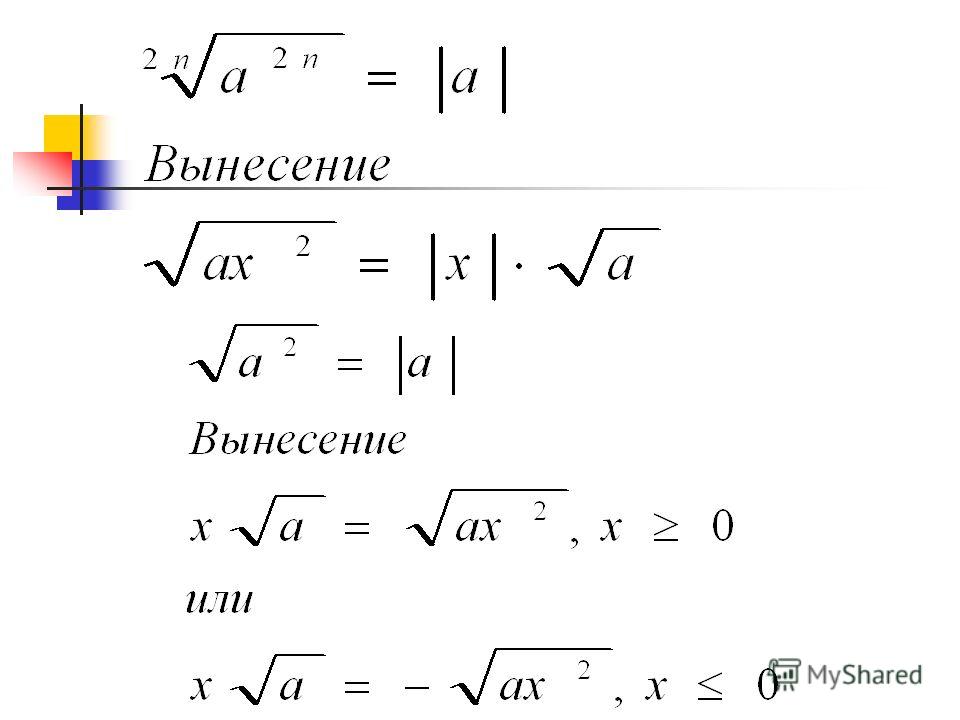 Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!  Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
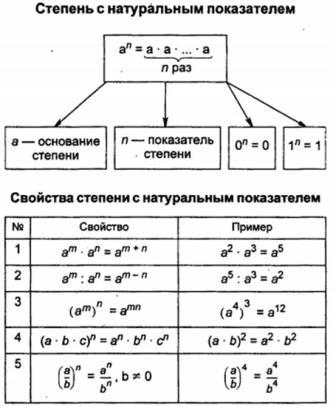
 После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:
После этого извлеките корень из квадратного числа и запишите найденное значение перед знаком корня (под знаком корня останется второй множитель). Например, 6√50 — 2√8 + 5√12. Числа, стоящее перед знаком корня, являются множителями соответствующих корней, а числа под знаком корня – это подкоренные числа (выражения). Вот как решать данную задачу:

 Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3.
Вы получите: (9-4)√5 -2√3 = 5√5 — 2√3. {3} = -125\)
{3} = -125\) {3*\frac{1}{3}} = -6\]
{3*\frac{1}{3}} = -6\] {2}}\) ?
{2}}\) ?
 После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .
После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .



 Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки.
Для этого подбираем два квадратных числа, которые стоят впереди и сзади подкоренного числа в цифровой линейки. Десятичные дроби делят так:
Десятичные дроби делят так: В нашем случае это 8.
В нашем случае это 8.
 megacampus.ru/xbookM0001/index.html?go=part-006*page.htm
megacampus.ru/xbookM0001/index.html?go=part-006*page.htm
 Для любого рациональных чисел r и s из неравенства > следует
Для любого рациональных чисел r и s из неравенства > следует Освободиться от иррациональности в знаменателе дроби
Освободиться от иррациональности в знаменателе дроби  Выполните действие
Выполните действие Упростить:
Упростить: Выполните действие
Выполните действие Упростить:
Упростить:
 А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней. А в ответе оставить их сумму.
А в ответе оставить их сумму. Если да, то снова выполнить второе действие.
Если да, то снова выполнить второе действие. Учитывая это, выражение будет записано так:
Учитывая это, выражение будет записано так: После вынесения множителей из-под знака корня имеем:
После вынесения множителей из-под знака корня имеем:

 коалиция различных политических и членских организаций запустила Lead Together, новый веб-сайт и центр для
коалиция различных политических и членских организаций запустила Lead Together, новый веб-сайт и центр для Лейтенант-губернатор Мандела Барнс, член палаты представителей США Ро Ханна, член палаты представителей штата Иллинойс Делия Рамирес, Бриттани Рамос ДеБаррос и наш собственный исполнительный директор Сульма Ариас!
Лейтенант-губернатор Мандела Барнс, член палаты представителей США Ро Ханна, член палаты представителей штата Иллинойс Делия Рамирес, Бриттани Рамос ДеБаррос и наш собственный исполнительный директор Сульма Ариас!  Сульма является национальным лидером в борьбе за справедливость для иммигрантов и рабочих. Добро пожаловать, Сульма!
Сульма является национальным лидером в борьбе за справедливость для иммигрантов и рабочих. Добро пожаловать, Сульма!
 Одиннадцать из его бывших клерков были назначены Трампом в федеральную скамью. Четверо из них заседают в Апелляционном суде, всего в одном шаге от Верховного суда.
Одиннадцать из его бывших клерков были назначены Трампом в федеральную скамью. Четверо из них заседают в Апелляционном суде, всего в одном шаге от Верховного суда.
 В своих мемуарах «Сын моего дедушки» 2007 года воспоминания Томаса о Пин-Пойнте носят пасторальный характер: он катил велосипедные диски по песчаным дорогам, ловил пескарей в ручье. Переезд его семьи в Саванну, когда Томасу было шесть лет, положил конец этой идиллии. В Пин-Пойнте Томас питался прямо с суши и воды, питаясь «обильным и постоянным запасом свежей пищи: креветками, крабами, раковинами, устрицами, черепахами, цыплятами, свиными ножками, окороками и большим количеством свежих овощей. ». В Саванне, прежде чем он переехал к бабушке и дедушке, он ел ложкой «кукурузные хлопья, смоченные смесью воды и сгущенного молока с сахаром».
В своих мемуарах «Сын моего дедушки» 2007 года воспоминания Томаса о Пин-Пойнте носят пасторальный характер: он катил велосипедные диски по песчаным дорогам, ловил пескарей в ручье. Переезд его семьи в Саванну, когда Томасу было шесть лет, положил конец этой идиллии. В Пин-Пойнте Томас питался прямо с суши и воды, питаясь «обильным и постоянным запасом свежей пищи: креветками, крабами, раковинами, устрицами, черепахами, цыплятами, свиными ножками, окороками и большим количеством свежих овощей. ». В Саванне, прежде чем он переехал к бабушке и дедушке, он ел ложкой «кукурузные хлопья, смоченные смесью воды и сгущенного молока с сахаром». «Если бы он был чернее, — подшучивали его одноклассники, — он был бы синим». Цвет был кодом класса. Смуглая кожа Томаса — наряду с диалектом галла-гичи, который он унаследовал от Пин-Пойнта, — была признаком его низкого статуса и происхождения. «У Кларенса были большие губы, пушистые волосы, и он был буквально черным», — сказал одноклассник Джейн Майер и Джилл Абрамсон в их 19-летнем возрасте.94 книга «Странное правосудие: продажа Кларенса Томаса». «Эти люди были у основания полюса. Ты просто не хотел тусоваться с этими детьми».
«Если бы он был чернее, — подшучивали его одноклассники, — он был бы синим». Цвет был кодом класса. Смуглая кожа Томаса — наряду с диалектом галла-гичи, который он унаследовал от Пин-Пойнта, — была признаком его низкого статуса и происхождения. «У Кларенса были большие губы, пушистые волосы, и он был буквально черным», — сказал одноклассник Джейн Майер и Джилл Абрамсон в их 19-летнем возрасте.94 книга «Странное правосудие: продажа Кларенса Томаса». «Эти люди были у основания полюса. Ты просто не хотел тусоваться с этими детьми». «Мой дедушка был внизу. Они будут смотреть на него свысока. Сейчас все пытаются это приукрасить, но так было на самом деле». Не было до 19В 64 года, когда он перешел в элитную католическую школу-интернат за пределами Саванны, Томас будет делить класс с белыми. Позже он назовет принудительную государством сегрегацию «настолько близкой к тоталитаризму, насколько мне хотелось бы».
«Мой дедушка был внизу. Они будут смотреть на него свысока. Сейчас все пытаются это приукрасить, но так было на самом деле». Не было до 19В 64 года, когда он перешел в элитную католическую школу-интернат за пределами Саванны, Томас будет делить класс с белыми. Позже он назовет принудительную государством сегрегацию «настолько близкой к тоталитаризму, насколько мне хотелось бы». В ходе опроса от четверти до половины одноклассников Томаса согласились со следующими утверждениями: что у чернокожих «меньше амбиций», чем у белых; что у чернокожих «более свободные нравы», чем у белых; что черные люди «пахнут иначе», чем белые. В 19В письме Wall Street Journal Томас написал: «Новая причуда СМИ состоит в том, чтобы постоянно рассказывать о бедственном положении чернокожих студентов колледжей в кампусах, где преобладают белые. Хотите верьте, хотите нет, но проблемы те же, что и 20 лет назад. . . . Главное отличие в том, что СМИ тогда уделяли им мало внимания».
В ходе опроса от четверти до половины одноклассников Томаса согласились со следующими утверждениями: что у чернокожих «меньше амбиций», чем у белых; что у чернокожих «более свободные нравы», чем у белых; что черные люди «пахнут иначе», чем белые. В 19В письме Wall Street Journal Томас написал: «Новая причуда СМИ состоит в том, чтобы постоянно рассказывать о бедственном положении чернокожих студентов колледжей в кампусах, где преобладают белые. Хотите верьте, хотите нет, но проблемы те же, что и 20 лет назад. . . . Главное отличие в том, что СМИ тогда уделяли им мало внимания».
 Женщина черного мужчины — самая красивая из всех женщин.
Женщина черного мужчины — самая красивая из всех женщин.  Когда он видел межрасовую пару, прогуливающуюся по кампусу, он громко спрашивал: «Я вижу черную женщину с белым мужчиной? Как это могло быть?» До 19В 86 году, когда Томас встретил Вирджинию Лэмп, белую девушку, которая станет его второй женой, он выступил против межрасового секса и брака.
Когда он видел межрасовую пару, прогуливающуюся по кампусу, он громко спрашивал: «Я вижу черную женщину с белым мужчиной? Как это могло быть?» До 19В 86 году, когда Томас встретил Вирджинию Лэмп, белую девушку, которая станет его второй женой, он выступил против межрасового секса и брака.
 Он защищал лидера «Черных пантер» Кэтлин Кливер и члена Коммунистической партии Анджелу Дэвис, которые бежали от американского правительства из-за радикальных причастностей и обвинений в преступной деятельности. Когда на слушаниях по его утверждению его спросили, чем он занимается, Томас ответил: «Английская литература». Когда его спросили, в чем он пренебрегает, он ответил: «Протест». Его первая поездка в Вашингтон состояла в том, чтобы выступить против Пентагона и войны во Вьетнаме. Последний митинг, на котором он присутствовал, в Кембридже — один из самых жестоких в истории города, на котором две тысячи полицейских напали на три тысячи протестующих — состоял в том, чтобы потребовать освобождения соучредителя «Черной пантеры» Бобби Сила и лидера «Пантеры» Эрики Хаггинс. «Я никогда не был либералом, — сказал он на выступлении в 1919 году.96. «Я был радикалом». Даже в своих мемуарах Томас отказывается высмеивать причину. «Чем больше я читал о движении за власть черных, — пишет он, — тем больше я хотел быть его частью».
Он защищал лидера «Черных пантер» Кэтлин Кливер и члена Коммунистической партии Анджелу Дэвис, которые бежали от американского правительства из-за радикальных причастностей и обвинений в преступной деятельности. Когда на слушаниях по его утверждению его спросили, чем он занимается, Томас ответил: «Английская литература». Когда его спросили, в чем он пренебрегает, он ответил: «Протест». Его первая поездка в Вашингтон состояла в том, чтобы выступить против Пентагона и войны во Вьетнаме. Последний митинг, на котором он присутствовал, в Кембридже — один из самых жестоких в истории города, на котором две тысячи полицейских напали на три тысячи протестующих — состоял в том, чтобы потребовать освобождения соучредителя «Черной пантеры» Бобби Сила и лидера «Пантеры» Эрики Хаггинс. «Я никогда не был либералом, — сказал он на выступлении в 1919 году.96. «Я был радикалом». Даже в своих мемуарах Томас отказывается высмеивать причину. «Чем больше я читал о движении за власть черных, — пишет он, — тем больше я хотел быть его частью».
 «Как бы ни было больно слышать, что я хорошо учился [в старшей школе], несмотря на мою расу, — писал он позже, — гораздо хуже было чувствовать, что я теперь в Йельском университете из-за этого».
«Как бы ни было больно слышать, что я хорошо учился [в старшей школе], несмотря на мою расу, — писал он позже, — гораздо хуже было чувствовать, что я теперь в Йельском университете из-за этого». Его классическая лирика — «Улыбающиеся лица, улыбающиеся лица лгут» — перекликается с его опытом общения с северными белыми либералами. По его словам, среди достоинств администрации Рейгана был тот факт, что никто не «улыбался вам в лицо».
Его классическая лирика — «Улыбающиеся лица, улыбающиеся лица лгут» — перекликается с его опытом общения с северными белыми либералами. По его словам, среди достоинств администрации Рейгана был тот факт, что никто не «улыбался вам в лицо». «Вы не отделяете сливки от сливок», — ответил профессор. «Ваша судьба, как студента юридического факультета Йельского университета, — стать одним из лидеров юридической профессии. Это произойдет не из-за вас лично, а из-за того, что вы здесь. Именно это происходит со студентами юридического факультета Йельского университета». Но чернокожие студенты Йельского университета были отделены от сливок; действительно, для осуществления этого разделения использовалось отсутствие ранжирования. Ближе к окончанию учебы Томас попытался устроиться в элитную юридическую фирму в Атланте, где не было чернокожих сотрудников. Одним из признаков против него было то, что у него не было оценок. Даже если он приехал из Йельского университета, как его потенциальные работодатели могли знать, насколько он хорош?
«Вы не отделяете сливки от сливок», — ответил профессор. «Ваша судьба, как студента юридического факультета Йельского университета, — стать одним из лидеров юридической профессии. Это произойдет не из-за вас лично, а из-за того, что вы здесь. Именно это происходит со студентами юридического факультета Йельского университета». Но чернокожие студенты Йельского университета были отделены от сливок; действительно, для осуществления этого разделения использовалось отсутствие ранжирования. Ближе к окончанию учебы Томас попытался устроиться в элитную юридическую фирму в Атланте, где не было чернокожих сотрудников. Одним из признаков против него было то, что у него не было оценок. Даже если он приехал из Йельского университета, как его потенциальные работодатели могли знать, насколько он хорош? Если вы хотите использовать службу Power BI, загрузите Supply Chain Sample.pbix, а затем загрузите его в рабочую область в службе Power BI.
Если вы хотите использовать службу Power BI, загрузите Supply Chain Sample.pbix, а затем загрузите его в рабочую область в службе Power BI. Добавьте эти поля в корзину «Объяснение по ». Обратите внимание, что рядом с вашим корневым узлом появился знак плюс. Нажав +, вы можете выбрать, какое поле вы хотите детализировать (вы можете детализировать поля в любом порядке).
Добавьте эти поля в корзину «Объяснение по ». Обратите внимание, что рядом с вашим корневым узлом появился знак плюс. Нажав +, вы можете выбрать, какое поле вы хотите детализировать (вы можете детализировать поля в любом порядке).


 Платформа не дает более высокой абсолютной стоимости, чем Nintendo (19 950 000 долларов против 46 950 000 долларов). Тем не менее, это ценность, которая выделяется.
Платформа не дает более высокой абсолютной стоимости, чем Nintendo (19 950 000 долларов против 46 950 000 долларов). Тем не менее, это ценность, которая выделяется. Вы также можете смешивать различные виды уровней ИИ (переход от высокого значения к низкому значению и обратно к высокому значению):
Вы также можете смешивать различные виды уровней ИИ (переход от высокого значения к низкому значению и обратно к высокому значению):
 Максимальное количество точек данных, которые можно одновременно визуализировать в дереве, — 5000. Мы усекаем уровни, чтобы показать n первых. В настоящее время верхнее n на уровень установлено равным 10.
Максимальное количество точек данных, которые можно одновременно визуализировать в дереве, — 5000. Мы усекаем уровни, чтобы показать n первых. В настоящее время верхнее n на уровень установлено равным 10.
 В большинстве исследований этой травы используются экстракты куркумы, которые содержат в основном сам куркумин, с дозировками, обычно превышающими 1 грамм в день.
В большинстве исследований этой травы используются экстракты куркумы, которые содержат в основном сам куркумин, с дозировками, обычно превышающими 1 грамм в день.
 Однако для получения лечебных результатов требуются очень высокие дозы (8, 9, 10).
Однако для получения лечебных результатов требуются очень высокие дозы (8, 9, 10).


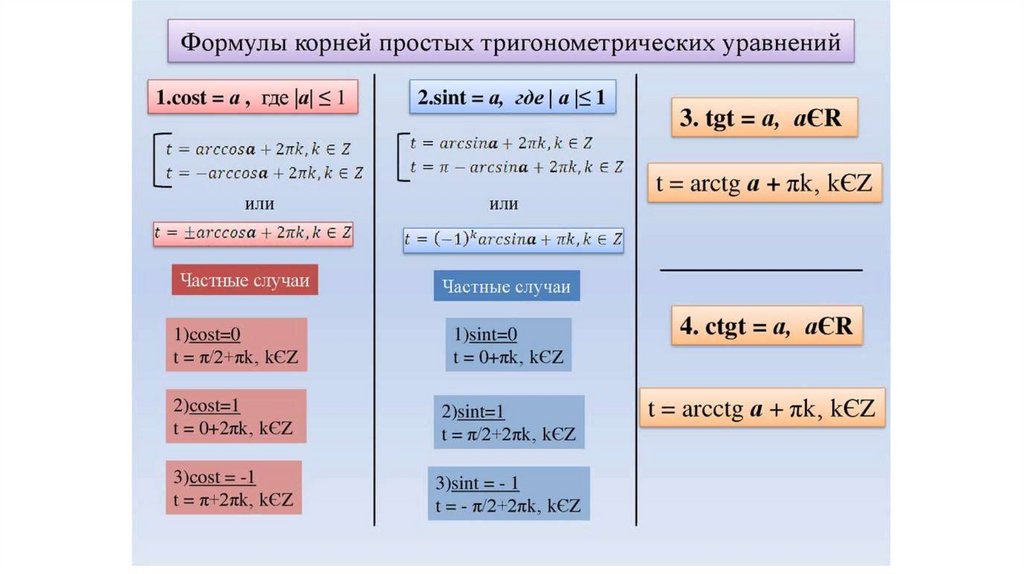 ).
).




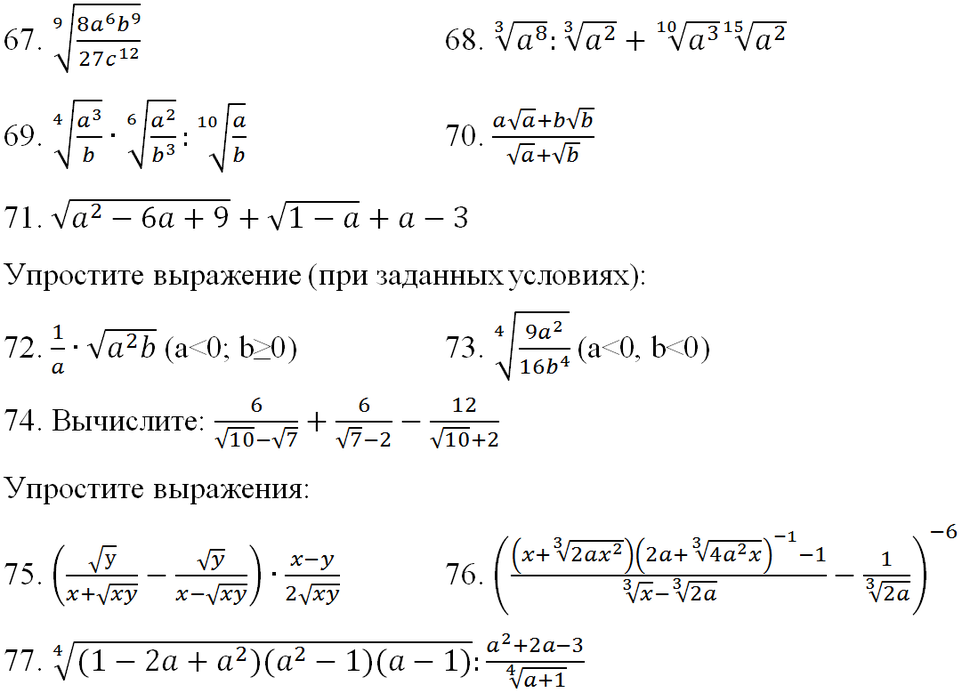
 Верховный король Гил-галад ( Бенджамин Уокер ), кажется, верит, что эта легенда верна, и принимает многие из своих недавних решений, основанных на этом убеждении. Из-за того, как был создан мифрил, король считает, что у металла есть какая-то божественная цель, которая будет спасением всех эльфов в Средиземье, поэтому он сосредоточился на том, чтобы Элронд восстановил свои отношения с Дурином ( Оуайн Артур ). Тем не менее, в теории короля Гил-галада есть много предположений, мотивирующих его действия, и может оказаться, что его желание получить мифрил для спасения эльфов может привести к катастрофе.
Верховный король Гил-галад ( Бенджамин Уокер ), кажется, верит, что эта легенда верна, и принимает многие из своих недавних решений, основанных на этом убеждении. Из-за того, как был создан мифрил, король считает, что у металла есть какая-то божественная цель, которая будет спасением всех эльфов в Средиземье, поэтому он сосредоточился на том, чтобы Элронд восстановил свои отношения с Дурином ( Оуайн Артур ). Тем не менее, в теории короля Гил-галада есть много предположений, мотивирующих его действия, и может оказаться, что его желание получить мифрил для спасения эльфов может привести к катастрофе. Чтобы защитить сильмариль от разрушения нападающим Балрогом, неизвестный эльф излил весь свой свет, который вы можете считать жизненной силой, в корни дерева. Одновременно огненный кнут Балрога хлестнул по дереву, и в дерево ударила огромная молния. Сочетание энергий чистого света эльфа, огня Балрога, света сильмарила и молнии отправило магию сильмарила глубоко в Туманную гору, создав тем самым минерал мифрил.
Чтобы защитить сильмариль от разрушения нападающим Балрогом, неизвестный эльф излил весь свой свет, который вы можете считать жизненной силой, в корни дерева. Одновременно огненный кнут Балрога хлестнул по дереву, и в дерево ударила огромная молния. Сочетание энергий чистого света эльфа, огня Балрога, света сильмарила и молнии отправило магию сильмарила глубоко в Туманную гору, создав тем самым минерал мифрил. Во времена правления старого Дурина III в этих первых нескольких эпизодах Кольца Власти , гномы добывали гору и развивали свой город на протяжении тысячелетий. Зрители слышат, как Дурин IV упоминает Миррормир, когда Элронд подслушивает, чтобы узнать, что скрывал Дурин, и секретная шахта, где Дурин добывает мифрил, находится под этим озером.
Во времена правления старого Дурина III в этих первых нескольких эпизодах Кольца Власти , гномы добывали гору и развивали свой город на протяжении тысячелетий. Зрители слышат, как Дурин IV упоминает Миррормир, когда Элронд подслушивает, чтобы узнать, что скрывал Дурин, и секретная шахта, где Дурин добывает мифрил, находится под этим озером. Эта легкая броня бесчисленное количество раз спасала их в приключениях. Галадриэль ( Cate Blanchett ) кольцо в фильмах Неня, сделано из мифрила. Двери Дурина, которые Гэндальф ( Ян МакКеллен ) забывает, как открыть, когда Братство пыталось проникнуть в шахты Мории, облицованы Этильденом, новым сплавом, который Келебримбор ( Чарльз Эдвардс ) создал с использованием мифрила. . Из него делали лунные буквы, поэтому дверь можно было увидеть только при лунном или звездном свете. Войдя в третью эпоху, мифрил стал гораздо более редким и дорогим, чем раньше. Гэндальф рассказывает сообществу о богатствах и богатстве, которые они получили от добычи мифрила, и о том, как гномы «копались слишком жадно и слишком глубоко и потревожили то, от чего они бежали, проклятие Дурина». Гномы разбудили Балрога, который спал глубоко в горах, и он уничтожил большую часть Казад-дума, заставив гномов покинуть свой дом. Когда добыча мифрила была фактически прекращена, цена на металл стала неизмеримой.
Эта легкая броня бесчисленное количество раз спасала их в приключениях. Галадриэль ( Cate Blanchett ) кольцо в фильмах Неня, сделано из мифрила. Двери Дурина, которые Гэндальф ( Ян МакКеллен ) забывает, как открыть, когда Братство пыталось проникнуть в шахты Мории, облицованы Этильденом, новым сплавом, который Келебримбор ( Чарльз Эдвардс ) создал с использованием мифрила. . Из него делали лунные буквы, поэтому дверь можно было увидеть только при лунном или звездном свете. Войдя в третью эпоху, мифрил стал гораздо более редким и дорогим, чем раньше. Гэндальф рассказывает сообществу о богатствах и богатстве, которые они получили от добычи мифрила, и о том, как гномы «копались слишком жадно и слишком глубоко и потревожили то, от чего они бежали, проклятие Дурина». Гномы разбудили Балрога, который спал глубоко в горах, и он уничтожил большую часть Казад-дума, заставив гномов покинуть свой дом. Когда добыча мифрила была фактически прекращена, цена на металл стала неизмеримой.
 Поскольку в Песне о корнях Хитаэглира рассказывается о сильмариле, содержащем свет Валар, магия которого распространилась на гору, он считает, что мифрил, созданный из него, буквально содержит свет Валар. Вот почему эльфам нужен мифрил, чтобы спасти свое существование в Средиземье. Независимо от того, есть ли за этой легендой какое-либо доверие, кажется, что она заставила Верховного Короля стать одержимым получением как можно большего количества этого, чтобы спасти свой народ.
Поскольку в Песне о корнях Хитаэглира рассказывается о сильмариле, содержащем свет Валар, магия которого распространилась на гору, он считает, что мифрил, созданный из него, буквально содержит свет Валар. Вот почему эльфам нужен мифрил, чтобы спасти свое существование в Средиземье. Независимо от того, есть ли за этой легендой какое-либо доверие, кажется, что она заставила Верховного Короля стать одержимым получением как можно большего количества этого, чтобы спасти свой народ. Тема и простая, и веселая. Мне нравится, что мы делаем это в начале года, потому что это выигрыш для студентов. Они могут «получить это», и они начинают с некоторой уверенностью. Это закладывает основу для аппроксимации иррациональных чисел и позволяет нам с легкостью начать учебный год.
Тема и простая, и веселая. Мне нравится, что мы делаем это в начале года, потому что это выигрыш для студентов. Они могут «получить это», и они начинают с некоторой уверенностью. Это закладывает основу для аппроксимации иррациональных чисел и позволяет нам с легкостью начать учебный год. Было совершенно очевидно, что он использовал один и тот же слайд из года в год, и он не мог потрудиться исправить пятно. Этот опыт навсегда запечатлелся в моей памяти. Я никогда не хочу, чтобы мои ученики думали, что делать что-то особенное для них — слишком большая работа для меня. Эти действия могут быть легко реализованы, но они также могут сделать процесс обучения более особенным и не грязным для учащихся.
Было совершенно очевидно, что он использовал один и тот же слайд из года в год, и он не мог потрудиться исправить пятно. Этот опыт навсегда запечатлелся в моей памяти. Я никогда не хочу, чтобы мои ученики думали, что делать что-то особенное для них — слишком большая работа для меня. Эти действия могут быть легко реализованы, но они также могут сделать процесс обучения более особенным и не грязным для учащихся. В течение первых двух дней в школе я просил учеников пройти эти 3 лабиринта на квадратных и кубических корнях, и я слышал от нескольких учеников, что они любовь лабиринты. Они настолько увлечены этой деятельностью, что почти кажется, что они даже не работают. Лабиринты для этой конкретной темы быстро и легко. Я использую их в начале урока как колокольчик. Когда я хожу по комнате, я даю ученикам обратную связь и штампую их бумагу, когда они точно завершают лабиринт.
В течение первых двух дней в школе я просил учеников пройти эти 3 лабиринта на квадратных и кубических корнях, и я слышал от нескольких учеников, что они любовь лабиринты. Они настолько увлечены этой деятельностью, что почти кажется, что они даже не работают. Лабиринты для этой конкретной темы быстро и легко. Я использую их в начале урока как колокольчик. Когда я хожу по комнате, я даю ученикам обратную связь и штампую их бумагу, когда они точно завершают лабиринт. Проверьте это!
Проверьте это! Так же, как в «Угадай, кто?» вы можете исключить ответы, задавая друг другу вопросы «да» или «нет».
Так же, как в «Угадай, кто?» вы можете исключить ответы, задавая друг другу вопросы «да» или «нет». Я использовал его со своими учениками в моем классе математической лаборатории на протяжении многих лет, и он работает как отличная поддержка для них.
Я использовал его со своими учениками в моем классе математической лаборатории на протяжении многих лет, и он работает как отличная поддержка для них.