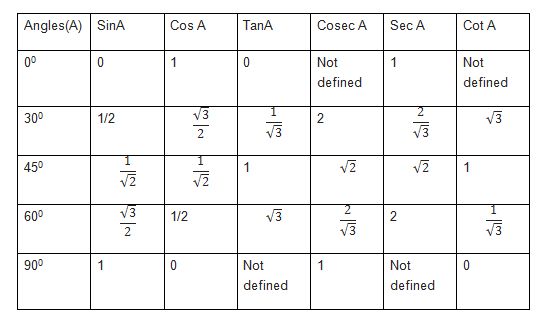
|
|
| |||||||||||||||||||||
Таблица Брадиса — ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОТ АРГУМЕНТА В РАДИАНАХ
Тригонометрически функции от аргумента в радианах (Таблица Брадиса 12)
Таблица брадиса 12 не содержит тех готовых поправок, какие даны почти во всех других таблицах брадиса, а потому, чтобы получить значение тригонометрической функции для промежуточного значения аргумента, надо полностью провести операцию линейного интерполирования, о которой говорится ниже. Особой осторожности требует интерполирование значений тангенса: необходимо предварительно выяснить, законна ли на данном участке таблицы операция линейного интерполирования, т. е. имеется ли на этом участке достаточно равномерное изменение функции; если не имеется, то значения функции надо округлить, чтобы их изменение стало почти равномерным. Так, при изменении х от 1,30 до 1,12 табличные разности равны 2,0143 — 1,9648 — 0,0495 и 2,0660 — 2,0143 = 0,0517, линейная интерполяция недопустима, но становится допустимой, если предварительно округлить табличные значения до тысячных, так как 2,014 — 1,965 = 0,049 и 2,066 — 2,014 = 0,052, соседние табличные разности отличаются одна от другой меньше чем на 4 единицы разряда последней цифры.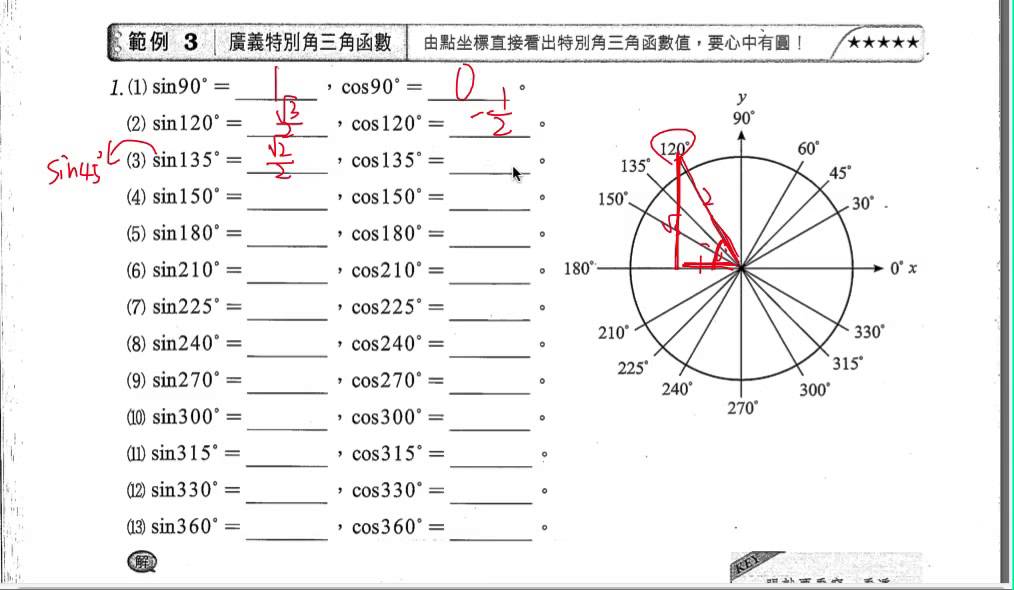
| X | sin х | cos x | tg x | X | sin x | cos x | tg x | sin x | cos x | tg x | |
| 0,00 | 0,0000 | 1,0000 | 0,0000 | 0,40 | 0,3894 | 0,9211 | 0,4228 | 0,80 | 0,7174 | 0,6967 | 1,0296 |
| 0,01 | 0100 | 1,0000 | 0100 | 0,41 | 3986 | 9171 | 4346 | 0,81 | 7243 | 6895 | 0505 |
| 0,02 | 0200 | 0,9998 | 0200 | 0,42 | 4078 | 9131 | 4466 | 0,82 | 7311 | 6822 | 0717 |
| 0,03 | 0300 | 9996 | 0300 | 0,43 | 4169 | 9090 | 4586 | 0,83 | 7379 | 6749 | 0934 |
| 0,04 | 0400 | 9992 | 0400 | 0,44 | 4259 | 9048 | 4708 | 0,84 | 7446 | 6675 | 1156 |
| 0,05 | 0500 | 9988 | 0500 | 0,45 | 4350 | 9004 | 4831 | 0,85 | 7513 | 6600 | 1383 |
| 0,06 | 0600 | 9982 | 0601 | 4439 | 8961 | 4954 | 0,86 | 7578 | 6524 | 1616 | |
| 0,07 | 0699 | 9976 | 0701 | 0,47 | 4529 | 8916 | 5080 | 0,87 | 7643 | 6448 | 1853 |
| 0,08 | 0799 | 9968 | 0802 | 0,48 | 4618 | 8870 | 5206 | 0,88 | 7707 | 6372 | 2097 |
| 0,09 | 0899 | 9960 | 0902 | 0,49 | 4706 | 8823 | 5334 | 0,89 | 7771 | 6294 | 2346 |
| 0,10 | 0,0998 | 0,9950 | 0,1003 | 0,50 | 0,4794 | 0,8776 | 0,5463 | 0,90 | 0,7833 | 0,6216 | 1,2602 |
| 0,11 | 1098 | 9940 | 1105 | 0,51 | 4882 | 8727 | 5594 | 0,91 | 7895 | 6137 | 2864 |
| 0,12 | 1197 | 9928 | 1206 | 0,52 | 4969 | 8678 | 5726 | 0,92 | 7956 | 6058 | 3133 |
| 0,13 | 1296 | 9916 | 1307 | 0,53 | 5055 | 8628 | 5859 | 0,93 | 8016 | 5978 | 3409 |
| 0,14 | 1395 | 9902 | 1409 | 0,54 | 5141 | 8577 | 5994 | 0,94 | 8076 | 5898 | 3692 |
| 0,15 | 1494 | 9888 | 1511 | o.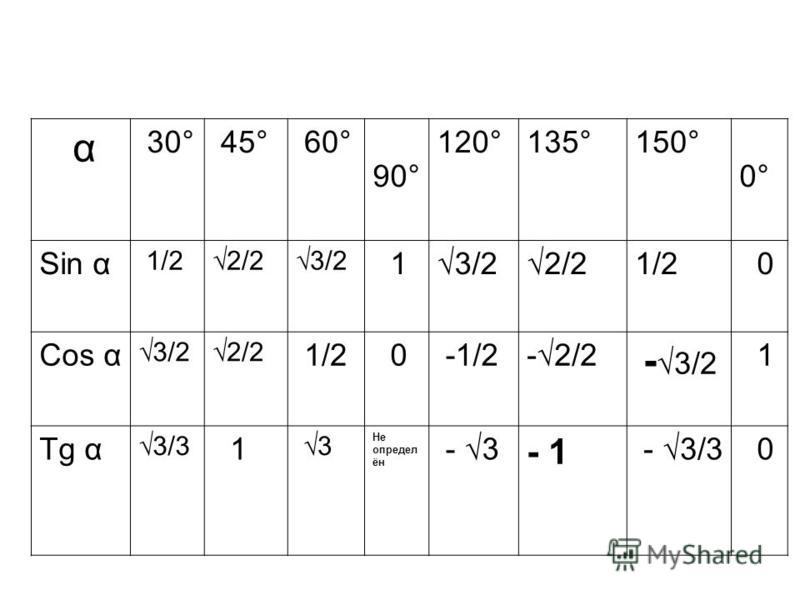 sa sa |
5227 | 8525 | 6131 | 0,95 | 8134 | 5817 | 3984 |
| 0,16 | 1593 | 9872 | 1614 | 0,56 | 5312 | 8473 | 6269 | 0,96 | 8192 | 5735 | 4284 |
| 0,17 | 1692 | 9856 | 1717 | 0,57 | 5396 | 8419 | 6410 | 0,97 | 8249 | 5653 | 4592 |
| 0,18 | 1790 | 9838 | 1820 | 0,58 | 5480 | 8365 | 6552 | 0,98 | 8305 | 5570 | 4910 |
| 0,19 | 1889 | 9820 | 1923 | 0,59 | 5564 | 8309 | 6696 | 0,99 | 8360 | 5487 | 5237 |
| 0,20 | 0,1987 | 0,9801 | 0,2027 | 0,60 | 0,5646 | 0,8253 | 0,6841 | 1,00 | 0,8415 | 0,5403 | 1,5574 |
| 0,21 | 2085 | 9780 | 2131 | 0,61 | 5729 | 8196 | 6989 | 1,01 | 8468 | 5319 | 5922 |
| 0,22 | 2182 | 9759 | 2236 | 0,62 | 5810 | 8139 | 7139 | 1,02 | 8521 | 5234 | 6281 |
| 0,23 | 2280 | 9737 | 2341 | 0,63 | 5891 | 8080 | 7291 | 1,03 | 8573 | 5148 | 6652 |
| 0,24 | 2377 | 9713 | 2447 | 0,64 | 5972 | 8021 | 7445 | 1,04 | 8624 | 5062 | 7036 |
| 0,25 | 2474 | 9689 | 2553 | 0,65 | 6052 | 7961 | 7602 | 1,05 | 8674 | 4976 | 7433 |
| 0,26 | 2571 | 9664 | 2660 | 0,66 | 6131 | 7900 | 7761 | 1,06 | 8724 | 4889 | 7844 |
| 0,27 | 2667 | 9638 | 2768 | 0,67 | 6210 |
7838 | 7923 | 1,07 | 8772 | 4801 | 8270 |
| 0,28 | 2764 | 9611 | 2875 | 0,68 | 6288 | 7776 | 8087 | 1,08 | 8820 | 4713 | 8712 |
| 0,29 | 2860 | 9582 | 2984 | 0,69 | 6365 | 7712 | 8253 | 1,09 | 8866 | 4625 | 9171 |
| 0,30 | 0,2955 | 0,9553 | 0,3093 | 0,70 | 0,6442 | 0,7648 | 0,8423 | 1,10 | 0,8912 | 0,4536 | 1,9648 |
| 0,31 | 3051 | 9523 | 3203 | 0,71 | 6518 | 7584 | 8595 | 1,11 | 8957 | 4447 | 2,0143 |
| 0,32 | 3146 | 9492 | 3314 | 0,72 | 6594 | 7518 | 8771 | 1,12 | 9001 | 4357 | 0660 |
| 0,33 | 3240 | 9460 | 3425 | 0,73 | 6669 | 7452 | 8949 | 1,13 | 9044 | 4267 | 1198 |
| 0,34 | 3335 | 9428 | 3537 | 0,74 | 6743 | 7385 | 9131 | 1,14 | 9086 | 4176 | 1759 |
| 0,35 | 3429 | 9394 | 3650 | 0,75 | 6816 | 7317 | 9316 | 1,15 | 9128 | 4085 | 2345 |
| 0,36 | 3523 | 9359 | 3764 | 0,76 | 6889 | 7248 | 9505 | 1,16 | 9168 | 3993 | 2958 |
| 0,37 | 3616 | 9323 | 3879 | 0,77 | 6961 | 7179 | 9697 | 1,17 | 9208 | 3902 | 3600 |
| 0,38 | 3709 | 9287 | 3994 | 0,78 | 7033 | 7109 | 0,9883 | 1,18 | 9246 | 3809 | 4273 |
| 0,39 | 3802 | 9249 | 4111 | 0,79 | 7104 | 7038 | 1,0092 | 1,19 | 9284 | 3717 | 4979 |
| X | sin х | cos x | tg x | X | sin x | cos x | tg x | X | sin x | cos x | tg x |
| X | sin х | cos x | tg x | X | sin x | cos x | tg x | X | sin x | cos x | tg x |
| 1,20 | 0,9320 | 0,3624 | 2,572 | 1,60 | 0,9996 | — 0,0292 | — 34,233 | 2,00 | 0,9093 | — 0,4161 | — 2,1850 |
| 1,21 | 9356 | 3530 | 650 | 1,61 | 9992 | 0392 | — 25,495 | 2,01 | 9051 | 4252 | 1285 |
| 1,22 | 9391 | 3436 | 733 | 1,62 | 9988 | 0492 | — 20,307 | 2,02 | 9008 | 4342 | 0744 |
| 1,23 | 9425 | 3342 | 820 | 1,63 | 9982 | 0592 | — 16,871 | 2,03 | 8964 | 4432 | 0224 |
| 1,24 | 9458 | 3248 | 912 | 1,64 | 9976 | 0691 | — 14,427 | 2.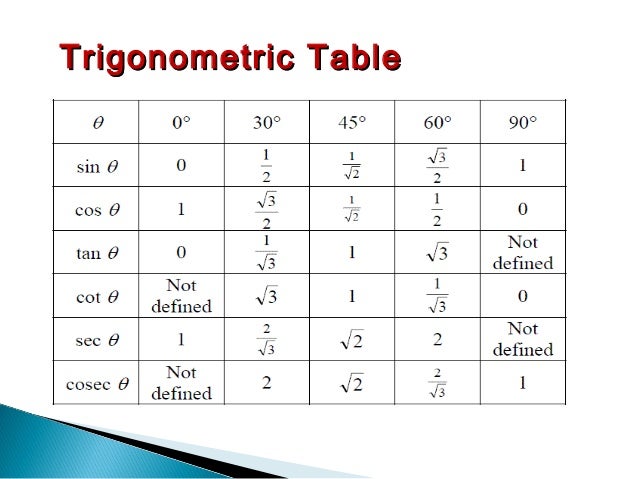 04 04 |
8919 | 4522 | — 1,9725 |
| 1.25 | 9490 | 3153 | 3,010 | 1,65 | 9969 | 0791 | — 12,599 | 2,05 | 8874 | 4611 | 9246 |
| 1,26 | 9521 | 3058 | 113 | 1,66 | 9960 | 0891 | — 11,181 | 2.06 | 8827 | 4699 | 8784 |
| 1,27 | 9551 | 2963 | 224 | 1,67 | 9951 | 0990 | — 10,047 | 2,07 | 8780 | 4787 | 8340 |
| 1,28 | 9580 | 2867 | 341 | 1,68 | 9940 | 1090 | — 9,1208 | 2,08 | 8731 | 4875 | 7911 |
| 1,29 | 9608 | 2771 | 467 | 1,69 | 9929 | 1189 | — 8,3492 | 2,09 | 8682 | 4962 | 7498 |
| 1,30 | 0,9636 | 0,2675 | 3,602 | 1,70 | 0,9917 | — 0,1288 | — 7,6966 | 2,10 | 0,8632 | — 0,5048 | — 1,7098 |
| 1,31 | 9662 | 2579 | 747 | 1,71 | 9903 | 1388 | — 7,1373 | 2,11 | 8581 | 5135 | 6713 |
| 1,32 | 9687 | 2482 | 903 | 1,72 | 9889 | I486 | — 6,6524 | 2,12 | 8529 | 5220 | 6340 |
| 1,33 | 9711 | 2385 | 4,072 | 1,73 | 9874 | 1585 | — 6,2281 | 2,13 | 8477 | 5305 | 5979 |
| 1,34 | 9735 | 2288 | 256 | 1,74 | 9857 | 1684 | — 5,8535 | 2,14 | 8423 | 5390 | 5629 |
| 1,35 | 9757 | 2190 | 455 | 1,75 | 9840 | 1782 | — 5,5204 | 2,15 | 8369 | 5474 | 5290 |
| 1,36 | 9779 | 2092 | 673 | 1,76 | 9822 | 1881 | — 5,2221 | 2,16 | 8314 | 5557 | 4961 |
| 1,37 | 9799 | 1994 | 913 | 1.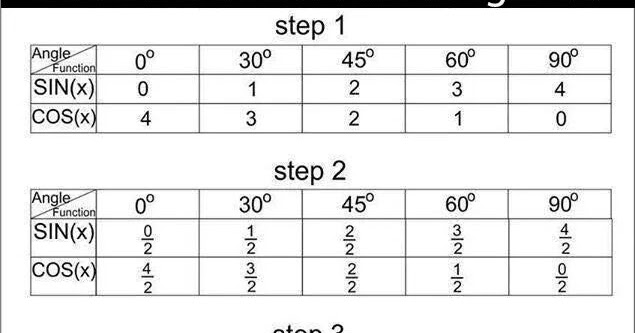 77 77 |
9802 | 1979 | — 4,9534 | 2,17 | 8258 | 5640 | 4642 |
| 1,38 | 9819 | 1896 | 5,177 | 1,78 | 9782 | 2077 | — 4,7101 | 2,18 | 8201 | 5722 | 4332 |
| 1,39 | 9837 | 1798 | 471 | 1,79 | 9761 | 2175 | — 4,4887 | 2,19 | 8143 | 5804 | 4031 |
| 1,40 | 0,9854 | 0,1700 | 5,798 | 1,80 | 0,9738 | — 0,2272 | — 4,2863 | 2,20 | 0,8085 | — 0,5885 | — 1,3738 |
| 1,41 | 9871 | 1601 | 6,165 | 1,81 | 9715 | 2369 | — 4,1005 | 2,21 | 8026 | 5966 | 3453 |
| 1,42 | 9887 | 1502 | 6,581 | 1,82 | 9691 | 2466 | — 3,9294 | 2,22 | 7966 | 6046 | 3176 |
| 1,43 | 9901 | 1403 | 7,055 | 1,83 | 9666 | 2563 | — 3,7712 | 2,23 | 7905 | 6125 | 2906 |
| 1,44 | 9915 | 1304 | 7,602 | 1,84 | 9640 | 2660 | — 3,6245 | 2,24 | 7843 | 6204 | 2643 |
| 1,45 | 9927 | 1205 | 8,238 | 1,85 | 9613 | 2756 | — 3,4881 | 2,25 | 7781 | 6282 | 2386 |
| 1,46 | 9939 | 1106 | 8,989 | 1,86 | 9585 | 2852 | — 3,3608 | 2,26 | 7717 | 6359 | 2136 |
| 1,47 | 9949 | 1006 | 9,887 | 1,87 | 9556 | 2948 | — 3,2419 | 2,27 | 7654 | 6436 | 1892 |
| 1,48 | 9959 | 0907 | 10,983 | 1,88 | 9526 | 3043 | — 3,1304 | 2,28 | 7589 | 6512 | 1653 |
| 1,49 | 9967 | 0807 | 12,350 | 1,89 | 9.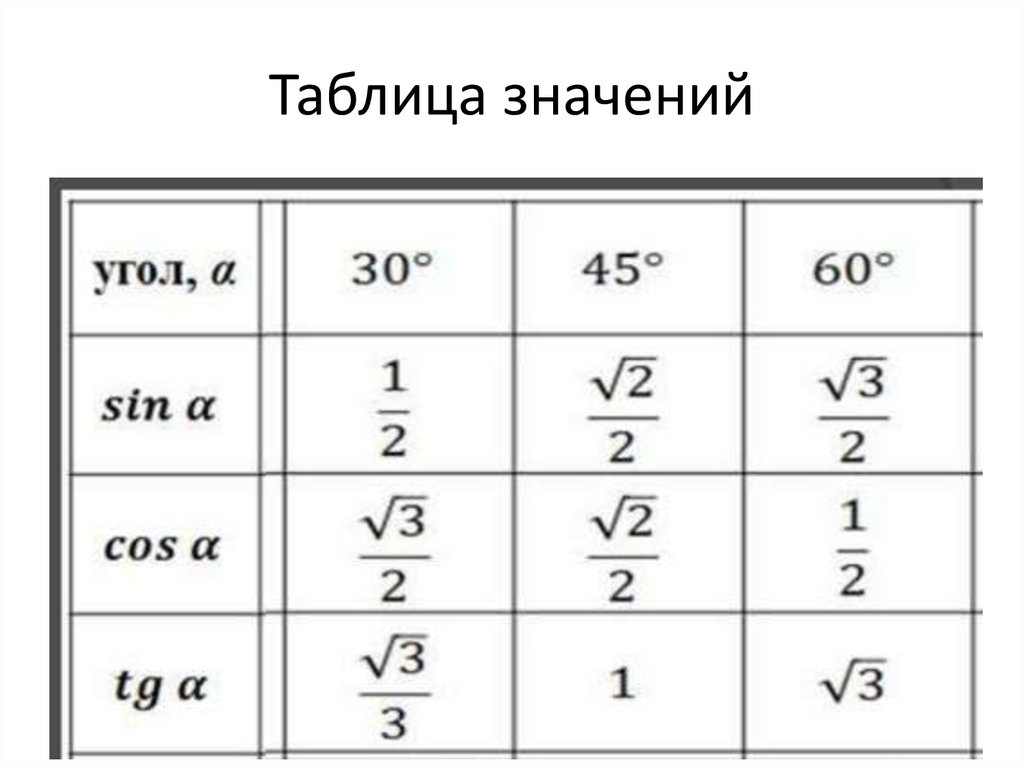 495 495 |
3138 | — 3,0257 | 2,29 | 7523 | 6588 | 1420 |
| 1,50 | 0,9975 | 0,0707 | 14,10 | 1,90 | 0,9463 | — 0,3233 | — 2,9271 | 2,30 | 0,7457 | — 0,6663 | — 1,1192 |
| 1,51 | 9982 | 0608 | 16,43 | 1,91 | 9430 | 3327 | 8341 | 2,31 | 7390 | 6737 | 0969 |
| 1,52 | 9987 | 0508 | 19,67 | 1,92 | 9396 | 3421 | 7463 | 2,32 | 7322 | 6811 | 0751 |
| 1,53 | 9992 | 0408 | 24,50 | 1,93 | 9362 | 3515 | 6632 | 2,33 | 7254 | 6883 | 0638 |
| 1,54 | 9995 | 0308 | 32,46 | 1,94 | 9326 | 3609 | 5843 | 2,34 | 7185 | 6956 | 0329 |
| 1,55 | 9998 | 0208 | 48,08 | 1,95 | 9290 | 3702 | 5095 | 2,35 | 7115 | 7027 | 0125 |
| 1,56 | 9999 | 0108 | 92,62 | 1,96 | 9252 | 3795 | 4383 | 2,36 | 7044 | 7098 | — 0,9924 |
| 1,57 | 1,0000 | 0008 | 1256 | 1,97 | 9214 | 3887 | 3705 | 2,37 | 6973 | 7168 | 9728 |
| 1,58 | 1,0000 | — 0,0092 | — 108,6 | 1,98 | 9174 | 3979 | 3058 | 2,38 | 6901 | 7237 | 9535 |
| 1,59 | 0,9998 | — 0,0192 | — 52,07 | 1,99 | 9134 | 4070 | 2441 | 2,39 | 6828 | 7306 | 9346 |
| X | sin х | cos x | tg x | X | sin X | cos x | tg x | X | sin x | cos x | tg x |
_______________
Источник информации: Брадис В.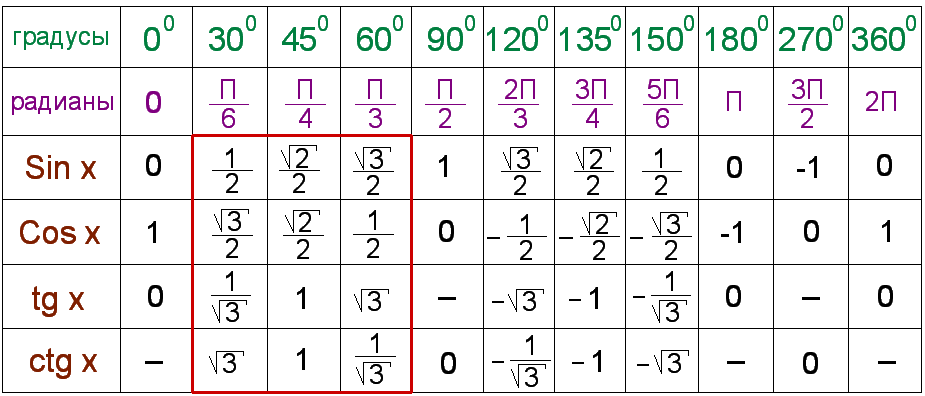 М. Четырехзначные математические таблицы: Для средней школы. / В.М. Брадис . — 57-е изд., — М.: Просвещение, 1990.
М. Четырехзначные математические таблицы: Для средней школы. / В.М. Брадис . — 57-е изд., — М.: Просвещение, 1990.
Таблица значений тангенсов, таблица Брадиса, таблица градусов, углов тангенсов
Вы можете самостоятельно найти тангенс при помощи инженерного онлайн калькулятора
Таблица тангенсов 0° — 180°
|
|
|
Таблица тангенсов 180° — 360°
|
|
|
Тригонометрические функции
Природные тригонометрические функции выражены как
SIN (θ D ) = A / C
= 1 / CSC ( θ D ) = 1 / CSC ( θ D )
= 1 / CSC ( θ D = 1 / CSC ( θ D ) = cos (π / 2 — θ R ) (1), где
θ D = Угол в градусах
θ R = угол в радианах
A
C
COS ( θ D ) = B / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / C / CS ( θ D ) Раздел ( θ D )
= SIN (π / 2 — θ R ) (2)
B
B
0054 CTAN ( θ D ) = A / B
= 1 / COT ( θ D )
D )
= SIN ) 9 = SIN ) 9 = SIN ) ) / cos ( θ D )
= COT (π / 2 — θ R ) (3)
9 A ).0055
b
cot( θ d ) = 1 / tan( θ d )
= cos( θ d ) / sin ( θ D )
= TAN (π / 2 — θ R ) (4)
θ (градусов)
TRIGOMOMOMET θ (DEGREES)
TRIGOMOMOMET θ (градусов)0008 0 to 90 degrees are tabulated below:
- Trigonometric functions in pdf-format
Inverse functions
arcsin (a) = sin -1 (a) (1a)
Arccos (A) = COS -1 (A) (2A)
Arctan (A) = TAN -1 (A) (3A)
-1 (A) (3A)
-1 (A) (3A)
9.0055Формула сложения.
a) cos (b) ± sin (a) sin (b) (5b)
tan (a ± b) = (tan(a) ± tan(b)) / (1 ± tan(a) tan(b)) (5c)
Формула суммы и разности
sin (a) + sin (b) = 2 sin ((a + b)/2) cos ((a + b)/2) (6)
sin (a) — sin (b) = 2 cos ((a + b)/2) sin ((a — b)/2) (6b)
cos (a) + cos (a) (b) = 2 cos ((a + b)/2) cos ((a — b)/2) (6c)
cos (a) — cos (b) = — 2 sin ((a + b )/2) sin ((a — b)/2) (6d)
tan (a) + tan (b) = sin (a + b) / (cos (a) cos (b)) ( 6e)
tan (a) — tan (b) = sin (a — b) / (cos (a) cos (b)) (6f)
Формула продукта
2 sin (a) cos (b) = sin (a — b) + sin (a + b) (7)
2 sin (a) sin (b) (a — b) — cos (a — b) (7b)
2 cos (a) cos (b) = cos (a — b) + cos (a + b) (7c) 9005 Формула углов и степеней
sin (2 a) = 2 sin (a) cos (a) (8)
COS (2 A) = COS 2 (A) — SIN 2 (A) (8B)
COS (2 A) = 2 COS 2 (A) — 1 (8C) )
COS (2 A) = 1 — 2 SIN 2 (A) (8D)
TAN (2 A) = 2 TAN A / (1 — TAN 2 (A) ) (8e)
sin 2 (a) + cos 2 (a) = 1 (8f)
sec 2 (a) = tan 2 (a) + 1 (8g)
Special Triangles
Trigonometric Values
sin(-θ d ) = — SIN (θ D ) (9A)
, где
θ D = угол в градусах
SIN (90 ° + θ D ) = COS (θ D . ) (9b)
) (9b)
SIN (90 ° — θ D ) = COS (θ D ) (9C)
SIN (180 ° + θ D ) = — SIN (θ D ) (9d)
SIN (180 ° — θ D ) = SIN (θ D ) (9E)
SIN (270 ° + θ D ) = — COS (θ D ) (9f)
sin(270° — θ d ) = — cos(θ d ) (9g)
SIN (360 ° + θ D ) = SIN (θ D ) (9H)
SIN (360 ° — θ D ) = — SIN (θ D ) (9H)
COS (-θ D ) = COS (θ D ) (10A)
COS (90 ° + θ D ) = — SIN (θ D ) (10B)
cos(90° — θ d ) = sin(θ d ) (10c)
cos(180° + θ d ) = — cos (θ D ) (10d)
COS (180 ° — θ D ) = — COS (θ D ) (10E)
COS (270 ° + θ D ) = SIN (θ D ) (10F)
COS (270 ° — θ D ) = — SIN (θ D ) (10G)
COS (360 ° + θ d ) = cos(θ d ) (10h)
cos(360° — θ d ) = cos(θ d ) (10H)
TAN (-θ D ) = — TAN (θ D ) (11A)
TAN (90 ° + θ D ) = — COT. ) (11B)
) (11B)
TAN (90 ° — θ D ) = COT (θ D ) (11C)
TAN (180 ° + θ D ) = TAN (θ D DA ) (11d)
tan(180° — θ d ) = — tan(θ d ) (11e)
TAN (270 ° + θ D ) = — COT (θ D ) (11F)
TAN (270 ° — θ D ) = COT (θ D ) (11G. )
TAN (360 ° + θ D ) = TAN (θ D ) (11H)
TAN (360 ° — θ D ) = — TAN (θ D ) ( 11h)
Используя таблицы, найдите значение 2 sin cos при тангенсе 2679…
Перейти к
- Тригонометрические таблицы. Упражнение 19.
- налог на товары и услуги
- Банковское дело
- Акции и дивиденды
- Квадратные уравнения с одной переменной
- Факторизация
- Соотношение и пропорция
- Матрицы
- Арифметика и геометрическая прогрессия
- Отражение
- Формула раздела
- Уравнение прямой линии
- Сходство
- Локус
- Круги
- Конструкции
- Измерение
- Тригонометрические тождества
- Тригонометрические таблицы
- Высоты и расстояния
Главная >
ML Aggarwal Solutions
Класс 10
Математика
>
Глава 19. Тригонометрические таблицы
>
Тригонометрические таблицы. Упражнение 19.>
Вопрос 27
Тригонометрические таблицы
>
Тригонометрические таблицы. Упражнение 19.>
Вопрос 27
Вопрос 27 Тригонометрические таблицы Упражнение 19
Используя таблицы, найдите значение 2 sin θ – cos θ, когда тангенс θ = 0,2679.
Ответ:
Решение:-
Таблицы натуральных синусов, натуральных косинусов и натуральных тангенсов можно использовать для получения приблизительных значений синуса, косинуса и тангенса с точностью до четырех знаков после запятой для любых углов. от 0 градусов до 90 градусов.
Из вопроса следует, что тангенс θ = 0,2679
Найдите в таблице натуральных синусов значение (≤ 0,2679), достаточно близкое к 0,2679.
Находим столбец значений, возглавляемый 15 o .
Получаем, θ = 15 o
Итак, подставляем значение θ,
= 2 sin 15 o – cos 15 o
значение 0 0
Из таблицы 0,2588 и cos 15 o = 0,9659
= (2 × 0,2588) – 0,9659
= -0,4483
Связанные вопросы
Найдите значение следующего выражения: cos 62o 27′
Найдите значение следующего выражения: sin 65o 20′
Найдите значение следующего выражения: sin 35o 22′
Найдите значение следующего выражения: sin 23o 56′
Найдите значение следующего выражения: cos 3o 11′
Используйте таблицы, чтобы найти острый угол θ, учитывая, что: sin θ = 0,2357
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Тригонометрические таблицы Упражнения 19
Главы
GST
Банковские
Акции и дивиденды
квадратичные уравнения в одном переменном
Фактория
.
Формула сечения
Уравнение прямой
Подобие
Геометрическое место
Окружности
Построения
Измерения
Тригонометрические тождества
Тригонометрические таблицы
Высоты и расстояния
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены0760 Purplemath
На предыдущей странице мы рассмотрели, как отношения синусов и косинусов прямоугольных треугольников могут быть расширены с помощью единичного круга до полноценных графических функций. Следующее тригонометрическое соотношение, которое мы рассмотрим, — это отношение тангенса. Но значения касательной трудно отобразить на единичной окружности. Это связано с тем, что тангенс формируется путем деления значения единичного круга для синуса на его значение для косинуса, каждое из которых иногда равно нулю, а мы не можем делить на ноль.
Итак, вместо этого, давайте подробнее рассмотрим графики синусов и косинусов, помня о том, что tan(θ) равен этому делению: sin(θ) ÷ cos(θ).
Содержание продолжается ниже
MathHelp.com
Тангенс, будучи дробью, будет равен нулю, если его числитель (то есть значение синуса для этой меры угла) равен нулю. Синус равен нулю в точках 0, π, 2π, 3π и т. д., а также в точках −π, −2π, −3π и т. д.; то есть тангенс будет иметь нулевое значение при каждом кратном π. Давайте пока рассмотрим только область от −π до 2π. Таким образом, касательная будет равна нулю (то есть пересечет x -ось) при -π, 0, π и 2π.
Тангенс, будучи дробью, будет равен undefined везде, где его знаменатель (то есть значение косинуса для этой меры угла) равен нулю. И, возвращаясь к тому времени, когда вы узнали о построении графиков рациональных функций, вы знаете, что ноль в знаменателе функции означает, что у вас будет вертикальная асимптота. Таким образом, тангенс будет иметь вертикальные асимптоты везде, где косинус равен нулю. Придерживаясь того же интервала от -π до 2π, вертикальные асимптоты будут при -π/2, π/2 и 3π/2. Другими словами, между каждым числом, кратным π, будет вертикальная асимптота.
Другими словами, между каждым числом, кратным π, будет вертикальная асимптота.
Точно так же, как отношения синуса и косинуса были преобразованы в функции, мы также можем преобразовать отношение тангенса в функцию. Тангенс неявно будет чем-то вроде рациональной функции, за исключением того, что его отношение образуется путем деления двух тригонометрических функций (а не двух многочленов). Эта функция обозначается как tan() или просто [TAN] на вашем калькуляторе. Эта функция периодична, как и синус и косинус, образующие тангенс. Но график не может быть хорошей простой волной, не в последнюю очередь из-за вертикальных асимптот.
График функции тангенса
Чтобы построить график тангенса, начнем с «интересных» точек, то есть с нулей и асимптот. Поставьте точки вместо нулей и пунктирные вертикальные линии для асимптот:
← смахните , сколько нужно, чтобы просмотреть полное изображение →
Но куда же идет функция от этих нулей? Здесь мы используем то, что знаем о синусе, косинусе и асимптотах, чтобы заполнить остальную часть графика касательной. Рассмотрим интервал между нулем в точке 0π и асимптотой в точке ½π.
Рассмотрим интервал между нулем в точке 0π и асимптотой в точке ½π.
- Мы знаем, что график никогда не коснется и не пересечет вертикальные асимптоты
- Мы знаем, что между нулем и асимптотой график будет либо ниже оси (и скользить вниз по асимптоте до отрицательной бесконечности), либо выше оси (и тоньше вверх по асимптоте до положительной бесконечности).
- Между нулем и π/2 и синус, и косинус положительны.
- Тогда тангенс, будучи их частным, также должен быть положительным, поэтому график скользит вверх по асимптоте.
С этой информацией мы можем начать наш график:
← пролистните , сколько нужно, чтобы просмотреть полное изображение →
Теперь рассмотрим следующий интервал. Между π/2 и π синус положительный, а косинус отрицательный. Эти противоположные знаки означают, что тангенсное частное будет отрицательным, поэтому оно будет скользить вверх по правой стороне асимптоты снизу, изгибаться и встречаться с осью x в точке x = π. Давайте нарисуем этот бит:
Давайте нарисуем этот бит:
← смахните , чтобы просмотреть полное изображение →
Поскольку синус и косинус являются периодическими, тангенс также должен быть периодическим. Быстрая проверка знаков говорит нам, как заполнить остальную часть графика:
- от −π до −π/2: синус отрицателен, а косинус отрицателен, поэтому тангенс положителен; эта часть графика должна дублировать график между 0 и ½π
- от −π/2 до 0: синус отрицательный, но косинус положительный, поэтому тангенс отрицательный; эта часть графика должна дублировать график между ½π и π
- π в 3π/2: синус отрицательный, а косинус отрицательный, поэтому тангенс положительный; часть графика должна дублировать график между 0 и ½π
- От 3π/2 до 2π: синус отрицательный, но косинус положительный, поэтому тангенс отрицательный; эта часть графика должна дублировать график между ½π и π
Используя эту периодичность (последовательность, которая повторяется для каждого числа, кратного π), теперь мы можем завершить наш график:
← смахните , чтобы просмотреть полное изображение →
Как видите, тангенс имеет период π, причем каждый период отделен вертикальной асимптотой.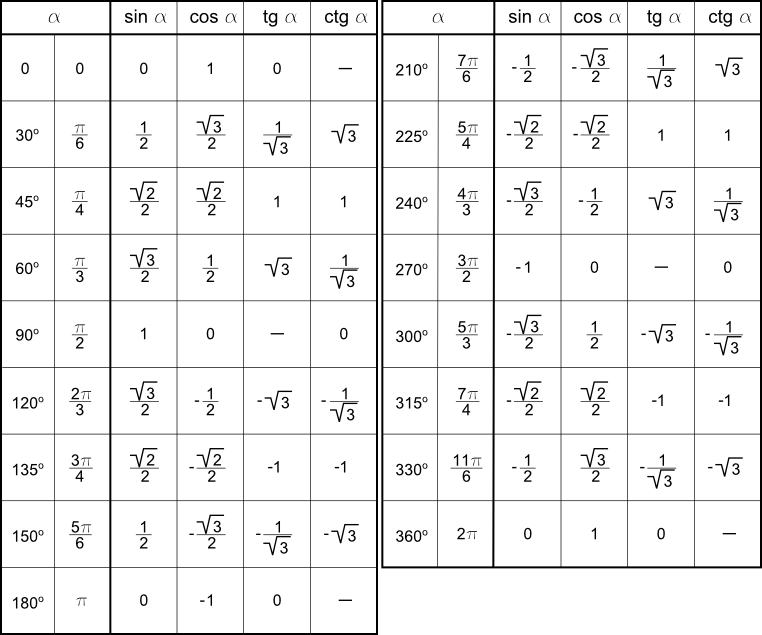 Понятие «амплитуда» действительно не применяется. Благодаря асимптотам значения тангенса не ограничены; то есть значения изменяются от -∞ до +∞; диапазон вывода y -значения «все».
Понятие «амплитуда» действительно не применяется. Благодаря асимптотам значения тангенса не ограничены; то есть значения изменяются от -∞ до +∞; диапазон вывода y -значения «все».
Для построения графика придерживайтесь «интересных» точек. Нарисуйте нули при x = 0, π, 2π и т. д. (они совпадают с нулями синуса), а затем прочеркните вертикальные асимптоты посередине между каждым нулем. Затем нарисуйте кривую. Вы можете нанести еще несколько точек, если хотите, но обычно от этого мало что выигрывают.
Если вы предпочитаете запоминать графики, запомните интервал по вашему выбору из графика выше. Вы можете предпочесть интервал 0 и π или, возможно, −½π и асимптоту при ½π. Все, что вы считаете полезным, является «правильной» вещью для запоминания. Что касается меня лично, у меня всегда были проблемы с поддержанием прямолинейности чего-либо, выходящего далеко за пределы синуса и косинуса, поэтому я использовал рассуждения, продемонстрированные выше, чтобы выяснить графики тангенса (и кофункции).

 narod.ru
Народ.Ру
Яндексе
narod.ru
Народ.Ру
Яндексе
 ….
…. 2867
2867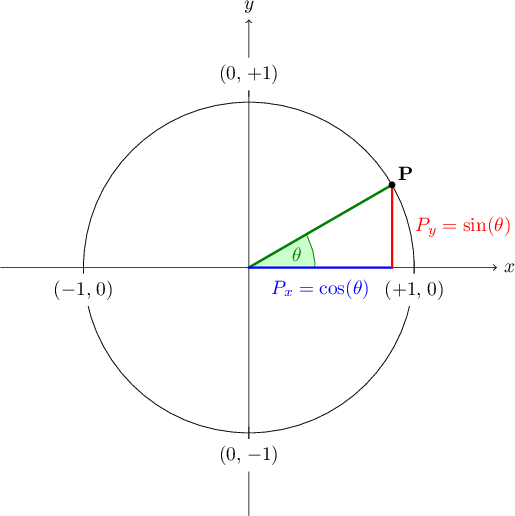 8391
8391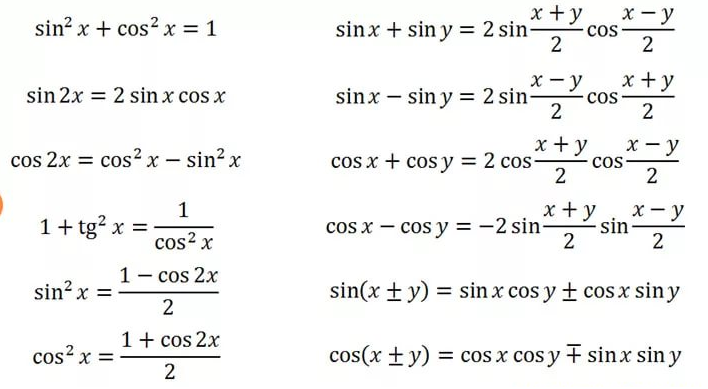 9626
9626 0811
0811 6051
6051 0724
0724 4452
4452 0175
0175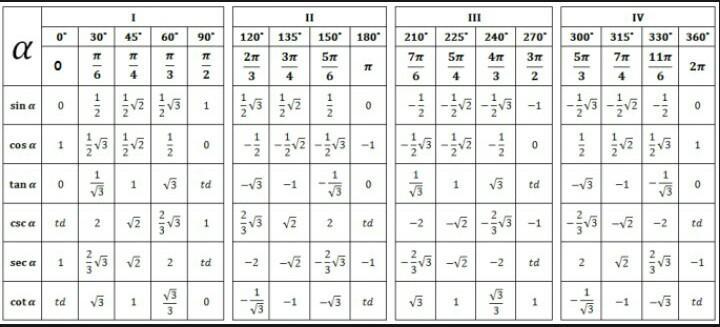 364
364 9657
9657 3559
3559 29
29 246
246 9657
9657 3839
3839 0055
0055 a) cos (b) ± sin (a) sin (b) (5b)
a) cos (b) ± sin (a) sin (b) (5b)