5.5. Асимптоты графика функции
Построение графика функции значительно облегчается, если знать его асимптоты.
Определение.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).
Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.
Рис. 5.10
Вертикальные асимптоты
Определение.
Прямая называетсявертикальной асимптотой графика функции , если выполнено одно из условий:
или (рис.5.11)
Рис. 5.11
Вертикальные
асимптоты, уравнение которых х=x0 , следует
искать в точках, где функция терпит
разрыв второго рода, или на концах ее
области определения, если концы не равны
.
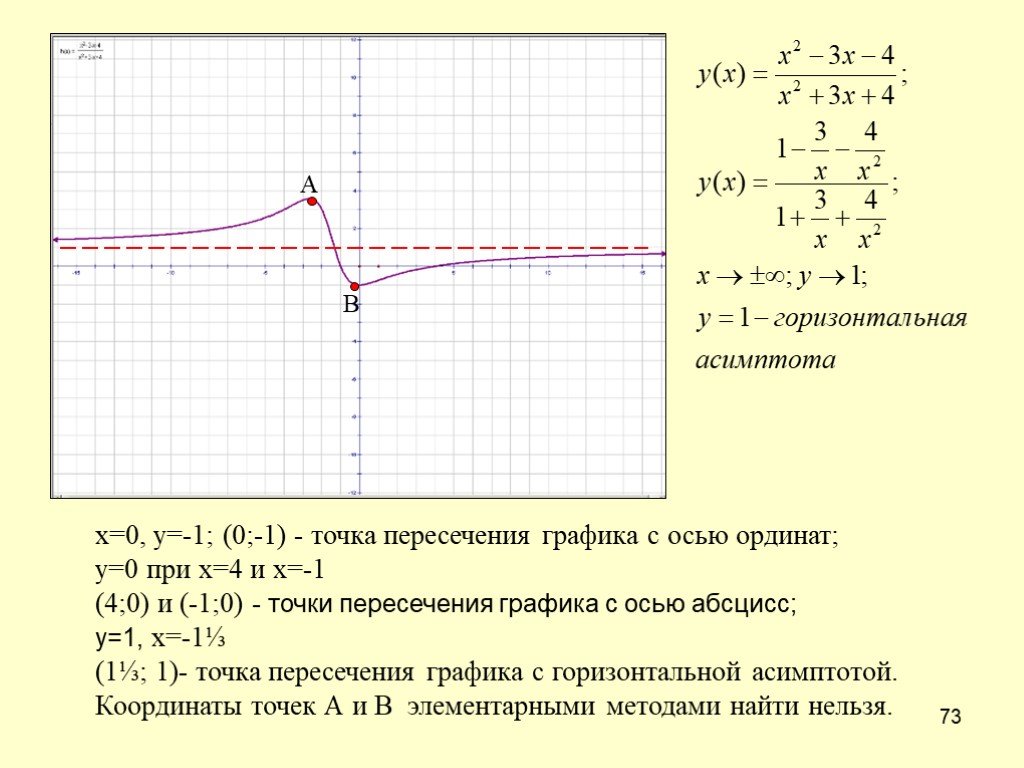
Например, для кривой , вертикальной асимптотой будет прямая, так как,. Вертикальной асимптотой графика функцииявляется прямая(осьОу), поскольку
.
Горизонтальные асимптоты
Определение.
Если при () функцияимеет конечный предел, равный числуb:
,
то прямая есть горизонтальная асимптота графика функции.
Например, для функции имеем
, .
Соответственно, прямая − горизонтальная асимптота для правой ветви графика функции, а прямая− для левой ветви.
В том случае, если
,
график функции не имеет горизонтальных асимптот, но может иметь наклонные.
Наклонные асимптоты
Определение.
Прямая называетсянаклонной асимптотой графика функции при(), если выполняется равенство
.
Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.
Теорема.
Для того, чтобы график функции имел при() наклонную асимптоту, необходимо и достаточно, чтобы существовали конечные пределы
и .
Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая наклонной асимптоты не имеет.
1. При отыскании асимптот следует отдельно рассматривать случаи и.
2. Если
и ,
то график функции имеет горизонтальную асимптоту.
3. Если
и ,
то прямая (осьОх) является горизонтальной асимптотой графика функции .
Из замечаний
следует, что горизонтальную асимптоту
можно рассматривать как частный случай
наклонной асимптоты при
.
Поэтому при отыскании асимптот графика
функции рассматривают лишь два случая:
1) вертикальные асимптоты,
2) наклонные асимптоты.
Пример
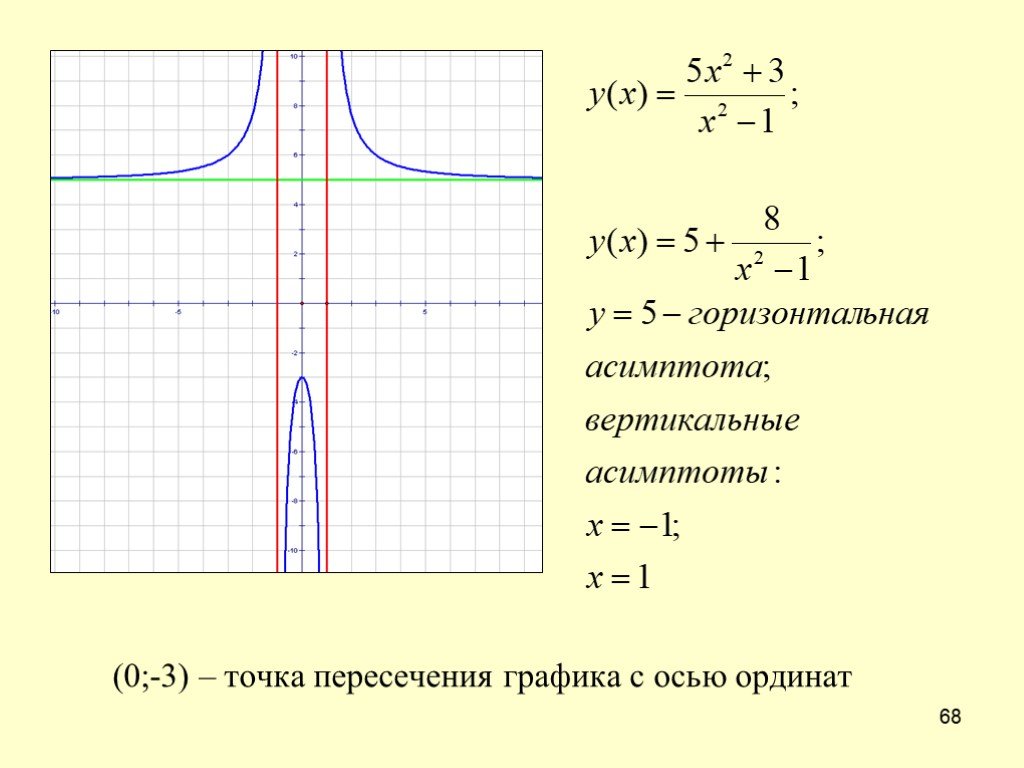
Найти асимптоты графика функции .
.
1) − точка разрыва второго рода:
, .
Прямая − вертикальная асимптота.
2) ,
,
.
Прямая − горизонтальная асимптота. Наклонной асимптоты нет.
5.6. Общая схема исследования функции и построение графика
В предыдущих параграфах было показано, как с помощью производных двух первых порядков изучаются общие свойства функции. Пользуясь результатами этого изучения, можно составить представление о характере функции и, в частности, построить ее график.
Исследование
функции
целесообразно проводить по следующей
схеме.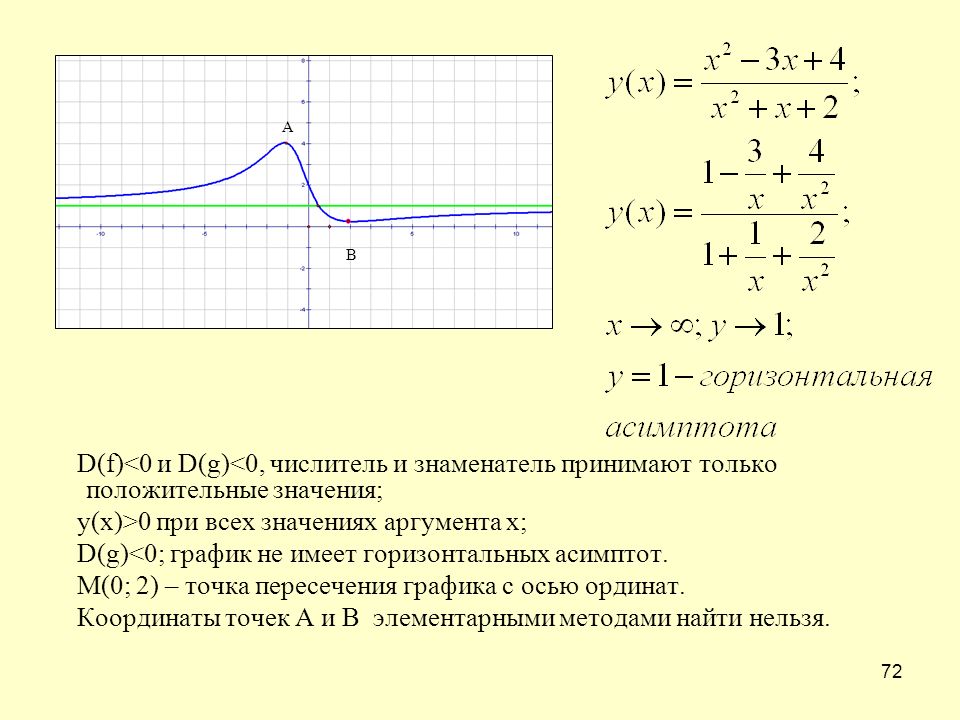
Найти область определения функции.
Исследовать функцию на периодичность.
Найти точки пересечения графика функции с осями координат.
Найти интервалы знакопостоянства функции (интервалы, на которых или).
Найти асимптоты графика функции.
Найти интервалы монотонности и точки экстремума функции.
Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
Построить график функции.
Пример
Исследовать функцию и построить ее график.
Область определения функции .
Функция нечетная: . График функции симметричен относительно начала координат
Функция непериодическая.
Точки пересечения с осями координат:
С осью Оу: , точка.
С осью Ох: ,,,.
Точки ,иразбивают осьОх на четыре интервала.
при ;
при ;
при ;
при .
Так как функция является непрерывной, то ее график не имеет вертикальных асимптот.
.
Наклонной и горизонтальной асимптот нет.
,
, ,− критические точки.
для «↑»,
для «↓»,
для «↑».
Сведем данные в таблицу.
х | -1 | 1 | |||
+ | 0 | − | 0 | + | |
↑ (возрастает) | mах 2 | ↓ (убывает) | min -2 | ↑ (возрастает) |
, ;
точка − максимум;
точка
− минимум.
, ,,.
при «»;
при «».
х | 0 | ||
− | 0 | + | |
(выпуклый) | 0 | (вогнутый) |
Точка − точка перегиба.
График функции (рис.
5.12)
5.12)Рис. 5.12
2.4.6. Асимптоты графика функции
Построение графика функции облегчается, если знать его асимптоты.
Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении точки по графику от начала координат (т.е. при стремлении аргумента к бесконечности).
Различают вертикальные и наклонные асимптоты. Частным случаем наклонной асимптоты является горизонтальная асимптота.
Прямая называется вертикальной асимптотой графика функции , если .
Вертикальные асимптоты проходят через точки бесконечного разрыва функции. Поэтому вертикальные асимптоты график функции может иметь только в точках разрыва второго рода или на границах области определения.
Наклонные асимптоты
получают при исследовании поведения
функции на бесконечности.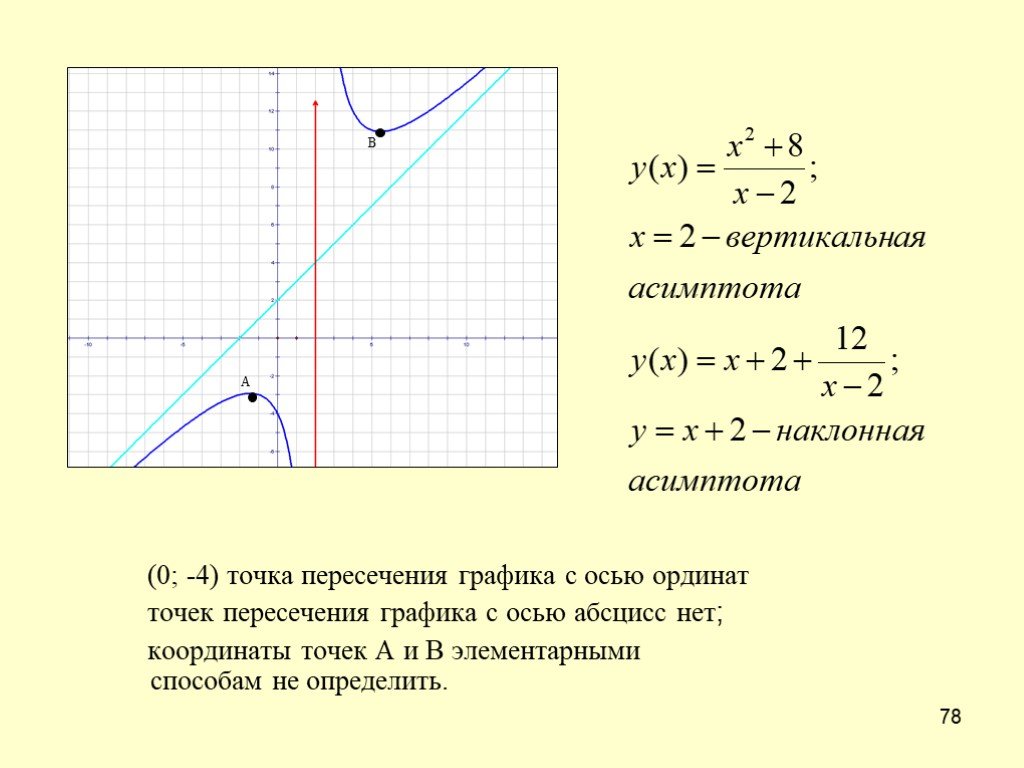
Уравнение наклонной асимптоты имеет вид , где
, .
Указанные пределы нужно находить отдельно при и.Если эти пределы будут различными, то график функции имеет две различные наклонные асимптоты: левостороннюю при и правостороннюю при . Если эти пределы равны при и, то функция имеет одну наклонную асимптоту.Если хотя бы один из указанных пределов, при отыскании и равен или не существует, то наклонных асимптот нет.
В частном случае, если , а, график функции имеет горизонтальную асимптоту, уравнение которой . Это прямая, параллельная оси .
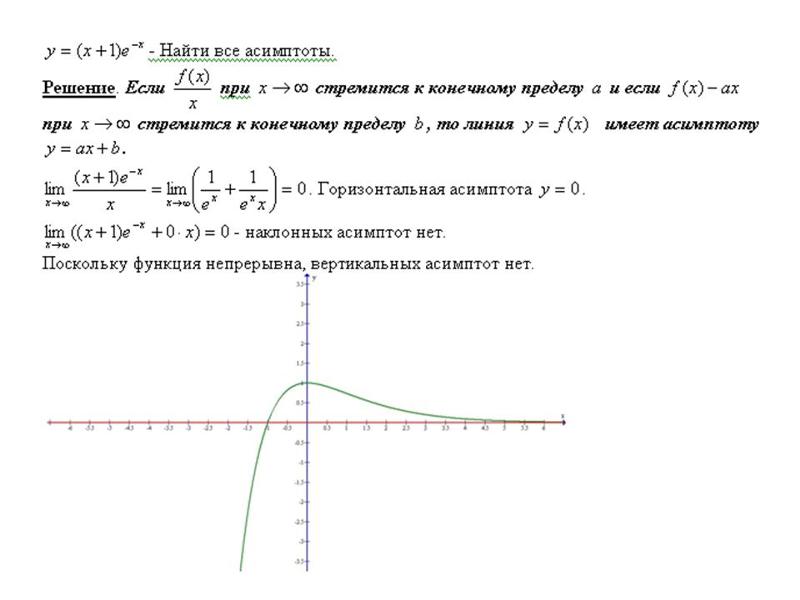
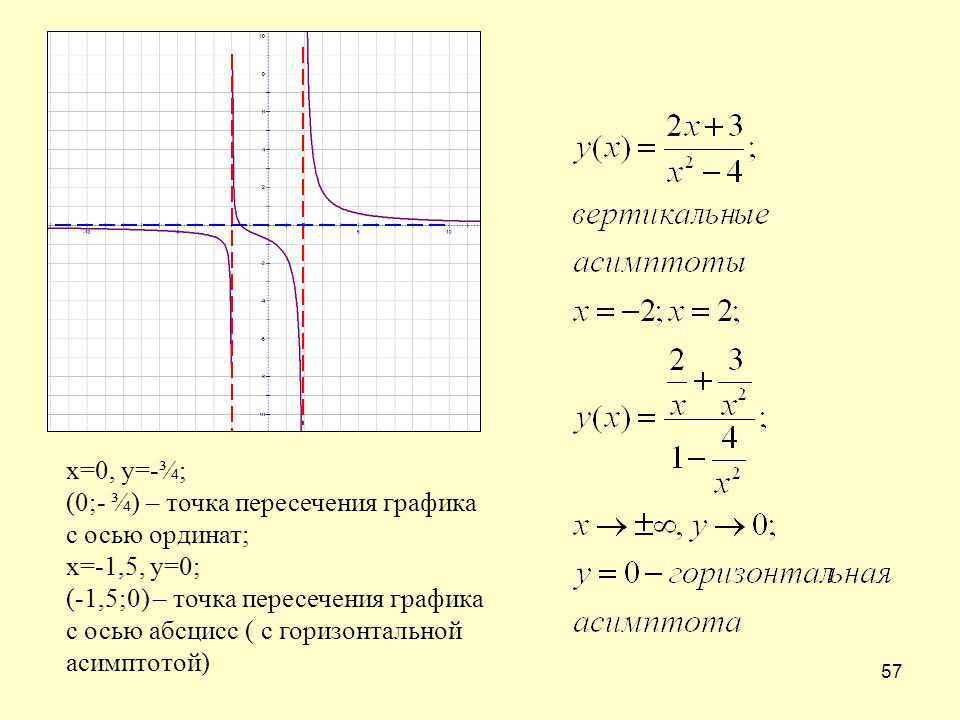
Пример 21.
Найти асимптоты графика функции .
Решение.
Функция определена на всей числовой оси, кроме . Область определения функции имеет вид: .
Следовательно,
точка – точка
разрыва функции. Исследуем точку разрыва
и вычислим односторонние пределы функции
в указанной точке.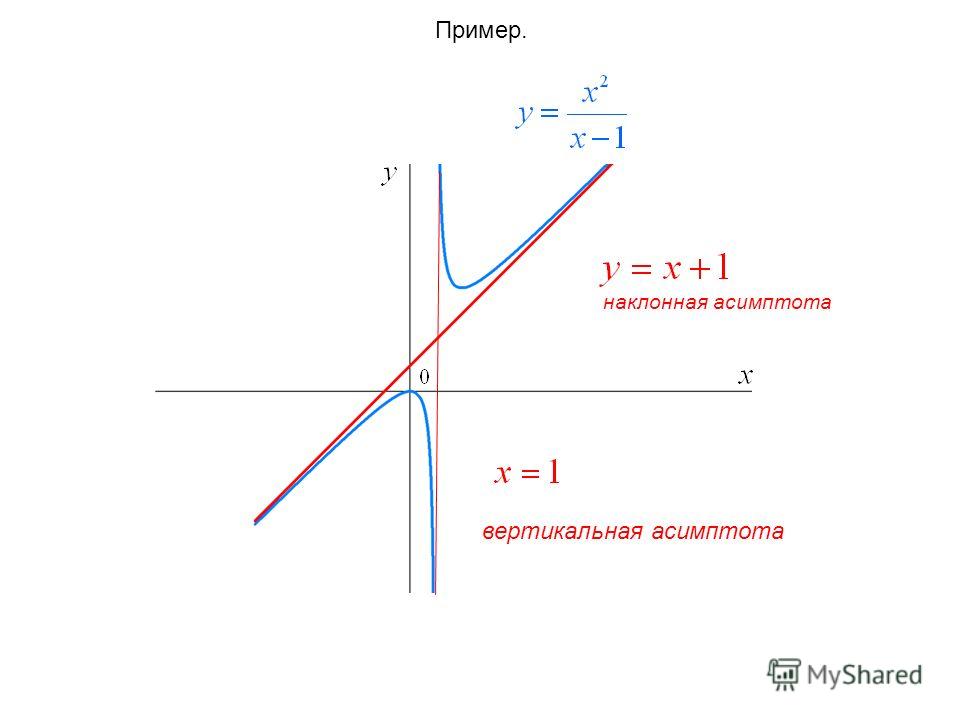
; .
Так как односторонние пределы равны , то в точке функция имеет разрыв второго рода. Соответственно график функции имеет вертикальную асимптоту (ось).
Возможное уравнение наклонной асимптоты будем искать в виде . Вычислим значения параметров и (для дробно-рациональной функции пределы будут одинаковы при ).
;
.
Подставляя найденные значения и, получим уравнение наклонной асимптоты .
График функции показан на рис.8
Для построения графика функции необходимо выяснить его характерные особенности, т.е. исследовать функцию. Полное исследование функции проводят по следующей схеме:
Найти область определения функции.
Исследовать функцию на непрерывность. Найти вертикальные асимптоты.
Исследовать функцию на чётность и нечётность.
Исследовать функцию на периодичность.
Найти точки пересечения графика функции с осями координат.
Определить промежутки монотонности и экстремумы функции.
Определить промежутки выпуклости, вогнутости и точки перегиба.
Найти наклонные асимптоты графика функции. Если график не имеет наклонных асимптот исследовать поведение функции при .
Построить график функции (при необходимости найти дополнительные точки графика функции).
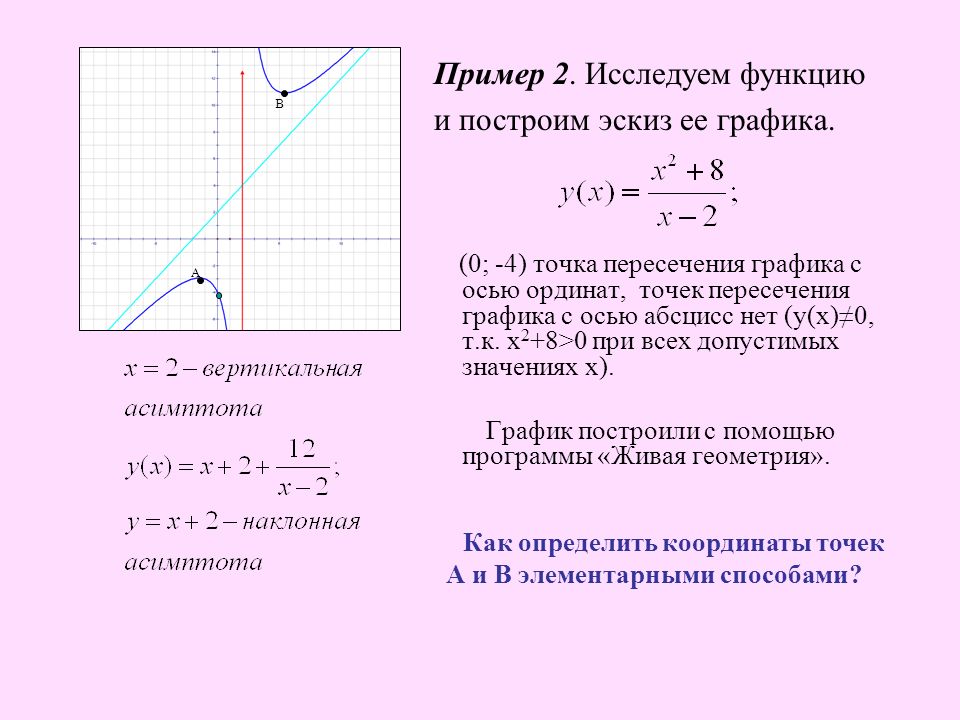
Пример 22.
Провести полное исследование функций и построить их графики:
а) ; б).
Решение.
а) .
1. Область определения функции.
Функция
определена при всех значениях
,
кроме тех, в которых знаменатель
обращается в ноль, т.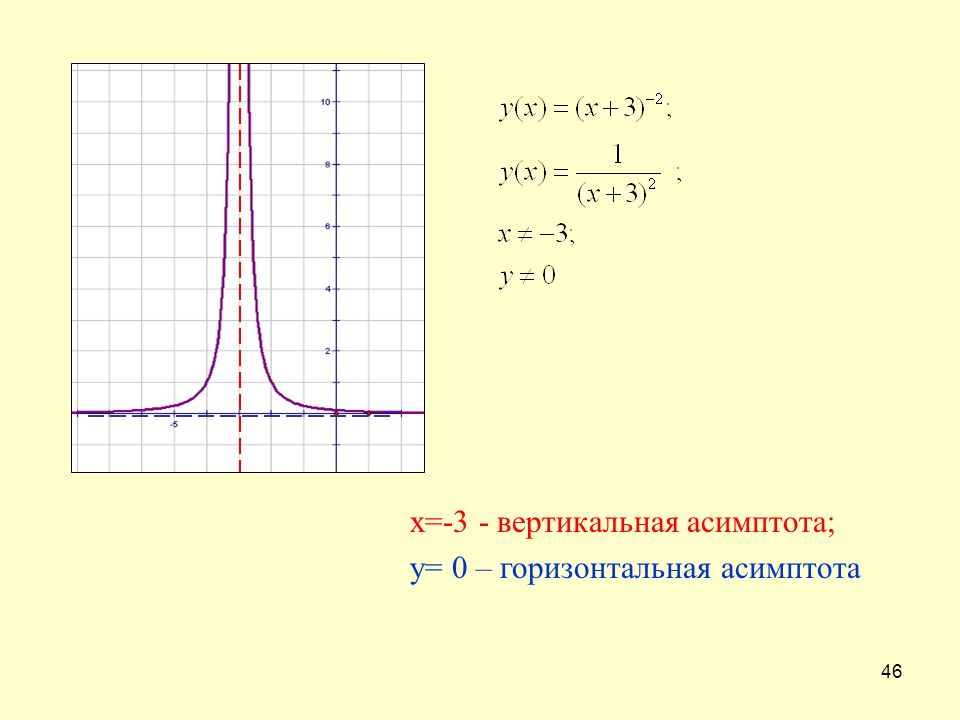
е.
, .
Область определения функции .
2. Непрерывность функции.
Функция определена при всех значениях , кроме . Следовательно, точки и – точки разрыва функции. Исследуем точки разрыва, найдем односторонние пределы функции в указанных точках.
;
;
;
.
Так как односторонние пределы равны , то в точках и функция терпит разрыв второго рода. Следовательно, график функции имеет две вертикальные асимптоты и .
3. Четность, нечетность.
Так как , то функция нечетная и ее график симметричен относительно начала координат.
4. Периодичность.
Так как не существует значения , при котором выполняется равенство , то функция непериодическая.
5. Точки пересечения
с осями координат.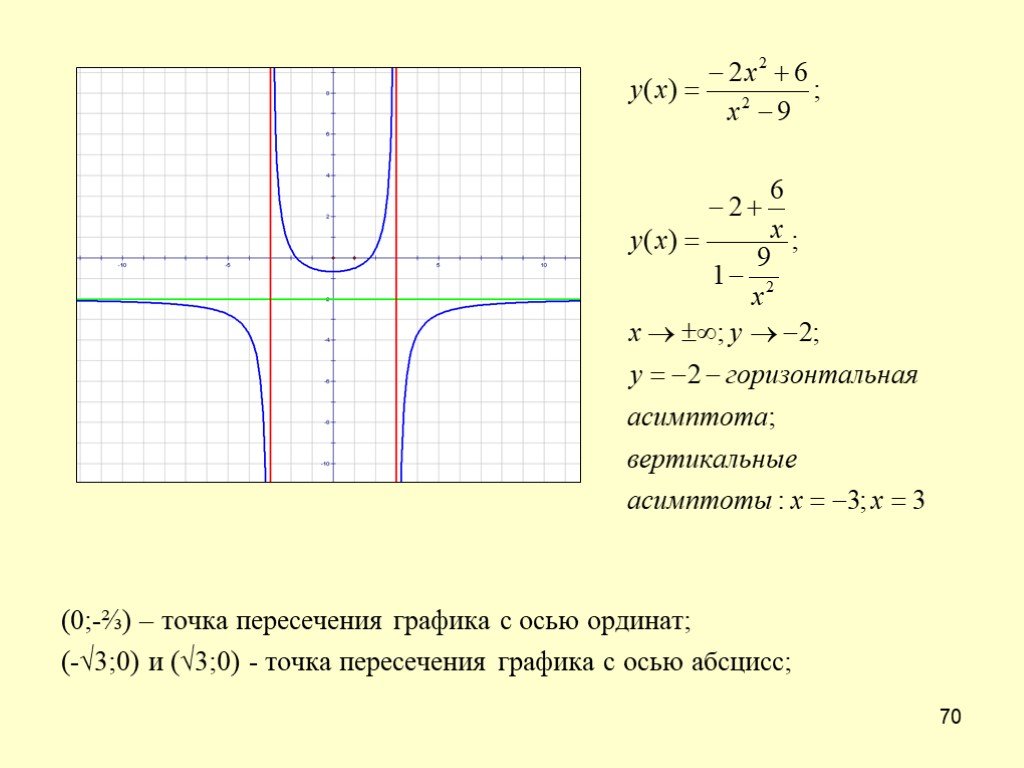
Точки пересечения графика функции с координатными осями ищем, приравнивая аргумент и функцию нулю.
С осью : ;;.
Точка пересечения графика функции с осью имеет координаты: .
С осью : .
Точка пересечения графика функции с осью имеет координаты: .
Следовательно, график функции проходит через начало координат, других точек пересечения графика функции с координатными осями нет.
6. Промежутки возрастания, убывания функции, экстремумы.
Найдем первую производную:
.
Найдем критические точки первого рода:
; .
Разобьем область определения критическими точками первого рода на интервалы и определим в каждом из них знак производной .
– 1 | 0 | 1 | |||||
+ | не
сущ. | + | 0 | + | не сущ. | + | |
↗ | не сущ. | ↗ | 0 | ↗ | не сущ. | ↗ |
Так как при переходе через критическую точку производная не меняет знак, то экстремума нет.
7. Промежутки выпуклости, вогнутости, точки перегиба.
Найдем вторую производную:
.
Найдем критические точки второго рода: ;
; ;.
Разобьем
область определения критическими
точками второго рода на интервалы и
определим в каждом из них знак второй
производной
.
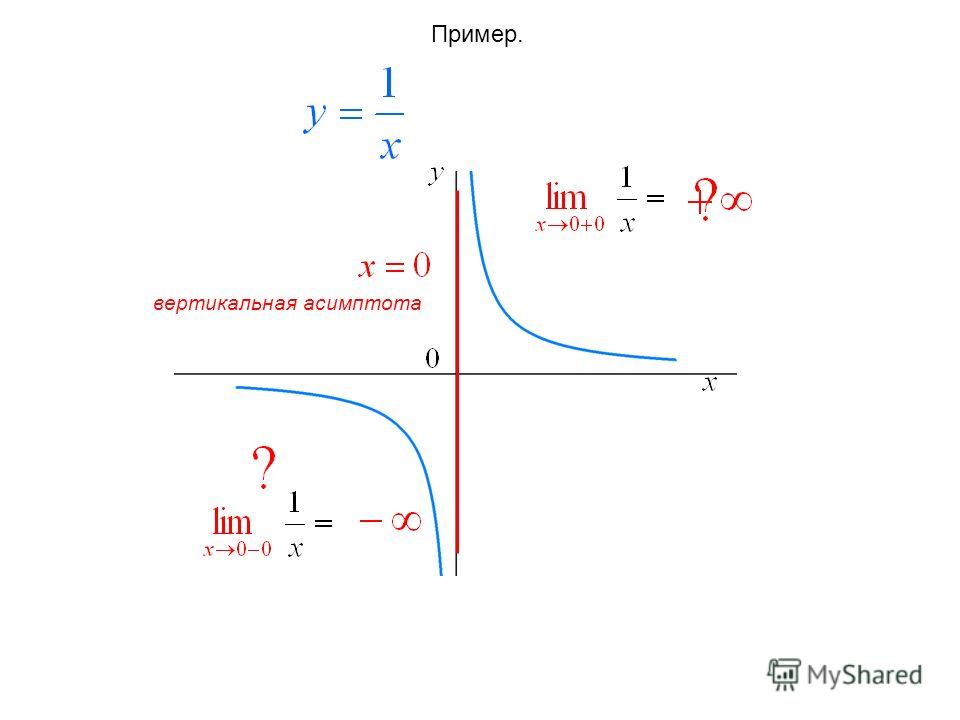
– 1 | 0 | 1 | |||||
+ | не сущ. | – | 0 | + | не сущ. | – | |
| не сущ. | | 0 | | не
сущ. | |
точка
перегиба
Так как при переходе через критическую точку вторая производная меняет знак, то – абсцисса точки перегиба. Точка перегиба: .
8. Наклонные асимптоты.
Уравнение наклонной асимптоты будем искать в виде . Вычислим значения параметров и (для дробно-рациональной функции пределы будут одинаковы при ).
;
Так как и, то график функции имеет горизонтальную асимптоту (ось).
9. Построение графика.
Построим график функции, учитывая пункты 1–8 (рис. 9).
Дополнительно найдем несколько точек графика функции:
–3 | –2 | –1,5 | –0,5 | 0,5 | 1,5 | 2 | 3 | |
0,38 | 0,67 | 1,2 | –0,67 | 0,67 | –1,2 | –0,67 | –0,38 |
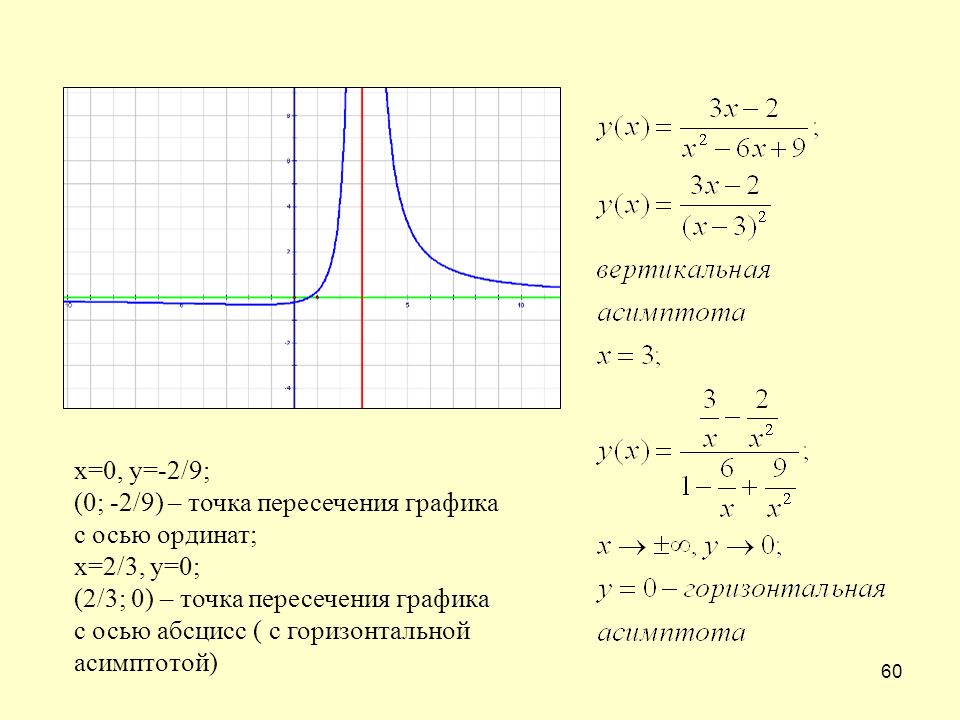
б)
.
1. Область определения функции.
Логарифмическая функция определена при, кроме этого знаменатель не может равняться нулю, т.е..
Тогда область определения функции имеет вид: .
2. Непрерывность функции.
Так как функция не определена в точке , то это точка разрыва. Исследуем характер точки разрыва, найдем односторонние пределы функции.
;
.
Так как односторонние пределы равны , то в точке функция терпит разрыв второго рода. Следовательно, функция в этой точке имеет вертикальную асимптоту .
Исследуем также поведение функции на границе области определения:
.
Значит при справа график функции стремится в точку .
3. Четность, нечетность.
Так
как
и,
то функция ни четная ни нечетная, т.е.
общего вида.
4. Периодичность.
Так как не существует значения , при котором выполняется равенство , то функция непериодическая.
5. Точки пересечения с осями координат.
С осью :;;.
Так как полученная система не имеет решений, значит точек пересечения графика с осью нет.
С осью : так какне входит в область определения, то точек пересечения с осьюнет.
График функции не пересекает координатные оси.
6. Промежутки возрастания, убывания функции, экстремумы.
Найдем первую производную:
.
Найдем критические точки первого рода:
; ;;.
Разобьем область определения критическими точками первого рода на интервалы и определим в каждом из них знак производной .
1 | е | ||||
– | не
сущ. | – | 0 | + | |
↘ | не сущ. | ↘ | 2е | ↗ |
min
Так как при переходе через критическую точку производная меняет знак с «–» на «+», то в этой точке – минимум функции.
Найдем значение функции в точке :.
7. Промежутки выпуклости, вогнутости, точки перегиба.
Найдем вторую производную:
.
Найдем критические точки второго рода: .
; ;.
Разобьем
область определения критическими
точками второго рода на интервалы и
определим в каждом из них знак второй
производной
.
1 | |||||
– | не сущ. | + | 0 | – | |
| не сущ. | | е2 | |
точка
перегиба
Так
как при переходе через критическую
точку
вторая производная меняет знак, то
– абсцисса
точки перегиба.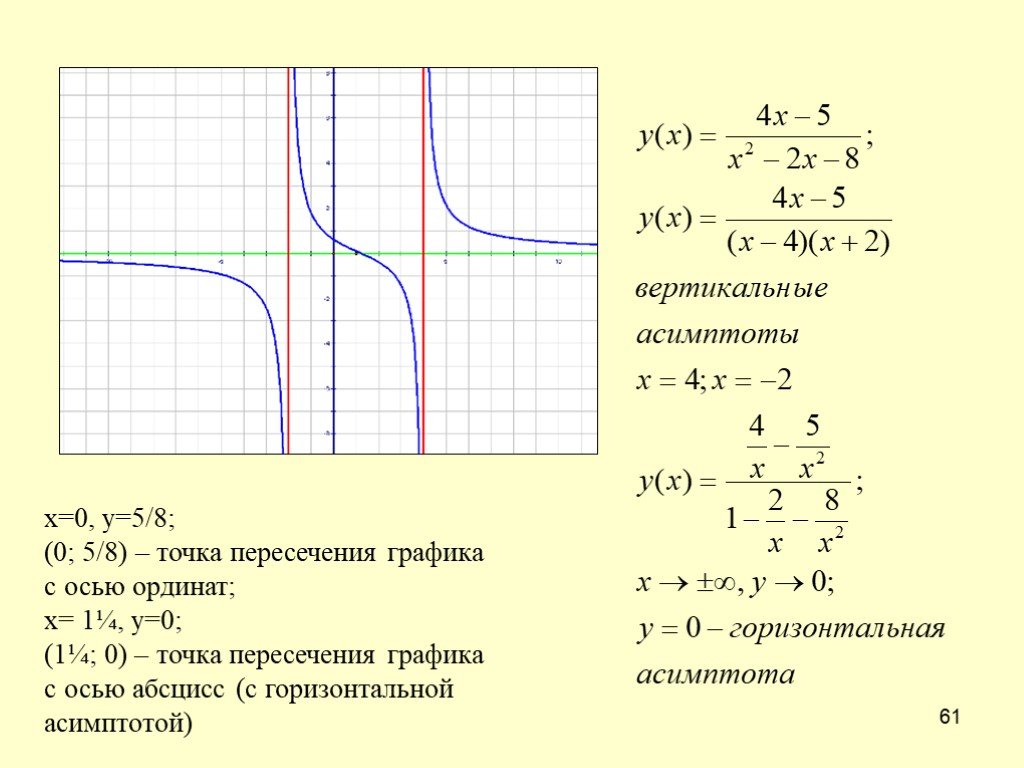
Найдем значение функции в точке :
.
8. Наклонные асимптоты.
Вычислим значения параметров и (учитывая область определения функции можно рассматривать лишь случай при).
;
.
Так как , то график функции наклонных асимптот не имеет.
Исследуем поведение функции при :
(см. выше нахождение параметра ).
9. Построение графика.
Построим график функции, учитывая пункты 1–8 (рис. 10).
Дополнительно найдем несколько точек графика функции:
0,5 | 1,5 | 2 | 5 | 8 | 11 | |
–1,44 | 7,4 | 5,77 | 6,21 | 7,69 | 9,11 |
Как найти горизонтальные асимптоты графика рациональной функции
График рациональной функции во многих случаях имеет одну или несколько горизонтальных линий, то есть когда значения x стремятся к положительной или отрицательной бесконечности, график Функции приближается к этим горизонтальным линиям, все ближе и ближе, но никогда не касается и даже не пересекает эти линии.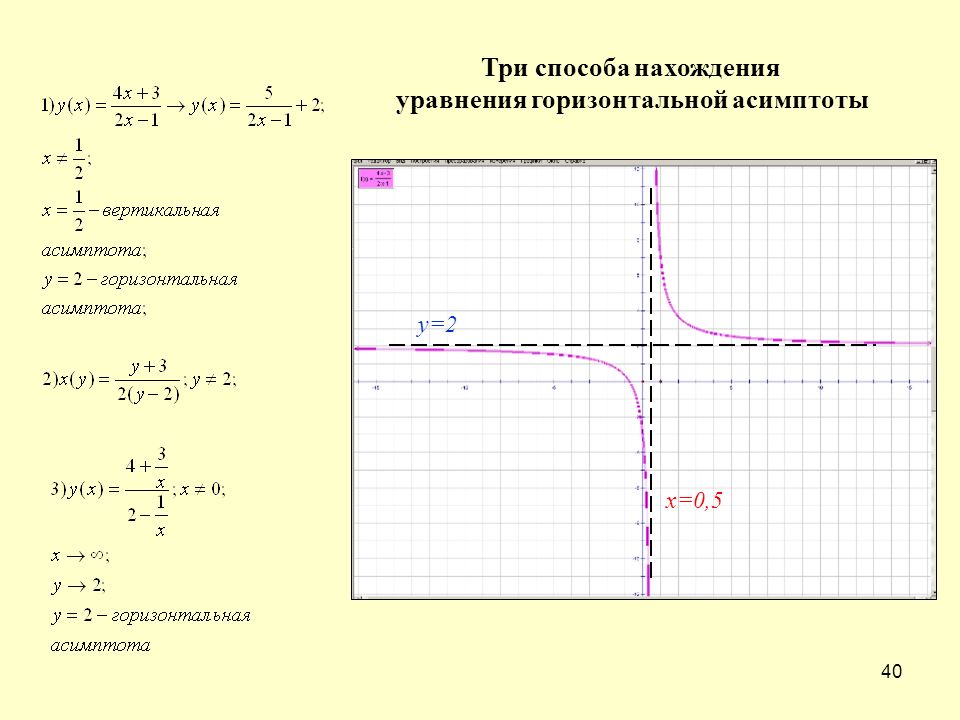
Эти линии называются горизонтальными асимптотами. Эта статья покажет, как найти эти горизонтальные линии, рассмотрев несколько примеров.
Учитывая рациональную функцию, f(x) = 1/(x-2), мы можем сразу увидеть, что когда x=2, у нас есть вертикальная асимптота (Чтобы узнать о вертикальных асимптотах, перейдите к статье, » Как найти разницу между вертикальной асимптотой…», того же автора, Z-MATH).
Горизонтальную асимптоту рациональной функции f(x) = 1/(x-2) можно найти, выполнив следующие действия: Разделив числитель ( 1 ) и знаменатель (x-2) на член высшей степени рациональной функции, которым в данном случае является терм ‘x’.
Итак, f(x)= (1/x)/[(x-2)/x]. То есть f(x) = (1/x)/[(x/x)-(2/x)], где (x/x)=1. Теперь мы можем выразить функцию как f(x) = (1/x)/[1-(2/x)]. Когда x приближается к бесконечности, оба термина (1/x) и (2/x) приближаются к нулю. , (0). Скажем, «Предел (1/x) и (2/x) при приближении x к бесконечности равен нулю (0)».
Горизонтальная линия y = f(x)= 0/(1-0) = 0/1 = 0, то есть y=0, есть уравнение горизонтальной асимптоты.
Пожалуйста, нажмите на изображение для лучшего понимания.
Учитывая рациональную функцию f(x)=x/(x-2), чтобы найти горизонтальную асимптоту, мы разделим числитель (x) и знаменатель (x-2) на член с наивысшей степенью в Рациональная функция, которая в данном случае является термином «х».
Итак, f(x)= (x/x)/[(x-2)/x]. То есть f(x) = (x/x)/[(x/x)-(2/x)], где (x/x)=1. Теперь мы можем выразить функцию как f(x) = 1/[1-(2/x)]. Когда x приближается к бесконечности, член (2/x) приближается к нулю, (0). Скажем, «Предел (2/x) при приближении x к бесконечности равен нулю (0)».
Горизонтальная линия y = f(x)= 1/(1-0) = 1/1 = 1, то есть y=1, есть уравнение горизонтальной асимптоты. Пожалуйста, нажмите на изображение для лучшего понимания.
Таким образом, для Рациональной функции f(x)=g(x)/h(x), где h(x) ≠ 0, если степень g(x) меньше степени h(x) , то уравнение горизонтальной асимптоты равно y=0. Если степень g(x) равна степени h(x), то уравнение горизонтальной асимптоты равно y=(отношению старших коэффициентов).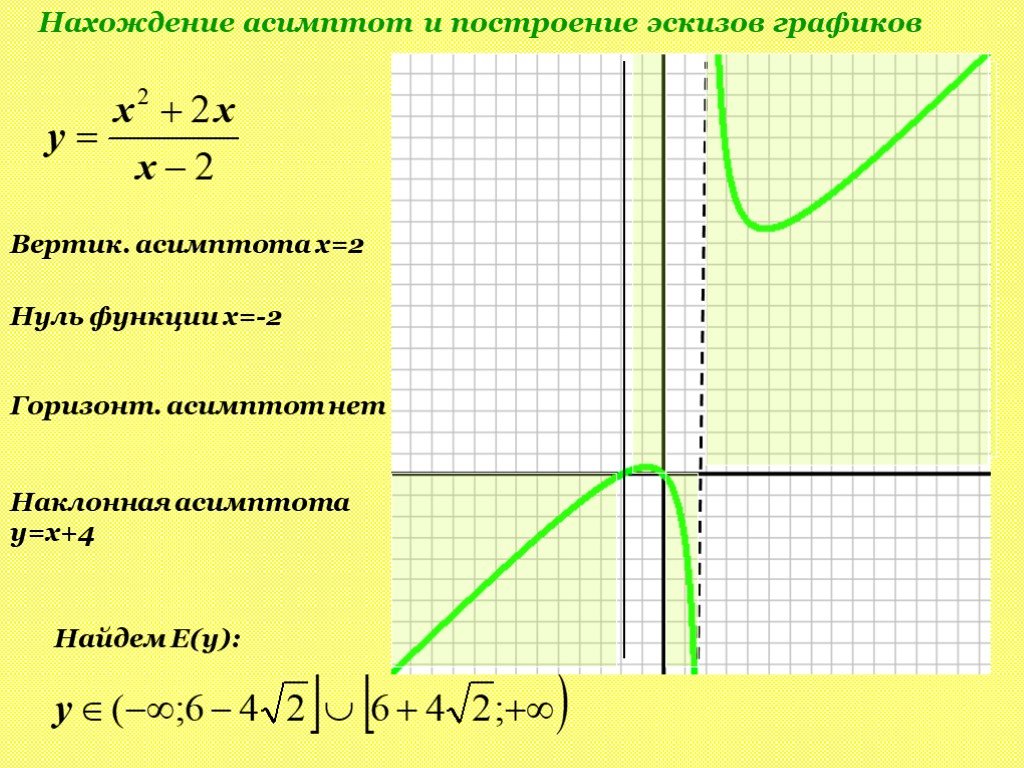
Если степень g(x) больше степени h(x), то горизонтальной асимптоты нет. 93 +5)/(2x -3), НЕТ горизонтальной асимптоты, поскольку степень функции числителя равна 3, что больше 1, где 1 является степенью функции знаменателя.
Вещи, которые вам понадобятся
- Бумага и
- Карандаш
Вертикальные асимптоты | Purplemath
HorizontalSlantExamples
Purplemath
Вертикальные асимптоты — это вертикальные линии, соответствующие нулям знаменателя рациональной функции. (Они также могут возникать в других контекстах, таких как логарифмы, но вы почти наверняка впервые столкнетесь с асимптотами в контексте рациональных чисел.)
Рассмотрим следующее уравнение:
Содержание продолжается ниже
MathHelp.com
Это рациональная функция. Точнее, это дробь. Может ли быть ноль в знаменателе дроби? Нет. Итак, если я установлю знаменатель приведенной выше дроби равным нулю и решу, это скажет мне значения, которые x могут быть , а не : 0
( х — 6)( x + 1) = 0
x = 6 или -1
Таким образом, x не может быть 6 или -1, потому что тогда я бы делил на ноль.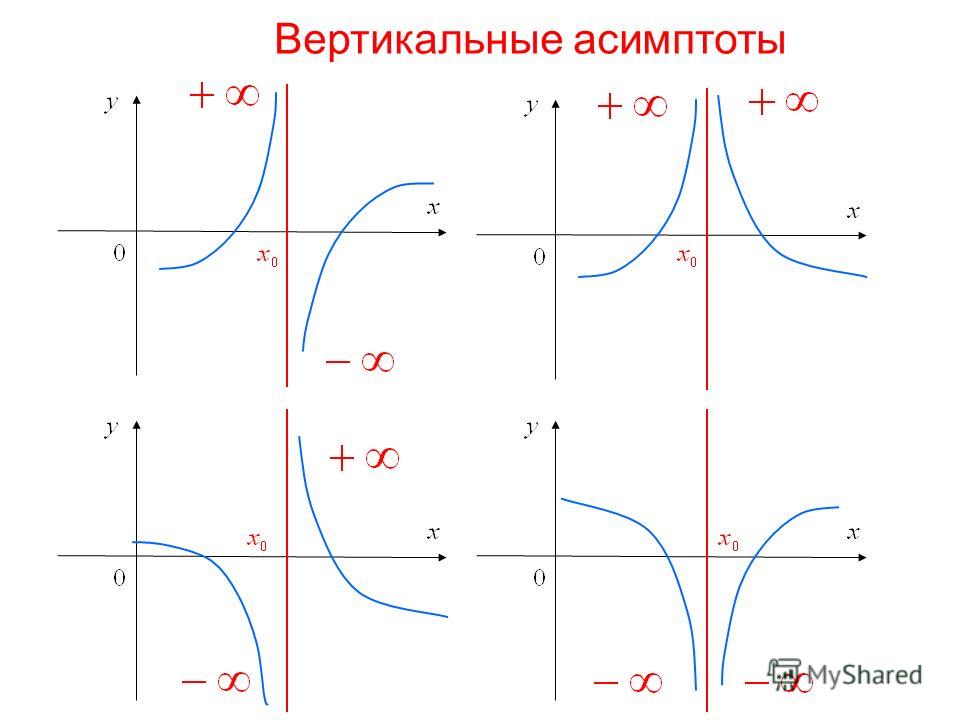
Теперь давайте посмотрим на график этой рациональной функции:
Вы можете видеть, что график избегает вертикальных линий x = 6 и x = −1. Это избегание произошло потому, что x не может быть равно ни -1, ни 6. Другими словами, тот факт, что домен функции ограничен, отражается на графике функции.
Мы рисуем вертикальные асимптоты в виде пунктирных линий, чтобы напомнить нам, что здесь нельзя строить графики, вот так:
Это нормально, что график поднимается вверх по сторонам асимптоты слева. Это обычное дело. Пока вы не нарисуете график , пересекающий вертикальную асимптоту, все будет в порядке.
Фактически, этот аспект «ползания вверх по стороне» является еще одной частью определения вертикальной асимптоты. Позже мы увидим пример, когда ноль в знаменателе не приводит к тому, что график поднимается вверх или вниз по вертикальной линии. Но на данный момент, и в большинстве случаев, нули знаменателя приведут к вертикальным пунктирным линиям и графикам, которые будут максимально приближены к этим вертикальным линиям.
Давайте попрактикуемся с этим соотношением между областью определения функции и ее вертикальными асимптотами.
Домен — это набор всех значений x , которые мне разрешено использовать. Единственные значения, которые могут быть запрещены, это те, которые дают мне ноль в знаменателе. Поэтому я приравняю знаменатель к нулю и решу.
х 2 + 2 х — 8 = 0
( х + 4)( х — 2) = 0
x = -4 или x = 2
Поскольку в знаменателе не может быть нуля, то и в домене не может быть x = -4 или x = 2. Это говорит мне о том, что вертикальные асимптоты (которые говорят мне, куда может пойти график , а не ) будут иметь значения x = -4 или x = 2.
область: x ≠ -4, 2
вертикальные асимптоты: x = −4, 2
Обратите внимание, что домен и вертикальные асимптоты являются «противоположными». Вертикальные асимптоты находятся в точках −4 и 2, а домен везде равен 9.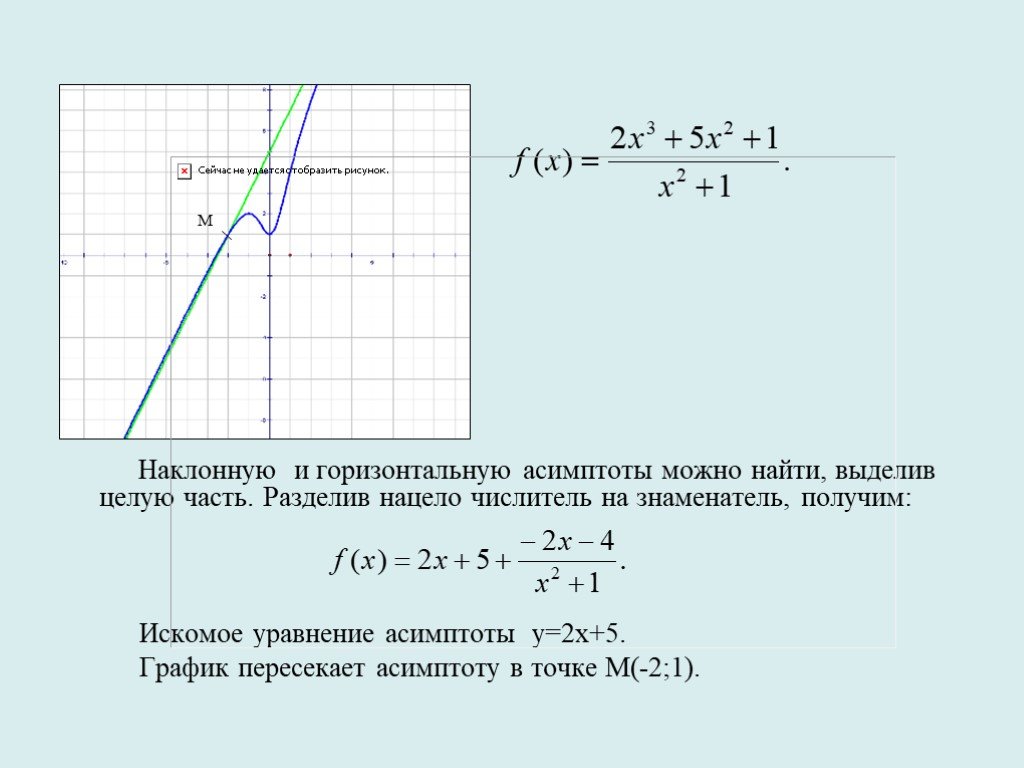
0049, но -4 и 2. Это соотношение всегда верно.
Чтобы найти область определения и вертикальные асимптоты, я приравняю знаменатель к нулю и решу. Решениями будут значения, недопустимые в области, а также вертикальные асимптоты.
x 2 + 9 = 0
x 2 = −9
Ой! Это не решает! Значит нулей в знаменателе нет. Так как нулей в знаменателе нет, то и запрещенных 9 нет.0049 x -значения, а домен «все x «. Кроме того, поскольку нет запрещенных для области значений, нет и вертикальных асимптот.
домен: все x
вертикальные асимптоты: нет
Обратите внимание еще раз, как домен и вертикальные асимптоты были «противоположны» друг другу. Домен — это «все значения x », или «все действительные числа», или «везде» (все это распространенные способы сказать одно и то же), а вертикальные асимптоты — «нет».
Я проверю нули знаменателя:
x 2 + 5 x + 6 = 0
( x + 3) ( x + 2) = 0 0003
.