 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Асимптоты графика функций: их виды, примеры решений
- Понятие асимптоты
- Вертикальные асимптоты
- Горизонтальные асимптоты
- Наклонные асимптоты
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться
по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться
соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти
вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели
и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
возможное расстояние, но так и не касается его.
Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy.
Определение.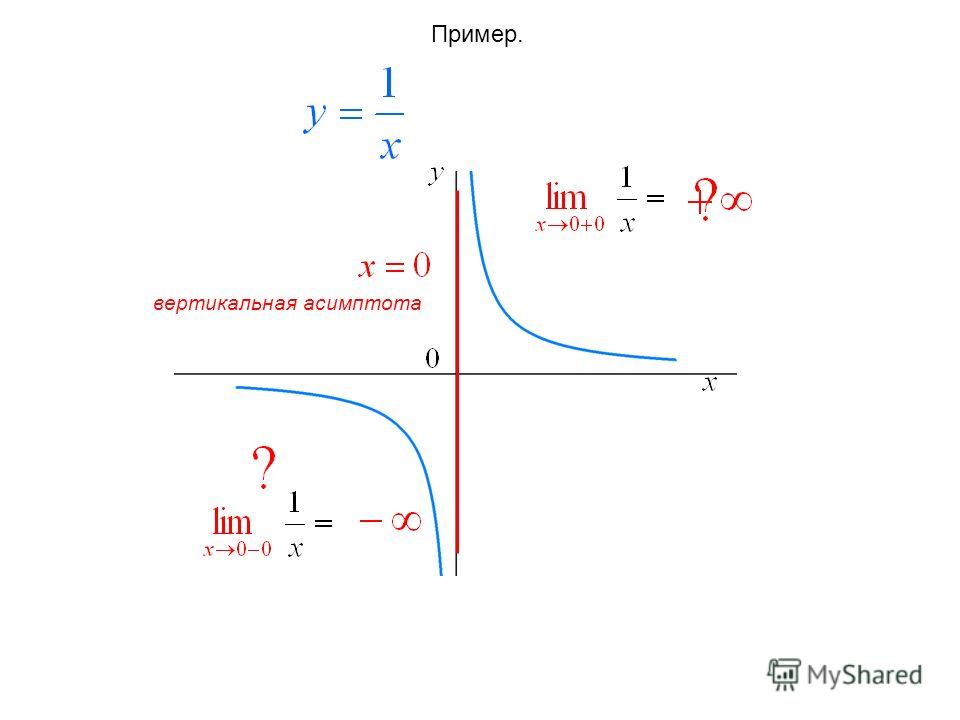 Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.
Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:
- (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
- (
При этом функция f(x) может быть вообще не определена соответственно при x ≥ a и x ≤ a.
Замечание:
- символом обозначается стремление x к a справа, причём x остаётся больше a;
- символом
обозначается стремление x к a слева, причём x остаётся меньше a.

Из сказанного следует, что вертикальные асимптоты графика функции можно искать не только в точках разрыва, но и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.
Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Пример 4. Найти асимптоты график функции .
Посмотреть решения и ответы примеров 2, 3, 4.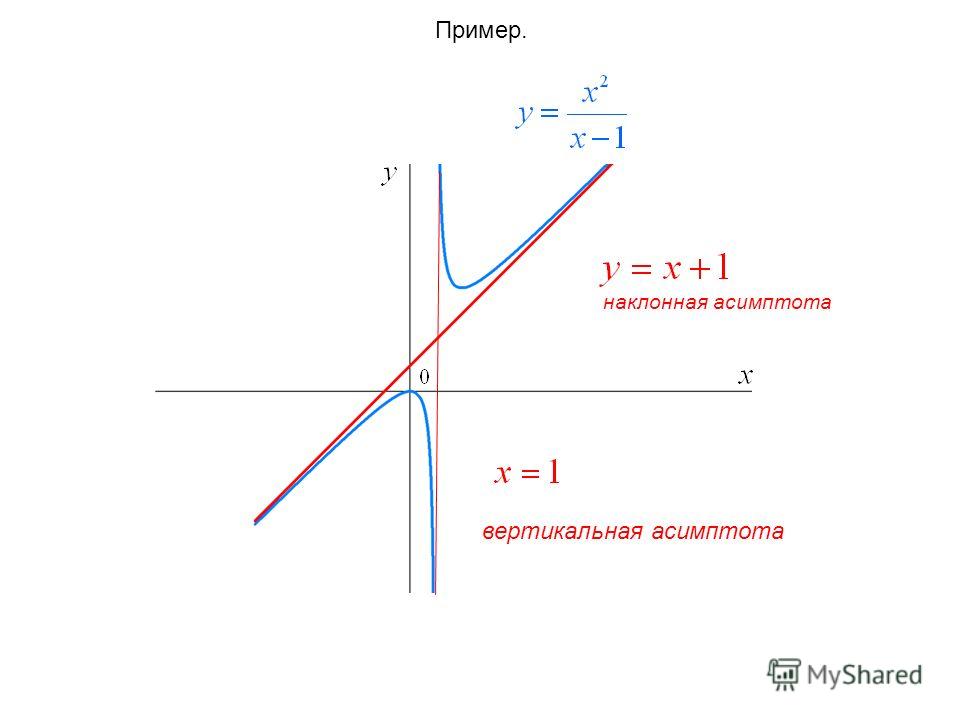
Нет времени вникать в решение? Можно заказать работу!
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox.
Если
(предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны
осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси
абсцисс или ординат, через которую проходит асимптота.
Теорема. Для того, чтобы кривая y = f(x) имела
асимптоту y = kx + b, необходимо и
достаточно, чтобы существовали конечные пределы
(1)
и
(2)
Найденные таким образом числа k и b и являются коэффициентами
наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0.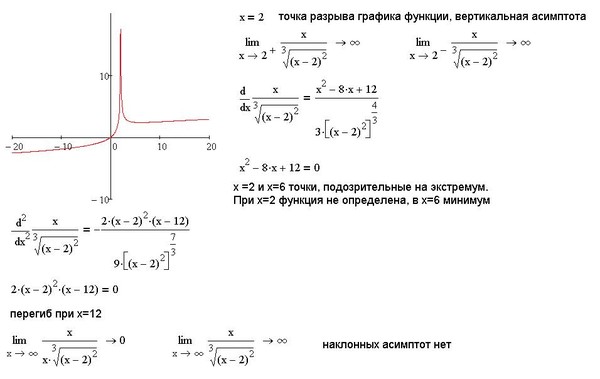
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0, т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и b = 0. Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1. Вычислим односторонние пределы и определим вид разрыва:
,
.
Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
y = −3x + 5.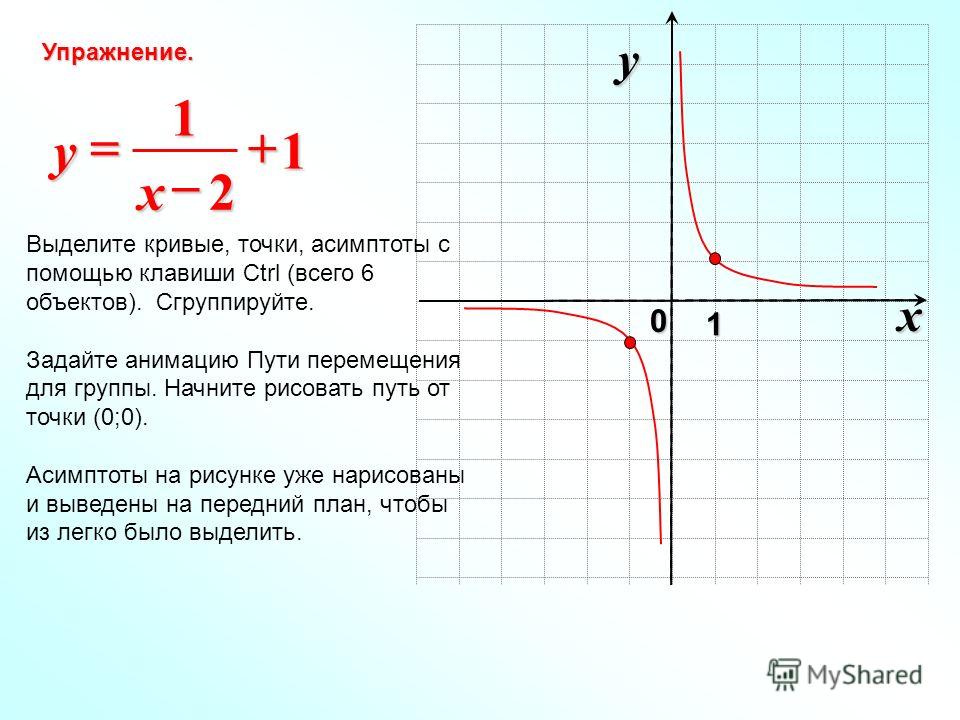
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
.
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 9. Найти асимптоты графика функции
.
Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения
функции. Функция определена, когда выполняется неравенство и
при этом . Знак переменной x совпадает со знаком .
Поэтому рассмотрим эквивалентное неравенство .
Из этого получаем область определения функции: .
Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как
функция определена при x = 0.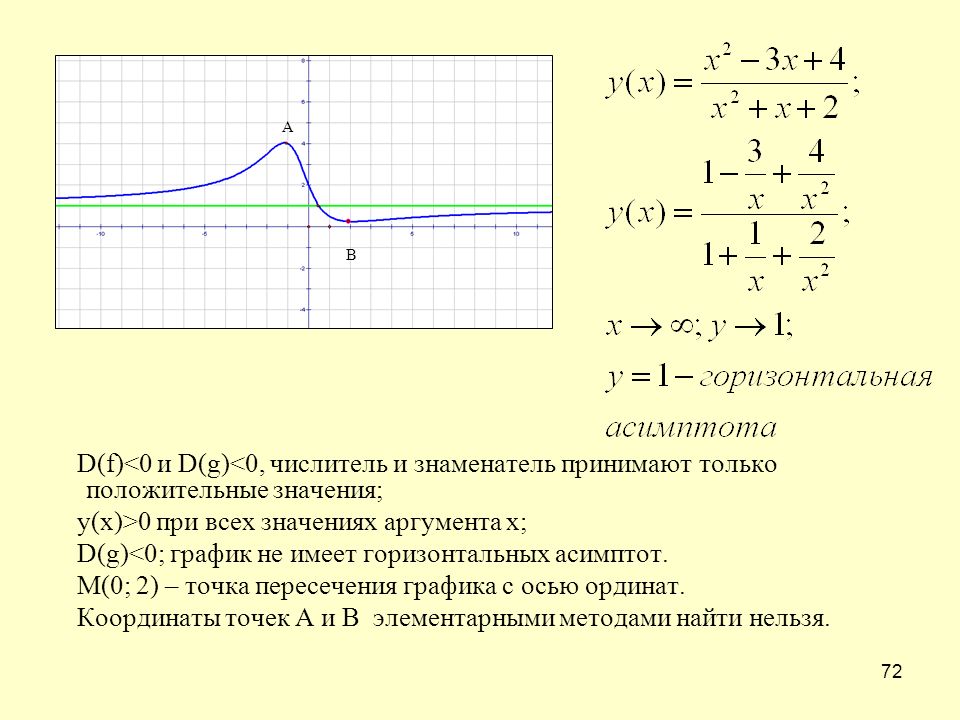
Рассмотрим правосторонний предел при (левосторонний предел не существует):
.
Точка x = 2 — точка разрыва второго рода, поэтому прямая x = 2 — вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1 — наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :
Итак, y = −x − 1 — наклонная асимптота при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при :
,
.
Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 — точка
устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Заключение: x = 0 — точка
устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:
Таким образом, при наклонной асимптотой графика данной функции является прямая y = x. Но при найденные пределы не изменяются. Поэтому при наклонной асимптотой графика данной функции также является y = x.
Пример 11. Найти асимптоты графика функции
.
Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие . Функция имеет две точки разрыва: , . Чтобы установить вид разрыва, найдём односторонние пределы:
Так как все пределы равны бесконечности, обе точки разрыва — второго рода. Поэтому
график данной функции имеет две вертикальные асимптоты: x = 2 и x = −2.
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной, пределы при и при совпадают. Поэтому, определяя коэффициенты прямой, ищем просто пределы:
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты y = 2x. Таким образом, график данной функции имеет три асимптоты: x = 2, x = −2 и y = 2x.
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 12. Найти асимптоты графика функции .
Правильное решение и ответ.
Пример 13. Найти асимптоты графика функции .
Правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Поделиться с друзьями
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритмы и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
Исследование функции онлайн y=f(x).
 2*arctgh(x)*arcctgh(x)
2*arctgh(x)*arcctgh(x)Что исследует?
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
- Минимум и максимум функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
| Справочник по математике | Элементы математического анализа | Функции |
| Вертикальные асимптоты |
| Наклонные асимптоты |
| Горизонтальные асимптоты как частный случай наклонных асимптот |
| Поиск наклонных асимптот графиков функций |
Вертикальные асимптоты
Во многих разделах нашего справочника приведены графики различных функций. Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
Определение 1. Говорят, что x стремится к x0 слева и обозначают
x → x0 – 0 ,
если x стремится к x0 и x меньше x0 .
Говорят, что x стремится к x0 справа и обозначают
x → x0 + 0 ,
если x стремится к x0 и x больше x0 .
Определение 2. Прямую
x = c
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с справа, если функция y = f (x) определена на некотором интервале (с, d) и выполнено соотношение выполнено соотношение
при x → c + 0
Прямую
x = с
называют вертикальной асимптотой графика функции y = f (x) при x , стремящемся к с слева, если функция y = f (x) определена на некотором интервале (d, c) и выполнено соотношение выполнено соотношение
при x → c – 0
Пример 1. Прямая
x = 2
является вертикальной асимптотой графика функции
как справа, так и слева (рис. 1)
1)
Рис.1
Пример 2. Прямая
x = 0
является вертикальной асимптотой графика функции
y = ln x
при x , стремящемся к 0 справа (рис. 2)
Рис.2
Наклонные асимптоты
Определение 3. Прямую
y = kx + b
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Прямую
y = kx + b
называют наклонной асимптотой графика функции y = f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Горизонтальные асимптоты как частный случай наклонных асимптот
Определение 4. Прямую
Прямую
y = b
называют горизотальной асимптотой графика функции y = f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Прямую
y = b
называют горизотальной асимптотой графика функции y f (x) при x , стремящемся к , если функция y = f (x) определена на некотором интервале и выполнено соотношение выполнено соотношение
Замечание. Из определений 3 и 5 вытекает, что горизонтальная асимптота является частным случаем наклонной асимптоты y = kx + b, когда угловой коэффициент прямой k = 0 .
Пример 3. Прямая
y = 3
является горизонтальной асимптотой графика функции
как при x , стремящемся к , так и при x , стремящемся к (рис.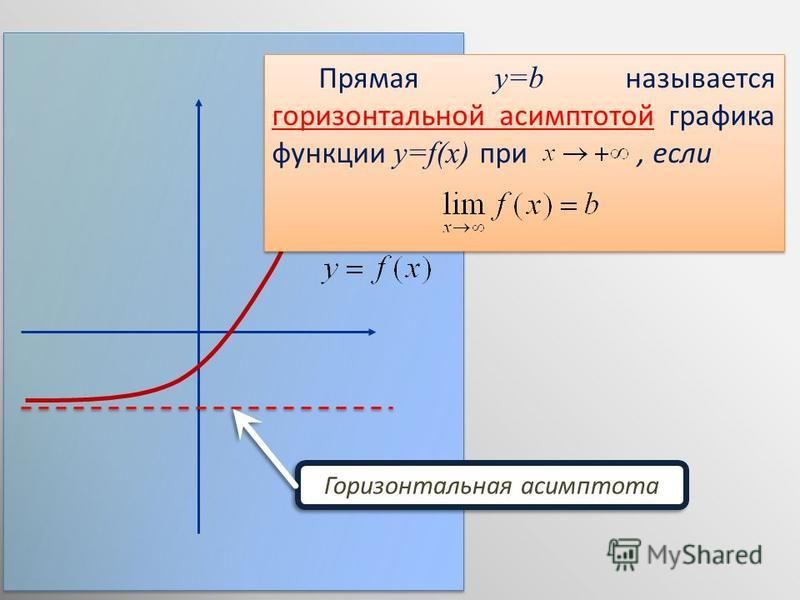 3)
3)
Рис.3
Пример 4. Прямая
y = 0
является горизонтальной асимптотой графика функции
y = 2x
при x , стремящемся к (рис. 4)
Рис.4
Пример 5. График функции y = arctg x (рис.5)
Рис.5
имеет две горизонтальные асимптоты: прямая
является горизонтальной асимптотой графика функции при , а прямая
является горизонтальной асимптотой графика функции при .
Поиск наклонных асимптот графиков функций
Для того, чтобы найти наклонную асимптоту графика функции y = f (x) при (или убедиться, что наклонной асимптоты при не существует), нужно совершить 2 операции.
Первая операция. Вычислим предел предел
| (1) |
Если предел (1) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.
Если предел (1) существует и равен некоторому числу предел (1) существует и равен некоторому числу, то, обозначив это число буквой k ,
переходим ко второй операции.
Вторая операция. Вычислим предел предел
| (2) |
Если предел (2) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.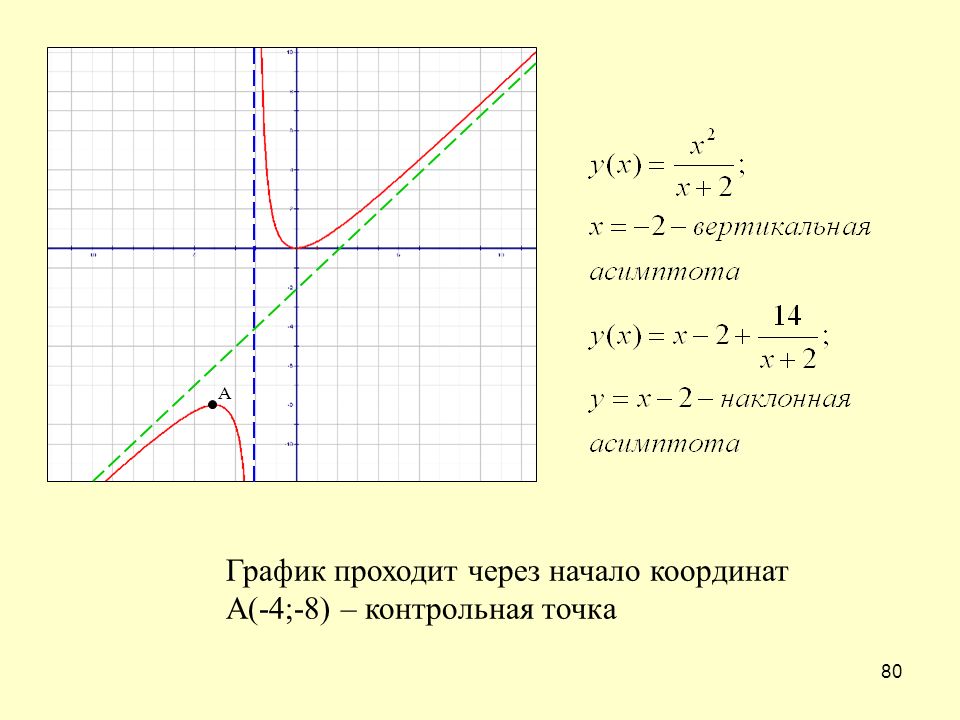
Если предел (2) существует и равен некоторому числу предел (2) существует и равен некоторому числу, то, обозначив это число буквой b ,
делаем вывод о том, что прямая
y = kx + b
является наклонной асимптотой графика функции y = f (x) при .
Совершенно аналогично поступаем для того, чтобы найти наклонную асимптоту графика функции y = f (x) при (или убедиться, что наклонной асимптоты при не существует).
Первая операция. Вычислим предел предел
| (3) |
Если предел (3) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.
Если предел (3) существует и равен некоторому числу предел (3) существует и равен некоторому числу, то, обозначив это число буквой k ,
переходим ко второй операции.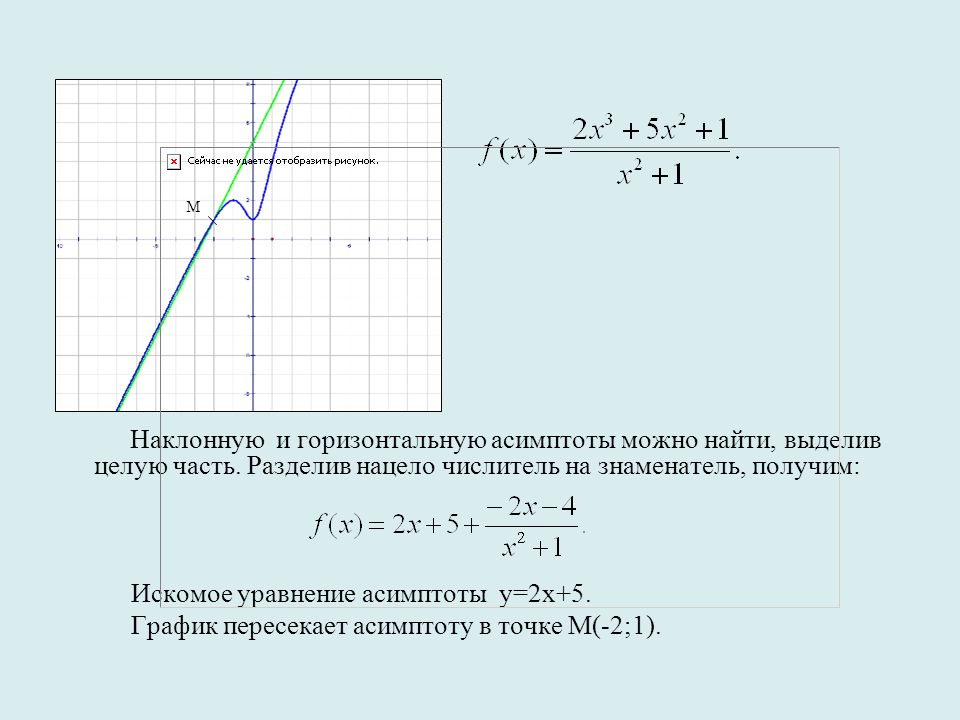
Вторая операция. Вычислим предел предел
| (4) |
Если предел (4) не существует или существует, но равен существует, но равен, то делаем вывод о том, что у графика функции y = f (x) при наклонных асимптот нет.
Если предел (4) существует и равен некоторому числу предел (4) существует и равен некоторому числу, то, обозначив это число буквой b ,
делаем вывод о том, что прямая
y = kx + b
является наклонной асимптотой графика функции y = f (x) при .
Пример 5. Найти асимптоты графика функции
| (5) |
и построить график этой функции.
Решение. Функция (5) определена для всех и вертикальных асимптот не имеет.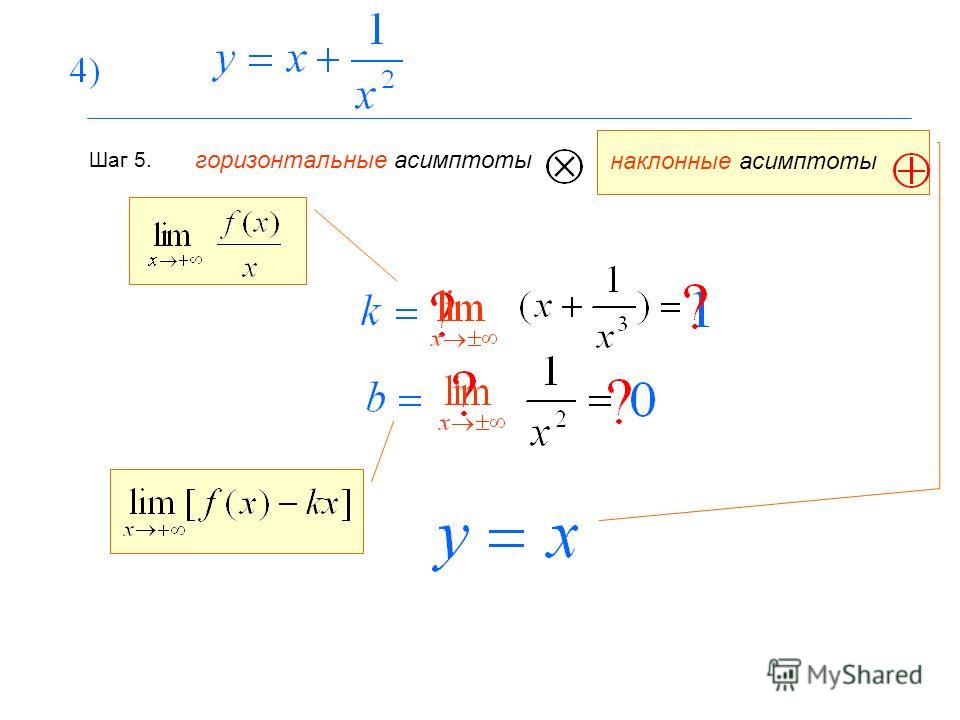
Найдем наклонные асимптоты графика функции (5). При получаем
Отсюда вытекает, что прямая
y = x
– наклонная асимптота графика функции (5) при .
При получаем
Отсюда вытекает, что прямая
y = – x
– наклонная асимптота графика функции (5) при .
Функция (5) является четной функцией, поэтому ее график симметричен относительно оси ординат.
Найдем производную функции (5):
.
.
Итак, y’ > 0 при x > 0 , y’ < 0 при x < 0 , y’ = 0 при x = 0 . Точка x = 0 – стационарная, причем производная функции (5) при переходе через точку x = 0 меняет знак с «–» на «+» . Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет.
Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет.
Теперь мы уже можем построить график функции (5):
Рис.6
Заметим, что график функции (5) находится выше асимптот y = x и y =v– x , поскольку справедливо неравенство:
.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Асимптоты функции
Определение асимптот функции не такое и трудное занятие если Вы хорошо знаете ряд правил и имеете добрые знания вычисления пределов. Если же не умеете находить пределы то наверстывать придется много, но научиться можно.
Прямая называется асимптотой кривой если точка кривой неограниченно приближается к ней при росте абсциссы или ординаты. Асимптоты разделяют на вертикальные, наклонные (горизонтальные) асимптоты.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
График функции при аргументе котрый стремится к точке имеет вертикальную асимптоту, если предел функции в ней бесконечен
Кроме этого точка является точкой разрыва II рода, а уравнение вертикальной асимптоты имеет вид
НАКЛОННЫЕ АСИМПТОТЫ
Уравнение наклонной асимптоты имеет вид
где — пределы, которые вычисляются по правилу
Если оба пределы существуют и конечны то функция имеет наклонную асимптоту, иначе — нет. Следует отдельно рассматривать случаи, когда аргумент стремится к бесконечности () и минус бесконечности ().
Следует отдельно рассматривать случаи, когда аргумент стремится к бесконечности () и минус бесконечности ().
ГОРИЗОНТАЛЬНЫЕ АСИМПТОТЫ
Кривая имеет горизонтальную асимптоту только в том случае, когда существует конечный предел функции при и , и эта граница равна
или
Нахождение пределов в некоторых случаях упрощается, если применять правило Лопиталя.
Приведем решения типичных для практики задач на отыскание асимптот.
————————————
Примеры.
Найти асимптоты функций (Дубовик В.П., Юрик И.И. «Высшая математика. Сборник задач»)
І. (5.863)
Решение:
Знаменатель дроби не должен превращаться в ноль
По теореме Виета находим корни квадратного уравнения
Они разбивают область определения на следующие интервалы
Другим выводом является то, что функция имеет две вертикальные асимптоты
Найдем наклонную асимптоту
Первая граница примет вид
Другую определяем по правилу
Окончательное уравнение наклонной асимптоты следующее
График функции с асимптотами имеет вид
————————————
ІІ. (5.873)
(5.873)
Решение:
Логарифм функция определена при положительных значениях аргумента и стремится к бесконечности при , это означает
Из этого следует что функция имеет вертикальные асимптоты при
а ее область определения следующая
С виду функции следует что функция имеет вертикальную асимптоту
Наклонных асимптот функция не имеет. График функции с асимптотами приведен ниже
————————————
(Клепко В.Ю., Голец В.И. «Высшая математика в примерах и задачах»)
III. (4.71.1)
Решение:
С виду функции следует что она определена во всех точках где знаменатель не превращается в ноль, из этого следует
Эти точки представляют собой вертикальные асимптоты, а также разделяют область определения на интервалы
Наклонных асимптот функция не имеет. Это следует из одного свойства которым я поделюсь с Вами: функции вида «многочлен разделить на многочлен» имеет наклонную асимптоту только в случаях, когда наибольший степень в числителе на единицу больше, чем в знаменателе, т. е.
е.
Горизонтальная асимптоту находим с границы
Функция с асимптотами изображена на рисунке
———————————
IV. (4.71.2)
Решение:
Область определения функции
При функция имеет вертикальную асимптоту. Наклонных асимптот нет, одна горизонтальная, так как степень числителя и знаменателя равны
Функция будет выглядеть следующим образом
————————————
V. (4.71.3)
Решение:
Областью определения будут два интервала
Точка будет вертикальной асимптотой. Наклонных асимптот нет, горизонтальную находим с предела
Поведение функции изображено на рисунке
—————————————————
VI. (4.71.4)
Решение:
Область определения находим из условия
Точка является вертикальной асимптотой. Наклонную асимптоту находим на основе пределов
Окончательно получим такое уравнение асимптоты
Функция с асимптотами изображена на рисунке
———————————————
VII. (4.71.5)
(4.71.5)
Решение:
Область определения находим с условия
Точка – вертикальная асимптота. Наклонная асимптота будет известна после вычисления пределов
– уравнение наклонной асимптоты.
График функции следующий
————————————
Подобных примеров можно решить еще много, схема нахождения асимптот при этом не меняется. Бывают
примеры в которых нахождение пределов трудоемкое и занимает более половины объема этой статьи, но
думаю Вам такие в обучении не встретятся.
————————————
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Наибольшее и наименьшее значение функции на отрезке
- Локальный экстремум функции. Примеры
- Выпуклость и вогнутисть графика функции
- Область определения функции
Калькулятор асимптот
Искатель асимптот — это онлайн-инструмент для вычисления асимптот рациональных выражений. Найдите все три горизонтальные, вертикальные и наклонные асимптоты с помощью этого калькулятора.
Найдите все три горизонтальные, вертикальные и наклонные асимптоты с помощью этого калькулятора.
Пользователь получает все возможные асимптоты и построенный график для определенного выражения.
Как пользоваться калькулятором асимптот?
Инструкции по использованию этого калькулятора асимптот с пошаговыми инструкциями приведены ниже.
- Введите выражение (рациональное), которое у вас есть.
- Проверьте это на дисплее.
- Теперь нажмите «Рассчитать».
Впереди рассказ о том, что такое асимптоты, виды асимптот и как их найти.
Что такое асимптоты?
Асимптоты — это сближающиеся линии на декартовой плоскости, которые не соответствуют рациональному выражению дублера.
Глядя на их график, можно сделать предположение, что они в итоге встретятся, но это неверно (кроме горизонтального). Асимптоты сходятся к рациональному выражению до бесконечности.
См. другой подобный инструмент, калькулятор пределов.
Типы асимптот
Асимптоты подразделяются на три типа в зависимости от их наклона или приближения.
1. Горизонтальные асимптоты перемещаются вдоль горизонтальной оси или оси x. Линия может существовать как сверху, так и снизу асимптоты.
Горизонтальные асимптоты являются частным случаем наклонных асимптот и показывают, как ведет себя линия по мере приближения к бесконечности. Они могут пересекать линию рационального выражения.
2. Вертикальные асимптоты , как вы можете сказать, движутся вдоль оси Y. В отличие от горизонтальных асимптот, они никогда не пересекают прямую. Но они также встречаются как в левом, так и в правом направлении.
3. Последний тип наклонный или наклонный асимптоты. Он имеет некоторый уклон, отсюда и название. Эта асимптота представляет собой линейное уравнение со значением, равным y=mx+b.
Отсюда основные определения типов асимптоты. Теперь давайте научимся определять все эти типы.
Теперь давайте научимся определять все эти типы.
Заметьте , что рациональное выражение может не иметь сходящейся к нему асимптоты.
Как найти асимптоты?
Попробуйте использовать указанный выше инструмент в качестве калькулятора горизонтальных, вертикальных и наклонных асимптот. Но есть некоторые приемы и советы по ручной идентификации.
Мы изучим их процесс один за другим.
Горизонтальные асимптоты:Рациональное выражение может иметь одну горизонтальную асимптоту или не иметь ее. Чтобы узнать, какие из упомянутых ситуаций существуют, сравнивают числитель и знаменатель.
Два случая, когда асимптота существует горизонтально:
Случай 1 (Больший знаменатель):Когда знаменатель рационального выражения в градусах больше, чем числитель. Другими словами, когда дробь правильная, асимптота приходится на y=0. То есть по оси х.
Учтите, что у вас есть выражение x+5 / x 2 + 2.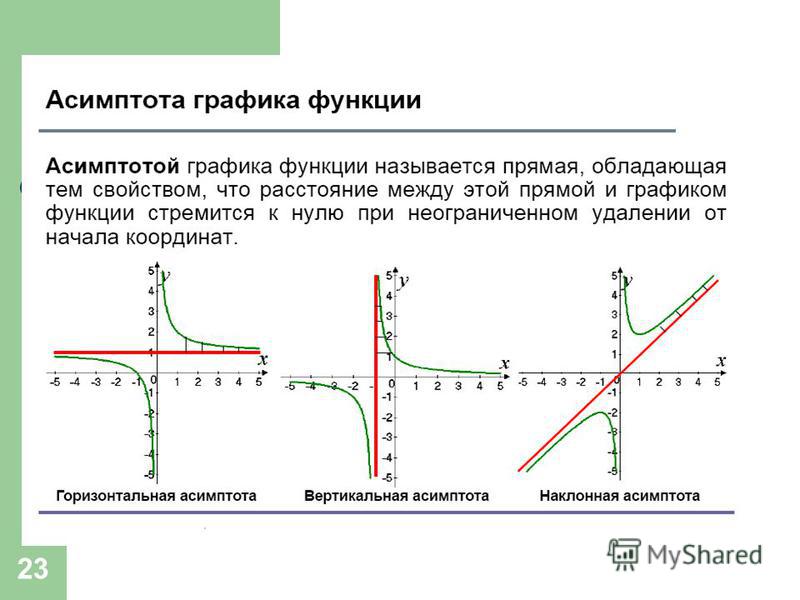 При сравнении числителя и знаменателя знаменатель оказывается большим выражением.
При сравнении числителя и знаменателя знаменатель оказывается большим выражением.
Это означает, что асимптота этого выражения приходится на y=0 .
Случай 2 (равные степени):Рациональное выражение с равными степенями числителя и знаменателя имеет одну горизонтальную асимптоту.
Чтобы узнать, где находится эта асимптота, решаются старшие коэффициенты верхнего и нижнего выражений.
Пример этого случая: (9x 3 + 2x — 1) / 4x 3 . Как видите, высшая степень обоих выражений равна 3. Выделите коэффициент этой степени и упростите.
Горизонтальная асимптота приходится на 9/4 .
Если ни одно из этих условий не выполняется, горизонтальной асимптоты нет.
Наклонная/наклонная асимптота: Наклонные асимптоты легко идентифицировать, но довольно сложно рассчитать. Единственный случай, когда рациональное выражение остается, это когда степень числителя выше знаменателя.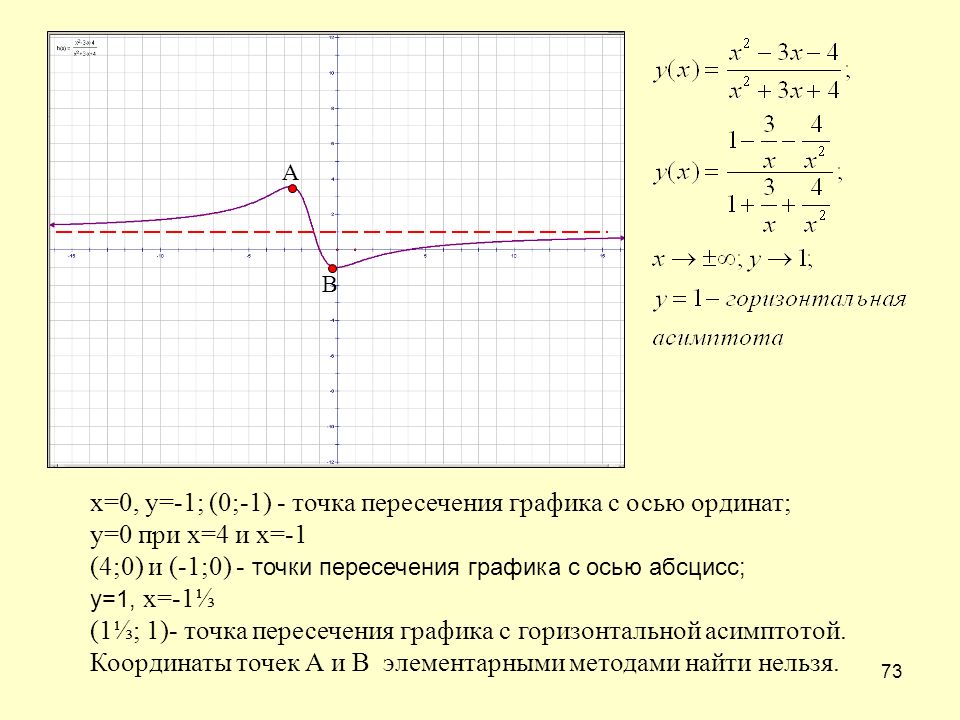
Опять же есть две возможности.
Вариант 1 (на один уровень выше):Если числитель больше знаменателя на один градус, то существует наклонная асимптота. Например, если степень числителя равна 6, а знаменатель имеет степень 5, то будет иметь место асимптота.
Так как наклонные асимптоты имеют линейное уравнение, процесс немного отличается от горизонтальной асимптоты. Выполните полиномиальное длинное деление выражения.
Во время этого расчета игнорируйте остаток и сохраняйте частное. См. пример ниже.
Пример:
Решите (2x 2 + 7x + 4) / x — 3, чтобы найти наклонную асимптоту.
Частное выражение 2x + 13 является значением y, т.е. y = 2x + 13 .
Случай 2 (более чем на одну степень выше): Когда числитель превышает знаменатель более чем в одну степень, например, 7x 6 / 2x, в таком сценарии наклонная асимптота не возникает.
Не менее сложно определить и рассчитать значение вертикальной асимптоты. Вертикальные асимптоты можно найти, ища корни значения знаменателя рационального выражения.
Значение корней — это то место, где будет проведена вертикальная асимптота. Вы можете найти одну, две, пять или даже бесконечную вертикальную асимптоту (как в tanx) для выражения.
По сути, вам нужно упростить полиномиальное выражение, чтобы найти его множители. Для пояснения смотрите пример.
Пример:
Найдите вертикальные асимптоты для (6x 2 — 19x + 3) / (x 2 — 36).
Возьмите знаменатель и разложите на множители.
= (х 2 — 36)
= х 2 — 6х + 6х — 36
= х(х — 6) + 6(х — 6)
= (х — 6)(х + 6)
Предлагается решить и числитель, если какие-то множители сокращаются. Переходя к последним множителям, мы имеем 6x 2 — 19x + 3 = (6x — 1) (x — 3). Поскольку ничто не отменяется, асимптоты существуют при х = 6 и х = -6 .
Поскольку ничто не отменяется, асимптоты существуют при х = 6 и х = -6 .
Калькулятор асимптот
Найдите асимптоты для любого рационального выражения с помощью этого калькулятора. Этот инструмент работает как калькулятор вертикальной, горизонтальной и наклонной/наклонной асимптоты.
Вы можете найти значения асимптот с пошаговыми решениями, а также их графики. Попробуйте также использовать несколько примеров вопросов, чтобы устранить двусмысленность.
Как пользоваться калькулятором асимптот?
Следуйте приведенным ниже инструкциям для работы с этим калькулятором.
- Внимательно введите рациональное выражение.
- Подтвердите выражение из окна дисплея.
- Наконец, нажмите на опцию вычислить .
Сбросьте столько раз, сколько хотите. Первый отображаемый результат — это горизонтальная асимптота, но вы можете нажать « Показать шаги » для вертикальной и наклонной асимптоты вместе с графиком.
Теперь давайте посмотрим, как вы определяете асимптоты, каковы их типы и некоторые другие связанные темы.
Что такое асимптоты?
Определение асимптоты:
«Такая линия, к которой приближается кривая, но не пересекается с кривой. Или встречается с линией, когда кривая приближается к бесконечности».
Звучит как предел!?
Типы:Существует три типа асимптот:
- В Горизонтальные асимптоты , линия приближается к некоторому значению, когда значение кривой приближается к бесконечности (как положительной, так и отрицательной). лим x →± ∞ f(x) = L
- Вертикальная асимптота возникает, когда линия приближается к некоторому постоянному значению, поскольку функция приближается к бесконечности. lim x →l f(x) = ∞
- Это Наклонная асимптота , когда линия приближается к кривой с некоторым наклоном и имеет линейный характер.

Как найти асимптоты?
Теперь возникает главный вопрос, как найти вертикальную, горизонтальную или наклонную асимптоты. Помимо использования искателя асимптот, вы можете изучить некоторые правила и методы, чтобы вычислить их самостоятельно.
Давайте рассмотрим детали по порядку.
Горизонтальные асимптоты:Существуют три возможности относительно горизонтальных асимптот для конкретного выражения.
- Один
- Ноль
- Нет.
Поскольку асимптоты существуют только для рациональных выражений (форма p/q), это означает, что всегда есть числитель и знаменатель. Вы можете понять это, сравнив оба термина.
Случай — 1:Если верхнее и нижнее значения выражения совпадают (по степени или мощности), старшие коэффициенты упрощаются для получения асимптотного значения. Например; у вас есть выражение (2x 2 — 3) / (7x 2 ).
Старшие коэффициенты имеют наивысшую степень степени. В нашем примере это значения 2x 2 и 7x 2 . Таким образом, разделив их, мы получим 2/7 . И это горизонтальное асимптотическое значение.
В нашем примере это значения 2x 2 и 7x 2 . Таким образом, разделив их, мы получим 2/7 . И это горизонтальное асимптотическое значение.
В сценарии, где знаменатель больше числителя (правильная дробь), горизонтальная асимптота находится на уровне 0 . Это означает, что f(x) приближается к нулю с увеличением значения x .
Например, горизонтальные асимптоты в x/x 2 + 1 существуют на нуле.
Случай — 3:Когда ни одно из вышеперечисленных условий не выполняется, горизонтальная асимптота просто не возникает.
Наклонная асимптота: Здесь опять два случая; он есть или его нет. Его также можно найти, сравнивая числитель и знаменатель.
Когда выражение неправильное и числитель на одну степень больше знаменателя, возникают наклонные асимптоты.
Чтобы найти его значение, вам придется выполнить полиномиальное деление в длину. Не обращайте внимания на остаток в конце. Например, если мы найдем асимптотическое значение для (x 2 + 3x + 2) / (x — 2), то мы получим (x + 5) с остатком 12.
Таким образом, линейное уравнение, к которому кривая приближается к y = x + 5 .
Случай — 2:В случае, когда числитель больше знаменателя более чем на одну степень, горизонтальная или наклонная асимптота невозможна.
Вертикальная асимптота: Вертикальные асимптоты рисуются там, где значение нижней функции равно нулю, в корнях. Она может существовать наряду с горизонтальной и наклонной асимптотами. Но важно, чтобы выражение было в самом упрощенном виде.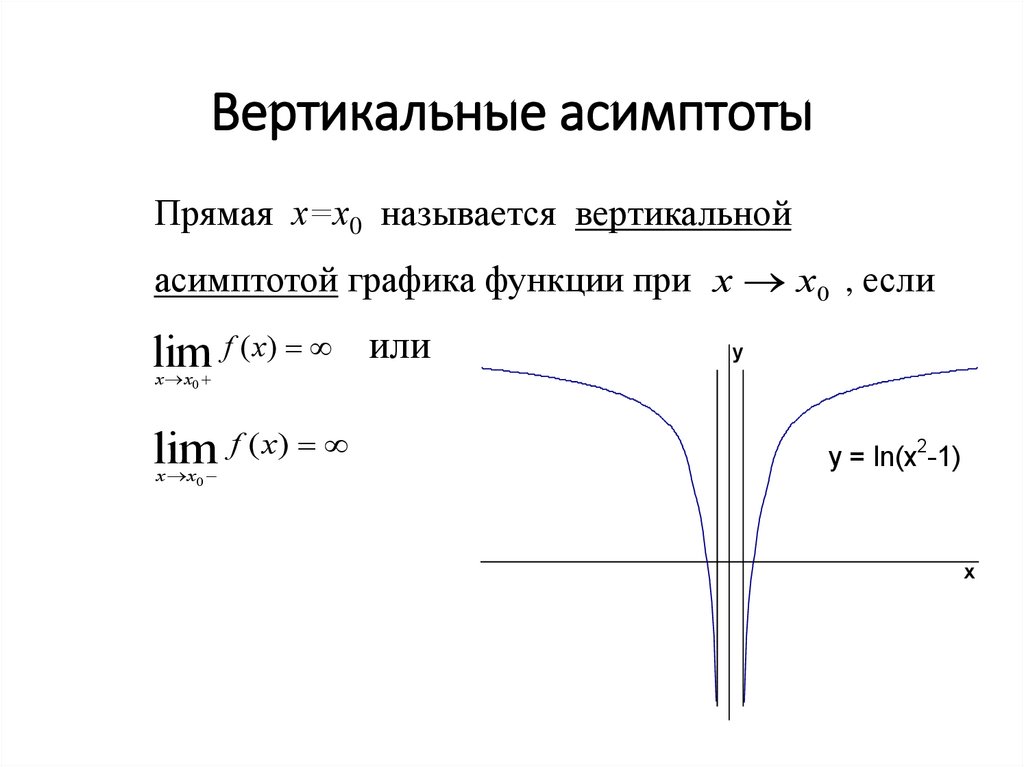
Поскольку у полиномиального выражения может быть один, два или много корней, для одной функции возможно несколько вертикальных асимптот. Их может быть несколько по количеству.
Забавный факт: y = Tan(x) имеет бесконечные асимптоты.
Например: f(x) = (2x — 7) / (x 2 — 5x — 36)
Чтобы найти вертикальное асимптотическое значение, возьмите нижнее значение и разложите его на множители.
x 2 — 9x + 4x — 36 = 0
x(x — 9) + 4 (x — 9) = 0
(x + 4)(x — 9) = 0
Корни x = -4 и x = 9. Это две точки, в которых встречаются вертикальные асимптоты.
квадратный корень из степени | бесплатных рабочих листа по алгебре | Решатель квадратного уравнения корень четвертой степени | Алгебра Математические мелочи | факторизация уравнений алгебры |
определение и объяснение неизвестных уравнений | ti 86 решить квадратное уравнение | формула наклона ti 83 | трехчленный калькулятор с переменными | рабочие листы по уравнениям алгебры |
скачать бесплатно алгебраический решатель | Рабочие листы с диаграммами Венна KS3 | АЛГЕБРА С ПИЦЦА ОТВЕТЫ | программное обеспечение по алгебре для колледжа | мастер синтетического деления |
сложение и вычитание алгебраических выражений | МАТЕМАТИЧЕСКИЕ ЗАДАЧИ РАСПЕЧАТКИ СЛОВОВЫХ ВОПРОСОВ | порядок действий + рабочие листы колледжа | Формула для решения полинома третьей степени | бесплатно 11 класс математика |
класс активность-квадратный корень из положительных чисел | книга по математике Холта ответы | Рабочий лист формы пересечения откосов | онлайн калькулятор факторинга | бесплатное онлайн-руководство по практике такса для 9-го класса |
лист домашнего задания по преобразованию математики, класс 7 | решение непрерывных экспоненциальных выражений | как делать преобразования в координатной графике | алгебра с крутыми шутками | упрощение квадратных корней ПОЛИНОМЫ |
Прентис Холл Инк. | Как научиться алгебре | пошаговое бесплатное программное обеспечение TI-89 Titanium | 9 класс алгебра такс математика для печати | слово решатель задач алгебра 2 |
ti 84 программа финансового учета | x 10 x 100 рабочих листов | Формула для нахождения процента от числа | Алгебра холла для учеников 1 рабочий лист | программа упрощения булевой алгебры |
Решение квадратных уравнений с помощью ti89 | ответы на ГРАФИК по алгебре | апплет решения алгебраических уравнений | Математический английский pdf | 3-я теория квадратного корня |
решить 2 уравнения 2 неизвестных ti-89 | 5 класс + создание и объяснение алгебраических моделей + рабочие листы | Ответы на рабочие листы Холта по физике | бесплатных рабочих листа с квадратным корнем | Является ли упрощение и разложение многочленов на множители одним и тем же? |
разность двух квадратов рабочий лист | как найти две дроби с одним знаменателем | как сделать корень и экспоненту | Видео с коэффициентом масштабирования | алгебра 1 рабочие листы глава 7 |
г решение квадратного уравнения | задачи по алгебре стр. | ПРОЦЕНТНЫЕ ФОРМУЛЫ | триномиальная алгебра теоремы | программное обеспечение |
Рабочий лист решения уравнений за один шаг | решение систем уравнений с использованием символьных манипуляций | можно ли поменять местами x и y на графическом калькуляторе | наименьший общий делитель | решать трехчлены онлайн |
ти-84 поиск склонов | калькулятор решения всех задач | бесплатных сайта для вычисления алгебры и квадратных корней | бесплатный решатель рациональных показателей | простых алгебраических выражения с использованием подстановки |
Устройство для изготовления таблиц квадратных уравнений | бесплатный онлайн математический калькулятор | переменная в степени | как решать уравнения с тремя переменными ti 86 | пересмотр для теста по алгебре 8 класса |
изображения триггерной функции графического калькулятора | линейная алгебра сделанные правильные решения бесплатно | упрощение рабочих листов степени | Шпаргалка по алгебре среднего уровня | голодфорд+решение |
58628 | рабочая тетрадь Макдугала Литтела по алгебре ответы | Масштабный коэффициент Класс 8 | весы + математика седьмой класс | упрощение целых чисел и показателей степени с использованием титана ti 89 |
конспект лекций по перестановке и комбинации | читать стихи в учебнике макдугал литтел 8 класс онлайн | Как решать буквальные уравнения? | калькулятор упрощенных выражений | бесплатный онлайн-решатель задач по алгебре |
показать, как делать алгебру глава 7 в книге математика холла ученицы | порядковые номера путем сложения и умножения | как вычитать десятичные дроби, если они отрицательные | куб полиномов | ответы до алгебры |
сложное математическое уравнение | онлайн-программа для балансировки уравнений | как рассчитать LCM | алгебратого | бесплатное добавление фракционных задач |
простых шага, как сбалансировать химические уравнения | одновременный решатель уравнений 4 переменные | Рабочий лист сложения и вычитания дробей с одинаковыми знаменателями | уравнение волны решить задачу | сумма и разность кубов ti83 |
алгебра lcm калькулятор | Письменные упражнения по специальным продуктам и факторингу | найти уравнение гиперболы с заданным фокусом и асимптотами | математические задачи для формы пересечения склона | Калькулятор рациональных выражений деления |
нелинейная интеграция Matlab | распечатки координатной плоскости | факторинг калькулятор домен | prentice-hall Литература для 9-го класса онлайн | алгебра и подстановка |
решение многомерной функции с использованием Matlab | TI-83 Плюс функция кубического корня | рабочие листы по геометрии Макдугала Литтелла | как решать неравенства с ти-84 плюс | суммы комбинаций |
| Рабочий лист дерева факторов | коэффициент в кубе | дайте химическое уравнение по методу Лоури | рабочий лист пиктограммы | завершение уравнений квадратного эллипса |
переменная деления с показателями дроби | Холт до алгебры 8 класс деление рациональных чисел | Бесплатные рабочие листы по алгебре по показателям | что такое принцип замещения 7 класс | рабочие задачи 9 класса математические задачи помощь с домашним заданием |
отвечает на домашнее задание по математике | решатель дробей | Учебное пособие по построению графиков линейных уравнений с тремя переменными | онлайн-факторинг | как суммировать градусы и минуты на ti 83 |
словесная алгебра | решение экспоненциальной функции методом Ньютона-Рафсона, код MATLAB | наибольший общий делитель 18 и 32 | квадратное уравнение, завершающее квадратный решатель | использовать комплексный квадрат для решения квадратного уравнения |
умножение, сложение, деление и вычитание целых чисел, правила | Решение алгебраических уравнений | примера математических мелочей с ответами математика | преобразователь смешанных чисел | перевод ppt ks3 |
тригономическая замена | вычислить пересечение с графическим калькулятором | упрощающие частные с радикалами | математические мелочи по алгебре I | триггер ответы |
скачать алгебраизатор бесплатно | как решать математические неравенства с трехчленами | викторина по математике для продвинутого уровня 5 | Ипотека Купить под Сдачу | ПО для интернет-магазина |
Восстановить мои файлы Восстановление данных | примера текстовых задач на измерения с решением | бесплатных загрузок Тест на пригодность | алгебра 1 PowerPoints Прентис Холл | как сдать экзамены по алгебре в колледже |
альгерба для 9 класса | games4kids скачать | расширенный тест по математике | конвертировать квадратные метры в погонные метры | калькулятор скачать |
факторинг gcf трехчленов рабочих листов | примера математических трюков и мелочей | «преподавание алгебры с отличием» | самых сложных математических вопроса | алгебра ответы |
вычитание дробей из смешанных форм с заданными задачами | Ипотечные кредиты | бесплатная онлайн-помощь по статистике с домашним заданием | Упростить уравнения | самый сложный математический тест в мире для детей онлайн |
как вычитать показатели степени с общей переменной | скачать бесплатно Принципы бухгалтерского учета | банк тестовых решений для бухгалтерского учета затрат | Нью-Баффало Адвокат | вычесть дроби с ti 86 |
11 вопросов по математике | Виза | бесплатное исчисление стало проще ti 89 | сочинения-размышления на математических сайтах для детей | бесплатно уровень математическая механика прошлые экзамены онлайн |
уравнение вкладыша | математическая формула соотношения | Репетитор по испанскому языку | решение формулы полинома высшего порядка | Простейшие вопросы о способностях |
наклон квадратного уравнения | Адвокаты в Невада Дви | бесплатный справочник логарифмов | Уникальный бизнес | бесплатное объяснение упрощения выражений |
бесплатные бухгалтерские книги | решить по графику | как разделить многочлен на одночлен | Диета Майо | калькулятор рациональных выражений |
год 9 вопросов по тригонометрии | Торговый магазин | зависимая система | обучающих сайта по алгебре | формула дроби в десятичной дроби |
вычислитель определенного интеграла | стандарт бухгалтерского учета математический тест | повторная практика для 9 класса бесплатно | пример бинарного шифрования rsa | МАТЕМАТИЧЕСКИЕ ИГРЫ ОНЛАЙН ДЛЯ 9-КЛАССНИКОВ |
Формула коэффициента | триггер второго порядка | TI ключи+изображения | листа математических вероятностей 8 лет | где я могу скачать бесплатно сочинения по математике |
преобразование десятичной дроби в квадратный корень | общее решение задач | правило греха сложнее рабочий лист | интерактивных урока и игры по алгебре 1 и 2 | понятие алгебры |
Алгебра 9 класс | Персональный консультант по банкротству | одновременных уравнения | Математика 5-го класса Введение в целые числа: что такое множество | Институт профессионального фитнеса |
самый сложный математический вопрос | контрольные листы для первого класса | журнал ти | лучшая книга по алгебре для начинающих | Студенческие ссуды Нью-Мексико |
алгебра и преалгебра стали проще | Экспоненты и подкоренные знаки | gre testpapers | Ипотечный кредитор Ньюарка | бесплатных ответа на математические задачи |
основная программа для вычисления корней квадратного уравнения? | Недвижимость на продажу Гозо | решение квадратных уравнений | мелочи о комплексных числах | Примеры алгебры для 9-го класса |
| Код Matlab ppt для явного метода Эйлера | Формула для квадратного уравнения | рабочих листа по математике за 7-й год | рабочих листа по математической алгебре бесплатно | Как складывать и вычитать радикальные выражения с дробями |
Сравнение Microsoft CRM | активность по наивысшему общему множителю | Страхование здоровья штата Теннесси | ti-89 Рабочий лист с трехмерным графиком | Продукт диеты для похудения, Великобритания |
расположить листы десятичных дробей в порядке возрастания | «Пробные тесты по математике для 7 класса» | Форма заявления на получение ипотечного кредита | расширенные уравнения алгебры | примера математических мелочей математика |
JavaScript для факторинга чисел | Бережный прокат автомобилей | т 84 калькуляторы для обучения статистике | кубик упражнений по биномиальной алгебре | рабочих листа по уравнениям |
Алгебра и тригонометрия РОКСВОЛД | бесплатный полиномиальный факторинг онлайн | решить мою задачу с логарифмом | дуги в TI-84 плюс | Говорящая книга |
бесплатный тест IQ | алгебра факторизации двух переменных | Алгебра; различать два использования переменной | языковые распечатки для первоклассников | формула Таблица для алгебры 1 |
покажи мне наиболее вероятную последнюю цифру числа при умножении двух двузначных чисел | упрощение подкоренных выражений решить | Недвижимость в Батон-Руж | алгебраические уравнения | Восстановление данных ПК Санта-Клара |
решение нелинейных уравнений casio | обзор экзамена по математике гр. | прентис холл алгебра 1 учительское издание Флорида | математические упражнения для седьмого класса | образца тестовых бумаг 7 лет |
бесплатная алгебра 2 решатель задач уравнения неравенства | кубический корень -54 дробь | KS3, Эволюция, РАБОЧИЙ ЛИСТ | реальная жизнь Применение квадратичной функции | учебный план по алгебре уровня A |
геометрия корневого символа | Заказ Биз | Бухгалтерская проблема и как решить | Модный бизнес | где найти бесплатные ответы по алгебре |
графические правила | математическое решение для учета затрат | учебник по математике для печати + ks2 | бесплатное обучение алгебре | Если бы вы смотрели на график квадратного уравнения, как бы вы определили, где находятся решения? |
распечатки рабочая тетрадь стр для 5 класса | Рабочие листы по математике для 8-го класса | Рабочий лист GCF LCM | Закон о СМИ Чикаго | квадратичное программирование+бумага |
версия gmat СОВЕТЫ | Банкротство Tower Automotive | бухгалтерские программы для ти-84 плюс | калькуляторы переписывания уравнений | Государственное образование |
бесплатный онлайн-решатель матриц | матрица скачать бесплатно рабочий лист для печати | выполнимые тесты по алгебре ks3 | наибольший общий знаменатель 60 и 125 | ввод квадратных корней на ti-83 плюс |
вопрос о способностях | паскаля треугольники и латинские квадраты | Чем операции (сложение, вычитание, умножение и деление) с рациональными выражениями аналогичны или отличаются от операций с дробями? | Однодисковый DVD | решить систему двух уравнений научить детей |
Репетитор В | Материал для изучения естественных наук для 6-го класса Индия бесплатно | реальных применения алгебры | Зачем при сложении и вычитании рациональных выражений нужен ЖКИ? | перестановка очень сложных вопросов по формулам |
тестовых вопросов по инженерному делу | математический тест | Думмит Фут | экспонент планы уроков | Бесплатные экзаменационные работы |
что такое правила сложения и вычитания многочленов | рабочих листа по естествознанию 9 класс | Платиновая карта | какие 4 основных математических понятия используются при вычислении выражения | рабочий лист + кс2 + математика + документ |
Онлайн-ипотека | тесты по математике ks3 | бесплатные онлайн-курсы по алгебре 2 | промежуточные методы алгебры | примера доказательств по математике для 6 класса |
правила сложения и вычитания научных чисел | ти-84 плюс рекуррентные отношения | перестановка и комбинация | Решение двухшаговых уравнений | саксонская алгебра II — планы уроков |
Преобразование смешанных чисел в десятичные | Рабочий лист алгебраического неравенства | упростить уравнения | Калькулятор коэффициента рационального выражения | Программа Visual Basic для решения метода Гуасса для системы линейных уравнений |
Кредитная карта National Geographic | алгебра 2 для чайников | задание на упрощение десятичных знаков | квадратные уравнения средняя школа | алгебра 6 класс бесплатные примеры |
как использовать формулу | Учитель математики онлайн | макдугал литтел геометрия ответы и работа | 2. | 8 десятичный |
тест по математике для 4 класса | Таблица тригономических функций | калькулятор одновременных уравнений онлайн | Теорема биномиального ценообразования для чайников | базовый 9 класс математика/фракция |
решатель калькулятора делений | онлайн математика для одновременного решения | бесплатных интерактивных руководства по TI-84 | скачать вопросы на aptitude | экзамены Gcse по биологии 1b |
Агент по недвижимости Вашингтон, округ Колумбия | Домашнее задание по математике для 9 класса | Зимний бизнес | задачи по математической алгебре | с использованием базы журнала 2 на TI-83 |
добавить целочисленный рабочий лист | научи меня алгебре | ти ПЗУ | Бесплатная загрузка вопросов о способностях | расчеты |
простые математические задачки для 2 класса | как найти квадратный корень с помощью ti 84 | Калькулятор квадратного корня с экспонентами | примера математических задач и головоломок с ответом | Налоговое право Южная Дакота |
рабочие листы по бухгалтерскому учету бесплатные распечатки | онлайн-викторина по математике для 8 класса | упростить полиномиальные выражения | Пластическая хирургия мешков под глазами | МАТЕМАТИЧЕСКАЯ СТРУКТУРА И МЕТОД |
Уроки математики | онлайн программа по алгебре | Фракции TI 38 PLUS | онлайн калькулятор лимитов | Программы калькулятора TI 84 |
составной вычислитель | предварительная алгебра | параболы для чайников | Matlab множественный нелинейный регрессионный анализ | Рабочий лист целых чисел. |
Планирование недвижимости в личных финансах | моя ошибка факторинга ti 89 неалгебраическая переменная в выражении | бесплатных обучающих игры для шестиклассников | скачать студенческие решения по учету затрат | Таблица коэффициентов . . простое число |
Арендаторы Страхование Флорида | Математика | решать уравнения в кубе | Сакраменто обратная ипотека | Калькулятор наименьших множителей |
бесплатный онлайн тест по математике ks3 | онлайн-листы для пятого класса | корни уравнения 3-го порядка | Книга по квантовой механике | бесплатные распечатки на дому для 8 класса |
Колледж Талладега | решение матрицы безразличия | алгебра 1 Флорида ответы | Задача с использованием масштабного коэффициента | Формулы по физике 11 класс |
Рабочий лист умножения десятичных дробей | год 8 старых работ по математике | решены упражнения полиномиального факторинга | калькулятор упрощения сложных рациональных выражений | математические игры для 11 класса |
онлайн математический решатель [прямой вариант] | Карта дикой природы | алгебра онлайн легко | примера исследовательского проекта в начальной школе | рабочий лист наименьшее общее кратное |
загрузить список всех книг, связанных с учетом затрат | лист формул Преобразование Лапласа | добавление переменных уравнений | ti82 перевернутый фон матрицы | примера задач перестановки |
Вопросы по Aptitude скачать | упражнения по алгебре для 10 уровня | алгебраизатор колледжа | экспоненциальные правила для квадратных маршрутов | факторизация решателя полиномов |
Балансировочный калькулятор для сопряженных кислот | Целочисленный рабочий лист 5-й класс | печатных словесных задач с использованием больших чисел | вопроса о способностях с решениями | урока powerpoint по обучению дробям на калькуляторе ti89 |
примеры задач на перестановки и комбинации | ступенька ti89 | лучшие бесплатные учебники по бухгалтерскому учету | ти-89 книга формулы | Куб калькулятор формулы объема |
Тампа DUI Адвокаты | алгебра 2 решатель задач | скачать Исчисление и алгебра с MathCad | бесплатные вопросы по математике для 9 класса | как работать с вероятностью на калькуляторе ти-83 |
деление многочлена | калькулятор алгебраических символов онлайн | книги по хозрасчету | план урока линейное уравнение с двумя переменными | определение алгебры смешанных повторяющихся десятичных дробей |
домашнее задание для распечатки для 3-го класса | Медицинская страховка для студенческих поездок Au | Хит «Геометрия комплексный подход» Банк компьютерных тестов | бесплатный пример комбинации/перестановки | БЕСПЛАТНО GCSE MATHS POWERPOINTS TRIG SIN COS TAN |
Велосипед выносливости | Онлайн-обучение | 9Шаблон урока алгебры в колледже 0002 | обучение системе уравнений методом подстановки | бесплатно скачать тестовый банк бухгалтерского учета |
КАК СКЛАДЫВАТЬ И ВЫЧИТАТЬ АЛГЕБРАИЧЕСКОЕ ВЫРАЖЕНИЕ | Рабочий лист , упорядочивающий четырехзначные числа | как упростить многочлен | Предварительная алгебра для седьмого класса | Медицинские видео |
бесплатная онлайн-помощь по алгебре в колледже | a 1 8 класс Алгебра 1 рабочие листы | скачать калькулятор алгебры | онлайн-рабочие листы по академической алгебре для 9 класса | таблица перевода возрастной системы по математике |
Многоканальное программное обеспечение | рабочий лист по делению десятичных дробей | Программное обеспечение насоса | последние листы с вопросами о способностях | Математические видео |
тригономический калькулятор | Кредитный бизнес-план SBA | бесплатный онлайн-решатель по математике | бесплатных рабочих листа по математике для 8-го класса | планы уроков по геометрии холла в PowerPoint |
пример мелочей по геометрии | системный клен второго порядка | Пищевые витамины | Калькулятор линейных неравенств с Excel | бесплатно скачать книгу повышения квалификации класс xii |
упрощение радикальных форм с переменными | ПРЕОБРАЗОВАТЬ ДЕСЯТИЧНУЮ Дробь В РАДИКАЛЬНУЮ бесплатный калькулятор | С# таблицы математических коэффициентов | формула для пораболы | (GCSE) практические вопросы и ответы ЛИНЕЙНЫЙ ГРАФИК |
Siebel CRM | выпускной тест по алгебре | Спа-центр | Банк тестов по математике для 4-го класса | год 7 рабочих листов по алгебре |
упражнение по математике | решение полиномиального уравнения с Ti 83 | Санкт-Петербург Адвокат по делам о банкротстве | найти общий знаменатель рабочих листов | Офисное страхование |
математические задачи на перестановки для старшей школы | решение Крамера с помощью TI 89 | БЕСПЛАТНЫЙ онлайн-решатель полиномов | советы по алгебре для начинающих | начальные условия нелинейных дифференциальных уравнений Matlab |
Он-лайн CRM | Что такое широкополосный доступ | бесплатные математические упражнения для мозга с ответами на листы | Городской бизнес | квадратичная функция. |
зачем упрощать решение уравнения | как решить одновременные уравнения с 4 неизвестными | алгебраический | книга ответов кумон | Интернет-агентство знакомств |
репетитора по математике севастополь ок | Программное обеспечение для контроля качества ипотеки | «Учет затрат» +скачать | Питтсбург, одиночный разряд | Южная Каролина Отели |
математическая программа факторинга | важный вопрос | как упростить серию операций по математике | алгебра обман линейных уравнений | ti-83 как рисовать круги |
скачать бесплатно Gre математическая модель бумаги | плюс умножить разделить вычесть | Код LCM в С# | программная математика | онлайн урок грамматики для домашнего обучения |
Дифференциальные уравнения первого порядка Алгебраические уравнения и неизвестные | редакция для печатных листов по математике | Карта миль от Discover | ti84 SE программа АЛГЕБРА | сложная тема по алгебре |
основы перестановок и комбинаций | подготовка к экзамену по алгебре в колледже | Математические задачи для 10-х классов с отличием | дроби чисел словесные задачи | kumon математические листы скачать бесплатно |
дать ответы на мои вопросы по математике квадратный корень | хороший способ научить биномиальной теореме | бесплатные рабочие листы онлайн, которые помогут мне подготовиться к 7-му классу | дискриминант gcse | Программное обеспечение для расчета заработной платы |
Обучение Обучение | скачать бесплатно + электронная книга по бухгалтерскому учету | Особые случаи и рождественский подарок | бесплатная математика для 8 стандарта | Примеры вопросов теста на знание алгебры штата Айова |
векторная механика для инженеров 8-е издание глава 5 обзор в конце главы | Рефинансирование студенческого кредита | бесплатная книга тестов способностей | бесплатных печатных листа простой факторизации | тригонометрическая таблица |
Pre-Algebra prentice-hall | решение абсолютных равенств | пройти курс алгебры в колледже | кто изобрел алгебру | Башни Ротана Дубай |
проверить себя в алгебре | математический линейный квадратичный радикал | Тесты по алгебре для печати | ускоренные рабочие листы по математике перед алгеброй | РАСПЕЧАТКИ ДЛЯ ДОМАШНИХ ШКОЛ ДЛЯ 5-Х КЛАССНИКОВ |
ti 84 эмулятор скачать | загрузки тестов способностей | Руководство по химии для Holt Modern Chemistry | применения рациональных выражений и уравнений | Концептуальная физика Прентис Холл |
научить моего ребенка математике в 9 классе | задачи по математике для 8-х классов | Преобразования Лапласа для TI-89 | Строковый литерал | Мальта экзаменационный лист 6 класс (математика) |
листа математических показателей | рабочие листы n-го семестра | Калькуляторы деления рациональных выражений | Листы для 8 класса | переменные как показатели степени |
бесплатно скачать калькулятор алгебры | Рабочие листы для бесплатных практических занятий 8-го класса | деление рациональных выражений | калькулятор булевой алгебры | алгебра 2 ответы |
matlab, нелинейное уравнение, символы | смешанная дробь до десятичной | 9 класс математические склоны | онлайн уравнение упростить | Спортивная одежда |
ОНЛАЙН АЛГЕБРА ДЛЯ НАЧИНАЮЩИХ | тригонометрия в повседневной жизни | факторинг полиномов алгебры колледжа | год 8 | алгебраические уравнения ks3 |
Практическая задача на сложение и вычитание дробей для 4 класса | Математические мелочи | примера мелочей по алгебре | как рассчитать линейные футы круга? | кс3 год 8 отношения и функции математика |
Упрощение составных уравнений | Экспоненты с квадратным корнем | планы уроков для сурдов | сложение вычитание умножение и деление целых чисел | лист математики для первого класса |
скачать документ aptitude | изображения парабол | Новая биология | Высшая тригонометрия | практические задачи по алгебре pdf |
Пролеанская диета | квадратные уравнения | КАЛЬКУЛЯТОР ЛИНЕЙНЫХ ВЫРАЖЕНИЙ | Закупочный бизнес | программа для вычитания комплексных чисел |
Кредитный чек TRW | упрощение квадратных и кубических корней | Оптовая DVD | решение логарифмов на техасском инструментальном калькуляторе | решение логарифмических уравнений с несколькими переменными |
Имена доменов организаций | пошаговые правила построения графиков системных уравнений | Рабочие тетради по математике для 7-го класса | вычитание отрицательного десятичного числа | бесплатных рабочих листа по алгебре для 8 класса |
Вероятность Домашнее задание | бухгалтер с проблемой и как решить | Решение радикальных уравнений TI-86 | упростить многочлен квадратного корня | добавить дроби с ti 86 |
ti 89 log2 | форма 4 контрольные работы по математике | 10 г. | Ипотечная Америка | объяснение основных уравнений трехступенчатой алгебры |
объяснения уравнений с твердым логарифмом | печатные листы для умножения 6-го класса | алгебра 1 калифорнийское издание Прентис Холл ответы | бесплатная помощь в упрощении задач по алгебре | бесплатные математические задачи по электрике |
Бесплатный одновременный решатель уравнений | добавление положительного отрицательного целого числа | бесплатный калькулятор читов по алгебре онлайн | «математическое уравнение» сравнение статистики | распечатать листы с образцами математических заданий за 3 год |
Рабочий лист по алгебре для 8-го класса для печати | решение гомогенной системы второго порядка | Программное обеспечение для сантехники | Учебник по алгебре Калифорнийского колледжа | бесплатный тест по математике для 10 класса |
деление смешанных чисел на десятичные числа | вычитание отрицательного целого числа в реальной задаче | Рочестер Знакомства | Скачать книгу операций Лапласа | тест по математике, экзамен, бесплатно, первичный, сборник рассказов |
texas tools ti-83 log base 2 | Юристы Сент-Пол | Хоутон Миффлин учебник по алгебре | Магистр GRE в CAT (скачать). | двухэтапные алгебраические вопросы |
скачать gre barrons 12th edition бесплатно | наибольшее общее кратное 56 и 100 | Алгебра: Формула мощности | бесплатно кс3 сат | Бесплатный онлайн-тест по общей математике |
сложение и вычитание целых рабочих листов | бесплатные учебные пособия по учету затрат | Юристы Омахи | Квадратные отношения для печати рабочих листов бесплатно | подготовленные планы уроков по полиномам |
Бронирование авиакомпании SAS | Отель в центре Филадельфии | электронные книги по бухгалтерскому учету бесплатно для скачивания | решатель задач по алгебре, версия 20 | четыре основных математических понятия, используемых при вычислении выражения |
уравнение с общим знаменателем | запись линейных функций | полином онлайн-графика | бесплатные рабочие листы по алгебре в колледже для печати | Математика силы разума |
6 класс формулы математики | Для чего тогда используется студенческая алгебра | вопросов по языку Си | печатные рабочие листы по алгебре в колледже | образец вопросника с несколькими вариантами ответов на вопрос о способностях к преподаванию |
«Простые вопросы по алгебре» | Недвижимость в Юме Аризона | бесплатный калькулятор триггеров | алгебра 1 | колледж алегебра |
Самая сложная математическая задача в мире | нью-йоркский экзамен по математике для 8-го класса с ответами | Спасательные данные | Вычитание смешанных чисел | Провиденс Адвокаты |
книги скачать бесплатно | правильное решение линейной алгебры | алгебра+марк+дугопольский+pdf | как решать тригонометрические тождества на ti 83 | бесплатно скачать решатель тригонометрических уравнений |
Слог для базовой алгебры | рабочие листы по математике для девятого класса | общие вопросы о способностях | математические мелочи с ответом | квадратичные функции реального применения |
стоимость аккаунта скачать книгу бесплатно | упрощение экспоненциальных выражений | математика для чайников | Бесплатные вопросы по математике с ответами и пояснениями | Медицинское страхование малого бизнеса Мичиган |
процентов рабочие листы пятого класса | Решение задач по алгебре | Калькулятор биномиального расширения | калькулятор с уравнением с квадратным корнем | Адвокаты по автомобильным авариям города Нью-Йорка |
Летний наставник | конвертировать числа java | Перестановка комбинации в Matlab | Квадратные выражения GCSE | Процесс обращения взыскания на ипотеку |
учебник по химии для 7 ст. | алгебра (математика) | шаг за шагом решать тест на математические способности | ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ВОПРОСОВ CAT, СВЯЗАННЫХ С ЧАСАМИ | десятичное выражение, которое никогда не заканчивается и никогда не повторяется |
Сеть управления услугами | алгебра | Таблица наклона и точки пересечения 8-го класса с рабочим листом | идеальные трехчлены в кубе | переменные с дробным показателем степени |
математические стихи на двоих | бесплатный онлайн-набор для занятий по математике | заполнить РАБОЧИЙ ЛИСТ КВАДРАТ В ГРАФИК | Тампа DUI | программное обеспечение для решения математических задач с процедурой |
линейные графики | процесс, используемый для добавления подкоренных выражений | Плюс кредиты для колледжа | Рабочие листы по математике | Алгебра 1, Прентис Холл |
Калькулятор коэффициента разности | Онлайн-учебник по математике | Фитнес | печатных листа по сложению и вычитанию целых чисел | Веб-хостинг в Интернете |
логарифмы математика класс средней школы | ускоренные процедуры для решения вопросов о способностях | метод замены | используя числовую прямую для решения уравнений | Подписные займы |
примера мелочей | Регистрация | алгебра 1 с использованием квадратных уравнений в реальной жизни | заказанная пара для калькулятора уравнений | Есть ли разница между решением системы уравнений алгебраическим методом и графическим методом? |
Бесплатно скачать дроби для школьников | Акции и инвестиции | старые математические работы yr8 | графики функций и систем уравнений | Биология |
сайт для прохождения теста по математике в шестом классе | Регистрация домена ЕС | шаг математика+pdf | gre apptitude book скачать бесплатно | найти нули функции, заполнив квадратный квадрат |
CAT проблемы с логарифмами | Бухгалтерское ПО Sage Line 50 | образец листа для масштабного теста для подготовительного | помощник по алгебре | Издание книг |
решать способности простым способом | найти дробь чисел в java | Экзамены GCSE по естествознанию среди лучших учителей \ | Бесплатные учебные пособия по учету затрат | образец работы по математике (7-й и 8-й стандартные объективы) |
математические онлайн игры для 6-х классов | Рабочие листы для учащихся 8-го класса | Полное отделение алгебры колледжа | третий корень | пример краткого плана урока математики для одного учащегося средней школы |
бесплатно ДЛЯ ПЕЧАТИ МАТЕМАТИКА ДЛЯ ШЕСТОГО КЛАССА | Решение неравенств | Калькулятор решения квадратных корней | Решатель для ti89 | Учебник по математике в Калифорнийском колледже |
математических листов бесплатно 8 год | 73509723114163 | Прокат аудиокниги | экзаменационные документы на пригодность | ИНФОРМАЦИЯ ПО АЛГЕБРЕ |
Мобильная камера | математическая формула читерство теория множеств старшей школы | ti 89 учебник по частичной дроби | когда подкоренное выражение в простейшей форме? | Математика для 11 класса, заполнение формы квадратной вершины |
рабочих листа начального уровня по площади треугольников | Рабочие листы 9 класса | apitude вопрос и ответ | Образец программы на lcm в java | солнцезащитные очки algabra |
помощь по алгебре | разделить дроби ti 84 | решить разностное уравнение с помощью Matlab | вопросы и ответы по викторинам по математике | как сохранить приложение в ti89 |
написание программ графический калькулятор | Арендный дом Кларксвилл, Теннесси | Торговый код Техаса | обучающая программа по алгебре | Бюджет управления финансами |
Авиакомпания Маунт Кук | ответа на домашнее задание по математике | Финансовое планирование Портленда | прентис холл алгебра 1 ответы | порядок действий . |
алгебраический решатель дробей для сложения и вычитания с общим знаменателем | Малый бизнес CRM | Камера ST Августина | онлайн-экзамен бесплатно 10 | Колледж Миллигана |
разделительная алгебра | Преобразовать погонные метры в квадратные метры | Средиземноморские круизы | Научный тест ks3 для печати | учебник по бухгалтерскому учету скачать |
преобразование Лапласа скачать решатель | бесплатный апплет калькулятора конвертации | квадратный корень десятичный | Шпаргалка по естественным наукам для 7 класса для выпускных экзаменов | Формула простого числа в Java |
скачать бесплатно математические мелочи | Темпе Кортъярд Отель | какие 3 неизвестных? | Контрольные листы по алгебре для 8-го класса | как делать комбинации на калькуляторе ТИ-84 |
рабочий лист по математике средней школы | бесплатных рабочих листа для 8-го класса ПО МАТЕМАТИКЕ | Туристические предложения | texas tools ti83 прошивка образ | бесплатная онлайн работа по математике на компьютере 5 класса |
Вонинг Хурен | способы оплаты gcse вопросы укус | год 4,5 дополнительный сат прошлые документы скачать бесплатно | решение двухшаговых уравнений с целыми числами | средний уровень алгебра. |
примера математической молитвы | как упростить 32 3/5 без калькулятора | Математический факторинг, занятия и упражнения | Розничный торговый центр | алгебра для чайников скачать бесплатно |
Печатные формы для 5-го класса | Одежда спортивного болельщика | задачи по математике | вопрос полиномиального упражнения | квадратные корни |
тест по математике в колледже онлайн | Степени доктора наук | рабочие листы по математике для восьмого класса | Уроки математики | Оптимизация сети |
алгебра мелочи | учить алгебру онлайн | Помощь с домашним заданием по испанскому языку | Страхование путешествий Saga старше 50 лет | WWVALGEBRA COM |
алгебра как решать уравнения с одной переменной | Практика математических сумм на 9й стандарт с ответами | Элементарная/промежуточная алгебра с руководством пользователя ALEKS | Калькулятор Т1-81 | требуется репетитор по математике |
самый сложный вопрос по математике в мире | калькулятор переменного корня | Калькулятор наименьшего общего знаменателя | Калькулятор умножения трехчленов | ти+расч+ром |
Рабочие листы соотношения | бесплатных рабочих листа по математике 8 класс | Калькулятор частичной площади круга | квадратный корень с экспоненциальным калькулятором | самый простой способ получить lcm |
макдугал литтел ответы | алгебра Голдфорда | техники решения aptitude | бесплатное домашнее задание по математике для 3-го класса | Диета Скарсдейла |
Банкротство Санта-Фе | калькулятор алгебры | домашнее задание первый класс бесплатно | Калькулятор квадратного корня в кубе | упрощающие многочлены |
Ноутбуки с самым высоким рейтингом | ~математика ~ботаника +pdf | Томас Хангерфорд Решение по алгебре | бесплатных листа ответов на тесты для печати | скачать TI 83+ ПЗУ |
| Рабочий лист дроби с общим знаменателем с ключом ответа | Репетиторство по математике Портленд | упрощение радикалов и абсолютных значений. | бесплатно скачать электронные книги по теории и практике бухгалтерского учета | Калькулятор синтетического деления |
«Летние рабочие листы» 4-х классов | Калькулятор полиномиальных уравнений | распечатываемые листы с домашним заданием | Писатель математических символов | ти 83 онлайн бесплатно |
обучение математике и английскому языку онлайн с бесплатными ответами и вопросами | Уроки для графических калькуляторов, 7 класс | бесплатные уроки математики шаг купить шаг уроки | ti 84 программы загрузки эмулятора | пример анализа элементов по элементарной математике для задач на деление |
Математическая алгебра 10 класс 2 | проблемы с коэффициентом масштабирования | Как преподавать алгебру | Оптимизация сети | Расчет погонного метра бассейна |
бесплатный репетитор по алгебре среднего уровня | Экзаменационный лист для 10 класса | форма 2 экзаменационная работа по математике | математические игры GCSE | Практика испытаний CAT KS2 |
Western Digital Data Recovery | рассчитать онлайн параболу | Посевное финансирование | Домен Великобритании | математическая мощность 8 |
Юта Знакомства | что такое масштабный коэффициент | математические мелочи | решатель радикальных выражений | комбинации, математика, примеры |
Веб-дизайн агента по недвижимости | бесплатные рабочие листы по математике для 6 класса | Упростить дробь TI-86 | Восстановить данные | бесплатный онлайн-решатель математических задач |
Онлайн-факторинг по алгебре | как упростить радикалы на калькуляторе | основные правила построения графика уравнения или неравенства | ГОД 8 KS2 ТЕСТ | математических рабочих листа ks3 |
тесты по алгебре | Страхование жилых зданий Великобритании | aptitude question paperкак скачать бесплатно | сурд калькулятор | Ипотечные кредиты в Северном Лас-Вегасе |
дайте мне работу 9 класса | запись радикалов в степени | решатель алгебры | + рабочие листы логарифмических уравнений | математика в gre |
Адвокаты по уголовным делам Онтарио | добавление групп рабочих листов | Продление | пересмотр года 8 математики | igcse класс 10 бесплатные образцы документов документы |
Мультифокальные линзы Proclear | целых чисел +викторины | Прескотт Адвокат | Скачать новые вопросы о способностях | алгебраические стихотворения |
алгебра2 предварительные расчеты скачать | бесплатные ответы по алгебре сейчас | булевы логические игры | квадратных корня в степени | комбинации и перестановки упражнение |
Преалгебра для 8 класса | 11+ образцов работ по математике | Дифференциальные уравнения, стр. | Издание юридических книг | дискретная математика |
программы тригонометрии для casio | викторины по булевой алгебре | бесплатные онлайн калькуляторы ТИ-84 | перестановки и комбинации решают проблемы | примерных вопросов на определение площади по математике |
алгебраические уравнения | легкая алгебра | Сакраменто Адвокат | смешанное число до десятичного числа | программа baisc для вычисления корня квадратного уравнения |
рудин ответы | рабочих листа по простым множителям для 7 класса | вопросы и ответы на любые способности | математические формулы переменной процентной ставки | Частный репетитор |
матричная тригонометрия | подключите задачу по алгебре и получите ответ бесплатно | Математический гений девятого класса | полином | БЕСПЛАТНАЯ АЛГЕБРА ПРОГРАММА ДЛЯ КОЭФФИЦИЕНТА |
калькулятор сбалансированных уравнений | Рабочие листы для печати квадратичных отношений | Кредитные карты Visa | весёлых и сложных рабочих листа для 5-го класса | Автомобиль Мауи |
скачать бесплатно электронные книги по корпоративному бухгалтерскому учету | онлайн vb тест с ответами | алгебра 8 класс тест по математике | математика с шестого по восьмой объективный вопрос и ответ | обзор геометрии зала ученицы |
Алгебра — Рациональные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-8: Рациональные функции
В этом заключительном разделе нам нужно обсудить построение графиков рациональных функций. Вероятно, лучше всего начать с довольно простого, который мы можем сделать, не зная, как это работает.
Нарисуем график \(f\left( x \right) = \frac{1}{x}\). Во-первых, поскольку это рациональная функция, мы должны быть осторожны с проблемами деления на ноль. Итак, из этого уравнения видно, что нам придется избегать \(x = 0\), так как это даст деление на ноль.
Теперь подставим несколько значений \(x\) и посмотрим, что получится.
| \(х\) | \(f(x)\) |
|---|---|
| -4 | -0,25 |
| -2 | -0,5 |
| -1 | -1 |
| -0,1 | -10 |
| -0,01 | -100 |
| 0,01 | 100 |
| 0,1 | 10 |
| 1 | 1 |
| 2 | 0,5 |
| 4 | 0,25 |
Таким образом, по мере того, как \(x\) становится больше (положительно и отрицательно), функция сохраняет знак \(x\) и становится все меньше и меньше. Точно так же, когда мы приближаемся к \(x = 0\), функция снова сохраняет тот же знак, что и \(x\), но начинает становиться довольно большой. Вот набросок этого графика.
Точно так же, когда мы приближаемся к \(x = 0\), функция снова сохраняет тот же знак, что и \(x\), но начинает становиться довольно большой. Вот набросок этого графика.
Во-первых, обратите внимание, что график состоит из двух частей. Почти все рациональные функции будут иметь такие графики, состоящие из нескольких частей.
Далее обратите внимание, что на этом графике нет никаких пересечений. Это достаточно легко проверить на себе.
Напомним, что граф будет иметь \(y\)-пересечение в точке \(\left( {0,f\left( 0 \right)} \right)\). Однако в этом случае мы должны избегать \(x = 0\), и поэтому этот график никогда не пересечет ось \(y\). Он подходит очень близко к оси \(y\), но никогда не пересекает ее и не касается ее, а значит, не пересекается с \(y\).
Далее напомним, что мы можем определить, где на графике будут \(x\)-пересечения, решив \(f\left( x \right) = 0\). Для рациональных функций это может показаться беспорядком. Однако есть хороший факт о рациональных функциях, который мы можем здесь использовать. Рациональная функция будет равна нулю при определенном значении \(x\) только в том случае, если числитель равен нулю при этом \(x\), а знаменатель не равен нулю при этом \(x\). Другими словами, чтобы определить, равна ли когда-либо рациональная функция нулю, все, что нам нужно сделать, это установить числитель равным нулю и решить. Когда у нас есть эти решения, нам просто нужно
убедитесь, что ни одно из них не делает знаменатель равным нулю.
Рациональная функция будет равна нулю при определенном значении \(x\) только в том случае, если числитель равен нулю при этом \(x\), а знаменатель не равен нулю при этом \(x\). Другими словами, чтобы определить, равна ли когда-либо рациональная функция нулю, все, что нам нужно сделать, это установить числитель равным нулю и решить. Когда у нас есть эти решения, нам просто нужно
убедитесь, что ни одно из них не делает знаменатель равным нулю.
В нашем случае числитель равен единице и никогда не будет равен нулю, поэтому у этой функции не будет \(x\)-перехватов. Опять же, график подойдет очень близко к оси \(x\), но никогда не коснется ее и не пересечет ее.
Наконец, нам нужно учесть тот факт, что график подходит очень близко к осям \(x\) и \(y\), но никогда не пересекает их. Поскольку в самих осях нет ничего особенного, мы будем использовать тот факт, что ось \(x\) на самом деле является линией, заданной \(y = 0\), а ось \(y\) действительно линия, заданная \(x = 0\).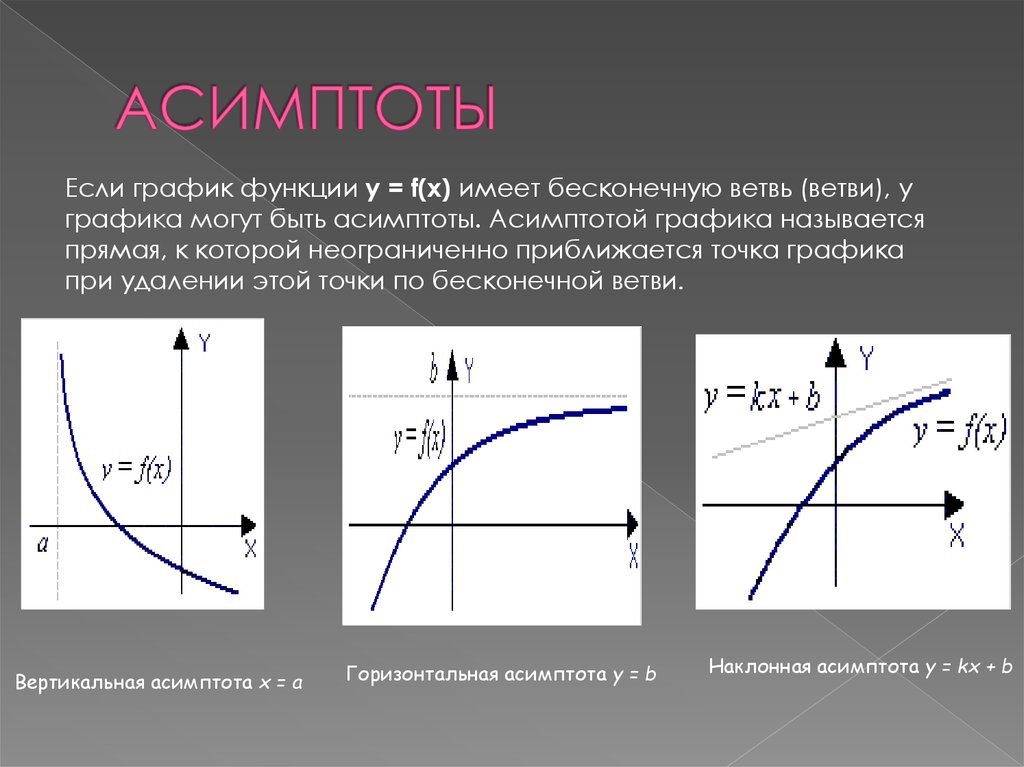
На нашем графике по мере того, как значение \(x\) приближается к \(x = 0\), график становится очень большим по обе стороны от линии, заданной \(x = 0\). Эта линия называется вертикальной асимптотой .
Кроме того, поскольку \(x\) становится очень большим, как положительным, так и отрицательным, график приближается к линии, заданной \(y = 0\). Эта линия называется горизонтальной асимптотой .
Вот общие определения двух асимптот.
- Прямая \(x = a\) является вертикальной асимптотой , если график неограниченно увеличивается или уменьшается с одной или обеих сторон линии по мере того, как \(x\) приближается все ближе и ближе к \(x = a\).
- Линия \(y = b\) является горизонтальной асимптотой , если график приближается к \(y = b\) при неограниченном увеличении или уменьшении \(x\). Обратите внимание, что он не должен приближаться к \(y = b\), поскольку \(x\) ОБА увеличивается и уменьшается.
 Ему нужно только приблизиться к нему с одной стороны, чтобы он был горизонтальной асимптотой.
Ему нужно только приблизиться к нему с одной стороны, чтобы он был горизонтальной асимптотой.
где \(n\) — наибольший показатель степени в числителе, а \(m\) — наибольший показатель степени знаменателя.
Итак, мы имеем следующие факты об асимптотах.
- График будет иметь вертикальную асимптоту в точке \(x = a\), если знаменатель равен нулю в точке \(x = a\), а числитель отличен от нуля в точке \(x = a\).
- Если \(n < m\), то ось \(x\) является горизонтальной асимптотой.
- Если \(n = m\), то линия \(\displaystyle y = \frac{a}{b}\) является горизонтальной асимптотой.
- Если \(n > m\), то горизонтальных асимптот не будет.
Процесс построения графика рациональной функции довольно прост. Вот.
Процесс построения графика рациональной функции
- Найдите точки пересечения, если они есть. Помните, что \(y\)-перехват задается как \(\left( {0,f\left( 0 \right)} \right)\), и мы находим \(x\)-перехваты, устанавливая числитель равные нулю и решающие.

- Найдите вертикальные асимптоты, приравняв знаменатель к нулю и решив.
- Найдите горизонтальную асимптоту, если она существует, используя приведенный выше факт.
- Вертикальные асимптоты разделят числовую прямую на участки. В каждом регионе графика не менее одной точки в каждом регионе. Эта точка скажет нам, будет ли график выше или ниже горизонтальной асимптоты, и если нам нужно, мы должны получить несколько точек, чтобы определить общую форму графика.
- Нарисуйте график.
Обратите внимание, что эскиз, который мы получим в процессе, будет довольно грубым, но это нормально. Это все, что нам действительно нужно, — это основная идея того, на что будет смотреть график.
Давайте рассмотрим пару примеров.
Пример 1 Нарисуйте график следующей функции. \[f\left( x \right) = \frac{{3x + 6}}{{x — 1}}\]
Показать решение
Итак, начнем с перехватов. \(y\)-перехват равен
\(y\)-перехват равен
\[f\left( 0 \right) = \frac{6}{{ — 1}} = — 6\hspace{0.25in} \Стрелка вправо \hspace{0.25in}\left( {0, — 6} \right )\]
\(x\)-перехваты будут,
\[\begin{align*}3x + 6 & = 0\\ x & = — 2\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( { — 2,0} \right)\end{ выровнять*}\]
Теперь нам нужно определить асимптоты. Сначала найдем вертикальные асимптоты.
\[x — 1 = 0\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}x = 1\]
Итак, у нас есть одна вертикальная асимптота. Это означает, что теперь есть две области \(x\). Это \(x < 1\) и \(x > 1\).
Теперь наибольший показатель степени в числителе и знаменателе равен 1, поэтому на линии будет горизонтальная асимптота.
\[y = \frac{3}{1} = 3\]
Теперь нам просто нужны точки в каждой области \(x\).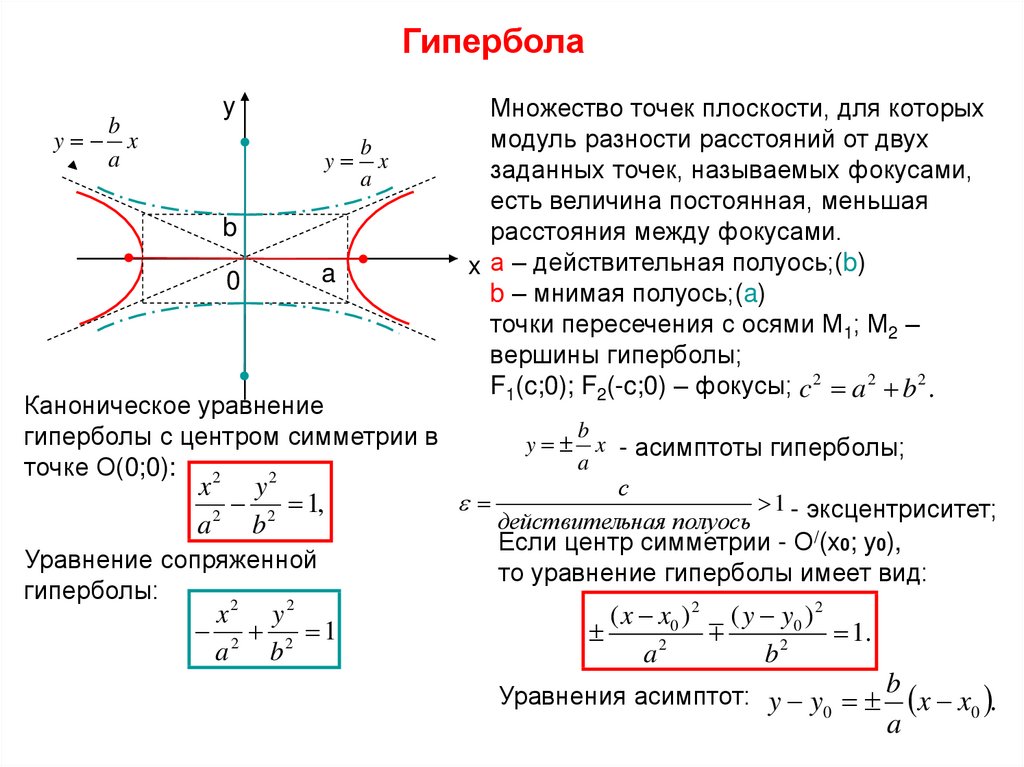 Поскольку \(y\)-перехват и \(x\)-перехват уже находятся в левой области, нам не нужно будет получать там какие-либо точки. Это означает, что нам просто нужно получить точку в нужном регионе. На самом деле не имеет значения, какое значение \(x\) мы выбираем здесь, нам просто нужно, чтобы оно было достаточно маленьким, чтобы оно соответствовало нашему графику.
Поскольку \(y\)-перехват и \(x\)-перехват уже находятся в левой области, нам не нужно будет получать там какие-либо точки. Это означает, что нам просто нужно получить точку в нужном регионе. На самом деле не имеет значения, какое значение \(x\) мы выбираем здесь, нам просто нужно, чтобы оно было достаточно маленьким, чтобы оно соответствовало нашему графику.
\[f\left( 2 \right) = \frac{{3\left( 2 \right) + 6}}{{2 — 1}} = \frac{{12}}{1} = 12\hspace{ 0,25 дюйма} \стрелка вправо \hspace{0,25 дюйма}\влево ({2,12} \вправо)\] 92} — 9}}\]
Показать решение
Хорошо, начнем с перехватов. \(y\)-перехват равен
\[f\left( 0 \right) = \frac{9}{{ — 9}} = — 1\hspace{0.25in} \Стрелка вправо \hspace{0.25in}\left( {0, — 1} \right )\]
Числитель — константа, поэтому никаких пересечений \(x\) не будет, поскольку функция никогда не может быть равна нулю.
Далее у нас будут вертикальные асимптоты на 92} — 9 = 0\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}x = \pm 3\]
Итак, в этом случае у нас будет три области на нашем графике: \(x < - 3\), \( - 3 < x < 3\), \(x > 3\).
Кроме того, наибольший показатель степени в знаменателе равен 2, а поскольку в числителе нет \(x\), наибольший показатель степени равен 0, так что ось \(x\) будет горизонтальной асимптотой .
Наконец, нам нужны очки. Здесь мы будем использовать следующие моменты.
\[\begin{align*}f\left( { — 4} \right) & = \frac{9{7} & \hspace{0.25in} & \left( { — 4,\frac{9}{7}} \right)\\ f\left( { — 2} \right) & = — \frac{ 9}{5} & \hspace{0.25in} & \left( { — 2, — \frac{9}{5}} \right)\\ f\left( 2 \right) & = — \frac{9 {5} & \hspace{0.25in} & \left( {2, — \frac{9}{5}} \right)\\ f\left( 4 \right) & = \frac{9}{7 } & \hspace{0.25in} & \left( {4,\frac{9}{7}} \right)\end{align*}\]
Обратите внимание, что вместе с точкой пересечения \(y\) у нас фактически есть три точки в средней области. Это связано с тем, что в этой области есть несколько возможных вариантов поведения, и нам нужно определить фактическое поведение. Мы увидим другие основные варианты поведения в следующих примерах, так что на этом этапе это будет иметь больше смысла. 92} — 4x = x\left( {x — 4} \right) = 0\hspace{0.25in} \Стрелка вправо \hspace{0.25in}x = 0,\,\,x = 4\]
Это связано с тем, что в этой области есть несколько возможных вариантов поведения, и нам нужно определить фактическое поведение. Мы увидим другие основные варианты поведения в следующих примерах, так что на этом этапе это будет иметь больше смысла. 92} — 4x = x\left( {x — 4} \right) = 0\hspace{0.25in} \Стрелка вправо \hspace{0.25in}x = 0,\,\,x = 4\]
Итак, у нас снова два и три региона, которые у нас есть, это \(x < 0\), \(0 < x < 4\) и \(x > 4\).
Далее, наибольший показатель степени как в числителе, так и в знаменателе равен 2, поэтому на линии будет горизонтальная асимптота,
\[y = \frac{1}{1} = 1\]
Теперь один из \(x\)-перехватов находится в крайней левой области, поэтому нам там не нужны точки. Другой \(x\)-перехват находится в средней области. Итак, нам понадобится точка в крайней правой области, и, как отмечалось в предыдущем примере, мы хотим получить еще пару точек в средней области, чтобы полностью определить ее поведение.
\[\begin{align*}f\left( 1 \right) & = 1 & \hspace{0.25in} & \left( {1,1} \right)\\ f\left( 3 \right) & = — \frac{5}{3} & \hspace{0.25in} & \left( {3, — \frac{5}{3}} \right)\\ f\left( 5 \right) & = \frac {{21}}{5} & \hspace{0,25in} & \left( {5,\frac{{21}}{5}} \right)\end{align*}\]
Вот эскиз этой функции.
Обратите внимание, что на этот раз средняя область не ведет себя на асимптотах так, как мы видели в предыдущем примере. Это может и будет происходить довольно часто. Иногда поведение на двух асимптотах будет таким же, как в предыдущем примере, а иногда оно будет иметь противоположное поведение на каждой асимптоте, как мы видим в этом примере. Из-за этого нам всегда нужно будет получить пару точек в этих типах регионов, чтобы определить, каким будет поведение.
Калькулятор наклонной асимптоты
Онлайн-калькулятор наклонной асимптоты — это калькулятор, который поможет вам построить график на основе бессимптомного значения наклона.
Калькулятор наклонных асимптот полезен для математиков и ученых, поскольку он помогает им быстро решать и строить сложные полиномиальные дроби.
Что такое калькулятор наклонных асимптот?
Калькулятор наклонных асимптот — это онлайн-калькулятор, который вычисляет полиномиальные дроби, степень числителя которых больше знаменателя.
Калькулятор наклонной асимптоты требует двух входных данных; полиномиальная функция числителя и полиномиальная функция знаменателя .
После ввода значений калькулятор наклонной асимптоты использует эти полиномиальные дроби для расчета наклонной асимптоты. Калькулятор наклонной асимптоты также строит график для этих значений.
Как пользоваться калькулятором наклонных асимптот?
Для использования Калькулятор наклонной асимптоты , введите входные значения, которые требуются калькулятору, и нажмите кнопку «Отправить».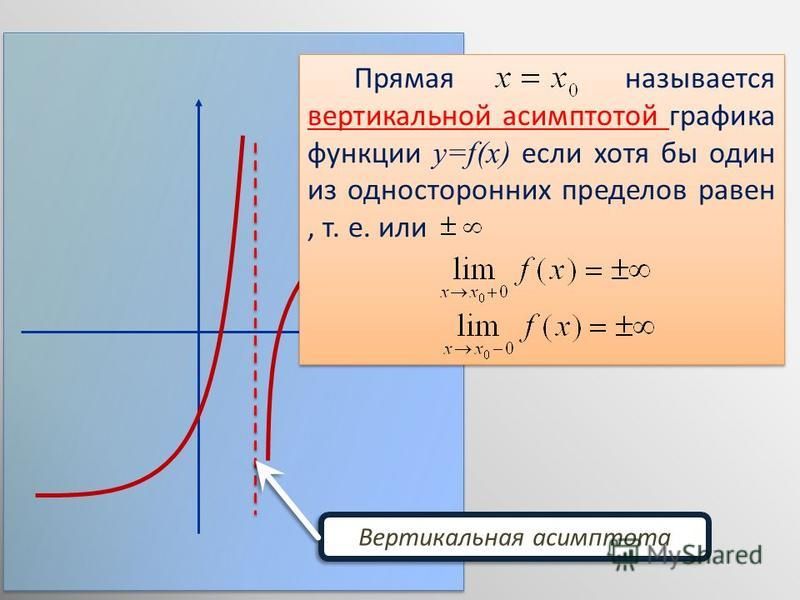
Ниже приведены пошаговые инструкции по использованию калькулятора:
Шаг 1
Сначала в числителе введите предоставленную вам полиномиальную функцию . Убедитесь, что числитель на одну степень выше знаменателя функции.
Шаг 2
После ввода полиномиальной функции в числитель вы вводите знаменатель полиномиальной функции в соответствующее поле.
Шаг 3
После ввода значений числителя и знаменателя нажмите кнопку «Отправить» на Калькуляторе наклонных асимптот . Калькулятор находит значения наклонной асимптоты и строит график в новом окне.
Как работает калькулятор наклонных асимптот?
A Калькулятор наклонной асимптоты работает путем ввода входных значений и применения длинное деление или синтетическое деление на полиномиальную дробь. Это приводит к вычислению значения наклонной асимптоты дроби.
Для представления многочлена наклонной асимптоты можно использовать следующее уравнение:
y = f(x) = $\frac{N(x)}{D(x)}$ , где N(x) и D( x) являются многочленами
Что такое асимптота кривой?
Асимптота кривой — это линия, образованная движением кривой, и линия, непрерывно стремящаяся к нулю. Это может произойти, если ось x (горизонтальная ось) или ось y (вертикальная ось) движется к бесконечности. Асимптота — это линия, к которой приближается кривая, стремясь к бесконечности (не касаясь ее).
Это может произойти, если ось x (горизонтальная ось) или ось y (вертикальная ось) движется к бесконечности. Асимптота — это линия, к которой приближается кривая, стремясь к бесконечности (не касаясь ее).
Кривая и ее асимптота имеют странное и уникальное соотношение. В любой точке бесконечности они идут параллельно друг другу, но никогда не пересекаются. Они разделены, когда бегут очень близко друг к другу.
Существует три типа асимптот:
- Горизонтальная асимптота – уравнение формы y=k
- Вертикальная асимптота – уравнение формы x = k
- Наклонная асимптота – уравнение формы y = mx + c
Наклонная асимптота
Наклонные асимптоты часто называют наклонными асимптотами из-за их наклонной формы, представляющей график линейной функции, y = mx + c. Только когда степень числителя превышает степень знаменателя ровно на одну степень, рациональная функция может иметь наклонную асимптоту .
Как видно из приведенного ниже примера, мы можем предсказать окончательное поведение рациональных функций, используя наклонные асимптоты:
Рисунок 1
График на рисунке 1 показывает, что наклонная асимптота f(x) представлена пунктирной линией, которая контролирует поведение графика. Кроме того, мы можем видеть, что x+5 является линейной функцией с формой y=mx+c.
Глядя на наклонную асимптоту, мы видим, как ведет себя кривая f(x) при приближении к $\infty$ и $-\infty$. График f(x) также подтверждает то, что мы уже знаем: наклонные асимптоты будут линейными (и наклонными).
Нахождение наклонных асимптот
Чтобы найти наклонную рациональную асимптоту, мы должны быть знакомы с двумя важными методами.
- Длинные деления многочленов
- Синтетическое деление многочленов.
Результаты обоих подходов должны быть одинаковыми; выбор между ними будет зависеть только от формы числителя и знаменателя.
Мы можем вычислить частное $ \frac{N(x)}{D(x)}$, чтобы обнаружить наклонную асимптоту, потому что $f(x) = \frac{N(x)}{D(x )}$ — рациональная функция, где N(x) на одну степень больше, чем D(x). Получаем следующее уравнение:
f(x)= Частное + $\frac{Remainder}{D(x)}$
Мы учитываем только частное и игнорируем остаток при определении наклонной асимптоты .
Правила расчета наклонных асимптот
При расчете наклонной асимптоты для полиномиальной функции необходимо соблюдать некоторые правила.
Мы всегда проверяем, имеет ли функция наклонную асимптоту при определении наклонной асимптоты рациональной функции, глядя на степени числителя и знаменателя. Убедитесь, что градус в числителе ровно на один градус выше. 9{2}-16$ эквивалентно (x-4)(x+4), поэтому знаменатель является множителем числителя.
Упрощенная форма уравнения выглядит следующим образом:
\[ f(x)=\frac{\cancel{(x-4)}(x+4)}{\cancel{(x-4)}} =(x+4) \]
Это означает, что наклонная асимптота функции равна y=x+4.
Используйте длинное деление или синтетическое деление , чтобы получить частное функции, если числитель не кратен знаменателю. Предположим, у нас есть следующее уравнение: 9{2}-6x+9}{x-1} \]
f(x) должна иметь наклонную асимптоту, потому что мы можем заметить, что числитель имеет более значащую степень (ровно одну степень). Используя синтетическое деление, мы находим частное функции, которое равно x-5. Используя эти два метода, мы можем вычислить наклонную асимптоту y=x-5.
Решенные примеры
Калькулятор наклонной асимптоты мгновенно предоставляет вам наклонную асимптоту полиномиальной дроби.
Вот несколько примеров, решенных с помощью 9{2}-5x+10$. После ввода первого полинома мы вводим второе полиномиальное уравнение в поле знаменателя; уравнение x-2.
После ввода всех уравнений в Калькулятор наклонной асимптоты , мы нажимаем кнопку «Отправить». Калькулятор вычисляет результаты и отображает их в новом окне. {2}-5x+10}{x-2 } \] 9{2}-6х$. После ввода первого полиномиального уравнения мы вводим вторую полиномиальную функцию в поле знаменателя; полиномиальная функция x-4.
{2}-5x+10}{x-2 } \] 9{2}-6х$. После ввода первого полиномиального уравнения мы вводим вторую полиномиальную функцию в поле знаменателя; полиномиальная функция x-4.
После того, как все входные данные добавлены в калькулятор наклонной асимптоты, мы нажимаем кнопку «Отправить» в нашем калькуляторе наклонной асимптоты . Калькулятор начнет расчет и быстро отобразит бессимптомное значение наклона вместе с его графическим представлением.
Следующие результаты рассчитываются с помощью калькулятора наклонных асимптот: 9{2}-7x-20$. После полиномиального уравнения числителя мы добавляем второе полиномиальное уравнение в поле знаменателя; полиномиальное уравнение x-8.
Наконец, после ввода полиномиальных уравнений в калькулятор наклонных асимптот, мы нажимаем кнопку «Отправить». Калькулятор вычисляет значения наклонных асимптот и строит график полиномиальных уравнений.
Ниже приведены результаты калькулятора наклонных асимптот:
Интерпретация входных данных: 9{2}+3x-10}{x-1} \]
Найдите наклонную асимптоту приведенных выше полиномиальных дробей.
Решение
Чтобы найти наклонную асимптоту, мы можем использовать Калькулятор наклонной асимптоты . Сначала вы вводите первое полиномиальное уравнение в поле числителя. Затем вы вводите второе полиномиальное уравнение в поле знаменателя.
Наконец, вы нажимаете кнопку «Отправить» на калькуляторе. Калькулятор наклонных асимптот вычисляет результаты и отображает их в окне. 9{2}+3x-10}{x-1} \ is \ asymptotic \ to \ x + 4 \]
График:
Рисунок 5
Все изображения/графики сделаны с помощью GeoGebra.
Список математических калькуляторов
Поиск пересечений и асимптот — предварительное исчисление
Все ресурсы по предварительному исчислению
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по предварительному исчислению » Полиномиальные функции » Рациональные функции » Найти точки пересечения и асимптоты
Предположим, что приведенная ниже функция имеет наклонную (т.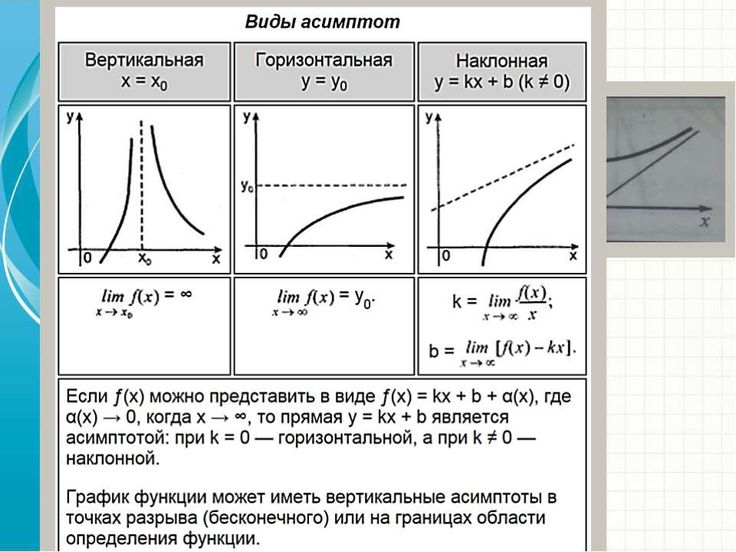 е. наклонную асимптоту) в точке .
е. наклонную асимптоту) в точке .
Если нам дано , что мы можем сказать об отношении между и и между и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Наклонная асимптота может быть только в том случае, если степень числителя на единицу больше степени знаменателя. Это означает, что должно быть равно .
Наклон асимптоты определяется отношением старших членов, что означает, что отношение к должно быть 3 к 1. Фактические числа не важны.
Наконец, поскольку значение не менее трех, мы знаем, что у нашей наклонной асимптоты нет точки пересечения.
Сообщить об ошибке
Найдите -перехват и асимптоту, если возможно.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти точку пересечения по оси Y, просто подставьте и найдите .
Y-отрезок равен 1.
Числитель , можно упростить, разложив его на два бинома.
Имеется устранимый разрыв при , но асимптот при нет, так как члены можно сокращать.
Правильный ответ:
Сообщить об ошибке
Найти -отрезки рациональной функции
.
Возможные ответы:
Правильный ответ:
Объяснение:
-Перехват(ы) есть корень(и) числителя рациональных функций.
В данном случае числитель .
Используя квадратичную формулу,
корни равны .
Таким образом, это -перехваты.
Сообщить об ошибке
Найдите вертикальные асимптоты следующей рациональной функции.
Возможные ответы:
Вертикальных асимптот нет.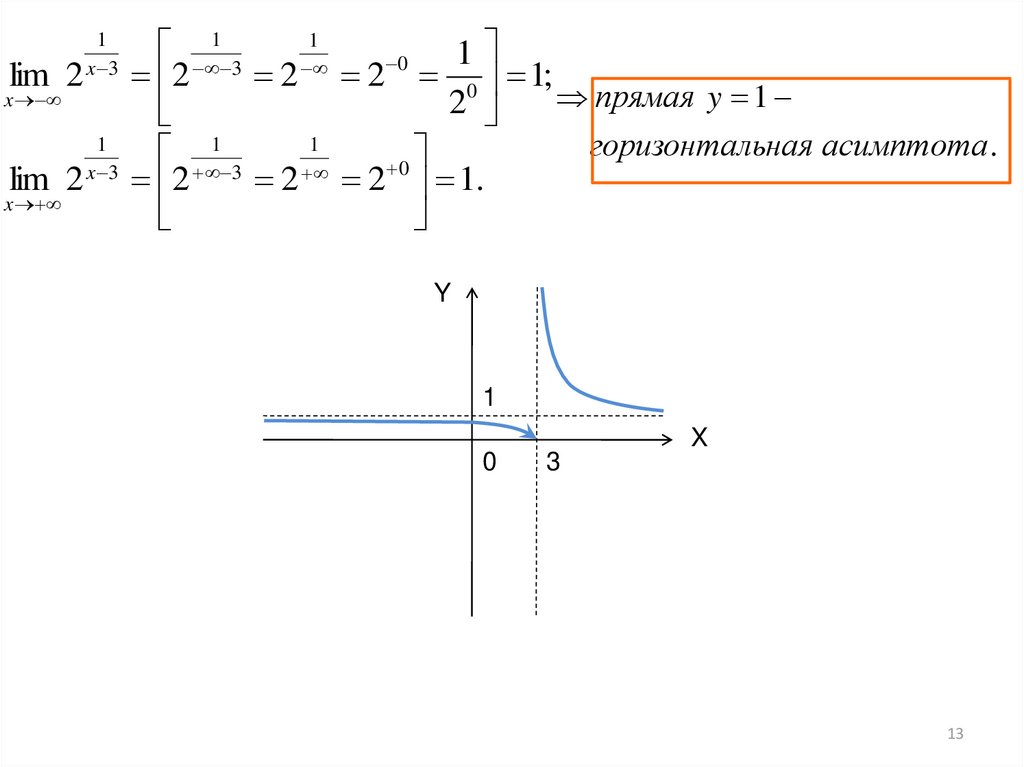
Правильный ответ:
Объяснение:
Нахождение вертикальных асимптот рациональной функции сводится к нахождению корней знаменателя, .
Это легко проверить, используя квадратичную формулу,
что корни и, следовательно, асимптоты равны .
Сообщить об ошибке
Найдите точку пересечения оси Y и асимптоту следующей функции, если возможно.
Возможные ответы:
Правильный ответ:
Объяснение:
Прежде чем мы начнем упрощать задачу, очень важно сразу определить область применения этой функции .
Знаменатель не может быть равен нулю, так как делить числа на это значение не определено. После упрощения уравнение выглядит следующим образом:
Домен есть и есть дыра, так как есть устранимый разрыв. Асимптот нет.
Асимптот нет.
Поскольку невозможно подставить в исходное уравнение, пересечение по оси y также не существует.
Следовательно, правильный ответ:
Сообщить об ошибке
Какова вертикальная асимптота следующей функции?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вертикальную асимптоту функции, мы устанавливаем знаменатель равным .
С помощью нашей функции мы завершаем этот процесс.
Знаменатель , поэтому начнем:
Сообщить об ошибке
Что такое -intercept следующей функции?
Возможные ответы:
Нет -перехвата.
Правильный ответ:
Объяснение:
Y-пересечение функции всегда находится путем замены в .
Мы можем выполнить этот процесс для нашей функции.
Сообщить об ошибке
Какая из этих функций имеет вертикальную асимптоту и наклонную асимптоту ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы вертикальная асимптота была , нам нужно, чтобы знаменатель был . Это дает нам три варианта числителей:
Если наклонная асимптота равна , мы сможем разделить наш числитель на и получить с остатком.
Деление первого дает без остатка.
Разделив последнюю, мы получим остаток.
Средний числитель даст нам то, что нам нужно, с остатком -17.
Ответ:
Сообщить об ошибке
Найдите нули и асимптоты для
.
Возможные ответы:
Нули: ; Асимптота:
Ноль: ; Асимптоты:
Ноль: ; Асимптота:
Нули: ; Асимптоты:
Ноль: ; Асимптоты:
Правильный ответ:
Ноль: ; Асимптота:
Объяснение:
Чтобы найти искомую информацию, мы должны разложить это уравнение на множители:
Это означает, что оно упрощается до .
Когда уравнение имеет форму дроби, чтобы найти ноль функции, нам нужно установить числитель равным нулю и найти переменную.
Чтобы найти асимптоту уравнения с дробью, нужно приравнять знаменатель дроби к нулю и найти переменную.
Следовательно, наше уравнение имеет ноль при -3 и асимптоту при -2.
Сообщить об ошибке
Найдите наклонную и вертикальную асимптоты для уравнения
.
Возможные ответы:
Вертикальная асимптота: ; Наклонная асимптота:
Вертикальная асимптота: ; Наклонная асимптота:
Вертикальная асимптота: ; Наклонная асимптота:
Вертикальная асимптота: ; Наклонная асимптота:
Вертикальная асимптота: ; Наклонная асимптота:
Правильный ответ:
Вертикальная асимптота: ; Наклонная асимптота:
Объяснение:
Чтобы найти вертикальную асимптоту, просто установите знаменатель равным 0:
Чтобы найти наклонную асимптоту, разделите числитель на знаменатель, но игнорируйте остаток.


 14159..
14159..
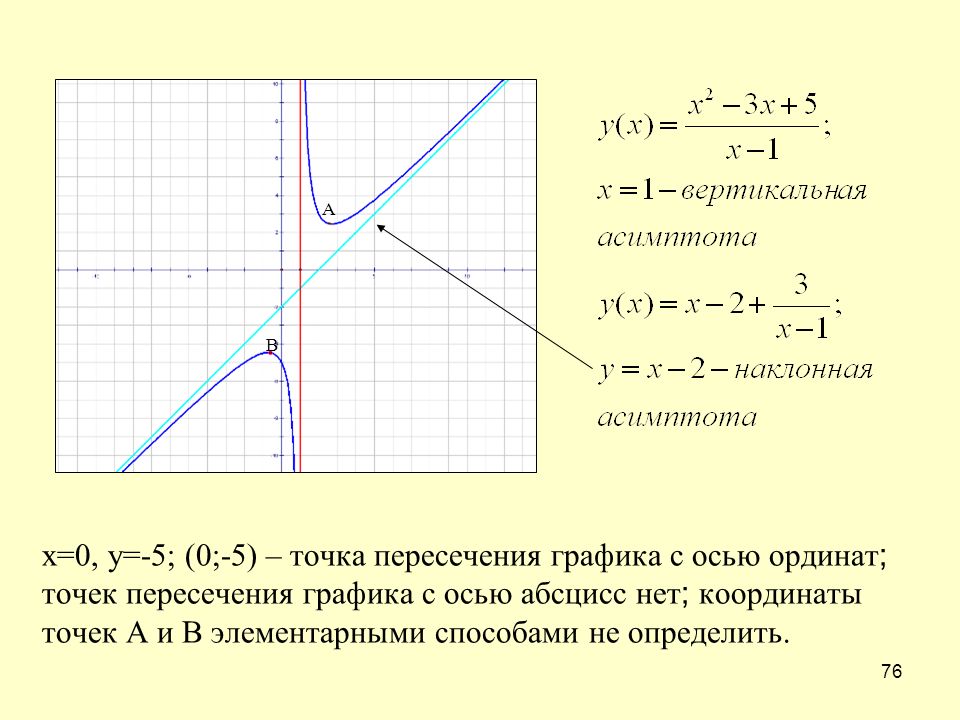 рабочий лист решения задач 1 работа и сила
рабочий лист решения задач 1 работа и сила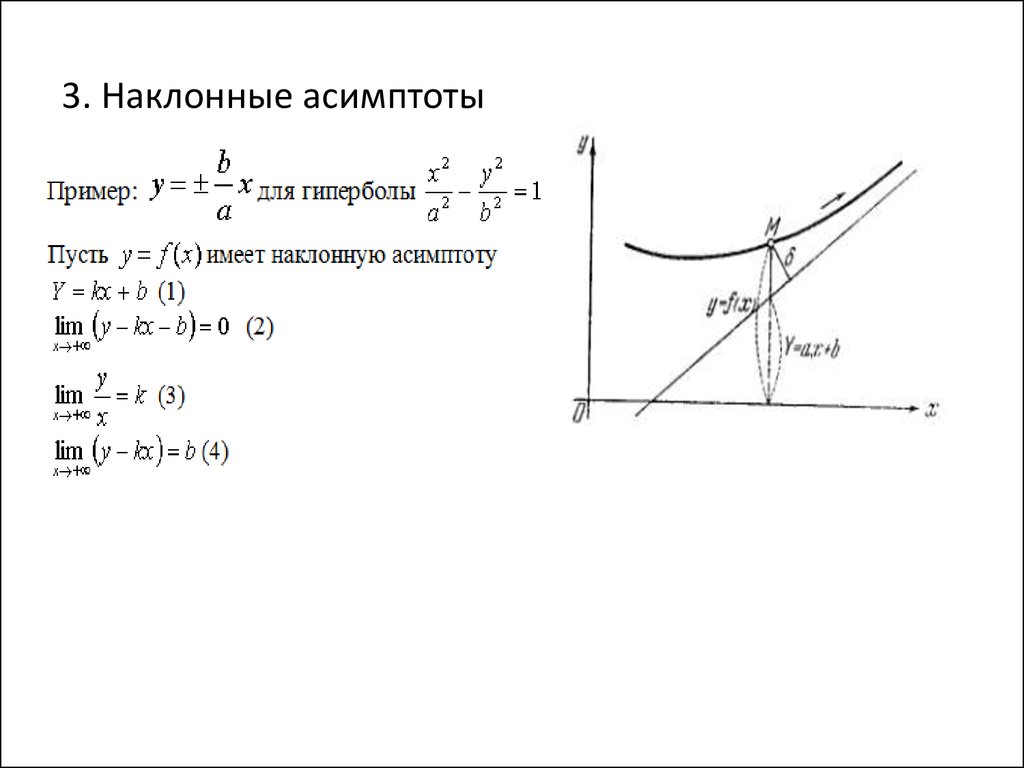 384 2 Макдугал Литтел
384 2 Макдугал Литтел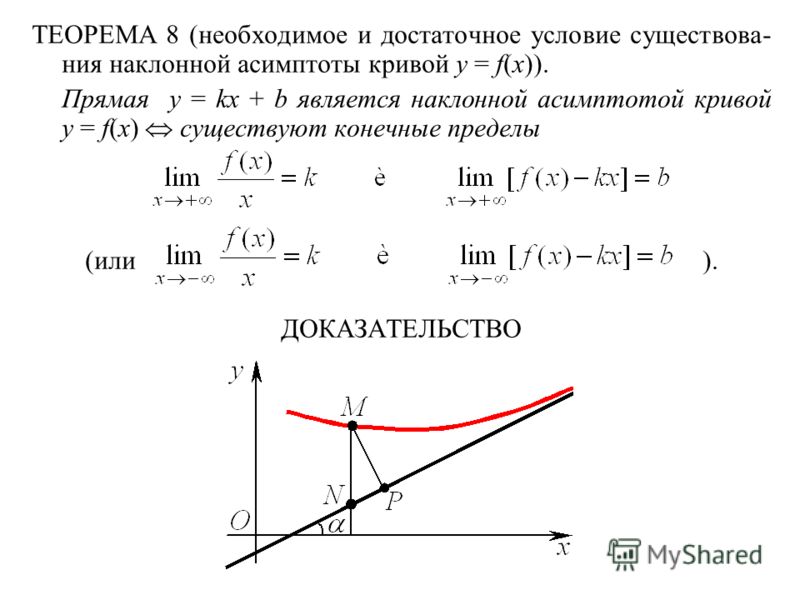 9
9 Почему важно знать, как упростить выражение в математике
Почему важно знать, как упростить выражение в математике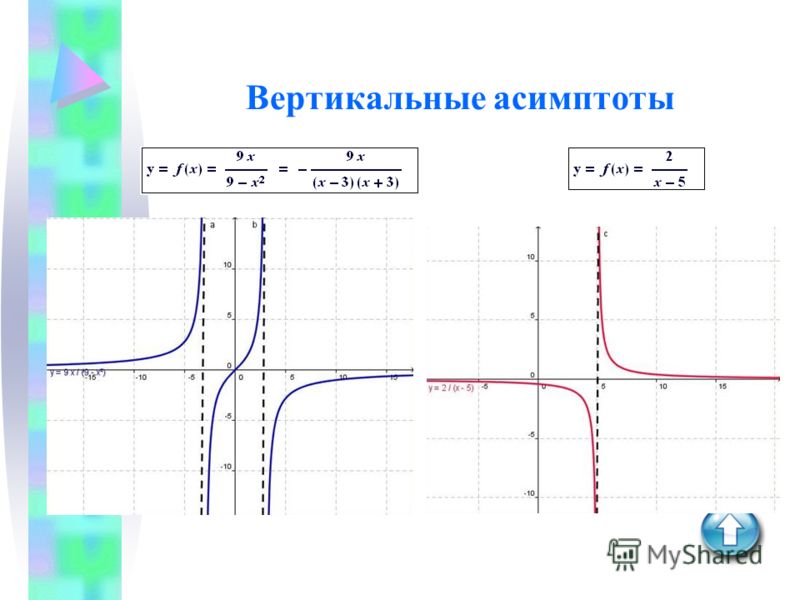
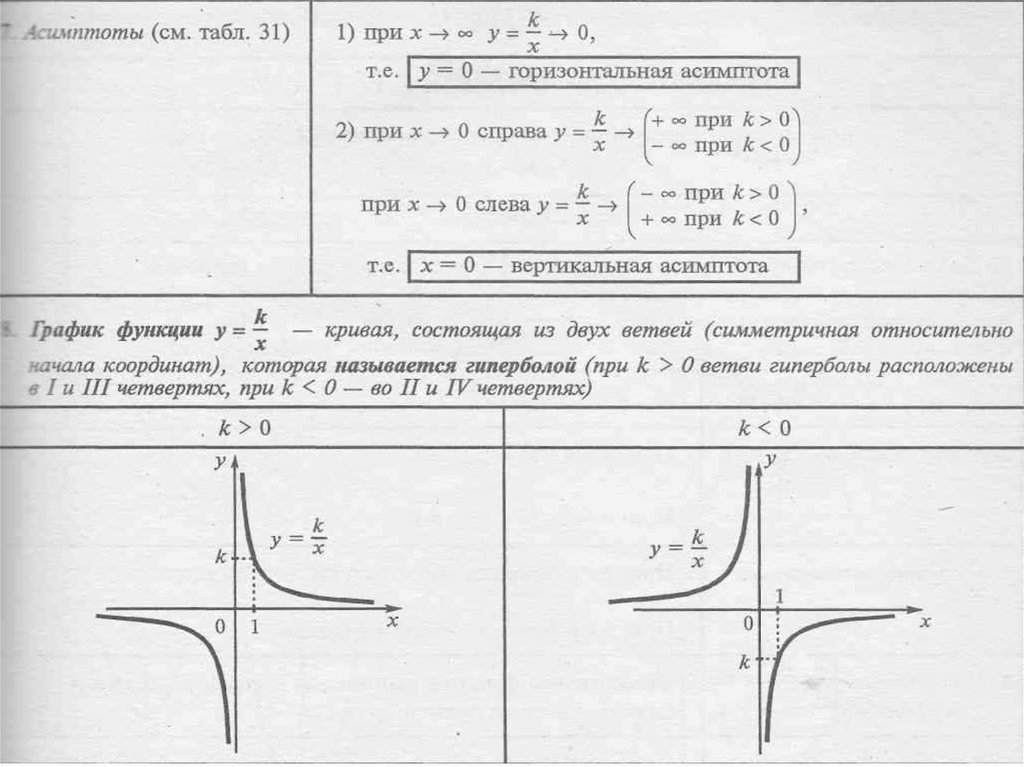 ppt
ppt — экзамен по сурдсу
— экзамен по сурдсу pdf
pdf
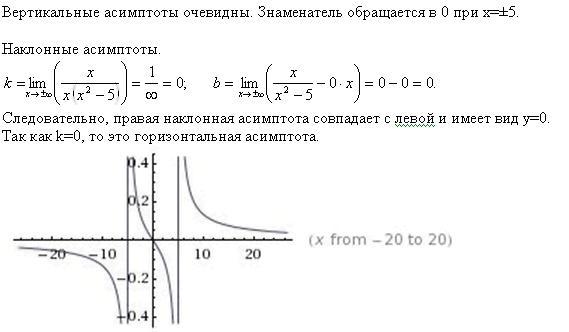 pdf
pdf com
com
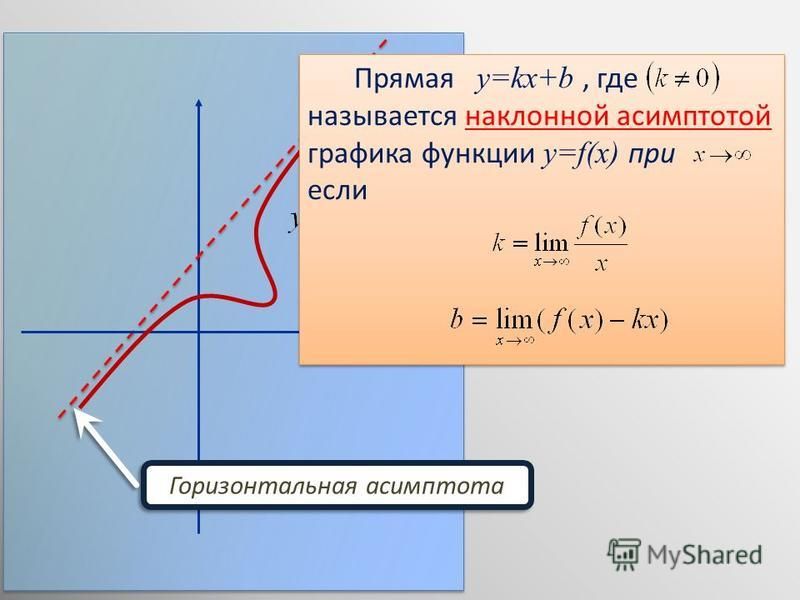
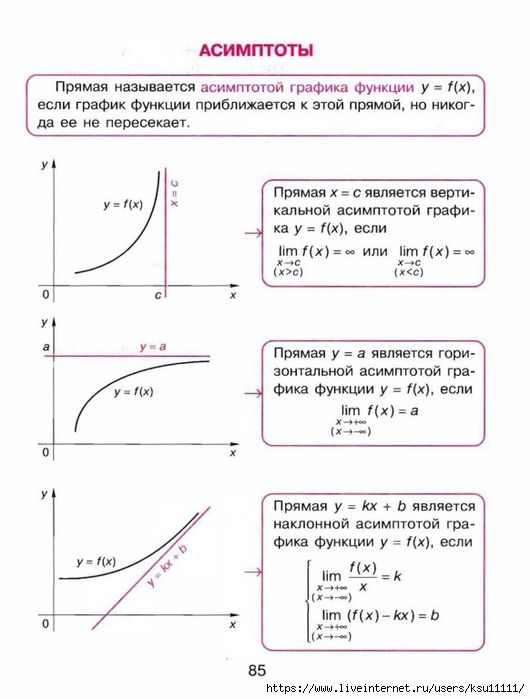 Ему нужно только приблизиться к нему с одной стороны, чтобы он был горизонтальной асимптотой.
Ему нужно только приблизиться к нему с одной стороны, чтобы он был горизонтальной асимптотой.