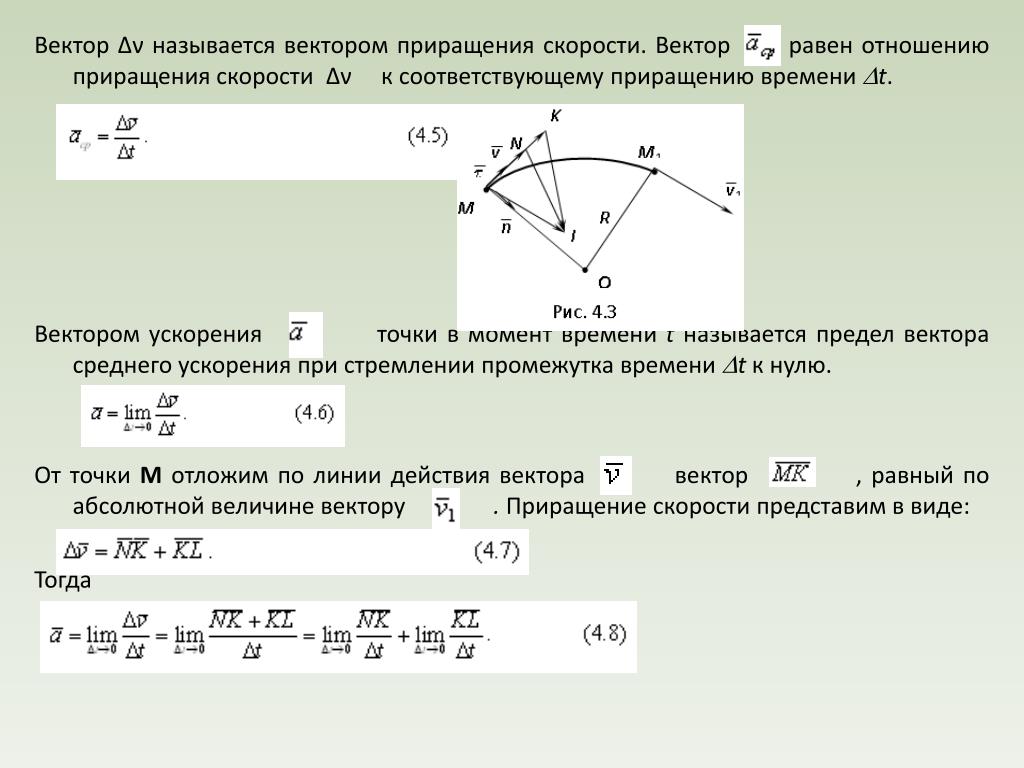
| ВЕКТОРЫ НА ПЛОСКОСТИ
Вектором называется направленный отрезок, то есть отрезок, у которого указаны начало (наз. также точкой приложения вектора) и конец. МОДУЛЬ ВЕКТОРА Длина направленного отрезка, изображающего вектор, называется длиной, или модулем, вектора. Длина вектора обозначается . Нуль-вектор () — вектор, начало и конец которого совпадают; его модуль равен 0, а направление неопределенное. КООРДИНАТНОЕ ПРЕДСТАВЛЕНИЕ Пусть на плоскости задана декартова система координат XOY. Тогда вектор может быть задан двумя числами: и Эти числа и в геометрии называют координатами вектора, а в физике – проекциями вектора на соответствующие оси координат. При таком определении вектора его модуль , а направление задается углом , который однозначно определяется соотношениями: Нуль-вектор: и ПРЕДСТАВЛЕНИЕ В СИСТЕМЕ КООРДИНАТ, ЗАДАННОЙ ЕДИНИЧНЫМИ ВЕКТОРАМИ (ОРТАМИ) Пусть на плоскости задана декартова система координат при помощи единичных векторов и : Тогда вектор может быть задан следующим образом: Очевидно, что: и При таком определении вектора его модуль , а направление задается углом , который однозначно определяется соотношениями: и Нуль-вектор: КОЛЛИНЕАРНЫЕ ВЕКТОРЫ Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. РАВЕНСТВО ВЕКТОРОВ Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаково направлены. Все нуль-векторы считаются равными. СУММА ВЕКТОРОВ Суммой векторов и называют вектор , идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора . Происхождение этого правила связано с правилом параллелограмма сложения векторов, источником которого является экспериментальный факт сложения сил (векторных величин) по этому правилу. Правило треугольника Правило параллелограмма
Координаты равных векторов удовлетворяют соотношениям: и Координаты вектора суммы двух векторов удовлетворяют соотношениям: и Координаты коллинеарных векторов удовлетворяют соотношению: Координаты равных векторов удовлетворяют соотношениям: и Вектор суммы двух векторов:
ПРОИЗВЕДЕНИЕ ВЕКТОРА НА ЧИСЛО Произведением вектора на число называют вектор, коллинеарный вектору , имеющий длину, равную , и направление, совпадающее с направлением при > 0 и противоположное при ПРОТИВОПОЛОЖНЫЕ ВЕКТОРЫ Вектор называется противоположным вектору и обозначается . СВОЙСТВА ДЕЙСТВИЙ НАД ВЕКТОРАМИ Операции сложения векторов и умножения вектора на число обладают след. свойствами: 1) , 2) , 3) , 4), 5) , 6) , 7) , 8). Координаты вектора суммы нескольких векторов удовлетворяют соотношениям: Координаты вектора произведения вектора на число удовлетворяют соотношениям:
Сумма нескольких векторов: Произведение вектора на число: Вектор, противоположный : Скалярное произведение векторов и (обозначается ) — скаляр, определяемый равенством , где — угол между векторами и , приведенными к общему началу:Скалярное произведение векторов: Скалярное произведение векторов: ДОПОЛНЕНИЕ: ТИПЫ ВЕКТОРНЫХ ВЕЛИЧИН В ФИЗИКЕ. Векторами называются такие геометрические и физические величины, которые однозначно определяются отрезками с заданным положением, направлением и длиной независимо от системы отсчета и подчиняются правилам I – IV (см. далее). Вектор называется осевым (аксиальным) в том случае, если соотношение между представляемой величиной и изображающим ее отрезком устанавливается посредством задания некоторой оси и определенного направления вращения вокруг этой оси. Принято, чтобы направление выбранного на оси отрезка составляло с осью вращения правый винт (угловая скорость, момент сил, вращательные импульсы). Длина отрезка – модуль вектора в определенном масштабе. Свободные векторы можно произвольно переносить в любое другое параллельное положение, сохраняя при этом их направление и длину (напр. Скользящие векторы неотделимы от несущей их прямой, от так называемой линии действия, но вдоль этой прямой они могут перемещаться произвольным образом (напр., угловая скорость; сила, приложенная к твердому телу). Связанные векторы неотделимы от определенной точки, от так называемой точки приложения вектора (напр., скорость точки тела, движущегося произвольным образом). I. Два вектора, и равны друг другу, если они имеют одинаковое направление и одинаковую длину; равные скользящие векторы должны иметь, кроме этого, общую линию действия, а равные связанные векторы – общую точку приложения. II. Вектор получается из вектора следующим образом: из точки приложения вектора откладывается в противоположном направлении отрезок с такой же длиной, как у вектора . III. Вектор : при m 0 – модуль в m раз больше, при m 0 – по правилу II/ IV. Каталог: inovation -> fisika жүктеу/скачать 319 Kb. Достарыңызбен бөлісу: |
Что значит модуль в векторах.
 Вычисление длины (модуля) вектора в MS EXCEL
Вычисление длины (модуля) вектора в MS EXCELВремя на чтение: 4 минут
Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).
Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.
1. Вычисление длины вектора по его координатам
Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле
В случае вектора в пространстве добавляется третья координата
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).
Функция СУММКВ()
возвращает сумму квадратов аргументов, т. е. в данном случае эквивалентна формуле =B8*B8+B9*B9
.
е. в данном случае эквивалентна формуле =B8*B8+B9*B9
.
В файле примера также вычислена длина вектора в пространстве.
Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .
2. Нахождение длины вектора через координаты точек
Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))
В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.
Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.
По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.
3. Нахождение длины вектора по теореме косинусов
Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))
В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ()
).
Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))
Примечание : для наглядности в ячейке со значением угла в градусах можно применить , см. например, статью
модуль вектора — величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector …
модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas
— (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия
Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика
модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика
Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа … Википедия
Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
Абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
Модуль вектора можно найти, если мы знаем его проекции на координатные оси .
на плоскости задан вектор а (рис. 15).
Опустим с начала и конца вектора перпендикуляры на координатные оси для нахождения его проекций. В соответствии с теоремой Пифагора
. Отсюда
.
Эту формулу надо знать НАИЗУСТЬ.
Запомните!
Чтобы найти модуль вектора надо извлечь корень квадратный из суммы квадратов его проекций.
Вы уже знаете, что проекцию вектора на ось можно найти, если из координаты точки конца вектора вычесть координату точки его начала. Тогда для нашего вектора, если он задан на плоскости, а x = х к − х н,
Тогда для нашего вектора, если он задан на плоскости, а x = х к − х н,
а y = y к − y н. Следовательно, модуль вектора можно найти по формуле
.
Нетрудно сообразить, как будет выглядеть формула, если вектор задан в пространстве.
Обратите еще внимание вот на что. Ведь модуль вектора — это длина отрезка, заключенного между двумя точками: точкой начала вектора и точкой его конца. А это ни что иное, как расстояние между двумя этими точками. Поэтому чтобы найти расстояние между любыми двумя точками, нужно вычислить модуль вектора , соединяющего эти точки.
Проекция вектора онлайн
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Прab = |b|cos(a,b) или
где a•b — скалярное произведение векторов,|a| — модуль вектора a.
Инструкция. Для нахождения проекции вектора Пpab в онлайн режиме необходимо указать координаты векторов a и b. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.
Для нахождения проекции вектора Пpab в онлайн режиме необходимо указать координаты векторов a и b. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.
две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A’B’, начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A’B’, взятая со знаком + или -, в зависимости от того, имеет ли вектор A’B’ то же направление, что и ось (вектор).

Виды проекций по системе координат
- проекции на плоскости (система координат OX,OY). Пример: a(2;-3), a=2i-3j
- проекции в пространстве (система координат OX,OY, OZ). Пример: a(2;-3;1), a=2i-3j+k
- проекции в N-мерном пространстве
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1. Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.AC’=AB’+B’C’
Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Прab = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.

- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.
| Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.
| Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
|
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.
| Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.
| Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.
|
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.
| Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.
| Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
|
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).
| Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).
| Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).
|
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120o. Длина |b| вектора b равна 4, поэтому прab=4·cos120o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Пример 3. Пусть вектор b задан через координаты точек M(1;1), N(4;5).
Координаты вектора: MN(4-1;5-1) = MN(3;4)
Тогда модуль вектора MN равен:
Направляющий вектор для оси OX равен вектору M’N’, где координаты точек M’(1;0) N’(4;0). Следовательно, вектор M’N’ имеет координаты: x = 4-1, y = 0-0 = 0.
M’N’(3;0)
Пример 4. Найти проекцию вектора c на вектор d;
с = АС = (-2;-1;3), d = CB(-5;-3;3)
Найдем проекцию вектора AC на вектор BC
Пример 5. Найти проекцию прb(-2a+4b)
где a=2m+3n и b=4m-n, |m|=k, |n|=l, угол между ∠(m,n)= π
Тогда -2a+4b = -4m+6n + 16m-4n = 12m+2n
а) Рассмотрим треугольник со сторонами a,b,c. По теореме косинусов:
a2 = b2 + c2 – 2bc∙cos(b,c), откуда
или б) Рассмотрим второй вариант решения.
Поскольку угол между векторами π, т.е. 180о, то векторы лежат на одной оси.
Таким образом, 4m-n = 4*1 – 1 = 3.
Находим проекцию.
прb(-2a+4b) = прb(12m+2n) =
Модуль вектора
Модуль вектора равен квадратному корню из суммы квадратов его элементов
Варианты
ввода операции модуля вектора. »
и ввести в показатель степени число
-1
»
и ввести в показатель степени число
-1
Функция
geninv(M), М – квадратная матрица с не нулевым определителем
На Рис. 2.9 приведен пример вычисления обратной матрицы.
Рис. 2.10. Операции транспонирования, обратной матрицы и ее определителя и получения модуля вектора
Векторное произведение векторов
Векторным произведением называется вектор, длина которого равна произведению длин исходных векторов и синуса угла между ними, а направление его совпадает с направлением перпендикуляра к плоскости этих двух векторов (по правилу «буравчика»).
Варианты ввода операции векторного произведения векторов.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Shift»+»|» |
На
Рис. 2.10
приведен пример векторного произведения
векторов.
2.10
приведен пример векторного произведения
векторов.
Скалярное произведение векторов
Скалярным произведением векторов называется число (или выражение), равное произведению длин перемножаемых векторов и косинуса угла между ними.
Варианты ввода операции скалярного произведения векторов.
Пиктограмма | в панели инструментов Calculator (Калькулятор) в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «*» |
На Рис. 2.10 приведен пример скалярного произведения векторов.
Суммирование элементов вектора
Варианты ввода операции суммирования элементов вектора.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Ctrl»+»4» |
На
Рис. 2.10
приведен пример суммирования элементов
вектора.
2.10
приведен пример суммирования элементов
вектора.
Рис. 2.11. Операции векторного и скалярного умножения векторов и суммирование элементов вектора
Исследование систем линейных алгебраических уравнений в пакете MathCad
Пример №1.
Задание. Показать, что столбцы и , составленные из коэффициентов уравнений
являются линейно независимыми.
______________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст «Пример №1» в правом верхнем углу листа.
Установить шрифт — MS Sans Serif сопроводительного текста, поддерживающий кириллицу. Для этого надо модифицировать текстовый стиль «Normal»:
Выбрать пункт меню Format4Style (Формат4Стиль) и загрузить диалоговое окно Text Styles (Стили текста) (Рис. 3.1).
В диалоговом окне Text Styles (Стили текста) выбрать из списка Styles (Стили) стиль «Normal», нажать кнопку Modify (Изменить) и загрузить диалоговое окно Define Style (Стиль по умолчанию) (Рис.
 3.2).
3.2).В диалоговом окне Define Style (Стиль по умолчанию) нажать кнопку Font (Шрифт) и загрузить диалоговое окно Text Format (Формат текста) (Рис. 3.3).
В списке Font (Шрифт) выбрать тип шрифта – MS Sans Serif и последовательно нажав кнопку OK (Да) закрыть диалоговые окна Text Format (Формат текста) и Style (Стиль по умолчанию).
Закрыть диалоговое окно Text Styles (Стили текста), нажав кнопку Close (Закрыть).
Перейти в русскую раскладку клавиатуры.
Установить курсор (красный крест) в верхнем правом углу листа, щелкнув правой кнопкой мыши.
Перейти в текстовый регион (при русской раскладке клавиатуры нажать кнопки «Shift» + «2»), .
Ввести текст «Пример № 1», .
Завершить процесс ввода сопроводительного текста, щелкнув левой кнопкой мыши на свободном месте листа,
Рис. 3.1.
Диалоговое окно Text Styles (Стили текста)
3.1.
Диалоговое окно Text Styles (Стили текста)
Рис. 3.2. Диалоговое окно Define Style (Стиль по умолчанию)
Рис. 3.3. Диалоговое окно Text Format (Формат текста)
2. Решить систему уравнений методом Крамера:
Ввести сопроводительный текст «Матрицы коэффициентов» (см. Рис. 3.4).
Составить матрицы коэффициентов – :
Матрица — D (см. Рис. 3.4):
Выбрать место для ввода матрицы коэффициентов.
Ввести имя матрицы, D, из панели инструментов математической панели.
Ввести знак присвоения, нажав клавиши «Shift» + «:»,
Ввести шаблон матрицы 2х2, нажав клавиши «Ctrl»+»M» и заполнив текстовые строки Rows (Строки) и Columns (Столбцы) цифрами -2 в диалоговом окне Insert Matrix (Вставить матрицы).
Заполнить ячейки шаблона,
Матрица
— D1
(Рис. 3.4):
3.4):
Выбрать место для ввода матрицы коэффициентов (см. )
Ввести символ, D, из панели инструментов математической панели.
Перейти в режим ввода нижнего индекса в имени переменной, нажав клавишу точка «.».
Вести 1
Ввести знак присвоения, шаблон матрицы 2х2 и заполнить ее последний, как это было сделано выше, .
Матрица — (проделать самостоятельно) (см. Рис. 3.4).
Ввести сопроводительный текст «Решить систему уравнений и найти неизвестные переменные» (см. параграф «Ввод пояснительного текста»).
Найти значение переменной a1.
Рассчитать определитель матрицы D (см. Рис. 3.4).
Выбрать место на экране и ввести имя переменной и знак присвоения, detD:=.
Ввести имя матрицы D и символ определителя матрицы |D|, нажав клавиши «Shift» +»|», detD:=|D|
Просмотреть содержимое переменной.
 Ввести имя
переменной и знак просмотра, нажав
кнопку «=», detD=-3.
Ввести имя
переменной и знак просмотра, нажав
кнопку «=», detD=-3.
Рассчитать определитель матрицы D1, detD1:=|D1|, detD1=0 (проделать самостоятельно) (см. Рис. 3.4).
Рассчитать значение коэффициента a1 (см. Рис. 3.4).
Ввести имя переменной, a1 и знак присвоения,
Ввести переменную detD1.
Ввести знак деления, нажав клавишу «/», .
Ввести в качестве делителя (в черный прямоугольник) переменную detD,
Просмотреть содержимое переменной. Ввести имя переменной и знак просмотра, нажав кнопку «=», a1=0.
Найти значение переменной a2.
Рассчитать определитель матрицы D2, detD2:=|D2|, detD2=0 (проделать самостоятельно) (см. Рис. 3.4).
Рассчитать и просмотреть значение коэффициента a2, (проделать самостоятельно) (см.
 Рис.
3.4).
Рис.
3.4).Просмотреть значение коэффициента a2, (проделать самостоятельно) (см. Рис. 3.4).
Следовательно, система уравнений имеет решение только в том случае, когда переменные a1 и a2 равны 0. Следовательно, столбцы b1 и b2 линейно не зависимы.
На (см. Рис. 3.4) приведен листинг с примером №1.
Вектор, модуль вектора. Коллинеарные векторы. Компланарные векторы. Координаты вектора
Напомним, что вектором называется направленный отрезок, то есть отрезок, имеющий длину и определённое направление. Если начало вектора находится в точке , а конец в точке , то такой вектор обозначается: . Часто векторы обозначаются и вот таким образом: .
Модулем, или длиной вектора, называется длина отрезка, который изображает вектор (, ).
Нулевым вектором называется
вектор, начало и конец которого совпадают ().
Направления нулевой вектор не имеет, а его длина равна нулю ().
Два отличных от нуля вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. При этом два коллинеарных вектора могут быть сонаправленными () или противоположно направленными (, ).
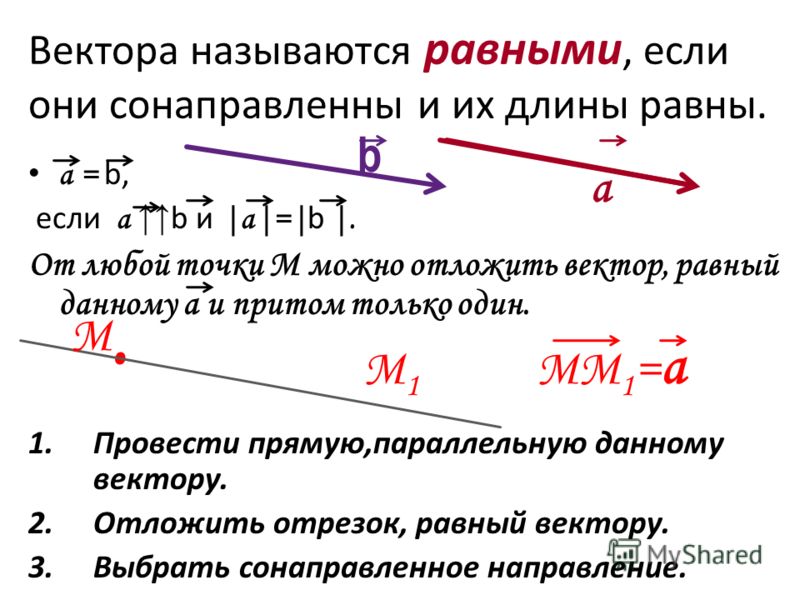
Векторы называются равными, если они одинаково направлены и их длины равны.
Сумму двух векторов можно найти по правилу треугольника:
А также по правилу параллелограмма:
Отметим, что для любого вектора справедливо равенство .
Также напомним, что для любых векторов , и справедливы:
1. (переместительный закон).
2. (сочетательный закон).
Разностью векторов и называется такой вектор, сумма которого с вектором даст вектор .
Для любых векторов и справедливо следующее равенство .
Произведением ненулевого вектора на число называется такой вектор , длина которого равна произведению .
При этом векторы и сонаправлены при и противоположно направлены при .
Основные свойства умножения вектора на число.
Для любых чисел , и любых векторов , справедливы:
1. (сочетательный закон).
2. (первый распределительный закон).
3. (второй распределительный закон).
Теорема. На плоскости любой вектор можно разложить по двум неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
,
, – неколлинеарные векторы,
, – коэффициенты разложения.
Векторы, лежащие в параллельных плоскостях (или в одной плоскости), называются компланарными.
При этом, если вектор можно разложить по векторам и , то есть представить в виде
,
где и – некоторые числа, то векторы , и компланарны.
Для сложения трёх некомпланарных векторов можно использовать правило параллелепипеда:
Теорема.
Любой вектор можно разложить по трём данным некомпланарным векторам, причём
коэффициенты разложения определяются единственным образом.
,
, , – некомпланарные векторы,
, , – коэффициенты разложения.
Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат.
, .
, .
Также напомним, что координатами вектора с началом в точке и концом в точке называются числа , .
В пространстве координатами вектора с началом в точке и концом в точке называются числа , , .
Теперь вспомним следующие правила.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
, ,
вектор имеет координаты .
, ,
вектор имеет координаты .
Каждая координата разности равна разности соответствующих координат этих векторов.
, ,
вектор имеет координаты .
, ,
вектор имеет координаты .
Каждая координата произведения вектора на число равна произведению
соответствующей координаты вектора на это число.
, – произвольное число,
вектор имеет координаты .
, – произвольное число,
вектор имеет координаты .
Также напомним, что длина вектора вычисляется .
В пространстве длина вектора по его координатам вычисляется аналогично.
, .
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Скалярный квадрат вектора (то есть скалярное произведение вектора на себя) равен квадрату его длины.
Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов. Скалярное произведение векторов и выражается следующей формулой:
.
В пространстве скалярное произведение векторов определяется аналогичным образом.
, , .
И напомним свойства скалярного произведения векторов.
Для любых векторов , , и любого числа справедливы соотношения:
1. ,
причём при
.
,
причём при
.
2. (переместительный закон).
3. (распределительный закон).
4. (сочетательный закон).
Отметим, что распределительный закон имеет место для любого числа слагаемых.
Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.
Задание первое. Стороны равностороннего треугольника равны . Найдите длину вектора, равного сумме векторов и .
Решение.
Задание второе. Найдите координаты вектора и его модуль, если , .
Решение.
Задание третье. Даны векторы и . Найдите координаты вектора и его модуль.
Решение.
Задание четвёртое. При каких значениях векторы и взаимно перпендикулярны?
Решение.
Задание
пятое. Найдите модуль суммы и модуль разности векторов и
.
Решение.
Задание шестое. Найдите косинус угла треугольника , если , и .
Решение.
Ы У С ОР А Т НИЛ ЕК
Ы: У С ОР А Т НИЛ ЕК О Л В П В Ы К О В А А Р И Н А 9 «В »
1. 1 КАКОВА РАЗНИЦА МЕЖДУ ВЕКТОРНЫМИ И СКАЛЯРНЫМИ ВЕЛИЧИНАМИ? СКАЛЯРНЫЕ ВЕЛИЧИНЫ ОПРЕДЕЛЯЮТСЯ ЗАДАНИЕМ СВОИХ ЧИСЛЕННЫХ ВЕЛИЧИН, А ХАРАКТЕРИЗУЮТСЯ НЕ ТОЛЬКО СВОИМ ЧИСЛОВЫМ ЗНАЧЕНИЕМ, НО И НАПРАВЛЕНИЕМ В ПРОСТРАНСТВЕ. 1. 2. ЧТО ТАКОЕ ВЕКТОР И КАК ЕГО ОБАЗНАЧАЮТ? ВЕКТОР-ЛЮБОЙ НАПРАВЛЕННЫЙ ОТРЕЗОК. ОБОЗНАЧАЮТ АВ ИЛИ a. 1. 3. КАКИЕ ВЕКТОРЫ НАЗЫВАЮТСЯ КОЛЛИНЕАРНЫМИ? ПРИВЕДИТЕ ПРИМЕР СОНАПРАВЛЕННЫХ И ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫХ. ЕСЛИ 2 ВЕКТОРЫ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ ИЛИ НА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ , ТО ТАКИЕ ВЕКТОРЫ НАЗЫВАЮТЯ КОЛЛИНЕАРНЫМИ(рис 1 ) СОНАПРАВЛЕННЫЕ ВЕКТОРЫ (рис2) ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕ (рис3) 1. 4. КАКИЕ ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ? ВЕКТОРЫ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ ОНИ СОНАПРАВЛЕННЫЕ И ИХ МОДУЛИ РАВНЫ. (рис4) 1. 5. КАКАЯ СВЯЗЬ МЕЖДУ РАВЕНСТВОМ ВЕКТОРОВ И ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ? РАВНЫЕ ВЕКТОРЫ МОЖНО СОВМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ, И, ОБРАТНО, ЕСЛИ ВЕКТОРЫ СОВМЕЩАЮТСЯ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ , ТО ЭТИ ВЕКТОРЫ ПАВНЫ.
(рис4) 1. 5. КАКАЯ СВЯЗЬ МЕЖДУ РАВЕНСТВОМ ВЕКТОРОВ И ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ? РАВНЫЕ ВЕКТОРЫ МОЖНО СОВМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ, И, ОБРАТНО, ЕСЛИ ВЕКТОРЫ СОВМЕЩАЮТСЯ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ , ТО ЭТИ ВЕКТОРЫ ПАВНЫ.
1. 6. ЧТО ТАКОЕ МОДУЛЬ ВЕКТОРА? ДЛИНА ОТРЕЗКА АВ НАЗЫВАЕТСЯ МОДУЛЕМ ВЕКТОРА АВ И ОБОЗНАЧАЕТСЯ /AB/. 1. 7. ЧТО ВЫ ЗНАЕТЕ О НУЛЕВОМ ВЕКТОРЕ? НУЛЕВОЙ ВЕКТОР – КОНЕЦ И НАЧАЛО КОТОРОГО СОВПАДАЮТ. ОБАЗНАЧАЕТСЯ 0. 2. 1 СФОРМУЛИРУЙТЕ ПРАВИЛО ТРЕУГОЛЬНИКА И ПАРАЛЛЕЛОГРАММА СЛОЖЕНИЯ ВЕКТОРОВ. ПРАВИЛО ТРЕУГОЛЬНИКА Для того чтобы сложить два вектора a и b нужно переместить вектор b параллельно самому себе так, чтобы его начало совпадало с концом вектора a . Тогда их суммой будет вектор c начало которого совпадает с началом , вектора a а конец — с концом вектора b , (рис1) ПРАВИЛО ПАРАЛЛЕЛОГРАММА Для того чтобы сложить два вектора a и b нужно переместить их параллельно самим себе так, чтобы начала векторов a и b находились в одной точке. Затем построить параллелограмм, сторонами которого будут эти вектора. Тогда суммой a будет +b вектор c начало которого совпадает с общим началом векторов, а конец — с , противоположной вершиной параллелограмма. (рис2)
Тогда суммой a будет +b вектор c начало которого совпадает с общим началом векторов, а конец — с , противоположной вершиной параллелограмма. (рис2)
2. 2 КАКИМИ СВОЙСТВАМИ ОБЛАДАЕТ СУММА ВЕКТОРОВ. Для любых векторов а , b и с верно: 1. а + b=b + а 2. (а+b)+c=а+(b+c) 2. 3. КАК ОПРЕДЕЛЯЕТСЯ РАЗНОСТЬ ВЕКТОРОВ? Разностью a – b векторов a и b называется такой вектор c, что c + b = a. Если отложить векторы от одной точки, то разность можно найти по «правилу треугольника» (рис1) 2. 4. 2 ВЕКТОРА , ИМЕЮЩИЕ РАВНЫЕ МОДУЛИ И ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕ , НАЗЫВАЮТСЯ ПРОТИВОПОЛОЖНЫМИ. (рис2) 2. 5. КАК МОЖНО РАЗЛОЖИТЬ ВЕКТОР НА СУММУ СОСТАВЛЯЮЩИХ ПО ДВУМ ПЕРЕСЕКАЮЩИМСЯ ПРЯМЫМ? ПУСТЬ ДАНЫ ДВЕ ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ. ТОГДА ЛЮБОЙ ВЕКТОР МОЖНО РАЗЛОЖИТЬ НА СУММУ СОСТАВЛЯЮЩИХ , РАСПОЛОЖЕННЫХ НА ДАННЫХ ПРЯМЫХ.
3. 1 КАКИМ МОЖЕТ БЫТЬ ПРОИЗВЕДЕНИЕ K*A, ЕСЛИ: 1) a=0; 2) K=0? Произведением вектора а≠ 0 на число к называется вектор , модуль которого равен числу /к/*/а/ и сонаправлен с вектором а при к>0 , противоположно направлен с вектором а при к 0 — вектора b и a сонаправленные, если число k > 0 a↑↓b, если k
3. 4 ДОКАЖИТЕ ПРИЗНАКИ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ. Два вектора будут коллинеарны при выполнении любого из этих условий: 1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b 2. Два вектора коллинеарны, если отношения их координат равны. ПРИЗНАК неприменимо, если один из компонентов вектора равен нулю. Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. 3. 5. КАКОЕ УСЛОВИЕ ЯВЛЯЕТСЯ НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ ДЛЯ ТОГО , ЧТОБЫ ТОЧКИ A, B, C ЛЕЖАЛИ НА ОДНОЙ ПРЯМОЙ. Для того чтобы точка С лежала на прямой АВ , необходимо и достаточно , чтобы существовала число а такое, что АС=АВ 4. 1 КАКОЙ УГОЛ НАЗЫВАЕТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ AB И AC ? УГЛОМ МЕЖДУ ВКТОРАМИ AB И AC НАЗЫВАЕТСЯ УГОЛ BAC. УГЛОМ МЕЖДУ НЕНУЛЕВЫМИ ВЕКТОРАМИ a И b НАЗЫВАЕТСЯ УГОЛ , ОБРАЗОВАННЫЙ ПРИОТКЛАДЫВАНИИ ЭТИХ ВЕКТОРОВ ОТ ОДНОЙ ТОЧКИ. ОБОЗНАЧАЕТСЯ (a, b) 4. 2. КАК ОПРЕДЕЛЯЕТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ a И b В ОБЩЕМ СЛУЧАЕ? Углом между двумя ненулевыми векторами называется величина заданного ими угла , когда они отложены от одной точки.
4 ДОКАЖИТЕ ПРИЗНАКИ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ. Два вектора будут коллинеарны при выполнении любого из этих условий: 1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b 2. Два вектора коллинеарны, если отношения их координат равны. ПРИЗНАК неприменимо, если один из компонентов вектора равен нулю. Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. 3. 5. КАКОЕ УСЛОВИЕ ЯВЛЯЕТСЯ НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ ДЛЯ ТОГО , ЧТОБЫ ТОЧКИ A, B, C ЛЕЖАЛИ НА ОДНОЙ ПРЯМОЙ. Для того чтобы точка С лежала на прямой АВ , необходимо и достаточно , чтобы существовала число а такое, что АС=АВ 4. 1 КАКОЙ УГОЛ НАЗЫВАЕТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ AB И AC ? УГЛОМ МЕЖДУ ВКТОРАМИ AB И AC НАЗЫВАЕТСЯ УГОЛ BAC. УГЛОМ МЕЖДУ НЕНУЛЕВЫМИ ВЕКТОРАМИ a И b НАЗЫВАЕТСЯ УГОЛ , ОБРАЗОВАННЫЙ ПРИОТКЛАДЫВАНИИ ЭТИХ ВЕКТОРОВ ОТ ОДНОЙ ТОЧКИ. ОБОЗНАЧАЕТСЯ (a, b) 4. 2. КАК ОПРЕДЕЛЯЕТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ a И b В ОБЩЕМ СЛУЧАЕ? Углом между двумя ненулевыми векторами называется величина заданного ими угла , когда они отложены от одной точки.
4. 3 ЧТО НАЗЫВАЕТСЯ СКАЛЯРНЫМ ПРОИЗВЕДЕНИЕМ ДВУХ ВЕКТОРОВ ? СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ЯВЛЯЕТСЯ ЧИСЛОМ ИЛИ ВЕКТОРОМ? СКАЛЯРНЫМ ПРОИЗВЕДЕНИЕМ ДВУХ ВЕКТОРОВ НАЗЫВАЕТСЯ ЧИСЛО, РАВНОЕ ПРОИЗВЕДЕНИЮ МОДУЛЕЙ ЭТИХ ВЕКТОРОВ НА КОСИНУС УГЛА МЕЖДУ НИМИ ЭТО ЧИСЛО. 4. 4 СФОРМУЛИРУЙТЕ СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЕ. 1. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору: a · a = 0 a = 0 Операция скалярного умножения коммуникативна: a · b = b · a Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны: a ≠ 0, b ≠ 0, a · b = 0 a ┴ b Операция скалярного умножения дистрибутивна: (a + b) · c = a · c + b · c
4. 5. КАКОЕ УСЛОВИЕ ЯВЛЯЕТСЯ НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ ДЛЯ ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ВЕКТОРОВ? ДЛЯ ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ВЕКТОРОВ НЕОБХОДИМО И ДОСТАТОНО, ЧТОБЫ ИХ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ РАВНЯЛОСЬ НУЛЮ. 4. 6. УКАЖИТЕ ПРИНЦИПЫ ПРИМЕНЕНИЯ ЭЛЕМЕНТОВ ВЕКТОРНОЙ АЛГЕБРЫ. 1. ВВОДЯ ВЕКТОРЫ В УДОБНОЙ ДЛЯ НАС ФОРМЕ , НУЖНО ПЕРЕПИСАТЬ УСЛОВИЕ ЗАДАЧИ С ПОМОЩЬЮ ВЕКТОРОВ. 2. ПРЕОБРАЗОВЫВАЯ ЗАДАЧУ , ЗАПИСАННУЮ В ВЕКТОРОЙ ФОРМЕ , ПОЛУЧАЕМ ЕЕ РЕШИЕМ В ВЕКТОРНОЙ ФОРМЕ. 3. РЕШЕНИЕ ЗАДАЧИ, ПОЛУЧЕННОЕ В ВЕКТОРНЫХ СООТНОШЕНИЯХ , НУЖНО ПЕРЕВЕСТИ НА ИСХОДНЫЙ «ЯЗЫК» ЗАДАЧИИ ЗАПИСАТЬ ОТВЕТ. 5. 1 СФОРМУЛИРУЙТЕ И ДОКАЖИТЕ ТЕОРЕМУ О РАЗЛОЖЕНИИ ВЕКТОРА ПО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ. ЕСЛИ НЕНУЛЕВЫЕ ВЕКТОРЫ a И b, ТО ДЛЯ ЛЮБОГО ВЕКТОРA c НАЙДУТСЯ ЧИСЛА x И y ТАКИЕ, ЧТО ВЫПОЛНЯЕТСЯ РАВЕНСТВО c=xa+yb; ПРИЧЕМ КОЭФФИЦЕНТ РАЗЛОЖЕНИЯ x и y, ОПРЕДЕЛЯЮТСЯ ЕДИНСТВЕННЫМ ОБРАЗОМ.
1. ВВОДЯ ВЕКТОРЫ В УДОБНОЙ ДЛЯ НАС ФОРМЕ , НУЖНО ПЕРЕПИСАТЬ УСЛОВИЕ ЗАДАЧИ С ПОМОЩЬЮ ВЕКТОРОВ. 2. ПРЕОБРАЗОВЫВАЯ ЗАДАЧУ , ЗАПИСАННУЮ В ВЕКТОРОЙ ФОРМЕ , ПОЛУЧАЕМ ЕЕ РЕШИЕМ В ВЕКТОРНОЙ ФОРМЕ. 3. РЕШЕНИЕ ЗАДАЧИ, ПОЛУЧЕННОЕ В ВЕКТОРНЫХ СООТНОШЕНИЯХ , НУЖНО ПЕРЕВЕСТИ НА ИСХОДНЫЙ «ЯЗЫК» ЗАДАЧИИ ЗАПИСАТЬ ОТВЕТ. 5. 1 СФОРМУЛИРУЙТЕ И ДОКАЖИТЕ ТЕОРЕМУ О РАЗЛОЖЕНИИ ВЕКТОРА ПО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ. ЕСЛИ НЕНУЛЕВЫЕ ВЕКТОРЫ a И b, ТО ДЛЯ ЛЮБОГО ВЕКТОРA c НАЙДУТСЯ ЧИСЛА x И y ТАКИЕ, ЧТО ВЫПОЛНЯЕТСЯ РАВЕНСТВО c=xa+yb; ПРИЧЕМ КОЭФФИЦЕНТ РАЗЛОЖЕНИЯ x и y, ОПРЕДЕЛЯЮТСЯ ЕДИНСТВЕННЫМ ОБРАЗОМ.
5. 2 КАКИЕ ВЕКТОРЫНАЗЫВАЮТСЯ БАЗИСНЫМИ ВЕКТОРАМИ НА ПЛОСКОСТИ? ИЗ ЭТОЙ ТЕОРЕМЫ ВЫТЕКАЕТ, ЧТО ЛЮБОЙ ВЕКТОР МОЖНО РАЗЛОЖИТЬ ПО ДВУМ ПРОИЗВОЛЬНЫМНЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ. ЕСЛИ НА ПЛОСКОСТИ ВЫБРАНЫ ТАКИЕ ЖЕ ДВА НЕКОЛЛИНЕАРНЫХ ВЕКТОРОВ, ТО ОНИ НАЗЫВАЮТСЯ БАЗИСНЫМИ ВЕКТОРАМИ ПЛОСКОСТИ. 5. 3 ЧТО ТАКОЕ КООРДИНАТЫ ВЕКТОРА И КАК ИХ ОБОЗНАЧАЮТ? КООРДИНАТАМИ ВЕКТОРА НАЗЫВАЮТСЯ КОЭФФИЦЕНТЫ ЕГО РАЗЛОЖЕНИЯ ПО БАЗИСНЫМ ВЕКТОРАМ. ОБОЗНАЧЕНИЕ: а=(х; у) 5. 4. НАПИШИТЕ КООРДИНАТЫ КООРДИНАТНЫХ ВЕКТОРОВ. Координаты нулевого вектора равны нулю. Координаты равных векторов соответственно равны. Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов. Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов. Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.
ОБОЗНАЧЕНИЕ: а=(х; у) 5. 4. НАПИШИТЕ КООРДИНАТЫ КООРДИНАТНЫХ ВЕКТОРОВ. Координаты нулевого вектора равны нулю. Координаты равных векторов соответственно равны. Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов. Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов. Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.
5. 5 КАКИЕ СВОЙСТВА КООРДИНАТЫ ВЕКТОРОВ ВЫ ЗНАЕТЕ? ДОКАЖИТЕ ИХ. 1. У РАВНЫХ ВЕКТОРОВ СООТВЕТСТВУЮЩИЕ КООРДИНАТЫ РАВНЫ. 2. ПРИ СЛОЖЕНИИ ВЕКТОРОВ СКЛАДЫВАЮТСЯ ИХ СОТВЕТСТВУЮЩИЕ КООРДИНАТЫ. 3. ПРИ УМНОЖЕНИИ ВЕКТОРА НА ЧИСЛО ЕГО КООРДИНАТЫ УМНОЖАЮТСЯ НА ЭТО ЖЕ ЧИСЛО. 5. 6. КАКОЙ ВЕКТОР НАЗЫВАЕТСЯ РАДИУС-ВЕКТОРОМ ТОЧКИ А? ЕСЛИ НА ПЛОСКОСТИ Оху ЗАДАНА ТОЧКА А(х; у) , ТО ВЕКТОР ОА НАЗЫВАЕТСЯ РАДИУСВЕКТОРОМ ТОЧКИ А. 5. 7. КАК ОПРЕДЕЛЯЮТСЯ КООРДИНАТЫ ВЕКТОРА , ЕСЛИ ЗАДАНЫ КООРДИНАТЫ ЕГО КОНЦОВ ? КООРДИНАТЫ ВЕКТОРА ОПРЕДЕЛЯЮТСЯ КАК РАЗНОСТИ СООТВЕТСТВУЮЩИХ КООРДИНАТ КОНЦА И НАЧАЛА ВЕКТОРА. 5. 8. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЕТСЯ МОДУЛЬ ВЕКТОРА?
5. 8. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЕТСЯ МОДУЛЬ ВЕКТОРА?
6. 1. КАК МОЖНО ОПРЕДЕЛИТЬ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ ПО ИХ КООРДИНАТАМ? ЗАПИШИТЕ СООТВЕТСТВУЮЩИЕ ФОРМУЛЫ. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ a=(x 1; y 1), и b(x 2; y 2) ОТЛОЖИТЬ ОТ НАЧАЛА КООРДИНАТ, ТО ОНИ ОПРЕДЕЛЯЮТСЯ ПО ФОРМУЛЕ: a*b=x 1*x 2+y 1*y 2 6. 2 НАПИШИТЕ УСЛОВИЯ ПЕРПЕНДИКУЛЯРНОСТИ ВЕКТОРОВ. ВЕКТОРЫ ЯВЛЯЮТСЯ ПЕРПЕНДИКУЛЯРНЫМИ ТОГДА И ТОЛЬКО, КОГДА ИХ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ РАВНО НУЛЮ. ДАНЫ 2 ВЕКТОРА a(xa; ya) и b(xb; yb). ЭТИ ВЕКТОРЫ БУДУТ ПЕРПЕНДИКУЛЯРНЫ , ЕСЛИ ВЫРАЖЕНИЕ xa xb + ya yb =0 6. 3. НАПИШИТЕ УСЛОВИЯ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ. 1. ДВА ВЕКТОРА a И B КОЛЛИНЕАРНЫ, ЕСЛИ СУЩЕСТВУЕТ ЧИСЛО n ТАКОЕ, ЧТО a = n · b. 2. ДВА ВЕКТОРА КОЛЛИНЕАРНЫ, ЕСЛИ ОТНОЖЕНИЕ КООРДИНАТ РАВНЫ. 3. ДВА ВЕКТОРА КОЛЛИНЕАРНЫ, ЕСЛИ ИХ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ РАВНО НУЛЕВОМУ ВЕКТОРУ. (рис1) 6. 4. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЮТСЯ УГОЛ МЕЖДУ ВЕКТОРАМИ? РИС 1
7. 1. КАКОЙ ВЕКТОР НАЗЫВАЕТСЯ НАПРАВЛЯЮЩИМ ВЕКТОРОМ ПРЯМОЙ? НАПРАВЛЯЮЩИЙ ВЕТОР ПРЯМОЙ- ЭТО ЛЮБОЙ НЕНУЛЕВОЙ ВЕКТОР, ЛЕЖАЩИЙ НА ДАННОЙ ПРЯМОЙ ИЛИ ПАРАЛЛЕЛЬНОЙ ЕЙ ПРЯМОЙ. (рис1) 7. 2. КАКАЯ ТОЧКА НАЗЫВАЕТСЯ НАЧАЛЬНОЙ ТОЧКОЙ ПРЯМОЙ? ТОЧКА М 0 НАЗЫВАЕТСЯ НАЧАЛЬНОЙ ТОЧКОЙ ПРЯМОЙ l. 7. 3. НАПИШИТЕ УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ? УРАВНЕНИК ПРЯМОЙ, ПРОХОДЯЩИЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ (x 1, y 1) и (x 2, y 2), ЗАПИСЫВАЕТСЯ ТАК: 7. 4. ЧТО ТАКОЕ ВЕКТОР НОРМАЛИ ПРЯМОЙ? НАПИШИТЕ УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И ВЕКТОРУ НОРМАЛИ. ВЕКТОР НОРМАЛИ- ЭТО ВЕКТОР, КОТОРЫЙ ПЕРПЕНДИКУЛЯРЕН ДАННОЙ ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО ВЕКТОРУ НОРМАЛИ: а(Х-Х 0)+в(У-У 0)=0 7. 5. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЕТСЯ УГОЛ МЕЖДУ ПРЯМЫМИ? Рис 2 7. 6. КАК ОПРЕДЕЛЯЕТСЯ РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ? РАССТОЯНИЕ ОТ Т. ДО ПРЯМОЙ –РАВНО ДЛИНЕ ПЕРПЕНДИКУЛЯРА ОПУЩЕННОГО ИЗ Т. НА ПРЯМУЮ. d = |A·Mx + B·My + C| √A 2 + B 2
(рис1) 7. 2. КАКАЯ ТОЧКА НАЗЫВАЕТСЯ НАЧАЛЬНОЙ ТОЧКОЙ ПРЯМОЙ? ТОЧКА М 0 НАЗЫВАЕТСЯ НАЧАЛЬНОЙ ТОЧКОЙ ПРЯМОЙ l. 7. 3. НАПИШИТЕ УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ? УРАВНЕНИК ПРЯМОЙ, ПРОХОДЯЩИЙ ЧЕРЕЗ ДВЕ ЗАДАННЫЕ ТОЧКИ (x 1, y 1) и (x 2, y 2), ЗАПИСЫВАЕТСЯ ТАК: 7. 4. ЧТО ТАКОЕ ВЕКТОР НОРМАЛИ ПРЯМОЙ? НАПИШИТЕ УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И ВЕКТОРУ НОРМАЛИ. ВЕКТОР НОРМАЛИ- ЭТО ВЕКТОР, КОТОРЫЙ ПЕРПЕНДИКУЛЯРЕН ДАННОЙ ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО ВЕКТОРУ НОРМАЛИ: а(Х-Х 0)+в(У-У 0)=0 7. 5. ПО КАКОЙ ФОРМУЛЕ ОПРЕДЕЛЯЕТСЯ УГОЛ МЕЖДУ ПРЯМЫМИ? Рис 2 7. 6. КАК ОПРЕДЕЛЯЕТСЯ РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ? РАССТОЯНИЕ ОТ Т. ДО ПРЯМОЙ –РАВНО ДЛИНЕ ПЕРПЕНДИКУЛЯРА ОПУЩЕННОГО ИЗ Т. НА ПРЯМУЮ. d = |A·Mx + B·My + C| √A 2 + B 2
СПАСИБО ЗА ВНИМАНИЕ!
Величина вектора — определение, формула
Величина векторной формулы помогает обобщить числовое значение для данного вектора. Вектор имеет направление и величину. Отдельные меры вектора вдоль оси x, оси y и оси z суммируются с использованием этой величины векторной формулы. Обозначается | против |. Величина вектора всегда является положительным числом или нулем, т. е. не может быть отрицательным числом. Давайте поймем величину векторной формулы, используя несколько решенных примеров в конце.
Вектор имеет направление и величину. Отдельные меры вектора вдоль оси x, оси y и оси z суммируются с использованием этой величины векторной формулы. Обозначается | против |. Величина вектора всегда является положительным числом или нулем, т. е. не может быть отрицательным числом. Давайте поймем величину векторной формулы, используя несколько решенных примеров в конце.
Какова величина вектора?
Величина вектора A равна длине вектора и обозначается | А |. Это квадратный корень из суммы квадратов компонентов вектора. Для заданного вектора с отношениями направлений по осям x, y и z величина вектора равна квадратному корню из суммы квадратов его отношений направлений. Это можно ясно понять из приведенной ниже величины векторной формулы.
Масштаб векторной формулы
- для вектора A = x 1 I + Y 1 J + Z 1 K , его магнит: | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A =√(x 1 2 + y 1 2 + z 1 2 )
- Для вектора v , когда одна из его конечных точек находится в начале координат (0,0), а другая конечная точка находится в (x, y), его величина равна: | против | =√(х 2 + у 2 )
- Для вектора v с концами в точках (x 1 , y 1 ) и (x 2 , y 2 ) его величина равна: | против | =√((х 2 — х 1 ) 2 + (у 2 — у 1 ) 2 )
Как найти модуль вектора?
Чтобы определить величину двумерного вектора по его координатам,
- Шаг 1: Определите его компоненты.

- Шаг 2: Найдите сумму квадратов каждой из его составляющих.
- Шаг 3: Извлеките квадратный корень из полученной суммы.
Таким образом,
- формула для определения величины вектора (в двумерном пространстве) v = (x, y): | против | =√(х 2 + у 2 ). Эта формула выводится из теоремы Пифагора.
- формула для определения величины вектора (в трехмерном пространстве) В = (х, у, г) это: | В | = √(х 2 + у 2 + z 2 )
Давайте рассмотрим применение формулы величины в следующем разделе.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Примеры использования величины векторной формулы
Пример 1: Используя формулу величины, найдите величину вектора с u = (2, 5)?
Решение:
Найти: Модуль данного вектора
Дано:
Вектор u = (2,5)
Используя формулу модуля,
| и | = √(x 2 + y 2 )
= √(2 2 + 5 2 )
= √(4 + 25)
2 |
и | = 5,385Ответ: Модуль заданного вектора = 5,385
Пример 2: Найти модуль вектора 3 i + 4 j — 5 k .
Решение:
Найти: Модуль заданного вектора
Заданный вектор A = 3 i + 4 j — 5 k2 , 90| = √(3
2 + 4 2 + (-5) 2 )
= √(9 + 16 + 25)
=√50
=5√2
Ответ: Величина заданного вектора = 5√2
Пример 3: Найти модуль вектора к .
Решение:
Найти: Величина данного вектора
Данного вектора A = 5 i — 4 j + 2 k5 , 90| =√(5
2 + (-4) 2 + 2 2 )
= √(25 + 16 + 4)
= √45
= 3√ 5
Ответ: Величина заданного вектора = 3√5
Часто задаваемые вопросы о величине вектора Формула
0 Величина векторной формулы?
Величина векторной формулы суммирует числовое значение для данного вектора. Обозначается | против |. Величины векторных формул следующие:
Обозначается | против |. Величины векторных формул следующие:
- | А | =√(х 2 + у 2 + z 2 ) для вектора A = x i + y j + z k
- | против | =√(x 2 + y 2 ), когда его конечные точки находятся в начале координат (0,0) и (x, y).
- | против | =√((x 2 — x 1 ) 2 + (y 2 — y 1 ) 2 ) при начальной и конечной точках вектора в определенных точках (x 1 , у 1 ) и (х 2 , у 2 ) соответственно.
Как использовать модуль векторной формулы?
Чтобы использовать величину векторной формулы, выполните шаги, указанные ниже.
- Шаг 1: Проверьте заданные параметры.
- Шаг 2: Подставьте значения в соответствующую формулу
Для вектора A = x i + y j + z k его величина равна |A| =√(х 2 + у 2 + z 2 )
Величина вектора, когда его конечная точка находится в начале координат (0,0), тогда | против | =√(x 2 + y 2 )
Начальная и конечная точки вектора находятся в определенных точках (x 1 , y 1 ) и (x 2 , y 2) 7 затем | против | =√((x 2 — x 1 ) 2 + (y 2 — y 1 ) 2 )
Какое понятие величины вектора стоит за формулой?
Величина вектора относится к длине или размеру вектора. Он также определяет его направление. Понятия, лежащие в основе этих формул, включают теорему Пифагора и формулу расстояния, которые используются для вывода формулы величины вектора.
Он также определяет его направление. Понятия, лежащие в основе этих формул, включают теорему Пифагора и формулу расстояния, которые используются для вывода формулы величины вектора.
Какова величина векторной формулы в словах?
Для заданного вектора с отношениями направлений по осям x, y и z величина вектора равна квадратному корню из суммы квадратов его отношений направлений.
Как найти модуль единичного вектора?
Векторы — это величины, которые обладают величиной и направлением. … Стрелка на линии указывает предполагаемое направление, а длина линии представляет величину. Величина также называется модулем или длиной вектора .
Является ли модуль вектора скаляром?
Модуль или модуль вектора равен скалярной величине . Вектор может быть представлен графически или геометрически прямой линией со стрелкой. Длина линии указывает величину вектора, а стрелка указывает его направление. 23 марта 2020 г.
Длина линии указывает величину вектора, а стрелка указывает его направление. 23 марта 2020 г.
Что такое коллинеарный вектор?
Коллинеарные векторы — это два или более векторов, которые параллельны одной и той же прямой, независимо от их величины и направления.
Как вычислить модуль?
Модуль — это другое название , остаток после деления 9.0105 . Например, 17 по модулю 5 = 2, так как если мы разделим 17 на 5, мы получим 3 с остатком 2. Модульную арифметику иногда называют арифметикой часов, поскольку аналоговые часы пересчитывают время после 12, то есть они работают по модулю 12.
Как вычислить вектор?
Чтобы работать с вектором, нам нужно уметь находить его 9Звездная величина 0104 и ее направление . Мы находим его величину, используя теорему Пифагора или формулу расстояния, и мы находим его направление, используя функцию арктангенса. Учитывая вектор положения →v=⟨a,b⟩, величина находится по формуле |v|=√a2+b2. 4 ноября 2018 г.
Связанные
Какие есть примеры скаляров?
скаляр, физическая величина, которая полностью описывается своей величиной; примеров скаляров 92 = А’А.
Связанные
Как найти скалярное значение вектора?
Скалярное произведение a и b: a · b = |a||b| cosθ Мы можем запомнить эту формулу как: «Модуль первого вектора, умноженный на модуль второго вектора, умноженный на косинус угла между ними».
Связанные
При каком значении a векторы 2i 3j 4k и Ai 6j 8k − − коллинеарны?
Другими словами, соответствующие компоненты коллинеарных векторов пропорциональны. Даны векторы 2i-3j+4k и ai+6j-8k. Следовательно, значение a равно -4 .Jul 2, 2019
Связанные
Что такое модуль вектора класса 11?
Длина вектора называется величиной или модулем вектора. 19 августа., 2018
Связанные
Что вы подразумеваете под модулем?
Определение модуля
1a : коэффициент, на который умножается логарифм числа по одному основанию для получения логарифма числа по новому основанию . b : смысл абсолютного значения 2.
Родственный
Какова величина двух векторов?
На этой странице выводятся формулы для величины векторов в двух и трех измерениях в терминах их координат. Для двумерного вектора a=(a1,a2) формула для его модуля имеет вид ∥a∥=√a21+a22.
Для двумерного вектора a=(a1,a2) формула для его модуля имеет вид ∥a∥=√a21+a22.
общий Информация СМИ Нажмите галерея иллюстрация
Поделиться этой записью:
Умножение векторов
Векторы — что это такое? дает введение в предмет.
Есть два полезных определения умножения векторов, в
один продукт является скаляром, а в другом продукт является
вектор. Нет операции деления векторов. В некоторых
в школьных программах вы встретите скалярные произведения, а не векторные
произведений, но мы обсуждаем оба типа умножения векторов в
эту статью, чтобы дать более полное представление об основах
предмет 92 \quad (2),$$ и если ${\bf i, j, k}$ единичные векторы вдоль
оси, то $${\bf i. i}={\bf j.j} = {\bf kk} = 1,\quad {\rm
и}\quad {\bf i.j}={\bf j.k} = {\bf k.i} = 0\quad (3).$$
читателю остается проверить из определения, что $${\bf u.v} =
{\bf v.u}, \ {\rm and} \ ({\bf u + v}).{\bf w} = {\bf u.w} +{\bf
v.w}.$$ Это показывает, что мы можем расширить или умножить $${\bf u.v}=
(u_1{\bf i}+u_2{\bf j}+u_3{\bf k}).(v_1{\bf i}+v_2{\bf j}+u_3{\bf
k})$$ дает девять терминов. Используя уравнение (3), шесть из этих членов равны
ноль, а остальные три дают выражение $u_1v_1+u_2v_2+u_3v_3$
в соответствии с определением в уравнении (1). 9{-1} \left({{\bf u.v}\over |{\bf
u}|||{\bf v}|}\right)\quad (7).$$ В трех измерениях мы можем использовать
более интуитивное определение угла с точки зрения поворота, но в
более высокие размеры необходимо иметь определение угла
например, формула (7). Если мы используем эту формулу для определения угла, то
Правило косинусов следует непосредственно, поскольку они эквивалентны.
i}={\bf j.j} = {\bf kk} = 1,\quad {\rm
и}\quad {\bf i.j}={\bf j.k} = {\bf k.i} = 0\quad (3).$$
читателю остается проверить из определения, что $${\bf u.v} =
{\bf v.u}, \ {\rm and} \ ({\bf u + v}).{\bf w} = {\bf u.w} +{\bf
v.w}.$$ Это показывает, что мы можем расширить или умножить $${\bf u.v}=
(u_1{\bf i}+u_2{\bf j}+u_3{\bf k}).(v_1{\bf i}+v_2{\bf j}+u_3{\bf
k})$$ дает девять терминов. Используя уравнение (3), шесть из этих членов равны
ноль, а остальные три дают выражение $u_1v_1+u_2v_2+u_3v_3$
в соответствии с определением в уравнении (1). 9{-1} \left({{\bf u.v}\over |{\bf
u}|||{\bf v}|}\right)\quad (7).$$ В трех измерениях мы можем использовать
более интуитивное определение угла с точки зрения поворота, но в
более высокие размеры необходимо иметь определение угла
например, формула (7). Если мы используем эту формулу для определения угла, то
Правило косинусов следует непосредственно, поскольку они эквивалентны.
Обратите внимание, что произведение вектора-строки и вектора-столбца равно
определяется в терминах скалярного произведения, и это согласуется с
умножение матриц. $$(u_1\ u_2\ u_3)\left(\begin{массив}{cc}
v_1 \\ v_2 \\ v_3 \end{массив} \right) = u_1v_1 + u_2v_2 +
u_3v_3.$$
$$(u_1\ u_2\ u_3)\left(\begin{массив}{cc}
v_1 \\ v_2 \\ v_3 \end{массив} \right) = u_1v_1 + u_2v_2 +
u_3v_3.$$
Умножение на вектор
Векторное произведение двух векторы ${\bf b}$ и ${\bf c}$, записанные ${\bf b}\times {\bf c}$ (и иногда называют крест произведение ), есть вектор $${\bf b}\times {\bf c} = \left( \begin{массив}{cc} b_2c_3-b_3c_2 \\ b_3c_1 -b_1c_3 \\ b_1c_2 -b_2c_1 \end{array} \right) \quad (8).$$ Существует альтернативное определение векторного произведения, а именно, что ${\bf b}\times {\bf c}$ является вектор величины $|{\bf b}||{\bf c}|\sin \theta$ перпендикулярен к ${\bf b}$ и ${\bf c}$ и подчиняясь «правилу правой руки», и мы докажем, что этот результат следует из данного определения и что эти два определения эквивалентны. Доказательство дано позже для полноты, но сначала мы рассмотрим ${\bf b}\times {\bf c}$, выраженное через компоненты по направлениям ${\bf i, у, к}$.
Из этого определения видно, что ${\bf b}\times {\bf c}=-{\bf
c}\times {\bf b}$, так что эта операция некоммутативна. Если $ {\ bf я,
j, k}$ — единичные векторы вдоль осей, тогда из этого определения:
$${\bf i}\times {\bf i} = {\bf j}\times {\bf j}= {\bf k}\times {\bf
k}, $$ и $$\eqalign{ {\bf i}\times {\bf j} &= {\bf k},\quad
{\bf j}\times {\bf i} = -{\bf k} \cr {\bf j}\times {\bf k} &=
{\bf i},\quad {\bf k}\times {\bf j} = -{\bf i} \cr{\bf k}\times
{\bf i} &= {\bf j},\quad {\bf i}\times {\bf k} = -{\bf j} .}$$
Из определения следует, что $$k({\bf b}\times {\bf c}) =
(k {\ bf b}) \ times {\ bf c} = {\ bf b} \ times (k {\ bf c}), \ quad \ quad
({\bf a+b})\times {\bf c} = ({\bf a}\times {\bf c}) + ({\bf
b}\times {\bf c}).$$ Раскрывая выражение $${\bf b}\times {\bf
c} = (b_1{\bf i} + b_2{\bf j} + b_3 {\bf k}) \times (c_1{\bf i}+
c_2{\bf j} + c_3 {\bf k})$$ дает $$ (b_2c_3-b_3c_2){\bf i}+
(b_3c_1-b_1c_3){\bf j} + (b_1c_2-b_2c_1){\bf k} \quad (9)$$ который
– формула векторного произведения, заданная в уравнении (8).
Если $ {\ bf я,
j, k}$ — единичные векторы вдоль осей, тогда из этого определения:
$${\bf i}\times {\bf i} = {\bf j}\times {\bf j}= {\bf k}\times {\bf
k}, $$ и $$\eqalign{ {\bf i}\times {\bf j} &= {\bf k},\quad
{\bf j}\times {\bf i} = -{\bf k} \cr {\bf j}\times {\bf k} &=
{\bf i},\quad {\bf k}\times {\bf j} = -{\bf i} \cr{\bf k}\times
{\bf i} &= {\bf j},\quad {\bf i}\times {\bf k} = -{\bf j} .}$$
Из определения следует, что $$k({\bf b}\times {\bf c}) =
(k {\ bf b}) \ times {\ bf c} = {\ bf b} \ times (k {\ bf c}), \ quad \ quad
({\bf a+b})\times {\bf c} = ({\bf a}\times {\bf c}) + ({\bf
b}\times {\bf c}).$$ Раскрывая выражение $${\bf b}\times {\bf
c} = (b_1{\bf i} + b_2{\bf j} + b_3 {\bf k}) \times (c_1{\bf i}+
c_2{\bf j} + c_3 {\bf k})$$ дает $$ (b_2c_3-b_3c_2){\bf i}+
(b_3c_1-b_1c_3){\bf j} + (b_1c_2-b_2c_1){\bf k} \quad (9)$$ который
– формула векторного произведения, заданная в уравнении (8).
Теперь мы докажем, что два определения векторного умножения верны.
эквивалент. На диаграмме показаны направления векторов ${\bf
b}$, ${\bf c}$ и ${\bf b}\times {\bf c}$, которые образуют «правильный
ручной набор».
Вы можете закончить чтение здесь, и это действительно больше важно понимать, что существует два определения вектора произведение, эквивалентность которого можно показать, чем оно механически проработать детали доказательства.
Теорема Вектор Произведение двух векторов ${\bf b}$ и ${\bf c}$ есть вектор ${\bf b}\times {\bf c}$ со следующими свойствами:
(i) ${\bf b}\times {\bf c}$ имеет величина $|{\bf b}||{\bf c}|\sin \theta$, где $\theta$ — угол между направлениями ${\bf b}$ и ${\bf c}$;
(ii) ${\bf b}\times {\bf c}$ перпендикулярно ${\bf b}$ и ${\bf c}$ с таким направлением, что векторы ${\bf b}$, ${\bf c}$ и ${\bf b}\times {\bf c}$ образуют правосторонний набор, как на диаграмме, так что ${\bf b}\times {\bf c}$ и ${\bf c}\times {\bf b}$ направлены в противоположные стороны.
Доказательство части (i)
Рассмотрим площадь параллелограмма со сторонами, равными
векторы ${\bf b}$ и ${\bf c}$ и угол $\theta$ между ними
стороны. Площадь этого параллелограмма равна $|{\bf b}||{\bf c}|\sin
\тета$. 2$. 92}
\cr &= |{\bf b}\times {\bf c}|. }$$
2$. 92}
\cr &= |{\bf b}\times {\bf c}|. }$$
Доказательство части (ii) Кому покажите, что ${\bf b}$ и ${\bf b}\times {\bf c}$ перпендикулярны мы показываем, что скалярное произведение равно нулю: $${\bf b}.{\bf b}\times {\bf c} = b_1(b_2c_3-b_3c_2) +b_2(b_3c_1-b_1c_3)+b_3(b_1c_2-b_2c_1) = 0,$$ и аналогично скалярное произведение ${\bf c}$ и ${\bf b}\times {\bf c}$ равен нулю, поэтому эти векторы перпендикулярны.
32.3: Векторы — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 38826
- Марсия Левитус
- Университет штата Аризона
В этой главе мы рассмотрим несколько понятий, которые вы, вероятно, знаете из курсов физики. В этой главе не предполагается исчерпывающее освещение темы, вместо этого мы коснемся нескольких понятий, которые вы будете использовать на уроках физической химии.
В этой главе не предполагается исчерпывающее освещение темы, вместо этого мы коснемся нескольких понятий, которые вы будете использовать на уроках физической химии.
Вектор — это величина, которая имеет как величину, так и направление, и поэтому они используются для определения положения, скорости и импульса частицы или для определения силы. Векторы обычно обозначаются жирным шрифтом (например, \(\mathbf{u}\)) или стрелкой над символом (например, \(\vec{u}\)). Тильда, помещаемая над или под именем вектора, также обычно используется в сокращении (\(\widetilde{u}\),\(\underset{\sim}{u}\)).
Если мы умножим число \(a\) на вектор \(\mathbf{v}\), мы получим новый вектор, параллельный исходному, но с длиной, которая \(a\) умножается на длину из \(\mathbf{v}\). Если \(a\) отрицательное \(a\mathbf{v}\) указывает в противоположном направлении, чем \(\mathbf{v}\) . Мы можем выразить любой вектор в терминах так называемых единичных векторов. Эти векторы, которые обозначаются как \(\hat{\mathbf{i}}\), \(\hat{\mathbf{j}}\) и \(\hat{\mathbf{k}}\), имеют единицу длину и точку вдоль положительных осей \(x, y\) и \(z\) декартовой системы координат (рисунок \(\PageIndex{1}\)). Символ \(\hat{\mathbf{i}}\) читается как «i-шляпа». Шляпы используются для обозначения того, что вектор имеет единичную длину. 9{1/2}\]
Символ \(\hat{\mathbf{i}}\) читается как «i-шляпа». Шляпы используются для обозначения того, что вектор имеет единичную длину. 9{1/2}\]
Если у нас есть два вектора \(\mathbf{u}=u_x\hat{\mathbf{i}}+u_y \hat{\mathbf{j}}+u_z \hat{\mathbf {k}}\) и \(\mathbf{v}=v_x \hat{\mathbf{i}}+v_y \hat{\mathbf{j}}+v_z \hat{\mathbf{k}}\), мы можем сложить их, чтобы получить
\[\mathbf{u}+\mathbf{v}=(u_x+v_x)\hat{\mathbf{i}}+(u_y+v_y)\hat{\mathbf{j} }+(u_z+v_z)\hat{\mathbf{k}} \nonumber\]
или вычесть их, чтобы получить:
\[\mathbf{u}-\mathbf{v}=(u_x-v_x)\ шляпа {\ mathbf {i}} + (u_y-v_y) \ шляпа {\ mathbf {j}} + (u_z-v_z) \ шляпа {\ mathbf {k}} \ nonumber \]
Когда дело доходит до умножения, мы можем выполнить произведение двух векторов двумя разными способами. Первый, который дает в результате скаляр (число), называется скалярным произведением или скалярным произведением. Второе, дающее в результате вектор, называется векторным (или перекрестным) произведением. Обе операции являются важными в физической химии.
Скалярное произведение
Скалярное произведение векторов \(\mathbf{u}\) и \(\mathbf{v}\), также известное как скалярное произведение или скалярное произведение, определяется как (обратите внимание на точку между символы, представляющие векторы)
\[\mathbf{u}\cdot \mathbf{v}=|\mathbf{u}||\mathbf{v}|\cos \theta \nonumber\]
где \(\theta\) угол между векторами. Обратите внимание, что скалярное произведение равно нулю, если два вектора перпендикулярны друг другу, и равно произведению их абсолютных значений, если они параллельны. Легко доказать, что
\[\mathbf{u}\cdot \mathbf{v}=u_xv_x+u_yv_y+u_zv_z \nonumber\]
Пример \(\PageIndex{1}\)
Покажите, что векторы
\[ \begin{align*} \mathbf{u_1} &=\dfrac{1}{\sqrt{3}}\hat{\mathbf{i}}+\dfrac{1}{\sqrt{3} }\шляпа{\mathbf{j}}+\dfrac{1}{\sqrt{3}}\шляпа{\mathbf{k}} \\[4pt] \mathbf{u_2} &=\dfrac{1}{ \ sqrt {6}} \ шляпа {\ mathbf {i}} — \ dfrac {2} {\ sqrt {6}} \ шляпа {\ mathbf {j}} + \ dfrac {1} {\ sqrt {6}} \hat{\mathbf{k}} \\[4pt] \mathbf{u_3} &=-\dfrac{1}{\sqrt{2}}\hat{\mathbf{i}}+\dfrac{1}{ \sqrt{2}}\шляпа{\mathbf{k}} \end{align*} \nonumber\] 9{1/2}=1 \end{align*} \nonumber\]
Чтобы проверить, перпендикулярны ли два вектора, мы выполняем скалярное произведение:
\[ \begin{align*} \mathbf{u_1}\cdot \mathbf{u_2}&=\left(\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}-\dfrac{1}{\sqrt{3}}\dfrac{ 2}{\sqrt{6}}+\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{6}}\right)=0 \\[4pt] \mathbf{u_1}\ cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{3}}\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}\ dfrac{1}{\sqrt{2}}\right)=0 \\[4pt] \mathbf{u_2}\cdot \mathbf{u_3} &=\left(-\dfrac{1}{\sqrt{6} }\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{6}}\dfrac{1}{\sqrt{2}}\right)=0 \end{align*} \ не число\]
Таким образом, мы только что доказали, что три пары взаимно перпендикулярны, а три вектора имеют единичную длину. Другими словами, эти векторы являются векторами \(\hat{\mathbf{i}}\), \(\hat{\mathbf{j}}\) и \(\hat{\mathbf{k}}\) вращается в пространстве.
Другими словами, эти векторы являются векторами \(\hat{\mathbf{i}}\), \(\hat{\mathbf{j}}\) и \(\hat{\mathbf{k}}\) вращается в пространстве.
Если скалярное произведение двух векторов (любой размерности) равно нулю, мы говорим, что эти два вектора ортогональны. Если векторы имеют единичную длину, мы говорим, что они нормализованы. Если два вектора нормализованы и ортогональны, мы говорим, что они ортонормированы. Набор векторов, показанный в предыдущем примере, образует ортонормированный набор. [vectors:orthonormal] Эти понятия также применимы к векторам, которые содержат комплексные элементы, но как мы выполняем скалярное произведение в этом случае? 9*\cdot \mathbf{v}=(\hat{\mathbf{i}}+(1+i)\hat{\mathbf{j}})((1+i)\hat{\mathbf{i}} +\hat{\mathbf{j}})=(1)(1+i)+(1+i)(1)=2+2i\neq 0 \nonumber\]
Следовательно, векторы неортогональны.
Произведение векторов
Векторное произведение двух векторов — это вектор, определенный как
\[\mathbf{u}\times \mathbf{v}=|\mathbf{u}| |\mathbf{v}| \mathbf{n} \sin\theta \nonumber\]
, где \(\theta\) снова угол между двумя векторами, а \(\mathbf{n}\) — единичный вектор, перпендикулярный образуемой плоскости на \(\mathbf{u}\) и \(\mathbf{v}\). Направление вектора \(\mathbf{n}\) задается правилом правой руки. Вытяните правую руку и укажите указательным пальцем в направлении \(\mathbf{u}\) (вектор слева от символа \(\times\)) и указательным пальцем в направлении \(\mathbf {v}\). Направление \(\mathbf{n}\), которое определяет направление \(\mathbf{u}\times \mathbf{v}\), является направлением вашего большого пальца. Если вы хотите отменить умножение и выполнить \(\mathbf{v}\times \mathbf{u}\), вам нужно указать указательным пальцем в направлении \(\mathbf{v}\), а указательным пальцем в направлении \(\mathbf{u}\) (по-прежнему используя правую руку!). Результирующий вектор будет указывать в противоположном направлении (рис. \(\PageIndex{1}\)).
Направление вектора \(\mathbf{n}\) задается правилом правой руки. Вытяните правую руку и укажите указательным пальцем в направлении \(\mathbf{u}\) (вектор слева от символа \(\times\)) и указательным пальцем в направлении \(\mathbf {v}\). Направление \(\mathbf{n}\), которое определяет направление \(\mathbf{u}\times \mathbf{v}\), является направлением вашего большого пальца. Если вы хотите отменить умножение и выполнить \(\mathbf{v}\times \mathbf{u}\), вам нужно указать указательным пальцем в направлении \(\mathbf{v}\), а указательным пальцем в направлении \(\mathbf{u}\) (по-прежнему используя правую руку!). Результирующий вектор будет указывать в противоположном направлении (рис. \(\PageIndex{1}\)).
Величина \(\mathbf{u}\times \mathbf{v}\) является произведением величин отдельных векторов, умноженных на \(\sin \theta\). Эта величина имеет интересную геометрическую интерпретацию: это площадь параллелограмма, образованного двумя векторами (рис. \(\PageIndex{1}\)).
Рисунок \(\PageIndex{1}\): Векторное произведение (CC BY-NC-SA; Marcia Levitus)Перекрестное произведение также может быть выражено в виде определителя:
\[\mathbf{u}\ раз \mathbf{v} = \begin{vmatrix} \шляпа{\mathbf{i}}&\шляпа{\mathbf{j}}&\шляпа{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \ конец {vmatrix} \номер\]
Пример \(\PageIndex{1}\):
Дано \(\mathbf{u}=-2 \hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\ mathbf{k}}\) и \(\mathbf{v}=3 \hat{\mathbf{i}}-\hat{\mathbf{j}}+\hat{\mathbf{k}}\), вычислить \(\mathbf{w}=\mathbf{u}\times \mathbf{v}\) и убедитесь, что результат перпендикулярен как \(\mathbf{u}\), так и \(\mathbf{v}\) .
Решение
\[ \begin{align*} \mathbf{u}\times \mathbf{v} &= \begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{ j}}&\hat{\mathbf{k}}\\ u_x&u_y&u_z\\ v_x&v_y&v_z\\ \end{vmatrix}=\begin{vmatrix} \hat{\mathbf{i}}&\hat{\mathbf{j} }&\шляпа{\mathbf{k}}\\ -2&1&1\\ 3&-1&1\\ \end{vmatrix} \\[4pt] &=\шляпа{\mathbf{i}}(1+1)-\ шляпа {\ mathbf {j}} (-2-3) + \ шляпа {\ mathbf {k}} (2-3) \\ [4pt] & = \ displaystyle {\ color {бордовый} 2 \ шляпа {\ mathbf {i}}+5 \hat{\mathbf{j}}-\hat{\mathbf{k}}} \end{align*} \nonumber\]
Чтобы убедиться, что два вектора перпендикулярны, мы выполняем скалярное произведение:
\[\mathbf{u} \cdot \mathbf{w}=(-2)(2)+(1)(5)+(1) (-1)=0 \nonumber\]
\[\mathbf{v} \cdot \mathbf{w}=(3)(2)+(-1)(5)+(1)(-1)= 0 \nonumber\]
Важным применением векторного произведения является определение углового момента. Если частица с массой \(m\) движется со скоростью \(\mathbf{v}\) (вектор), ее (линейный) импульс равен \(\mathbf{p}=m\mathbf{v}\). Пусть \(\mathbf{r}\) — положение частицы (другой вектор), тогда угловой момент частицы определяется как
Пусть \(\mathbf{r}\) — положение частицы (другой вектор), тогда угловой момент частицы определяется как
\[\mathbf{l}=\mathbf{r}\times\mathbf{p} \nonumber\]
Таким образом, угловой момент является вектором, перпендикулярным как \(\mathbf{r}\), так и \( \mathbf{p}\). Поскольку положение частицы необходимо определить относительно определенного источника, это начало необходимо указать при определении углового момента.
Рисунок \(\PageIndex{2}\): Угловой момент частицы с положением \(\mathbf{r}\) от начала координат и импульсом \(\mathbf{p}=m\mathbf{v}\) (CC BY-NC-SA; Марсия Левитус) 92+(-i)(i)=3\rightarrow |\mathbf{u}|=\sqrt{3} \nonumber\]Следовательно, чтобы нормализовать этот вектор, мы делим все компоненты на его длину:
\ [\ шляпа {\ mathbf {u}} = \ гидроразрыва {1} {\ sqrt {3}} \ шляпа {\ mathbf {i}} + \ гидроразрыва {1} {\ sqrt {3}} \ шляпа {\ mathbf {j}}+\frac{i}{\sqrt{3}}\hat{\mathbf{k}} \nonumber\]
Обратите внимание, что мы используем «шляпу», чтобы указать, что вектор имеет единичную длину.
Нужна помощь? Ссылки ниже содержат решенные примеры.
Операции с векторами: http://tinyurl.com/mw4qmz8
Внешние ссылки:
- Точечный продукт: http://patrickjmt.com/vectors-the-dot-product/
- Перекрестное произведение: http://patrickjmt.com/the-cross-product/
- Скалярное произведение: http://www.youtube.com/watch?v=enr7JqvehJs
Эта страница под названием 32.3: Vectors распространяется по незаявленной лицензии и была создана, изменена и/или курирована Марсией Левитус с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Марсия Левитус
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет на странице
- Теги
- источник@https://www.
 public.asu.edu/~mlevitus/chm240/book.pdf
public.asu.edu/~mlevitus/chm240/book.pdf
- источник@https://www.
Векторы
Это вектор:
Вектор имеет величины (размер) и направления :
Длина линии показывает ее величину, а стрелка указывает направление.
Мы можем добавить два вектора, соединив их лоб в лоб:
И неважно в каком порядке мы их складываем, получаем один и тот же результат:
Пример: Самолет летит на север, но ветер дует с северо-запада.
Два вектора (скорость, создаваемая пропеллером, и скорость ветра) приводят к несколько меньшей скорости относительно земли в направлении немного к востоку от севера.
Если смотреть на самолет с земли, то может показаться, что он немного скользит вбок.
Вы когда-нибудь видели такое? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают объяснить это.
Скорость, ускорение, сила и многое другое являются векторами.
Вычитание
Мы также можем вычесть один вектор из другого:
- Сначала мы меняем направление вектора, который хотим вычесть,
- , затем добавьте их как обычно:
а − б
Обозначение
Вектор часто записывается жирным шрифтом , например a или b .
| Вектор также можно записать в виде букв его головы и хвоста со стрелкой над ними, например: |
Расчеты
Теперь… как мы будем производить расчеты?
Самый распространенный способ — сначала разбить вектор на части x и y, например:
Вектор a разбит на
два вектора a x и a y
(Позже мы увидим, как это сделать.)
Добавление векторов
Затем мы можем сложить векторы по , добавив части x и , добавив части y :
Вектор (8, 13) и вектор (26, 7) в сумме дают вектор (34, 20)
Пример: добавить векторы
а = (8, 13) и б = (26, 7)в = а + б
в = (8) + 13 (8+26, 13+7) = (34, 20)
Когда мы разбиваем вектор таким образом, каждая часть называется компонентом :
Вычитание векторов
Чтобы вычесть, сначала инвертируйте вектор, который мы хотим вычесть, затем сложите.
Пример: вычесть
k = (4, 5) из v = (12, 2)a = v + − k
a = (12, 2) + −(4, 5) = (12, 2) + (−4, −5) = (12− 4, 2−5) = (8, −3)
Величина вектора
Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:
| и |
ИЛИ можно написать двойными вертикальными черточками (чтобы не путать с абсолютным значением):
|| и ||
Для расчета используем теорему Пифагора:
| и | = √( х 2 + у 2 )
Пример: какова величина вектора
b = (6, 8) ?| б | = √( 6 2 + 8 2 ) = √( 36+64) = √100 = 10
Вектор с величиной 1 называется единичным вектором.
Вектор против скаляра
Скаляр имеет величину (размер) только .
Скаляр: просто число (например, 7 или −0,32) … определенно не вектор.
Вектор имеет величину и направление и часто пишется жирным шрифтом , поэтому мы знаем, что это не скаляр:
- , поэтому c — это вектор, он имеет величину и направление
- , но c — это просто значение, например 3 или 12,4
Пример: k
b на самом деле скаляр, умноженный на k вектор b .Умножение вектора на скаляр
Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем размер вектора.
Пример: умножить вектор
m = (7, 3) на скаляр 3| a = 3 м = (3×7, 3×3) = (21, 9) |
Он по-прежнему указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Умножение вектора на вектор (скалярное произведение и векторное произведение)
Как нам умножить два вектора вместе? Существует более чем один способ!
(Дополнительную информацию см. на этих страницах.) |
Более двух измерений
Векторы также отлично работают в трех и более измерениях:
Вектор (1, 4, 5)
Пример: сложите векторы
a = (3, 7, 4) и b = (2, 9, 11)c = a + b
c = 02 9 (3,2 9 , 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
Пример: какова величина вектора
w = (1, −2, 3) ?| с | = √( 1 2 + (−2) 2 + 3 2 ) = √( 1+4+9) = √14
Вот пример с 4-мя измерениями (но это сложно нарисовать!):
Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)
(3, 3, 3, 3) + −(1, 2, 3, 4)
= (3, 3, 3, 3) + (−1,−2,−3,−4)
= (3−1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1 )
Величина и направление
Мы можем знать величину и направление вектора, но нам нужны его длины x и y (или наоборот):
| <=> | ||
| Вектор a в полярных координатах | Вектор a в декартовых координатах Координаты |
Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткий обзор:
| Из полярных координат (r, θ ) в декартовы координаты (x,y) | Из декартовых координат (x,y) в полярные координаты (r, θ) | |
|---|---|---|
|
|
Пример
Сэм и Алекс тянут коробку.
- Сэм тянет с силой 200 ньютонов под углом 60°
- Алекс тянет с усилием 120 ньютонов под углом 45°, как показано
Что такое объединенная сила и ее направление?
Сложим два вектора «голова к хвосту»:
Первое преобразование из полярной системы в декартову (до 2 десятичных знаков):
Вектор Сэма:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0,5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0,8660 = 173,21
Вектор Алекса:
- x = r × cos( θ ) = 120 × cos(−45°) = 120 × 0,7071 = 84,85
- y = r × sin( θ ) = 120 × sin(−45°) = 120 × -0,7071 = −84,85
Теперь у нас есть:
Добавьте их:
(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)
Этот ответ верный, но давайте обратимся к полярному, поскольку вопрос был полярным:
- r = √ (x 2 + y 2 ) = √ (184,85 2 + 88,36 2 ) = 204,04
- θ = тангенс -1 ( y / x ) = тангенс -1 ( 88,36 / 184,85 ) = 25,5°
И у нас есть этот (округленный) результат:
А для Сэма и Алекса это выглядит так:
Они могли бы получить лучший результат, если бы стояли плечом к плечу!
Объяснение урока: полярная форма вектора
В этом объяснении мы узнаем, как преобразовывать прямоугольную форму вектора в полярную.
Когда мы думаем о векторах на плоскости, мы обычно думаем о декартовых координатах, поскольку это наиболее распространенная система координат, которая приводит к прямоугольной форме вектора. В частности, прямоугольные формы вектора используются в линейном движении, где просто указать движение оси и где движение будет проходить по линейному пути к определенному местоположению.
Прямоугольные формы вектора определяют положение как линейное расстояние от начала координат в двух или более взаимно перпендикулярных направлениях. Стандартные единичные векторы в координатной плоскости: ⃑𝑖=(1,0),⃑𝑗=(0,1).
Начало — это точка пересечения осей, а векторы на координатной плоскости задаются линейной комбинацией единичных векторов с использованием обозначения ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗=(𝑥,𝑦).
Для прямоугольной формы вектора любой вектор может быть определен уникальным набором компонентов, заданным как линейная комбинация единичных векторов 𝑥⃑𝑖+𝑦⃑𝑗; эта форма допускает как положительные, так и отрицательные компоненты по отношению к происхождению.
Однако существуют и другие способы представления вектора a — мы рассмотрим один из таких способов, известный как полярная форма вектора. Эта полярная форма определяет вектор в пространстве с использованием комбинации радиальных и угловых единиц, а вектор определяется расстоянием по прямой от начала координат и углом от положительной оси 𝑥.
Они известны как радиальные и угловые компоненты вектора, а полярная форма вектора, как показано на диаграмме выше, имеет вид ⃑𝑣=(𝑟,𝜃).
Полярные формы вектора часто используются в нелинейном движении, например, если движение включает круговой путь. Это делает полярную форму полезной при расчете уравнений движения для многих механических систем. У него также есть другие реальные приложения, такие как радары, использующие индикатор положения в плане, описание характеристик микрофона и управление промышленными роботами в различных производственных приложениях и гравитационных полях, и это лишь некоторые из них.
Для полярной формы вектора ⃑𝑣 мы помечаем вектор его линейным расстоянием или длиной от начала координат, обозначаемым 𝑟, и его углом от положительной оси 𝑥, обозначаемым 𝜃. Другими словами, радиальная составляющая 𝑟 определяется как длина модуля вектора,
𝑟≡‖‖⃑𝑣‖‖.
Другими словами, радиальная составляющая 𝑟 определяется как длина модуля вектора,
𝑟≡‖‖⃑𝑣‖‖.
Поскольку мы можем построить прямоугольный треугольник, используя 𝑟 в качестве гипотенузы, мы выражаем стороны треугольника через sin𝜃 и cos𝜃.
Это также позволяет нам выразить компоненты прямоугольной формы вектора ⃑𝑣 через компоненты его полярной формы.
Определение: Преобразование полярной формы в прямоугольную форму вектора
Компоненты полярной формы (𝑟,𝜃) вектора могут быть преобразованы в прямоугольную форму 𝑥⃑𝑖+𝑦⃑𝑗 как 𝑥=𝑟𝜃,𝑦=𝑟𝜃.cossin
Итак, если нам даны компоненты полярной формы вектора, модуль или длина 𝑟 и угол 𝜃, мы можем определить компоненты прямоугольной формы, 𝑥 и 𝑦, используя эти уравнения.
В качестве примера давайте преобразуем вектор из полярной формы в градусах в прямоугольную форму, используя модуль вектора и острый угол, представленные геометрически.
Пример 1: Геометрическое представление векторов
Рассмотрим вектор ⃑𝑣 с модулем 3 и углом 45∘, отсчитываемым против часовой стрелки от положительной оси 𝑥. Используя тригонометрию, вычислить 𝑥- и 𝑦-компоненты вектора и, следовательно, записать ⃑𝑣 в виде (𝑥,𝑦). Округлите ответ до двух знаков после запятой.
Используя тригонометрию, вычислить 𝑥- и 𝑦-компоненты вектора и, следовательно, записать ⃑𝑣 в виде (𝑥,𝑦). Округлите ответ до двух знаков после запятой.
Ответ
В этом примере мы хотим найти прямоугольную форму вектора, используя графическое представление и заданную длину вектора.
Напомним, что полярная форма определяет вектор согласно расстоянию от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃.
Радиальная составляющая равна длине или модулю вектора ⃑𝑣, 𝑟=‖‖⃑𝑣‖‖, и задается как 𝑟=3, и нам говорят, что вектор находится под углом 45 ∘ над положительной 𝑥-осью.
Подставляя радиальную и угловую компоненты вектора ⃑𝐴, 𝑟=3 и 𝜃=45∘, компоненты прямоугольной формы определяются как 𝑥=345=3×1√2=2,121320343…cos∘ а также 𝑦=345=3×1√2=2,121320343….sin∘
Следовательно, с точностью до двух знаков после запятой имеем ⃑𝑣=(2.12,2.12).
Теперь давайте рассмотрим другой пример, в котором мы преобразуем вектор из полярной формы в градусах в прямоугольную, используя графическое представление вектора.
Пример 2. Преобразование вектора из полярной формы в векторную форму с использованием графического представления вектора
Заполните пропуск: Если ‖‖⃑𝐴‖‖=4см, то ⃑𝐴=.
- 4√3,4
- 2,2√3
- √3,2
- 2√3,2 1
- 4⃑𝑖 — 4√3⃑𝑗
- 4⃑𝑖+4√3⃑𝑗
- 4√3⃑𝑖 — 4⃑𝑗
- 4√3⃑𝑖+4⃑𝑗
- (3,4)
- (−3,4)
- (−3,−4)
- (3,−4)
- 72⃑𝑖+7чина.0050
- 6
- 11
- 10
- 15
- 8, 𝜋3
- 8, 𝜋4
- (8, 𝜋)
- 8, 𝜋6
- √2,5𝜋4
- √2, 𝜋4
- √2,7𝜋4
- чина (𝑟,𝜃) в радианах для конкретного вектора в прямоугольной форме ⃑𝐴=−⃑𝑖−⃑𝑗.
Напомним, что полярная форма определяет вектор согласно расстоянию от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃. Мы используем соглашение, где угол 𝜃 является положительным углом против часовой стрелки. Мы также ограничиваем углы до 0≤𝜃2𝜋, чтобы записать их в стандартизированной форме.
Компоненты прямоугольной формы вектора через основные единицы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 могут быть выражены через компоненты полярной формы ⃑𝑣=(𝑟,𝜃) как 𝑥=𝑟𝜃,𝑦=𝑟𝜃.cossin
Теперь найдем полярную форму вектора ⃑𝐴=−⃑𝑖−⃑𝑗, используя графическое представление непосредственно с определением. Радиальная составляющая — это расстояние от начала координат до вектора ⃑𝐴, и мы можем найти его, применив теорему Пифагора о прямоугольном треугольнике, как показано на диаграмме ниже.
Мы можем найти гипотенузу этого треугольника из 𝑟=√1+1=√2.

Поскольку вектор ⃑𝐴 расположен в третьем квадранте, угловая составляющая 𝜃 для полярной формы будет положительным углом против часовой стрелки от положительной оси 𝑥, а угол 𝛼 измеряется от отрицательной оси 𝑥. Мы можем составить прямоугольный треугольник с углом 𝛼 и сторонами длиной 2 и 5, как показано на диаграмме выше. Поскольку 𝛼 — острый угол, мы можем записать это через стороны, используя арктангенс, как 𝛼=11.tan
У нас также есть 𝜃=𝛼+𝜋. Подставляя угол 𝛼, мы можем изменить это, чтобы найти 𝜃=𝛼+𝜋=11+𝜋=𝜋4+𝜋=5𝜋4.tan
Мы могли бы также прийти к этому ответу, используя тот факт, что мы можем преобразовать вектор из прямоугольной формы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗, расположенной в третьем квадранте в полярную форму ⃑𝑣=(𝑟,𝜃) с помощью 𝑟=√𝑥+𝑦,𝜃=𝑦𝑥+𝜋.tan
Это дает те же радиальные и угловые компоненты полярной формы после замены 𝑥=−1 и 𝑦=−1.
Следовательно, полярная форма ⃑𝐴 √2,5𝜋4.
Это вариант A.
Ключевые точки
- Полярная форма вектора обозначается (𝑟,𝜃), где 𝑟 представляет собой расстояние от начала координат, а 𝜃 представляет собой угол, измеренный от оси 𝑥.

- Компоненты прямоугольной формы вектора ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 могут быть получены из компонент полярной формы ⃑𝑣=(𝑟,𝜃) из 𝑥=𝑟𝜃,𝑦=𝑟𝜃.коссин Полярная форма вектора ⃑𝑣=(𝑟,𝜃) не уникальна, и существуют эквивалентные способы описания одного и того же вектора, поскольку тригонометрические функции, используемые для их определения, являются периодическими.
- Используемые соглашения принимают угол против часовой стрелки как положительный, а угол по часовой стрелке как отрицательный, и мы используем стандартизированную форму с 0≤𝜃2𝜋 в радианах или 0≤𝜃360∘∘ в градусах.
- Мы можем найти эквивалентную полярную форму вектора, добавляя или вычитая любое целое число, кратное полному обороту (360∘ или 2𝜋): (𝑟,𝜃)=(𝑟,𝜃+2𝜋𝑛).
- Компоненты полярной формы вектора ⃑𝑣=(𝑟,𝜃) могут быть выражены через компоненты прямоугольной формы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 как
𝑟=√𝑥+𝑦,
а значение 𝜃 будет зависеть от квадранта, в котором лежит вектор ⃑𝑣, для 0≤𝜃2𝜋 в радианах или 0≤𝜃360∘∘ в градусах.

- Полярная форма вектора обозначается (𝑟,𝜃), где 𝑟 представляет собой расстояние от начала координат, а 𝜃 представляет собой угол, измеренный от оси 𝑥.
- прямоугольная форма вектора с использованием графического представления и заданной длины вектора.
Напомним, что полярная форма определяет вектор согласно расстоянию от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃.
Компоненты прямоугольной формы вектора ⃑𝑣=(𝑥,𝑦) могут быть выражены через компоненты полярной формы ⃑𝑣=(𝑟,𝜃) как 𝑥=𝑟𝜃,𝑦=𝑟𝜃.cossin
Радиальная составляющая равна длине или модулю вектора ⃑𝑣: 𝑟=‖‖⃑𝑣‖‖.
Подставляя радиальную и угловую компоненты вектора ⃑𝐴, 𝑟=4 см и 𝜃=30∘, компоненты прямоугольной формы определяются как
𝑥=430=4×√32=2√3cos∘
а также
𝑦=430=4×12=2. sin∘
sin∘
Следовательно, имеем ⃑𝐴=2√3,2.
Это вариант D.
Теперь давайте преобразуем вектор из полярной формы в градусах в прямоугольную, чтобы решить конкретную задачу со словами, связанную с силой.
Пример 3: Преобразование вектора из полярной формы в прямоугольную в текстовой задаче
Заполните пропуск: Если сила 𝐹=8N действует в направлении 30∘ к востоку от севера, где восток представляет положительную ось 𝑥 а север представляет собой положительную 𝑦-ось, тогда ⃑𝐹=.
Ответ
В этом примере мы хотим найти прямоугольную форму вектора силы. проблема со словом.
Напомним, что полярная форма определяет вектор согласно расстоянию от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃.
Компоненты прямоугольной формы вектора через основные единицы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 могут быть выражены через компоненты полярной формы ⃑𝑣=(𝑟,𝜃) как
𝑥=𝑟𝜃,𝑦=𝑟𝜃. коссин
коссин
Радиальная составляющая эквивалентна длине или модулю вектора ⃑𝑣: 𝑟=‖‖⃑𝑣‖‖.
Поскольку 𝐹=8 действует в направлении 30∘ к востоку от севера, радиальная составляющая полярной формы равна 𝑟=|𝐹|=8, а угловая составляющая, угол против часовой стрелки от положительной оси 𝑥, равна 𝜃=90 −30=60∘∘∘.
Это связано с тем, что заданный угол составляет 30° к востоку от севера, а углы обычно измеряются с востока на север в направлении против часовой стрелки от положительной оси 𝑥, как показано на диаграмме выше.
Подставляя радиальную и угловую компоненты вектора ⃑𝐹, 𝑟=8 и 𝜃=60∘, компоненты прямоугольной формы определяются как 𝑥=860=8×12=4cos∘ а также 𝑦=860=8×√32=4√3.sin∘
Следовательно, имеем ⃑𝐹=4⃑𝑖+4√3⃑𝑗.
Это вариант B.
Угол против часовой стрелки считается положительным, а угол по часовой стрелке отрицательным. В предыдущих примерах и диаграммах угловые компоненты были острыми, поскольку векторы в примерах находились в первом квадранте. Если вектор лежит в другом квадранте, как показано на диаграмме ниже, его угол не является острым.
Если вектор лежит в другом квадранте, как показано на диаграмме ниже, его угол не является острым.
На самом деле, хотя мы и вывели уравнения для компонентов прямоугольной формы, 𝑥=𝑟𝜃,𝑦=𝑟𝜃,коссин от острых углов, 0≤𝜃𝜋2, мы знаем, что они остаются верными для любого угла 𝜃.
Рассмотрим пример, в котором мы преобразуем вектор, лежащий во втором квадранте с неострым углом, из полярной формы в радианах в прямоугольную, чтобы найти разность двух векторов.
Пример 4. Решение задачи с векторами прямоугольной и полярной форм
Заполните пропуск: Если ⃑𝐴=(6,𝜋) и ⃑𝐵=−3⃑𝑖+4⃑𝑗, то 𝐴𝐵=.
Ответ
В этом примере мы хотим найти вектор направления 𝐴𝐵 в прямоугольной форме, где вектор ⃑𝐴 задан в полярной форме, а ⃑𝐵 задан в прямоугольной форме. Начнем с построения векторов ⃑𝐴 и ⃑𝐵,
. Напомним, что полярная форма определяет вектор в соответствии с расстоянием от начала координат, обозначаемым 𝑟, и угловым направлением от положительной оси 𝑥, обозначаемой 𝜃.
Компоненты прямоугольной формы вектора через основные единицы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 могут быть выражены через компоненты полярной формы ⃑𝑣=(𝑟,𝜃) как 𝑥=𝑟𝜃,𝑦=𝑟𝜃.cossin
Подставляя радиальную и угловую компоненты вектора ⃑𝐴, 𝑟=6 и 𝜃=𝜋, компоненты прямоугольной формы определяются как 𝑥=6(𝜋)=6×−1=−6cos а также 𝑦=6(𝜋)=6×0=0.sin
Таким образом, ⃑𝐴 в прямоугольной форме ⃑𝐴=−6⃑𝑖+0⃑𝑗=−6⃑𝑖.
Теперь мы можем определить 𝐴𝐵: 𝐴𝐵=⃑𝐵−⃑𝐴=−3⃑𝑖+4⃑𝑗−−6⃑𝑖=3⃑𝑖+4⃑𝑗.
Следовательно, имеем 𝐴𝐵=(3,4).
Это вариант A.
В следующем примере давайте преобразуем вектор в четвертом квадранте, 3𝜋2𝜃2𝜋, из полярной формы в радианах в прямоугольную форму.
Пример 5: Преобразование вектора из полярной формы в прямоугольную
Заполните пропуск: Если ⃑𝐴=7,5𝜋3, то ⃑𝐴 в терминах фундаментальных единичных векторов равно .
Ответ
В этом примере мы хотим определить прямоугольную форму вектора из полярной формы 7,5𝜋3.
Напомним, что полярная форма определяет вектор согласно расстоянию от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃.
Компоненты прямоугольной формы вектора через основные единицы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 могут быть выражены через компоненты полярной формы ⃑𝑣=(𝑟,𝜃) как 𝑥=𝑟𝜃,𝑦=𝑟𝜃.коссин
Мы знаем, что расстояние от начала координат равно 7, а стандартный угол вектора равен 5𝜋3. Поскольку этот угол находится между 3𝜋2 и 2𝜋, мы знаем, что вектор расположен в четвертом квадранте, как показано на диаграмме ниже.
Подставляя радиальную и угловую компоненты вектора ⃑𝐴, 𝑟=7 и 𝜃=5𝜋3, компоненты прямоугольной формы определяются как 𝑥=75𝜋3=7×12=72cos а также 𝑦=75𝜋3=7×−√32=−7√32.sin
Отметим, что 𝑥>0 и 𝑦0, что указывает на то, что этот вектор, как и ожидалось, лежит в четвертом квадранте.
Таким образом, вектор ⃑𝐴 в терминах фундаментальных ортов равен 72⃑𝑖−7√32⃑𝑗.
Это вариант B.
До сих пор мы видели примеры преобразования вектора из полярной формы в прямоугольную с помощью тригонометрии. Но что, если мы хотим сделать обратное, то есть преобразовать вектор из прямоугольной формы в полярную?
Начнем с того, что вспомним уравнения, выражающие компоненты прямоугольной формы 𝑥 и 𝑦 через компоненты полярной формы 𝑟 и 𝜃: 𝑥=𝑟𝜃,𝑦=𝑟𝜃.коссин
Используя их, мы хотим записать компоненты полярной формы в терминах 𝑥 и 𝑦, независимо от того, в каком квадранте лежит вектор.
Если мы возьмем квадрат каждого из них и сложим их, используя Пифагорейское тождество, мы можем устранить 𝜃 и показать, что они удовлетворяют 𝑥+𝑦 = 𝑟𝜃+𝑟𝜃 = 𝑟𝜃+𝜃 = 𝑟. +𝑦⃑𝑗, который мы определяем как 𝑟, задается выражением 𝑟=‖‖⃑𝑣‖‖=√𝑥+𝑦.
Используя это, мы можем решить задачу на сложение длин трех векторов.
Пример 6: Решение проблемы с участием векторов в прямоугольной форме и полярной форме
, если ⃑𝐴 = 3⃑𝑖+4⃑𝑗, ⃑𝐵 = 4⃑𝑗 и ⃑𝐶 = 6, 𝜋10, то ‖⃑𝐴⃑𝐴⃑𝐴‖+‖⃑𝐵⃑𝐵‖ +‖‖⃑𝐶‖‖=.
Ответ
В этом примере мы хотим найти сумму длины трех векторов, где ⃑𝐴 и ⃑𝐵 находятся в прямоугольной форме, а ⃑𝐶 — поля. . Начнем с построения графика трех заданных векторов.
Напомним, что полярная форма определяет вектор согласно смещению от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃.
Модуль вектора ⃑𝑣 в прямоугольной форме в основных единицах ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 определяется выражением ‖‖⃑𝑣‖‖=√𝑥+𝑦.
Следовательно, для заданных векторов ⃑𝐴 и ⃑𝐵 имеем ‖‖⃑𝐴‖‖=√3+4=5 а также ‖‖⃑𝐵‖‖=√0+4=4.
Мы также можем увидеть длину вектора ⃑𝐵 на графике.
Вектор ⃑𝐶 задан в полярной форме (𝑟,𝜃), где 𝑟 — радиальная составляющая, равная длине или модулю вектора ‖‖⃑𝐶‖‖, а 𝜃 — угловая составляющая. Следовательно, модуль вектора равен ‖‖⃑𝐶‖‖=6.
Следовательно, имеем
‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖+‖‖⃑𝐶‖‖=5+4+6=15.
Это вариант D.
Кроме того, когда мы делим уравнение для 𝑦 на уравнение для 𝑥, мы можем отменить появившееся 𝑟, чтобы получить 𝑦𝑥=𝑟𝜃𝑟𝜃=𝜃𝜃=𝜃.sincossincostan
Отметим, что это верно только для 𝑥≠0. У нас есть частный случай, когда 𝑥=0,𝑦=𝑎∈ℝ или (0,𝑎) в прямоугольной форме. Для этого у нас есть 𝑟𝜃=0, потому что что приводит к 𝜃=𝜋2, 𝜃=−𝜋2 или 𝑟=0. Мы можем игнорировать случай 𝑟=0, так как это означало бы 𝑦=0, что соответствует нулевому вектору, который в полярной форме обозначается (0,𝜃), для любого угла 𝜃.
Таким образом, 𝜃=𝜋2 или 𝜃=−𝜋2, которые соответствуют оси 𝑦. Эти углы помещают вектор на 𝑦-ось, поэтому модуль вектора равен абсолютному значению 𝑦-координаты, 𝑟=|𝑎|. Представление полярной формы этого вектора: |𝑎|,𝜋2 для 𝑎>0 и |𝑎|,−𝜋2 для 𝑎0.
Итак, если 𝑥≠0, у нас есть следующее уравнение для определения угла 𝜃: загар𝜃=𝑦𝑥.
Диапазон функции арктангенса равен −𝜋2,𝜋2, когда область определения функции тангенса ограничена одним и тем же интервалом, известным как главная ветвь. Это делается для того, чтобы функция тангенса была один к одному, чтобы функция арктангенса оценивалась как одно значение, известное как основное значение.
Это делается для того, чтобы функция тангенса была один к одному, чтобы функция арктангенса оценивалась как одно значение, известное как основное значение.
Таким образом, пока 𝜃∈−𝜋2,𝜋2, мы можем взять арктангенс обеих частей уравнения, чтобы получить 𝜃=𝑦𝑥.tan
Угловые координаты 𝜃∈−𝜋2,𝜋2 соответствуют первому и четвертому квадрантам или квадрантам, где 𝑥>0.
В следующем примере давайте преобразуем вектор из прямоугольной формы в полярную в радианах.
Пример 7: Преобразование вектора из векторной формы в полярную форму
Заполните пропуск: Если 𝑃𝑀=4√3,4, то полярная форма вектора 𝑃𝑀 равна .
. ), в радианах, для заданного вектора в прямоугольных координатах 𝑃𝑀=4√3,4. Начнем с построения этого вектора на координатной плоскости.
Напомним, что полярная форма определяет вектор согласно расстоянию от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃. Мы используем соглашение, где угол 𝜃 является положительным углом против часовой стрелки.
Мы используем соглашение, где угол 𝜃 является положительным углом против часовой стрелки.
Компоненты прямоугольной формы вектора через основные единицы ⃑𝑣=𝑥⃑𝑖+𝑦⃑𝑗 могут быть выражены через компоненты полярной формы ⃑𝑣=(𝑟,𝜃) как 𝑥=𝑟𝜃,𝑦=𝑟𝜃.cossin
Теперь найдем полярную форму вектора 𝑃𝑀, используя графическое представление непосредственно с определением. Радиальная координата — это расстояние от начала координат до вектора 𝑃𝑀, которое мы можем найти из теоремы Пифагора о прямоугольном треугольнике, как показано на диаграмме. Сначала найдем гипотенузу этого треугольника. 𝑟=4√3+4=√64=8.
Поскольку вектор 𝑃𝑀 расположен в первом квадранте, угловая составляющая 𝜃 для полярной формы будет положительным углом против часовой стрелки от положительной оси 𝑥, и мы можем построить прямоугольный треугольник с углом 𝜃 и длинами сторон 4 √3 и 4, как показано на диаграмме. Поскольку 𝜃 — острый угол, используя тригонометрию прямоугольного треугольника, мы можем записать это в терминах арктангенса как
𝜃=44√3=1√3=𝜋6. tantan
tantan
Мы могли бы также получить этот ответ, используя тот факт, что мы можем преобразовать вектор из прямоугольной формы, ⃑𝑣=(𝑥, 𝑦), расположенных в первом квадранте в полярной форме, ⃑𝑣=(𝑟,𝜃), с помощью 𝑟=√𝑥+𝑦,𝜃=𝑦𝑥.загар
Это дает те же радиальные и угловые компоненты полярной формы после замены 𝑥=4√3 и 𝑦=4.
Следовательно, полярная форма вектора 𝑃𝑀 равна 8,𝜋6.
Это вариант D.
Теперь давайте рассмотрим пример, в котором мы идентифицируем графическое полярное представление данного вектора.
Пример 8: Определение графического полярного представления вектора
Что из следующего является полярным представлением ⃑𝐴=2√3,2?
Ответ
В этом примере мы хотим определить графическое полярное представление в градусах для конкретного вектора в прямоугольной форме, ⃑𝐴=2√3,2.
Напомним, что полярная форма определяет вектор согласно расстоянию от начала координат, обозначенному 𝑟, и угловому направлению от положительной оси 𝑥, обозначенному 𝜃. Мы используем соглашение, где угол 𝜃 является положительным углом против часовой стрелки. Мы также ограничиваем углы до 0≤𝜃2𝜋, чтобы записать их в стандартизированной форме.
Мы используем соглашение, где угол 𝜃 является положительным углом против часовой стрелки. Мы также ограничиваем углы до 0≤𝜃2𝜋, чтобы записать их в стандартизированной форме.
Компоненты прямоугольной формы вектора ⃑𝑣=(𝑥,𝑦) могут быть выражены через компоненты полярной формы ⃑𝑣=(𝑟,𝜃) как 𝑥=𝑟𝜃,𝑦=𝑟𝜃.cossin
Поскольку вектор лежит в первом квадранте, мы можем определить полярную форму, используя 𝑟=√𝑥+𝑦,𝜃=𝑦𝑥.tan
Для данного вектора ⃑𝐴 мы можем определить радиальную составляющую как 𝑟=2√3+2=√12+4=√16=4 а угловая составляющая как 𝜃=22√3=1√3=30.tantan∘
Таким образом, графическим полярным представлением является то, в котором отрезок имеет длину 4 и находится на расстоянии 30∘ от положительной оси 𝑥 в направление против часовой стрелки.
Это вариант B.
В предыдущем примере мы преобразовали прямоугольную форму вектора в первом квадранте в полярную форму. Как видно из этого примера, мы можем вычислить угловую координату вектора, используя
𝜃=𝑦𝑥тан
в первом и четвертом квадрантах. Однако это уже не так, если вектор лежит во втором или третьем квадранте. Для второго и третьего квадрантов значение 𝜋 в радианах или 180∘ в градусах необходимо добавить к углу 𝜃, чтобы настроить угловую координату так, чтобы вектор лежал в правильном квадранте. Это не влияет на саму касательную функцию, поскольку мы имеем тождество
тантан𝜃=(𝜃+180),∘
или в более общем смысле
тантан𝜃=(𝜃+180𝑘),𝑘∈ℤ.∘
Однако это уже не так, если вектор лежит во втором или третьем квадранте. Для второго и третьего квадрантов значение 𝜋 в радианах или 180∘ в градусах необходимо добавить к углу 𝜃, чтобы настроить угловую координату так, чтобы вектор лежал в правильном квадранте. Это не влияет на саму касательную функцию, поскольку мы имеем тождество
тантан𝜃=(𝜃+180),∘
или в более общем смысле
тантан𝜃=(𝜃+180𝑘),𝑘∈ℤ.∘
Чтобы убедиться в этом, рассмотрим вектор в прямоугольных координатах, лежащий во втором квадранте, (𝑥,𝑦)=(−𝑎,𝑏) с 𝑎>0 и 𝑏>0.
Угловой компонент 𝜃 для этого вектора в полярной форме будет положительным углом против часовой стрелки от положительной оси 𝑥, а угол 𝛼 измеряется от отрицательной оси 𝑥, как показано на диаграмме. Мы можем построить прямоугольный треугольник с углом 𝛼 и длинами сторон 𝑎 и 𝑏. Поскольку 𝛼 — острый угол, мы можем записать это через стороны, используя арктангенс, как 𝛼=𝑏𝑎.тан
У нас также есть 𝛼+𝜃=180∘. Подставляя угол 𝛼, мы можем изменить это, чтобы найти
𝜃=−𝛼+180=−𝑏𝑎+180=𝑏−𝑎+180,∘∘∘тантан
где для последнего равенства мы использовали тот факт, что функция тангенса, а значит и функция арктангенса, является нечетной функцией.
Поскольку (𝑥,𝑦)=(−𝑎,𝑏), это эквивалентно 𝜃=𝑦𝑥+180.tan∘
В следующем примере мы найдем угловую координату определенного вектора в градусах, лежащего во втором квадранте.
Пример 9. Нахождение угла направления заданного вектора
Рассмотрим вектор (−2,3). Вычислите направление вектора, задав ваше решение как угол с точностью до градуса, измеренный против часовой стрелки от положительной оси 𝑥.
Ответ
В этом примере мы хотим определить направление вектора в градусах для конкретного вектора в прямоугольной форме (−2,3). Мы хотим найти угол, измеренный против часовой стрелки от положительной оси 𝑥. Начнем с построения этого вектора на координатной плоскости.
Поскольку вектор (−2,3) расположен во втором квадранте, направлением вектора является угол 𝜃, отсчитываемый против часовой стрелки от положительной оси 𝑥. Рассмотрим угол 𝛼, который измеряется в том же направлении, что и 𝜃, как показано на схеме. Мы можем составить прямоугольный треугольник с углом 𝛼 и длинами сторон 2 и 3. Поскольку 𝛼 — острый угол, мы можем использовать тригонометрию прямоугольного треугольника, чтобы записать стороны через арктангенс как
𝛼=32.tan
Поскольку 𝛼 — острый угол, мы можем использовать тригонометрию прямоугольного треугольника, чтобы записать стороны через арктангенс как
𝛼=32.tan
Поскольку сумма углов на прямой составляет 180∘, мы также имеем 𝛼+𝜃=180∘. Подставляя угол 𝛼, мы можем изменить это, чтобы найти 𝜃=−𝛼+180=−32+180=−56,3099324…+180=123,65….∘∘∘∘∘tan
Мы могли бы также прийти к этому ответу, используя тот факт, что вектор прямоугольной формы (𝑥,𝑦), расположенный во втором квадранте, имеет угол 𝜃=𝑦𝑥+𝜋,загар где 𝜃 отсчитывается против часовой стрелки от положительной оси 𝑥. Это дает тот же угол после замены 𝑥=−2 и 𝑦=3. Этот угол эквивалентен угловой составляющей полярной формы (−2,3).
Следовательно, с точностью до градуса направление вектора, отсчитываемого против часовой стрелки от положительной оси 𝑥, равно 124∘.
Для третьего квадранта мы можем показать аналогичным образом, что нам также нужно добавить 180∘ к tan𝑦𝑥, чтобы получить угловую координату 𝜃 в правильном квадранте.
Полярные формы вектора не уникальны, если только мы не ограничиваем угол определенным диапазоном, и существует множество способов представления одного и того же вектора. В качестве примера определим полярную форму вектора ⃑𝑖+⃑𝑗 в прямоугольных координатах.
Радиальная составляющая 𝑟 — это расстояние от начала координат, которое мы можем определить, используя теорему Пифагора о прямоугольном треугольнике со стороной 1 и углом 𝜃. Особенно, 𝑟=√1+1=√2.
Существует много способов выразить угловую составляющую 𝜃. Один из них — это положительный угол против часовой стрелки от положительной оси 𝑥, который от прямоугольного треугольника дает нам тангенс с точки зрения отношения противоположной и смежной сторон: загар𝜃=11=1.
Поскольку вектор лежит в первой четверти, а 𝜃 — острый угол на диаграмме, мы можем найти угол непосредственно из арктангенса, 𝜃=(1)=45.tan∘
Таким образом, полярная форма вектора ⃑𝑖+⃑𝑗 есть √2,45∘.
Другая полярная форма может быть найдена, если мы используем отрицательный угол по часовой стрелке от положительной оси 𝑥, что даст эквивалентную полярную форму как √2,45−360=√2,−315∘∘∘. На самом деле, если мы совершим полный оборот от этого вектора по часовой или против часовой стрелки, мы вернемся обратно к тому же вектору. Таким образом, другим представлением будет √2,45+360=√2,405∘∘∘.
На самом деле, если мы совершим полный оборот от этого вектора по часовой или против часовой стрелки, мы вернемся обратно к тому же вектору. Таким образом, другим представлением будет √2,45+360=√2,405∘∘∘.
Это показывает ключевое отличие при использовании полярных форм по сравнению с прямоугольной формой, поскольку позволяет бесконечное количество наборов для описания любого заданного вектора. Это потому, что мы можем добавить любое целое число, кратное полному обороту (360∘ или 2𝜋), к угловой координате 𝜃, чтобы получить эквивалентную точку в полярных координатах. Это следует из того, что тригонометрические функции, используемые для определения полярных форм, сами по себе являются периодическими.
Это условие эквивалентности можно резюмировать следующим образом.
Определение: условие периодичности для полярных форм
Если (𝑟,𝜃) описывает полярную форму вектора, то мы можем выразить эквивалентные полярные формы как
(𝑟,𝜃)=(𝑟,𝜃+2𝜋𝑛)(),=(𝑟,𝜃+360𝑛)(),радианыградусы∘
для любого 𝑛∈ℤ.
Таким образом, чтобы стандартизированно выразить полярную форму с 0≤𝜃2𝜋 в радианах или 0≤𝜃360∘∘ в градусах, нам, возможно, придется скорректировать значение угловой координаты 𝜃. В частности, для четвертого квадранта нам, возможно, придется добавить полный оборот (2𝜋 или 360∘), чтобы получить эквивалентный угол в стандартном диапазоне, поскольку арктангенс дает отрицательный угол по часовой стрелке, а не положительный угол против часовой стрелки от положительного 𝑥-ось.
Используемые нами соглашения принимают угол против часовой стрелки как положительный, а угол по часовой стрелке как отрицательный. Угол измеряется против часовой стрелки от положительной оси 𝑥.
Мы можем обобщить то, что мы рассмотрели до сих пор, в определении, которое можно использовать для преобразования прямоугольной формы вектора в полярную форму и наоборот.
Определение: Преобразование прямоугольной формы в полярную форму вектора 𝑟=√𝑥+𝑦,𝜃=⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩𝑦𝑥𝑥>0,𝑦>0;𝑦𝑥+(3602𝜋)𝑥>0,𝁇80;𝑦 )𝑥0;90𝜋2𝑥=0,𝑦>0;2703𝜋2𝑥=0,𝑦0;∘∘∘∘танфортанорфортанорфорфорорфор для 0≤𝜃2𝜋 в радианах или 0≤𝜃360∘∘ в градусах.

Эту информацию можно эффективно передать с помощью следующей схемы.
В качестве примера рассмотрим векторы ⃑𝑣=(4,3),⃑𝑣=(−4,3), ⃑𝑣=(−4,−3) и ⃑𝑣=(4,−3) в прямоугольной форме, где каждый вектор расположен в другом квадранте, как показано на графике. Мы хотим определить полярные формы этих векторов стандартизированным способом, с точностью до двух знаков после запятой и в градусах с 0≤𝜃360∘∘.
Радиальная составляющая 𝑟 для этих векторов в полярной форме будет одинаковой, так как 𝑟=√4+3=√(−4)+3=√(−4)+(−3)=√4+(−3)=5.
Разница будет с угловой составляющей 𝜃, так как это будет определять направление и, следовательно, в каком квадранте будет лежать вектор в полярной форме.
из общей формулы как 𝜃=34=34=36,86989765….tantan∘
Как и ожидалось, этот угол острый, так как 0≤𝜃90∘∘, что помещает вектор в первый квадрант.
Вектор ⃑𝑣=−4⃑𝑖+3⃑𝑗 находится во втором квадранте, а угловая составляющая равна
𝜃=3−4+180=−34+180=−36,86989765…+180=143,1301024…. tantan∘∘∘∘∘
tantan∘∘∘∘∘
Как и ожидалось, у нас есть 90𝜃180, что помещает вектор во втором квадранте.
Вектор ⃑𝑣=−4⃑𝑖−3⃑𝑗 находится в третьем квадранте, а угловая составляющая равна 𝜃=−3−4+180=34+180=36,86989765…+180=216,8698976….tantan∘∘∘∘∘
Как и ожидалось, мы имеем 180𝜃270, где вектор в третьем квадранте.
Наконец, вектор ⃑𝑣=4⃑𝑖−3⃑𝑗 находится в четвертом квадранте, а угловая составляющая 𝜃=−34+360=−34+360=−36,86989765…+360=323,1301024….tantan∘∘∘∘∘
Как и ожидалось, мы имеем 270𝜃360, что помещает вектор в четвертом квадранте.
Таким образом, представление полярной формы векторов с точностью до двух знаков после запятой дается выражением ⃑𝑣=(5,36,87),⃑𝑣=(5,143,13),⃑𝑣=(5,216,87),⃑𝑣=(5,323,13).∘∘∘∘
Наконец, давайте рассмотрим пример, где мы преобразуем вектор в третьем квадрант от прямоугольной формы к полярной форме, в радианах.
Пример 10. Преобразование вектора из прямоугольной формы в полярную
Заполните пропуск: Если ⃑𝐴=-⃑𝑖-⃑𝑗, то
⃑𝐴 есть .

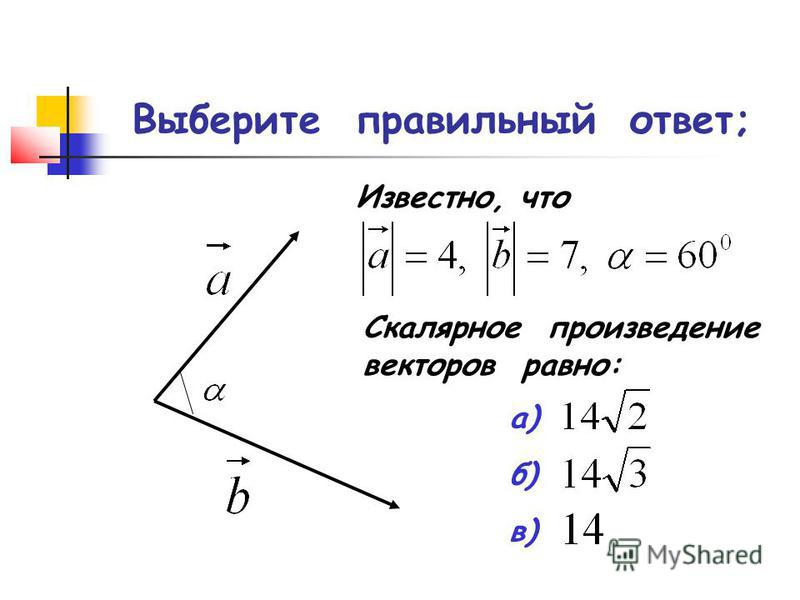

 , вектор скорости при поступательном движении тела).
, вектор скорости при поступательном движении тела). Два вектора, и , имеющие общую точку приложения, складываются по правилу параллелограмма. Разность векторов: .
Два вектора, и , имеющие общую точку приложения, складываются по правилу параллелограмма. Разность векторов: . 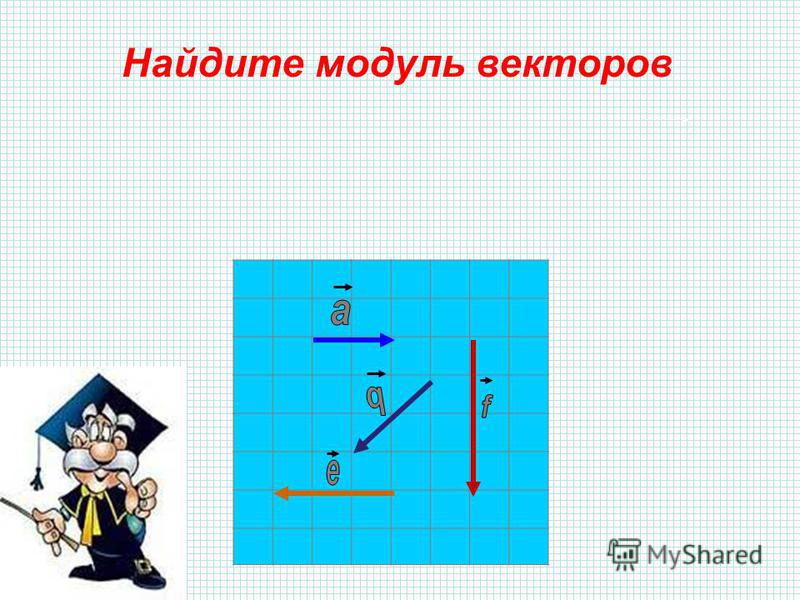
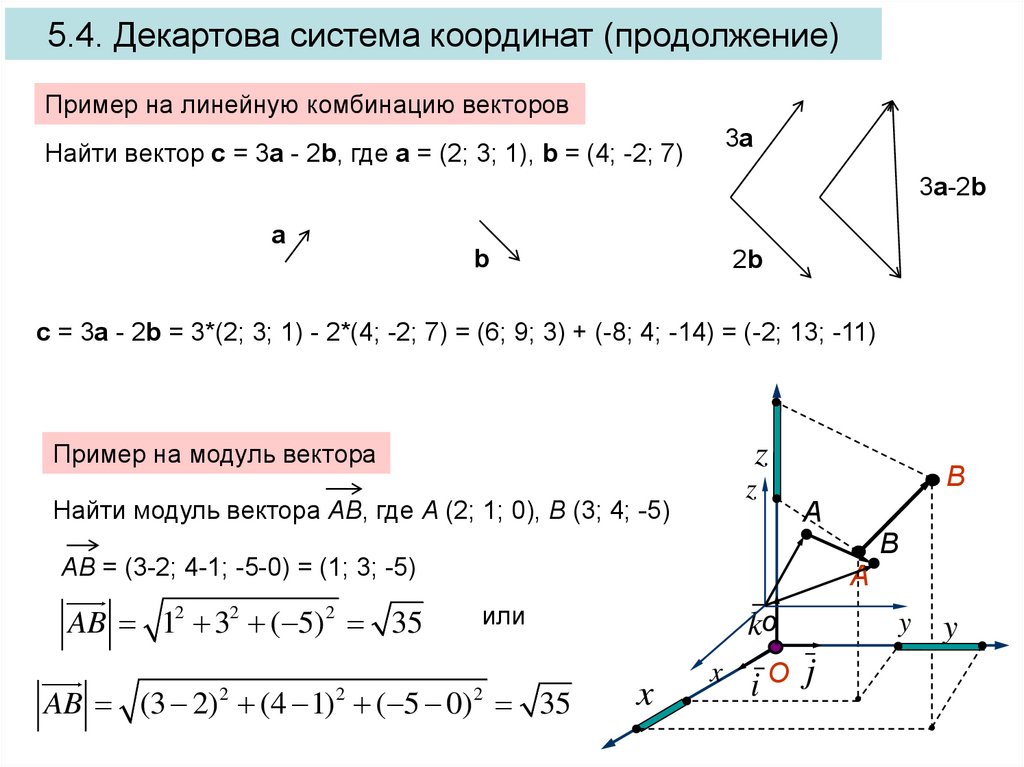
 3.2).
3.2). Ввести имя
переменной и знак просмотра, нажав
кнопку «=», detD=-3.
Ввести имя
переменной и знак просмотра, нажав
кнопку «=», detD=-3. Рис.
3.4).
Рис.
3.4).