Белоусов А.И., Ткачев С.Б. Дискретная математика
- формат djvu
- размер 5.39 МБ
- добавлен 05 апреля 2007 г.
М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. 744 стр. (Сер. Математика
в техническом университете; Вып. XIX).
В девятнадцатом выпуске серии «Математика в техническом
университете» изложены теория множеств и отношений, элементы
современной абстрактной алгебры, теория графов, классические
понятия теории булевых функций, а также основы теории формальных
языков, куда включены теории конечных автоматов, регулярных языков,
контекстно-свободных языков и магазинных автоматов. В анализе
графов и автоматов особое внимание уделено алгебраическим
методам.
Содержание учебника соответствует курсу лекций, который авторы
читают в МГТУ им.
Для студентов технических университетов. Может быть полезен преподавателям, аспирантам и инженерам.
Множества и отношения
Множества
Кортеж. Декартово произведение
Соответствия и бинарные отношения
Операции над соответствиями
Семейства множеств
Специальные свойства бинарных отношений
Отношения эквивалентности
Упорядоченные множества. Теорема о неподвижной точке
Мощность множества
Об одном парадоксе теории множеств
Метод характеристических функций
Вопросы и задачи
Алгебры: группы и кольца
Операции. Понятие алгебраической структуры
Группоиды, полугруппы, группы
Кольца, тела, поля
Области целостности
Модули и линейные пространства
Подгруппы и подкольца
Теорема Лагранжа
Гомоморфизмы групп и нормальные делители
Гомоморфизмы колец
Кватернионы
Вопросы и задачи
Полукольца и булевы алгебры
Полукольца. Основные примеры
Замкнутые полукольца
Решение систем линейных уравнений
Решетки
Вопросы и задачи
Алгебраические системы
Модели и алгебры
Подсистемы
Конгруэнции и фактор-системы
Гомоморфизмы
Прямые произведения алгебраических систем
Конечные булевы алгебры
Многосортные алгебры
Вопросы и задачи
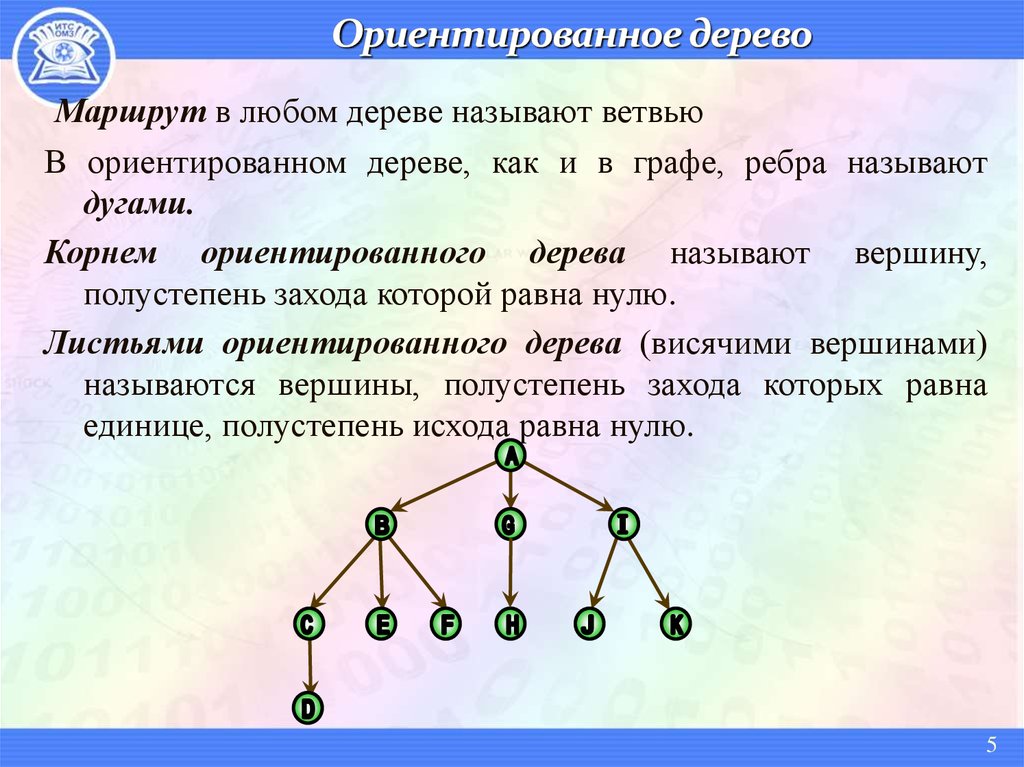
Теория графов
Основные определения
Способы представления
Деревья
Остовное дерево наименьшего веса
Методы систематического обхода вершин графа
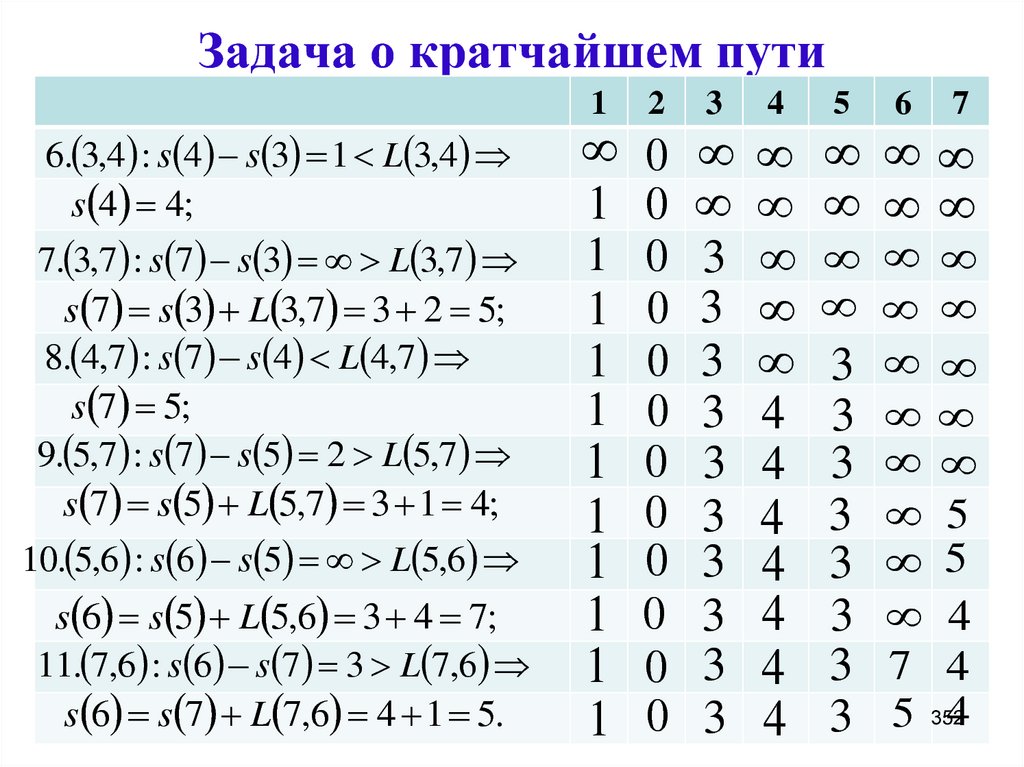
Задача о путях во взвешенных ориентированных графах
Изоморфизм графов
Топологическая сортировка
Элементы цикломатики
Вопросы и задачи
Булевы функции
Понятие булевой функции.
Булев куб
Таблицы булевых функций
Фиктивные переменные. Равенство булевых функций
Формулы и суперпозиции
Дизъюнктивные и конъюнктивные нормальные формы
Построение минимальных ДНФ
Теорема Поста
Схемы из функциональных элементов
Конечные автоматы и регулярные языки
Алфавит, слово, язык
Порождающие грамматики
Классификация грамматик и языков
Регулярные языки и регулярные выражения
Конечные автоматы. Теорема Клини
Детерминизация конечных автоматов
Минимизация конечных автоматов
Лемма о разрастании для регулярных языков
Обоснование алгоритма детерминизации конечных автоматов
Конечные автоматы с выходом. Структурный синтез
Морфизмы и конечные подстановки
Машины Тьюринга
Вопросы и задачи
Контекстно-свободные языки
КС-грамматики. Деревья вывода. Однозначность
Приведенная форма КС-грамматики
Лемма о разрастании для КС-языков
Магазинные автоматы
Алгебраические свойства КС-языков
О методах синтаксического анализа КС-языков
Семантика формальных языков
Графовое представление МП-автоматов
Вопросы и задачи
На сайте также имеются следующие книги из этой серии:
http://www.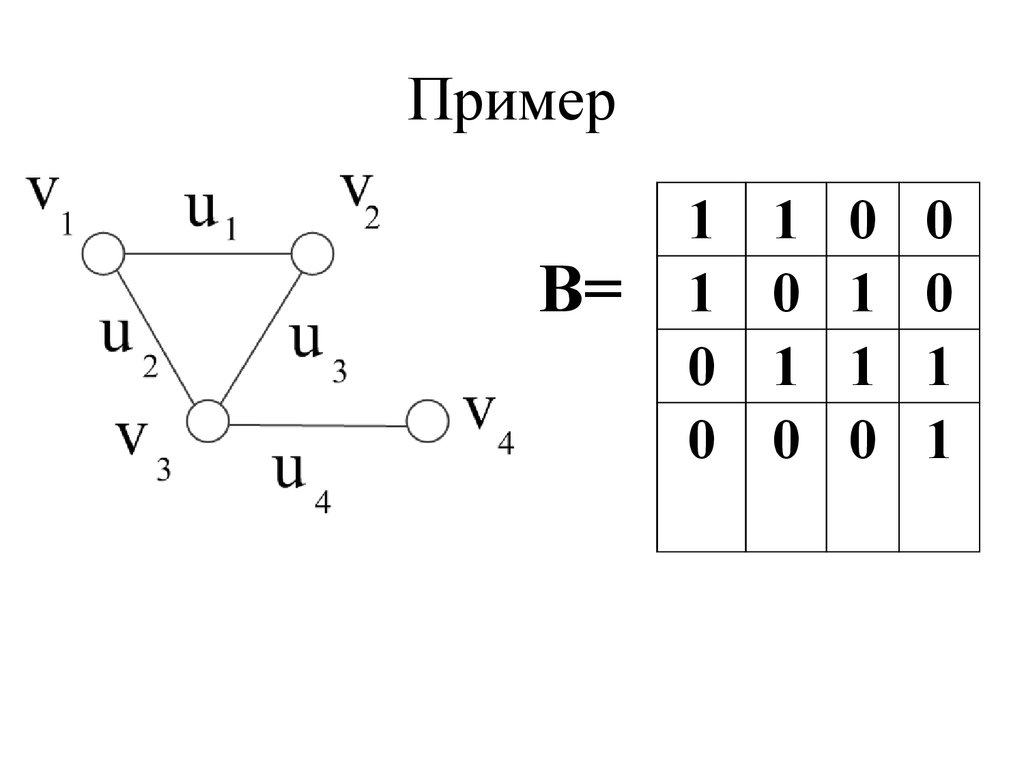
http://www.twirpx.com/file/112170/ — Выпуск II. Дифференциальное исчисление функций одного переменного
http://www.twirpx.com/file/16492/ — Выпуск III. Аналитическая геометрия
http://www.twirpx.com/file/85529/ — Выпуск IV. Линейная алгебра
http://www.twirpx.com/file/112171/ — Выпуск V. Дифференциальное исчисление функций многих переменных
http://www.twirpx.com/file/112174/ — Выпуск VI. Интегральное исчисление функций одного переменного
http://www.twirpx.com/file/112175/ — Выпуск VII. Кратные и криволинейные интегралы. Элементы теории поля
http://www.twirpx.com/file/32977/ — Выпуск VIII. Дифференциальные уравнения
http://www.twirpx.com/file/118507/ — Выпуск IX. Ряды
http://www.twirpx.com/file/118500/ — Выпуск X. Теория функций комплексного переменного
http://www.twirpx.com/file/28647/ — Выпуск XI. Интегральные преобразования и операционное исчисление
Дифференциальные уравнения математической физикиhttp://www.twirpx.com/file/111179/ — Выпуск XIII. Приближенные методы математической физики
http://www.twirpx.com/file/110869/ — Выпуск XIV. Методы оптимизации
http://www.twirpx.com/file/24117/ — Выпуск XV. Вариационное исчисление и оптимальное управление
http://www.twirpx.com/file/32544/ — Выпуск XVI. Теория вероятностей
http://www.twirpx.com/file/112177/ — Выпуск XVII. Математическая статистика
http://www.twirpx.com/file/64741/ — Выпуск XVIII. Случайные процессы
http://www.twirpx.com/file/1821/ — Выпуск XIX. Дискретная математика
http://www.twirpx.com/file/53173/ — Выпуск XX. Исследование операций
http://www.twirpx.com/file/101503/- Выпуск XXI. Математическое моделирование в технике
Купить и скачать книгу «Дискретная математика»
Похожие разделы
- Академическая и специальная литература
- Математика
- Математическая логика
- Академическая и специальная литература
- Математика
- Математическая логика
- Теория множеств
Смотрите также
- формат pdf
- размер 453.
45 КБ - добавлен 09 апреля 2011 г.
45 КБИзд-во МГТУ им. Баумана, 1998г. — 36с. Теория множеств. Операции над множествами. Бинарные отношения и функции. Специальные бинарные отношения. Мощность множества. Элементы общей алгебры. Полугруппы и группы. Кольца и поля. Теория графов. Неориентированные графы. Ориентированные графы. Способы представления. Деревья. Алгоритм Краскала. Сети. Алгоритм Демукрона. Поиск в глубину и поиск в ширину. Задача о путях во взвешенных орграфах….
Практикум
- формат doc
- размер 289.73 КБ
- добавлен 01 мая 2011 г.
Методические указания предназначены для студентов второго курса заочной формы обучения по направлению «Телекоммуникации», изучающих курс «Дискретная математика».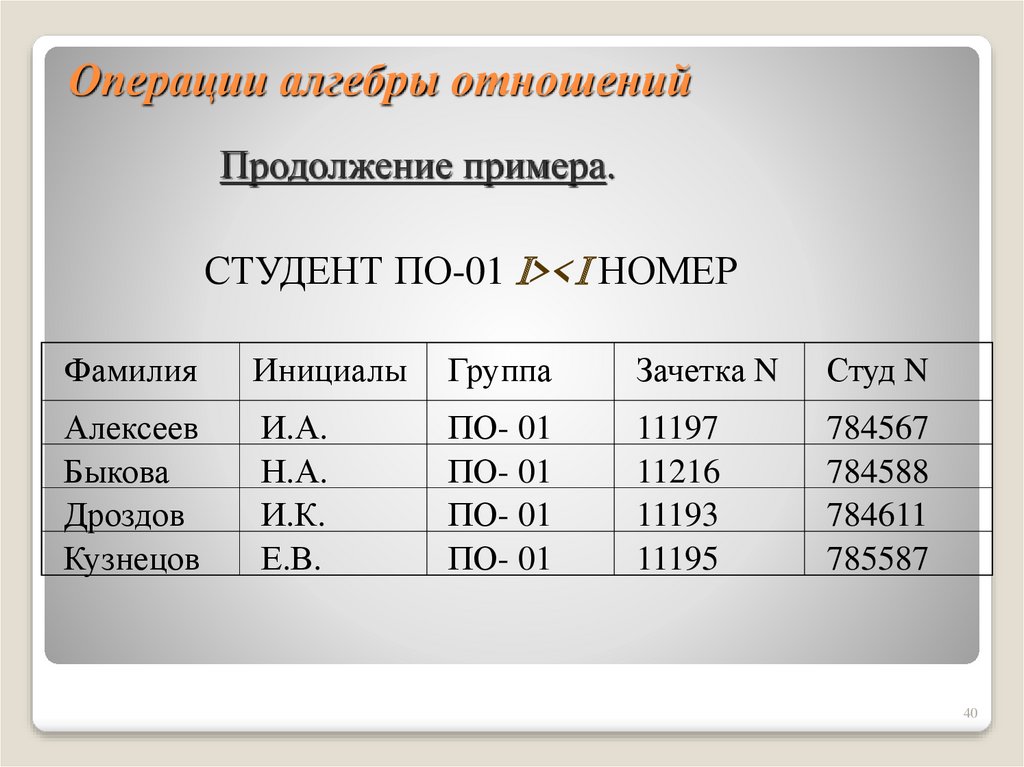
- формат djvu
- размер 3.25 МБ
- добавлен 03 декабря 2010 г.
Учебное пособие. — Симферополь: Издат. «СОНАТ», 2000г. — 360с. Для студентов университетов. Соответствует программе курса «Дискретная математика» и «Прикладная математика».
- формат doc
- размер 117 КБ
- добавлен 16 января 2012 г.
Карпова И.В., Монина М. Занимательная дискретная математика. Миф-2, №4, Занимательная дискретная математика. принцип Дирихле. Логические задачи. Графы. Комбинаторика. Контрольные задания.
- формат doc
- размер 558.04 КБ
- добавлен
12 декабря 2009 г.
Математика. Дискретная математика: методические указания для самостоятельной работы студентов очной формы обучения (I семестр). — Брянск: БГТУ, 2008. – 35 с. БГТУ, 1 семестр Предисловие Разбор типичных задач Элементы теории множеств Множества. Операции над множествами Отображения. Инъективные и сюръективные отображения Отношение эквивалентности Элементы теории кодирования Элементы теории графов Поиск путей в графе Представление графов в памяти…
Статья
- формат doc
- размер 740.69 КБ
- добавлен 07 мая 2009 г.
Дискретная математика – самостоятельное направление современной математики. Она изучает математические модели объектов, процессов, зависимостей, существующих в реальном мире, с которыми имеют дело в технике, информатике и других областях знаний.
В данном учебном пособии содержание разделов дискретной математики определяются требованиями государственного образовательного стандарта профессионального образования, предъявляемыми к дисциплине «Дискрет…
- формат doc
- размер 229.74 КБ
- добавлен 04 марта 2009 г.
Лекции по курсу “Дискретная математика”. Введение в теорию множеств. Элементы комбинаторики. Математическая логика. Теория кодирования. Зачем нужна криптография. Теория графов.rn
- формат doc
- размер 742.91 КБ
- добавлен 27 февраля 2010 г.
В данном учебном пособии содержание разделов дискретной математики определяются требованиями государственного образовательного стандарта профессионального образования, предъявляемыми к дисциплине «Дискретная математика» специальности «Прикладная информатика в экономике» и родственных специальностей.
К этим разделам относятся: элементы теории множеств, математической логики, теории графов.
- формат tif, jpg
- размер 66.18 МБ
- добавлен 29 марта 2007 г.
Дискретная математика. Сканированные листы [26-61].rn
- формат pdf
- размер 982.38 КБ
- добавлен 29 января 2009 г.
Челябинск, ЮУрГУ, 1998 г. Задачник соответствует курсу дискретной математики для студентов специальности «Прикладная математика» (на сайте выложен соответствующий учебник Эвнина «Дискретная математика»)
Решение задач по математике
Дискретная математика
| Год издания: 2004 | Количество страниц: 744 |
Размер файла: 5. 4 Мб
|
Формат книги: djvu |
Белоусов А.И., Ткачев СБ. Дискретная математика: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. -3-е изд., стереотип. — М.: Изд-во МГТУ им. Н.Э. Баумана, (Сер. Математика в техническом университете; Вып. XIX). (Вып. XIX)
В девятнадцатом выпуске серии „Математика в техническом университете» изложены теория множеств и отношений, элементы современной абстрактной алгебры, теория графов, классические понятия теории булевых функций, а также основы теории формальных языков, куда включены теории конечных автоматов, регулярных языков, контекстно-свободных языков и магазинных автоматов. В анализе графов и автоматов особое внимание уделено алгебраическим методам.
Содержание учебника соответствует курсу лекций, который авторы читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен преподавателям, аспирантам и инженерам.
Ил. 200. Табл. 27. Библиогр. 65 назв.
Дискретная математика для программистов
| Год издания: 2003 | Количество страниц: 320 | Размер файла: 4.6 Мб | Формат книги: pdf |
Р. Хаггартн Москва: Техносфера.
Элементарное введение в дискретную математику, без знания которой невозможно успешно заниматься
информатикой и программированием. Ни одно из немногочисленных изданий по этой дисциплине, вышедших
на русском языке, не читается с таким удовольствием и пользой. В доступной и весьма увлекательной
форме автор рассказывает о фундаментальных понятиях дискретной математики — о логике, множествах,
графах, отношениях и булевых функциях. Теория изложена кратко и иллюстрируется многочисленными
простыми примерами, что делает её доступной даже школьнику.
После каждой главы (начиная со второй)
рассматривается приложение описанных методов к информатике.
Книга будет полезна студентам, изучающим курс дискретной математики, а также всем желающим проникнуть в технику написания и проверки корректности алгоритмов, включая программистов-практиков.
Дискретная математика: графы, матроиды, алгоритмы
| Год издания: 2001 | Количество страниц: 288 | Размер файла: 3.1 Мб | Формат книги: djvu |
Асанов М. О., Баранский В. А., Расин В. В. — Ижевск: ННЦ «Регулярная и хаотическая динамика»
Изложен ряд основных разделов теории графов и матроидов. Рассмотрены алгоритмы дискретной оптимизации на сетях и графах, наиболее часто используемые программистами.
Для студентов и аспирантов, специализирующихся в области компьютерных наук, для практикующих программистов, для всех желающих
изучить основы современной дискретной компьютерной математики.
Дискретная математика: алгоритмы и программы
| Год издания: 2003 | Количество страниц: 282 | Размер файла: 14.5 Мб | Формат книги: pdf |
Иванов Б. Н. Учебное пособие — М.: Лаборатория Базовых Знаний, 2003.
Книга посвящена современному курсу дискретной математики. Теоретические основы курса сопровождаются практически значимыми алгоритмами, реализованными в конкретных компьютерных программах. Книгу можно рассматривать в качестве хорошего справочника методов и алгоритмов дискретной математики, широко применяемых в практическом программировании.
Пособие рассчитано на студентов специальностей, учебные планы которых
предполагают изучение каких-либо разделов курса дискретной математики, в
первую очередь на математиков-прикладников, а также программистов, занятых
разработкой прикладного программного обеспечения.
Обучающий курс по дискретной математике.
| Год издания: 2008 | Количество страниц: 44 | Размер файла: 1.4 Мб | Формат книги: Файл справки |
Разработан на основе учебного пособия Коротеева Г.И. «Дискретная математика. элементы теориимножеств, отношений, графов и булевых функций»
Учебный курс содержит следующие разделы:
ВВЕДЕНИЕ
1. МНОЖЕСТВА, ОТНОШЕНИЯ И ФУНКЦИИ
2. ГРАФЫ
3. ОРИЕНТИРОВАННЫЕ ГРАФЫ И СЕТИ
4. БУЛЕВЫ ФУНКЦИИ
КОНТРОЛЬНАЯ РАБОТА
ТИПОВОЙ РАСЧЕТ
ТРЕНИНГИ
Тренинги данного электронного обучающего курса представляют собой разбор контрольной работы и типового расчета по курсу «Дискретная математика»
Обучающий курс содержит следующие тренинги:
1.
Элементарные операции с множествами
2. Доказательство тождества
3. Нахождение отношения эквивалентности
4. Нахождение отношения частичного порядка
5. Операции с графом
6. Паросочетание в графе
7. Пути в орграфе
8. Максимальный поток в транспортной сети
9. Представление булевой функции в различных видах
Дискретная математика для программистов.
| Год издания: 2000 | Количество страниц: 304 | Размер файла: 1.4 Мб | Формат книги: Файл справки |
Автор: Ф. А. Новиков
В учебнике изложены основные разделы дискретной математики и описаны важнейшие алгоритмы на дискретных структурах данных. Основу книги составляет материал лекционного курса, который автор читает в Санкт-Петербургском государственном техническом университете последние полтора десятилетия.
Учебник содержит:
1. Систематическое изложение основных разделов дискретной математики.
2. Описание важнейших алгоритмов над объектами дискретной математики.
3. Основные способы представления объектов дискретной математики с помощью стандартных структур данных.
Для студентов вузов, практикующих программистов и всех желающих изучить дискретную математику.
Математика | Бесплатный полнотекстовый | Динамика стохастической модели химической реакции Белоусова-Жаботинского
1. Введение
Теоретический анализ повторяющихся колебательных процессов в открытых системах был начат Лоткалем [1,2]. Бак [3] и Хиггинс [4] рассматривали как закрытые, так и открытые системы и обобщали теорию таких реакций, а Спэнглер и Снелл [5] рассматривали модельную систему. Интерес к колебательным реакциям был вызван большим количеством таких процессов, наблюдаемых в биологических системах, и эти идеи были развиты Пригожиным с сотрудниками [6,7].
Колебательные реакции обычно включают две автокаталитические реакции, которые включают и выключают друг друга и в чем-то аналогичны известной схеме триггера в электронике. Филд и др. [8] показали, что можно разработать механизм колебаний, включающий только один автокаталитический процесс.
Катализируемое йодом разложение перекиси водорода [9] было первой реакцией, которая, как считается, колебалась гомогенно. Белоусов наблюдал второй пример осциллирующих химических реакций в гомогенных растворах — окисление четырехвалентно-трехвалентного иона церия, связанного каталитической лимонной кислотой, броматом калия. Реакция Белоусова-Жаботинского была открыта в 1950-х годах бывшими советскими биофизиками Белоусовым и Жаботинским [10]. Поэтому мы назвали реакцию реакцией Белоусова-Жаботинского, именуемой реакцией Б-З. В 1969 Пригожин предложил теорию диссипативной структуры, ясно объясняющую причину возникновения колебательной реакции. Это делает реакцию B-Z снова в центре внимания исследования.
Теория диссипативной структуры утверждает, что когда система находится далеко от равновесного состояния, то есть находится в состоянии нелинейном и неравновесном, неупорядоченное однородное состояние не обязательно является устойчивым.
Существует много объяснений механизма реакции B-Z [11,12]. В одном варианте суммарная реакция состоит из двух процессов: A и B. Суммарная реакция процесса A равна:
Суммарная реакция процесса B:
Процесс A представляет собой ионную реакцию двойного переноса электрона, процесс B включает свободные радикалы и перенос одиночного электрона. При концентрации бромид-иона выше критической концентрации в основном возникает процесс А, а при концентрации бромид-иона ниже критической концентрации в основном возникает процесс Б. Бромид-ион является здесь контрольным веществом. При этом ион бромата B не только окисляет ионы металла, но и образует бром. Такие колебания могут поддерживаться тысячи раз в замкнутой системе, и в процессе реакции не нужно добавлять реагенты.
Таким образом, этот вид реакции очень удобен для изучения химической волны. Реакционные растворы окрашиваются в два цвета. Если решение неглубокое, оно будет похоже на явление интерференции волн, когда два цвета волны распространяются попеременно. Волна того же цвета исчезла, когда произошел контакт, который отличается от электромагнитной волны.
В 1990 г. Л.Дьердь, Т.Тураньи, Р.Дж. Филд [8] разработал скелетный механизм реакции. Реакции, составляющие механизм колебательной реакции B-Z, можно разделить на неорганическую и органическую подгруппы. Он содержит восемьдесят элементарных реакций и настолько сложен, что люди выдвинули упрощенный механизм из шести стадий, который выражается как:
BrO3-+Br-+2H+→HBrO2+HOBr(k1);
HBrO2+Br−+H+→2HOBr(k2);
BrO3-+HBrO2+H+→2BrO2+h3O(k3);
BrO2+Ce3++H+→HBrO2+Ce4+(k4);
2HBrO2→BrO3-+HOBr+H+(k5);
4Ce4++BrCH(COOH)2+h3O+HOBr→2Br−+4Ce3++3CO2+6H+(k6).
Субстраты реакции включали бромат, сульфат аммония церия (или сульфат церия), малоновую кислоту и разбавленную серную кислоту, причем бромат является субстратом, который нельзя изменить. Ионы металлов обычно представляют собой Ce или Mn, но также могут быть комплексными ионами, образованными Fe, Ru, Co, Cu, Cr, Ag, Ni, Os. Малоновая кислота может быть вместо другого восстановителя. Образование других галогенсодержащих оксисолей и анионов, таких как ионы хлорида, может мешать реакции. В реакцию Б-З обычно в качестве индикатора включается соседний ферроин, это комплексы фенантролина и иона двухвалентного железа, который в восстановленном состоянии имеет красный цвет, а в окисленном — синий. Ион церия имеет желтый цвет в степени окисления, а трехвалентный ион церия бесцветен в восстановленном состоянии. Таким образом, эффект синтеза: степень окисления зеленая, степень восстановления красная.
Теперь мы представим построение математической модели химической реакции B-Z и рассмотрим изменение концентрации некоторых основных реагентов.
Во-первых, объясним, почему мы не рассмотрели кислотность или концентрацию воды в этой статье? Это потому, что их вариации в среде незначительны из-за использования тампона. Тогда отметим X = [HBrO 2 ]; Y = [Br — ]; Z = 2[Се 4+ ]; А = [BrO3-]; P = [HOBr], Q – концентрация образования отходов. Мы описываем вышеупомянутые реакции в следующие пять шагов: (i) Описываем преобразование из Y в X; (ii) одновременная инактивация X и Y; (iii) и (iv) автокаталитический продукт X; (v) бимолекулярное разложение X; (vi) Всеобъемлющая реакция заменяет Z на Y. Мы выражаем эти шаги как:
где f – стехиометрический коэффициент общей стадии реакции, а ki(i=1,⋯,6) – константа скорости реакции, которая содержит эффект концентрации H+.
Из основного принципа моделирования получаем математическую модель реакции, которую часто называют моделью реакции B-Z:
Обратите внимание, как в [13] с безразмерным преобразованием
система (1) преобразуется в:
Тайсон и др.
В [14,15] изучалась динамика модели (3) и система (3) имеет два равновесия O(0,0,0) и P(x*,y*,z*), причем O неустойчива. Здесь,
Глобальную асимптотическую устойчивость состояния равновесия можно увидеть и в [13,16]. Теорема 1.10 из [13] показывает, что положительное состояние равновесия модели (2) глобально асимптотически устойчиво при f∈(0,f1)⋃(f2,∞). В [17] Танг доказал, что для системы (3) B является положительным инвариантным множеством, и все положительное начальное решение в конечном счете войдет в B, здесь
и y1=fq1+q,y2=f2q.
Обратите внимание, что модель (1) является детерминированной и не учитывает влияние окружающего шума, который всегда присутствует. На самом деле на модели химических реакций влияет белый шум окружающей среды, потому что температура и давление меняются во время процессов химической реакции и тесно связаны с процессом. Две стохастические модели химических реакций обсуждались в [18,19,20], где модель химической реакции рассматривалась при стохастическом возмущении методом Ляпунова.
В данной работе мы вводим стохастические возмущения в систему (1) и рассматриваем стохастическую систему:
где W1(t),W2(t),W3(t) — независимые броуновские движения, а δ12>0,δ22>0,δ32>0 — интенсивности белого шума. Рассмотрим безразмерное преобразование этой стохастической модели и соотношение коэффициента, как в (2), за исключением того, что
Тогда система (4) становится:
где B1(τ),B2(τ),B3(τ) — независимые броуновские движения, а σ12>0,σ22>0,σ32>0 — интенсивности белого шума.
Целью данной работы является исследование динамического поведения системы (5). В разделе 2 мы показываем, что решение системы является положительным и глобальным. В разделе 3 мы доказываем, что система (5) обладает эргодичностью и стационарным распределением, а в последнем разделе представлены некоторые модели для иллюстрации наших теоретических результатов.
2. Существование и единственность положительного решения
Необходимо, чтобы решения стохастической модели были положительными в модели химической реакции, поэтому мы доказываем существование и единственность положительного решения для модели (5).
Если не указано иное, пусть (Ω,F,{Ft}t≥0,P) — полное вероятностное пространство с фильтрацией {Ft}t≥0, удовлетворяющей обычным условиям (т. е. непрерывной справа и F0 содержит все P-нулевые множества) на протяжении всей этой статьи. Обозначать
В общем случае мы рассматриваем следующее d-мерное стохастическое дифференциальное уравнение с начальным значением x(t0)=x0∈Rd
а B(t) обозначает стандартные d-мерные броуновские движения, определенные в приведенном выше вероятностном пространстве. Дифференциальный оператор L, связанный с верхним уравнением, определяется формулой
Если дифференциальный оператор L действует на функцию V∈C2,1(Sh×R¯+;R¯+), то имеем
где Vt=∂V∂t,Vx=(∂V∂x1,…,∂V∂xd) и Vxx=(∂2V∂xixj)d×d.
можно получить
Доказательство
Чтобы проиллюстрировать, что положительное локальное решение (x(τ),y(τ),z(τ)),τ∈[0,τe) стохастической системы B-Z (5) является глобальным, мы просто нужно доказать, что τe=∞п.н. Пусть m0≥0 — достаточно большое число, такое, что оба x0,y0,z0 лежат в интервале [1m0,m0]. Установите m≥m0 и определите время остановки
мы полагаем infϕ=∞ (как обычно, ϕ обозначает пустое множество) на протяжении всей статьи. Ясно, что τm возрастает при m→∞. Положим τ∞=limm→∞τm, где τ∞≤τea.s. Если мы докажем, что τ∞=∞п.н., то, очевидно, τe=∞, т. е. (x(0),y(0),z(0))∈R+3п.н. для всех t≥0. Позвольте мне сказать иначе, стремитесь завершить доказательство, нам просто нужно доказать, что τe=∞a.s. Если нет, то существуют T>0 и ε∈(0,1) такие, что 9формулы, мы можем вывести, что
Выбрав значение k1,k2 как в (7), тогда
где K — положительная константа.
Кроме того, у нас есть
Получение ожидаемых результатов
Для m≥m1 положим Ωm={Tm≤T}, и по формуле (6) мы знаем, что P(Ωm)≥ε. Заметим, что существует хотя бы одно из значений x(τm,ω),y(τm,ω),z(τm,ω), равных m или 1m для каждого ω∈Ωm. Следовательно,
Тогда по формулам (6) и (8) имеем
где IΩm(ω) — индикаторная функция Ωm. Если мы позволим m→∞, это приведет к противоречию ∞>V(x(0),y(0),z(0)+KT=∞. Таким образом, мы должны иметь τ∞=∞a.s. □
3. Эргодичность
Прежде чем мы начнем доказывать эргодичность модели стохастической реакции B-Z, приведем результат, который можно найти в [21] (мы также отсылаем читателя к [22]).
Пусть X(t) — однородный марковский процесс, описанный стохастическим уравнением в El (El обозначает евклидово l-пространство)
и его диффузионная матрица
Дифференциальный оператор L, связанный с уравнением (9), определяется формулой
Замечание 1.
Доказательство леммы 1 приведено в [21]. В теореме 4.1, с.119 и лемме 9.4, с.138 дается существование стационарного распределения с плотностью. Эргодичность и слабая сходимость получены в теореме 5.1, с.121 и теореме 7.1, с.130. Для проверки (i) достаточно доказать, что F равномерно эллиптична в любой ограниченной области D, где Fu=b(x)ux+12tr(Λ(x)uxx), т. е. существует положительное число M, такое что ∑i,j=1kλij(x)ξiξj≥M|ξ|2,x∈D¯,ξ∈Rk (см. [23, гл. 3, с. 103] и принцип Рэлея в [24, гл. 6, с. 349). Для проверки (ii) достаточно показать, что существуют некоторая окрестность U и неотрицательная C2-функция, поэтому для любого El\U LV отрицательна (подробнее см. [25], с. 1163) .
Доказательство
Чтобы доказать эту теорему, все, что нам нужно сделать, это проверить, что (i) и (ii) выполняются согласно лемме 1. Во-первых, стохастическая система (5) может быть записана как:
Здесь матрица диффузии
Теперь существует M=min{σ12×2,σ22y2,σ32z2,(x,y,z)∈U¯}>0 такое, что
что означает, что условие (i) выполнено.
Теперь нам нужно проверить условие (ii). Сначала построим неотрицательную C2-функцию V и замкнутое множество U∈∑ (полностью лежащее в R+3) так, чтобы
что гарантирует выполнение условия (ii). Учтем C2-функцию h(x,y,z):
Здесь l1,l2,l3 — положительные числа с 0 Очевидно, что если σ12<2s, достаточно выбрать l2,l3 достаточно малыми, чтобы выполнялось условие (10). Несложно проверить, что h(x,y,z) имеет единственную точку минимума (l1,2s2l2,3sfωl3), и где Dk=(1/k,k)×(1/k,k)×(1/k,k). Далее мы определяем неотрицательную C2-функцию, принимая следующую форму: Непосредственным вычислением получаем, что Пусть C=l1(σ122−s)+l2(1s+σ222)+l3(ω+σ322), и из (11) имеем C<0. Тогда мы можем получить Определить закрытый набор где и ε — достаточно малое число такое, что Пусть Тогда R+3\U=D1∞⋃D2∞⋃D3∞⋃D1⋃D2⋃D3. Случай 1. Если (x,y,z)∈D1∞, где M1=supx∈(0,+∞){−12qsx2+(s+3sf+l1sq+l2s)x}. Тогда мы можем получить LV<−1 на D1∞ из (12) и (13). Случай 2. На D2∞, имеем LV<−1 в силу (12) и (14). Случай 3. Если (x,y,z)∈D3∞, Обратите внимание на (12) и (15), и мы имеем LV<−1 на D3. Корпус 4. На D1, из (12) и (16). Корпус 5. На D2, поскольку выполняются (12) и (17), что дает LV<−1 в этой области. Случай 6. На D3 тем же методом, что и в случае 5, имеем следующее неравенство: что дает LV<−1 в этой области, поскольку выполняются (12) и (18). Таким образом, условие (ii) выполнено. Затем мы завершаем доказательство теоремы 1. □ Теперь мы проверим выводы нашей теории с помощью моделирования в этом разделе. В этом разделе мы предполагаем, что единицей времени является минута, а концентрация реагентов измеряется в единицах моль/л·мин. Мы всегда используем метод дискретизации и выбираем Δt = 0,002. Выберем параметры в системе (5) как соответственно. Очевидно, что в двух указанных выше условиях различается только значение параметра f. Мы устанавливаем начальное значение (x (0), y (0), z (0)) = (0,8, 0,8, 0,5) и моделируем распределение рассеяния и стационарные фигуры распределения модели стохастического дифференциального уравнения (5) с помощью Matlab при условии (19) и (20). Результаты моделирования показаны на рис. 1, рис. 2, рис. 3 и рис. 4 соответственно. Соответствующая детерминированная модель (3), значения параметров в (19) не удовлетворяют условию теоремы 1. В этой статье мы добавили мультипликативные члены шума в уравнение (1) как представление окружающего белого шума, кроме того, мы доказали, что существование положительного решения и стохастической модели является эргодичным. По сути, эргодичность — это своего рода слабая устойчивость, т. е. устойчивость по распределению. Независимо от того, в каком состоянии находится система, химическая реакция всегда продолжается в слабоустойчивом состоянии. Вывод, который мы получаем, очень интересен, что первоначальные ограничения на параметр f в детерминистке исчезли, все условие — белый шум удовлетворяет неравенству σ12<2s. Поэтому мы считаем, что белый шум способствует стабильности стохастической системы реакции Б-З на практике. Письмо — подготовка первоначального проекта: YY; методика: D.J.; написание—рецензирование и редактирование: Д.О. и А.А. Все авторы прочитали и согласились с опубликованной версией рукописи. Работа выполнена при поддержке Молодежного фонда Национального фонда естественных наук Китая (№ 11701044), Национального фонда естественных наук Китая (№ 11871473) и Фонда естественных наук провинции Шаньдун (№ ZR2019MA010, ZR2019MA006) . Авторы заявляют об отсутствии конфликта интересов. Рисунок 1. Распределение разброса для модели стохастической реакции (5) методом компьютерного моделирования при выборе параметров как в (19). Рисунок 1. Распределение разброса для модели стохастической реакции (5) методом компьютерного моделирования при выборе параметров как в (19). Рисунок 2. Распределение разброса для модели стохастической реакции (5) методом компьютерного моделирования при выборе параметров, как в (20). Рисунок 2. Распределение разброса для модели стохастической реакции (5) методом компьютерного моделирования при выборе параметров, как в (20). Рис. 3. Решение стохастической системы и ее гистограмма при выборе параметров как в (19). Рисунок 3. Решение стохастической системы и ее гистограмма при выборе параметров как в (19). Синие линии представляют решение соответствующей невозмущенной системы (3), а красные линии представляют решение стохастической системы (5). Правый рисунок — гистограммы стохастической системы (5). Рисунок 4. Решение стохастической системы и ее гистограмма при выборе параметров как в (20). Синие линии представляют решение соответствующей невозмущенной системы (3), а красные линии представляют решение стохастической системы (5). Правый рисунок — гистограммы стохастической системы (5). Рисунок 4. Решение стохастической системы и ее гистограмма при выборе параметров как в (20). Синие линии представляют решение соответствующей невозмущенной системы (3), а красные линии представляют решение стохастической системы (5). . 2013 май; 112(2):145-62. doi: 10.1016/j.biosystems.2013.03.003.
Epub 2013 13 марта. Паоло Дини 1 , Кристофер Л. Неханив, Аттила Эгри-Надь, Мария Дж. Шилстра Бесплатная статья Паоло Дини и др.
Биосистемы.
2013 май. Бесплатная статья . 2013 май; 112(2):145-62. doi: 10.1016/j.biosystems.2013.03.003.
Epub 2013 13 марта. Паоло Дини 1 , Кристофер Л. Неханив, Аттила Эгри-Надь, Мария Дж. Интерактивные вычисления (IC) направлены на сопоставление свойств интегрируемых низкоразмерных нелинейных динамических систем с дискретной областью конечных автоматов в попытке воспроизвести в программном обеспечении самоорганизующиеся и динамически стабильные свойства субклеточных биохимических систем. Copyright © 2013 Elsevier Ireland Ltd. Все права защищены. Структура симметрии в дискретных моделях биохимических систем: естественные подсистемы и слабая иерархия управления в новой модели вычислений, управляемой взаимодействиями. Неханив С.Л., Родс Дж., Эгри-Надь А., Дини П., Моррис Э.Р., Хорват Г., Карими Ф., Шреклинг Д., Шилстра М.Дж.
Неханив С.Л. и соавт.
Philos Trans A Math Phys Eng Sci. 2015 28 июля; 373 (2046): 20140223. дои: 10.1098/рста.2014.0223.
Philos Trans A Math Phys Eng Sci. 2015.
PMID: 26078349 Алгебраические свойства автоматов, связанных с сетями Петри, и приложения к вычислениям в биологических системах. Егри-Надь А, Неханов кл.
Эгри-Надь А. и др.
Биосистемы. 2008 г., октябрь-ноябрь; 94 (1-2): 135-44. doi: 10.1016/j.biosystems.2008.05.019. Epub 2008 20 июня.
Биосистемы. 2008.
PMID: 18611428 Собственные химические вычисления. Общее применение колебательной химии на примере реакции Белоусова-Жаботинского. Обзор. Дуэньяс-Диес М., Перес-Меркадер Х.
Дуэньяс-Диес М. и соавт.
Фронт хим. 2021 11 мая; 9:611120. doi: 10.3389/fchem.2021.611120. Электронная коллекция 2021.
Фронт хим. 2021.
PMID: 34046394
Бесплатная статья ЧВК.
Обзор. Динамический контроль и обработка информации в реакции Белоусова-Жаботинского с использованием коэволюционного алгоритма.
Для любого (x,y,z)∈R+3\U мы рассматриваем следующие шесть случаев:
4. Моделирование
10 [13], так как значение f=1 не удовлетворяет ни (1), ни (2). Значение f=0,1 в (20) удовлетворяет условиям теоремы 1.10 [13]. В этих двух случаях стохастическая модель (5) всегда имеет эргодичность и стационарное распределение. 5. Выводы
В дальнейшей работе мы постараемся сделать прорыв в этой модели. Авторские вклады
Финансирование
Конфликт интересов
Ссылки
«> Бак, Т. Вклад в теорию химической кинетики: исследование связи между термодинамикой и процессами химической скорости; WA Benjamin Inc.: Нью-Йорк, штат Нью-Йорк, США, 1963; Том 25. [Google Scholar]
Дж. Физ. хим. 1990 , 94, 7162–7170. [Google Scholar] [CrossRef]
«> Тайсон Дж.Дж. реакция Белоусова-Жаботинского; Спрингер: Нью-Йорк, штат Нью-Йорк, США, 19 лет.76. [Google Scholar]
«> Yang Y.; Цзян, Д. Динамика стохастической модели тримолекулярной химической реакции с низкой концентрацией. Дж. Матем. хим. 2014 , 52, 2532–2545. [Google Scholar] [CrossRef]
«> Странг, Г. Линейная алгебра и ее приложения; Thomson Learning Inc.: Boston, MA, USA, 1988. [Google Scholar]
Синие линии представляют решение соответствующей невозмущенной системы (3), а красные линии представляют решение стохастической системы (5). Правый рисунок — гистограммы стохастической системы (5).
Правый рисунок — гистограммы стохастической системы (5).
© 2020 авторами. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (http://creativecommons.org/licenses/by/4.0/). Изучение концепции интерактивных вычислений посредством дискретно-алгебраического анализа реакции Белоусова-Жаботинского
принадлежность
[email protected] Авторы
Шилстра принадлежность
Абстрактный
. Поскольку работа, о которой сообщается в этой статье, все еще находится на ранних стадиях развития теории, она сосредоточена на анализе особенно простого химического осциллятора, реакции Белоусова-Жаботинского (БЖ). После пересмотра обоснования IC, разработанного за последние несколько лет с точки зрения физики, биологии, математики и информатики, в статье представлено элементарное обсуждение декомпозиции Крона-Родса автоматов с конечным числом состояний, включая декомпозицию голономии простого автомата и его интерпретации как абстрактной позиционной системы счисления. Затем метод применяется к анализу алгебраических свойств дискретных автоматов с конечным числом состояний, полученных из упрощенной сетевой модели Петри реакции BZ. Неудивительно, что в простейшем и симметричном случае соответствующий автомат содержит исключительно циклические группы. Во втором, асимметричном случае разложение намного сложнее и включает пять различных простых неабелевых групп, потенциальная значимость которых возникает из-за их способности кодировать функционально полные алгебры. Обсуждается возможная вычислительная значимость этих результатов и делаются возможные выводы. Похожие статьи