Формула Бернулли. Примеры решения задач по теории вероятности.
Калинина Елена Ивановна
МКОУ «Средняя школа №1 имени А.М.Горького» городского округа город Фролово
Учитель математики.
Стать на тему «Формула Бернулли.Примеры решения задач по теории вероятности.
Формула Бернулли.
Примеры решения задач по теории вероятности.
Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.
Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p.
Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.
Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:
A — появление события A с вероятностью p;
«не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.
Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.
Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.
Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:
Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:
где Cnk — число сочетаний, q = 1 − p.
Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.
Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:
герб выпадет три раза;
герб выпадет один раз;
герб выпадет не менее двух раз.
Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.
Таким образом, имеем: n = 6; p = 0,5; q = 0,5.
Определим вероятность того, что герб выпал три раза, т.е. k = 3:
Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:
Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P6(2) + P6(3) + … + P6(6).
Заметим, что эта сумма также равна (1 − P6(0) − P6(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0).
Поскольку P6(1) нам уже известно, осталось найти P6(0):
Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?
Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.
Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.
Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3):
Очевидно, P20(3) > P20(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.
Небольшое замечание по поводу факториалов.
Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/497857-formula-bernulli-primery-reshenija-zadach-po-
Решение задач на формулу Бернулли. Часть 1
Задача №1. У дикорастущей земляники красная окраска ягод доминирует над розовой; этот признак передается по наследству. В некоторой популяции земляники вероятность встретить растение с красными ягодами равна 0,7. Какова вероятность того, что среди отобранных случайным образом 8-ми растений этой популяции красные ягоды будут иметь:
а) б растений;
б) не менее шести растений?
Решение. В каждом испытании может появиться или не появиться событие
, которое состоит в том, что у растения земляники будут красные ягоды. Общее число испытаний n = 8; испытания являются независимыми. Вероятность появления события в каждом из восьми испытаний постоянна и равна р=0,7; вероятность непоявления события в каждом испытании равна q = 1 — р = 0,3.
а) Обозначим событие:
— ровно б растений из восьми отобранных будут иметь красные ягоды. Число испытаний, в которых ожидается появление события , равно .
Искомую вероятность найдем по формуле (1) при значении :
б) Обозначим событие:
— не менее шести растений из восьми отобранных будут иметь красные ягоды.
Рассмотрим события, составляющие событие :
, , — красные ягоды будут иметь, соответственно, б растений, 7 растений, 8 растений из 8 отобранных. , , — несовместные события, причем событие равно событию , рассмотренному в пункте а) задачи.
Событие состоит в том, что красные ягоды будут иметь или б, или 7, или 8 растений. Это означает, что событие представляет собой сумму событий , и : . Вероятность события найдем по теореме сложения вероятностей несовместных событий:
Вероятность . Вероятности и найдем по формуле Бернулли при значениях m, соответственно равных и :
Подставив значения
, и в равенство (*), получим
В рассмотренном случае вероятность
равна вероятности того, что событие появится в 8-ми испытаниях от до раз.
Итак, при небольших значениях и вероятность того, что примет определенное значение из заданного интервала, находят с применением формулы Бернулли и теоремы сложения вероятностей несовместных событий.
Задача №2. Исследование инкубации яиц яичного кросса Беларусь-9 показало, что цыплята выводятся в среднем из 70% заложенных в инкубатор яиц. Из общего количества заложенных в инкубатор яиц случайным образом отобраны и помечены шесть. Найти вероятности того, что из помеченных яиц выведутся:
а) менее трех цыплят;
б) более трех цыплят;
в) не менее трех цыплят;
г) не более трех цыплят.
д) Есть ли среди событий, вероятности которых требуется найти в пунктах: а) — г), такие, которые составляют полную группу? (если есть, то какие?).
Решение. Общее число независимых испытаний n = 6. Событие
, которое может произойти или не произойти в каждом испытании, состоит в том, что из заложенного в инкубатор яйца выведется цыпленок.
Вероятность наступления события в каждом испытании постоянна и равна р = 0,7; вероятность q = 0,3.
Рассмотрим события:
— из б-ти яиц выведутся менее трех цыплят;
— из 6-ти яиц выведутся более трех цыплят;
— из 6-ти яиц выведутся не менее трех цыплят;
— из 6-ти яиц выведутся не более трех цыплят.
По формуле Бернулли найдем:
Вероятности событий
, , и найдем, применив формулу Бернулли и теорему сложения вероятностей несовместных событий:
События
и составляют полную группу несовместных событий, так как событие достоверно.
Вероятность этого события .
События и — взаимно противоположные; можно обозначить: .
Так же можно показать, что полную группу несовместных событий составляют события
и . События и — взаимно противоположные; можно обозначить: .
Узнать все об уравнении Бернулли и его приложениях
Последнее обновление: 12 декабря 2022 г.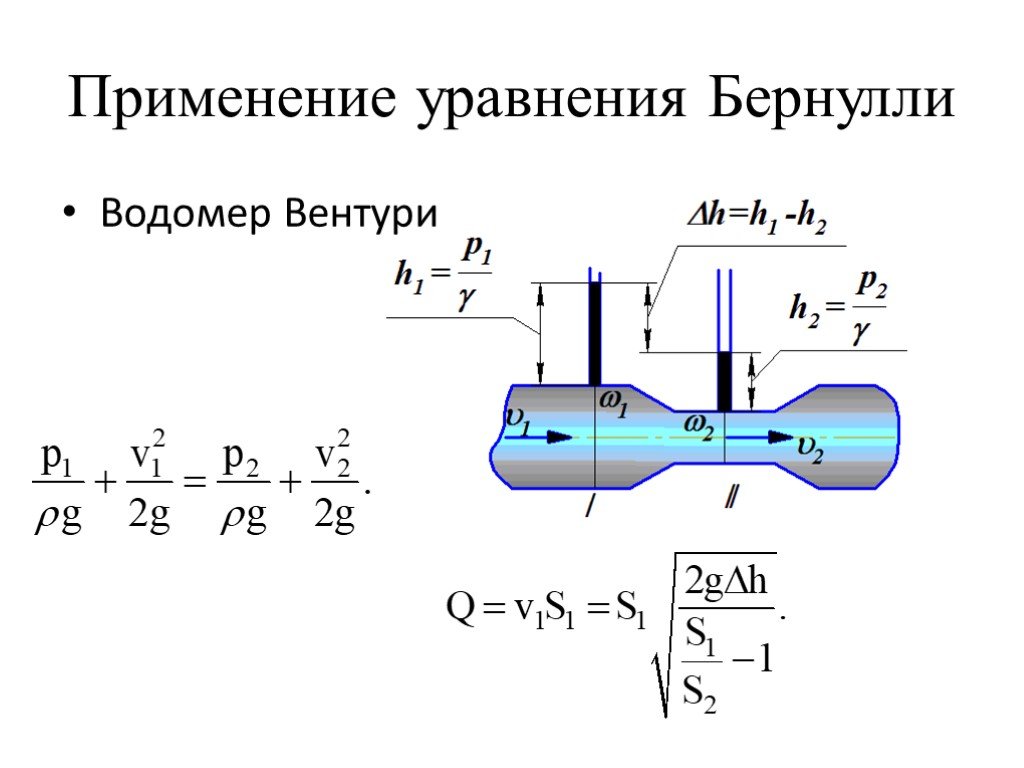
, автор: Нурхан Эссам
Уравнение Бернулли, или уравнение энергии установившегося потока несжимаемой жидкости, считается одним из самых известных уравнений в физике (гидромеханике). и это объясняет сохранение механической работы-энергии. Уравнение было опубликовано в 1738 году Даниэлем Бернулли (швейцарским физиком), чтобы помочь нам понять поток жидкости.
Даниил Бернулли родился 8 февраля 1700 года в Нидерландах. Он изучал математику и медицину под руководством своего отца Иоганна Бернулли.
В этой статье мы обсудим уравнение Бернулли, его принцип, вывод, применение и многое другое.
Начало начало PraxIlabs для бесплатных
Содержание
Уравнение БернуллиP — статическое давление (давление жидкости)
ρ — плотность
vocity velocity.
G ускорение свободного падения
H высота жидкости
Теорема Бернулли описывает связь между скоростью, давлением и высотой жидкости, текущей по линии тока.
В нем указано, что динамическое давление плюс статическое давление в потоке, равное половине плотности (r), умноженной на квадрат скорости (V), равны константе во всем потоке. Константа называется полным давлением потока (pt).
Или, проще говоря, уравнение Бернулли утверждает, что сумма потенциальной, кинетической энергии и энергии потока жидкости постоянна в линии тока при стационарном течении.
Примечание:
Линия тока при установившемся течении — это путь, пройденный одной частицей в жидкости.
На следующем рисунке показана линия тока при установившемся течении:
Чтобы применить уравнение Бернулли:
- Поток должен быть установившимся (скорость, плотность и давление не должны изменяться ни в одной точке линии тока).
- Поток должен быть несжимаемым: даже при изменении давления плотность вдоль линии тока должна оставаться постоянной.
- Трение вязких сил должно быть незначительным или минимальным.
Примечание:
Несжимаемые потоки — это газы и газы с малым числом Маха и постоянной плотностью жидкости независимо от напорного потока. Используя несжимаемый поток, мы получим простейшую форму уравнения Бернулли
Принцип БернуллиПринцип Бернулли утверждает, что увеличение скорости (скорости жидкости) происходит одновременно и должно сопровождаться уменьшением потенциала энергия жидкости (или статическое давление).
Принцип Бернулли можно вывести из закона сохранения энергии. В случае стационарного течения сумма форм энергии в жидкости останется неизменной во всех точках этой линии тока. В то время как вся энергия остается постоянной, увеличение скорости жидкости будет означать увеличение кинетической энергии или динамического давления. Это происходит при уменьшении потенциальной энергии (статического давления и внутренней энергии).
Принцип Бернулли Формула Формула уравнения Бернулли считается отношением между давлением, потенциальной энергией и кинетической энергией жидкости.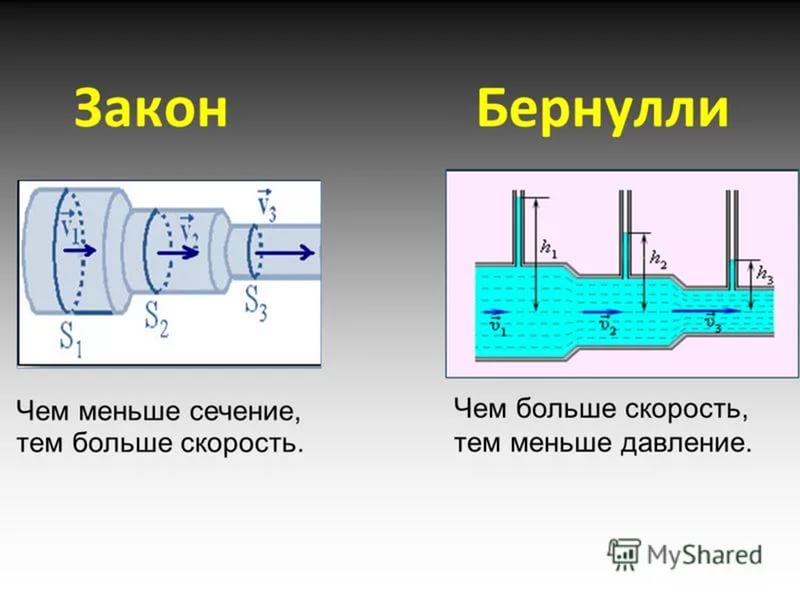
Приведенная формула выглядит следующим образом:
Уравнение Бернулли можно рассматривать как принцип сохранения энергии для текущих жидкостей. Эффект Бернулли заключается в снижении давления жидкости в случаях, когда скорость увеличивается. В случае высокоскоростного потока через сужение кинетическая энергия должна увеличиваться за счет энергии давления.
Ограничения на использование теоремы БернуллиУравнение Бернулли применимо к установившемуся потоку, как мы объясняли ранее, но в некоторых случаях мы не можем использовать уравнение Бернулли.
Теорема Бернулли неприменима в проточной части, такой как машины (например, вентилятор, турбина или насос), потому что эти машины могут повредить линии тока и вступить в энергетическое взаимодействие с жидкостью. Поэтому в этих случаях вместо уравнения Бернулли следует использовать уравнение энергии.
Уравнение также не следует использовать для секций потока со значительным изменением температуры, таких как секции охлаждения или нагрева, поскольку плотность газа обратно пропорциональна температуре.
В каждом потоке присутствует некоторое трение, и если эффектами трения нельзя пренебречь, то в этом случае теорема Бернулли неприменима.
Итак, уравнение Бернулли нельзя использовать в потоке:
- Внезапное расширение
- Секция нагрева
- Клапан
- Вентилятор
- Узкая длинная трубка
Дифференциальное уравнение Бернулли можно вывести следующим образом:
Будем считать, что у нас есть труба различной высоты и диаметра, по которой течет несжимаемая жидкость. Зависимость между площадями поперечных сечений A, давлением p, скоростью потока v и высотой h в двух различных точках 1 и 2 представлена на следующем рисунке:
Предположения:
- Плотность несжимаемой жидкости остается постоянной в обеих точках.
- Энергия жидкости сохраняется, потому что в жидкости нет сил вязкости.
Итак, работа над жидкостью записывается как:
dW = F1dx1 – F2dx2
dW = p1A1dx1 – p2A2dx2
dW = p1dv – p2dv = (p1 – p2)dv
3 900 работа на жидкости было обусловлено сохранением изменения как кинетической энергии, так и гравитационной потенциальной энергии
Изменение кинетической энергии жидкости определяется как:
Изменение потенциальной энергии определяется как:
dU = m2gy2 – m1gy1 = ρdvg(y2 – y1)
Тогда уравнение энергии дается как:
dW = dK + dU
И, наконец, переставляя вышеприведенное уравнение, мы получаем
Для большего понимания, посмотрите следующее видео о выводе уравнения Бернулли 0002 Виртуальные научные лаборатории PraxiLabs позволяют проводить различные лабораторные эксперименты по физике, химии и биологии онлайн в любое время и в любом месте. Создайте бесплатную учетную запись и попробуйте наши виртуальные лаборатории прямо сейчас. Закажите БЕСПЛАТНУЮ демо-версию прямо сейчас Уравнение Бернулли имеет множество применений. Например, мы можем использовать его для объяснения того, как самолеты создают подъемную силу, для расчета скорости потока жидкости или почему судам приходится убегать друг от друга при прохождении, а также для других применений, которые мы находим в нашей повседневной жизни. Мы подробно рассмотрим некоторые из наиболее популярных приложений теоремы Бернулли. Уравнение Бернулли применяется ко всем задачам о течении несжимаемой жидкости. Уравнение Бернулли можно применять к таким устройствам, как расходомер с диафрагмой, расходомер Вентури и трубка Пито, а также к его приложениям для измерения расхода в открытых каналах и внутри труб. Расходомер Вентури — это устройство, основанное на принципе Бернулли и используемое для определения скорости потока в трубе. Примечание: принцип Бернулли гласит, что в области уменьшенного диаметра должен быть перепад давления. Это явление известно как эффект Вентури. Расходомер Вентури Как мы упоминали ранее, скорость потока жидкости можно измерить с помощью таких устройств, как расходомер Вентури, который используется для уменьшения диаметра потока и помещается в трубопровод. Максимально возможная скорость нагнетания для резервуара с отверстием или носиком в основании может быть рассчитана непосредственно по уравнению Бернулли, и было обнаружено, что он пропорционален квадратному корню из высоты жидкости в резервуаре (это является законом Торричелли), и это показывает, что закон Торричелли совместим с принципом Бернулли. Как крылья самолета создают подъемную силу, можно объяснить уравнением Бернулли для жидкостей. В случае полета жидкость, текущая над крылом самолета, движется быстрее, чем текущая под крылом, что, согласно принципу Бернулли, вызывает создание над поверхностью воздуха области пониженного давления и области повышенного давление под самолетом, и эта разница давлений создает высоту. То есть причину формы крыльев и их загнутости вверх (по теории Бернулли) мы можем объяснить тем, что по верхней поверхности воздух проходит с большей скоростью, чем по нижней. Разность скоростей воздуха рассчитывается по принципу разности давлений Бернулли. В некоторых случаях течения жидкости нам известны скорости в двух точках линии тока и давление только в одной точке. Итак, в этом случае (если к нему применимо уравнение Бернулли) мы можем использовать уравнение Бернулли, чтобы найти неизвестное давление. В случаях, когда высота и давление в двух точках линии тока известны, а также известна скорость в одной точке, и мы хотим найти неизвестную скорость, применяется уравнение Бернулли для расчета и нахождения требуемой скорости. Например: поток через сифон В этом случае нам нужно найти скорость, с которой жидкость выходит из сифона. Применяя уравнение Бернулли между поверхностью резервуара и точкой выхода сифона, где жидкость покидает трубку, давление в обеих точках одинаково и равно атмосферному давлению, а скорость в резервуаре пренебрежимо мала, поскольку резервуар большой. Мы можем рассчитать скорость в точке выхода, используя значения высоты в двух точках. В эхокардиографии принцип Бернулли может применяться при интерпретации кровотока для описания локализованного снижения давления, вызванного высокой скоростью потока вблизи закупорки. В клинической медицине это уравнение используется для простой оценки градиентов давления по скорости. Уравнение Бернулли также можно использовать в маске Вентури. Маска Вентури — это медицинское кислородное устройство, которое обеспечивает подачу кислорода пациентам, проходящим контролируемую оксигенотерапию. Маска имеет трубку, соединенную с соплом, которое соединяется с подачей чистого кислорода. Трубка, непосредственно подсоединенная к маске, имеет небольшое окошко, которое позволяет комнатному воздуху поступать в маску. Маска Вентури может контролировать количество поступающего кислорода, а также чистого кислорода, подаваемого из подсоединенного сопла. В масках Вентури используется принцип Бернулли. По мере поступления кислорода в трубку давление снижается из-за прохождения кислорода через узкое отверстие трубки. Воздух поступает в маску за счет падения давления, смешиваясь с чистым кислородом из сопла, что является следствием принципа Бернулли.
Он работает путем измерения перепада давления на участке рядом с трубой. Для несжимаемой жидкости уменьшение диаметра увеличит скорость потока жидкости.
Вязкость снижает скорость разряда.
Неизвестным является давление в другой точке жидкости.
Другие применения принципа Бернулли
- Теория Бернулли используется для изучения неустойчивого потенциального течения, используемого в теории поверхностных волн и акустики океана.
- Когда мы стоим на вокзале и подъезжает поезд, мы склонны падать прямо на поезд. Мы можем объяснить это, используя принцип Бернулли. По мере прохождения поезда скорость воздуха между нами и поездом увеличивается. Следовательно, из уравнения можно сказать, что давление уменьшается. Так что давление сзади подталкивает нас к поезду, и это зависит от эффекта Бернулли.
- Уравнение Бернулли также объясняет, как работает горелка Бунзена. Когда газовый клапан открыт, газ поступает в ствол с высокой скоростью. Согласно теории Бернулли, эта высокая скорость создает в стволе область низкого давления (которая втягивает воздух через регулятор), что позволяет газу сгорать более эффективно.
- Многие расходомеры основаны на принципе Бернулли для определения скорости потока жидкости. Самым известным из этих устройств является статическая трубка Пито, которая используется в самолетах для измерения скорости полета.
- Принцип Бернулли также применим к раскачиванию мяча для крикета. Во время матча игроки постоянно полируют одну сторону мяча. Через некоторое время одна сторона становится совершенно шероховатой, а другая все еще гладкой. Следовательно, когда мяч подбрасывается в воздух, скорость на одной стороне мяча больше, чем на другой, из-за этой разницы в гладкости. И это приводит к разнице в давлении между двумя сторонами. Это заставляет мяч вращаться («раскачиваться»), когда он путешествует по воздуху.
Виртуальные научные лаборатории PraxiLabs позволяют проводить различные лабораторные эксперименты по физике, химии и биологии онлайн в любое время и в любом месте.
Создайте бесплатную учетную запись и попробуйте виртуальные лаборатории PraxiLabs прямо сейчас.
Присоединяйтесь к нам БЕСПЛАТНО
Уравнение Бернулли | Инженерная библиотека
На этой странице представлена глава об уравнении Бернулли из «Справочника DOE по основам: термодинамика, теплопередача и поток жидкости», DOE-HDBK-1012/3-9.2, Министерство энергетики США, июнь 1992 г.
Другие связанные главы из «Справочника по основам Министерства энергетики: термодинамика, теплопередача и поток жидкости» можно увидеть справа.
Уравнение Бернулли — это частный случай общего уравнения энергии, которое, вероятно, является наиболее широко используемым инструментом для решения задач о течении жидкости. Он обеспечивает простой способ соотнесения напора по высоте, скоростного напора и напора жидкости. Можно изменить уравнение Бернулли таким образом, чтобы он учитывал потери напора и работу насоса.
Общее уравнение энергии
Принцип сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена.
Это эквивалентно Первому закону термодинамики, который был использован для построения общего уравнения энергии в модуле по термодинамике. Уравнение 3-8 представляет собой формулировку общего уравнения энергии для открытой системы.
В + (U + PE + KE + PV) в = W + (U + PE + KE + PV) из + (U + PE + KE + PV) хранится
(3-8)
где:
Упрощенное уравнение Бернулли
Уравнение Бернулли является результатом применения общего уравнения энергии и первого закона термодинамики к стационарной системе, в которой не совершается никакой работы над жидкостью или ею, тепло не передается к жидкости или от жидкости и не происходит никаких изменений в внутренней энергии (т. е. без изменения температуры) жидкости. В этих условиях общее уравнение энергии упрощается до уравнения 3-9.2 \over 2 g_c} + P_2 V_2 $$
(3-10)
где:
| м | = | масса (фунт) |
| из | = | высота над эталоном (футы) |
| против | = | средняя скорость (фут/сек) |
| г | = | ускорение свободного падения (32,17 фут/сек 2 ) |
| г в | = | гравитационная постоянная, (32,17 ft-lbm/lbf-sec 2 ) |
Примечание.
Коэффициент g c требуется только в том случае, если используется английская система измерения и масса измеряется в фунтах. По сути, это коэффициент преобразования, необходимый для прямого вывода единиц измерения. Никакой фактор не требуется, если масса измеряется в порциях или если используется метрическая система измерения.
Каждый член в уравнении 3-10 представляет форму энергии, которой обладает движущаяся жидкость (потенциальная, кинетическая энергия и энергия, связанная с давлением). По сути, уравнение физически представляет собой баланс энергий KE, PE, PV, так что если одна форма энергии увеличивается, одна или несколько других уменьшаются, чтобы компенсировать это, и наоборот. 92 \над 2 г} + P_2 \nu_2 {г_с \над г} $$
(3-11)
где:
| с | = | высота над контрольным уровнем (футы) |
| против | = | средняя скорость жидкости (фут/сек) |
| Р | = | давление жидкости (фунт-сила/фут 2 ) |
| ν | = | удельный объем жидкости (фут 3 /фунт) |
| г | = | ускорение свободного падения (фут/сек 2 ) |
| г в | = | гравитационная постоянная, (32,17 ft-lbm/lbf-sec 2 ) |
Головка
Поскольку единицы для всех различных форм энергии в уравнении 3-11 измеряются в единицах расстояния, эти термины иногда называют «напором» (напорный напор, скоростной напор и подъемный напор). Срок 9Головка 0500 используется инженерами по отношению к давлению. Это ссылка на высоту, обычно в футах, столба воды, который будет поддерживать данное давление. Каждая из энергий, которыми обладает жидкость, может быть выражена в терминах напора. Высота напора представляет собой потенциальную энергию жидкости из-за ее подъема над опорным уровнем. Скоростной напор представляет собой кинетическую энергию жидкости. Это высота в футах, на которую текущая жидкость поднялась бы в столбе, если бы вся ее кинетическая энергия была преобразована в потенциальную энергию. Напор представляет собой энергию потока столба жидкости, вес которого эквивалентен давлению жидкости.
Сумма подъемного, скоростного и напорного напора жидкости называется полным напором. Таким образом, уравнение Бернулли утверждает, что общий напор жидкости постоянен.
PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице уравнения Бернулли. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Просмотреть курс сейчас:
Просмотреть курс
Преобразование энергии в жидкостных системах
Уравнение Бернулли позволяет легко исследовать, как происходит передача энергии между подъемным напором, скоростным напором и напором. Можно исследовать отдельные компоненты трубопроводных систем и определить, какие свойства жидкости изменяются и как это влияет на энергетический баланс.
Если труба, содержащая идеальную жидкость, подвергается постепенному расширению в диаметре, уравнение неразрывности говорит нам, что по мере увеличения диаметра и проходного сечения скорость потока должна уменьшаться, чтобы поддерживать тот же массовый расход. Поскольку скорость на выходе меньше скорости на входе, скоростной напор потока должен уменьшаться от входа к выходу. Если труба расположена горизонтально, напор не меняется; следовательно, уменьшение скоростного напора должно компенсироваться увеличением напора.
Поскольку мы рассматриваем идеальную несжимаемую жидкость, удельный объем жидкости не изменится. Единственный способ увеличения напора несжимаемой жидкости — это увеличение давления. Таким образом, уравнение Бернулли показывает, что уменьшение скорости потока в горизонтальной трубе приведет к увеличению давления.
Если труба постоянного диаметра, содержащая идеальную жидкость, подвергается уменьшению высоты, возникает тот же чистый эффект, но по другим причинам. В этом случае скорость потока и скоростной напор должны быть постоянными, чтобы удовлетворять уравнению неразрывности массы.
Таким образом, уменьшение высоты подъема может быть компенсировано только увеличением напора. Опять же, жидкость несжимаема, поэтому увеличение напора должно привести к увеличению давления.
Хотя на уравнение Бернулли наложено несколько ограничений, оно применяется во многих задачах с физическими жидкостями. Как и в случае сохранения массы, уравнение Бернулли может быть применено к задачам, в которых более чем один поток может входить или выходить из системы одновременно.
2 } $$
$$ v_1 = 40 ~{\text{ft} \over \text{sec}} $$ 92} }\справа) } \номер \\
&=& 39.3 ~\text{ft}
\end{эквнаррай}
$$
Ограничения на упрощенное уравнение Бернулли
Практическое применение упрощенного уравнения Бернулли к реальным трубопроводным системам невозможно из-за двух ограничений. Одним из серьезных ограничений уравнения Бернулли в его нынешнем виде является то, что при решении задач о трубопроводах не допускается жидкостное трение. Следовательно, уравнение 3-10 применимо только к идеальным жидкостям. Однако в действительности полный напор, которым обладает жидкость, не может быть полностью перенесен из одной точки в другую из-за трения. Учет этих потерь напора дал бы гораздо более точное описание того, что происходит физически. Это особенно верно, потому что одной из целей насоса в жидкостной системе является преодоление потерь давления из-за трения в трубах.
Второе ограничение уравнения Бернулли состоит в том, что жидкость не может совершать работу над жидкостью.
Это ограничение предотвращает анализ двух точек в потоке жидкости, если между двумя точками есть насос. Поскольку большинство проточных систем включают насосы, это является существенным ограничением. К счастью, упрощенное уравнение Бернулли можно изменить так, чтобы оно удовлетворительно учитывало как потери напора, так и работу насоса.
Расширенный Бернулли
Уравнение Бернулли можно изменить, чтобы учесть прирост и потерю напора. Полученное уравнение, называемое расширенным уравнением Бернулли, очень полезно при решении большинства задач о течении жидкости. На самом деле расширенное уравнение Бернулли, вероятно, используется чаще, чем любое другое уравнение течения жидкости. Уравнение 3-12 является одной из форм расширенного уравнения Бернулли. 92 \более 2 г} + P_2 \nu_2 {g_c \более g} + H_f $$
(3-12)
где:
| с | = | высота над контрольным уровнем (футы) |
| против | = | средняя скорость жидкости (фут/сек) |
| Р | = | давление жидкости (фунт-сила/фут 2 ) |
| ν | = | удельный объем жидкости (фут 3 /фунт) |
| Н р | = | напор добавлен насосом (ft) |
| Н f | = | потеря напора из-за жидкостного трения (футы) |
| г | = | ускорение свободного падения (фут/сек 2 ) |
| г в | = | гравитационная постоянная, (32,17 ft-lbm/lbf-sec 2 ) |
Потеря напора из-за жидкостного трения (H f ) представляет собой энергию, используемую для преодоления трения, вызванного стенками трубы.
Хотя это представляет собой потерю энергии с точки зрения потока жидкости, обычно это не представляет собой значительную потерю общей энергии жидкости. Это также не нарушает закон сохранения энергии, поскольку потеря напора из-за трения приводит к эквивалентному увеличению внутренней энергии (u) жидкости. Эти потери максимальны, когда жидкость протекает через входы, выходы, насосы, клапаны, фитинги и любые другие трубопроводы с шероховатой внутренней поверхностью.
Большинство методов оценки потери напора из-за трения являются эмпирическими (основаны почти исключительно на экспериментальных данных) и основаны на константе пропорциональности, называемой коэффициентом трения (f), которая будет обсуждаться в следующем разделе.
Пример: Расширенный Бернулли
Вода перекачивается из большого резервуара в точку на 65 футов выше резервуара. Сколько футов напора должен добавить насос, если через 6-дюймовую трубу протекает 8000 фунтов/ч, а потеря напора на трение составляет 2 фута? Плотность жидкости составляет 62,4 фунта/фут 9 .
0404 3 , а площадь поперечного сечения 6-дюймовой трубы составляет 0,2006 фута 2 .
Решение:
Для использования модифицированной формы уравнения Бернулли опорные точки выбирают на поверхности резервуара (точка 1) и на выходе из трубы (точка 2). Давление на поверхности резервуара такое же, как давление на выходе из трубы, т. е. атмосферное давление. Скорость в точке 1 будет практически нулевой.
Используя уравнение для массового расхода, определить скорость в точке 2: 92} }\right) } + 0 ~\text{ft} + 2 ~\text{ft} \nonumber \\ H_p &=& 67 ~\text{ft} \end{эквнаррай} $$
Студент должен отметить, что решение этой примерной задачи имеет числовое значение, которое «имеет смысл» из данных, приведенных в задаче. Общее увеличение напора на 67 футов связано в первую очередь с увеличением оценки на 65 футов и на 2 фута фрикционного напора.
Применение уравнения Бернулли к трубке Вентури
Многие компоненты установки, такие как трубка Вентури, могут быть проанализированы с использованием уравнения Бернулли и уравнения неразрывности.
Вентури представляет собой устройство для измерения расхода, состоящее из постепенного сжатия, за которым следует постепенное расширение. Пример трубки Вентури показан на рисунке 6. Путем измерения перепада давления между входом трубки Вентури (точка 1) и горловиной трубки Вентури (точка 2) можно определить скорость потока и массовый расход на основе уравнения Бернулли. уравнение.
92 \над 2 г} + P_2 \nu_2 {г_с \над г} $$
(3-13)
Применение уравнения неразрывности к точкам 1 и 2 позволяет нам выразить скорость потока в точке 1 как функцию скорости потока в точке 2 и отношения двух площадей потока.
$$ \rho_1 A_1 v_1 = \rho_2 A_2 v_2 $$ $$ v_1 = { \rho_2 A_2 v_2 \над \rho_1 A_1 } $$ $$ v_1 = v_2 ~{A_2 \over A_1} $$
Используя алгебру, чтобы изменить уравнение 3-13 и подставив приведенный выше результат вместо v 1 92 } $$
Следовательно, скорость потока в горловине трубки Вентури и объемный расход прямо пропорциональны квадратному корню из дифференциального давления.