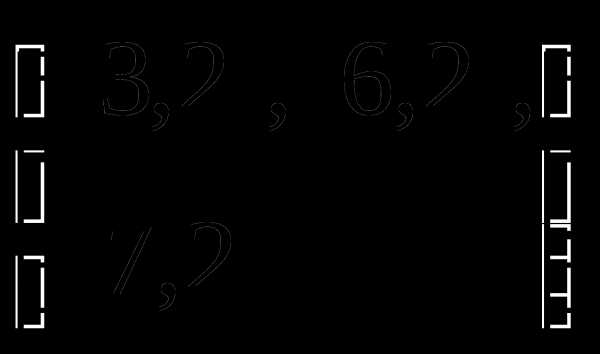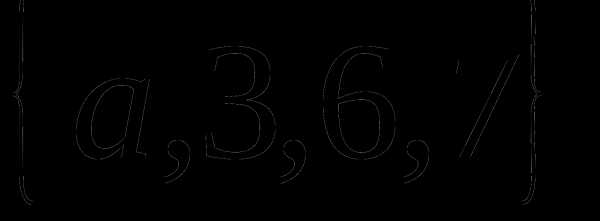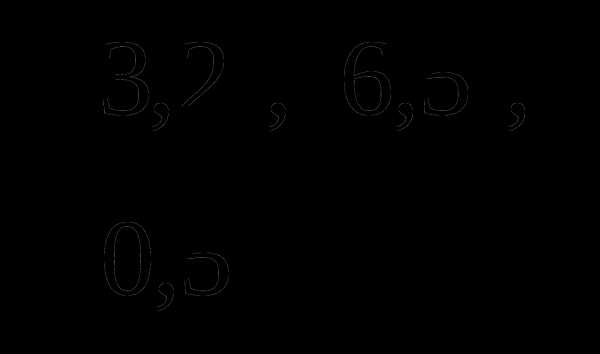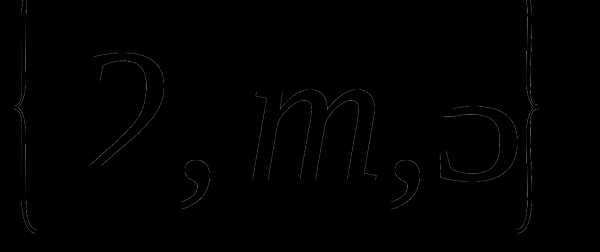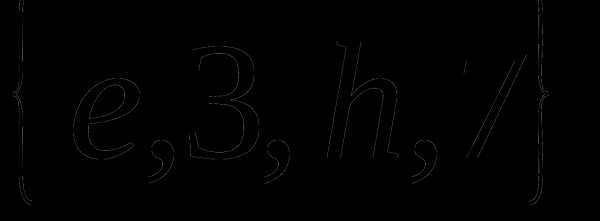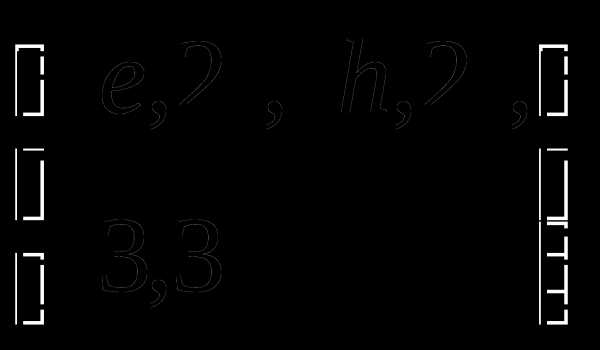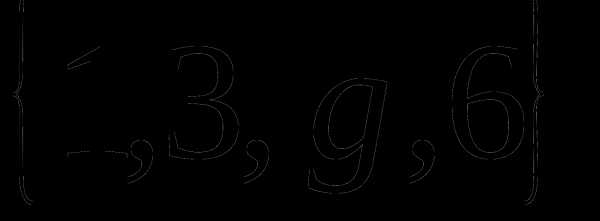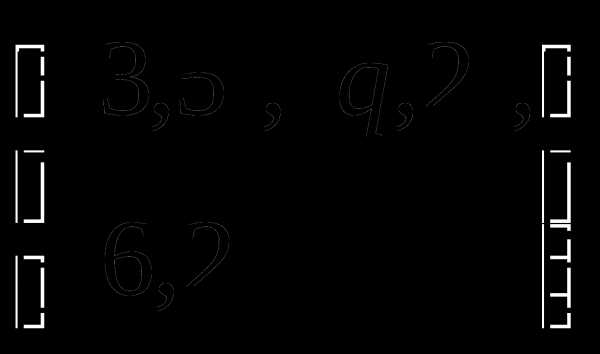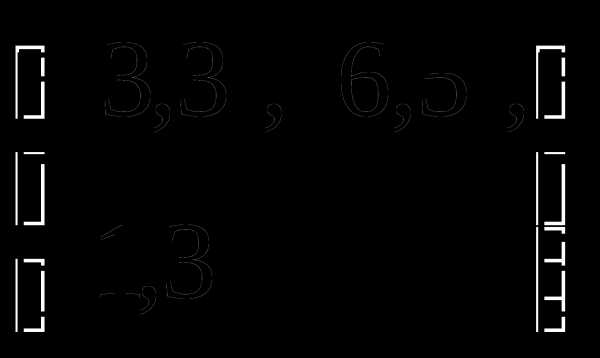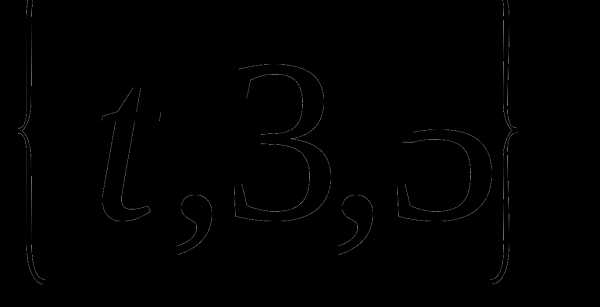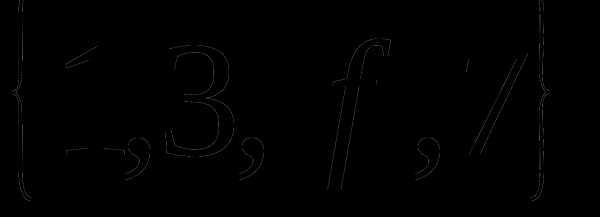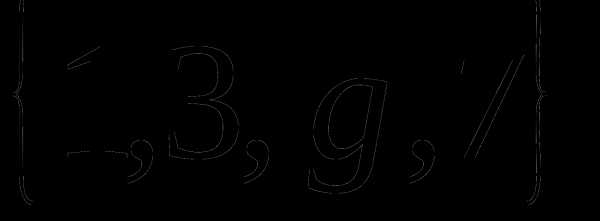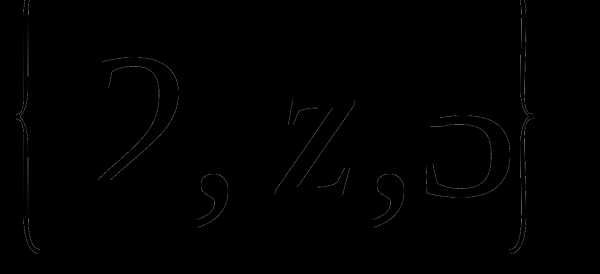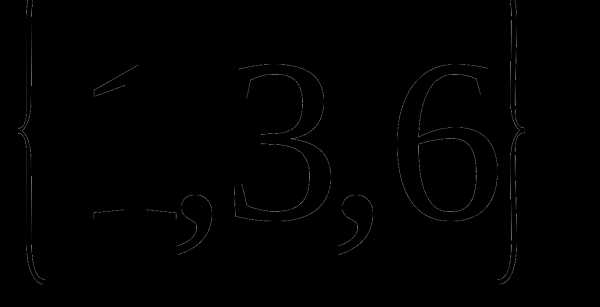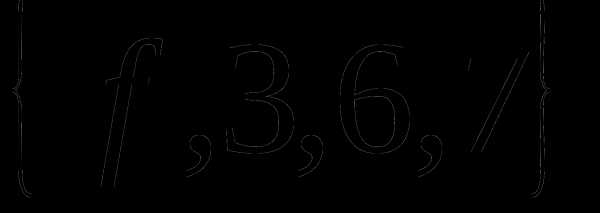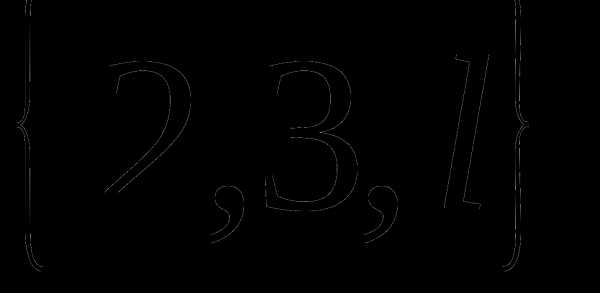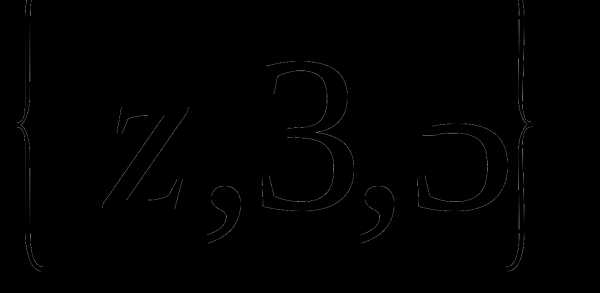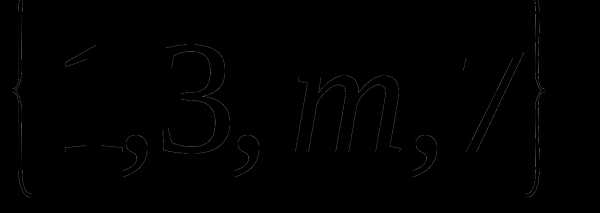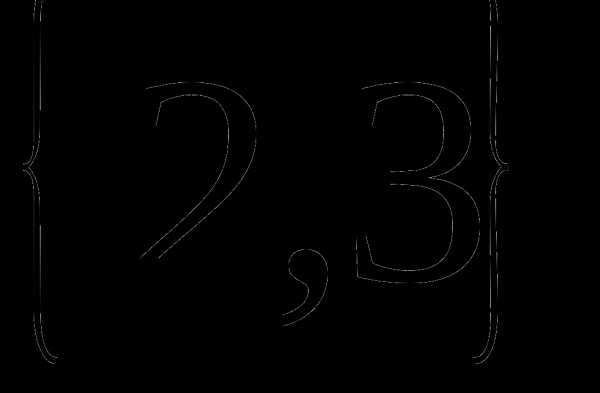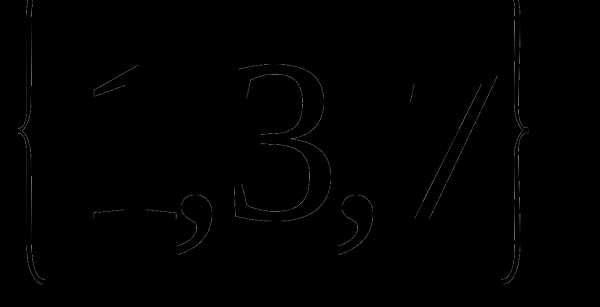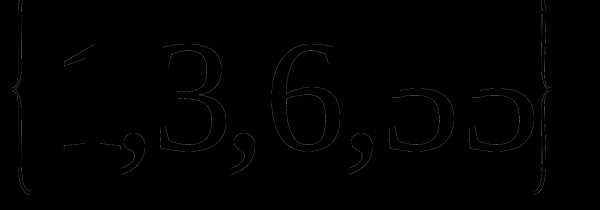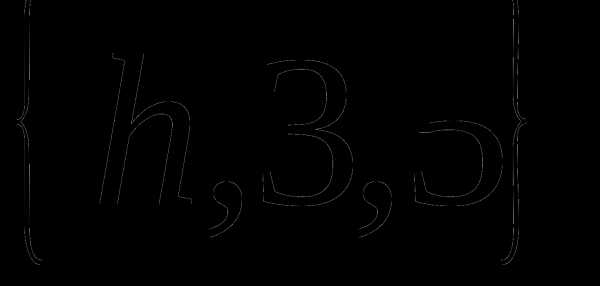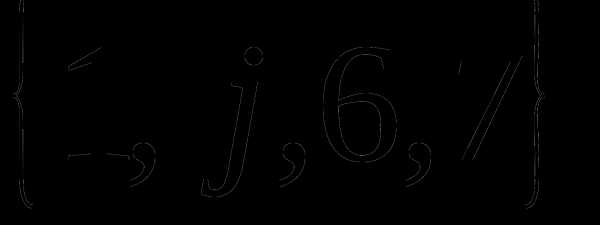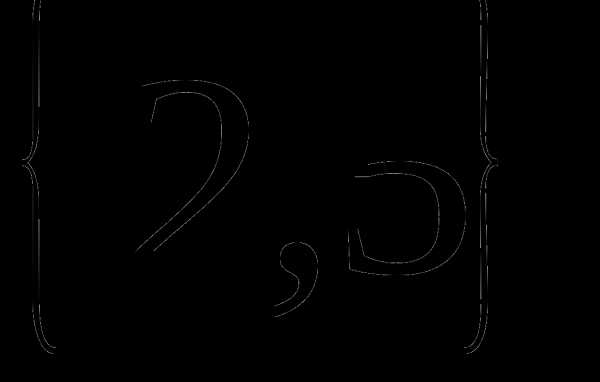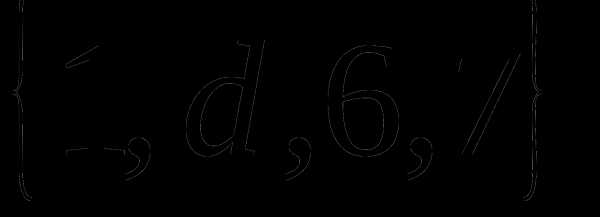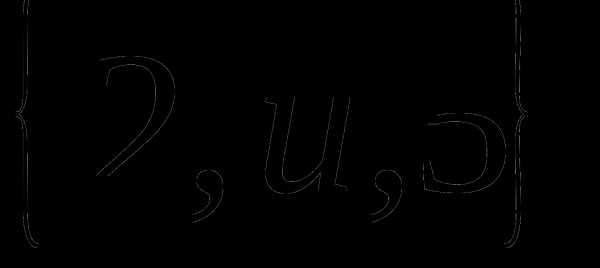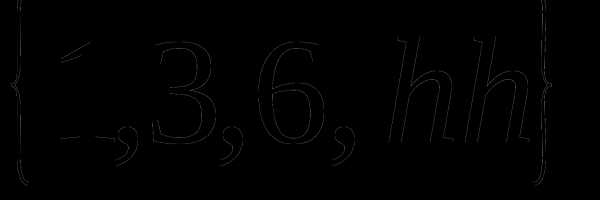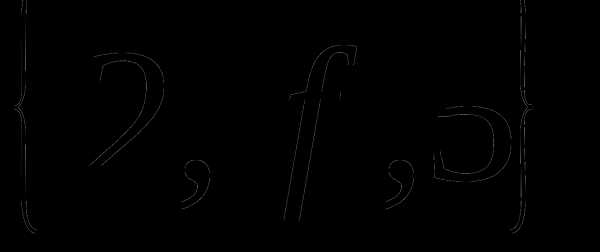Определение 9 (инъекция, сюръекция, биекция). — КиберПедия
Отображение называется инъекцией, если для любых элементов , для которых следует, что . (рис. 2.4)
Рисунок 2.4. Отображение – инъекция
Сюръекцией (или отображением «на» ) называется отображение, при котором (рис. 2.5).
Рисунок 2.4. Отображение –сюръекция
Биекция – это одновременно и сюръекция и инъекция (рис.2.5).
Рисунок 2.5. Отображение – биекция
Примерыотображений.
1) Функция – отображаетмножество действительных чисел на множество действительных положительных чисел. Это отображение – сюръекция, т.к. разным x соответствуют одинаковые y;
2) Функция – отображаетмножество положительных действительных чисел на множество действительных положительных чисел. Это отображение – инъекция, но не сюръекция, т.к. для любых ;
3) Функция y = 4x+7 – отображает всю числовой ось на себя. Это отображение –
2.4. Способы задания функций
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Существует табличный, графический, аналитический и словесный способ задания функции.
Табличный способзаключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. В этом состоит преимущества табличного способа задания функции. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графический способ задания функции вляяниет наглядно представить себе функцию по ее графику. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Однако этот способ не всегда дает возможность точно определить численные значения аргумента и функции. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Определение 2.6. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым вляяниием вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Словесный способ состоит в том, что функциональная зависимость выражается словами. Главное преимущество этого способа заключается в возможности задания тех функций, которые не удается выразить аналитически, а основными недостатками словесного способа задания функции вляяются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности.
2.5. Сложные функции
Определение 2.7. Сложная функция –это функция от функции. Если величина y является функцией от переменной u,т.е. у = f (u), а и,в свою очередь, функцией от переменной х, т.е. u =g(х), то функция у является cложной функцией от переменной х, т.е. y = f [g(x)]. Она определёна для тех значений х, для которых значения g(х) входят в множество определения функции
Например, если у = u2, u =sinx ,то у = sin2х для всех значений х – это сложная функция. Или если , а, , то – сложная функция, причём, если ограничиваться действительными значениями функции у как функции от переменной х, то cложная функция определена только для таких значений х, для которых , то есть для , где k = 0, ± 1, ± 2,….
Если определены отображения f: X Y и g: Y Z, то можно задать композицию этих отображений: g ° f : X Z (рис. 2.6), значения которой определяются формулой (g° f)(x) = g(f(x)).
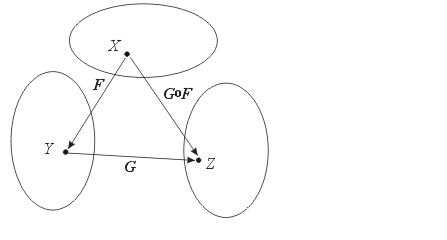
Рисунок 2.6. Отображение сложной функции
Ограниченные функции
Определение 2.8. Функция называется ограниченной функцией на множестве X, если существует такое положительное число М, что для всех х измножества X значения функции по абсолютной величине не превосходят числа М. Или
{ Функция называется ограниченной функцией на множестве X} .
Определение 2.9. Функция называется ограниченнойфункцией при , если существует такое число и такое число , что при всех , для которых справедливо неравенство , имеет место следующее неравенство: .
Множество ограниченнойфункцией при , принято обозначать символом . Иногда вместо записи при используют запись: при , понимая под этим, что является одной из функций, принадлежащих классу при .
Приведем символическую запись определения ограниченной функции при :
Аналогично можно определять при или
Примерыограниченных функций: при для ; при для ; при для .
cyberpedia.su
Ответы по Matemat_logike2013
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
Федеральное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет водных коммуникаций»
Кафедра Комплексного обеспечения информационной безопасности
Дисциплина «Математическая логика и теория алгоритмов» ( ИЗ — I )
Специальность «090900.62 — Информационная безопасность» профиль «Безопасность автоматизированных систем»
Список вопросов
Свойства операций над множествами.
Свойства операций над множествами.
Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами :
Коммутативность.
A B=B A(объединение) A B=B A(Пересечение)
Ассоциативность.
(A B) C=A (B C) (A B) C= A (B C)
Дистрибутивность.
(A B) C = (A
A A=A, A A=A A = A, A
Законы де Моргана (законы двойственности).
1) A B= A B 2 ) A B= A B
Доказательство данных свойств проводится на основе определения равенства двух множеств.
Заметим, что закон ассоциативности при комбинировании операций объединения и вычитания, вообще говоря, не имеет места.
Отношения: инъекция, сюръекция, биекция, их свойства.
Определение 9 ( инъекция , сюръекция , биекция ).
Отображение называется инъекцией , если для любых элементов x1, x2 X , для которых f(x1) = f(x2) следует, что x1 = x2 . (рис. 7)
Сюръекцией (или отображением «на» ) называется отображение, при котором f(X) = Y (рис. 8).
Биекция – это одновременно и сюръекция и инъекция (рис.9).
Отношение эквивалентности. Классы эквивалентности, их свойства.
Важным видом бинарного отношения является отношение эквивалентности.
Определение 5.1. Бинарное отношение на множестве X называется отношением эквивалентности на X, если рефлексивно, симметрично и транзитивно.
Отношение эквивалентности часто обозначают символами ~,.
Примерами отношения эквивалентности служат:
отношение тождества
отношение подобия на множестве фигур плоскости;
отношение равносильности на множестве уравнений;
С отношением эквивалентности тесно связано разбиение множества на классы.
Определение 6.1. Система непустых подмножеств
{M1, M2, …}
множества M называется разбиением этого множества, если
M = M1M2 …
и при ij
MiMj =O.
Сами множества M1, M2, … называются при этом классами данного разбиения.
Примерами разбиений служат:
разложение всех многоугольников на группы по числу вершин — треугольники, четырехугольники, пятиугольники и т. д.;
разбиение всех треугольников на классы подобных треугольников;
разбиение множества всех учащихся данной школы по классам.
Классом эквивалентности, порождённым элементом х называется подмножество множества χ.
Теорема 6.1. Всякое разбиение непустого множества M на классы определяет (индуцирует) на этом множестве отношение эквивалентности такое, что:
всякие два элемента одного класса находятся в отношении ;
всякие два элемента различных классов не находятся в отношении .
Отношения частичного и линейного порядка. Теорема об изоморфизме частично упорядоч. множеств.

Непустое множество X с заданным на этом множестве отношением частичного (линейного) порядка называется частично (линейно) упорядоченным множеством. Для отношения порядка на произвольном множестве часто используют символ <=, соответственно для строгого порядка можно использовать символ ≺
Два частично упорядоченных множества называются изоморф-
ными, если между ними существует изоморфизм, то есть взаимно
однозначное соответствие, сохраняющее порядок. (Естественно, что
в этом случае они равномощны как множества.) Можно сказать так:
биекция f : A → B называется изоморфизмом частично упорядочен-
ных множеств A и B, если
a1 6 a2 ⇔ f(a1) 6 f(a2)
для любых элементов a1, a2 ∈ A (слева знак 6 обозначает порядок в
множестве A, справа — в множестве B).
Очевидно, что отношение изоморфности рефлексивно (каждое
множество изоморфно самому себе), симметрично (если X изоморф-
но Y , то и наоборот) и транзитивно (два множества, изоморфные
третьему, изоморфны между собой). Таким образом, все частично
упорядоченные множества разбиваются на классы изоморфных, ко-
торые называют порядковыми типами.
Равносильность формул. Основные свойства.

Основные тавтологии.

Правильные рассуждения. Основные схемы.
Правильным называется рассуждение, в котором из конъюнкции посылок следует заключение, и оно является тавтологией. В этом случае, если посылки – истинны, заключение – истинно.
В этом случае, если посылки – истинны, заключение – истинно.
А⇒В ≡ (А⇒В) ∨ Л ≡ ¬(А⇒В) ⇒(С & ¬С) ≡ (А & ¬В) ⇒(С & ¬С).
А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨ (С & ¬С) ≡¬ (¬А ∨ В) ⇒ (С & ¬С)
А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨¬А ≡¬ (¬А ∨ В) ⇒¬А ≡(А & ¬В) ⇒¬А
А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨ В ≡¬ (¬А ∨ В) ⇒ В≡ (А & ¬В) ⇒В
А⇒В≡ ¬А ∨ В ≡ В ∨ ¬А ≡ ¬В ⇒¬А – закон контрапозиции
Двойственные формулы. Лемма. Теорема – принцип двойственности.
НЕПОЛНЫЙ ОТВЕТ!!!!!!!!
Связки & и ∨ Называются двойственными.
Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций.( & на ∨)(∨ на &). Для таких формул есть свойство:
F*(X1…Xn)= -F(-X1…-Xn)
Теорема о представлении булевой функции формулой логики высказываний.
Каждая булева функция порождается некой формулой, в которую кроме пропозиц.переменных входят только пропозиц.связки из множества(И, ИЛИ, НЕ)
Док-во.
Пусть F(X1-Xn) задана таблицей
1)Если она является тождественным нулём, то формула (А1 & ¬А1)∨ (А2 & ¬А2)∨…∨ (Аn & ¬Аn) является такой порождающей формулой.
2) Пусть среди значений функции есть хотя бы одна 1. Пусть это строка таблицы истинности с номером j.
Эта формула принимает значение Истина только на «своей» строистинности. На всех остальных она принимает значение Ложь
f=D1vD2v…vDn составленная по всем строкам со значением 1 является формулой порождающей исходную булеву функцию
Полные системы связок.
Дизъюнктивная нормальная форма. Совершенная ДНФ. Теорема о представлении в ДНФ.
Теоремы о приведении к СДНФ и об единственности СДНФ.
Конъюнктивная нормальная форма. Совершенная КНФ. Теорема о представлении в КНФ.

Теорема о представимости булевых функций многочленами Жегалкина.


Приложение логики высказываний: к синтезу логических схем вычисл. устройств, и др.
http://cs323524.vk.me/v323524284/7907/ilnj3Kv_tSs.jpg
http://cs309131.vk.me/v309131284/6914/enoGWqwlJ90.jpg
Простейшие свойства выводимых формул в аксиоматических теориях (1- 8).

Вывод в теории Черча: .

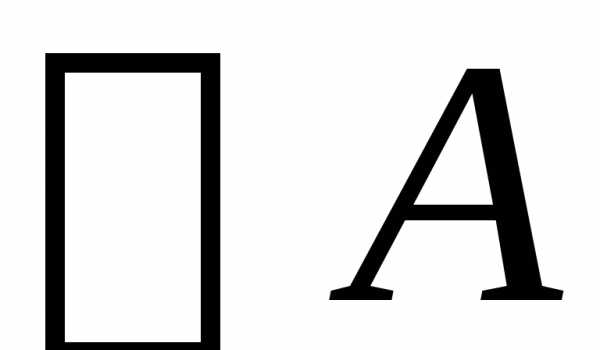
Вывод в теории Черча: если
 ,
то
.
,
то
.
Вывод в теории Черча: .

Вывод в теории Черча: .

Вывод в теории Черча:
 и
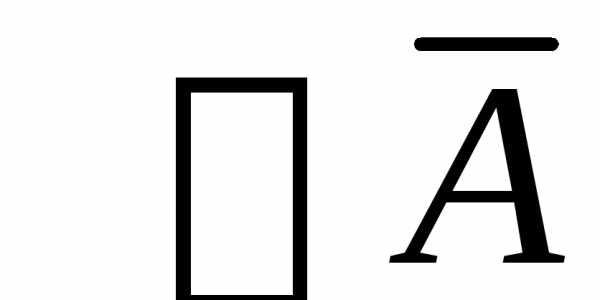
и  .
.

Теорема о дедукции.


Правило силлогизма.

Вывод формулы: .

Правило перевертывания.

Производное правило вывода: .

Производное правило вывода: .

Производное правило вывода: .

Производное правило вывода: и .

Производное правило вывода: если , то

Производное правило вывода: если , то
 .
.

Лемма к теореме о полноте (в широком смысле).

Теорема о корректности АТЧ.
Теорема. (о корректности АТЧ)
Любая теорема АТЧ является тавтологией.
Доказательство
Аксиомы А1, А2, А3 являются тавтологиями (см. стр. 8). Далее, единст-39
венное правило вывода MP, примененное к тавтологиям, снова приводит к
тавтологии (см. стр. 9). Поэтому каждая теорема является тавтологией. ■
Теорема о полноте (в широком смысле).

Теорема о непротиворечивости.

Теорема о абсолютной непротиворечивости. Теорема об альтернативности АТ.
Частично–рекурсивные и примитивно–рекурсивные функции: ; .
Машина Тьюринга для простейших функций.
Машина Тьюринга для копирования слов.

Машина Тьюринга для удвоения чисел.
Машина Тьюринга для сложения двух чисел
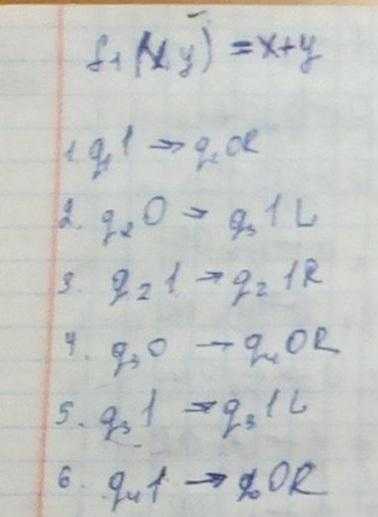
studfiles.net
Дискретная математика, комбинаторика, теория чисел
Отображение (функция) называется сюръективным (или сюръекцией, или отображением на ), если каждый элемент множества является образом хотя бы одного элемента множества , то есть .
Отображение (функция) множества в множество называется инъекцией (или вложением, или взаимно однозначным отображением множества в множество ), если разные элементы множества переводятся в разные элементы множества ,
Биекция — это отображение (функция), которое является одновременно и сюръективным, и инъективным.
А как называется такое отображение (функция) ?
Например,
Вроде бы свойство сюрьекции выполняется, свойство инъекции тоже выполняется, т.к. в обоих определениях ничего не сказано о единственности существования, однако, биекции явно нет.
Как это отображение (функция) называется в математике, где об этом можно почитать ?
dxdy.ru
| Отображения
Пусть даны два множества X и Y. Такое соответствие, при котором каждому элементу x из Х соответствует (единственный) элемент y из У, называется отображением множества X в множество Y; в частности, если каждый элемент y из У соответствует по крайней мере одному элементу x из Х, то такое соответствие называется отображением X на Y. Если элементу x из Х соответствует y из У, то y называется образом элемента x, а x — прообразом элемента y. Пример.Даны два множества X={с,е,н,т,я,б,р,ь} и Y={1,2,3,4,5,9,10,11} Отображение из множества X в множество Y имеет следующий вид: {с, е, н, т, я, б, р, ь} ↨ ↨ ↨ ↨ ↨ ↨ ↨ ↨ {1, 2, 3, 4, 5, 9, 10, 11} Сюръе́кция -сюръективное отображение — отображение множества {\displaystyle X} X на множество {\displaystyle Y}Y ({\displaystyle (f\colon X\to Y)}f:X→Y), при котором каждый элемент множества {\displaystyle Y}Y является образом хотя бы одного элемента множества {\displaystyle X}X, то есть для любого {\displaystyle \forall y\in Y\exists x\in X:y=f(x)}у∈Y ∃ x∈X: y=f(x) , иными словами — функция, принимающая все возможные значения. Иногда говорят, что сюръективное отображение {\displaystyle f\colon X\to Y}f:X→Y отображает {\displaystyle X}X на {\displaystyle Y}Y (в противоположность инъективному отображению, которое отображает {\displaystyle X}X в {\displaystyle Y}Y). Инъекция в математике — отображение {\displaystyle f}f множества {\displaystyle X}X в множество {\displaystyle Y}Y ({\displaystyle f\colon X\to Y}f:X→Y), при котором разные элементы множества {\displaystyle X}X переводятся в разные элементы множества {\displaystyle Y}Y, то есть, если два образа при отображении совпадают, то совпадают и прообразы: f(x) = f(y)=> x=y Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно однозначным отображением (соответствием), одно-однозначным отображением. Мо́щность мно́жества, кардина́льное число́ мно́жества — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества. В основе этого понятия лежат естественные представления о сравнении множеств: 1. Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность). 2 .Обратно: множества, равные по мощности, должны допускать взаимно-однозначное соответствие. 3. Часть множества не превосходит полного множества по мощности (то есть по количеству элементов). В теории множеств, счётное мно́жество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формально: множество {\displaystyle X}X является счётным, если существует биекция {\displaystyle X\leftrightarrow \mathbb {N} }X↔N , где {\displaystyle {\mathbb {N} }}N обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел. Конти́нуум в теории множеств — мощность (или кардинальное число) множества всех вещественных чисел. Обозначается строчной латинской буквой “c” во фрактурном начертании{\displaystyle {\mathfrak {c}}}. Множество, имеющее мощность континуум, называется континуальным множеством. Континуум является бесконечной мощностью (алефом), превосходящей мощность счётного множества {\displaystyle \aleph _{0}}. Любое континуальное множество содержит счётное подмножество. Поделитесь с Вашими друзьями: |
refnew.ru
Математики, помогите пожалуйста. Объясните, в элементарной форме, в чем разница между инъекцией, сюръекцией и биекцией.
Ну вот возьмем два множества: множество учеников и множество стульев в классе. И будем устанавливать соответсвие между этими двумя множествами, т. е. просто рассаживать учеников на стулья. 1. Если каждый ученик сел на отдельный стул (некоторые стулья могут остаться свободными) , то это инъекция. Понятно, что при таком отображение количество стульев не может быть меньше количества учеников (ученики не могут садится по два на один стул) . 2. Если все стулья оказались заняты (на некоторых могут сидеть и по два или больше учеников) , то это сюръекция. В этом случает уже количество учеников не может быть меньше стульев. 3. Если каждый ученик сидит на отдельном стуле, и нет ни свободных стульев, ни учеников, которым стульев не хватило — это биекция. Т. е. биекция это одновременно и инъекция (каждый ученик сидит на отдельном стуле) и сюръекция (все стулья заняты) . Для возможности такого отображения (биекции) количество учеников должно быть в точности равно количеству стульев. Естественно вместо учеников и стульями может быть что угодно, например числовые множества. Все эти соответсвия могут устанавляваться и между бесконечными множествами. И кроме того, между конечным и бесконечным — инъекция, или бесконечным и конечным — сюръекция. Да и маленькое замечание к ответу Андре Дедыка, он в общем-то все вам понятно объяснил, только немного неправильно. В определении инъекции требуется, чтобы разным элементам первого множества соответствовали разные элементы второго. Так что в его примере парням нужно обязательно целовать разных девушек
Это виды взаимно-однозначных отображений. Инъекцию куда делают медики? В тебя. Значит, это отображение В. То есть ВСЁ множество А отображается в какую-то часть множества В. Сюръекция — отображение НА. То есть какая-то часть множества А отображается на ВСЁ множество В. Биекция — это инъекция и сюръекция одновременно. То есть в этом случае ВСЁ множество А отображается на ВСЁ множество В.
Всё это отношения (ЧТО-ТО отображается КУДА-ТО) инъекция — все элементы ЧТО-ТО отображены в некоторые элементы КУДА-ТО (но ну во все) сюръекция — все элементы КУДА-ТО заняты некоторыми элементами ЧТО-ТО (но ну во все) биекция — все элементы ЧТО-ТО отображены на все элементы КУДА-ТО. А теперь примеры: Есть два множества. Каждый состоит из двух элементов (для простоты) . Например, «парни» — Андрей (первый элемент) и Борис (второй) «девушки» — Вика и Галя. Значит первое множество состоит из двух элементов А и Б. Второе множество — из В и Г. Пока все понятно? ? Можно задать любое отображение — иньективное, сюрьективное, биективное, короче любое. Взаимодействие должно быть только между элементами разных множеств. А и Б между собой не могут взаимодействовать.. . Придумал взаимодействие = «целоваться» 1)Задаю иньективное: А поцеловался с В. Б поцеловался с В. Отсюда видно что все парни кого-то поцеловали, но не все девушки целованные. 2) сюрьекция А поцеловался с В. А поцеловался с Г Видно что все девушки поцеловались, но не все парни!! ! (Здесь я немножко ошибся, но это суть не меняет. Специально не поправляю что бы не сбивать… ) 3) биекция Тут все просто. Каждый парень должен хоть с кем то поцеловаться. И каждая девушка должна хоть с кем-то поцеловаться. И по этому А целуется с В. Б целуется с Г. Понятно? Могу еще таких примеров наготовить, но лучше для усвоения если вы сами попробуете придумать такие примеры (но для троих элементов) и написать в комментариях. Вот и проверим.
Не. Инъекция — это другое (чем у выходца из народа) . Тут лучше на картинке посмотреть. Вот <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Инъекция_(математика)» target=»_blank» >здесь</a> все коротко и ясно
touch.otvet.mail.ru
Отображения инъекция сюръекция биекция свойства обратимости слева и справа
6. Отображения. Инъекция, сюръекция, биекция, свойства обратимости слева и справа.
Функция для которой 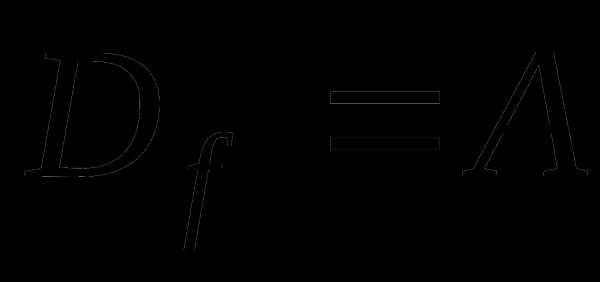 называется всюду
определенной,
обозначается или и называется также отображением.
называется всюду
определенной,
обозначается или и называется также отображением.
Тождественным
отображением 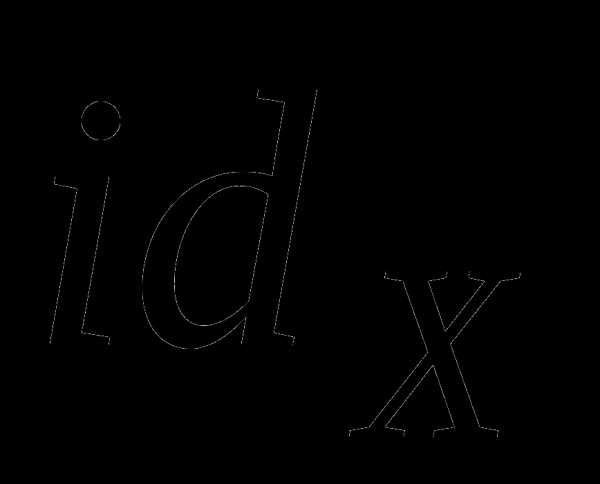 на множестве
на множестве  называется отображение
,
обладающее свойством
,т.е.
это отображение оставляет каждый элемент
области определения на месте.
называется отображение
,
обладающее свойством
,т.е.
это отображение оставляет каждый элемент
области определения на месте.
Пусть
—
функция и  —
подмножество ее области определения. Сужением функции на множество
—
подмножество ее области определения. Сужением функции на множество  называется функция
.
Эта функция является отображением вида
.
Имеет место формула:
.
называется функция
.
Эта функция является отображением вида
.
Имеет место формула:
.
Пример. Дано . Найти сужение .
Решение. Имеем:
Ответ: .
Функция называется продолжением функции  ,
если выполняется включение
,
если выполняется включение  .
.
Отображение называется сюръективным или сюръекцией (отображением
“на”, накрытием) если  ,
т.е. если его образ совпадает со всем
конечным множеством отображения. Это
условие можно записать также в виде:
,
т.е. каждый элемент конечного множества
является образом некоторого элемента
начального множества отображения.
,
т.е. если его образ совпадает со всем
конечным множеством отображения. Это
условие можно записать также в виде:
,
т.е. каждый элемент конечного множества
является образом некоторого элемента
начального множества отображения.
Отображение называется инъективным или инъекцией, если выполняется свойство , т.е. разные переходят в разные.
Отображение называется биективным или биекцией (взаимно- однозначным отображением, перестановкой) если оно одновременно сюръекция и инъекция.
Пусть дано отображение . Отображение называется левым обратным к отображению если выполняется свойство . Отображение называется правым обратным к , если . Отображение называется обратным к отображению , если оно одновременно является правым обратным и левым обратным по отношению к , т.е. если выполняются свойства .
Теорема 1. Пусть имеется отображение . Оно обладает левым обратным тогда и только тогда, когда отображение является инъекцией. При этом левое обратное находится по формуле:
Отображение обладает правым обратным
,
если
является
сюръекцией, при этом обратное  находится по формуле:
находится по формуле:
Отображение обладает как левым обратным , так и правым обратным в том и только том случае, если — биекция. В этом случае левое и правое обратные отображения совпадают, определяются однозначно и их общее значение называется обратным (двусторонним) отображением к отображению .
Задание функции программой ЭВМ.
Пример.
Функция задана C++ программой:
int f(int x)
{
if (x>5) return x*2;
else if (3
else return x%2;
}
Найти
значение 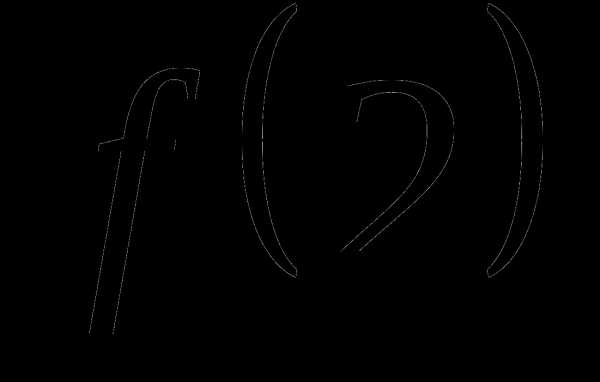 .
.
Решение. Для большей ясности действия указанной функции построим блок-схему алгоритма данной функции:

Используя
входные данные  осуществим прохождение от точки входа
то точки выхода блок-схемы.
осуществим прохождение от точки входа
то точки выхода блок-схемы.
1)  —
вход в схему;
—
вход в схему;
2.Безусловный 1 переход на блок 2;
3)
Проверка  —
нет, переход по дуге 2 на блок 3;
—
нет, переход по дуге 2 на блок 3;
4)
Проверка  —
нет, переход по дуге на исполнительный
блок 5;
—
нет, переход по дуге на исполнительный
блок 5;
5) Операция . Результат :
6) Безусловный переход на блок 7:
7) Вывод данных .
Итак,
выполняя алгоритм данной функции по
указанной блок-схеме получили ответ 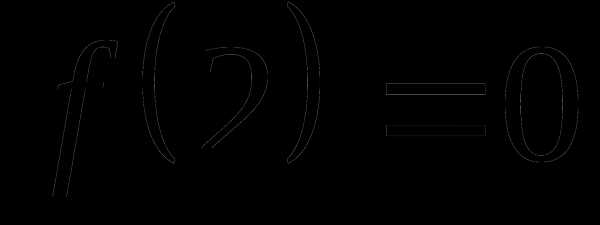 .
.
Лабораторная работа 3. Функции и операции над ними.
Цель. Изучить понятие функции и научиться решать типовые задачи по теме “функция”.
Задание. Выполнить задания 1-5, записать решения, ответить на контрольные вопросы.
Задание
1. Кортежное задание функции. Даны начальное и конечные множества 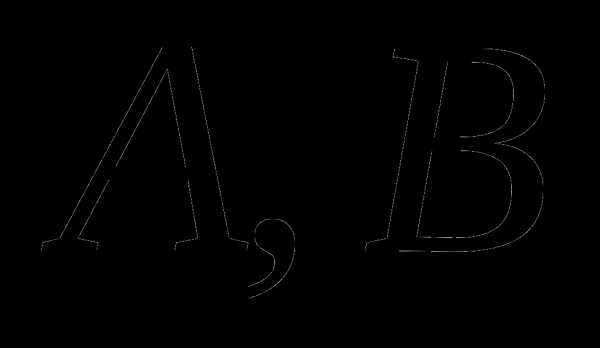 ,
функция
,
найти область определения
,
функция
,
найти область определения 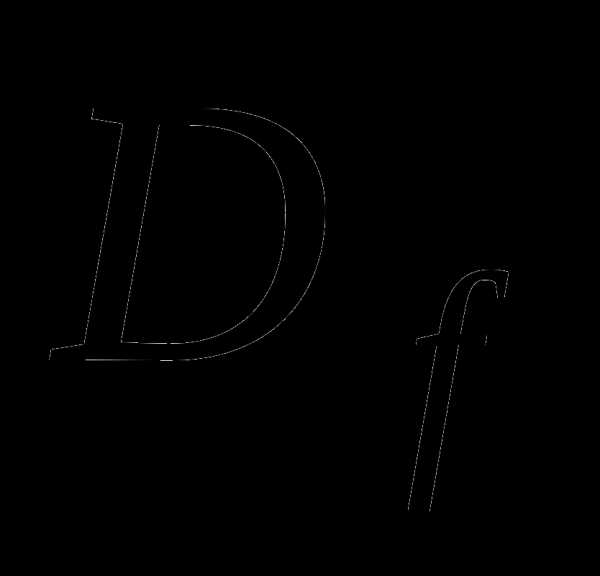 ,
область значений
,
область значений  функции, получить табличное представление
функции. Привести визуальное изображение
функции в виде двудольного орграфа.
функции, получить табличное представление
функции. Привести визуальное изображение
функции в виде двудольного орграфа.
Пример выполнения. Дано .
Решение. Область определения функции — это множество первых компонент ее кортежей. Получаем . Область значений- это множество вторых координат ее кортежей. Получаем . Табличное представление функции — это таблица аргумент-значение для всех элементов области определения функции. Получаем таблицу:
Изображение:
Индивидуальное задание 1.
Nv | Nv | ||||||
1 |
| 2 |
| ||||
3 |
| 4 |
|
| |||
5 |
| 6 |
| ||||
7 |
|
| 8 |
| |||
9 |
|
| 10 |
| |||
11 |
| 12 |
| ||||
13 |
|
|
| 14 |
| ||
15 |
| 16 |
| ||||
17 |
| 18 |
| ||||
19 |
| 20 | |||||
21 |
| 22 |
| ||||
23 | 24 |
| |||||
25 |
| 26 |
| ||||
27 |
| 28 |
| ||||
29 | 30 |
| |||||
31 | 32 | ||||||
33 | 34 |
| |||||
35 | 36 |
| |||||
37 | 38 |
| |||||
39 | 40 |
|
gigabaza.ru
Сюръекция — это… Что такое Сюръекция?
сюръекция — сущ., кол во синонимов: 3 • наложение (10) • отображение (14) • функция (49) … Словарь синонимов
СЮРЪЕКЦИЯ — сюръективное отображение множества Ав множество В отображение f такое, что f(A)=B. Вместо лf сюръективно … Математическая энциклопедия
Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
Реляционная СУБД — (РСУБД; иначе Система управления реляционными базами данных, СУРБД) СУБД, управляющая реляционными базами данных. Понятие реляционный (англ. relation отношение) связано с разработками известного английского специалиста в области… … Википедия
Синонимы — У этого термина существуют и другие значения, см. Синоним (значения). Синонимы слова одной части речи, различные по звучанию и написанию (ср. омонимы), но имеющие одинаковое или очень близкое лексическое значение (ср. антонимы). Примеры… … Википедия
Инъекция (математика) — У этого термина существуют и другие значения, см. Инъекция (значения). Инъективная функция. Отображение … Википедия
Полисемия — (от греч. πολυσημεία «многозначность») многозначность, многовариантность, то есть наличие у слова (единицы языка, термина) двух и более значений, исторически обусловленных или взаимосвязанных по смыслу и происхождению. В современном… … Википедия
Николя Бурбаки — Шарль Дени Бурбаки, французский генерал, фамилия которого была взята в качестве псевдонима Николя Бурбаки (фр. Nicolas Bourbaki) коллективный псевдоним группы французских математиков (позднее в неё вошли несколько иностранцев),… … Википедия
Ключ отношения — Первичный ключ (англ. primary key) понятие теории реляционных баз данных, минимальное множество атрибутов, являющееся подмножеством заголовка данного отношения, составное значение которых уникально определяет кортеж отношения. На практике термин… … Википедия
Иерархические базы данных — Иерархическая модель базы данных состоит из объектов с указателями от родительских объектов к потомкам, соединяя вместе связанную информацию. Иерархические базы данных могут быть представлены как дерево, состоящее из объектов различных уровней.… … Википедия
dic.academic.ru

 ,
то
.
,
то
.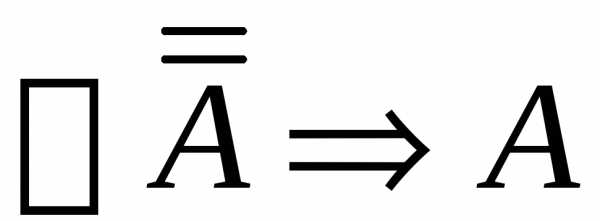 и
и 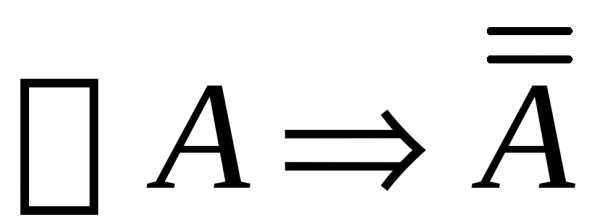 .
. .
.