|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа… Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом. Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Отображение называется инъекцией, если для любых элементов , для которых следует, что .
Рисунок 2.4. Отображение – инъекция
Сюръекцией (или отображением «на» ) называется отображение, при котором (рис. 2.5).
Рисунок 2.4. Отображение –сюръекция
Биекция – это одновременно и сюръекция и инъекция (рис.2.5).
Рисунок 2.5. Отображение – биекция
Примерыотображений. 1) Функция – отображаетмножество действительных чисел на множество действительных положительных чисел. Это отображение – сюръекция, т.к. разным x соответствуют одинаковые y; 2) Функция – отображаетмножество положительных действительных чисел на множество действительных положительных чисел. Это отображение – 3) Функция y = 4x+7 – отображает всю числовой ось на себя. Это отображение – биекция. 2.4. Способы задания функций Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Табличный способзаключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. В этом состоит преимущества табличного способа задания функции. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента. Графический способ. Графический способ задания функции вляяниет наглядно представить себе функцию по ее графику. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Определение 2.6. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым вляяниием вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений. Словесный способ состоит в том, что функциональная зависимость выражается словами. Главное преимущество этого способа заключается в возможности задания тех функций, которые не удается выразить аналитически, а основными недостатками словесного способа задания функции вляяются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. 2.5. Сложные функции Определение 2.7. Сложная функция –это функция от функции. Если величина y является функцией от переменной u,т.е. у = f (u), а и,в свою очередь, функцией от переменной х, т.е. u =g(х), то функция у является cложной функцией от переменной х, т.е. y = f [g(x)]. Она определёна для тех значений х, для которых значения g(х) входят в множество определения функции f (u). В таком случае говорят, что функция у является cложной функцией независимого аргумента х, а u — промежуточным аргументом. Например, если у = u2, u =sinx ,то у = sin2х для всех значений х – это сложная функция. Или если , а, , то – сложная функция , причём, если ограничиваться действительными значениями функции у как функции от переменной х, то cложная функция определена только для таких значений х, для которых , то есть для , где k = 0, ± 1, ± 2,. Если определены отображения f: X Y и g: Y Z, то можно задать композицию этих отображений: g ° f : X Z (рис. 2.6), значения которой определяются формулой (g° f)(x) = g(f(x)).
Рисунок 2.6. Отображение сложной функции
Ограниченные функции Определение 2.8. Функция называется ограниченной функцией на множестве X, если существует такое положительное число М, что для всех х измножества X значения функции по абсолютной величине не превосходят числа { Функция называется ограниченной функцией на множестве X} . Определение 2.9. Функция называется ограниченнойфункцией при , если существует такое число и такое число , что при всех , для которых справедливо неравенство , имеет место следующее неравенство: . Множество ограниченнойфункцией при , принято обозначать символом . Иногда вместо записи при используют запись: при , понимая под этим, что является одной из функций, принадлежащих классу при . Приведем символическую запись определения ограниченной функции при : Аналогично можно определять при или Примерыограниченных функций: при для ; при для ; при для . ⇐ Предыдущая1234Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). |
Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения
Содержание:
- Сюръекция, инъекция и биекция
- Произведение множеств
По этой ссылке вы найдёте полный курс лекций по математике:
| Решение задач по математике |
Правило, задающее отображение f: X (или функцию /), можно условно изобразить стрелками (рис. 2.1). Бели в множестве У есть хотя бы один элемент) на который не указывает ни одна из стрелок, то это свидетельствует о том, что область значений функции f не заполняет все множество У, т.е. f(X) С У. Если же область значений / совпадает с У, т.е. f{X) = У, то такую функцию называют сюръективной} или короче — сюръекцией, и говорят, что функция / отображает множество X на множество У (в отличие от общего случая отображения множества X в множество У согласно определению 2.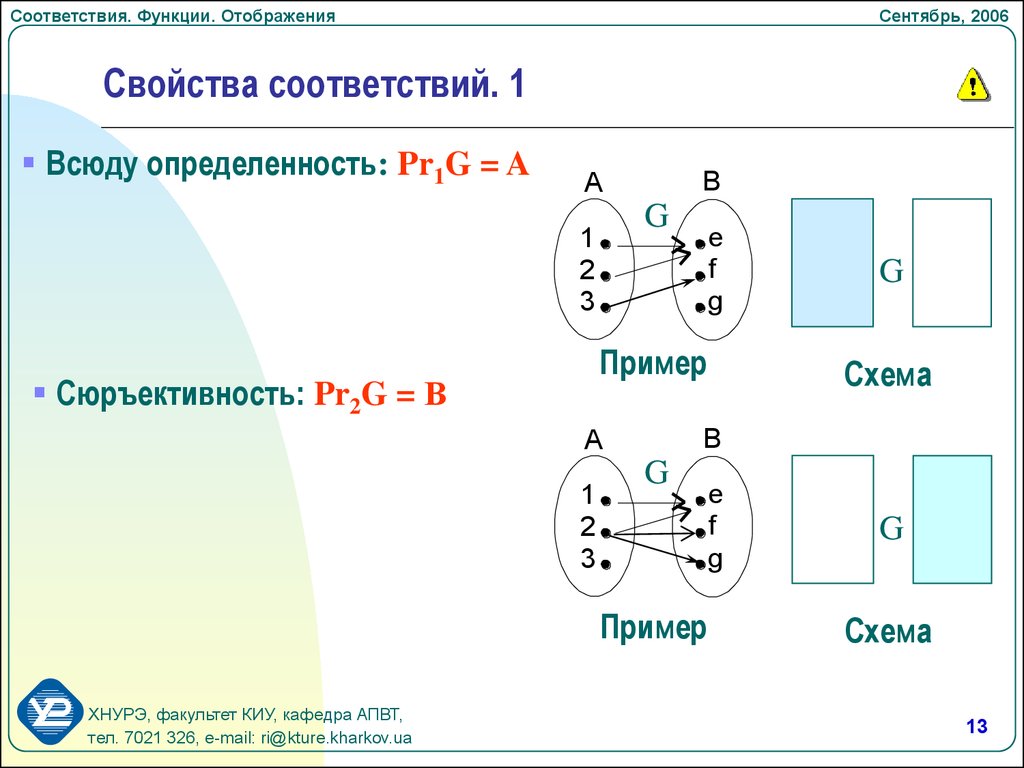 1). Итак, / : X есть сюръекция, если Vy 6 У Зх € X : /(х) = у. На рисунке в таком случае к каждому элементу множества У ведет хотя бы одна стрелка (рис. 2.2). При этом к некоторым элементам из У могут вести несколько стрелок. Если к любому элементу у € У ведет не более одной стрелки, то / называют инъективной функцией, или инъекцией. Эта функция не обязательно сюръективна, т.е. стрелки ведут не ко всем элементам множества У (рис. 2.3).
1). Итак, / : X есть сюръекция, если Vy 6 У Зх € X : /(х) = у. На рисунке в таком случае к каждому элементу множества У ведет хотя бы одна стрелка (рис. 2.2). При этом к некоторым элементам из У могут вести несколько стрелок. Если к любому элементу у € У ведет не более одной стрелки, то / называют инъективной функцией, или инъекцией. Эта функция не обязательно сюръективна, т.е. стрелки ведут не ко всем элементам множества У (рис. 2.3).
- Итак, функция /: X —У У представляет собой инъекцию, если два любых различных элемента из X имеют своими образами при отображении / два различных элемента из У, или Vy £ f{X) С У 3хеХ: f{x) = y. Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. Отображение /: X->У именуют биективным, или би-екцией, если каждый элемент у 6 У является образом некоторого и призом единственного элемента из X, т.е. Vy € f(X) = У Э!х € X : f(x) = у.
По сути, функция / в этом случае устанавливает взаимно однозначное соответствие между множествами X и У, и потому ее часто называют взаимно однозначной функцией. Очевидно, что функция / биективна тогда и только тогда, когда она одновременно инъективна и сюръективна. В этом случае стрелки (рис. 2.4) соединяют попарно каждый элемент из X с каждым элементом из У.
Очевидно, что функция / биективна тогда и только тогда, когда она одновременно инъективна и сюръективна. В этом случае стрелки (рис. 2.4) соединяют попарно каждый элемент из X с каждым элементом из У.
При этом никакие два элемента из X не могут быть соединены стрелкой с одним и тем же элементом из У, ибо / инъективна, и никакие два элемента из У не могут быть соединены стрелками с одним и тем же элементом из X из-за требования единственности образа в определении 2.1 отображения.
Каждый элемент из X участвует в попарном соединении, поскольку X — область определения функции /. Наконец, каждый элемент из У тоже участвует в одной из пар, ибо / сюръективна. Роли X и У в этом случае как бы совершенно одинаковы, и если повернуть все стрелки вспять (рис. 2.5), то получим иное отображение или иную функцию д), которое тоже и инъективно, в сюръективно. Отображения (функции), допускающие такое обращение, будут играть большую роль в дальнейшем.
В частном случае множества X и У могут совпадать (X = У).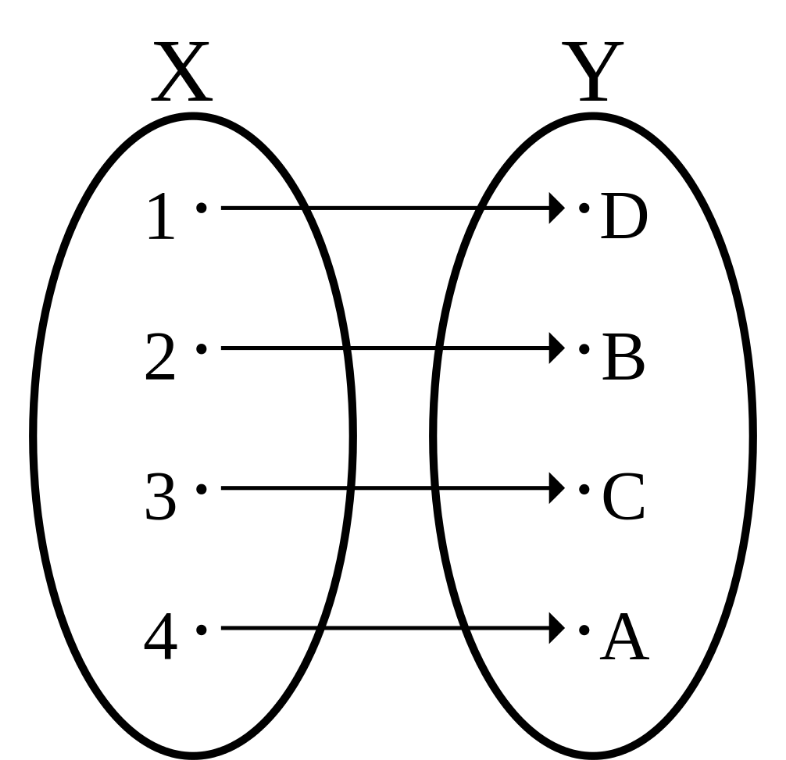 |
Тогда биективная функция будет осуществлять отображение множества X на себл. Биекцию множества на себя называют также пре-образов анием. 2.3. Обратное отображение Пусть /: X —? У — некоторая биекция и пусть у € У. Обозначим через /_1(у) единственный элемент х€Х, такой, что /(г) = у. Тем самым мы определим некоторое отображение 9 : Y Xу которое является снова биекцией. Ее называют обратным отображением, или обратной биекцией к /. Часто ее также называют просто обратной функцией и обозначают /»*. На рис. 2.5 функция д как раз и является обратной к /, т.е. д = f’1.
Возможно вам будут полезны данные страницы:
| Концентрация растворенного вещества |
| Ионно-молекулярные уравнения реакции |
| Объемно-планировочное решение здания (ОПР) Расположение (компоновка) помещений |
| Круги Эйлера фигуры, условно изображающие множества |
Функция /, определяемая формулой у = За — 2, я,у € R, является биекцией. комсество действительных чисел.
комсество действительных чисел.
- Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. 2.4. Композиция отображений Если f:X-*Y и g:Y-*Zy то отображение (р:Х -+Z, заданное для каждого а: 6 А» формулой =, именуют композицией (суперпозицией) отображений (функций) / и д> или сложной функцией, и обозначают ро/ (рис. 2.6).
- Таким образом, сложная функция до f реализует правило: я Применяй сначала /, а затем ди, т.е. в композиции операций «до/ надо начинать с операции /, расположенной справа. Отметим, что композиция Рис. 2.6 отображений ассоциативна, т.е.если /: X -+Y , д: Y Z и h: Z-*H> то тогда (hog)of = = ho(gof)i что проще записывают в виде ho до /. Проверим это следующим образом: На любом wK«oaicecmee X определено отображение 1х -X X, называемое тождественным, обозначаемое часто также idx и задаваемое формулой Ix(x) = x Vx € А». Его -действие состоит в том, что оно оставляет все на своих местах.

Так, если является биекцией, обратной к биекции /: Х-+У, то /»1о/ = /х, а /о/-1 = /у, где и /у — тождественные отображения множеств X и У соответственно. Обратно, если отображения f: X ->Y и р : У Л» таковы, что gof = Ix и fog = /у, то функция / является биекцией, а у — ее обратной биекцией.
Очевидно, что если / — биекция Л» на У, а $ — биекция У на Z, то gof является биекцией X на Z, а будет по отношению к ней обратной биекцией. 2.5. Произведение множеств. График отображения Напомним, что две взаимно перпендикулярные координатные оси с масштабом, одинаковым для обеих осей, задают на плоскости прямоугольную декартову систему координат (рис. 2.7). Точку О пересечения координатных осей называют начало* координат. Каждой точке М можно поставить в соответствие пару (я, у) действительных чисел где х — координата точки Мх на ко-ординатной оси Ох, а у — координата точки Му на координатной оси Оу. Точки Мх и Му являются основаниями перпендикуляров, опущенных из точки М соответственно на оси Ох и Оу. Числа х и у называют координатами точки М ( в выбранной системе координат), причем х называют абсциссой точки М, а у — ординатой этой точки.
Числа х и у называют координатами точки М ( в выбранной системе координат), причем х называют абсциссой точки М, а у — ординатой этой точки.
Очевидно, что каждой паре (а, Ь) действительных чисел а, 6 6R соответствует на плоскости точка М, имеющая эти числа своими координатами. И обратно, каждой точке М плоскости соответствует пара (а, 6) действительных чисел а и 6. В общем случае пары (а, Ь) и (6, а) определяют разные точки, т.е. существенно, какое из двух чисел а и b стоит в обозначении пары на первом месте. Таким образом, речь идет об упорядоченной паре. В связи с этим пары (а, 6) и (6, а) считают равными между собой, и они определяют одну и ту же точку на плоскости, если только а = 6. Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. Множество всех пар действительных чисел, а также множество точек плоскости обозначают R2. Это обозначение связано с важным в теории множеств понятием прямого (или дек ар-това) произведения множеств (часто говорят просто о произведении множеств). Определение 2.2.
Определение 2.2.
Произведением множеств А и В называют множество Ах В возможных упорядоченных пар (ж, у), где первый элемент взят из А, а второй — из В, так что Равенство двух пар (х, у) и (&’, у’) определяют условиями х = х’ и у = у7. Пары (я, у) и (у, х) считают различными, если хфу. Это особенно важно иметь в виду, когда множества А и В совпадают. Поэтому в общем случае А х В ф В х Л, т.е. произведение произвольных множеств не коммутативно, но оно дистрибутивно по отношению к объединению, пересечению и разности множеств: где обозначает одну из трех названных операций.
Произведение множеств
Произведение множеств существенно отличается от указанных операций над двумя множествами. Результатом выполнения этих операций является множество, элементы которого (если оно не пустое) принадлежат одному или обоим исходным множествам. Элементы же произведения множеств принадлежат новому множеству и представляют собой объекты иного рода по сравнению с элементами исходных множеств. Аналогично определению 2.2 можно ввести понятие произведения более чем двух множеств. Множества (А х В) х С и А*х (В х С) отождествляют и обозначают просто А х В х С, так что . Произведения Ах Ау Ах Ах А и т.д. обозначают, как правило, через А2 , А3 и т.д. Очевидно, плоскость R2 можно рассматривать как произведение R х R двух экземпляров множества действительных чисел (отсюда и происходит обозначение множества точек плоскости как произведения двух множеств точек числовой прямой). Множеству точек геометрического (трехмерного) пространства соответствует произведение R х R х R трех экземпляров множества точек числовой прямой, обозначаемое R3.
Аналогично определению 2.2 можно ввести понятие произведения более чем двух множеств. Множества (А х В) х С и А*х (В х С) отождествляют и обозначают просто А х В х С, так что . Произведения Ах Ау Ах Ах А и т.д. обозначают, как правило, через А2 , А3 и т.д. Очевидно, плоскость R2 можно рассматривать как произведение R х R двух экземпляров множества действительных чисел (отсюда и происходит обозначение множества точек плоскости как произведения двух множеств точек числовой прямой). Множеству точек геометрического (трехмерного) пространства соответствует произведение R х R х R трех экземпляров множества точек числовой прямой, обозначаемое R3.
- Произведение п множеств действительных чисел обозначают Rn. Это множество представляет собой всевозможные наборы (xj, Х2, хп) из п действительных чисел Х2) хп £ R, а любая точка х* из Rn есть такой набор (xj, х, х*) действительных чисел хп € К*
- Произведение п произвольных множеств есть множество упорядоченных наборов из п (в общем случае разнородных) элементов.
 Для таких наборов употребляют названия кортеж или n-ка (произносят „энка»). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У.
Для таких наборов употребляют названия кортеж или n-ка (произносят „энка»). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У. - Такое множество называют графиком отображения f (или графиком функции я*»- Пример 2.5. В случае XCR и Y = К каждая упорядоченная пара задает координаты точки на плоскости R2. Если при этом X является промежутком числовой прямой R, то график функции может представлять некоторую линию (рис. 2.9). Пример 2.6. Ясно, что при XCR2 и У = R график функции есть некоторое множество точек в R3, которое может представлять некоторую поверхность (рис. 2.10).
Если же X С R, а У = R2, то график функции также есть множество точек в R3, которое может представлять некоторую линию, пересекаемую плоскостью х = const лишь в одной точке М с тремя координатами х} yi, у2 (рис. 2.11). # Все упомянутые примеры графиков функции являются важнейшими объектами математического анализа, и в дальнейшем они будут подробно рассмотрены.
2.11). # Все упомянутые примеры графиков функции являются важнейшими объектами математического анализа, и в дальнейшем они будут подробно рассмотрены.
Бинарное отношение. Биекция .Сюръекция. Инъекция. в теории…
Бинарное отношение. Биекция .Сюръекция. Инъекция. в теории…Привет, сегодня поговорим про бинарное отношение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое бинарное отношение, биекция, сюръекция, инъекция , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
бинарное отношение в математике — двухместное отношение между любыми двумя множествами и , то есть всякое подмножество декартова произведения этих множеств: . Бинарное отношение на множестве — любое подмножество , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.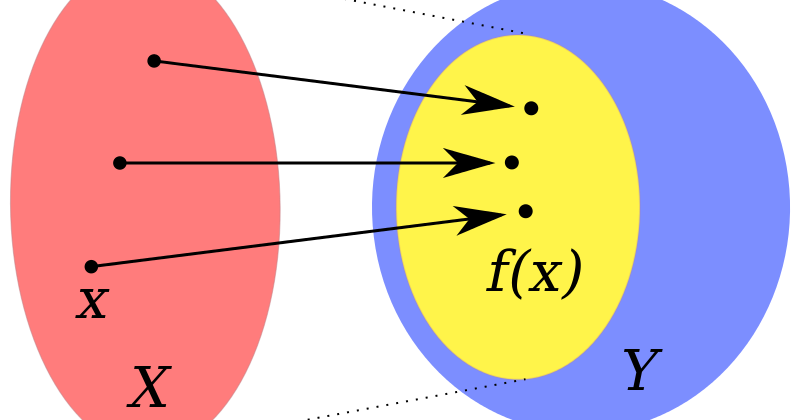
Бинарным отношением между двумя множествами называется соответствие элементов одного из них элементам второго.
Определение
Пусть даны два множества и , и пусть — подмножество их декартова произведения. Тогда тройка называется бинарным отношением между и Утверждение обычно записывается в виде и читается » соотносится с » Если то пишут или
Связанные определения
Множество всех первых элементов пар из называется областью определения отношения и обозначается как .
- Множество всех вторых элементов пар из называется областью значения отношения и обозначается как .
- Инверсия (обратное отношение) — это множество и обозначается, как .
- Композиция (суперпозиция) бинарных отношений и — это множество и обозначается, как .
Свойства отношений
Бинарное отношение на некотором множестве может обладать различными свойствами, например:
- рефлексивность: ,
- антирефлексивность (иррефлексивность): ,
- корефлексивность: ,
- симметричность: ,
- антисимметричность: ,
- асимметричность: , эквивалентна одновременной антирефлексивности и антисимметричности отношения,
- транзитивность: ,
- евклидовость: ,
- полнота (или связность): ,
- связность (или слабая связность): ,
- коннексность (англ.
 connex): ,
connex): , - трихотомия: верно ровно одно из трех утверждений: , или .
Виды отношений
- Рефлексивное транзитивное отношение называется отношением квазипорядка.
- Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
- Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.
- Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка.
- Полное антисимметричное (для любых выполняется или ) транзитивное отношение называется отношением линейного порядка.
- Антирефлексивное антисимметричное отношение называется отношением доминирования.
Виды бинарных отношений
- Обратное отношение (отношение, обратное к ) — это двухместное отношение, состоящее из пар элементов , полученных перестановкой пар элементов данного отношения .
 Обозначается: . Для данного отношения и обратного ему верно равенство: .
Обозначается: . Для данного отношения и обратного ему верно равенство: . - Взаимо-обратные отношения (взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу . Об этом говорит сайт https://intellect.icu . Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого.
- Рефлексивное отношение — двухместное отношение , определенное на некотором множестве и отличающееся тем, что для любого этого множества элемент находится в отношении к самому себе, то есть для любого элемента этого множества имеет место . Примеры рефлексивных отношений: равенство,одновременность, сходство.
- Антирефлексивное отношение (иррефлексивное отношение; так же, как антисимметричность не совпадает с несимметричностью, иррефлексивность не совпадает с нерефлексивностью) — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любого элемента этого множества неверно, что оно находится в отношении к самому себе (неверно, что ), то есть возможен случай, что элемент множества не находится в отношении к самому себе.

- Транзитивное отношение — двухместное отношение , определенное на некотором множестве и отличающееся тем, что для любых из и следует (). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».
- Нетранзитивное отношение — двухместное отношение , определенное на некотором множестве и отличающееся тем, что для любых этого множества из и не следует (). Пример нетранзитивного отношения: «x отец y»
- Симметричное отношение — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любых элементов и этого множества из того, что находится к в отношении , следует, что и находится в том же отношении к — . Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность.
- Антисимметричное отношение — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любых и из и следует (то есть и выполняются одновременно лишь для равных между собой членов).

- Асимметричное отношение — бинарное отношение , определенное на некотором множестве и отличающееся тем, что для любых и из следует . Пример: отношения «больше» (>) и «меньше» (<).
- Отношение эквивалентности — бинарное отношение между объектами и , являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность.
- Отношение порядка — отношение, обладающие только некоторыми из трех свойств отношения эквивалентности: отношение рефлексивное и транзитивное, но несимметричное (например, «не больше») образует нестрогий порядок, а отношение транзитивное, но нерефлексивное и несимметричное (например, «меньше») — строгий порядок.
- Функция одного переменного — бинарное отношение , определенное на некотором множестве, отличающееся тем, что каждому значению отношения соответствует лишь единственное значение . Свойство функциональности отношения записывается в виде аксиомы: .

- биекция (взаимно-однозначное отношение) — бинарное отношение , определенное на некотором множестве, отличающееся тем, что в нем каждому значению соответствует единственное значение , и каждому значению соответствует единственное значение .
- Связанное отношение — бинарное отношение , определенное на некотором множестве, отличающееся тем, что для любых двух различных элементов и из этого множества, одно из них находится в отношении к другому (то есть выполнено одно из двух соотношений: или ). Пример: отношение «меньше» (<).
Операции над отношениями
Так как отношения, заданные на фиксированной паре множеств и суть подмножества множества , то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных , :
,
,
.
Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.
Например, , , то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрого порядка, а их пересечение пусто.
Кроме перечисленных важное значение имеют еще операции обращения и умножения отношений, определяемые следующим образом. Если , то обратным отношением называется отношение , определенное на паре , и состоящее из тех пар , для которых . Например, .
Пусть , . Композицией (или произведением) отношений и называется отношение такое, что:
.
Например, для отношения строгого порядка на множестве натуральных числе его умножение на себя определено следующим образом: .
Бинарные отношения и называются перестановочными, если . Для любого бинарного отношения , определенного на , имеет место , где символом обозначено равенство, определенное на . Однако равенство не всегда справедливо.
Имеют место следующие тождества:
- ,
- ,
- ,
- ,
- ,
- ,
- .

Аналоги последних двух тождеств для пересечения отношений не имеют места.
Типы отношений
сюръекция , инъекция и биекция.
— Отображение f:x->y называется СЮРЪЕКЦИЕЙ, если Ay∈Y ∃ x∈X:y=f(x). Тогда y — образ, x — прообраз y.
— Отображение f:x->y называется ИНЪЕКЦИЕЙ, если x1 ≠ x2 => f(x1)≠f(x2), те разные элементы множества X переводятся в разные элементы множества Y.
или f(x1)≠f(x2) => x1=x2
— Отображение f:x->y называется БИЕКЦИЕЙ, если оно одновременно сюръективно и инъективно. При биективном отражении каждому элементу одного множества соответсвует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает теми же свойствами.
Бинарное отношение называется
- инъективным, если
- полным слева, если
- сюръективным (или полным справа), если
- функциональным, если
- функцией, если оно полно слева и функционально;
- биективным, если оно полно слева и справа, а также инъективно и функционально.

Виды отношений
- Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
- Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.
Бинарное отношение на множестве называется отношением частичного порядка, если оно удовлетворяет свойствам
- рефлексивности: для всех ;
- антисимметричности: для всех ;
- транзитивности: для всех .
Определение. Бинарное отношение f называется функцией, если из Îf и Îf следует, что y=z.
Поскольку функции являются бинарными отношениями, то две функции f и g равны, если они состоят из одних и тех же элементов. Область определения функции обозначается Df, а область значений – Rf. Определяются они так же, как и для бинарных отношений.
Если f – функция, то вместо Îf пишут y=f(x) и говорят, что y – значение, соответствующее аргументу х, или y – образ элемента х при отображении f.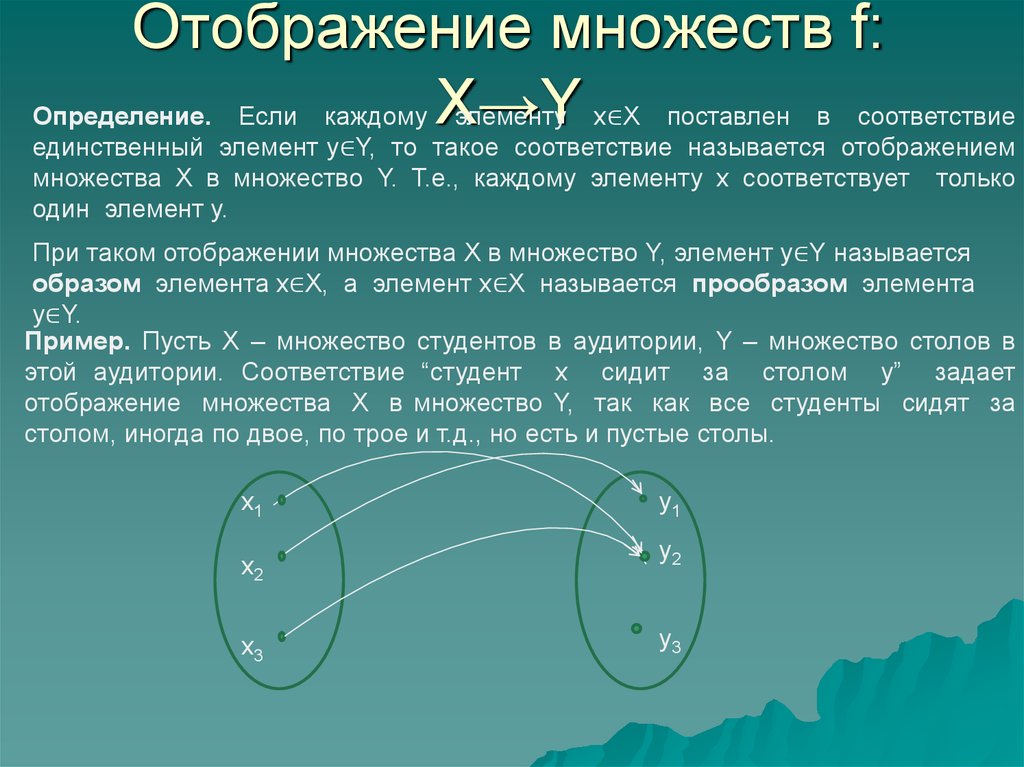 При этом хназывается прообразом элемента y.
При этом хназывается прообразом элемента y.
Определение. Назовем f n-местной функцией из Х в Y если f:Xn®Y. Тогда пишем y=f(x1, x2, …, xn) и говорим, что y – значение функции при значении аргументов x1, x2, …, xn.
Пусть f:X®Y.
Определение. Функция f называется инъективной, если для любых х1, х2, y из y=f(x1) и y=f(x2) следует, что x1=x2, то есть каждому значению функции соответствует единственное значение аргумента.
Определение. Функция f называется сюръективной, если для любого элемента yÎY существует элемент хÎХ такой, что y=f(x).
Определение. Функция f называется биективной, если f одновременно сюръективна и инъективна.
Рисунок 9 иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.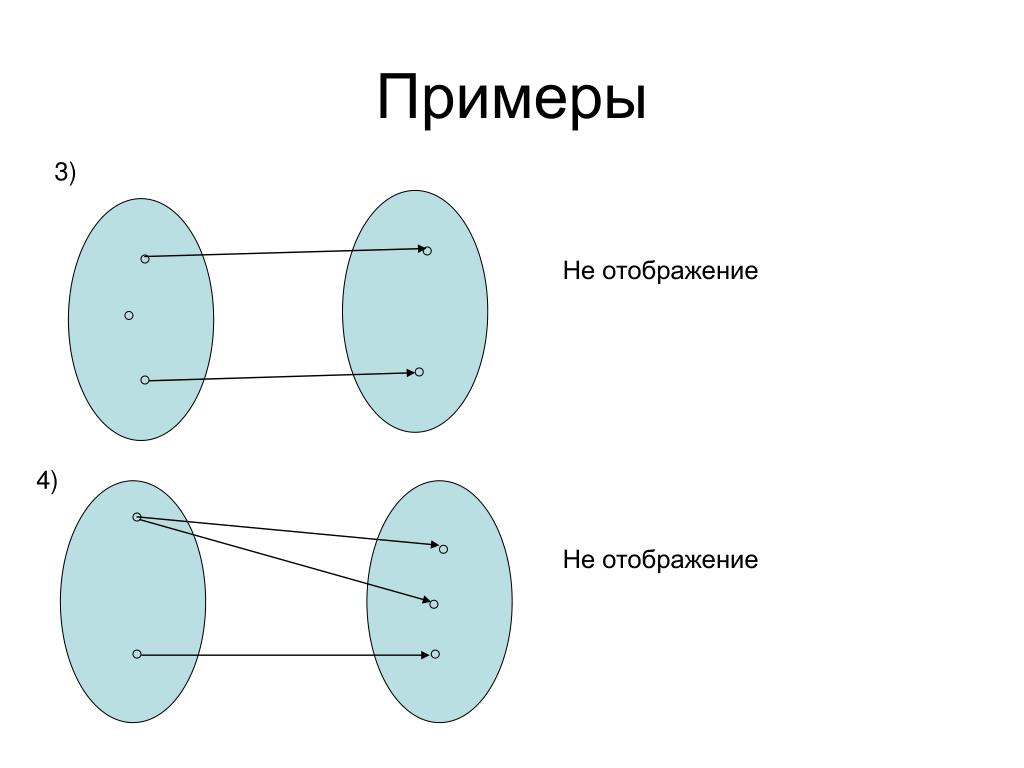
Пример 9.
Рассмотрим три функции, заданные на множестве действительных чисел и принимающих значение в этом же множестве:
- функция f(x)=ex — инъективна, но не сюръективна;
- функция f(x)=x3-x – сюръективна, но не инъективна;
- функция f(x)=2x+1 – биективна.
Ну вот возьмем два множества: множество учеников и множество стульев в классе. И будем устанавливать соответсвие между этими двумя множествами, т. е. просто рассаживать учеников на стулья.
1. Если каждый ученик сел на отдельный стул (некоторые стулья могут остаться свободными) , то это инъекция. Понятно, что при таком отображение количество стульев не может быть меньше количества учеников (ученики не могут садится по два на один стул) .
2. Если все стулья оказались заняты (на некоторых могут сидеть и по два или больше учеников) , то это сюръекция. В этом случает уже количество учеников не может быть меньше стульев.
3. Если каждый ученик сидит на отдельном стуле, и нет ни свободных стульев, ни учеников, которым стульев не хватило — это биекция. Т. е. биекция это одновременно и инъекция (каждый ученик сидит на отдельном стуле) и сюръекция (все стулья заняты) . Для возможности такого отображения (биекции) количество учеников должно быть в точности равно количеству стульев.
Естественно вместо учеников и стульями может быть что угодно, например числовые множества.
Все эти соответсвия могут устанавляваться и между бесконечными множествами. И кроме того, между конечным и бесконечным — инъекция, или бесконечным и конечным — сюръекция.
См. также
- толерантности ослабленная форма эквивалентности.
- Отношение порядка отношение порядка ,
- отношение эквивалентности ,
- Эквиваленция логическая операция .
- Знак равенства
Я хотел бы услышать твое мнение про бинарное отношение Надеюсь, что теперь ты понял что такое бинарное отношение, биекция, сюръекция, инъекция
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Инъективный, Сюръективный и Биективный
«Инъективный, Сюръективный и Биективный» говорит нам о том, как ведет себя функция.
Функция — это способ сопоставления элементов набора «А» – набора «В»:
Давайте посмотрим на это более внимательно:
A Общая функция точек от каждого члена «A» до члена «B».
Это никогда не имеет одного «А», указывающего на несколько «В», поэтому «один ко многим» не подходит в функции (так что что-то вроде «f(x) = 7 или 9″ не допускается)
Но несколько «A» могут указывать на один и тот же «B» ( в порядке )
Инъективное число означает, что у нас не будет двух или более «А», указывающих на одно и то же «В».
Таким образом, «многие к одному» НЕ ОК, (что подходит для общей функции).
Поскольку это тоже функция «один ко многим» не подходит
Но у нас может быть «В» без соответствующего «А»
Инъективный также называется « Один-к-одному »
Сюръективный означает, что каждое «В» имеет по крайней мере одно , соответствующее «А» (может быть, более одного).
Не будет пропущена буква «Б».
Bijective означает одновременно Injective и Surjective.
Думайте об этом как об «идеальном сочетании» между наборами: у каждого есть партнер, и никто не остается в стороне.
Так что есть идеальное » Индивидуальное соответствие » между элементами наборов.
(но не путайте это с термином «один к одному», используемым для обозначения инъективных).
Биективные функции имеют обратное !
Если каждый » A» переходит в уникальное «B», и каждому «B» соответствует «A», тогда мы можем двигаться вперед и назад, не сбиваясь с пути.
Прочтите обратные функции, чтобы узнать больше. Давайте посмотрим несколько примеров, чтобы понять, что происходит.
Когда A и B являются подмножествами действительных чисел, мы можем изобразить взаимосвязь.
Пусть у нас есть A по оси x и B по оси y, и посмотрите на наш первый пример:
Это не функция , потому что у нас есть A со многими
5 B 90. Это все равно, что сказать f(x) = 2
или 4. Это не проходит «Тест вертикальной линии» и, следовательно, не является функцией. Но это все еще действительные отношения, так что не сердитесь на это.
Теперь общая функция может быть такой:
A Общая функция
МОЖЕТ (возможно) иметь B со многими A . Например, синус, косинус и т.д. Совершенно допустимые функции.
Но « Инъективная функция » более строгая и выглядит так:
«Инъективная» (один к одному)
На самом деле мы можем провести «Проверку горизонтальной линии»:
Чтобы быть Injective , Горизонтальная линия никогда не должна пересекать кривую в 2 или более точках.
(Примечание: строго возрастающие (и строго убывающие) функции являются инъективными, вы можете прочитать о них для более подробной информации)
Итак:
- Если она также проходит тест горизонтальной линии , это инъективная функция
Формальные определения
Хорошо, ожидайте более подробной информации обо всем этом:
Инъективный
Функция f является инъективной тогда и только тогда, когда когда-либо f(x) = f(y) , x = y .
Пример: f ( x ) = x+5 из множества действительных чисел в является инъективной функцией.
Верно ли, что всякий раз, когда f(x) = f(y) , x = y ?
Представьте, что x=3, тогда:
- f(x) = 8
Теперь я говорю, что f(y) = 8, каково значение y? Оно может быть только 3, поэтому x=y
Пример: f ( x ) = x 2 из набора действительных чисел не является инъективной функцией . что-то вроде этого:
что-то вроде этого:
- f ( 2 ) = 4 и
- ф ( -2 ) = 4
Это противоречит определению f(x) = f(y) , x = y , потому что f(2) = f(-2), но 2 ≠ -2
6
Другими словами, есть два значения A , которые указывают на одно B .
НО если бы мы сделали его из набора натуральных числа к, то оно инъективно, потому что:
- ф ( 2 ) = 4
- f(-2) не существует, потому что -2 не является натуральным номер
Так что домен и кодовый домен каждого набора важны!
Сюръективный (также называемый «на»)
Функция A f (из набора A по B 6 9)0005 сюръективно тогда и только тогда, когда для каждого Y в B , в x .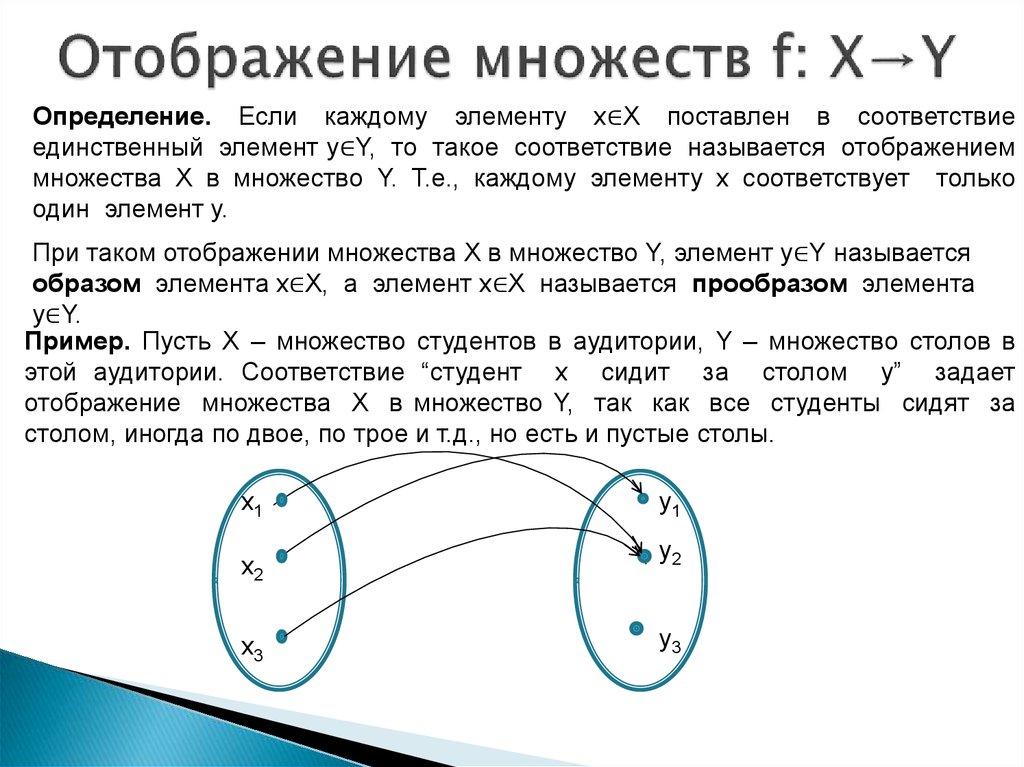 сюръективно
если и только если f(A) = B .
сюръективно
если и только если f(A) = B .
Проще говоря: каждое B имеет некоторое A.
Пример: Функция ф ( х ) = 2х из набора натуральных чисел к множеству неотрицательных четных чисел является сюръективной функцией.
А ф ( х ) = 2х из набора натуральных числа не являются сюръективными , потому что, например, ни один член in не может быть сопоставлен с 3 с помощью этой функции.
Биективное
A function f (from set A to B ) is bijective if, for every y in B , there is exactly one x в A такое, что f ( x ) = y
В качестве альтернативы, f является биективным, если оно соответствует 9-к-одному 901. 0411 между этими наборами, другими словами, как инъективное, так и сюръективное.
0411 между этими наборами, другими словами, как инъективное, так и сюръективное.
Пример: Функция f ( x ) = x 2 из множества положительных вещественных числа в положительные вещественные числа одновременно инъективны и сюръективны. Таким образом, это также биективное .
Но одна и та же функция из множества всех действительных чисел не является биективной, потому что мы могли бы иметь, например, оба
- f ( 2 )=4 и
- ф ( -2 )=4
Биекция, инъекция и сюръекция | Brilliant Math & Science Wiki
Функция f :X→Yf \двоеточие X\to Yf:X→Y — это правило, согласно которому каждому элементу x∈X, x\in X,x∈X ставится в соответствие элемент f (х)∈Y. f(x) \in Y.f(x)∈Y. Элемент f(x) f(x)f(x) иногда называют образом элемента x, x,x, а подмножество Y Y Y, состоящее из образов элементов из X XX, называют образом элемента f. с.ф. то есть
с.ф. то есть
image(f)={y∈Y:y=f(x) для некоторого x∈X}.\text{image}(f) = \{ y \in Y : y = f(x) \text{ для некоторого } x \in X\}.image(f)={y∈Y:y=f(x) для некоторого x∈X}.
Пусть f :X→Yf \ двоеточие X \to Yf:X→Y — функция. Тогда fff является инъективным , если различные элементы XXX отображаются в различные элементы Y.Y.Y.
То есть, если x1x_1x1 и x2x_2x2 находятся в XXX так, что x1≠x2x_1 \ne x_2x1=x2, то f(x1)≠f(x2)f(x_1) \ne f(x_2)f( x1)=f(x2).
Это эквивалентно тому, что если f(x1)=f(x2)f(x_1) = f(x_2)f(x1)=f(x2), то x1=x2x_1 = x_2x1=x2.
Синоним слова «инъективный» — «один к одному».
Функция f :Z→Z f\colon {\mathbb Z} \to {\mathbb Z}f:Z→Z, определяемая выражением f(n)=2n f(n) = 2nf(n)=2n, является инъективной: если 2×1=2×2, 2x_1=2x_2,2×1=2×2, деление обеих сторон на 2 2 2 дает x1=x2. х_1=х_2.х1=х2.
Функция f :Z→Z f\colon {\mathbb Z} \to {\mathbb Z}f:Z→Z определяется как f(n)=⌊n2⌋ f(n) = \big\lfloor\frac n2 \big\rfloorf(n)=⌊2n⌋ не является инъективным; например, f(2)=f(3)=1f(2) = f(3) = 1f(2)=f(3)=1, но 2≠3.
2 \ne 3.2=3.
Функция f :{немецкие футболисты, одетые для финала ЧМ-2014}→N f\colon \{ \text{немецкие футболисты, одетые для финала ЧМ-2014}\} \to {\mathbb N} f: {Немецкие футболисты, одетые для финала чемпионата мира по футболу 2014 года}→N, определяемые формулой f(A)=номер футболки Af(A) = \text{номер футболки команды } Af(A)=номер футболки команды A инъективен ; никаким двум игрокам не разрешалось носить один и тот же номер.
Существование инъективной функции дает информацию об относительных размерах ее области определения и диапазона:
Если X X X и Y Y Y конечные множества и f :X→Y f\colon X\to Y f:X→Y инъективно, то ∣X∣≤∣Y∣. |Х| \le |Y|.∣X∣≤∣Y∣.
ххх гггг ззз Ничего из вышеперечисленного
Пусть fff — взаимно однозначная (инъективная) функция с областью определения Df={x,y,z}D_{f} = \{x,y,z\} Df={x,y,z} и диапазон {1,2,3}.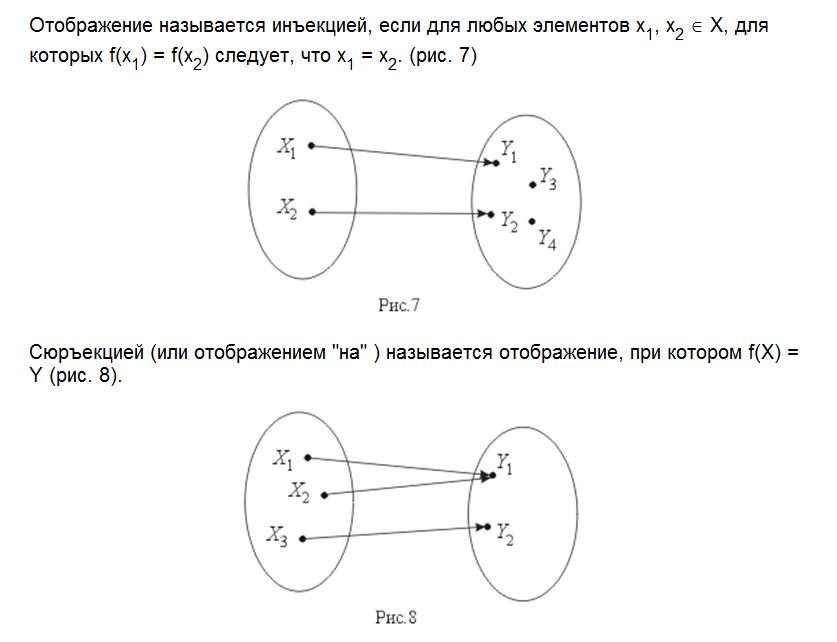 \{1,2,3\}.{1,2,3}. Дано, что только одно из следующих 333 утверждений верно, а остальные утверждения ложны: 9{-1} (1). f−1(1).
\{1,2,3\}.{1,2,3}. Дано, что только одно из следующих 333 утверждений верно, а остальные утверждения ложны: 9{-1} (1). f−1(1).
Пусть f :X→Yf \colon X\to Yf:X→Y — функция. Тогда fff является сюръективным , если каждый элемент YYY является образом хотя бы одного элемента X.X.X. То есть изображение(f)=Y. \text{изображение}(f) = Y.image(f)=Y.
Символически,
∀y∈Y,∃x∈X такие, что f(x)=y.\для всех y \in Y, \существует x \in X \text{ такое, что } f(x) = y.∀y∈Y, ∃x∈X такой, что f(x)=y.
Синоним слова «сюръективный» — «на».
Функция f :Z→Z f\colon {\mathbb Z} \to {\mathbb Z}f:Z→Z, определяемая как f(n)=2n f(n) = 2nf(n)=2n, не является сюръективной : не существует целого числа n nn такого, что f(n)=3, f(n)=3,f(n)=3, так как 2n=3 2n=32n=3 не имеет решений в Z. \mathbb З.З. Так что 3 33 не входит в образ f. с.ф.
Функция f :Z→Z f\colon {\mathbb Z} \to {\mathbb Z}f:Z→Z определяется как f(n)=⌊n2⌋ f(n) = \big\lfloor\frac n2 \big\rfloorf(n)=⌊2n⌋ сюръективно.
Для любых целых чисел m, m,m заметим, что f(2m)=⌊2m2⌋=m, f(2m) = \big\lfloor \frac{2m}2 \big\rfloor = m,f(2m)=⌊ 22m⌋=m, поэтому m m m находится в образе f. с.ф. Таким образом, образ fff равен Z.\mathbb Z.Z.
Функция f :{сенаторы США}→{штаты США}f \двоеточие \{\text{сенаторы США}\} \to \{\text{штаты США}\}f:{сенаторы США}→{штаты США } определяется как f(A)=состояние, которое представляет Af(A) = \text{состояние, которое } A \text{ представляет}f(A)=состояние, которое представляет A, является сюръективным; в каждом штате есть хотя бы один сенатор.
Существование сюръективной функции дает информацию об относительных размерах ее области определения и диапазона:
Если X X X и Y Y Y конечные множества и f :X→Y f\colon X\to Y f:X→Y сюръективно, то ∣X∣≥∣Y∣. |Х| \ge |Y|.∣X∣≥∣Y∣.
Пусть E={1,2,3,4} E = \{1, 2, 3, 4\} E={1,2,3,4} и F={1,2}.F = \ {1, 2\}.F={1,2}. Тогда каково число онтофункций из E E E в F? Ф? Ф?
Функция биективна для двух множеств, если каждый элемент одного множества сопряжен только с одним элементом второго множества, а каждый элемент второго множества сопряжен только с одним элементом первого множества. Это означает, что все элементы спарены и спарены один раз.
Это означает, что все элементы спарены и спарены один раз.
Пусть f :X→Yf \ двоеточие X \to Y f:X→Y — функция. Тогда fff является биективным , если оно инъективно и сюръективно; то есть каждый элемент y∈Y y \in Yy∈Y является образом ровно одного элемента x∈X. х \in X.x∈X.
Функция f :R→R f \colon {\mathbb R} \to {\mathbb R} f:R→R, определяемая формулой f(x)=2x f(x) = 2xf(x)=2x, является биекцией .
Функция f :Z→Z f \colon {\mathbb Z} \to {\mathbb Z} f:Z→Z, определяемая как f(n)={n+1if n нечетноn−1if n четно f( n) = \begin{cases} n+1 &\text{если } n \text{ нечетно} \\ n-1&\text{если } n \text{ четно}\end{cases}f(n) ={n+1n−1если n нечетноесли n четно является биекцией. 9\text{th} \text{ month}f(M)= число n такое, что M – n-й месяц, является биекцией.
Обратите внимание, что приведенные выше обсуждения подразумевают следующий факт (примеры см. Вики биективных функций):
Если X X X и Y Y Y — конечные множества и f :X→Y f\colon X\to Y f:X→Y биективно, то ∣X∣=∣Y∣.
|Х| = |Y|.∣X∣=∣Y∣.
Следующая альтернативная характеристика биекций часто полезна в доказательствах:
Предположим, что X X X непусто. Тогда f :X→Y f \colon X \to Y f:X→Y является биекцией тогда и только тогда, когда существует функция g :Y→X g\colon Y \to X g:Y→X такая, что g∘f g \circ f g∘f — тождество на X X X и f∘g f\circ gf∘g — тождество на Y; Г;Г; то есть g(f(x))=xg\big(f(x)\big)=xg(f(x))=x и f(g(y))=y f\big(g(y)\ big)=y f(g(y))=y для всех x∈X,y∈Y.x\in X, y \in Y.x∈X,y∈Y. Когда это происходит, функция g g g называется 92.f(x)=x2. Почему бы и нет?)\большое))
4.3 Инъекции и операции
Два простых свойства, которыми могут обладать функции, оказываются
исключительно полезно. Если кодовый домен функции также является ее диапазоном,
тогда функция на или сюръективно . Если функция не отображает два
различных элементов в домене к одному и тому же элементу в диапазоне, это один к одному или инъективный . В этом разделе мы определяем эти понятия
«официально» с точки зрения прообразов и изучить несколько простых примеров
и последствия.
В этом разделе мы определяем эти понятия
«официально» с точки зрения прообразов и изучить несколько простых примеров
и последствия.
Определение 4.3.1 Функция $f\colon A\to B$ является инъективным, если каждый $b\in B$ имеет не более одного прообраза в $A$, т. е. не более одного $a\in A$ такое, что $f(a)=b$. $\квадрат$
Пример 4.3.2 Предположим, что $A=\{1,2,3\}$ и $B=\{r,s,t,u,v\}$ и
$$ \начать{массив}{} f(1)=s&g(1)=r\\ f(2)=t&g(2)=t\\ f(3)=r&g(3)=r\\ \конец{массив} $$
Здесь $f$ инъективен, так как $r,s,t$ имеют один прообраз и
$u,v$ не имеют прообразов. С другой стороны, $g$ не может быть инъективным,
поскольку $r$ имеет более одного прообраза.
$\квадрат$
9х$. Функция $f$ не может быть инъективной, так как любое положительное
число имеет два прообраза (его положительный и отрицательный квадратный корень). На
с другой стороны, $g$ инъективен, так как если $b\in \R$, то $g(x)=b$
имеет не более одного решения (если $b>0$, то имеет одно решение, $\log_2 b$,
и если $b\le 0$ не имеет решений). $\квадрат$
$\квадрат$
Пример 4.3.4. Если $A\subseteq B$, то включение отображение из $A$ в $B$ инъективно. $\квадрат$
Инъективная функция называется инъекцией . Инъекцию также можно назвать функция «один к одному» (или 1–1); некоторые люди считают это менее формальным чем «инъекция».
Существует еще один способ характеризовать инъективность, который полезен для делать доказательства. Сказать, что элементы домена кода имеют не более один прообраз должен сказать, что никакие два элемента домена не берутся в тот же элемент, как мы указали в первом абзаце. В других словами, $f\colon A\to B$ инъективен тогда и только тогда, когда для всех $a,a’\in A$, $a\ne a’$ влечет $f(a)\ne f(a’)$. Принимая во внимание противоположность, $f$ инъективен тогда и только тогда, когда для всех $a,a’ \in A$ $f(a)=f(a’)$ влечет $а=а’$.
Теорема 4.3.5. Если $f\colon A\to B$ и $g\,\colon B\to C$ инъективны, то $g\circ f\colon A \to C$ инъективна также.
Доказательство. Предположим, что $g(f(a))=g(f(a’))$. Поскольку $g$ инъективен,
$f(а)=f(а’)$. Поскольку $f$ инъективен, $a=a’$. Таким образом, $(g\circ
f)(a)=(g\circ f)(a’)$ влечет $a=a’$, поэтому $(g\circ f)$ инъективен. $\qed$
Предположим, что $g(f(a))=g(f(a’))$. Поскольку $g$ инъективен,
$f(а)=f(а’)$. Поскольку $f$ инъективен, $a=a’$. Таким образом, $(g\circ
f)(a)=(g\circ f)(a’)$ влечет $a=a’$, поэтому $(g\circ f)$ инъективен. $\qed$
Определение 4.3.6 Функция $f\colon A\to B$ сюръективна, если каждый $b\in B$ имеет хотя бы один прообраз, т. е. существует хотя бы один $a\in A$ такой, что $f(a)=b$. $\квадрат$ 9х $ это всегда положительна, $f$ не сюръективна (любая $b\le 0$ не имеет прообразов). На с другой стороны, для любого $b\in \R$ уравнение $b=g(x)$ имеет решение (а именно $x=\root 3 \of b$), поэтому $b$ имеет прообраз под $g$. Поэтому $g$ есть сюръективный. $\квадрат$
Пример 4.3.9. Предположим, что $A$ и $B$ — множества с $A\ne \emptyset$. затем $p\,\colon A\times B\to B$, заданный $p((a,b))=b$, является сюръективным и называется проекцией на $B$ . $\квадрат$
Пример 4.3.10. Для любого множества $A$ тождество карта $i_A$ одновременно инъективна и сюръективна. $\квадрат$
Сюръективная функция называется сюръекцией . Сюръекцию также можно назвать
на функцию; некоторые люди считают это менее формальным, чем
«сюръекция». Сказать, что функция $f\colon A\to B$ является
сюръекция означает, что каждое $b\in B$ находится в пределах $f$, т. е.
диапазон такой же, как кодовый домен, как мы указали выше.
Сюръекцию также можно назвать
на функцию; некоторые люди считают это менее формальным, чем
«сюръекция». Сказать, что функция $f\colon A\to B$ является
сюръекция означает, что каждое $b\in B$ находится в пределах $f$, т. е.
диапазон такой же, как кодовый домен, как мы указали выше.
Теорема 4.3.11. Предположим, что $f\colon A\to B$ и $g\,\colon B\to C$ сюръективные функции. затем $g\circ f\colon A \to C$ также сюръективен. 93-x$
| c) $\sin x$ | f) $|x|$ |
Пример 4.3.2
а) Найдите пример инъекции $f\colon A\to B$ и сюръекция $g\,\colon B\to C$ такая, что $g\circ f$ не является ни инъективным, ни сюръективным.
б) Найдите пример сюръекции $f\colon A\to B$ и вложение $g\,\colon B\to C$ такое, что $g\circ f$ не является ни инъективным, ни сюръективным.
Пример 4.3.3
а) Предположим, что $A$ и $B$ — конечные множества и
$f\colon A\to B$ инъективен.

 ..
.. (рис. 2.4)
(рис. 2.4) Существует табличный, графический, аналитический и словесный способ задания функции.
Существует табличный, графический, аналитический и словесный способ задания функции. Однако этот способ не всегда дает возможность точно определить численные значения аргумента и функции. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением.
Однако этот способ не всегда дает возможность точно определить численные значения аргумента и функции. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Функция может быть определена разными формулами на разных участках области своего задания.
Функция может быть определена разными формулами на разных участках области своего задания.
 ...
...
 ..
..
 Для таких наборов употребляют названия кортеж или n-ка (произносят „энка»). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У.
Для таких наборов употребляют названия кортеж или n-ка (произносят „энка»). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У. connex): ,
connex): , Обозначается: . Для данного отношения и обратного ему верно равенство: .
Обозначается: . Для данного отношения и обратного ему верно равенство: .




 2 \ne 3.2=3.
2 \ne 3.2=3.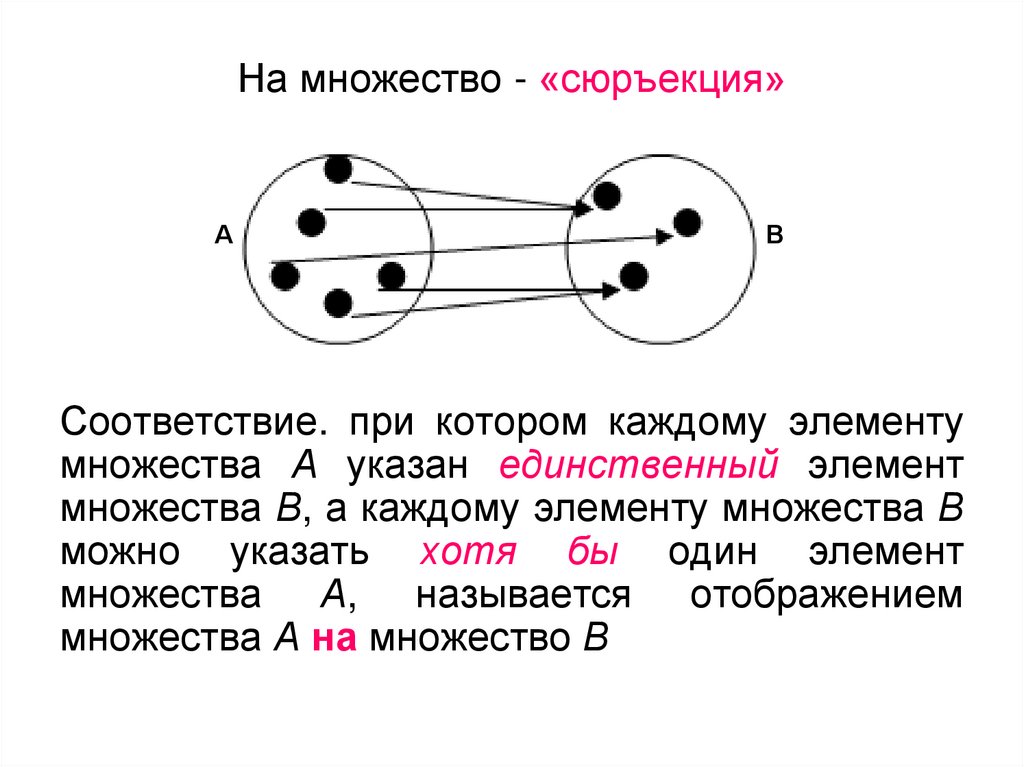 Для любых целых чисел m, m,m заметим, что f(2m)=⌊2m2⌋=m, f(2m) = \big\lfloor \frac{2m}2 \big\rfloor = m,f(2m)=⌊ 22m⌋=m, поэтому m m m находится в образе f. с.ф. Таким образом, образ fff равен Z.\mathbb Z.Z.
Для любых целых чисел m, m,m заметим, что f(2m)=⌊2m2⌋=m, f(2m) = \big\lfloor \frac{2m}2 \big\rfloor = m,f(2m)=⌊ 22m⌋=m, поэтому m m m находится в образе f. с.ф. Таким образом, образ fff равен Z.\mathbb Z.Z. |Х| = |Y|.∣X∣=∣Y∣.
|Х| = |Y|.∣X∣=∣Y∣.