Конфигурация | Название фигуры | Формула | Правило |
Треугольник | Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне | ||
Треугольник | Площадь треугольника равна половине произведения двух его сторон на синус угла между ними | ||
Треугольник | Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон | ||
Треугольник | Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла
| ||
Треугольник | Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов
| ||
Треугольник | Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника | ||
Прямоугольный треугольник | Площадь прямоугольного треугольника равна половине произведения его катетов | ||
Равнобедренный треугольник | Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания | ||
Равносторонний треугольник | Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх | ||
Равносторонний треугольник | Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх | ||
Треугольник | Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности | ||
Треугольник | Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов
| ||
Треугольник | Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник) | ||
Треугольник | Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника | ||
Прямоугольник | Площадь прямоугольника равна произведению двух соседних его сторон | ||
Квадрат | Площадь квадрата равна квадрату его стороны | ||
Квадрат | Площадь квадрата равна половине квадрата его диагонали | ||
Параллелограмм | Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне | ||
Параллелограмм | Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними | ||
Ромб | Площадь ромба равна произведению квадрата его стороны на синус одного из его углов
| ||
Ромб (дельтоид) | Площадь ромба (как и дельтоида) равна половине произведения его диагоналей | ||
Трапеция | Площадь трапеции равна произведению полусуммы её оснований на высоту | ||
Трапеция | Площадь трапеции равна произведению её средней линии на высоту | ||
Выпуклый четырёхугольник | Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними | ||
Вписанный четырёхугольник | Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон | ||
Круг | Площадь круга равна произведению числа «пи» на квадрат радиуса | ||
Круг | Площадь круга равна четверти произведения числа «пи» на квадрат диаметра | ||
Круговой сектор | формулы для случаев градусной и радианной мер центральных углов | Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору | |
Круговое кольцо | Площадь кругового кольца равна произведению числа «пи» на разность квадратов внешнего и внутреннего радиусов | ||
Круговое кольцо | Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров | ||
Круговое кольцо | Площадь кругового кольца равна удвоенному произведению числа «пи», среднего радиуса кольца и его ширины |
3.
 Площадь фигур — Фигуры В Пространстве
Площадь фигур — Фигуры В ПространствеПлощадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры. 1. Площадь поверхности куба равна произведению квадрата длины его грани и числа шесть. Формула площади куба: S = 6 a 2 где S — площадь куба,a — длина грани куба.
2. Площадь призмы Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы — сумма площадей ее боковых граней.
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
3. Площадь прямоугольного параллелепипеда Формула площади прямоугольного параллелепипеда: S = 2( a · b + a · h + b · h )
где S — площадь прямоугольного параллелепипеда,a — длина,b — ширина,h — высота.4. Площадь пирамиды Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметра оснований на апофему. 5. Площадь цилиндра Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту. Формула для вычисления площади боковой поверхности цилиндра: S = 2 π R h Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.Формула для вычисления площади полной поверхности цилиндра: S = 2 π R h + 2 π R 2 = 2 π R ( R + h ) где S — площадь,R — радиус цилиндра,h — высота цилиндра,π = 3,141592 . 6. Площадь конуса Площадь боковой поверхности конуса равна произведению его радиуса и образующей, умноженному на число π . Формула для вычисления площади боковой поверхности конуса: S = π R l Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.Формула для вычисления площади полной поверхности конуса: S = π R 2 + π R l = π R ( R + l ) где S — площадь,R — радиус основания конуса,l — образующая конуса,π = 3,141592 . 7. Площадь шара Площадь поверхности шара равна четырем его радиусам в квадрате, умноженным на число π. Формула площади шара: S = 4 π R 2 Площадь поверхности шара равна квадрату его диаметра, умноженного на число π. Формула площади шара: S = π D 2 где V — площадь шара,R — радиус шара,D — диаметр шара,π = 3,141592 . |
Площади фигур | Математические формулы
Формула площади треугольника по стороне и высоте
Найти
Известно, что:
Sah =
Вычислить ‘S’Формула площади треугольника по двум сторонам и углу между ними
Найти
Известно, что:
SabC =
Вычислить ‘S’Формула площади треугольника по трем сторонам (Формула Герона)
Найти
Известно, что:
Spabc =
Вычислить ‘S’Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Найти
Известно, что:
Spr =
Вычислить ‘S’Формула площади треугольника по трем сторонам и радиусу описанной окружности
Найти
Известно, что:
SabcR =
Вычислить ‘S’Формула площади прямоугольнogo треугольника
Найти
Известно, что:
Sab =
Вычислить ‘S’Площадь равностороннего треугольника
НайтиИзвестно, что:
Sa =
Вычислить ‘S’Формула площади квадрата по длине стороны
Найти
Известно, что:
Sa =
Вычислить ‘S’Формула площади квадрата по длине диагонали
Найти
Известно, что:
Sd =
Вычислить ‘S’Площадь прямоугольника
Найти
Известно, что:
Sab =
Вычислить ‘S’Площадь прямоугольника по длине диагонали
Найти
Известно, что:
Sdφ =
Вычислить ‘S’Формула площади параллелограмма по длине стороны и высоте
Найти
Известно, что:
Sah =
Вычислить ‘S’Формула площади параллелограмма по двум сторонам и углу между ними
Найти
Известно, что:
Sabα =
Вычислить ‘S’ Формула площади параллелограмма по диагоналям и углу между нимиНайти
Известно, что:
Sd1d2φ =
Вычислить ‘S’Формула площади ромба по длине стороны и углу
Найти
Известно, что:
Saα =
Вычислить ‘S’Формула площади ромба по длинам его диагоналей
Найти
Известно, что:
Sd1d2 =
Вычислить ‘S’Площадь произвольного вписанного четырёхугольника (формула Брахмагупты)
Найти
Известно, что:
Spabcd =
Вычислить ‘S’Формула площади трапеции
Найти
Известно, что:
Sabh =
Вычислить ‘S’Площадь трапеции через среднюю линию
Найти
Известно, что:
Smh =
Вычислить ‘S’Площадь правильного многоугольника вписанного в окружность
Найти
Известно, что:
SRn =
Вычислить ‘S’Площадь правильного многоугольника
Найти
Известно, что:
Snar =
Вычислить ‘S’Площадь равностороннего треугольника по радиусу описанной окружности
Найти
Известно, что:
SR =
Вычислить ‘S’Площадь равностороннего треугольника по радиусу вписанной окружности
Найти
Известно, что:
Sr =
Вычислить ‘S’Площадь равностороннего треугольника по висоте
Найти
Известно, что:
Sh =
Вычислить ‘S’Площадь квадрата по радиусу описанной окружности
Найти
Известно, что:
SR =
Вычислить ‘S’Площадь квадрата по радиусу вписанной окружности
Найти
Известно, что:
Sr =
Вычислить ‘S’ Площадь правильного шестиугольникаНайти
Известно, что:
Sa =
Вычислить ‘S’Площадь правильного шестиугольника по радиусу описанной окружности
Найти
Известно, что:
SR =
Вычислить ‘S’Площадь правильного шестиугольника по радиусу вписанной окружности
Найти
Известно, что:
Sr =
Вычислить ‘S’Площадь круга
Найти
Известно, что:
SπR =
Вычислить ‘S’Площадь сектора круга
Найти
Известно, что:
SRl =
Вычислить ‘S’Площадь сектора круга через угол
Найти
Известно, что:
SπRα =
Вычислить ‘S’Площадь меньшего сегмента круга
Найти
Известно, что:
SπRαS_ΔAOB =
Вычислить ‘S’Площадь большего сегмента круга
Найти
Известно, что:
SπRαS_ΔAOB =
Вычислить ‘S’Площадь сегмента круга
Найти
Известно, что:
SRπα =
Вычислить ‘S’Какие формулы площади для различных геометрических фигур?
Существует множество доступных геометрических форм/фигурок, и мы можем найти площадь каждой фигуры, используя различные формулы, основанные на их форме. Площадь фигуры можно определить как пространство, ограниченное замкнутой геометрической фигурой на двумерной плоскости. В этой статье мы найдем площадь нескольких геометрических фигур, используя разные формулы.
Площадь фигуры можно определить как пространство, ограниченное замкнутой геометрической фигурой на двумерной плоскости. В этой статье мы найдем площадь нескольких геометрических фигур, используя разные формулы.
Площадь треугольника
Площадь треугольника вычисляется путем умножения половины основания на высоту.
Площадь треугольника = (1/2) × основание × высота
Пример: Найдите площадь треугольника с высотой 6 см и основанием 4 см.
Решение:
Чтобы найти площадь треугольника, у нас была формула, т. е. (1/2) × основание × высота
Итак, для этого треугольника основание = 4 и высота = 6
Площадь = (1/2) × 4 × 6
= (1/2) × 24
= 12
Таким образом, площадь данного треугольника равна 12 см 2 .
Площадь квадрата
В квадрате длины всех сторон одинаковы, и чтобы найти площадь квадрата, нам нужно найти квадрат длины стороны.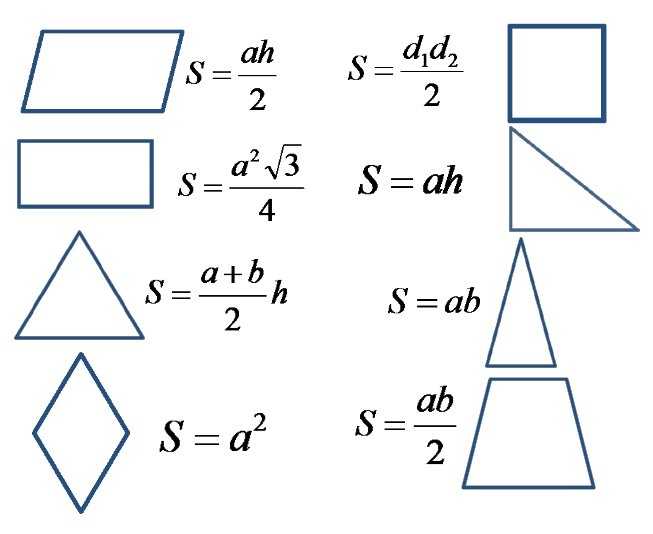
Площадь квадрата = сторона × сторона = сторона 2
Пример: Найдите площадь квадрата , каждая сторона которого имеет длину 4 см.
Решение:
Из данного рисунка имеем квадрат, каждая сторона которого равна 4см. Мы можем найти его площадь на
Площадь квадрата = сторона х сторона
Площадь прямоугольника
Площадь прямоугольника можно вычислить, умножив его длину на ширину. Потому что в прямоугольнике противоположные грани имеют одинаковую длину (размеры).
Площадь прямоугольника = длина × ширина
Примечание: Формула площади параллелограмма такая же, как и формула нахождения площади прямоугольника.
Пример: Какова площадь прямоугольника длиной 10 см и шириной 5 см.
Решение:
Площадь кругаИз данного рисунка,
Длина = 10 см
Ширина = 5 см
Площадь прямоугольника = длина × ширина
= 10 × 5
= 50 0003
SO, зона из области из области из области из области из области из области из области из зоны.
данный прямоугольник 50см 2
Площадь круга можно рассчитать по формуле πr 2 , где r — радиус круга, а π = 22/7
100002
3
3 Пример: Найдите площадь круга с радиусом 5см. Решение:
Из данных данных,
Радиус R = 5 см
Область круга = π × радиус 2
= (22/7) × 5 2
= (22/7) × 25
= 78,57 Приблизительно
, поэтому площадь круга составляет 78,57 см 2
Площадь трапеции
в трапезе. т. е. длины верха и низа. Для нахождения площади трапеции используется формула полусуммы длин двух оснований, умноженных на высоту.
Площадь трапеции = (1/2) × (основание1 + основание2) × высота
Пример. Найдите площадь приведенной ниже данной трапеции
Решение:
Из данного рисунка
Длина основания1 = 7см
Длина основания2 = 5 см
высота трапезии = 4cm
2 = 5 см
Площадь трапеции = (1/2) × (Base1 + Base2) × высота
= (1/2) × (5 + 7) × 4
= (1/2) × 12 × 4
= 24CM 2
Значит площадь данной трапеции 24см 2 .
Район затмения Прежде чем узнать формулу нахождения затмения, нам нужно узнать о затмении.
В геометрии затмение имеет форму овала и имеет большую и малую оси, как показано на рисунке. Чтобы найти площадь затмения, нам нужно выполнить умножение длины большой полуоси, малой полуоси и π.
Площадь затмения = π × (длина большой полуоси) × (длина малой полуоси)
Длина большой полуоси = длина большой оси/2
Длина малой полуоси = длина малой оси/ 2
Пример: Какова площадь затмения , если длина его большой оси и малой оси составляет 6 см и 3 см соответственно.
Решение:
Исходя из данных,
длина большой оси = 6
Длина незначительной оси = 3
Длина полу -основной оси = длина основной оси/2
= 6/2
= 3
Длина полуножной оси = длина незначительной оси/2
= 3 /2
=1,5
площадь затмения = π × (длина большой полуоси) × (длина малой полуоси)
= (22/7) × 3 × 1,5
= 14,14 Приблизительно
, поэтому для данной зоны затмения составляет 14,14 см 2
Площадь Ромб
Площадь расчеты по половине половины. произведение длин двух диагоналей ромба. Формула:
произведение длин двух диагоналей ромба. Формула:
Площадь ромба = (1/2) × длина (диагональ 1 ) × длина (диагональ 2 )
Графическое изображение ромба приведено ниже:
Пример: Найдите площадь ромба, диагонали которого равны 3 см и 6 см.
Решение:
Из данных данных,
Длина диагонального 1 = 3 см
Длина диагонального 2 = 6CM
Область пороба = (1/2). 1 ) × длина (диагональ 2 )
= (1/2) × 3 × 6
Значит площадь ромба 9см 2 .
Как запомнить формулы площади? – The Math Doctors
Студенты часто спрашивают о формулах для площадей или объемов. Иногда они просто ошеломлены количеством формул, которые им нужно знать; в других случаях им любопытно, откуда мы знаем, что они верны. Ответ на оба вопроса отчасти один и тот же: если вы хоть что-то знаете о том, откуда они берутся, вы можете либо легче их запомнить, либо просто извлечь их, когда они вам понадобятся.
Ответ на оба вопроса отчасти один и тот же: если вы хоть что-то знаете о том, откуда они берутся, вы можете либо легче их запомнить, либо просто извлечь их, когда они вам понадобятся.
Доктор Ян подчеркнул здесь, что мы не должны полагаться на память для большинства формул:
Математика для будущего в науках
Последние три года у меня были проблемы с математикой. Теоремы, уравнения, закономерности и т. д. кажутся громоздкими — запомнить их все невозможно. Или иногда я не понимаю концепцию... . Можете ли вы что-нибудь порекомендовать тем, кто хочет изучать математику самостоятельно и иметь возможность сохранять информацию на долгие годы?
Часть его ответа:
Могу вам посочувствовать, у меня похожая проблема. Я _никогда_ не мог запомнить формулы, и способ, который мне приходилось компенсировать, заключался в том, что всякий раз, когда я изучаю новую формулу, я должен научиться выводить ее из первых принципов - под которыми я подразумеваю вещи, которые настолько простые, что я не могу их забыть. D
D
Вот еще одно обсуждение, в частности, о формулах области , которая является моей основной темой здесь:
Запоминание формул области
Привет, мне было интересно, есть ли хороший способ помочь мне запомнить формулы для областей различной формы. У меня много проблем с этим, и мне нужна помощь. Есть забавная поговорка или что-то в этом роде?
Доктор Ян снова дал несколько хороших советов по запоминанию, начав с того, что простое заучивание — плохая идея:
Вам нужно запоминать только то, чего вы не понимаете, поэтому ощущение, что вам нужно что-то запомнить, является признаком того, что вы все еще этого не понимаете.
А когда что-то запоминаешь, легко вспомнить неправильно, опустив знак минус, или перепутав числитель и знаменатель, или сотней других способов.
Он ссылается на места, где мы дали необходимое понимание негеометрических тем, и заключает:
Понимание подобных примеров похоже на хранение запасного ключа под керамической лягушкой рядом с задней дверью. .. вы можете использовать его, чтобы войти, если вы когда-нибудь заперлись из дома.
Если вы хотите написать мне и рассказать о некоторых вещах, которые вы пытаетесь запомнить, я могу попытаться помочь вам понять их таким образом, чтобы сделать заучивание ненужным. Хотели бы вы попробовать это?
.. вы можете использовать его, чтобы войти, если вы когда-нибудь заперлись из дома.
Если вы хотите написать мне и рассказать о некоторых вещах, которые вы пытаетесь запомнить, я могу попытаться помочь вам понять их таким образом, чтобы сделать заучивание ненужным. Хотели бы вы попробовать это?
Затем д-р Ахиллес приводит несколько конкретных примеров, показывая, как можно выучить базовые формулы площади с точки зрения их вывода:
Во-первых, вам нужно запомнить две вещи. Только два, однако! 1) Площадь прямоугольника равна ширине * длине. 2) Площадь круга пи*радиус*радиус. Затем, когда вы видите какую-либо другую проблему с областью, просто используйте эти два факта, чтобы определить область. Квадрат достаточно легко вычислить. Квадрат — это просто особый тип прямоугольника, в котором ширина = длине. Таким образом, вы просто умножаете сторону на сторону, и все готово.
Он использует изображения, чтобы сделать каждую из основных формул «очевидной». Вот мои варианты их:
Для треугольника заключите его в прямоугольник с тем же основанием и высотой, и проведите высоту к основанию; красный треугольник слева конгруэнтен желтому треугольнику, и точно так же справа; поэтому красная площадь равна желтой площади, которая составляет половину прямоугольника. Таким образом, площадь треугольника равна половине площади прямоугольника с тем же основанием и высотой: \(A = \frac{1}{2} bh\).
Таким образом, площадь треугольника равна половине площади прямоугольника с тем же основанием и высотой: \(A = \frac{1}{2} bh\).
Для параллелограмма нарисуйте прямоугольник с тем же основанием и высотой. Вы можете видеть, что если вы отрежете желтый треугольник от правой стороны параллелограмма и переместите его вправо, вы получите прямоугольник; поэтому площади двух фигур одинаковы: \(A = bh\).
Для трапеции нарисуйте прямоугольник, вершина и низ которого лежат на тех же линиях, что и у трапеции, но левая и правая стороны которого проходят через середины сторон трапеции. Опять же, если вы отрежете желтые треугольники от нижних углов и поместите их на верхние углы, вы сделали прямоугольник; так что площади одинаковые. Площадь трапеции равна площади прямоугольника той же высоты, а основание равно среднему значению оснований трапеции: \(A = \frac{B+b}{2} h\).
(Это не полные доказательства; если бы угол при основании треугольника или трапеции был бы тупым, или если бы угол параллелограмма не лежал над основанием, то эти построения не работали бы. Но наша цель здесь лишь напомнить
Но наша цель здесь лишь напомнить
Доктор Ахиллес закончил словами, подобными словам доктора Яна:
Кроме того, если вы выучите причины, по которым площади равны тому, что они делают, вместо того, чтобы выучивать забавную рифму, тогда если вы когда-нибудь совсем забудете формулы, вы всегда сможете снова их вычислить; но если ты когда-нибудь забудешь рифму, тебе будет некуда идти. Изучение математики требует много практики, но если вы попытаетесь понять, почему вещи такие, какие они есть, вместо того, чтобы просто запоминать формулы без какой-либо причины, вы добьетесь большего успеха и получите больше удовольствия. 92\)). Так получилось, что это одна из формул , которую, по словам доктора Ахиллеса, нужно запомнить, – хотя на днях я покажу вам несколько способов понять площади прямоугольника и круга, а также способы определить, помните ли формулу, которую вы помните, для области или что-то еще. Подобные выводы можно найти здесь (соответственно доктор Джеремайя и доктор Рик):
Определение формул для площади
Нахождение площади квадратов и треугольников
Последнее дает другой способ обращения с трапецией, как и
Формула площади трапеции
Один ученик спросил немного о другом: существует ли единая формула , применимая к каждой фигуре? Это вычислил доктор Ян (хотя, конечно, это не охватывает все — только те случаи, которые мы рассмотрели здесь:
Общая формула площади
Я слышал, что существует всеобъемлющая формула площади квадрата, прямоугольника, параллелограмма, трапеции и треугольника. Это правда? Я искал везде, но я ничего не могу найти.
Это правда? Я искал везде, но я ничего не могу найти.
Ответ заключается в том, что все эти фигуры можно рассматривать как трапеции, потому что все они имеют параллельные основания — если вы готовы думать о «верхнем основании» треугольника как об одной точке с нулевой длиной. Таким образом, вы всегда можете умножить высоту на среднюю ширину (среднее значение верха и низа), чтобы получить площадь!
Наконец, позвольте мне отослать вас к этой странице, которая делает то же самое для трехмерных фигур:
Полезные способы запомнить формулы цилиндра и призмы
Секрет всех областей — математика с плохими рисунками
(кроме области 51, которую я не уполномочен разглашать) или «Мир сквозь прямоугольные очки»
Теперь, когда я преподаю в средней школе , я обнаружил, что борюсь с огромным количеством формул площади, которые мои ученики должны знать (или, по крайней мере, быть с ними поверхностно знакомы). Прямоугольники, треугольники, параллелограммы, трапеции…
Прямоугольники, треугольники, параллелограммы, трапеции…
Логика такова: Горстка геометрических фигур постоянно повторяется в нашем мире. Как только вы узнаете, как их обнаружить, они повсюду, как Вильгельм Крик. Полезно легко определять размеры этих фигур с помощью формул.
Это все правда, насколько это возможно. Но сведение геометрии к одним только формулам может привести к трагическим недоразумениям, как, например, когда студент спросил моего друга: "Есть ли простой способ запомнить разницу между объемом и площадью поверхности?" Это все равно, что просить простой способ запомнить разницу между океанами и пустынями: вы можете спутать их, только если у вас есть глубокие неправильные представления о каждом из них.
Поэтому, когда я учу эти формулы, я пытаюсь напомнить себе элегантную истину: когда дело доходит до площади, все является прямоугольником.
И да, я имею в виду все .
Итак, начнем. Имея прямоугольников , найти площадь — это просто вопрос умножения. В каждом прямоугольнике у вас есть небольшой массив квадратов:
В каждом прямоугольнике у вас есть небольшой массив квадратов:
В этом случае у нас есть массив 5 квадратных сантиметров на 3 квадратных сантиметра. Всего 15 квадратных сантиметров. Или, в более общем смысле: A = bh.
А как насчет треугольников ?
Ну, просто нарисуйте их внутри прямоугольников.
Обратите внимание, что мы можем разделить прямоугольник на две стороны. Треугольник заполняет половину левых сторон и половину правых. Так что это должна быть половина всей площади.
Далее: параллелограмм .
Обратите внимание, что вы можете отрезать одну сторону параллелограмма и переместить ее на другую сторону, получив…
…прямоугольник! Значит, его площадь равна площади прямоугольника.
Как насчет трапеции (или, как странно настаивают мои новые британские соседи, трапеция )? Это немного сложнее.
Один из способов: сложите трапецию и посмотрите, что получится: параллелограмм!
Площадь всего этого объекта, согласно нашей формуле параллелограмма, равна (b 1 + b 2 ) x h, но это в два раза больше. Итак, делим на 2, чтобы получить ответ.
Итак, делим на 2, чтобы получить ответ.
Кроме того, вы можете заметить, что у трапеции есть маленький прямоугольник, который помещается внутри…
…и что трапеция, в свою очередь, помещается внутри большего прямоугольника:
Площадь меньшего прямоугольника b 1 h. Больший имеет площадь b 2 h. А трапеция находится ровно посередине между ними. Отсюда: та же формула площади!
Далее: запускаем воздушного змея !
Применив уже знакомый нам трюк, мы можем поместить воздушного змея внутри большего прямоугольника и заметить, что он заполняет ровно половину:
Отсюда наша формула: площадь d 1 d 2 /2.
Как насчет ромба ? Тот самый трюк!
Если вы вспомните, что квадрат является одновременно особым прямоугольником (поскольку все его углы равны) и особым ромбом (поскольку его стороны равны), вы увидите, что мы можем найти его площадь двумя способами. :
:
Комбинируя эти две формулы, мы даже получаем классный результат:
(И вам не нужно звонить Пифагору за помощью с доказательством.)
До сих пор мы ограничивались простыми формами с прямыми сторонами. Возможно, неудивительно, что их площади можно найти с помощью умного применения прямоугольников. Но как насчет чего-то более экзотического, менее прямоугольного?
Как насчет, скажем… круга ?
Сначала нарежьте круг, как пиццу. Затем переставьте ломтики в чередующемся порядке, чтобы получилась вот такая форма:
Это похоже на параллелограмм, верно? Он имеет «высоту» примерно r (радиус круга) и «основание» примерно πr .
(Примечание: если вы помните, длина окружности 2πr. Обратите внимание, что это основание составляет половину окружности. Это πr.)
Теперь нарежьте его еще мельче и повторите процесс. Что ты заметил?
Это выглядит даже больше как параллелограмм. И в самом деле, он начинает выглядеть как прямоугольник.
И в самом деле, он начинает выглядеть как прямоугольник.
Здесь вы можете проявить свое воображение. Представьте себе, что круг разрезается на все более и более тонкие кусочки, как одна пицца, которую делят между населением всего мира. Затем нарежьте его даже тоньше , чтобы на каждую мышь, лося и бактерию на земле нашлось по кусочку. Затем нарежьте его еще мельче, чем и !
Что мы получим?
Чем тоньше мы нарезаем, тем ближе получается прямоугольник. И если бы вы могли представить, что разрезаете его на «бесконечные» кусочки — это невозможно, но потерпите меня, — вы бы получили идеальный прямоугольник.
Какова будет его площадь? Итак, основание умножить на высоту… что равно πr умножить на r… что равно πr 2 . Формула площади доказана! КЭД! (На латыни это означает «гейм, сет, матч».)
Хорошо. Итак, мы свели следующие фигуры к прямоугольникам:
Но я обещал вам, что все будут прямоугольниками. И мы не все рассмотрели. Например, мы не нашли площади таких фигур:
И мы не все рассмотрели. Например, мы не нашли площади таких фигур:
Итак, что мы можем сделать? Что ж, мы можем попытаться оценить площадь такой фигуры с помощью одного прямоугольника, но мы не будем очень близки:
Тот, что сверху, слишком мал, а тот, что снизу, слишком велик. И мы понятия не имеем, насколько НАМНОГО больше — это не очевидная дробь.
Что делать, если прямоугольник не работает? Добавьте больше прямоугольников!
Лучше, но все равно не очень. А 8 прямоугольников?
Это выглядит ближе. И это указывает на закономерность: чем больше узких прямоугольников мы позволяем себе использовать, тем ближе мы подходим к истинной области.
Суммируйте все это с помощью некоторых уравнений, и вы получите объект, знакомый изучающим математику: интеграл!
Правильно: интеграл. Мы говорим о всемогущем математическом механизме для нахождения площади любой формы, в которую вы можете ввести уравнение.
Из данных данных,
Радиус R = 5 см
Область круга = π × радиус 2
= (22/7) × 5 2
= (22/7) × 25
= 78,57 Приблизительно
, поэтому площадь круга составляет 78,57 см 2
Площадь трапеции = (1/2) × (основание1 + основание2) × высота
Из данного рисунка
Длина основания1 = 7см
Длина основания2 = 5 см
высота трапезии = 4cm
2 = 5 см
Площадь трапеции = (1/2) × (Base1 + Base2) × высота
= (1/2) × (5 + 7) × 4
= (1/2) × 12 × 4
= 24CM 2
Значит площадь данной трапеции 24см 2 .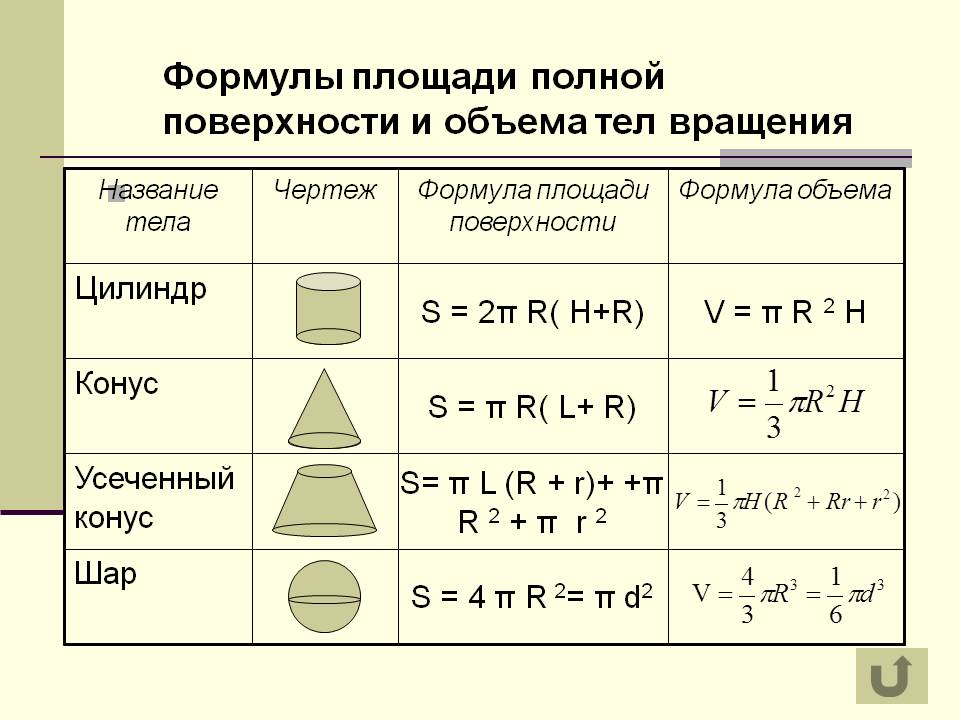
Площадь затмения = π × (длина большой полуоси) × (длина малой полуоси)
Длина большой полуоси = длина большой оси/2
Длина малой полуоси = длина малой оси/ 2
Исходя из данных,
длина большой оси = 6
Длина незначительной оси = 3
Длина полу -основной оси = длина основной оси/2
= 6/2
= 3
Длина полуножной оси = длина незначительной оси/2
= 3 /2
=1,5
площадь затмения = π × (длина большой полуоси) × (длина малой полуоси)
= (22/7) × 3 × 1,5
= 14,14 Приблизительно
, поэтому для данной зоны затмения составляет 14,14 см 2
 произведение длин двух диагоналей ромба. Формула:
произведение длин двух диагоналей ромба. Формула:Площадь ромба = (1/2) × длина (диагональ 1 ) × длина (диагональ 2 )
Из данных данных,
Длина диагонального 1 = 3 см
Длина диагонального 2 = 6CM
Область пороба = (1/2). 1 ) × длина (диагональ 2 )
= (1/2) × 3 × 6
Значит площадь ромба 9см 2 .
 Ответ на оба вопроса отчасти один и тот же: если вы хоть что-то знаете о том, откуда они берутся, вы можете либо легче их запомнить, либо просто извлечь их, когда они вам понадобятся.
Ответ на оба вопроса отчасти один и тот же: если вы хоть что-то знаете о том, откуда они берутся, вы можете либо легче их запомнить, либо просто извлечь их, когда они вам понадобятся.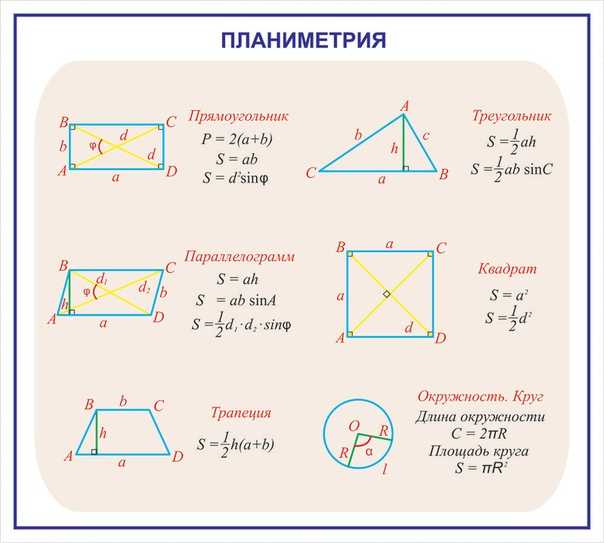 D
D  .. вы можете использовать его, чтобы войти, если вы когда-нибудь заперлись из дома.
Если вы хотите написать мне и рассказать о некоторых вещах, которые вы пытаетесь запомнить, я могу попытаться помочь вам понять их таким образом, чтобы сделать заучивание ненужным. Хотели бы вы попробовать это?
.. вы можете использовать его, чтобы войти, если вы когда-нибудь заперлись из дома.
Если вы хотите написать мне и рассказать о некоторых вещах, которые вы пытаетесь запомнить, я могу попытаться помочь вам понять их таким образом, чтобы сделать заучивание ненужным. Хотели бы вы попробовать это? 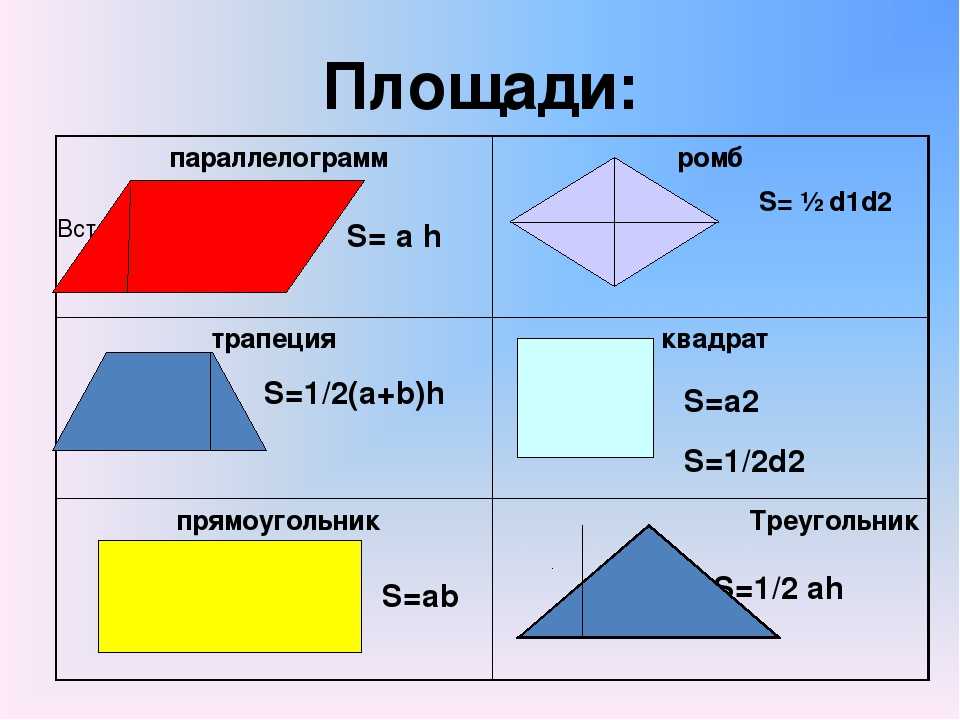 Таким образом, площадь треугольника равна половине площади прямоугольника с тем же основанием и высотой: \(A = \frac{1}{2} bh\).
Таким образом, площадь треугольника равна половине площади прямоугольника с тем же основанием и высотой: \(A = \frac{1}{2} bh\). Но наша цель здесь лишь напомнить
Но наша цель здесь лишь напомнитьПодобные выводы можно найти здесь (соответственно доктор Джеремайя и доктор Рик):
Определение формул для площади Нахождение площади квадратов и треугольников
Последнее дает другой способ обращения с трапецией, как и
Формула площади трапеции
Один ученик спросил немного о другом: существует ли единая формула , применимая к каждой фигуре? Это вычислил доктор Ян (хотя, конечно, это не охватывает все — только те случаи, которые мы рассмотрели здесь:
Общая формула площади Я слышал, что существует всеобъемлющая формула площади квадрата, прямоугольника, параллелограмма, трапеции и треугольника.Это правда? Я искал везде, но я ничего не могу найти.
Ответ заключается в том, что все эти фигуры можно рассматривать как трапеции, потому что все они имеют параллельные основания — если вы готовы думать о «верхнем основании» треугольника как об одной точке с нулевой длиной. Таким образом, вы всегда можете умножить высоту на среднюю ширину (среднее значение верха и низа), чтобы получить площадь!
Наконец, позвольте мне отослать вас к этой странице, которая делает то же самое для трехмерных фигур:
Полезные способы запомнить формулы цилиндра и призмы
Секрет всех областей — математика с плохими рисунками
(кроме области 51, которую я не уполномочен разглашать)или «Мир сквозь прямоугольные очки»
Теперь, когда я преподаю в средней школе , я обнаружил, что борюсь с огромным количеством формул площади, которые мои ученики должны знать (или, по крайней мере, быть с ними поверхностно знакомы). Прямоугольники, треугольники, параллелограммы, трапеции…
Прямоугольники, треугольники, параллелограммы, трапеции…
Логика такова: Горстка геометрических фигур постоянно повторяется в нашем мире. Как только вы узнаете, как их обнаружить, они повсюду, как Вильгельм Крик. Полезно легко определять размеры этих фигур с помощью формул.
Это все правда, насколько это возможно. Но сведение геометрии к одним только формулам может привести к трагическим недоразумениям, как, например, когда студент спросил моего друга: "Есть ли простой способ запомнить разницу между объемом и площадью поверхности?" Это все равно, что просить простой способ запомнить разницу между океанами и пустынями: вы можете спутать их, только если у вас есть глубокие неправильные представления о каждом из них.
Поэтому, когда я учу эти формулы, я пытаюсь напомнить себе элегантную истину: когда дело доходит до площади, все является прямоугольником.
И да, я имею в виду все .
Итак, начнем. Имея прямоугольников , найти площадь — это просто вопрос умножения.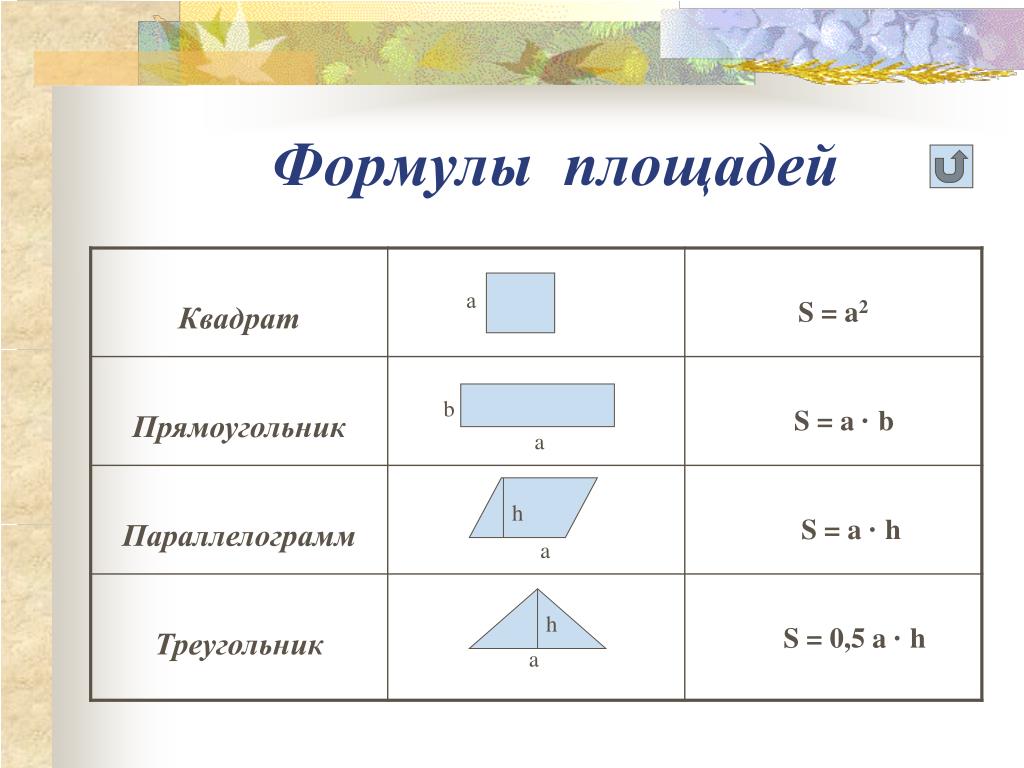 В каждом прямоугольнике у вас есть небольшой массив квадратов:
В каждом прямоугольнике у вас есть небольшой массив квадратов:
В этом случае у нас есть массив 5 квадратных сантиметров на 3 квадратных сантиметра. Всего 15 квадратных сантиметров. Или, в более общем смысле: A = bh.
А как насчет треугольников ?
Ну, просто нарисуйте их внутри прямоугольников.
Обратите внимание, что мы можем разделить прямоугольник на две стороны. Треугольник заполняет половину левых сторон и половину правых. Так что это должна быть половина всей площади.
Далее: параллелограмм .
Обратите внимание, что вы можете отрезать одну сторону параллелограмма и переместить ее на другую сторону, получив…
…прямоугольник! Значит, его площадь равна площади прямоугольника.
Как насчет трапеции (или, как странно настаивают мои новые британские соседи, трапеция )? Это немного сложнее.
Один из способов: сложите трапецию и посмотрите, что получится: параллелограмм!
Площадь всего этого объекта, согласно нашей формуле параллелограмма, равна (b 1 + b 2 ) x h, но это в два раза больше.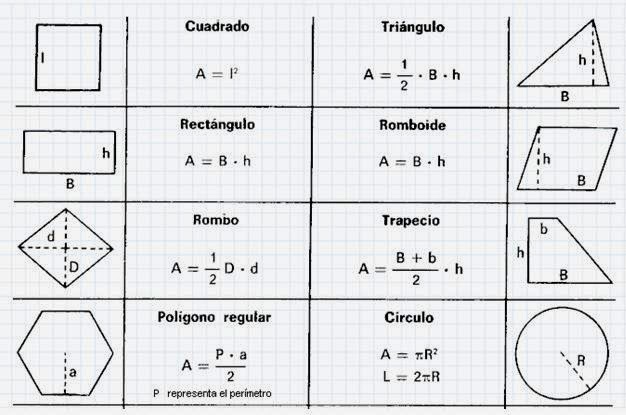 Итак, делим на 2, чтобы получить ответ.
Итак, делим на 2, чтобы получить ответ.
Кроме того, вы можете заметить, что у трапеции есть маленький прямоугольник, который помещается внутри…
…и что трапеция, в свою очередь, помещается внутри большего прямоугольника:
Площадь меньшего прямоугольника b 1 h. Больший имеет площадь b 2 h. А трапеция находится ровно посередине между ними. Отсюда: та же формула площади!
Далее: запускаем воздушного змея !
Применив уже знакомый нам трюк, мы можем поместить воздушного змея внутри большего прямоугольника и заметить, что он заполняет ровно половину:
Отсюда наша формула: площадь d 1 d 2 /2.
Как насчет ромба ? Тот самый трюк!
Если вы вспомните, что квадрат является одновременно особым прямоугольником (поскольку все его углы равны) и особым ромбом (поскольку его стороны равны), вы увидите, что мы можем найти его площадь двумя способами. :
:
Комбинируя эти две формулы, мы даже получаем классный результат:
(И вам не нужно звонить Пифагору за помощью с доказательством.)
До сих пор мы ограничивались простыми формами с прямыми сторонами. Возможно, неудивительно, что их площади можно найти с помощью умного применения прямоугольников. Но как насчет чего-то более экзотического, менее прямоугольного?
Как насчет, скажем… круга ?
Сначала нарежьте круг, как пиццу. Затем переставьте ломтики в чередующемся порядке, чтобы получилась вот такая форма:
Это похоже на параллелограмм, верно? Он имеет «высоту» примерно r (радиус круга) и «основание» примерно πr .
(Примечание: если вы помните, длина окружности 2πr. Обратите внимание, что это основание составляет половину окружности. Это πr.)
Теперь нарежьте его еще мельче и повторите процесс. Что ты заметил?
Это выглядит даже больше как параллелограмм. И в самом деле, он начинает выглядеть как прямоугольник.
И в самом деле, он начинает выглядеть как прямоугольник.
Здесь вы можете проявить свое воображение. Представьте себе, что круг разрезается на все более и более тонкие кусочки, как одна пицца, которую делят между населением всего мира. Затем нарежьте его даже тоньше , чтобы на каждую мышь, лося и бактерию на земле нашлось по кусочку. Затем нарежьте его еще мельче, чем и !
Что мы получим?
Чем тоньше мы нарезаем, тем ближе получается прямоугольник. И если бы вы могли представить, что разрезаете его на «бесконечные» кусочки — это невозможно, но потерпите меня, — вы бы получили идеальный прямоугольник.
Какова будет его площадь? Итак, основание умножить на высоту… что равно πr умножить на r… что равно πr 2 . Формула площади доказана! КЭД! (На латыни это означает «гейм, сет, матч».)
Хорошо. Итак, мы свели следующие фигуры к прямоугольникам:
Но я обещал вам, что все будут прямоугольниками.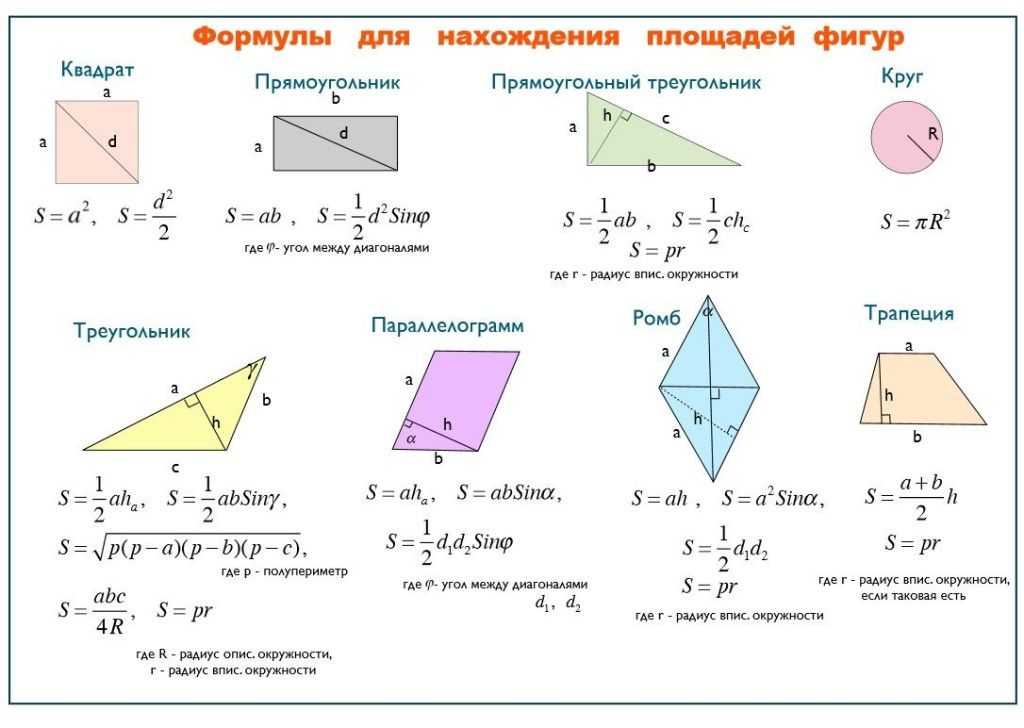 И мы не все рассмотрели. Например, мы не нашли площади таких фигур:
И мы не все рассмотрели. Например, мы не нашли площади таких фигур:
Итак, что мы можем сделать? Что ж, мы можем попытаться оценить площадь такой фигуры с помощью одного прямоугольника, но мы не будем очень близки:
Тот, что сверху, слишком мал, а тот, что снизу, слишком велик. И мы понятия не имеем, насколько НАМНОГО больше — это не очевидная дробь.
Что делать, если прямоугольник не работает? Добавьте больше прямоугольников!
Лучше, но все равно не очень. А 8 прямоугольников?
Это выглядит ближе. И это указывает на закономерность: чем больше узких прямоугольников мы позволяем себе использовать, тем ближе мы подходим к истинной области.
Суммируйте все это с помощью некоторых уравнений, и вы получите объект, знакомый изучающим математику: интеграл!
Правильно: интеграл. Мы говорим о всемогущем математическом механизме для нахождения площади любой формы, в которую вы можете ввести уравнение.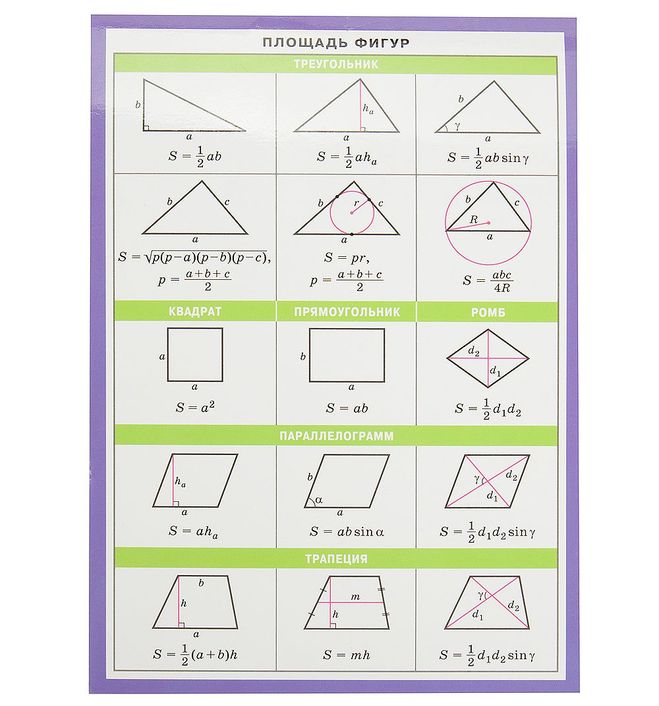


 е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней.
е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней. данный прямоугольник 50см 2
данный прямоугольник 50см 2  Это правда? Я искал везде, но я ничего не могу найти.
Это правда? Я искал везде, но я ничего не могу найти.