Биквадратное уравнение как решать: Решение биквадратных уравнений

видео. Биквадратное уравнение, решение биквадратных уравнений

Инструкция

Способ подстановкиВыразите одну переменную и подставте ее в другое уравнение. Выражать можно любую переменную по вашему усмотрению. Например, выразите «у из второго уравнения:
х-у=2 => у=х-2Затем подставьте все в первое уравнение:
2х+(х-2)=10Перенесите все без «х в правую часть и подсчитайте:
2х+х=10+2
3х=12 Далее, чтобы «х, разделите обе части уравнения на 3:
х=4.Итак, вы нашли «х. Найдите «у. Для этого подставьте «х в то уравнение, из которого вы выразили «у:
у=х-2=4-2=2
у=2.

Сделайте проверку. Для этого подставьте получившиеся значения в уравнения:
2*4+2=10
4-2=2
Неизвестные найдены верно!

Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.
Так как в «у со знаком «+ , а во втором «- , то вы можете выполнить операцию сложения, т.е. левую часть складываем с левой, а правую с правой:
2х+у+(х-у)=10+2Преобразуйте:
2х+у+х-у=10+2

3х=12
х=4Подставьте «х в любое уравнение и найдите «у:
2*4+у=10
8+у=10
у=10-8
у=2По 1-ому способу можете , что найдены верно.

Если нет четко выраженных переменных, то необходимо немного преобразовать уравнения.
В первом уравнении имеем «2х, а во втором просто «х. Для того, чтобы при сложении или «х сократился, второе уравнение умножьте на 2:
х-у=2
2х-2у=4Затем вычтите из первого уравнения второе:
2х+у-(2х-2у)=10-4Заметим, если перед скобкой стоит минус, то после раскрытия поменяйте на противоположные:
2х+у-2х+2у=6
3у=6
у=2«х найдите, выразив из любого уравнения, т.е.
х=4

Видео по теме

Уравнение , в общем виде записанное ах+bу+с=0, называется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит бесконечное множество решений, поэтому в задачах оно всегда чем-либо дополняется – еще одним уравнением или ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя

переменными следует разными способами.

Вам понадобится

• — линейное уравнение с двумя переменными;
• — второе уравнение или дополнительные условия.

Инструкция

Если дана система из двух линейных уравнений, решайте ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными поменьше и выразите одну из переменных, например, х. Затем подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные – в правую. Найдите у и подставьте в любое из первоначальных уравнений, найдите х.

Решить систему из двух уравнений можно и другим способом. Умножьте одно из уравнений на число, чтобы коэффициент перед одной из переменных, например, перед х, был одинаков в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть аналогично и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте найденное значение у в любое из первоначальных равенств. Найдите х.

Третий способ решения системы двух линейных уравнений – графический. Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.

Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если

переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.

Источники:

• как решить уравнение с одной переменной

Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.

Вам понадобится

• — система из трех уравнений с тремя неизвестными.

Инструкция

Если два из трех системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в

уравнение с тремя неизвестными . Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.

Некоторые системы уравнений можно вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из на или переменную так, чтобы сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.

Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя

неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.

Найдите матрицу А в степени (-1) предварительно отыскав , обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.

Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов.

Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.

Источники:

• решений уравнений с тремя неизвестными

Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше. Решать системы можно несколькими методами.

Инструкция

Самый распространенный метод решения системы уравнений — это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.

Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.

Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.

2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.

Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений . Если решение было одно, то будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.

Видео по теме

Одним из классических способов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований переводится в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.

Инструкция

Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z — после Y и так далее. В правой части каждого уравнения неизвестных быть не должно.

Мысленно определите коэффициенты, стоящие перед каждой неизвестной, а также коэффициенты в правой части каждого уравнения.

Всем еще со школы известно такое понятие, как уравнения. Уравнение — это равенство, содержащее одну или несколько переменных. Зная то, что одна из частей данного равенства равна другой, можно вычленять отдельные части уравнения, перенося те или иные его составляющие за знак равенства по четко оговоренным правилам. Можно упростить уравнение до необходимого логического завершения в виде х=n, где n — это любое число.

С начальной школы все дети проходят курс изучения различной сложности. Позже в программе появляются более сложные линейные уравнения — квадратные, затем идут кубические уравнения. Каждый последующий вид уравнений имеет новые методики решения, становится труднее в изучении и повторении.

Однако после этого возникает вопрос о решении такого вида уравнений, как биквадратные уравнения. Данный вид, несмотря на кажущуюся сложность, решается достаточно просто: главное — уметь привести такие уравнения в должный вид. Их решение изучается за один-два урока вместе с практическими заданиями, если у учащихся имеются базовые знания о решении квадратных уравнений.

Что необходимо знать человеку, столкнувшемуся с этим типом уравнений? Для начала то, что они включают в себя только четные степени переменной «икс»: четвертая и, соответственно, вторая. Чтобы биквадратное уравнение было решаемо, необходимо привести его к виду Как это сделать? Достаточно просто! Нужно всего лишь заменить «икс» в квадрате на «игрек». Тогда устрашающий для многих школьников «икс» в четвертой степени превратится в «игрек» в квадрате, а уравнение примет вид обычного квадратного.

Далее оно решается как обычное квадратное уравнение: раскладывается на множители, после чего находится значение таинственного «игрека». Чтобы решить биквадратное уравнение до конца, нужно найти из числа «игрек» — это и будет искомая величина «икс», после нахождения значений которого можно будет поздравить себя с успешным завершением расчетов.

Что же следует помнить, решая уравнения данного вида? Первое и самое главное: игрек не может быть отрицательным числом! Само условие, что игрек — это квадрат числа икс, исключает подобный вариант решения. Поэтому если при первичном решении биквадратного уравнения одно из значений «игрек» получается у вас положительным, а второе — отрицательным, необходимо взять только его положительный вариант, иначе биквадратное уравнение будет решено неверно. Лучше сразу ввести правило, что переменная «игрек» больше либо равна нулю.

Второй немаловажный нюанс: число «икс», являясь квадратным корнем числа «игрек», может быть как положительным, так и отрицательным. Допустим, если «игрек» равен четырем, то биквадратное уравнение будет иметь два решения: два и минус два. Это происходит по той причине, что отрицательное число, возведенное в четную степень, равно числу того же модуля, но отличного знака, возведенному в ту же степень. Поэтому всегда стоит помнить об этом немаловажном моменте, иначе можно попросту потерять один или несколько ответов уравнения. Лучше всего сразу писать, что «икс» равен плюс-минус квадратному корню от «игрек».

В общем и целом, решение биквадратных уравнений — это достаточно просто и не требует больших временных затрат. {2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]

Мы получили снова четыре корня:

Вот так решаются все биквадратные уравнения. Конечно, это не самый быстрый способ, зато он самый надежный. Попробуйте самостоятельно прорешать такие же примеры, как и в этом видео. В ответе значения иксов нужно записывать через точку с запятой — вот так, как я записывал. На этом урок закончен. Удачи!

Перед тем, как решать биквадратные уравнения, необходимо разобраться, что собой являет данное выражение. Итак, это уравнение четвертой степени, которое можно записать в таком виде: «(ах 4) + (bx 2) + с = 0 ». Его общий вид можно записать в виде «ах ». Чтобы решить уравнение подобного рода, необходимо применить метод под названием «подстановка неизвестных». Согласно ему, выражение «х 2 » необходимо заменить другой переменной. После такой подстановки получается простое квадратное уравнение, решение которого в дальнейшем не составляет особого труда.

Необходимо:

— чистый лист бумаги;
— пишущая ручка;
— элементарные математические навыки.

Инструкция:

• Итак, необходимо изначально записать выражение на листке бумаги. Первый этап его решения состоит в простой процедуре замены выражения «х 2 » на простую переменную (например «к »). После того, как Вы это сделали, у Вас должно получиться новое уравнение: «(ак 2) – (bк) + с = 0 ».
• Далее, чтобы правильно решить биквадратное уравнение, нужно вначале найти корни для «(ак 2 ) – (bк) + с = 0 », которое у Вас получилось после замены. Чтобы это сделать, необходимо будет посчитать значение дискриминанта по известной формуле: «D = (b 2 ) − 4*ас ». При этом все эти переменные (а , b и с ) являются коэффициентами вышеприведенного уравнения.
• В ходе расчета дискриминанта мы можем узнать, имеет ли решение наше биквадратное уравнение, ведь если в итоге данное значение получится со знаком минус, то оно просто-напросто может не иметь решения в дальнейшем. В случае же если дискриминант будет равняться нулю, тогда у нас будет одно единственное решение, определенное такой формулой: «к = — (b / 2 * а) ». Ну и в случае, если наш дискриминант окажется больше нуля, тогда у нас получится два решения. Для нахождения двух решений необходимо будет взять квадратный корень от «D » (то есть с дискриминанта). Полученное значение нужно будет записать в виде переменной «QD ».
• Следующий шаг – непосредственное решение квадратного уравнения , которое у Вас получилось. Для этого Вам необходимо будет подставить в формулу уже известные значения. Для одного из решений: «к1 = (-b + QD) / 2 * а », а для другого: «к2 = (-b — QD) / 2 * а ».
• И, наконец, завершающий этап – нахождение корней биквадратного уравнения . Для этого необходимо будет взять квадратный корень из полученных до этого решений обычного квадратного уравнения. Если же дискриминант был равен нулю, и у нас было только одно решение, тогда в этом случае корней получится два (с отрицательным и с положительным значением квадратного корня). Соответственно, если дискриминант был больше нуля, то наше биквадратное уравнение будет иметь целых четыре корня.

Конспект урока по Алгебре «Биквадратное уравнение и его корни» 8 класс

Учитель математики Апенькина Наталья Александровна

Конспект урока

Класс – 8.

Тема – «Биквадратное уравнение и его корни».

Цели урока: 

образовательная: дать определение биквадратного уравнения, научиться решать биквадратные уравнения, исследовать число корней биквадратного уравнения;

воспитательная: формировать умение работать в парах, выслушивать мнение товарища, доказывать свою точку зрения;

развивающая: развивать навыки самостоятельной и исследовательской работы.

 Тип урока: изучение и первичное закрепление новых знаний.

Форма урока: урок-исследование.

Оборудование: учебник «Алгебра, 8 кл. компьютер, плакат с кроссвордом.

Приложение: презентация «Биквадратное уравнение и его корни», для создания которой использована программа PowerPoint из пакета программ Microsoft Office.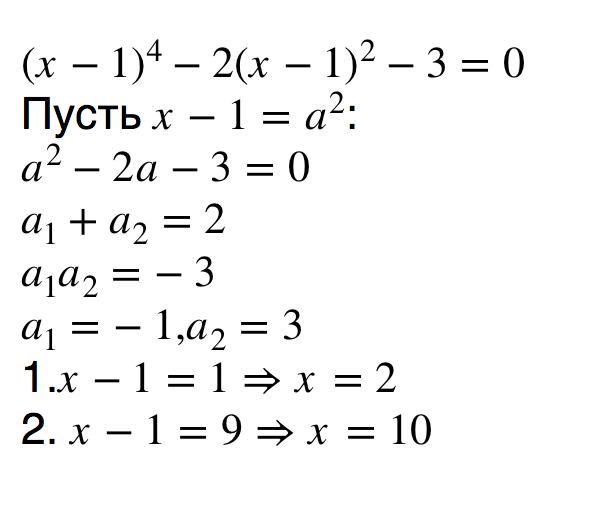  

План урока.

1. Организационный момент. Слайд 1.

2. Актуализация знаний.

3. Открытие детьми темы урока (кроссворд). Слайд 2.

4. Постановка детьми целей урока.

5. Самостоятельная работа. Слайд 3.

6. Итог самостоятельной работы. Слайды 4, 5.

7. Пример решения биквадратного уравнения. Слайд 6.

8. Исследование. 

9. Итоги исследования. Слайд 7.

10. Итог урока.

11. Задание на дом. Слайд 8. Слайд 9.

Ход урока.

1. Организационный момент.

— Здравствуйте, ребята! Садитесь.

Начинаем урок алгебры. Сегодня вы будете исследователями! Желаю вам удачи, хорошего настроения и взаимопонимания! Девизом урока пусть будут слова Л. Н. Толстого. Слайд 1. 

2. Актуализация знаний.

— В начале для разминки выполним устные упражнения (на доске записаны упражнения) и повторим формулы дискриминанта и корней квадратного уравнения.

(х²)² = …; (у²)² = …; выполните обратную задачу: а⁴ = …; решить уравнения: х² = 9, а² = 16, у² = 1, в² = 0, с² = 17, р² = — 25, к² = — 6, х² = ¼. Придумайте уравнение такого же вида (х² = а), которое имеет 2 корня, 1 корень и не имеет корней.

— Какой общий вид имеет квадратное уравнение? По какой формуле находим дискриминант? Корни уравнения?

+ Отвечают дети.

3. Открытие темы урока.

— Для того чтобы узнать тему урока, давайте разгадаем кроссворд. 

1. 
   Третья степень числа. (Куб) 

2. 
   Подкоренное выражение в формуле корней квадратного уравнения. (Дискриминант) 

3. 
   Значение переменной, обращающее уравнение в верное равенство. (Корень) 

4. 
   Уравнения, имеющие одинаковые корни. (Равносильные) 

5. 
   Равенство с переменной. (Уравнение) 

6. 
   Квадратное уравнение, с первым коэффициентом равным нулю. (Приведенное) 

7. 
   Многочлен в правой части квадратного уравнения. (Трехчлен) 

8. 
   Равенство, содержащее числа и переменные. (Формула) 

9. 
   Французский математик. (Виет) 

10. 
    Числовой множитель — в произведении. (Коэффициент) 

11. 
    Один из видов квадратного уравнения. (Неполное) 

12. 
    Множество корней уравнения. (Решения) 

— Прочитайте слово, которое получилось в выделенной горизонтальной строке. 

+ Биквадратное.

— Как вы думаете, к какому математическому понятию относится это определение?

+ Оно относится к слову «уравнение».

— Совершенно верно! Теперь вы можете сказать, какова тема нашего сегодняшнего урока.

+ Тема урока «Биквадратное уравнение». Слайд 2.

4. Постановка целей урока.

— Каковы для вас цели урока?

+ Мы должны узнать, какое уравнение называется биквадратным.

— Хорошо. Но ведь, как и любое уравнение, оно должно иметь корни. Значит, чему ещё вы должны научиться?

+ Как найти его корни. 

— Верно.

Слайд 3.

5. Самостоятельная работа.

— Всё это вы будете узнавать самостоятельно. Посмотрите, по какому плану вы будете работать. Слайд 4.

Тому, кто закончит быстрее всех, предложить решить биквадратное уравнение.(№ 278, д) Ответ: ±√1/3, ±√2/3.

6. Итог самостоятельной работы.

— Итак, что же вы узнали?

+ Биквадратным называется уравнение вида ах⁴ + вх² + с = 0, где а ≠ 0.

— Существенно ли замечание, что а ≠ 0? 

+ Да, т.к. если а будет равно 0, то уравнение будет квадратным (неполным).

— Хорошо. Приведите пример биквадратного уравнения.  Дети приводят примеры биквадратных уравнений).

Слайд 5.

— Какой алгоритм решения биквадратного уравнения вы записали?

+ Алгоритм следующий:

1) Ввести замену переменной: пусть х² = t.

2) Составить квадратное уравнение с новой переменной: at² + bt + c=0.

3) Решить новое квадратное уравнение.

4) Вернуться к замене переменной.

5) Решить получившиеся квадратные уравнения.

6) Сделать вывод о числе решений биквадратного уравнения.

7) Записать ответ.

— Молодцы! Посмотрите слайд 6.

У кого что-то не так – исправьте.

7. Пример решения биквадратного уравнения.

Прокомментируйте устно пример решения биквадратного уравнения 

(слайд 7). 

8.Исследование.

— Сейчас мы проведём исследование: сколько корней имеет биквадратное уравнение. Каждая пара получит своё уравнение и решит его. (Учитель раздаёт уравнения: х⁴-10х²+9=0, 2х⁴ –х²-1=0, х⁴+5х²+4=0, 2х⁴+5х²+4=0, 

х⁴-8х²+16=0, х⁴+8х²+16=0. )

А потом мы сделаем выводы о том, сколько корней имеют биквадратные уравнения.

+ Дети решают уравнения……………………………………………………………

— Итак, что получилось? Рассказывает 1 пара.

+ х⁴-10х²+9=0. У нас получился дискриминант положительный, значит, квадратное уравнение имеет 2 корня, корни тоже положительные, значит всего 4 корня.

-Хорошо. Вторая пара.

+ 2х⁴ –х²-1=0. Дискриминант положительный, один корень положительный, а другой отрицательный, значит, биквадратное уравнение имеет 2 корня.

— Третья пара.

+ х⁴+5х²+4=0. Дискриминант квадратного уравнения положительный, но корни отрицательные, значит, биквадратное уравнение не имеет корней.

— Четвёртая пара.

+ 2х⁴+5х²+4=0. А у нас дискриминант отрицательный, поэтому уравнение не имеет корней.

— Молодцы! Следующая пара.

+ Уравнение х⁴-8х²+16=0 имеет 2 корня, т.к. квадратное уравнение имеет 1 корень (Д=0).

— И последняя пара.

+ Уравнение х⁴+8х²+16=0 не имеет корней, т.к. хотя и Д=0, но корень-то отрицательный.

9. Итог исследования.

Итоги исследования мы поместим в таблицу.

Посмотрите и прокомментируйте. Слайд 8.

+ Ученики комментируют по цепочке.

10. Итог урока.

— Подведём итог урока. Чем пополнился ваш багаж знаний? 

Скажите, что понравилось на уроке? А что не понравилось? Чем отличается квадратное уравнение от биквадратного? Что означает приставка «би»? Зачем нам нужно изучать биквадратные уравнения? 

+ Дети отвечают.

11. Задание на дом (дифференцированное). Слайд 9. 

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Уравнения, сводящиеся к квадратным уравнениям

      Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.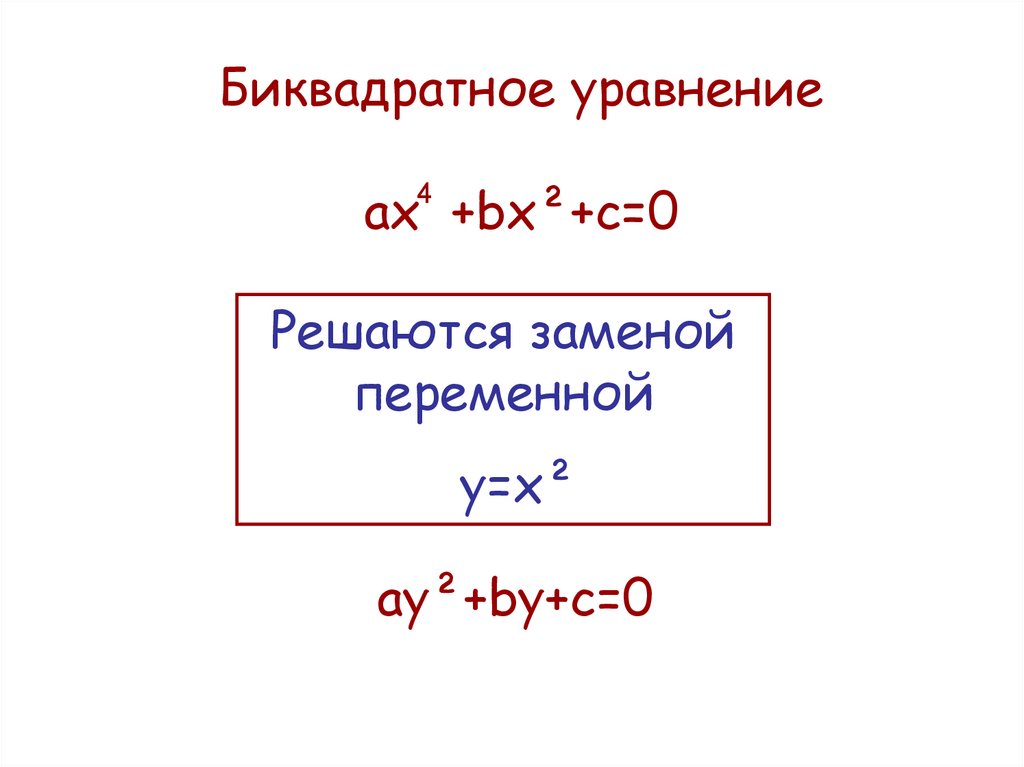

      К таким уравнениям, в частности, относятся уравнения следующих типов:

	Трёхчленные уравнения
	Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
	Возвратные (симметричные) уравнения 3-ей степени
	Возвратные (симметричные) уравнения 4-ой степени
	Обобщенные возвратные уравнения 4-ой степени

      Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».

Трехчленные уравнения

      Трёхчленными уравнениями называют уравнения вида

a f 2(x)+ b f (x) + c = 0,

(1)

а также уравнения вида

(2)

где a, b, c – заданные числа, а    f (x) – некоторая функция.

      Для того, чтобы решить трехчленное уравнения вида (1), обозначим

y = f (x),

(3)

тогда уравнение (1) станет квадратным уравнением относительно переменной y :

ay2 + by + c = 0 .

(4)

      Затем найдем корни уравнения (4), а после этого, подставив каждый из найденных корней в равенство (3), решим полученное уравнение относительно x .

      Для того, чтобы решить трехчленное уравнение вида (2), сначала введем обозначение (3), а затем умножим полученное уравнение на знаменатель. В результате уравнение (2) примет вид (4), а схема решения уравнения (4) уже описана выше.

      Покажем, как это осуществляется на примерах.

      Пример 1. Решить уравнение

(x2 – 2x)2 – – 2(x2 – 2x) – 3 = 0 .

(5)

      Решение. Если обозначить

y = x2 – 2x ,

(6)

то уравнение (5) превратится в квадратное уравнение

y2 – 2y – 3 = 0 .

(7)

      Решим уравнение (7):

      В первом случае из равенства (6) получаем:

      Во втором случае из равенства (6) получаем:

      Ответ:     – 1,     1,     3.

      Пример 2. Решить уравнение

(8)

      Решение. Если обозначить

,

(9)

то уравнение (8) превратится в квадратное уравнение

которое эквивалентно уравнению

2y2 – 3 y – 2 = 0 .

(10)

      Решим уравнение (10):

      В первом случае из равенства (9) получаем уравнение:

которое, в силу неотрицательности арифметического корня, решений не имеет.

      Во втором случае из равенства (9) получаем:

      Ответ:

      Пример 3. Решить уравнение

(11)

      Решение. Если обозначить

(12)

то уравнение (11) превратится в квадратное уравнение

y² – 9 + 3 – 5y = 0 ,

которое эквивалентно уравнению

y2 – 5y – 6 = 0 .

(13)

      Решим уравнение (13):

y₁ = – 1,     y₂ = 6 .

      В первом случае из равенства (12) получаем уравнение:

которое, в силу неотрицательности арифметического корня, решений не имеет.

      Во втором случае из равенства (12) получаем:

      Ответ:

      Пример 4. Решить биквадратное уравнение

x4 – x2 – 12 = 0 .

(14)

      Решение. Если обозначить

y = x2,

(15)

то уравнение (14) превратится в квадратное уравнение

y2 – y – 12 = 0 .

(16)

      Решим уравнение (16):

y₁ = – 3,     y₂ = 4 .

      В первом случае из равенства (15) получаем уравнение:

x² = – 3,

которое решений не имеет.

      Во втором случае из равенства (15) получаем:

      Ответ:    – 2,     2 .

      Пример 5. Решить уравнение

(17)

      Решение. Если обозначить

y = x2 – 3x,

(18)

уравнение (17) превращается в уравнение

которое при умножении на   y   принимает вид

y2 + 2y – 8 = 0 .

(19)

      Решим уравнение (19):

y₁ = – 4,     y₂ = 2 .

      В первом случае из равенства (18) получаем квадратное уравнение:

которое решений не имеет.

      Во втором случае из равенства (18) получаем:

      Ответ:

      Пример 6. Решить уравнение

(20)

      Решение. Если обозначить

,

(21)

уравнение (20) превращается в уравнение

которое при умножении на   y   принимает вид

3y2 – 2y – 1 = 0 .

(22)

      Решим уравнение (22):

      В первом случае из равенства (21) получаем уравнение

которое, в силу неотрицательности арифметического корня, решений не имеет.

      Во втором случае из равенства (21) получаем:

      Ответ:     – 2 .

Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии

      Рассмотрим уравнение

(ax + b)(ax + b + + c)(ax + + b + 2c)(ax + + b + 3c) = d ,

(23)

где a, b, c, d –  заданные числа, и заметим, что левая часть этого уравнения представляет собой произведение четырёх последовательных членов арифметической прогрессии, первый член которой равен ax+b, а разность равна c.

      Схема решения уравнений вида (23) заключается в следующем.

      Сначала обозначим

y = ax + b.

(24)

      Тогда уравнение (23) примет вид:

y (y + c)(y + + 2c)(y + 3c) = d .

(25)

      Перегруппируем сомножители в левой части уравнения (25) следующим образом:

[y (y + 3c)][(y + + c)(y + 2c)] = d .

(26)

      Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (26), то получим:

[y2 + 3cy][y2 + + 3cy + 2c2] = d .

(27)

      Если теперь в уравнении (27) обозначить

z = y2 + 3cy ,

(28)

то уравнение (27) станеи квадратным уравнением

z2 + 2c2 z – d = 0 .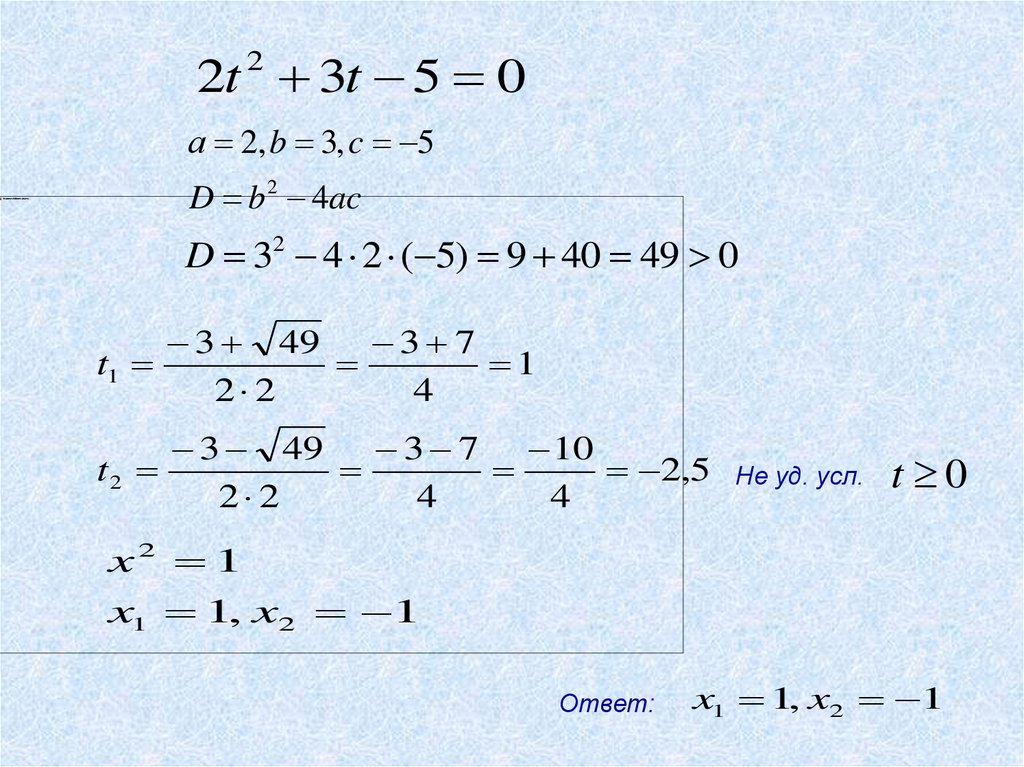

(29)

      Для того, чтобы найти корни уравнения (23), остаётся решить уравнение (29), затем для каждого корня уравнения (29) решить уравнение (28) относительно   y , а затем в каждом из полученных случаев решить уравнение (24) относительно   x .

      Пример 7 . Решить уравнение

(2x + 3)(2x + 5)(2x + + 7)(2x + 9) = 384 .

(30)

      Решение.Если обозначить

y = 2x + 3,

(31)

уравнение (30) превращается в уравнение

y (y + 2)(y + + 4)(y + 6) = 384 .

(32)

      Перегруппируем сомножители в левой части уравнения (32):

[y (y + 6)][(y + + 2)(y + 4)] = 384 .

(33)

      Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (33), то уравнение (33) примет вид:

[y2 + 6y][y2 + + 6y + 8] = 384 .

(34)

      Если теперь обозначить

z = y2 + 6y ,

(35)

то уравнение (34) станет квадратным уравнением

z2 + 8 z – 384 = 0 .

(36)

      Решим уравнение (36):

z₁ = – 24,     z₂ = 16 .

      В первом случае из равенства (35) получаем уравнение:

которое корней не имеет.

      Во втором случае из равенства (35) получаем:

      В первом из этих случаев, из равенства (31) получаем:

      Во втором случае из равенства (31) получаем:

      Ответ:

 

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Модульные технологии на уроке математики по теме: «Биквадратные уравнения». 9-й класс

«Ум человеческий только тогда понимает обобщения, когда он сам его сделал или проверил.»
Л.Н. Толстой.

Тип урока: изучение новых знаний.

Цели урока:

• познакомить учащихся с новым видом уравнения с одной переменной;
• изучить и закрепить способ решения биквадратных уравнений;
• продолжать работу по развитию речи учащихся;
• учить составлять алгоритм решения задания по образцу;
• развивать умения работать с книгой, самостоятельно добывать знания.

I. Организационный момент

Приветствие учащихся, мобилизация внимания.

II. Актуализация опорных знаний.

Учитель: Мы продолжаем изучение темы: “ Квадратные уравнения”. Сегодня на уроке мы познакомимся с новым видом уравнения, приводимого к квадратному, поэтому повторим изученное, вспомнив основные определения, формулы и теоремы.Проведем экскурс в тему. Задача отвечающего ученика у доски, донести до слушателей логичный рассказ по изученным вопросам темы, задача остальных учащихся внимательно слушать и дополнить рассказ.
Ученик: (у доски рассказывает о «квадратных» уравнениях).
Перед учащимися демонстрируются формулы, рассказывается об истории вопроса, напоминается прямая и обратная теорема Виета, ее применение для нахождения и проверки корней квадратного уравнения.
На доске помещена тематическая газета. Ученик сопровождает свой рассказ с опорой на готовый материал.
Учитель: Дополнения (к классу)…
Вопросы к учащимся:

• Устно решите уравнения, назовите корни этих уравнений, если они есть:
  (Демонстрирует карточки с условиями уравнений).

Учитель оценивает устную работу учащихся на уроке. Акцентирует внимание учащихся на том, что они должны уметь решать неполные и полные квадратные уравнения на “ отлично” для успешного усвоения новой темы.

III. Мотивация обучения. (3 мин, кроссворды лежат на партах у всех учащихся)

Учитель: Нам предстоит работа по разгадыванию кроссворда. Разгадав его, мы узнаем название нового вида уравнений, который научимся решать на уроке. Работаем по цепочке. Учащиеся читают вопрос вслух по цепочке, допускаются хоровые ответы. Записывает ответ учащийся I варианта, учащиеся II варианта — читают вопрос вслух.
Разгадав кроссворд, ребята прочитают слово “ биквадратные”.
Учитель: Вам предстоит изучить эту тему самостоятельно с опорой на учебник и учебный модуль. Время на изучение темы отводится один урок. Цели и задачи по теме вы прочитаете в учебном модуле.
Запишем тему урока в тетрадях. ( Учитель пишет тему на доске, учащиеся в тетрадях).

IV. Самостоятельное изучение новой темы по модульной программе.

Учитель: Приступайте к изучению новой темы по учебному модулю.

1. УЭ -0 — 1 мин.
2. УЭ- 1 — 4 мин.
3. Защита составленного алгоритма решения биквадратного уравнения.
   (3 мин коллективная работа)

Учитель (после сигнала учащихся о готовности к работе) во фронтальной беседе с учащимися проговаривают определение биквадратного уравнения, составленный алгоритм решения нового вида уравнения.
Затем, сверяют составленный самостоятельно «алгоритм», с алгоритмом записан ном заранее на срытой части доски. Еще раз читают его по пунктам. Идет вторичное осмысление алгоритма.
Учитель: Проверьте составленный алгоритм.
Кто сможет решить сам биквадратное уравнение по этому алгоритму?
Ученик решает у доски, комментируя свои действия по алгоритму.
Закрепление действий учащихся по алгоритму. Показ образца решения.

• Задача учителя: дать образец записи решения нового упражнения через ученика.
• Задача ученика: используя алгоритм по шагам дойти до конца, решив новое упражнение.

Остальные учащиеся работают в тетрадях.
Учитель: (классу после решения уравнения)
Обратите внимание на форму записи на доске нового типа уравнения.
Есть ли затруднения при его решении?

V. Формирование навыков решения биквадратного уравнения.

Учитель: Учимся применять полученные знания. Выполните следующий учебный элемент. Работайте парами. УЭ-2— 15 мин.
Учащиеся работают самостоятельно над решением биквадратных уравнений по вариантам, решая по 3 уравнения. Примеры уравнений подобраны так, чтобы охватить разные случаи решения. В учебном элементе 2 перед учащимися стоят задачи:

1. Применять полученные знания по алгоритму;
2. Провести взаимоконтроль с соседним вариантом;
3. Заполнить таблицу по результатам решенных уравнений из двух вариантов;
4. Сделать вывод о числе решения биквадратных уравнений;
5. Провести исследование по новой теме.

Во время самостоятельной работы учитель помогает в случае необходимости учащемуся индивидуально, контролирует ход работы, оценивает отдельных учащихся за работу на уроке по новой теме.
По мере решения уравнений, после проверки учителем работы ученика, ученики записывают результат, заполняя таблицу. 15 минут класс работает самостоятельно.

VI. Взаимопроверка задания.

Результаты работы постепенно появляются в таблице на доске и на партах учащихся.
Учитель: Заполните таблицу. Обсудите полученные данные в парах. Выполните УЭ -3 (6 мин).
Подготовьтесь для обобщения проведенного исследования.
Учитель: Подведем итоги самостоятельной работы над новыми уравнениями. Поговорим о числе решений биквадратных уравнений.
Ученики: (анализируют данные таблицы) — фронтальный метод.

VII. Итог урока.

Учитель: Оцените, достигли ли вы намеченных целей и задач урока? (УЭ -0)
Ученики читают п. 1-3, отвечая на вопросы.
Учитель:

1. Какие же уравнения называются биквадратными? (Определение)
2. Алгоритм решения биквадратного уравнения?
3. От чего зависит число решений биквадратного уравнения?

VIII. Домашнее задания.

Запишем д/з. Стр. 123-124, № 468 ( 2,4), 469 (2,4). Дополнительно 474*(2)

Учитель: Домашние упражнения аналогичны классным, кроме одного, № 474*(2).
Это упражнение для тех ребят, кто хочет углубить свои знания по изученной теме, работает над своим образованием.
Мы разберем приемы решения подобных упражнений на следующем уроке.
Сегодня на уроке выполнены все задачи. В оставшееся время — выполняйте УЭ – 4.
УЭ – 4 дан для тех учащихся, кто быстро выполняет задания в классе, легко понимает и применяет алгоритм решения.

Оцените свою работу на уроке в листе самоконтроля

№	Ф. И. ученика	Устные ответы на уроке	УЭ-1 алгоритм	УЭ-2 решение уравнений	УЭ-3 выводы	УЭ-4 дополн. упр-е	Итоговая оценка
1.
2.
3.
4.
5.
…

 

Аналогичный лист контроля на столе у учителя, где по ходу урока он работает, оценивая учащихся.

Модульная программа по теме: “Биквадратные уравнения».
(раздаточный материал каждому ученику для работы на уроке)

Интегрируемая цель:

1. Познакомиться с новым видом уравнения с одной переменной.
2. Учиться составлять алгоритм решения заданий по готовому образцу.
3. Научиться приему решения биквадратного уравнения.
4. Освоение данного модуля будет способствовать развитию вашего логического мышления, умений работать самостоятельно с учебной литературой.

У Э — О (установочный) — 1 мин.
В процессе работы над УЭ — 1, УЭ — 2 вы должны:

1. Выучить определение биквадратного уравнения;
2. Научиться решать биквадратные уравнения, используя составленный вами алгоритм.

У Э — 1 — 5 мин.
Цели: изучив УЭ — 1 , вы должны

1. Познакомиться с новым видом уравнения с одной переменной.
2. Составить алгоритм решения биквадратного уравнения по готовому образцу в учебнике.
3. Уметь объяснять решение уравнения, используя учебник.

Работайте с учебником стр. 123., пример 1.

Задание 1.

а) Прочитайте определение биквадратного уравнения.
б) Запишите определение в тетрадь.
в) Расскажите определение друг другу.
г) Существенно ли замечание, что а не равно нулю?

Задание 2.

а) Разберите решенное уравнение в учебнике. Устно составьте алгоритм решения этого уравнения.
б) Работайте парами. Обсудите составленный алгоритм друг с другом.
в) Подготовьтесь к защите составленного алгоритма у доски.

Дайте учителю сигнал о готовности к защите задания 2, подняв руку.
Составив алгоритм, до обсуждения его в классе, продолжайте работать над вопросами по самоконтролю.

Вопросы для самоконтроля:

1. “БИ” — дважды, биквадратное — дважды квадратные. Как это проявляется в алгоритме?
2. Можно ли назвать метод решения биквадратного уравнения — “метод замены переменной”?
3. Сможете ли вы по составленному алгоритму решить аналогичное уравнение?
4. Примите участие в обсуждении составленного алгоритма в классе.

 

УЭ — 2 — 15 мин.
Изучив УЭ — 2 , вы должны:

а) Научиться приему решения биквадратного уравнения.
б) Научиться записывать решение уравнения.
в) Сделать вывод о числе решений биквадратных уравнений.

Учимся применять полученные знания.

Задание 3. Решайте задания по вариантам

В.1 1. х4 + 7х2 + 12 = 0 2. 2х4 + х2 + 3 = 0 3. х4 + 4х2 = 0

В.2 1. 9х4 + 5х2 — 4 = 0 2. х4 — 3х2 + 2 = 0 3. х4 + 2х2 + 1 = 0

УЭ -3. – 5 минут.

Задание 4.

1. Обсудите полученные результаты самостоятельной работы..
2. Сверьте записи в ваших тетрадях с образцом.
3. Проведите взаимоконтроль. Примените теорему Виета для проверки корней уравнения.
4. Заполните таблицу.
5. Проанализируйте таблицу.
6. Обсудите в парах результаты своей работы.
7. Оцените свою работу в оценочном листе.

Дайте учителю сигнал о готовности к защите задания 3, подняв руку.
До обсуждения задания 3 и 4 в классе, продолжайте работать над вопросами по самоконтролю.

Задание 5. Проведите самоконтроль, ответив на вопросы:

1. Сколько решений может иметь биквадратное уравнение?
2. От чего зависит число решений биквадратного уравнения?
3. Может ли биквадратное уравнение иметь ровно 3 действительных корня?
4. Самостоятельно оцените: достигли ли вы цели работы на уроке. Для этого вернитесь к началу модуля УЭ — 0.
5. Участвуйте в обсуждении работы по исследованию числа решений биквадратных уравнений.

Запишите домашнее задание к следующему уроку: стр. 123-124, № 468 (2 ,4 ), № 469 (4 ),
Вы должны знать алгоритм и уметь применять прием решения биквадратного уравнения.
Дополнительно 474*(2).
Испытайте себя. Сможете, ли вы применить изученный метод замены переменной в более сложной ситуации?

УЭ -4. Дополнительное задание:
Если у вас осталось время на уроке, начните решать новое уравнение:

( х² + 2х) ² — (х² + 2х) = 56.

Решение.

Пусть t = ( . . . ), тогда t²=( . . . )² .
Составлю …

Кроссворд. Если вписать верные слова, то получится название одного из видов уравнений.

Алгоритм решения биквадратного уравнения. Метод решения — замены переменной.

1. Ввести замену переменной: пусть х² = t,
2. Составить квадратное уравнение с новой переменной: аt² + bt + с = 0 (2)
3. Решить новое квадратное уравнение (2).
4. Вернуться к замене переменной.
5. Решить получившиеся квадратные уравнения.
6. Сделать вывод о числе решений биквадратного уравнения.
7. Записать ответ.

Таблица для исследования числа решения биквадратных уравнений

№	Уравнение	Знак дискриминананта (D)	Корни промежуточного (нового) уравнения t1 и t2	Знаки корней нового уравнения	Корни исходного уравнения	Количество решений биквадрат. уравнения
1	х4 + 7х2 + 12 = 0
2	9х4 — 5х2 — 4 = 0
3	2х4 + х2 + 3 = 0
4	х4 + 4х2 = 0
5	х4 — 3х2 + 2 = 0
6	х4 + 2х2 + 1 = 0

Примерный текст выступление ученика.

«Ум человеческий только тогда понимает обобщения, когда он сам его сделал или проверил.»
Л.Н. Толстой.

Знаете ли вы, что квадратные уравнения умели решать еще 4000 лет назад, например, в Древнем Вавилоне, Древней Греции?
Думаете, им был известен способ, который мы изучали на уроках алгебры? Скорее всего, нет.
Древние все известные им алгебраические приемы решения уравнений выражали в геометрической форме.
Геометрическую алгебру в решении уравнений широко применял еще Евклид в своих «Началах».
Только в XIX веке, когда Ф. Виет ввел буквенную символику, под влиянием Декарта и Ньютона исторический процесс перехода к алгебре в нашем понимании был в основном завершен.
Теперь мы легко решаем любые квадратные уравнения, применяя общую формулу, умеем определять число корней уравнения по дискриминанту. А когда-то поиск решения отдельных видов квадратных уравнений затягивался на века.

По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше скажи, постоянства такого:
Умножишь ты корни – и дробь уж готова.
В числителе «c», в знаменателе «а».
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта,
Что за беда –
В числителе «b», в знаменателе «а».

Франсуа Виет. Отец современной буквенной алгебры. А между тем, Виет по образованию и профессии юрист. А его знаменитая теорема дает нам возможность часто устно найти корни квадратного уравнения и всегда проверить их верность.

Кроссворд.

1. Третья степень числа. (Куб)
2. Подкоренное выражение в формуле корней квадратного уравнения. (Дискриминант)
3. Значение переменной, обращающее уравнение в верное равенство. (Корень)
4. Уравнения, имеющие одинаковые корни. (Равносильные)
5. Равенство с переменной. (Уравнение)
6. Квадратное уравнение, с первым коэффициентом равным нулю. (Приведенное)
7. Многочлен в правой части квадратного уравнения. (Трехчлен)
8. Равенство, содержащее числа и переменные. (Формула)
9. Французский математик. (Виет)
10. Числовой множитель — в произведении. (Коэффициент)
11. Один из видов квадратного уравнения. (Неполное)
12. Множество корней уравнения. (Решения)

Урок алгебры на тему «Квадратные и биквадратные уравнения». 9-й класс

Цель: расширение знаний учащихся, повторение материала в рамках подготовки к экзаменам, проконтролировать и оценить знания.

Тип урока: игра, урок проводится во время декады математики в школе.

Оформление класса

Мудрые мысли:

• “Предмет математики настолько серьезен, что полезно не упускать случаев, делать его немного занимательным” Б. Паскаль.
• “Неустанный труд все препятствия преодолеет” М.В.Ломоносов

Все учащиеся разбиты на две команды, каждая команда занимает свое место

Пожелания:

• “Не всегда уравнения разрешают сомнения, но итогом сомнения может быть озарение”
• “Чтобы ум владыкой стал, язык вперед не забегал”
• “Больше думай, не болтай, но и формул ты не забывай”

Урок начинается торжественно, звучит тихая музыка, на ее фоне читается стихотворение

О, математика земная,
Гордясь, прекрасная собой
Ты всем наукам мать родная
И дорожат они тобой.
В веках овеяна ты славой,
Светило всех земных светил
Тебя “Царицей величавой”
Недаром Гаусс окрестил
Строга, логична, величава,
Стройна в полете, как стрела
Твоя не меркнувшая слава
В веках бессмертье обрела
Я славлю разум человека,
Дела его волшебных рук;
Надежду нынешнего века —
Царицу всех земных наук.

Представление команд:

“Математики”

Девиз: “Посредством уравнений, теорем, мы уйму разрешим проблем”

“Иксы в квадрате”

Девиз: “Наша команда иксы в квадрате, мы сегодня в неадеквате, чтобы вам нас победить, нужно очень умными быть!”

1 конкурс «Из истории математики» (это задание было дано заранее)

А) Квадратные уравнения в древнем Вавилоне

Необходимость решать уравнения в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и полные квадратные уравнения:

• х² +х= 3/4
• х²— х= 14. 5

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решением, изложенным в виде рецептов, без указаний относительно того, каким образом, они были найдены, отсутствуют общие методы решения квадратных уравнений

Б) “Квадратные уравнения в Индии”

Задачи на квадратные уравнения встречаются уже в астрономическом трактате “Ариабхаттиам”, составленном в 499 г индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: aх² +bх = c a>o. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: “ Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предполагая и решая алгебраические задачи”. Задачи часто облекались в стихотворную форму. Вот одна из задач индийского математика VII в Бхаскары

“Обезьянок резвая стая
Всласть поевши, развлекалась,
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам…
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?”

Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Соответствующее задаче уравнение

(х/ 8)² + 12 = х Бхаскара пишет под видом х² –64х = -768, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 ², получая х²-64х+ 32 ²= -768+ 1024

(х -32)²=256

х-32=+16

х-32= -16

х₁=-16

х₂= 48

В) “Квадратные уравнения в Европе XIII-XVII в.в.” Формулы решения квадратных уравнений в Европе были впервые изложены в “ Книге абака”, написанной в 1202г итальянским математиком Леонардо Фибоначчи. Этот труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из “Книги абака” переходили почти во все европейские учебники XVI-XVII вв. и частично XVIII.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х²+ bх = с при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Конкурс капитанов

1)

Что за чиж на черном поле
чертит клювом белый след?
У чижа ни ног, ни крыльев
ни пера, ни пуха нет (Мел)

2)

Говорит она беззвучно,
Но понятно и не скучно,
Ты беседуй чаще с ней
Станешь лучше и умней (Книга)

3)

Она всегда с трудом дается нам,
Зато потом, когда ответ получен,
То словно свет блеснет по сторонам,
Где только, что еще бродили тучи. (Задача)

Разминка команд

На доске записаны уравнения.

Задание: Найти дискриминант (от каждой команды выходит по 4 человека и выполняют каждый свое задание)

1 команда	2 команда
а) 2х2-5х-3=0 (49)	а) 3х2+5х-2=0 (49)
б) х2+х-6=0 (25)	б) х2-3х-4=0 (25)
в) 9х2-12х+4=0 (0)	в) 2х2-12х+18=0 (0)
г) х2-11х=10=0 (81)	г) х2+6х-7=0 (64)

Заморочки из бочки

Каждый участник команды берет в бочке вопрос и дает ответ

Вопросы:

1 Какое уравнение называют квадратным уравнением общего вида?

2 Определение приведенного квадратного уравнения

3 Какое уравнение называют неполным квадратным уравнением?

4 Запиши формулу дискриминанта полного квадратного уравнения

5 Что означает по – латыни слово дискриминант (различитель)

6 При каком условии полное квадратное уравнение имеет один корень

7 При каком условии квадратное уравнение имеет два корня.

8 В каком случае квадратное уравнение не имеет корней

9 Как читается теорема Виета.

10 Запиши формулу корней квадратного уравнения

Проверка навыков решения уравнений.

Каждая команда получает 10 карточек с заданием: “Реши уравнения”, так как учащиеся имеют свои места, то они не могут общаться

1. а) 3х2-7х+2=0 б) х2-2х=0	2. а) 2х2+5х-18=0 б) х2-16=0	3. а) 2х2-7х-30=0 б) х2-4=0
4. а) х2+2х-24=0 б) 7х-2х2=0	5. а) 5х2-12х+4=0 б) 9-х2=0	6. а) 3х2-8х+5=0 б) 5х2-10х=0
7. а) 2х2+3х-14=0 б) 2х2-32=0	8. а) 3х2-8х-3=0 б) 3х2-12х=0	9. а) Х2-8х+7=0 б) 2х+х2=0
10. а) 4х2+х-3=0 б) 3х2+27=0

Веселая перемена

Жюри проверяет работы, а учащиеся получают карточки с занимательными задачками “Бирюльки”. Задание выполняется путем вычеркивания букв, вычеркнутые буквы дают одно слово, а из оставшихся букв получается другое слово

1 Длаяйтекал прогони собаку, не тревожа птицу.(дятел, лайка)

2. Маидспраниияд со страной расстанься, но оставь столицу. (Мадрид, Испания)

3.Гакрвозадиська где цветок, где рыба, отыскать попробуй. (карась, гвоздика)

4.Нкиквеальс выплесни напиток, а метал не трогай. (Квас, никель)

5.Сммасоролединнока гриб клади в корзинку, ягоду в лукошко (масленок, смородина)

6.Пакнетдерыа разберись, где обувь, где большая кошка (кеды, пантера)

7. Брбуоськся отыщи вид спорта и снаряд спортивный (бокс, брусья)

8.Кфрувешигант где сосуд из глины? Где корабль старинный? (кувшин, фрегат)

9.Ксоамобсврала от змеи опасной отдели машину (кобра, самосвал)

10.Бтрелиткаон кто грызет орехи? Кто зарылся в тину (белка, тритон)

11Сгререадкла здесь герой античный спрятан в дне недели (Геракл, среда)

12Пчеанасыл что над школьной дверью? Что в твоем портфеле? (часы, пенал)

В жюри подается один лист, на котором записаны все ответы, работа на скорость и сплоченность команды

Биквадратные уравнения

Каждая команда получает 10 карточек, задача капитана правильно распределить, от этого зависит успех команды

1) х4-5х2+4=0	2) х4+3х2+2=0	3) х4-25х2+144=0
4) х4+14х2+48=0	5) х4-5х2-36=0	6) х4-4х2-45=0
7)2х4-9х2+4=0	8)9х4-9х2+2=0
9) (2х2+3)2 – 12 (2х2+3) +11=0	10) (х2+х-1)(х2+х+2)=40

Жюри проверяет работы, для учащихся проводится

Веселая перемена

Команды получают карточки с заданием, это же задание изображено на плакате в цвете для психологической разгрузки, ответ подается один от команды.

Сколько весит крокодил?

Вот крокодил и павиан,
Их вес – две бочки и диван.
Павиан без крокодила
Весит две корзинки ила.
Ровно шесть корзинок ила
Весит черная горилла.
Две гориллы — посмотри —
Сколько бочек весят? Три.
И все та же обезьяна
Весит ровно полдивана.
Сколько весит крокодил
В пересчете на горилл?

Литература

1) Г.И. Глейзер “История математики в школе 7-8 классы”

2) Учебник “Алгебра 9 класс” под редакцией С.А. Теляковского

3) Календарь для школьника

Биквадратные уравнения | Методическая разработка по алгебре (9 класс) на тему:

Урок по алгебре 9 класса по теме: «Биквадратные уравнения»

План урока

1. Устная работа.
2. Объяснение нового материала.
3. № 278 (а).
4. Составление алгоритма.
5. № 278 (в) (I, II способы).
6. № 278 (б) (С помощью выделения квадрата двучлена).
7. Графический способ решения биквадратных уравнений.
8. Биквадратное уравнение со знаком модуля.
9. Самостоятельная работа.

Ход урока

Устная работа

1. Представьте  в виде квадрата двучлена квадратный трехчлен

4 + 12х + 9

2. Замените ☺ таким одночленом, чтобы полученное выражение можно было представить в виде квадрата двучлена.

 + 20b + ☺

А теперь представьте данный квадратный трехчлен в виде квадрата двучлена

    –  квадрат суммы  b и 10.

3. Выделите квадрат двухчлена из квадратного трехчлена:

  – 6х – 2

Объяснение

На предыдущем уроке мы с вами решали уравнения методом введения новой переменной.

Метод введения новой переменной позволяет легко решать уравнения четвертой степени, имеющие вид:      + b  + C = 0 (пишу на доске).

Уравнения вида:       + b  + C = 0, где   0, являющиеся квадратными относительно , называют биквадратными уравнениями (“би”, т.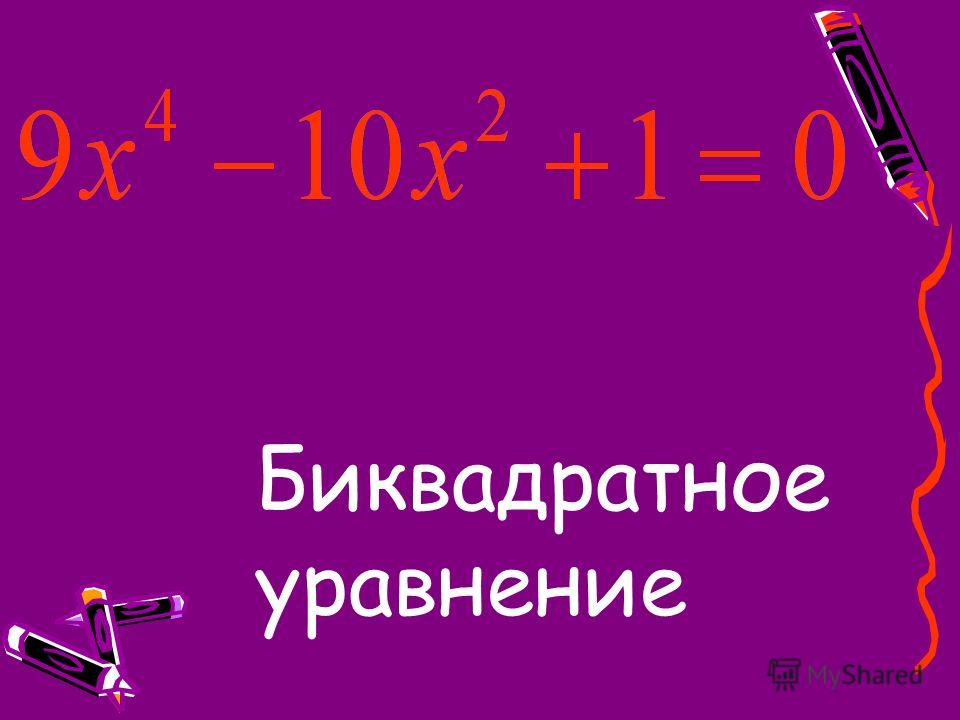 е. два, значит дважды квадрат).

Сегодня на уроке мы будем учиться решать биквадратные уравнения. И начнем с примера.

Запишем:   9 – 10 + 1 = 0    –   биквадратное уравнение.

Обозначим  через y. Запишем:

Пусть  = y, где  y0, (т.к.  всегда принимает неотрицательные значения). Следовательно уравнение х сведется к переменной y :

9 – 10y + 1 = 0,

D = 100 – 49 = 64, D  0,

Таким образом,    ,  1 0

       или    

 ,  

Ответ: ;  ; ;

 

№ 222 (а)

А теперь решаем 222 (а). ( Решает ученик у доски)

а)

Пусть =у, где у0 , тогда

 

D=25 – 4*(–36)= 169, D > 0,

   не удовлетворяет условию у0

 

Ответ:  – 3; 3.

А теперь давайте составим алгоритм решения  биквадратных уравнений.

 

 + b  + C = 0, где   0

Пусть =у, где у0 , тогда

 + b + C = 0

1. D > 0, два корня

Если , то =, =

Если , то =, =

2. D = 0, один корень

Если , то =, =

Если у

3. D

№ 222 (в)

в) ,

I способ:

      Внимание !

Ребята! Обратите внимание на это уравнение:

Представим левую часть в виде квадрата двучлена

Получим

Отсюда

             

Ответ: нет корней.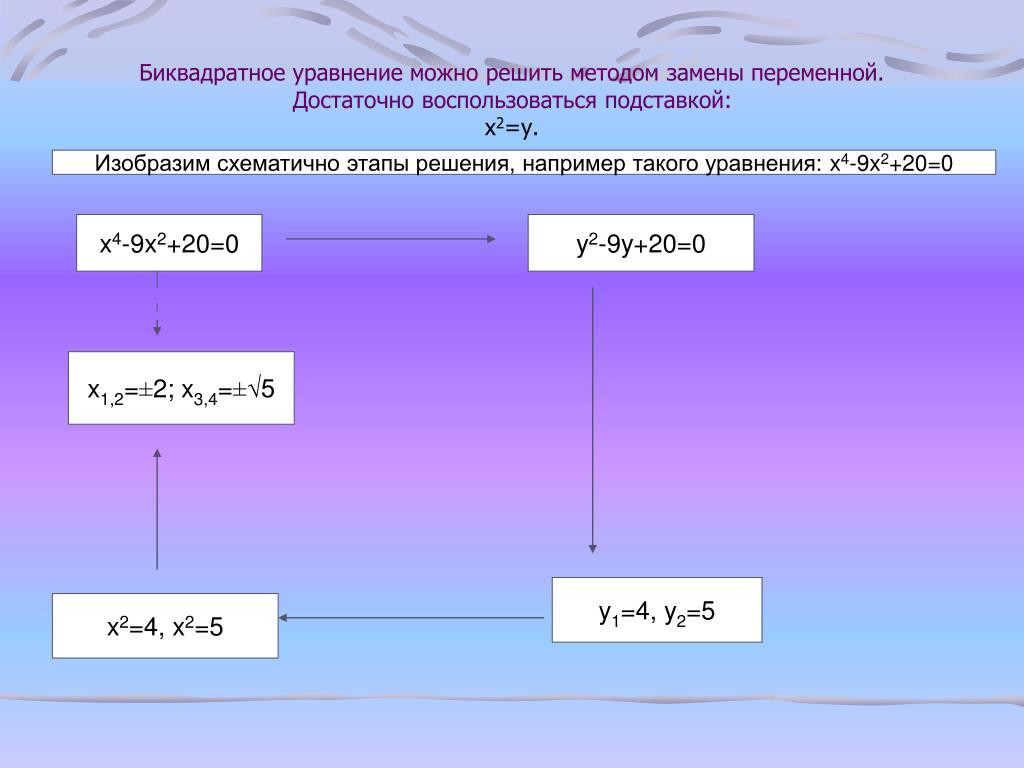

II способ:

Посмотрите, как можно еще проще решить это уравнение.

, ,  , значит квадратный трехчлен при любом t принимает положительные значения.

Ответ: нет корней.

№ 222 (б)

Решим еще одно биквадратное уравнение

б)

Решим биквадратное уравнение выделением квадрата двухчлена:

 

Отсюда

 или ,

                 

,        ,

Ответ: , , 2 , 2

Графический способ

Рассмотрим еще один способ решения биквадратных уравнений: графический

Представим данное уравнение в виде :

Построим схематически с помощью шаблонов в одной системе координат графики функций:

y  , у  ( графиком функции y  является парабола ветви которой направлены вверх с вершиной в точке с координатами (0;0), графиком функции

у  является парабола ветви, которой направлены вниз с вершиной в точке (0;6))

Они не пересекаются, значит данное уравнение не имеет корней.

Ответ: нет корней.

Ребята!

Но этот способ не всегда эффективен, т.к. графический способ не обеспечивает высокую точность результата

Уравнение с модулями

Решим уравнение с модулем

 

 

  если произведение равно нулю, то хотя бы один из множителей  равен нулю

 или

      = 0                      

                     ,   

 ,  

Ответ: 0 ,   – 2, 2 ,     

Самостоятельная работа

А теперь самостоятельная работа: два варианта.

Мне хочется посмотреть как вы усвоили новую тему и какие способы решения биквадратных уравнений вы выберете.

Вариант 1.

Вариант 2.

      Вариант 1 (ответы).

     1)4

Пусть =у, где у0 , тогда

4

D=25 – 4*4= 9, D > 0,

  

 

    или

 ,

Ответ:   ,

     2)

, ,  , значит квадратный трехчлен при любом t (x) принимает положительные значения.

Ответ: нет корней.

Вариант 2 (ответы).

Пусть =у, где у0 , тогда

 

D=9 – 4*(–10)= 49, D > 0,

   не удовлетворяет условию у0

 

Ответ:  

,

Ответ: ,

Какие же способы вы выбрали? Молодцы!

Сдал тетради.

Спасибо за урок!

Мне очень понравилось, как вы работали, но особенно хочу отметить…

Домашнее задание

п.12 № 279, 347(в), 352(а).

Биквадратное уравнение, два корня которого равны 1+i класс 10 по математике CBSE

Ответ

Подтверждено

218.1k+ просмотров

Подсказка: Биквадратное уравнение — это уравнение, имеющее 4 корня. В данной задаче заданы два корня биквадратного уравнения, у которых один из корней мнимый, а другой иррациональный. Коэффициенты уравнения вещественные и рациональные, два других корня уравнения найдем, решая сопряженные к данным корням. Мы должны взять сопряженные как $1-i,1+\sqrt{2}$ . Тогда мы можем выразить корни как \[\left[ x-\left( 1+i \right) \right]\text{ }and\text{ }\left[ x-\left( 1-i \right) \right]\] , затем умножьте их и приравняйте к 0, чтобы получить одно уравнение. Точно так же мы найдем другое уравнение для следующего набора корней. Наконец, мы снова перемножим полученные уравнения, чтобы получить окончательный ответ.

Полный пошаговый ответ:
Даны два корня биквадратного уравнения: \[1+i\], \[1-\sqrt{2}\].
Мы можем найти два других корня биквадратного уравнения, используя сопряженные корни данных корней.
Чтобы найти сопряженные комплексные числа, мы должны изменить знак мнимой части.
Итак, мы получим сопряжение \[1+i=1-i\].
Аналогичным образом вычисляется сопряжение иррационального числа путем изменения знака иррациональной части.
Итак, мы получим сопряжение \[1-\sqrt{2}=1+\sqrt{2}\].
Теперь мы вычислили все 4 корня биквадратного уравнения.
Все четыре корня биквадратного уравнения равны \[1+i\], \[1-\sqrt{2}\], \[1-i\], \[1+\sqrt{2}\]. {2}}$ , мы имеем 9{2}}-2x-2=0\], правильный вариант А.

Примечание:
Избегайте глупых ошибок при решении сопряженных данных мнимого и иррационального корней биквадратного уравнения. Имейте ясность в отношении формирования квадратного уравнения с заданными корнями, а также биквадратного уравнения, образованного произведением двух квадратных уравнений. Есть вероятность, что некоторые учащиеся попытаются подставить корни в заданные варианты и проверить, удовлетворяет это или нет. Это совсем не рекомендуется, так как это отнимает очень много времени, и мы должны проверить, все ли четыре корня \[1+i\], \[1-\sqrt{2}\], \[1-i\] , \[1+\sqrt{2}\] удовлетворяют уравнениям или нет.

Недавно обновленные страницы. Нихром имеет высокую стойкость 12 класса по физике CBSE

Если альфа и бета альфа и гамма альфа и дельта относятся к 10 классу математики JEE_Main

Значение р, для которого оба корня уравнения 10 класса математики JEE_Main

Значения электроотрицательности Полингса для элементов относятся к 11 классу химии CBSE

Для частицы, совершающей простое гармоническое движение, 11 класс физики CBSE

Дальнозоркий человек, потерявший очки, читает 10 класс физики JEE_Main

Обладает ли нихром высоким сопротивлением 12 классу физика CBSE

Если альфа и бета альфа и гамма альфа и дельта относятся к 10 классу математики JEE_Main

Значение p, для которого оба корня уравнения 10 класса математики JEE_Main

Тенденции сомнений

Уравнения с двумя переменными.

Решение биквадратных уравнений Решение уравнений с параметром

Понятие об уравнениях с двумя переменными впервые формируется в курсе математики для 7 класса. Рассмотрены конкретные задачи, процесс решения которых приводит к этому типу уравнений.

При этом изучены они достаточно поверхностно. Программа ориентирована на системы уравнений с двумя неизвестными.

Это стало причиной того, что задачи, в которых на коэффициенты уравнения накладываются определенные ограничения, практически не рассматриваются. Недостаточно внимания уделяется методам решения задач типа «Решить уравнение в натуральных или целых числах». Известно, что материалы ЕГЭ и билеты на вступительные экзамены часто содержат такие упражнения.

Какие уравнения определяются как уравнения с двумя переменными?

ху = 8, 7х + 3у = 13 или х 2 + у = 7 являются примерами уравнений с двумя переменными.

Рассмотрим уравнение x — 4y = 16. Если x = 4 и y = -3, это будет верное равенство. Следовательно, эта пара значений является решением этого уравнения.

Решением любого уравнения с двумя переменными является множество пар чисел (x; y), которые удовлетворяют этому уравнению (превращают его в истинное равенство).

Часто уравнение преобразуют так, чтобы из него можно было получить систему нахождения неизвестных.

Примеры

Решить уравнение: ху — 4 = 4х — у.

В этом примере можно использовать метод факторизации. Для этого нужно сгруппировать слагаемые и вынести за скобки общий множитель:

ху — 4 = 4х — у;

ху — 4 — 4х + у = 0;

(ху + у) — (4х + 4) = 0;

у(х + 1) — 4(х + 1) = 0;

(x + 1)(y — 4) = 0.

Ответ: Все пары (x; 4), где x — любое рациональное число и (-1; y), где y — любое рациональное число.

Решите уравнение: 4x 2 + y 2 + 2 = 2(2x — y).

Первый шаг — группировка.

4х 2 + у 2 + 2 = 4х — 2у;

4x 2 + y 2 + 1 — 4x + 2y + 1 = 0;

(4x 2 — 4x + 1) + (y 2 + 2y + 1) = 0.

Применяя формулу квадрата разности, получаем:

(2x — 1) 2 + (y + 1) 2 = 0 .

При суммировании двух неотрицательных выражений ноль получится только в том случае, если 2x — 1 = 0 и y + 1 = 0. Отсюда следует: x = ½ и y = -1.

Ответ: (1/2; -1).

Решите уравнение (x 2 — 6x + 10) (y 2 + 10y + 29) = 4.

Рационально применить метод оценки, выделив в скобках полные квадраты.

((x — 3) 2 + 1) ((y + 5) 2 + 4) = 4.

Кроме того, (x — 3) 2 + 1 ≥ 1 и (y + 5) 2 + 4 ≥ 4. Тогда левая часть уравнения всегда не меньше 4. Равенство возможно в случае

(х — 3) 2 + 1 = 1 и (у + 5) 2 + 4 = 4. Отсюда х = 3, у = -5.

Ответ: (3; -5).

Решить уравнение в целых числах: х 2 + 10у 2 = 15х + 3.

Можно записать это уравнение в таком виде:

х 2 = -10у 2 + 15х + 3. Если верно часть равенства делится на 5, тогда в остатке 3. Отсюда следует, что x 2 не делится на 5. Известно, что квадрат числа, которое не делится на 5, должен давать в остатке либо 1, либо 4. Это означает, что уравнение не имеет корней.

Ответ: Решений нет.

Пусть вас не обескураживает сложность поиска правильного решения уравнения с двумя переменными. Упорство и практика обязательно принесут свои плоды.

Цели:

1. Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
2. Углубить знания, выполнив ряд заданий, некоторые из которых не знакомы ни по своему типу, ни по способу решения.
3. Формирование интереса к математике через изучение новых разделов математики, воспитание графической культуры через построение графиков уравнений.

Тип урока : комбинированный.

Оборудование: графопроектор.

Видимость: таблица «Теорема Виета». 1. Умственный счет

.+a 1 x 1 + a 0 биномом x-a?

б) Сколько корней может иметь кубическое уравнение?

в) С помощью чего решаем уравнение третьей и четвертой степени?

г) Если b четное число в квадратном уравнении, то чему равно D и x 1; х 2

2. Самостоятельная работа (в группах)

Составить уравнение, если известны корни (ответы на задания закодированы) Использовать «Теорему Виета»

1 группа

Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6

Напишите уравнение:

B=1 -2-3+6=2; b=-2

c=-2-3+6+6-12-18=-23; с= -23

d=6-12+36-18=12; d=-12

e=1(-2)(-3)6=36

x 4 — 2 x 3 — 23 x 2 — 12 x + 36 = 0 (это уравнение затем решается формулой группа 2 на плате)

Решение . Ищем целые корни среди делителей числа 36.

p = ±1; ±2; ±3; ±4; ±6…

p 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, поэтому =1 является корнем уравнения. Схема Горнера

р 3 (х) = х 3 -х 2 -24х -36

р 3 (-2) = -8 -4 +48 -36 = 0, х 2 = -2

р 2 ( х) = х 2 -3х -18 = 0

х 3 = -3, х 4 = 6

Ответ: 1; -2; -3; 6 сумма корней 2 (Р)

2 группа

Корни: х 1 = -1; х 2 = х 3 =2; х 4 = 5

Напишите уравнение:

В=-1+2+2+5-8; b=-8

c=2(-1)+4+10-2-5+10=15; c=15

D=-4-10+20-10=-4; д=4

e=2(-1)2*5=-20;e=-20

8 + 15 + 4x-20 = 0 (группа 3 решает это уравнение на доске)

p = ±1; ±2; ±4; ±5; ±10; ±20.

стр 4 (1)=1-8+15+4-20=-8

стр 4 (-1)=1+8+15-4-20=0

р 3 (х) = х 3 -9х 2 + 24х -20

р 3 (2) = 8 -36 + 48 -20 = 0

р 2 (х) = х 2 — 7х+10=0 х 1=2; х 2 = 5

Ответ: -1;2;2;5 сумма корней 8(P)

3 группа

Корни: х 1 = -1; х 2 =1; х 3 = -2; х 4 = 3

Напишите уравнение:

B=-1+1-2+3=1;b=-1

s=-1+2-3-2+3-6=-7; s=-7

D=2+6-3-6=-1; d=1

e=-1*1*(-2)*3=6

x 4 — x 3 — 7x 2 + x + 6 = 0 (позже это уравнение решается на доске с помощью группа 4)

Раствор. Ищем целые корни среди делителей числа 6.

p = ±1; ±2; ±3; ±6

р 4 (1)=1-1-7+1+6=0

р 3 (х) = х 3 — 7х -6

р 3 (-1) = -1 + 7-6 \ u003d 0

р 2 (х) = х 2 -х -6=0; х 1 = -2; х 2 = 3

Ответ: -1; 1; -2; 3 Сумма корней 1 (О)

4 группа

Корни: х 1 = -2; х 2 = -2; х 3 = -3; x 4 = -3

Напишите уравнение:

B=-2-2-3+3=-4; б=4

с=4+6-6+6-6-9=-5; c=-5

D=-12+12+18+18=36; d=-36

e=-2*(-2)*(-3)*3=-36; е=-36

x 4+ 4x 3 — 5x 2 — 36x -36 = 0 (затем это уравнение решается группой 5 на доске)

Решение. Ищем целые корни среди делителей числа -36

p = ±1; ±2; ±3…

р(1)= 1 + 4-5-36-36 = -72

р 4 (-2) = 16 -32 -20 + 72 -36 = 0

р 3 (х ) = х 3 + 2х 2 -9х-18 = 0

р 3 (-2) = -8 + 8 + 18-18 = 0

р 2 (х) = х 2 -9 = 0; х=±3

Ответ: -2; -2; -3; 3 Сумма корней-4 (F)

5 группа

Корни: х 1 = -1; х 2 = -2; х 3 = -3; x 4 = -4

Запишите уравнение

x 4 + 10x 3 + 35x 2 + 50x + 24 = 0 (это уравнение затем решает 6-я группа на доске)

Решение . Ищем целые корни среди делителей числа 24.

р = ±1; ±2; ±3

р 4 (-1) = 1 -10 + 35 -50 + 24 = 0

р 3 (х) = х- 3 + 9х 2 + 26х + 24 = 0

р 3 (- 2) = -8 + 36-52 + 24 = О

р 2 (х) = х 2 + 7х + 12 = 0

Ответ: -1; -2; -3; -4 сумма-10 (I)

6 группа

Корни: х 1 = 1; х 2 = 1; х 3 = -3; x 4 = 8

Напишите уравнение

B=1+1-3+8=7;b=-7

c=1 -3+8-3+8-24= -13

Д=-3-24+8-24=-43; d=43

х 4 — 7 х 3 — 13 х 2 + 43 х — 24 = 0 (это уравнение затем решается 1 группой на доске)

Решение . Ищем целые корни среди делителей числа -24.

р 4 (1)=1-7-13+43-24=0

р 3 (1)=1-6-19+24=0

р 2 (х) = х 2 -5х — 24 = 0

х 3 = -3, х 4 = 8

Ответ: 1; 1; -3; 8 сумма 7 (L)

3. Решение уравнений с параметром

1. Решить уравнение x 3 + 3x 2 + mx — 15 = 0; если один из корней равен (-1)

Ответ в порядке возрастания

R=P 3 (-1)=-1+3-m-15=0

x 3 + 3x 2 -13x — 15 = 0 ; -1+3+13-15=0

По условию x 1 = — 1; Д=1+15=16

Р 2 (х) = х 2 + 2х-15 = 0

х 2 = -1-4 = -5;

х 3 = -1 + 4 = 3;

Ответ: — 1; -5; 3

В порядке возрастания: -5;-1;3. (b n s)

2. Найти все корни многочлена х 3 — 3х 2 + ах — 2а + 6, если остатки его деления на двучлены х-1 и х + 2 равны.

Решение: R = R 3 (1) = R 3 (-2)

Р 3 (1) = 1-3 + а- 2а + 6 = 4-а

Р 3 (-2) ) = -8-12-2а-2а + 6 = -14-4а

х 3 -3х 2 -6х + 12 + 6 = х 3 -3х 2 -6х + 18

х 2 (х- 3)-6(х-3) = 0

(х-3)(х 2 -6) = 0

3) а = 0, х 2 -0 * х 2 +0 = 0; х 2 =0; х 4 = 0

а=0; х=0; х=1

а>0; х=1; x=a ± √a

2. Напишите уравнение

1 группа . Корни: -4; -2; один; 7;

2 группа . Корни: -3; -2; один; 2;

3 группа . Корни: -1; 2; 6; 10;

4 группа . Корни: -3; 2; 2; 5;

5 группа . Корни: -5; -2; 2; четыре;

6 группа . Корни: -8; -2; 6; 7.

Предлагаем Вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Можно быстро получить и понять, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн , сначала приведите уравнение к общему виду:
ax2 + bx + c = 0
Заполните поля формы соответственно:

Как решить квадратное уравнение:	Типы корней:
1. Привести квадратное уравнение к общему виду: Общий вид Ax 2 +Bx+C=0 Пример: 3x — 2x 2 +1=-1 Уменьшить до -2x 2 +3x+2=0 2. Находим дискриминант D. D=B 2 -4*A*C. В нашем примере D= 9-(4*(-2)*2)=9+16=25. 3. Находим корни уравнения. х1 = (-В + Д 1/2)/2А. Для нашего случая x1=(-3+5)/(-4)=-0,5 x2=(-B-D 1/2)/2A. Для нашего примера x2=(-3-5)/(-4)=2 Если B четное число, то дискриминант и корни удобнее вычислять по формулам: D = K 2 -ac х1=(-К+Д 1/2)/А х2 = (-К-Д 1/2)/А, Где К=В/2	1. Реальные корни. А также. x1 не равно x2 Ситуация возникает, когда D>0 и A не равно 0. 2. Настоящие корни совпадают. x1 равно x2 Ситуация возникает, когда D=0. Однако ни А, ни В, ни С не должны быть равны 0, 3. Два сложных корня. x1=d+ei, x2=d-ei, где i=-(1) 1/2 Ситуация возникает, когда D 4. Уравнение имеет одно решение. A=0, B и C не равны нулю. Уравнение становится линейным. 5. У уравнения есть бесконечное число решений. А=0, В=0, С=0. 6. Уравнение не имеет решений. A=0, B=0, C не равно 0.

Для закрепления алгоритма вот еще наглядные примеры решений квадратных уравнений .

Пример 1. Решение обыкновенного квадратного уравнения с различными вещественными корнями.
x 2 + 3x -10 = 0
В этом уравнении
A=1, B=3, C=-10
D=B 2 -4*A*C = 9-4*1*(-10) = 9 +40 = 49
квадратный корень будет обозначаться как число 1/2!
х1 = (-В + Д 1/2) / 2А = (-3 + 7) / 2 = 2
х2 = (-В-Д 1/2) / 2А = (-3-7) / 2 = -5

Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x — 10 = x2 + 3x -10

Пример 2. Решение квадратного уравнения с одинаковыми вещественными корнями.
х 2 — 8х + 16 = 0
А=1, В=-8, С=16
D = k 2 — AC = 16 — 16 = 0
X=-k/A=4

Заменить
(х-4) * (х-4) = (х-4) 2 = Х 2 — 8х + 16

Пример 3. Решение квадратного уравнения с комплексными корнями.
13х 2 — 4х + 1 = 0
А=1, В=-4, С=9
D = b 2 — 4AC = 16 — 4 * 13 * 1 = 16 — 52 = -36
Дискриминант отрицательный — корни комплексные.

Х1 = (-В + Д 1/2) / 2А = (4 + 6и) / (2 * 13) = 2/13 + 3и / 13
х2 = (-В-Д 1/2) / 2А = (4-6i)/(2*13) = 2/13-3i/13
, где I корень квадратный из -1

Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор будет вам очень полезен.
Если материал был полезен, можно

» (Внеклассное чтение по произведениям современных писателей и поэтов о школе и учителях) 92 + bx + c = 0,$$

, где $a,  b,  c \in \mathbb{R}$ равны  и $a\neq 0$.

Если $a = 0$, наше уравнение сводится к $bx + c = 0$, что является линейным уравнением. Подробнее о решении линейных уравнений вы можете узнать в уроках Уравнения в один шаг, Уравнения в два шага и Уравнения в несколько шагов.

Число $a$ в этом уравнении называется старшим коэффициентом , число $b$ — линейным коэффициентом , а $c$ — постоянным .

Каждый $x$ (вещественный или комплексный), который удовлетворяет этому уравнению, называется 92 = – \frac {c}{a}.$$

Это уравнение всегда имеет два различных решения. Решения могут быть действительными или комплексными числами, в зависимости от знака чисел $a$ и $c$.
Если $- \frac {c}{a}>0$, то квадратное уравнение имеет два действительных решения:
$$x_1 = \sqrt{\left(-\frac{c}{a}\right)}  \text { и }  x_2 =-\sqrt{\left(-\frac{c}{a}\right)}.$$
Если $-\frac{c}{a} < 0$, то решения представляют собой комплексные числа
$$x_1 = я \sqrt{\left|-\frac{c}{a}\right|}  \text{ и }  x_2 = — i \sqrt{\left|-\frac{c}{a}\ правильно|}.$$ 92 – 4ac.$$

Тогда решения квадратного уравнения, записанные с использованием дискриминанта, будут:

$$x_{1,2}= \frac{-b \pm \sqrt{D}}{2a}. $$

Если $\D > 0$, то квадратное уравнение имеет два различных действительных решения, если $\D < 0$, то квадратное уравнение имеет два комплексно-сопряженных решения, а если $\D = 0$ квадратное уравнение имеет одно действительное решение кратности два.

 

Формулы Виета

 

Французский математик Франсуа Виет также изучал квадратное уравнение и пришел к важной связи между квадратным уравнением и системой двух уравнений с двумя неизвестными. Эти неизвестные являются решениями наблюдаемого квадратного уравнения. 92 + bx + 8 = 0$, какое другое решение и что такое $b$?

Раствор :

По формулам Виета находим, что:

$$x_1 + x_2 = -\frac{b}{1}$$

$$x_1 \cdot x_2 = \frac{8} {1}.$$

Поскольку у нас уже есть одно решение, это можно записать как:

$$ 2 + x_2 = -b$$

$$2x_2 = 8.$$

Из второго уравнения находим что $\x_2 = 4$, что приводит нас к $\b = -6$.

Пример: 92 + Dx + Ey + F = 0,$$

 

где $A, B, C, D, E, F$ – действительные числа – коэффициенты.

Уравнение такого типа не может быть решено без каких-либо связанных с ним условий, однако, если у нас есть еще одно дополнительное условие, такое как линейное уравнение, его можно решить.

Это потому, что из линейного уравнения мы получаем информацию о том, в каком отношении находятся неизвестные $x$ и $y$, и затем мы можем извлечь одно из другого, чтобы получить квадратное уравнение только с одним неизвестным. Решениями этой системы являются две пары упорядоченных чисел $(x_1, y_1)$ и $(x_2, y_2)$. 92 – 4 \cdot 7 \cdot 24}}{2\cdot 7} = \frac{28 \pm \sqrt{784-672}}{14} =\frac{28 \pm \ 4\sqrt{7}} {14} = 2 \pm \frac{2\sqrt{7}}{7}$$.

Теперь нам нужно решить линейные уравнения $y_1 = 2 – x_1$  и  $y_2 = 2 – x_2$.

Следующим образом:

$$y_1 = 2 – 2 – \frac{2\sqrt{7}}{7} = – \frac{2\sqrt{7}}{7},$$

$$ y_2 = 2 – 2 + \frac{2\sqrt{7}}{7} =   \frac{2\sqrt{7}}{7}.$$

 

Решения: $(2+\frac {2\sqrt{7}}{7}, – \frac{2\sqrt{7}}{7})$ и $(2-\frac{2\sqrt{7}}{7}, \frac {2\sqrt{7}}{7})$. 92 = -4 \Rightarrow  x_3 = -2i, \quad  x_4 = 2i$$.

Мы надеемся, что эти формулы для квадратных уравнений были вам полезны. Посмотрите:

Бесплатные рабочие листы квадратичных уравнений.

2263 совпадения)

   Решить с помощью квадратичной формулы (308,2 КиБ, 1536 совпадений)

   Поиск дискриминанта (473,2 КиБ, 986 совпадений)

   Факторизация квадратных выражений (315,0 КиБ, 1756 совпадений)

Квадратные уравнения | Brilliant Math & Science Wiki

Ашиш Менон, Сандип Бхардвадж, Ришик Джейн, а также

способствовал

Содержимое

• Решение с помощью факторинга
• Нахождение квадратного уравнения из корней
• Решение путем заполнения квадрата
• Решение квадратной формулы
• Параболы
• Природа корней квадратного уравнения
• Словесные задачи — основные
• Биквадратные уравнения
• Квадратные уравнения — решение задач
• Смотрите также
92+2х+3х+6&=0 \\ х(х+2)+3(х+2)&=0. \end{выровнено}x2+2x+3x+6x(x+2)+3(x+2)​=0=0.​ Приняв (x+2)(x+2)(x+2) как общий множитель, мы имеем (x+3)(x+2)=0x+3=0  ⟹  x=−3x+2=0  ⟹  x=−2.\begin{выровнено} (х+3)(х+2)&=0 \\ х+3&=0 \подразумевает х=-3 \\ x+2&=0 \подразумевает x=-2. \end{выровнено}(x+3)(x+2)x+3x+2​=0=0⟹x=−3=0⟹x=−2.​ Следовательно, два корня данного уравнения равны −3-3−3 и −2-2−2. □_\квадрат□​

Метод решения квадратного уравнения с помощью факторизации:

92 + 6a -6 a2+6a−6 равно aaa, тогда найдите минимальное значение aaa.

Когда задано два места переменной, мы должны записать их в виде (переменная — значение = 0)\текст{(переменная — значение = 0)}(переменная — значение = 0).

Чтобы найти уравнение из корней:

Шаг 1. Если задана переменная xxx и заданы два значения x=ax=ax=a и x=bx=bx=b, то мы должны упростить их до x−a=0 и x−b=0 .x-a=0 \quad\text{ и }\quad x-b=0.x-a=0 и x-b=0. Шаг 2. Перемножая уравнения и упрощая их, приходим к следующему: (x−a)(x−b)=0x2−(a+b)x+ab=0. 2-11х+30 & =0.\ _\квадрат \end{выровнено}(x−5)(x−6)x(x−6)−5(x−6)x2−6x−5x+30×2−11x+30​=0=0=0=0. □​​ 92 -4×1×-69}}{2×1}\\ & = \dfrac {20 \pm \sqrt {400 +276}}{2}\\ & = \dfrac {20 \pm \sqrt {676}}{2}\\ & = \dfrac {20 \pm 26}{2}\\ \Стрелка вправо x & = 23 \, \text{ или }\, x=-3.\ _\квадрат \end{выровнено}x⇒x​=2×1−(−20)±(−20)2−4×1×−69=220±400+276=220±676=220± 26​=23 или х=−3. □​​

Попробуйте решить следующие задачи. sqrt{4841}-69\big)}{2}2−(4841

​−69)​ 4681−692.\ _\квадрат \end{выровнено}2A⇒y​=A×(2−1​)2=8=8×2. □​​

Попробуйте решить следующие задачи:

0,84 1,05 1,00 0,95

Если бы логотип McDonald’s хранился в виде набора пикселей, увеличение быстро привело бы к искажению или пикселизации изображения, что раздражает. 2-25х-15х+375 &=0\\ х(х-25)-15(х-25) &=0\\ (х-15)(х-25) &=0\\ \Стрелка вправо x&=15, x=25. \end{выровнено}x(40−x)40x−x2x2−40x+375×2−25x−15x+375x(x−25)−15(x−25)(x−15)(x−25)⇒x​= 375=375=0=0=0=0=15,x=25.​ 92 +n -90 = (n — 9)(n+10)=0, n2+n−90=(n−9)(n+10)=0,

, что означает n=9 n = 9 n=9. Тогда два числа равны 9 и 10, а их сумма равна 19. □_\квадрат□​

Попробуйте решить следующие проблемы:

600 655 Ни один из вышеперечисленных 625

Учитель, пытаясь расположить учеников сплошным квадратом для массовых учений, обнаружил, что 24 ученика не учитываются. Когда он увеличил размер квадрата на единицу, то обнаружил, что ему не хватает 25 учеников. Найдите количество учеников.

Разность кубов двух последовательных нечетных натуральных чисел на 400 больше, чем сумма их квадратов. Найдите сумму двух целых чисел.

---

Пояснение : Нечетные положительные целые числа равны 1,3,5,7,9,…. 1, 3, 5, 7, 9, точки 1,3,5,7,9,…. Два последовательных нечетных положительных целых числа относятся к двум последовательным числам в этой последовательности. Это не относится к двум последовательным целым числам (из которых одно не будет нечетным).

Иногда квадратичная формула может быть полезна при решении уравнений большей степени. 92 — 100x + 5a = \ 0 x2−5ax+100= 0x2−100x+5a= 0

Найдите сумму всех возможных значений xxx, удовлетворяющих приведенным выше уравнениям. Обратите внимание, что aaa — произвольная константа.

х(х+1)(х+2)(х+3)=120 х(х+1)(х+2)(х+3)=120х(х+1)(х+2)(х +3)=120

Найдите сумму всех действительных корней приведенного выше уравнения.

• Факторные полиномы
• Завершение Квадрата
• Квадратичная формула

Цитировать как: Квадратные уравнения. Brilliant. org . Извлекаются из https://brilliant.org/wiki/quadratic-equations/

калькулятор, как их решать, примеры

Вам нужно решить биквадратные уравнения ? Воспользуйтесь нашим онлайн-калькулятором и получите сразу четыре решения уравнения.

Напомним, что биквадратное уравнение представляет собой уравнение четвертой степени (не путать с уравнением второй степени) без членов нечетной степени. То есть выглядят они так:

ax ⁴  + bx ²  + c = 0

Чтобы использовать наш калькулятор биквадратных уравнений , просто введите значения a, b и c и нажмите кнопку расчета, чтобы получить результат.

Разделы статей

• Как решать биквадратные уравнения
• Упражнения на решение уравнений двух квадратов
• Пример биквадратных уравнений
• Сколько решений имеет уравнение двух квадратов?
• Решение неполных уравнений двух квадратов

Как решать биквадратные уравнения

Мы уже видели, что уравнение двух квадратов имеет вид: Чтобы решить его, мы собираемся преобразовать его в уравнение второй степени , которое мы знаем, как решить. Для этого сделаем замену переменной в которой:

х ² = t

Следовательно, если заменить переменную в уравнении двух квадратов, мы получим уравнение второй степени вида: знать, как ее решить (нажмите на ссылку, которую мы только что оставили, если вы не знаете, как это сделать), поэтому мы получим два решения:

t = t ₁

t = t ₂

Но поскольку мы сделали замену переменной, в которой x ² = t, у нас будет это для извлечения четырех решений биквадратного уравнения путем решения следующих квадратных корней:

x ₁ = +√ t √ t ₁
x ₃ = +√ t ₂
x ₄ = -√ t ₂

Упражнения на решение уравнений двух квадратов

Чтобы применить теорию, которую мы только что рассмотрели, на примере биквадратных уравнений, упражнения Давайте решим следующее уравнение: переменной x ² = t и преобразуем его в следующее уравнение второй степени:0703, который позволяет нам получить решения уравнения второй степени:

Делая замены в приведенной выше формуле и решая, мы имеем следующее:

Теперь, когда мы знаем решения, мы отменяем замену переменной мы составили в начале статьи:

х ₁ = +√ t ₁ = +√ 25 = 5
х ₂ = -√ t ₁ = -√ 901 = -5 х 901 ₃ = +√ t ₂ = +√ -9
x ₄ = -√ t ₂ = -√ -9

Мы не решаем третье и четвертое решения, так как нет действительных чисел квадратного корня из -9 (мы можем только найти квадратный корень из положительных числа). Достаточно оставить это указанным в упражнении.

Пример биквадратичного уравнения

В случае, если предыдущее упражнение с уравнением двух квадратов было не очень ясным, давайте посмотрим еще одно, в котором нас просят решить:

x ⁴  — 13x ² + 36 = 0

Мы изменяем переменную x ² = T, чтобы преобразовать его в уравнение второй степени:

T ² — 13 ^T + 36 = 0 0003

7

и We решить его:

Наконец, мы отменяем замену переменной и извлекаем четыре решения исходного уравнения двух квадратов:
x ₂ = -√ t ₁ = -√ 9= -3
x ₃ = +√ t ₂ = +√ 4 = 2
x ₄ = -√ t ₂ = -√ 4 = -2

Легко, не правда ли? Если у вас есть какие-либо сомнения или вы хотите проверить решения, вы всегда можете использовать наш калькулятор биквадратичного уравнения или оставить нам комментарий, и мы поможем вам решить упражнение.

Сколько решений имеет уравнение двух квадратов?

Хотя уравнение двух квадратов обычно имеет четыре решения В некоторых случаях их может быть три, два, одно решение или вообще ни одного.

Например:

• Если t ₁ = 0 или t ₂ = 0, у нас будет только одно решение при отмене замены переменной, и оно будет x = 0
• Если t ₁ < 0, у нас не будет никакого решения, как мы видели в первом примере, так как нет корней отрицательного числа. То же самое, если t ₂ < 0,

Если вы используете наш Калькулятор биквадратичного уравнения и вы видите, что в некоторых полях решений не отображаются данные, это связано с тем, что некоторые из вышеперечисленных условий были выполнены.

Решение неполного уравнения двух квадратов

Когда дело доходит до решения неполного уравнения двух квадратов Процедура, которую необходимо использовать, такая же, как и в первом пункте теории.

Другими словами, мы меняем переменную и в результате получаем неполное квадратное уравнение, которое нужно будет решить по процедуре, которую мы указываем на странице ссылки, которую мы вам только что оставили.

Nacho

Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.

• Градусы в радианы
• Апофема
• Калькулятор антилогарифмов
• Калькулятор деления
• Калькулятор экспоненты
• Exponential Function Calculator
• Logarithm Calculator
• Neperian logarithm calculator
• Prime Number Calculator
• Odd or even calculator
• Exponent calculator
• Cube root calculator
• Calculator for n-th root of a number
• Quadratic equation calculator
• Калькулятор факториала онлайн
• Калькулятор гипотенузы
• Калькулятор наибольшего общего делителя
• Калькулятор наименьшего общего кратного
• Калькулятор умножения
• Онлайн-калькулятор

Формула для нахождения биквадратного уравнения?

Вопрос задан: Доктор Сэмми Кози

Оценка: 4,1/5 (43 голоса)

Биквадратное уравнение — это уравнение 4-й степени без членов степени 1 и 3. Чтобы решить биквадратное уравнение, необходимо сделать замену переменной: z = x ² . Затем вам нужно решить квадратное уравнение и, наконец, отменить изменение.

Какова общая форма биквадратного уравнения?

В общем случае g(x) = ax3 + bx2 + cx + d , a ≠ 0 — квадратичный многочлен. Многочлен, имеющий наивысшую степень 4, известен как биквадратный многочлен.

Существует ли формула четвертой степени?

Существует аналогичная формула для общего уравнения четвертой степени: ax4 + bx3 + cx2 + dx + e = 0 . Под этим мы подразумеваем четыре различные формулы, каждая из которых дает один корень уравнения. … Настоящая цель статьи — познакомить читателей с рядом математических тонкостей, связанных с решением общей квартики.

Как решать кубические уравнения?

Общая стратегия решения кубического уравнения состоит в том, чтобы свести его к квадратному уравнению, а затем решить квадратное уравнение обычными средствами , либо факторизуя, либо используя формулу. все кубические уравнения. Точно так же, как квадратное уравнение может иметь два действительных корня, кубическое уравнение может иметь три.

Что такое формула 3 b 3?

Формула a ³ — b ³ также известна как одно из важных алгебраических тождеств. Читается как куб минус b куб. это ³ — b ³ формула выражается в виде

Квадратное уравнение: Как решить биквадратное уравнение | Камальдхирия

Найдено 36 связанных вопросов

Что такое формула Кардано?

Формула Кардано для корней (1) имеет вид: x=3√−q2+√q24+p327+3√−q2−√q24+p327 . для которого выполняется соотношение αβ=−p/3 (такое значение β всегда существует).

Есть ли формула для решения уравнений пятой степени?

(1) Из теории Галуа известно, что не существует формулы для решения общего уравнения пятой степени . Но известно, что общую квинтику можно решить точно для 5 корней. Еще в 1858 году Эрмит и Кронекер независимо друг от друга показали, что квинтику можно точно решить (используя эллиптическую модулярную функцию).

Как написать уравнение четвертой степени?

Функция четвертой степени — это полином четвертой степени: функция, в которой член старшего порядка представляет собой переменную, возведенную в четвертую степень. Это можно записать как: f(x) = a ₄ x ⁴ + a ₃ x ³ + a ₂ x ² +a _{1 6 4 509 1} x 4.4

Является ли алгебра линейных уравнений?

Линейное уравнение в алгебре — это уравнение , которое можно записать в виде ax + by = c.

Является ли корень 2 многочленом?

Квадратный корень из 2 — это число. Аполиномиальное — это выражение от переменной x, состоящее из сумм, кратных неотрицательным степеням x. Корень 2 не является полиномом .

Какая степень биквадратичности?

Мы знаем, что степень квадратного многочлена равна 2. Таким образом, степень биквадратного многочлена равна 2×2=4 .

Что такое метод Феррари?

Метод Феррари — это метод сведения решения уравнения степени 4 над комплексными числами (или, в более общем случае, над любым полем характеристики ≠2,3) к решению одного кубического и двух квадратных уравнений; открыт Л. Феррари (опубликовано в 1545 г.). =(x2+p2+α)2−[2αx2−qx+(α2+pα+p24−r)].

Какие корни биквадратного уравнения?

Теперь мы вычислили все 4 корня биквадратного уравнения. Все четыре корня биквадратного уравнения равны \[1+i\], \[1-\sqrt{2}\], \[1-i\], \[1+\sqrt{2}\].

Какие корни кубического уравнения?

Три корня x3 + ax + b — это действительные числа 2R, -R + /3I и -R — /3I . Эти четыре шага вместе составляют кубическую формулу. Он использует комплексные числа (D и z) для создания действительных чисел (2R, -R + /3I и -R — /3I), которые являются корнями кубического многочлена x3 + ax + b.

Почему нет формулы пятой степени?

Любая кубическая формула, построенная исключительно из операций с полями, непрерывных функций и радикалов, должна содержать вложенные радикалы. … Не существует не существует какой-либо формулы пятой степени, построенной из конечной комбинации полевых операций, непрерывных функций и радикалов.

Как решить уравнение 5 степени?

Чтобы решить многочлен степени 5, мы должны разложить данный многочлен на множители как можно больше . После факторизации многочлена степени 5 мы находим 5 множителей и приравнивая каждый множитель нулю, мы можем найти все значения x. Решение: Поскольку степень многочлена равна 5, у нас есть 5 нулей.

Почему нет формулы для полиномов 5-й степени?

И простая причина, по которой уравнение пятой степени неразрешимо, состоит в том, что не существует аналогичного набора из четырех функций в A, B, C, D и E, который сохраняется при перестановках этих пяти букв .

No related posts.