Биквадратные уравнения — примеры с решениями » Kupuk.net
Впервые с решением биквадратных уравнений сталкиваются на уроках алгебры. Степенные равенства высокого порядка решаются по аналогии с квадратными уравнениями. Существует несколько способов, позволяющих найти ответ, но чаще используется метод введения новой переменной. Такой подход простой и разобраться с ним будет под силу даже семикласснику. При этом существуют и онлайн-сервисы, проводящие вычисление корней квадратичного равенства.
Появление методики
Уравнения начали составлять ещё в Древнем Вавилоне. Это было вызвано потребностью находить площади земельных участков, выполнять инженерные работы. Составляли равенства и астрономы, высчитывая расстояния до обнаруживаемых космических тел. Квадратные равенства встречаются в клинописных текстах греков и вавилонян. При этом в этих записях попадаются уравнения, содержащие кубическую или биквадратную степень.
Несмотря на довольно хорошее развитие алгебры в стародавнее время, находимые упоминания о равенствах содержат только ответы, без указаний способов решений. Задачи с примерами решения биквадратных уравнений встречаются у астронома Ариабхатта и индийского учёного Брахмапутра. Формулы для решения сложных уравнений были изложены в сборнике «Книга абака», написанной в 1202 году итальянцем Фибоначчи. Это издание способствовало развитию математики, в частности, алгебре, в Италии, Германии, Франции. Большой вклад в развитие теории решения внесли и советские учёные-математики: Чеботарев, Четаев.
Задачи с примерами решения биквадратных уравнений встречаются у астронома Ариабхатта и индийского учёного Брахмапутра. Формулы для решения сложных уравнений были изложены в сборнике «Книга абака», написанной в 1202 году итальянцем Фибоначчи. Это издание способствовало развитию математики, в частности, алгебре, в Италии, Германии, Франции. Большой вклад в развитие теории решения внесли и советские учёные-математики: Чеботарев, Четаев.
В XVI веках в Китае был разработан способ нахождения корней равенств высшей степени методом Цинь Цзю-шао, после успешно применявшимся в работах Руффини и Горнера.
Этот метод использовал способ подбора, но применим был только для случаев, когда в ответе присутствовали только целые числа.
Все способы решения биквадратных уравнений сводились к приведению их к простому квадратному равенству. Была найдена формула, позволяющая решать уравнения с помощью радикалов (корней). Впервые этот метод предложил Виета, но он был рассчитан только на положительные ответы. Итальянские же учёные Тарталья, Кордано, Бомбелли стали учитывать и отрицательные корни. В итоге Декарт, Жирар и Ньютон привели способы решения к современному виду.
Итальянские же учёные Тарталья, Кордано, Бомбелли стали учитывать и отрицательные корни. В итоге Декарт, Жирар и Ньютон привели способы решения к современному виду.
Биквадратные выражения стали разделять на полные и неполные. В алгоритмическом языке корнями уравнения начали называть такие значения неизвестной составляющей, при которой решаемое выражение обращается в правильное числовое равенство. То есть чтобы решить задачу, нужно найти всевозможные его корни или доказать, что решения быть не может.
Основные понятия
Биквадратным уравнением будет называться равенство вида: a*p 4 + b*p 2 + c = 0. Переменные a, b, c могут быть различными числами, при этом A не должно равняться нулю. Символ C называют свободным членом. За P принимают неизвестную переменную, требующую вычисления. Решение уравнений сводится к поиску чисел, которые при подстановке вместо P сделают равенство верным.
Согласно теореме Безу, число корней многочлена, не равного нулю, не может превосходить величину его степени. При этом любой многочлен с коэффициентами ненулевой степени должен иметь хотя бы одно решение. Тут следует отметить, что корень уравнения может быть комплексным. То есть таким выражением, степень которого равна wx = z, где x — степень, а w — комплексное число. Понятие комплексного числа уже относится к высшей математике. Обозначают его символом (z)1/x.
Для того чтобы доказать справедливость утверждения Безу, нужно за корень многочлена f принять c1 и составить равенство f = (p — c1) f1 . Тогда (f 1 Є K [p]), где К — является элементом поля многочлена, но лишь при условии, что f можно разделить на (p — c). Если принять за c2 корень f1, то f1 = (p — c 2)* f 2 (f 2 Є K [ p ]), а это значит что будет верным выражение: f = (p — c 1) * (p — c 2) * f2. Для длинного многочлена вида: f = (p — c 1) * (p — c 2) *…* (p — c) * s, где многочлен (s Є K [p]) не имеет решений.
Так как значения с1, с2… Cm — это все возможные корни f, то для любого поля будет верным: f (p) = (c — c1) * (c — c2)…(c — cm) * s (p). Учитывая, что s (p) не равно нулю, а f (p) = 0 только в том случае, если C равно некоторому числу I, величина корней многочлена f не может быть более значения m.
Таким образом, уравнение может иметь четыре, три, два, или одно решение. При этом есть вероятность, что ответа может совсем и не быть. Принцип, по которому решаются биквадратные уравнения, следующий:
- вводят новую переменную y = p2;
- подставляют используемую переменную в решаемое уравнение;
- используя методы решения квадратных уравнений, находят корни равенства;
- найденные величины подставляют в выражение y = p2 и вычисляют исходные корни.
Квадратные уравнения можно решать любым удобным способом. Типичная схема состоит всего из четырёх шагов и редко вызывает трудности понимания. Пожалуй, сложности могут возникнуть только при нахождении комплексных корней.
Решение равенств
Без знания методов нахождения корней в квадратных уравнениях решить самостоятельно биквадратное равенство не удастся, так как исходное неравенство в итоге приводится к виду квадратичного. Существует несколько способов, позволяющих быстро найти нужные корни или доказать невозможность существования равенства.
К основным относят:
- разложение части уравнения с неизвестной на множители;
- вынос за скобки полного квадрата;
- использование специальных формул;
- графический метод;
- теорему Виета.
Разложение многочлена на множители основано на группировании и нахождении дискриминанта, то есть знака, по виду которого можно судить о существовании корней. Для решения используется формула: a * p 2 + b * p + c = a * (p — p 1) * (p — p 2), где p и являются корнями уравнения. Этот способ понятен и используется при обучении учащихся решению задач такого типа.
Этот способ понятен и используется при обучении учащихся решению задач такого типа.
Нахождение корней методом выделения полного квадрата требует опыта использования формул сокращённого умножения, особенно если коэффициентами являются рациональные числа. При решении используется выражение: (a + b)2 = a 2 + 2* a * b + b 2 и (a — b)2 = a 2 — 2* a * b + b 2.
Существуют специальные формулы нахождения корней квадратного, а значит, и биквадратного уравнения. Выглядят они следующим образом: p 1 = (- b — (b 2— 4 ac)½) / (2* a) и p 2 = (- b + (b 2 + 4 ac)½) / (2* a). С их помощью можно решить любое уравнение. При этом часто для упрощения решения вводят замену подкоренному выражению (b 2— 4 ac) обозначая его буквой D — дискриминант. Если D больше нуля, то есть два корня, если меньше — решений нет. Если же D = 0, то существует только один корень.
Франсуа Виет, проводя математические исследования, смог обнаружить зависимость между корнями уравнения и его коэффициентами. Он установил, что если p1 и p2 являются решениями равенства, то их сумма будет равна второму коэффициенту с другим знаком, а произведение свободному члену. То есть для уравнения вида: p2 +r*p + k = 0, будет справедливо записать, что p1 + p2 = — r, p1 * p2 = k.
Он установил, что если p1 и p2 являются решениями равенства, то их сумма будет равна второму коэффициенту с другим знаком, а произведение свободному члену. То есть для уравнения вида: p2 +r*p + k = 0, будет справедливо записать, что p1 + p2 = — r, p1 * p2 = k.
Графическое решение требует построения зависимостей. График первой представляет собой параболу, проходящую через начало координат, а второй — прямую. Для того чтобы выделить зависимости используют перенос. В результате получается две функции: y = a * p 2 и y = -(r * p+k). Построение функций и нахождение точек пересечения занимает много времени, поэтому этот метод практически никогда не используется.
Примеры уравнений
Решения любым из способов имеют свои достоинства и недостатки. По мнению математиков, проще решать уравнения, используя теорему Виета. Например, пусть дано выражение: 4p4 — 5p + 1 = 0, необходимо найти все бинарные корни. В первую очередь задание нужно привести к виду квадратного равенства. Для этого вводится переменная m = p2. Тогда заданное уравнение можно записать как 4 m2 — 5m + 1 = 0.
В первую очередь задание нужно привести к виду квадратного равенства. Для этого вводится переменная m = p2. Тогда заданное уравнение можно записать как 4 m2 — 5m + 1 = 0.
Теперь можно определить дискриминант: D = (-5)2 — 4 * 4 * 1 = 9. Используя формулы нахождения корней, вычисляют: m1 = (5+3) / 8 = 1, m2 = (5−3) / 8 = ¼. Оба ответа удовлетворяют условию, то есть больше нуля. Подставив полученные значения в исходные выражения, решают неполные квадратные уравнения: p1 = 1; p2 = -1; p3 = ½; p4 = -½. Это цифры и будут искомыми корнями.
Довольно легко решаются уравнения с помощью метода Виета. Вероятность допущения ошибки при определении корней в этом случае стремится к нулю. Например, p4 — 10 * p2 + 9 = 0. Чтобы избавиться от четвёртой степени, вводят переменную p. В результате уравнение принимает вид: p2 — 10 * p2 + 9 = 0. Теперь можно найти корни, используя обратную теорему Виета: p 1 = 9, p 2 = 1. Так как оба ответа больше нуля, то действительными корнями уравнения будут: p 1 = 3, p 2 = -3, p 3 = 1, p 2 = -1.
Определить, что решать биквадратное уравнение не имеет смысла, можно, используя комбинаторный анализ. Например, p4 + 11*p2 + 10 = 0. Для его решения необходимо расписать каждые члены уравнения, используя определение равенства. Так как каждый член p4, 11*p2, 10 должен быть больше либо равен нулю, то справедливым будет выражение: p4 + 11*p2 + 10 > 0.
Отсюда можно сделать вывод, что p4 + 11*p2 + 10 решения не имеет, ведь сумма неотрицательных чисел с положительным не может быть равной нулю. И также можно разложить и доказать бесперспективность поиска для задания с одними минусами, например, -2 p4 — 45 p2 — 12 = 0.
Но не всегда уравнение будет иметь четыре корня. Например, p 4 +4 *p 2 — 21=0. Если принять p2 = m, квадратное уравнение изменится до вида: m 2 +4*m -21=0, отсюда m 1 = -7, m 2 =3. Теперь нужно решить первоначальное уравнение. Первый ответ не имеет действительных корней, из второго же находят решение. Им будут корни: m 1 = (3)½ и m 2 = -(3)½.
Разложение на множители
Самостоятельная работа, дающаяся в школе, часто предполагает решение биквадратных равенств методом разложения на множители. Связанно это с тем, что этот способ позволяет понять принцип нахождения корней для многочлена любой степени.
Например, нужно разложить уравнение p4 + p3 — 6p2 на множители. В первом действии неизвестное выносится за скобки p2 (p2 + p — 6). Во втором, используя формулу нахождения решений, вычисляют: p 1 = (-1 + (12 — 4 * (-6))½) / 2, p 2 = (-1 — (12 — 4 * (-6))½) / 2. Отсюда корни уравнения будут p1 = -3, p2 = 2. Подставив полученные значения в заданное выражение, можно записать: p 2 + p — 6 = (p — p 1)*(p — p 2) = (p + 3) * (p-2).
Пошагово описать разложение многочлена можно на следующем примере: p4 + 2p3 + 3p2 + 4p +2. Решают его в следующей последовательности:
 Значит, он будет любым из цифр: -2, -1, 1, 2.
Значит, он будет любым из цифр: -2, -1, 1, 2. Вычисление корней требует внимательности и усердия. Для проверки своих навыков можно использовать онлайн-калькуляторы. Это сервисы, использующие специальное программное обеспечение, часто написанное на Паскале, умеют быстро и безошибочно рассчитывать корни любого примера.
Чтобы решить биквадратное уравнение онлайн, особых умений или знаний правил не нужно. Всё, что требуется — это ввести в предложенную форму параметры решаемого равенства. Из наиболее популярных интернет-порталов выделяют Allcalc. Используя его, можно проверить свои знания, исправить допущенные ошибки при самостоятельном расчёте. Причём свои услуги сайт предлагает совершенно бесплатно.
Квадратные и биквадратные уравнения
Впервые квадратные уравнения сумели решить математики древнего Египта. Вавилоняне умели решать неполные квадратные уравнения, так же частные виды полных квадратных уравнений около 2 тысяч лет до нашей эры. Древнегреческие математики умели решать некоторые виды квадратных уравнений, сводя их к геометрическим построениям. Примеры решения уравнений без использования геометрических знаний дает Диофант Александрийский (3 век). Диофант в своих книгах «Арифметика» изложил способ решения полных квадратных уравнений, однако эти книги не сохранились. В Европе формулы для решения квадратных уравнений были впервые изложены итальянским математиком Леонардо Фибоначчи в 1202 году.
В Европе формулы для решения квадратных уравнений были впервые изложены итальянским математиком Леонардо Фибоначчи в 1202 году.
Общее правило решения квадратных уравнений, преобразованных в вид х2 + bх = с, было описано немецким математиком М. Штифелем. Он и сформулировал в 1544 году общее правило решения квадратных уравнений, приведенных к единому каноническому виду
Франсуа Виет вывел формулы квадратного уравнения в общем виде, однако он работал только с положительными числами.
Тарталья, Кардано, Бомбелли – итальянские ученые, которые среди первых в XVI веке учитывают кроме положительных еще и отрицательные корни.
Выводом формулы решения квадратных уравнений общего вида занимался Виет. Одно свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал).
После трудов нидерландского математика Альберта Жирара, а также Декарта и Ньютона, методы решения квадратных уравнений приняли современный вид.
Квадратные уравнения
1. Вспомним уже знакомые способы решения и исследования квадратных уравнений:
- выделение полного квадрата;
- по формуле корней для квадратного уравнения;
- по теореме Виета;
- на основании свойств квадратичной функции.
В процессе решения уравнений необходимо следить за множеством допустимых значений неизвестного, т.к. оно может изменяться. В случае его расширения следует проверять найденное решение, не является ли оно посторонним для данного уравнения. В случае, если произошло сужение, необходимо убедиться, не являются ли потерянные значения неизвестных решениями данного уравнения. Процесс нахождения выпавших решений не всегда легко выполним, поэтому желательно избегать сужение множества допустимых значений неизвестных уравнения.
2. Типичные ошибки при решении уравнений.
По правилам можно преобразовывать исходное уравнение в равносильное ему, при этом, вы знаете, что: обе части уравнения можно делить или умножать на одно и то же, отличное от нуля, число.
1) Если уравнение имеет вид f(х) · g(х) = p(х) · g(х), то деление обеих частей на одинаковый множитель g(x), как правило, недопустимо. Данное действие может привести к потере корней: могут быть потеряны корни уравнения g(х) = 0, если ни существуют.
Пример 1.
Решить уравнение 2(х – 3) = (х – 3)(х + 5).
Решение.
Здесь нельзя сокращать на множитель (х – 3).
2(х – 3) – (х – 3)(х + 5) = 0, вынесем общую скобку:
(х – 3)(-х – 3) = 0, теперь
х – 3 = 0 или -х – 3 = 0;
х = 3 или х = -3.
Ответ: -3; 3.
2) Уравнение вида f(х) / g(х) = 0 можно заменить системой:
{f(x) = 0,
{g(x) ≠ 0.
Она равносильна исходному уравнению.
Или можно решить уравнение f(x) = 0, а уже затем исключить найденных корней те, которые обращают в нуль знаменатель g(x).
Встречаются дробно-рациональные уравнения, которые сводятся к квадратным уравнениям.
Пример 2.
Решить уравнение: (х + 3) / (х – 3) + (х – 3) / (х + 3) = 10/3 + 36/(х – 3)(х + 3).
Решение.
Умножив обе части уравнения на общий знаменатель и заменив исходное уравнение целым, получим равносильную систему:
{3(х + 3)2 + 3(х – 3)2 = 10(х – 3)(х + 3) + 3 · 36;
{(х – 3)(х +3) ≠ 0.
В результате получим два корня: х = 3 или х = -3, но х ≠ 3 и х ≠ -3.
Ответ: уравнение корней не имеет.
Пример 3.
Решить уравнение: (х + 5)(х2 + 4х — 5)/(х + 5)(х + 2) = 0.
Решение.
Часто ограничиваются таким решением:
(х2 + 4х – 5) / (х + 2) = 0.
{х = -5, х = 1,
{х ≠ -2.
Ответ: -5; 1.
Правильный ответ: 1.
Пример 4.
При выполнении распространенных заданий на исследование квадратного уравнения следующего вида: «Не вычисляя действительных корней х1 и х2 уравнения 2х2 + 3х + 2 = 0, найти значение х12 + х22» банальная невнимательность приводит к грубой ошибке.
Действительно, по теореме Виета,
х12 + х22 = (х1 + х2)2 – х1х2 = (-3/2)2 – 2 · 1 = 1/4.
Однако, теоремой можно было воспользоваться при существовании действительных корней. В данном примере D < 0 и корней нет.
Ответ: значение х 12 + х22 не существует.
Пример 5.
Вычислить отрицательный коэффициент b и корни уравнения х2 + bх – 1 = 0, если с увеличением каждого из этих корней на единицу они становятся корнями уравнения х2 – b2х – b = 0.
Решение.
Пусть х1 и х2 – корни уравнения х2 + bх – 1 = 0. Тогда по т. Виета
х1 + х2 = -b и х1х2 = -1 (*). С другой стороны, по условию
(х1 + 1) + (х2 + 1) = b2 и (х1 + 1)(х2 + 1) = -b.
Перепишем:
х1 + х2 = b2 – 2 и (х1 + 1)(х2 + 1) = -b.
Теперь, учитывая условия (*), получим b
b1 = -2, b2 = 1. По условию подходит b1 = -2.
Значит, исходное уравнение имеет вид х2 – 2х – 1 = 0, корнями являются числа х1,2 = 1 ± √2.
Ответ: b1 = -2, х1,2 = 1 ± √2.
Уравнения, приводимые к квадратным. Биквадратные уравнения
Уравнения вида ах4 + bх2 + c = 0, где а ≠ 0, называются биквадратными уравнениями с одной переменной.
Для решения биквадратного уравнения нужно сделать подстановку х2 = t, найти корни t1 и t2 квадратного уравнения аt2 + bt + c = 0 и решить уравнения х2 = t1 и х2 = t2. Они имеют решения лишь в случае, когда t1,2 ≥ 0.
Пример 1.
Решить уравнение х4 + 5х2 – 36 = 0.
Решение.
Подстановка: х2 = t.
t2 + 5t – 36 = 0. По т. Виета t1 = -9 и t2 = 4.
х2 = -9 или х2 = 4.
Ответ: В первом уравнении корней нет, из второго: х = ±2.
Пример 2.
Решить уравнение (2х – 1)4 – 25(2х – 1)2 + 144 = 0.
Решение.
Подстановка: (2х – 1)2 = t.
t2 – 25t + 144 = 0. По т. Виета t1 = 9 и t2 = 16.
(2х – 1)2 = 9 или (2х – 1)2 = 16.
2х – 1 = ±3 или 2х – 1 = ±4.
Из первого уравнения два корня: х = 2 и х = -1, из второго тоже: х = 2,5 и х = -1,5.
Ответ: -1,5; -1; 2; 2,5.
Таким образом, процесс решения любых уравнений состоит в последовательной замене данного уравнения другим, равносильным ему и более простым уравнением.
Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как решаются биквадратные уравнения. Как решать биквадратное уравнение: видео
Впервые квадратные уравнения сумели решить математики древнего Египта. Вавилоняне умели решать неполные квадратные уравнения, так же частные виды полных квадратных уравнений около 2 тысяч лет до нашей эры. Древнегреческие математики умели решать некоторые виды квадратных уравнений, сводя их к геометрическим построениям. Примеры решения уравнений без использования геометрических знаний дает Диофант Александрийский (3 век). Диофант в своих книгах «Арифметика» изложил способ решения полных квадратных уравнений, однако эти книги не сохранились.
Общее правило решения квадратных уравнений, преобразованных в вид х 2 + bх = с , было описано немецким математиком М. Штифелем. Он и сформулировал в 1544 году общее правило решения квадратных уравнений, приведенных к единому каноническому виду
х 2 + bх + с = 0 при всевозможных вариациях знаков и коэффициентов b и с.
Франсуа Виет вывел формулы квадратного уравнения в общем виде, однако он работал только с положительными числами.
Тарталья, Кардано, Бомбелли – итальянские ученые, которые среди первых в XVI веке учитывают кроме положительных еще и отрицательные корни.
Выводом формулы решения квадратных уравнений общего вида занимался Виет. Одно свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал).
После трудов нидерландского математика Альберта Жирара, а также Декарта и Ньютона, методы решения квадратных уравнений приняли современный вид.
Квадратные уравнения
1. Вспомним уже знакомые способы решения и исследования квадратных уравнений:
- выделение полного квадрата;
- по формуле корней для квадратного уравнения;
- по теореме Виета;
- на основании свойств квадратичной функции.
В процессе решения уравнений необходимо следить за множеством допустимых значений неизвестного, т.к. оно может изменяться. В случае его расширения следует проверять найденное решение, не является ли оно посторонним для данного уравнения. В случае, если произошло сужение, необходимо убедиться, не являются ли потерянные значения неизвестных решениями данного уравнения. Процесс нахождения выпавших решений не всегда легко выполним, поэтому желательно избегать сужение множества допустимых значений неизвестных уравнения.
2. Типичные ошибки при решении уравнений.
По правилам можно преобразовывать исходное уравнение в равносильное ему, при этом, вы знаете, что: обе части уравнения можно делить или умножать на одно и то же, отличное от нуля, число.
1) Если уравнение имеет вид f(х) · g(х) = p(х) · g(х), то деление обеих частей на одинаковый множитель g(x), как правило, недопустимо. Данное действие может привести к потере корней: могут быть потеряны корни уравнения g(х) = 0, если ни существуют.
Пример 1.
Решить уравнение 2(х – 3) = (х – 3)(х + 5).
Решение.
Здесь нельзя сокращать на множитель (х – 3).
2(х – 3) – (х – 3)(х + 5) = 0, вынесем общую скобку:
(х – 3)(-х – 3) = 0, теперь
х – 3 = 0 или -х – 3 = 0;
х = 3 или х = -3.
Ответ: -3; 3.
2) Уравнение вида f(х) / g(х) = 0 можно заменить системой:
{f(x) = 0,
{g(x) ≠ 0.
Она равносильна исходному уравнению.
Или можно решить уравнение f(x) = 0, а уже затем исключить найденных корней те, которые обращают в нуль знаменатель g(x).
Встречаются дробно-рациональные уравнения, которые сводятся к квадратным уравнениям.
Пример 2.
Решить уравнение: (х + 3) / (х – 3) + (х – 3) / (х + 3) = 10/3 + 36/(х – 3)(х + 3).
Решение.
Умножив обе части уравнения на общий знаменатель и заменив исходное уравнение целым, получим равносильную систему:
{3(х + 3) 2 + 3(х – 3) 2 = 10(х – 3)(х + 3) + 3 · 36;
{(х – 3)(х +3) ≠ 0.
В результате получим два корня: х = 3 или х = -3, но х ≠ 3 и х ≠ -3.
Ответ: уравнение корней не имеет.
Пример 3.
Решить уравнение: (х + 5)(х 2 + 4х — 5)/(х + 5)(х + 2) = 0.
Решение.
Часто ограничиваются таким решением:
(х 2 + 4х – 5) / (х + 2) = 0.
{х = -5, х = 1,
{х ≠ -2.
Ответ: -5; 1.
Правильный ответ: 1.
Пример 4.
При выполнении распространенных заданий на исследование квадратного уравнения следующего вида: «Не вычисляя действительных корней х 1 и х 2 уравнения 2х 2 + 3х + 2 = 0, найти значение х 1 2 + х 2 2 » банальная невнимательность приводит к грубой ошибке.
Действительно, по теореме Виета,
х 1 2 + х 2 2 = (х 1 + х 2) 2 – х 1 х 2 = (-3/2) 2 – 2 · 1 = 1/4.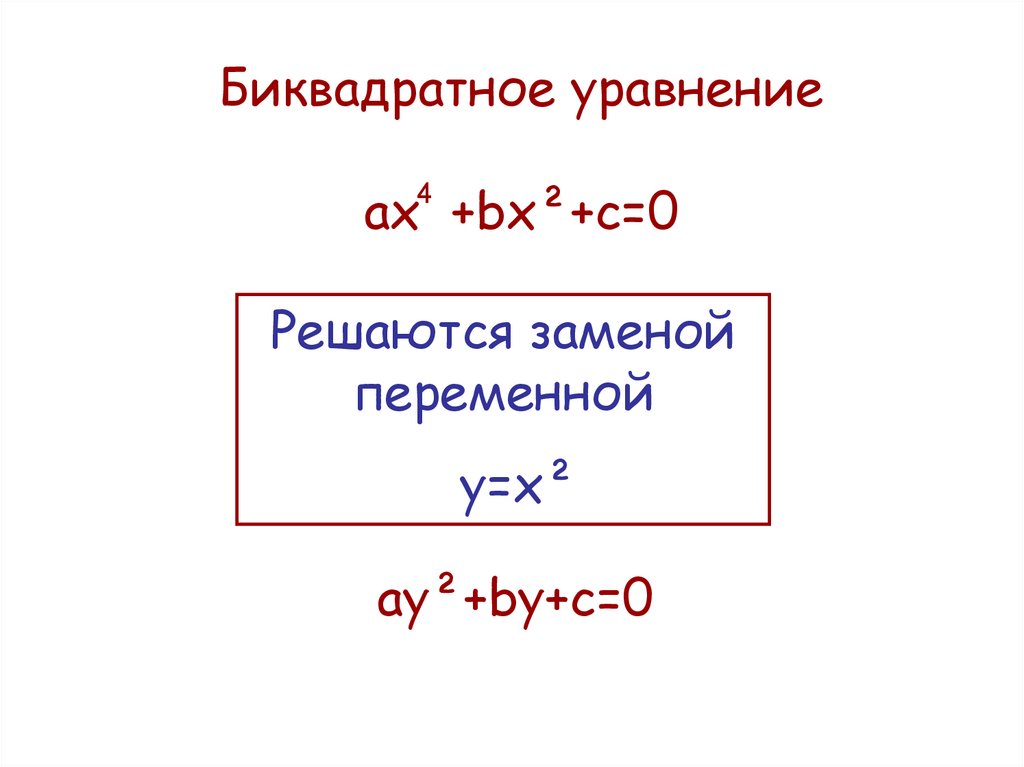
Однако, теоремой можно было воспользоваться при существовании действительных корней. В данном примере D
Ответ: значение х 1 2 + х 2 2 не существует.
Пример 5.
Вычислить отрицательный коэффициент b и корни уравнения х 2 + bх – 1 = 0, если с увеличением каждого из этих корней на единицу они становятся корнями уравнения х 2 – b 2 х – b = 0.
Решение.
Пусть х 1 и х 2 – корни уравнения х 2 + bх – 1 = 0. Тогда по т. Виета
х 1 + х 2 = -b и х 1 х 2 = -1 (*). С другой стороны, по условию
(х 1 + 1) + (х 2 + 1) = b 2 и (х 1 + 1)(х 2 + 1) = -b.
Перепишем:
х 1 + х 2 = b 2 – 2 и (х 1 + 1)(х 2 + 1) = -b.
Теперь, учитывая условия (*), получим b 2 – 2 = -b, следовательно,
b 1 = -2, b 2 = 1. По условию подходит b 1 = -2.
Значит, исходное уравнение имеет вид х 2 – 2х – 1 = 0, корнями являются числа х 1,2 = 1 ± √2.
Ответ: b 1 = -2, х 1,2 = 1 ± √2.
Уравнения, приводимые к квадратным.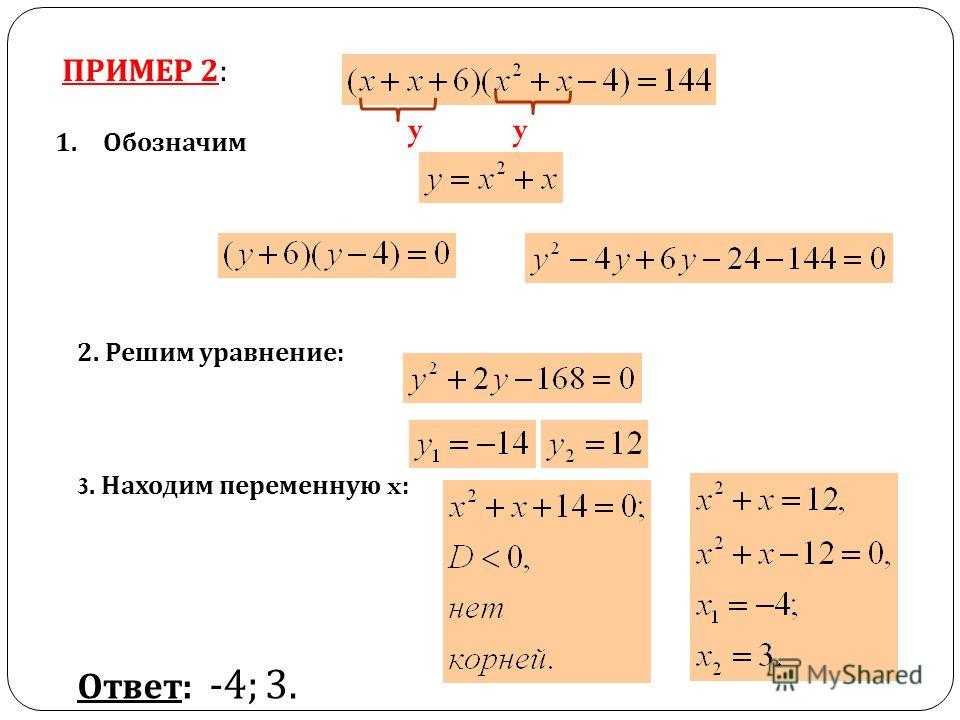 Биквадратные уравнения
Биквадратные уравнения
Уравнения вида ах 4 + bх 2 + c = 0, где а ≠ 0 , называются биквадратными уравнениями с одной переменной.
Для решения биквадратного уравнения нужно сделать подстановку х 2 = t, найти корни t 1 и t 2 квадратного уравнения аt 2 + bt + c = 0 и решить уравнения х 2 = t 1 и х 2 = t 2 . Они имеют решения лишь в случае, когда t 1,2 ≥ 0.
Пример 1.
Решить уравнение х 4 + 5х 2 – 36 = 0.
Решение.
Подстановка: х 2 = t.
t 2 + 5t – 36 = 0. По т. Виета t 1 = -9 и t 2 = 4.
х 2 = -9 или х 2 = 4.
Ответ: В первом уравнении корней нет, из второго: х = ±2.
Пример 2.
Решить уравнение (2х – 1) 4 – 25(2х – 1) 2 + 144 = 0.
Решение.
Подстановка: (2х – 1) 2 = t.
t 2 – 25t + 144 = 0. По т. Виета t 1 = 9 и t 2 = 16.
(2х – 1) 2 = 9 или (2х – 1) 2 = 16.
2х – 1 = ±3 или 2х – 1 = ±4.
Из первого уравнения два корня: х = 2 и х = -1, из второго тоже: х = 2,5 и х = -1,5.
Ответ: -1,5; -1; 2; 2,5.
Таким образом, процесс решения любых уравнений состоит в последовательной замене данного уравнения другим, равносильным ему и более простым уравнением.
Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Всем еще со школы известно такое понятие, как уравнения. Уравнение — это равенство, содержащее одну или несколько переменных. Зная то, что одна из частей данного равенства равна другой, можно вычленять отдельные части уравнения, перенося те или иные его составляющие за знак равенства по четко оговоренным правилам. Можно упростить уравнение до необходимого логического завершения в виде х=n, где n — это любое число.
С начальной школы все дети проходят курс изучения различной сложности. Позже в программе появляются более сложные линейные уравнения — квадратные, затем идут кубические уравнения. Каждый последующий вид уравнений имеет новые методики решения, становится труднее в изучении и повторении.
Каждый последующий вид уравнений имеет новые методики решения, становится труднее в изучении и повторении.
Однако после этого возникает вопрос о решении такого вида уравнений, как биквадратные уравнения. Данный вид, несмотря на кажущуюся сложность, решается достаточно просто: главное — уметь привести такие уравнения в должный вид. Их решение изучается за один-два урока вместе с практическими заданиями, если у учащихся имеются базовые знания о решении квадратных уравнений.
Что необходимо знать человеку, столкнувшемуся с этим типом уравнений? Для начала то, что они включают в себя только четные степени переменной «икс»: четвертая и, соответственно, вторая. Чтобы биквадратное уравнение было решаемо, необходимо привести его к виду Как это сделать? Достаточно просто! Нужно всего лишь заменить «икс» в квадрате на «игрек». Тогда устрашающий для многих школьников «икс» в четвертой степени превратится в «игрек» в квадрате, а уравнение примет вид обычного квадратного.
Далее оно решается как обычное квадратное уравнение: раскладывается на множители, после чего находится значение таинственного «игрека». Чтобы решить биквадратное уравнение до конца, нужно найти из числа «игрек» — это и будет искомая величина «икс», после нахождения значений которого можно будет поздравить себя с успешным завершением расчетов.
Чтобы решить биквадратное уравнение до конца, нужно найти из числа «игрек» — это и будет искомая величина «икс», после нахождения значений которого можно будет поздравить себя с успешным завершением расчетов.
Что же следует помнить, решая уравнения данного вида? Первое и самое главное: игрек не может быть отрицательным числом! Само условие, что игрек — это квадрат числа икс, исключает подобный вариант решения. Поэтому если при первичном решении биквадратного уравнения одно из значений «игрек» получается у вас положительным, а второе — отрицательным, необходимо взять только его положительный вариант, иначе биквадратное уравнение будет решено неверно. Лучше сразу ввести правило, что переменная «игрек» больше либо равна нулю.
Второй немаловажный нюанс: число «икс», являясь квадратным корнем числа «игрек», может быть как положительным, так и отрицательным. Допустим, если «игрек» равен четырем, то биквадратное уравнение будет иметь два решения: два и минус два. Это происходит по той причине, что отрицательное число, возведенное в четную степень, равно числу того же модуля, но отличного знака, возведенному в ту же степень. Поэтому всегда стоит помнить об этом немаловажном моменте, иначе можно попросту потерять один или несколько ответов уравнения. Лучше всего сразу писать, что «икс» равен плюс-минус квадратному корню от «игрек».
Поэтому всегда стоит помнить об этом немаловажном моменте, иначе можно попросту потерять один или несколько ответов уравнения. Лучше всего сразу писать, что «икс» равен плюс-минус квадратному корню от «игрек».
В общем и целом, решение биквадратных уравнений — это достаточно просто и не требует больших временных затрат. На изучение этой темы в школьной программе хватает двух академических часов — не считая, конечно, повторений и контрольных работ. Биквадратные уравнения стандартного вида решаются очень легко, если соблюдать перечисленные выше правила. Их решение не составит для вас никакого труда, потому что оно подробно расписано в учебниках математики. Удачной вам учебы и успехов в решении любых, не только математических, задач!
Перед тем, как решать биквадратные уравнения, необходимо разобраться, что собой являет данное выражение. Итак, это уравнение четвертой степени, которое можно записать в таком виде: «(ах 4) + (bx 2) + с = 0 ». Его общий вид можно записать в виде «ах ». Чтобы решить уравнение подобного рода, необходимо применить метод под названием «подстановка неизвестных». Согласно ему, выражение «х 2 » необходимо заменить другой переменной. После такой подстановки получается простое квадратное уравнение, решение которого в дальнейшем не составляет особого труда.
Чтобы решить уравнение подобного рода, необходимо применить метод под названием «подстановка неизвестных». Согласно ему, выражение «х 2 » необходимо заменить другой переменной. После такой подстановки получается простое квадратное уравнение, решение которого в дальнейшем не составляет особого труда.
Необходимо:
— чистый лист бумаги;
— пишущая ручка;
— элементарные математические навыки.
Инструкция:
- Итак, необходимо изначально записать выражение на листке бумаги. Первый этап его решения состоит в простой процедуре замены выражения «х 2 » на простую переменную (например «к »). После того, как Вы это сделали, у Вас должно получиться новое уравнение: «(ак 2) – (bк) + с = 0 ».
- Далее, чтобы правильно решить биквадратное уравнение, нужно вначале найти корни для «(ак 2 ) – (bк) + с = 0 », которое у Вас получилось после замены. Чтобы это сделать, необходимо будет посчитать значение дискриминанта по известной формуле: «D = (b 2 ) − 4*ас ».
 При этом все эти переменные (а , b и с ) являются коэффициентами вышеприведенного уравнения.
При этом все эти переменные (а , b и с ) являются коэффициентами вышеприведенного уравнения. - В ходе расчета дискриминанта мы можем узнать, имеет ли решение наше биквадратное уравнение, ведь если в итоге данное значение получится со знаком минус, то оно просто-напросто может не иметь решения в дальнейшем. В случае же если дискриминант будет равняться нулю, тогда у нас будет одно единственное решение, определенное такой формулой: «к = — (b / 2 * а) ». Ну и в случае, если наш дискриминант окажется больше нуля, тогда у нас получится два решения. Для нахождения двух решений необходимо будет взять квадратный корень от «D » (то есть с дискриминанта). Полученное значение нужно будет записать в виде переменной «QD ».
- Следующий шаг – непосредственное решение квадратного уравнения , которое у Вас получилось. Для этого Вам необходимо будет подставить в формулу уже известные значения. Для одного из решений: «к1 = (-b + QD) / 2 * а », а для другого: «к2 = (-b — QD) / 2 * а ».
 {2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]
{2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]Мы получили снова четыре корня:
Вот так решаются все биквадратные уравнения. Конечно, это не самый быстрый способ, зато он самый надежный. Попробуйте самостоятельно прорешать такие же примеры, как и в этом видео. В ответе значения иксов нужно записывать через точку с запятой — вот так, как я записывал. На этом урок закончен. Удачи!
Инструкция
Способ подстановкиВыразите одну переменную и подставте ее в другое уравнение. Выражать можно любую переменную по вашему усмотрению. Например, выразите «у из второго уравнения:
х-у=2 => у=х-2Затем подставьте все в первое уравнение:
2х+(х-2)=10Перенесите все без «х в правую часть и подсчитайте:
2х+х=10+2
3х=12 Далее, чтобы «х, разделите обе части уравнения на 3:
х=4.Итак, вы нашли «х. Найдите «у. Для этого подставьте «х в то уравнение, из которого вы выразили «у:
у=х-2=4-2=2
у=2.
Сделайте проверку. Для этого подставьте получившиеся значения в уравнения:
2*4+2=10
4-2=2
Неизвестные найдены верно!Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.
Так как в «у со знаком «+ , а во втором «- , то вы можете выполнить операцию сложения, т.е. левую часть складываем с левой, а правую с правой:
2х+у+(х-у)=10+2Преобразуйте:
2х+у+х-у=10+2
3х=12
х=4Подставьте «х в любое уравнение и найдите «у:
2*4+у=10
8+у=10
у=10-8
у=2По 1-ому способу можете , что найдены верно.Если нет четко выраженных переменных, то необходимо немного преобразовать уравнения.
В первом уравнении имеем «2х, а во втором просто «х. Для того, чтобы при сложении или «х сократился, второе уравнение умножьте на 2:
х-у=2
2х-2у=4Затем вычтите из первого уравнения второе:
2х+у-(2х-2у)=10-4Заметим, если перед скобкой стоит минус, то после раскрытия поменяйте на противоположные:
2х+у-2х+2у=6
3у=6
у=2«х найдите, выразив из любого уравнения, т. е.
е.
х=4Видео по теме
Уравнение , в общем виде записанное ах+bу+с=0, называется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит бесконечное множество решений, поэтому в задачах оно всегда чем-либо дополняется – еще одним уравнением или ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя переменными следует разными способами.
Вам понадобится
- — линейное уравнение с двумя переменными;
- — второе уравнение или дополнительные условия.
Инструкция
Если дана система из двух линейных уравнений, решайте ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными поменьше и выразите одну из переменных, например, х. Затем подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные – в правую.
 Найдите у и подставьте в любое из первоначальных уравнений, найдите х.
Найдите у и подставьте в любое из первоначальных уравнений, найдите х.Решить систему из двух уравнений можно и другим способом. Умножьте одно из уравнений на число, чтобы коэффициент перед одной из переменных, например, перед х, был одинаков в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть аналогично и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте найденное значение у в любое из первоначальных равенств. Найдите х.
Третий способ решения системы двух линейных уравнений – графический. Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.

Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.
Источники:
- как решить уравнение с одной переменной
Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.
Вам понадобится
- — система из трех уравнений с тремя неизвестными.
Инструкция
Если два из трех системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными .
 Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.
Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.Некоторые системы уравнений можно вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из на или переменную так, чтобы сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.
Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В).
 Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.
Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.Найдите матрицу А в степени (-1) предварительно отыскав , обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.
Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.
Источники:
- решений уравнений с тремя неизвестными
Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше.
 Решать системы можно несколькими методами.
Решать системы можно несколькими методами.Инструкция
Самый распространенный метод решения системы уравнений — это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.
Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.
Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.
В первом выражении все члены 2, можно вынести 2 за скобку распределительному свойству умножения:2*(2х-у-3)=0. Теперь обе части выражения можно сократить на это число, а затем выразить у, так как коэффициент по модулю при нем равен единице:-у=3-2х или у=2х-3.
Так же, как и в первом случае, подставляем данное выражение во второе уравнение и получаем:3х+2*(2х-3)-8=0;3х+4х-6-8=0;7х-14=0;7х=14;х=2.
 2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.
2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений . Если решение было одно, то будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.
Видео по теме
Одним из классических способов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований переводится в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.
Инструкция
Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z — после Y и так далее. В правой части каждого уравнения неизвестных быть не должно.
 2=6\)
2=6\)
Главное, что надо запомнить про дробно-рациональные уравнения – в них надо писать ОДЗ. И после нахождения корней – обязательно проверять их на допустимость. Иначе могут появиться посторонние корни, и все решение будет считаться неверным.
Алгоритм решения дробно-рационального уравнения:
-
Выпишите и «решите» ОДЗ.
-
Найдите общий знаменатель дробей.
-
Умножьте каждый член уравнения на общий знаменатель и сократите полученные дроби. Знаменатели при этом пропадут.
-
Запишите уравнение, не раскрывая скобок.
-
Раскройте скобки и приведите подобные слагаемые.
-
Решите полученное уравнение.
-
Проверьте найденные корни с ОДЗ.
 2+9x-5=0\)
2+9x-5=0\)Находим корни уравнения
\(x_1=-5;\) \(x_2=\frac{1}{2}.\)
Один из корней не подходи под ОДЗ, поэтому в ответ записываем только второй корень.
Ответ: \(\frac{1}{2}\).
Смотрите также:
Дробно-рациональные неравенстваУравнения, приводящие к квадратным или биквадратные уравнения
Тема урока: Уравнения, приводящие к квадратным уравнениям.
Школа-гимназия имени Ш.Қалдаякова
Класс: 8
ФИО учителя: Тәшімбет Зияш Мамырқызы
Цель обучения
Изучив данную тему, учащиеся ознакомятся с понятием биквадратные уравнения, с некоторыми другими уравнениями, приводящимися к решению квадратных уравнений.

Все учащиеся смогут:
Большинство учащихся смогут:
Некоторые учащиеся смогут:
Цель учителя:
Проводить сравнительный анализ, делать выводы.
Предыдущее обучение:
Обобщение знаний, полученные по теме «Квадратные уравнения»,
Учащиеся могут:
Применять термины, связанные с биквадратными уравнениями,
Ключевые слова:
Дискриминант, корни уравнения, биквадратные уравнения,
Ход урока
Планируемые действия учителя
Планируемые действия учащихся
Ресурсы
І.
 Актуализация знаний
Актуализация знанийВопросы для обсуждения:
Какой общий вид имеет квадратное уравнение ?
Назовите формулу Дискриминанта?
Когда уравнение имеет один корень, два корня, не имеет корней?
Квадратным уравнением называется уравнение вида
,где
x — переменная,
a,b,c — постоянные (числовые) коэффициенты.
В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
Формула дискриминанта:
.
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
D0 — уравнение имеет 2 различных вещественных корня
D=0 — уравнение имеет 2 совпадающих вещественных корня
D — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет)
В общем случае корни уравнения равны:
.

Очевидно, в случае с нулевым дискриминантом, оба корня равны
.
Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:
В таком случае корни уравнения вычисляются по формуле:
Мячик
Метод «снежный ком»
Самостоятельная работа
Раздает карточки каждой группе, приложение №1
Учитель открывает ответы уравнений
— Чем они отличаются?
— Вы уже знаете способы решения квадратных уравнений различных видов. Теперь переходим к рассмотрению уравнений, приводящихся к решению квадратных уравнений.
— Составьте алгоритм решения биквадратного уравнения.
Показывает ролик
АЛГОРИТМА решения уравнения на сайте BILIM land
— Как бы вы назвали эти уравнения?
-Вот перед вами примеры. Научимся находить корни биквадратные уравнения.
Скажите, что нового мы сегодня узнаем?
— От чего зависит количество корней квадратного уравнения?
-Всё это вы будете узнавать вместе самостоятельно, в задании №2 Упражнение №2
-Сейчас мы проведём исследование: сколько корней имеет биквадратное уравнение? Задание №4. Проверь себя! Упражнение
— Сколько корней имеет биквадратное уравнение
Работа на доске
Работа с книгой
Домашнее задание №190/1-3/, 191 /1-2/
Задание №1.
Укажите виды уравнений:
а) х2+9х-20=0; в) х2 —8х=0;
б) 2х2-7х-30=0; г) 35х2+150=0;Ответы записывают в тетрадь.
1 группа х2+4х-5=0; х2-х-72=0; х2+3х-28=0; х4-13х2+36=0;
2 группа х2-10х+16=0;х2-10х+21=0;х2-6х+8=0;х4-34х2+225=0;
3 группа х2-7х+12=0; х2-9х+18=0; х2-4х-5=0; х4— 20х2+64=0;
4 группа х2+5х-6=0; х2-7х-18=0; х2-9х+14=0; х4— 4х2+45=0;
5 группа х2-8х+15=0; х2-6х+8=0; х2-7х-18=0; х4— 20х2+100=0;
Ребята сверяются, выясняют , что есть в задании такие уравнения, которые они не смогли решить.
 Представители групп записывают свои биквадратные уравнения на доске.:
Представители групп записывают свои биквадратные уравнения на доске.:х2-7х-18=0; х4— 20х2+100=0.
— 1 слагаемое в 2 раза меньше
Каждая группа получает карточку с 1 биквадратным уравнением, с его решением по алгоритму . Приложение № 2
Объясняют решение уравнения
На плакате каждая группа расписывает алгоритм решения биквадратного уравнения.Алгоритм решения биквадратного уравнения.
Ввести замену переменной: пусть у2=х
Составить квадратное уравнение с новой переменной: aх2+bx+c=0
Решить новое квадратное уравнение.
Вернуться к замене переменной.
Решить получившиеся квадратные уравнения
Сделать вывод о числе решений биквадратного уравнения.
Записать ответ.
Биквадратными — так как «би» означает «два»
Задание №3 Приложение №4
Упражнение №1 завершить условия относительно х и tОт дискриминанта.

Каждая группа решает пример в ноутбуке, После выполнения задания учащиеся производят самопроверку по результатам.
Выполняют задание №№
1 карточка: х4-10х2+9=0, /4 корня /
2 карточка: х4-13х+36=0 , /4корня/
3 карточка: х4+5х2+4=0, /корни отрицательное, биквадратное уравнение не имеет корней/
4 карточка: х4-8х2 +16 /биквадратное уравнение имеет 2 корня/
5 карточка: х4+8х2+16=0 /не имеет корней. /Каждая группа меняется карточками и проверяют ответы выполненных работ с ключами ответов на слайде.
Упражнение 5
Каждая группа выполняет по одному примеру из задачи №189. После выполненных работ сверяют с ключами ответов на слайде.
Карточки
Карточки
Слайд
В сайте BILIM land, в разделе Курсы→Математика→Алгебра→Уравнения и неравенства→Биквадратные уравнения→содержание урока →Биквадратные уравнения /просмотреть видео «Решение биквадратного уравнения»/
Биквадратные уравнения→содержание урока →Биквадратные уравнения→ Упражнение №1
Прежде чем приступить к работе в разделе Биквадратные уравнения → нахождение биквадратных уравнений→ Важно!
Карточки
Слайд из презентации
Биквадратные уравнения→содержание урока →Биквадратные уравнения→ Упражнение 5
Доска
Алгебра 8 класс, стр 78
Слайд
Дополнительная информация
Дифференциация.
 Поощряется каждый правильный ответ, неуверенно ответившему задается направляющие вопросы.
Поощряется каждый правильный ответ, неуверенно ответившему задается направляющие вопросы.Оценивание. Критериальное оценивание каждого задания в ходе приобретения знаний учащихся позволяет реально оценивать каждого ученика.
Межпредметные связи: руский язык, информатика.
ИКТ компетентность: ученики умеют пользоваться компьютером, исспользовать интернет ресурсы.
Связи с ценностями: в группе слушаются доводы каждого.
Итоги урока, ответы на самые актуальные вопросы из блока слева.
Рефлексия
Цели обучения были реалистичными.
Сегодняшний урок был направлен на изучение уравнений, приводящим к квадратным уравнениям. В процессе обучения учащиеся ознакомились с биквадратными уравнениями и нахождением его корней.

Обучение было направлено на развитие критического мышления при работе в групах..Расширение кругозора учащихся, развитие интереса к предмету, развитие личностных качеств учащихся их коммуникативных характеристик, развитие умения самостоятельно приобретать новые знания.
Дифференциация хорошо соблюдалась. Время обучения выдерживалось.Итоговая оценка
Какие два аспекта в обучении прошло очень хорошо (с учетом преподавания и учения)? Аспекты с применением сайта BILIM land в ресурсах Курсы, раздел Математика, а также эффективное применение ИКТ.
Какие два обстоятельства могли бы улучшить урок (с учетом преподавания и учения)?
Увеличить количество заданий в паре.
Предварительное задание для знакомства задания на сайте
Как решать неполные квадратные уравнения? Примеры и Формулы
Основные понятия
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин.
 Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
- если D < 0, корней нет;
- если D = 0, есть один корень;
- если D > 0, есть два различных корня.
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
Неполные квадратные уравнения бывают трех видов: - Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.

- Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax² + c = 0, при b = 0;
- ax² + bx = 0, при c = 0.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как решить уравнение ax² = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.
Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.
Пример 1. Решить −5x² = 0.
Как решаем:
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
−5x² = 0
x² = 0
x = √0
x = 0
Ответ: 0.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Как решить уравнение ax² + с = 0
Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
- перенесем c в правую часть: ax² = — c,
- разделим обе части на a: x² = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р² = — c/а не является верным.
Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.
В двух словах квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
- не имеет корней при — c/а < 0;
- имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.
Пример 1. Найти решение уравнения 9x² + 4 = 0.
Как решать:
- Перенесем свободный член в правую часть:
9x² = — 4
- Разделим обе части на 9:
x² = — 4/9
- В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.
Пример 2. Решить -x² + 9 = 0.
Как решаем:
- Перенесем свободный член в правую часть:
-x² = -9
- Разделим обе части на -1:
x² = 9
- Найти корни:
x = √9
x = -3, 3
Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.
Как решить уравнение ax² + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.
Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0.
 А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:
- x = 0;
- x = −b/a.
Пример 1. Решить уравнение 2x² — 32x = 0
Как решать:
- Вынести х за скобки
х(2x — 32) = 0
- Это уравнение равносильно х = 0 и 2x — 32 = 0.
- Решить линейное уравнение:
2x = 32,
х = 32/2
- Разделить:
х = 16
- Значит корни исходного уравнения — 0 и 16.
Ответ: х = 0 и х = 16.
Пример 2. Решить уравнение 3x² — 12x = 0
Как решать:
Разложить левую часть уравнения на множители и найти корни:
Ответ: х = 0 и х = 4.
Для удобства мы собрали все виды неполных квадратных уравнений и способы их решения на одной картинке-шпаргалке.

Предварительное исчисление алгебры — Существует ли общая формула для решения уравнений четвертой степени (степень $4$)?
Наверняка есть, но он уродливый, сложный и не стоит запоминать. Люди знают об этом и цитировали или цитировали это для вас, но на самом деле они никогда не использовали бы это. Если вам нужно что-то действительно полезное для бумажных решений, вы можете понять реальную теорию, лежащую в основе решения. Я предоставлю один метод ниже.
Формула четвертой степени — это всего лишь конечный результат этой методологии, записанный в терминах исходных коэффициентов. Из-за этого метод гораздо легче запомнить, чем формулу, поэтому меня раздражает, когда люди приводят только формулу и говорят вам: «Не беспокойтесь, используйте вместо этого компьютер». Решение с ручкой и бумагой не сложное, оно просто требует времени.
Понимание того, как это делается, даже если вы никогда этим не пользуетесь, расширяет ваш мозг и ваше понимание, позволяет реализовать это в программировании и позволяет вам воссоздавать его, когда вам это может понадобиться, вместо чрезмерной зависимости от компьютеров, которые всегда будут рядом.
 для вас, что, на мой взгляд, делает его плохим математиком.
для вас, что, на мой взгляд, делает его плохим математиком.Есть три метода решения квартик, которые я знаю и знаю:
- Квадратичная факторизация Декарта
- Метод Эйлера
- Метод Феррари
Если кто-то знает больше, пожалуйста, дайте мне знать.
Метод Феррари исторически является первым открытым методом. Метод Эйлера очень похож на метод Кардано для куба и, вероятно, был смоделирован на основе того же подхода. Но я неравнодушен к технике квадратичной факторизации Декарта. Это относительно простой процесс, который я буду использовать ниже. Если вы хотите посмотреть, как работают другие, дайте мне знать.
Все вышеперечисленные методы начинаются одинаково: депрессия (удаление члена степени $n-1$, в данном случае кубического члена) и нормализация (приведение опережающего коэффициента к 1, т. е. преобразование многочлена в монический). 92 + qz + r = 0\;\;\;\;\;\;\;\;\;\;\;\;(1)$$
Для некоторых $p,q,r\in\mathbb {Р} $.
 Это не влияет на корневые позиции; все, что делал опережающий коэффициент, — это увеличивал ненулевые значения. Относительно нулей нет абсолютно никакой потери общности. Все эти константы $p,q,r$ можно вычислить из исходных коэффициентов $a,b,c,d,e$. Кубического члена по-прежнему нет, а опережающего коэффициента теперь тоже нет.
Это не влияет на корневые позиции; все, что делал опережающий коэффициент, — это увеличивал ненулевые значения. Относительно нулей нет абсолютно никакой потери общности. Все эти константы $p,q,r$ можно вычислить из исходных коэффициентов $a,b,c,d,e$. Кубического члена по-прежнему нет, а опережающего коэффициента теперь тоже нет.Было бы интересно отметить, что произошло с многочленом. Мы начали с 5 произвольных констант и сократили их до 3, нормализовав шаг и удалив кубический член. Первоначально у нас были произвольные значения $a,b,c,d,e\in\mathbb{R}$, а теперь у нас есть произвольные значения $p,q,r\in\mathbb{R}$. Хотя последние три вычисляются из первоначальных пяти, они имеют произвольные значения, и нет потери общности. Это существенное упрощение задачи. Несуществование кубического члена окажется жизненно важным.
До сих пор все было просто установкой: запись полинома в сокращенной монической форме. Напомним, что все методы четвертой степени достигают по крайней мере этого.
 Затем мы реализуем метод факторизации Декарта.
Затем мы реализуем метод факторизации Декарта.Метод факторизации Декарта
Мы должны предположить, что все коэффициенты действительны, $p,q,r\in\mathbb{R}$. Это необходимое условие для того, чтобы методология работала. Причина в том, что теперь все решения с ненулевыми мнимыми компонентами входят в комплексно-сопряженные пары. Большое дело? Это позволяет нам сгруппировать два решения вместе, даже если они чисто действительные, в квадратичные множители с действительными коэффициентами. Мы знаем, что 92 -\frac{q}{m}$$ Обратите внимание на то, что в левой части оба этих уравнения могут быть легко решены для $n$ и $\frac{r}{n}$ в терминах $m$, оба из которых входят в квадратичные множители (3). Их можно использовать позже, когда мы узнаем $m$ для завершения квадратичного множителя.
Мы можем найти $m$, взяв последние два уравнения и перемножив их, тем самым исключив неизвестное $n$. Обратите внимание, что $n$ в числителе одного и в знаменателе другого.
 2 }$$ 92 =0$$
2 }$$ 92 =0$$На этом мы по существу закончили. У нас остался кубический полином от $w$, который разрешим собственными методами. Методы, о которых я только предполагаю, что вы уже знаете, если пытаетесь решить квартики. Как и в случае с квартиками, как вы уже знаете, существуют кубические формулы, но я рекомендую изучить методы, лежащие в их основе.
Если вам нужна помощь с кубиками, я рекомендую метод Кардано (оригинальное решение) или тригонометрическое решение Виета (мой любимый). Есть еще Completing the Cube, хорошее доказательство концепции, но я никогда не буду его использовать. Не стесняйтесь задавать отдельный вопрос для кубика, и я буду рад ответить. 92 — mz + \frac{r}{n})=0$.
Еще не сделано. Каждый из этих квадратичных множителей теперь должен быть решен с помощью квадратичной формулы, и у вас есть решения в $z$. Это решает депрессивную моническую квартику, с которой мы начали метод квадратичной факторизации Декарта.
Наконец
Не забывайте об исходной квартике, которая была у нас в самом начале, до депрессии и нормализации.
 Мы ввели горизонтальный сдвиг $x = z-\frac{b}{4a}$. Выполнение этого последнего шага решит исходную квартику в терминах $ x $, что является решением, которое вам нужно.
Мы ввели горизонтальный сдвиг $x = z-\frac{b}{4a}$. Выполнение этого последнего шага решит исходную квартику в терминах $ x $, что является решением, которое вам нужно.Когда закончишь, ты придешь к набору решений. Обязательно проверьте свои ответы. У вас могут быть избыточные или лишние решения. Некоторые избыточные решения могут быть записаны очень разными алгебраическими способами, но будут представлять одно и то же числовое значение.
Если вы выразите окончательный ответ $x$ через исходные $a,b,c,d,e$, вы получите те же самые «формулы четвертой степени», которые вам приводят другие люди. Выражение, конечно, будет немного отличаться в зависимости от того, какой из методов четвертой степени вы используете.
Опасения
Если вас беспокоит предположение о том, что коэффициенты $p,q,r$ реальны, не беспокойтесь. Все это означает, что $a,b,c,d,e$ реальны, что обычно является хорошим предположением. На самом деле, мы можем обобщить. Значения $p,q,r$ можно сделать комплексными, подразумевая только, что исходная квартика имеет комплексные $a,b,c,d,e$.
 Это также означает, что вам придется решать кубик с комплексными коэффициентами. Это выполнимо, и математика все еще работает нормально.
Это также означает, что вам придется решать кубик с комплексными коэффициентами. Это выполнимо, и математика все еще работает нормально.Решение уравнений четвертой степени
3X 4 + 6X 3 — 123X 2 — 126X + 1,080 = 0 Уравнения четвертой степени решаются в несколько шагов. Сначала упростим уравнение, разделив все члены обозначаются буквой «а», поэтому уравнение становится таким:
x 4 & NBSP + & NBSP 2x 3 & NBSP — & NBSP 41x 2 & NBSP — & NBSP 42x & NBSP AMPSP 360 & NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP.   d   =   -42   и   e   =   360 Далее мы определяем переменную ‘f’:
f = с — (3b 2 /8) «Подставив» числа из приведенного выше уравнения, мы получим:
ф = -41 — (3*2*2/8) f = -42,5 Далее мы определяем «г»:
г = d + (b 3 / 8) — (b*c/2) «Вставляем» цифры:г = -42 + (8/8) — (2 * -41/2) г = 0 Далее мы определяем «h»:
ч = е — (3*б 4 /256) + (б 2 * с/16) — ( б*д/4) Подстановка цифр:
ч = 370,5625 Затем мы «подставляем» числа «f», «g» и «h» в следующее кубическое уравнение:
Y 3 + (f/2)*Y 2 + ((f 2 -4*h)/16)*Y -g 2 /64 = 0 Y 3 -21,25*Y 2 + (1806,25 -4 * 370,5625 )/16*Y -0 2 /64 = 0 Д 3 -21,25*Д 2 + (1 806,25 -1 482,25)/16*Д -0 2 /64 = 0 Д 3 -21,25*Д 2 + 20,25*Д -0 = 0 Далее, мы решаем это кубическое уравнение, используя метод, расположенный в решение кубических уравнений   ИЛИ (гораздо проще) с помощью КАЛЬКУЛЯТОРА КУБИЧЕСКИХ УРАВНЕНИЙ
. 
И 3 корня уравнения:
Y 1 =  20,25     Y 2 =  0     Y 3 =  1 Пусть «p» и «q» будут квадратными корнями из ЛЮБОГО 2 ненулевые корня (Y 1 Y 2 или Y 3 ).
p=SqRoot(20,25) = 4,5 q=SqRoot(1) = 1 r= -g/(8*pq) = 0 s= b/(4*a) = 6/(4* 3) = 0,5 Тогда четыре корня уравнения четвертой степени равны:
X 1 = p + q + r -s = 4,5 + 1 + 0 — 0,5 = 5
X 2 = p — q — r -s = 4,5 — 1 — 0 — 0,5 = 3
X 3 = -p + q — r -s = -4,5 + 1 — 0 — ,5 = -4
X 4 = -p — q + r -s = -4,5 — 1 + 0 — ,5 = — 6Пример № 2 Уравнение четвертой степени с 2 действительными и 2 комплексными корнями -20X 4 + 5X 3 + 17X 2 — 29X + 87 = 0 Упростите уравнение, разделив все члены на «а», чтобы уравнение тогда становится:
X 4   —   .  25X 3   —   .85X 2   +   1,45X   —   4,35   =   0
25X 3   —   .85X 2   +   1,45X   —   4,35   =   0Где   a  =  1   b  =  -.25   c  =  -.85   d   =   +1,45   и   e   =   -4,35 f = с — (3b 2 /8) f = -0,8734375 г = d + (b 3 / 8) — (b*c/2) г = 1,341796875 h = e — (3*b 4 /256) + (b 2 * c/16) — (b*d/4) ч = -4,262741088867187 Затем мы «подставляем» числа «f», «g» и «h» в следующее кубическое уравнение:
Y 3 + (f/2)*Y 2 + ((f 2 -4*h)/16)*Y -g 2 /64 = 0 Y 3 -0,436718750000*Y 2 + 1,113366088867*Y -0,028131544590 = 0 Затем мы получаем 3 корня этого кубического уравнения, перейдя к:
КУБИЧЕСКОЕ УРАВНЕНИЕ   КАЛЬКУЛЯТОР. 
а корни такие:
Д 1 = 0,0255074144632 Y 2 =  0,2056056677683 + i* 1,029856038619 Y 3 =  0,2056056677683 — i* 1,029856038619 Пусть «p» и «q» будут квадратными корнями из ЛЮБЫХ 2 ненулевых корней (Y 1 Y 2 или Y 3 ).
Всякий раз, когда у нас есть 1 действительный корень и 2 сложных корня, мы ВСЕГДА выбираем 2 комплексных корня.
Найдите квадратные корни, перейдя к: Калькулятор комплексных чисел.p=SqRoot(Y2) = 0.79239675 + i* 0.6498360995438
q=SqRoot(Y3) = 0.79239675 — i* 0.6498360995438
r= -g/(8*pq) = -1.341796875000/(8*1.0501795803089815) = -0,159710408124 с = b/(4*a) = 5/(4*-20) = -0,0625 Тогда четыре корня уравнения четвертой степени равны:
X 1 = p + q + r -s = + (0,79239675 + я * 0,6498360995438)
+ (0,79239675 — i* 0,6498360995438)
+ (-0,159710408124) — (-.  0625)
0625)Обратите внимание, что «мнимые» части p и q в сумме равны нулю, поэтому мы имеем: X 1 = 2*(.79239675 ) -0,1597109408124 -0,1597109408124 
X 1 = 1,5847935184606 -0,097210408124 х 1 = 1,48758311033 X 2 = р-к-р-с = + (0,79239675 + я * 0,6498360995438)
— (0,79239675 — я* 0,6498360995438)
— (-0,159710408124) — (-.0625) Здесь «действительные» части p и q в сумме равны нулю, и поэтому: X 2 = 2*(0,6498360995438*i) + 0,159710408124 + 0,0625 X 2 = 0,222210408124 + i*1,29967219908 X 3 = -p + q — r -s = — (0,79239675 + я* 0,6498360995438)
+ (0,79239675 — i* 0,6498360995438)
— (-0,159710408124) — (-.  0625)
0625)Опять же, «действительные» части p и q в сумме равны нулю, и поэтому: X 3 = -2*(0,6498360995438*i) + 0,159710408124 + 0,0625 X 3 = 0,222210408124 — i*1,29967219908 X 4 = -p — q + r -s = — (0,79239675 + я* 0,6498360995438)
— (0,79239675 — я * 0,6498360995438)
+ (-0,159710408124) — (-.0625) Здесь «мнимые» части p и q в сумме равны нулю, и поэтому: X 4 = -2*(.79239675 )   -0,159710408124 +.0625
X 4 = -1,5847935184606   -0,097210408124 х 4 = -1,68200392658 Пример № 3 Уравнение четвертой степени без действительного и с 4 комплексными корнями 2X 4 + 4X 3 + 6X 2 + 8X + 10 = 0 Упростите уравнение, разделив все члены на «а», чтобы уравнение тогда становится:
x 4 & NBSP + & NBSP 2x 3 & NBSP + & NBSP 3X 2 & NBSP + & NBSP 4x & NBSP + NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBSP = NBS.  д   =   4   и   e   =   5
д   =   4   и   e   =   5f = c — (3b 2 /8) = 3 — (3*2 2 /8) ф = 1,5 г = d + (b 3 / 8) — (b*c/2) = 4 + (2 3 / 8) — ((2 * 3) / 2) = г = 2 h = e — (3*b 4 /256) + (b 2 * c/16) — ( b*d/4) = 5 — (3*2 4 /256) + (2 2 * 3/16) — (2*4/4) ч = 3,5625 Затем мы «подставляем» числа «f», «g» и «h» в следующее кубическое уравнение:
Д 3 + (f/2)*Д 2 + ((f 2 -4*h)/16)*Y -g 2 /64 = 0 Д 3 +,75*Д 2 -0,75*Д -0,0625 = 0 Затем мы получаем 3 корня этого кубического уравнения, перейдя к:
КУБИЧЕСКОЕ УРАВНЕНИЕ   КАЛЬКУЛЯТОР. а корни такие:
Д 1 = 0,62065322983065 Д 2 =  -1,29275744640077 Д 3 =  -0,07789578342988 Пусть «p» и «q» будут квадратными корнями из ЛЮБОГО 2 ненулевые корня (Y 1 Y 2 или Y 3 ).

В этом случае возьмем квадратные корни из двух отрицательных чисел.Чтобы найти квадратный корень из отрицательного числа:
• возьмите квадратный корень из абсолютного значения числа, затем
• умножьте его на «i».
Например, квадратный корень из -9 равен 3i.P = SQROOT (Y2) = 1,136994020 I Q = SQROOT (Y3) = 0,2760 9 I R = -G/(8*PQ) = -2 /.3 -3 -2/3 = 3-3.0940058) = 0,787815479557647 с = b/(4*a) = 2/(4*1) = 0,5 Тогда четыре корня уравнения четвертой степени равны:
X 1 = p + q + r -s = 1.136994 02 i + 0.27609 i + 0.787815479557647 -.5 = +1.41609308017191 i +0.28781547955765 X 1 = 0,28781547955765 + i*1,41609308017191 X 2 = р-к-р-с = 1,136994 02 I -0. 2760
27609 I -0,787815479557647 -5 0,857896758328492 I -1.1.1.27896758328492 I -1.1.1.27896758328492 I -1.1.1.27896758328492 I -1,2777758328492 I 02 I +0.2760.1778758328492 I .177896758328492 I .177896758328492 . X 2 = -1,287815479557650 + i*0,857896758328492 X 3 = -p + q — r -s = -1.136994 9 I -0,787815479557647 -5 -0,8578955834497 -0,8578975834497 -0,8578955734497 -0,8578955734497 -0,8578955734497 -0,85789557147 .х 3 = -1,28781547955765 — i*0,857896758328492 X 4 = -p — q + r -s = -1. 02 i -0.2760 136994
1369949 i +0.787815479557647 -.5 -1.41609308017191 i +0.287815479557647 X 4 = 0,287815479557647 — i*1,41609308017191 ВОЗВРАТ   В   QUARTIC УРАВНЕНИЕ   КАЛЬКУЛЯТОР
_____________________ Вернуться на главную страницу Авторское право © 1999 — 1728 программных систем
KryssTal : Introduction To Algebra
KryssTal : Введение в алгебру[Домашняя страница]
[Страница математики][Введение в числа]
[Введение в алгебру]
[Треугольник Паскаля]
[Тригонометрия]
[Рассмотрение логарифмов]
[Графики]
[Тригонометрические уравнения]
[Исчисление: дифференцирование]
[Сферическая тригонометрия1]
]
[Веселье с формулами][Отзывы читателей (математика)]
[Язык]
[Путешествия]
[Затмения]
[Лондон]
[Астрономия]
[Математика]
[Физика]
[Химия]
[Биология]
[Футбол]
[Телевидение]
[Другое] 903 Рекламная ссылка
Чтобы разместить здесь ссылку, свяжитесь с веб-мастером.
Слово, Алгебра — это арабское слово, означающее , объединяющее сломанные части . Этот полезный инструмент математики был изобретен арабским математиком 9-го века, Мохаммедом Ибн Мусой Аль-Хорезми (от европеизированного имени которого происходит слово, алгоритм ). Вот два примера задач, которые можно решить с помощью алгебры.Пример 1: Если к этому числу добавить шесть, получится девять. Какой номер?
Пример 2: Число умножается само на себя. Трижды вычитается одно и то же число. Наконец, добавляется два. Итого теперь ноль. Какой номер?
Пример 1 тривиален. Число должно быть три. Пример 2 гораздо труднее угадать. Я вернусь к этому позже.
В алгебре вместо неизвестных чисел используются буквы. Эти буквы затем манипулируют в соответствии с определенными правилами, пока не появится ответ. Обычная буква для неизвестного числа — 9.0028 х . Обычно используются маленькие x , но это слишком похоже на знак умножения ( × ), поэтому я буду использовать заглавные X . Два числа, сложенные вместе, показаны как:
Эти буквы затем манипулируют в соответствии с определенными правилами, пока не появится ответ. Обычная буква для неизвестного числа — 9.0028 х . Обычно используются маленькие x , но это слишком похоже на знак умножения ( × ), поэтому я буду использовать заглавные X . Два числа, сложенные вместе, показаны как:A + B Два вычитаемых числа показаны как:
A — B Два числа, умноженные вместе, показаны как:
A × B но чаще:
АВ Два разделенных числа показаны как:
A / B Число, умножающее сумму чисел, отображается как:
A(B + C) Это можно расширить, умножив все, что внутри скобок, на число снаружи:
AB + AC Число, делящее сумму чисел, отображается как:
(B + C) / A Это можно расширить, разделив все, что внутри скобок, на число снаружи:
Б/А + С/А Два положительных числа, умноженные вместе, дают положительное число:
A × A = B Два отрицательных числа, умноженные вместе, также дают положительное число:
-A × -A = B Отрицательное число, умноженное на положительное число, дает отрицательное число:
-A × A = -B
Возвращение к Пример 1 сверху, на алгебре это можно записать какX + 6 = 9 Это называется уравнением , потому что в нем есть знак равенства. Если мы хотим найти значение неизвестного числа X, мы должны получить X с одной стороны уравнения и числа с другой стороны.
Если мы хотим найти значение неизвестного числа X, мы должны получить X с одной стороны уравнения и числа с другой стороны.Мы можем делать что угодно с этим уравнением , если мы делаем то же самое с обеими частями уравнения .
Мы можем легко изолировать X, вычитая 6 с обеих сторон:
Х + 6 = 9 Х + 6 — 6 = 9 — 6 Х = 3 Таким образом, неизвестное число равно 3. Всегда полезно проверить ответ, подставив значение 3 обратно в исходное уравнение:
. Проверка путем замены X на 3 дает: 3 + 6 = 9 ….. верно.
Пример 2 выше будет рассмотрен позже. Пример 3: Решите уравнение X — 6 = 2,Опять же, мы должны изолировать X на одной стороне уравнения и числа на другой стороне. Это можно сделать, добавив 6 к обеим сторонам.
Х — 6 = 2 Х — 6 + 6 = 2 + 6 Х = 2 + 6 Х = 8 Проверка путем замены X на 8 дает: 8 — 6 = 2 . Теперь мы можем вычесть 3 с обеих сторон. …. верно. Пример 4: Решите уравнение 2X — 3 = -1
…. верно. Пример 4: Решите уравнение 2X — 3 = -1 Этот немного сложнее. X умножается на 2, а затем вычитается 3. Сначала мы должны разобраться с вычитанием 3. Мы можем сделать это, добавив 3 к обеим сторонам.
2X — 3 = -1 2X — 3 + 3 = -1 + 3 2X = 2 Следующий шаг — разделить обе части на 2.
2X = 2 2X / 2 = 2 / 2 X = 1 Проверка путем замены X на 1 дает: (2 × 1) — 3 = 2 — 3 = -1 ….. верно.
Пример 5: Решите уравнение 2(X + 3) = 4.В этом уравнении на 2 умножается все, что находится внутри скобки. С этим 2 нужно разобраться в первую очередь. Его можно удалить, разделив обе части на 2.
2 (x + 3) = 4 2 (x + 3) / 2 = 4/2 (x + 3) = 2 x + 3 = 2 
Х + 3 — 3 = 2 — 3 Х = -1 Проверка путем замены X на -1 дает: 2 × (-1 + 3) = 2 × 2 = 4 ….. верно.
Пример 6: Решите уравнение 4 / (X + 1) = 2.В этом уравнении часть, содержащая X, находится внизу. X + 1 в скобке — это все, что делит 4. Его нужно вывести наверх. Это делается путем умножения обеих сторон на (X + 1).
4 / (Х + 1) = 2 4 = 2(Х + 1) Следующий шаг — разделить обе части на 2.
4 / 2 = X + 1 2 = X + 1 Вычтите 1 с обеих сторон.
2 = Х + 1 2 — 1= Х + 1 — 1 1= Х или Х = 1 Проверка путем замены X на 1 дает: 4 / (1 + 1) = 4 / 2 = 2 .
Пример 7: Решите уравнение -X — 3 = -2. …. верно.
…. верно. Перед X стоит знак минус. Умножается на -1:
-1X — 3 = -2 Чтобы удалить -1, нам нужно умножить обе части на -1.
-1X — 3 = -2 -1 × (-1X — 3) = -2 × -1 X + 3 = 2 Умножение на -1 равносильно изменению всех знаков. Следующим шагом будет вычитание 3 с обеих сторон.
Х + 3 — 3 = 2 — 3 Х = -1 Проверка путем замены X на -1 дает: -(-1) — 3 = 1 — 3 = -2 ….. правильно.
Обратите внимание, что два минуса, умноженные вместе, дают плюс.
Пример 8: Решите следующее уравнение 2X — 5 = 4 — X.Применяются обычные правила: поместите X на одной стороне и цифры на другой стороне. Добавьте X с обеих сторон, чтобы удалить X с правой стороны.

2X — 5 = 4 — X 2X — 5 + X = 4 — X + X 2X + X — 5 = 4 Два X и один X могут быть добавлены, чтобы получить 3 X.
2Х + Х — 5= 4 3X — 5 = 4 Добавьте 5 к обеим сторонам.
3X — 5 = 4 3X — 5 + 5 = 4 + 5 3X = 9 Разделите обе части на 3.
3X = 9 3X / 3 = 9/3 X = 3 Проверка путем замены X (в 2X — 5) на 3 дает: (2 × 3) — 5 = 6 — 5 = 1
Проверка заменой X (в 4 — X) на 3 дает: 4 — 3 = 1 ….. согласны обе стороны.
До сих пор у нас были уравнения с одним неизвестным числом. Что делать, если у нас есть два неизвестных числа? Давайте посмотрим на уравнение X + Y = 3 . Это может быть удовлетворено:
Что делать, если у нас есть два неизвестных числа? Давайте посмотрим на уравнение X + Y = 3 . Это может быть удовлетворено:X = 1 и Y = 2 (потому что 1 + 2 = 3).
Но это не единственный ответ.
X = 0 и Y = 3 (потому что 0 + 3 = 3).
X = -1 и Y = 4 (потому что -1 + 4 = 3).
X = 4 и Y = -1 (потому что 4 + -1 = 4 — 1 = 3).
На самом деле уравнение с двумя неизвестными имеет бесконечное число пар ответов. Чтобы исправить одну пару чисел в качестве ответа, нам нужно еще одно уравнение . Пара уравнений, в каждом из которых есть два неизвестных числа, называется одновременных уравнений . Их можно решить вместе, чтобы получить значения неизвестных, которые удовлетворяют ОБЕИХ уравнений одновременно (отсюда и название). Пример 9: Решить одновременные уравнения: X + Y = 3 и X — Y = 7.
Сначала мы перечислим и пронумеруем два уравнения:
X + Y = 3 ….. (i) X — Y = 7 ….. (ii) Затем мы манипулируем двумя уравнениями, чтобы создать новое уравнение, которое исключает либо X, либо Y из одного из уравнений. В приведенном выше примере мы можем сделать это, добавив два уравнения (i) и (ii).
X + Y + (X — Y) = 3 + 7 ….. (i) + (ii) X + Y + X — Y = 10 X + X = 10 2Х = 10 Х = 5 Это дает нам значение для X. Заменив X в (i) на 5, мы можем получить значение для Y.
X + Y = 3 ….. (i) 5 + Y = 3 5 + Y — 5 = 3 — 5 Y = -2 Итак, у нас есть пара значений, X = 5 и Y = -2 .
 Их можно проверить, поместив их в (ii).
Их можно проверить, поместив их в (ii).Проверка значений X = 5, Y = -2 в (ii) дает: X — Y = 5 — (-2) = 5 + 2 = 7 ….. правильно.
Пример 10: Решить одновременные уравнения: 2X + 3Y = -4 и X — Y = 3.Перечислите и пронумеруйте два уравнения:
2X + 3Y = -4 ….. (i) Х-Y = 3 ….. (ii) Простого сложения или вычитания недостаточно, чтобы исключить ни X, ни Y. Нам нужно начать с удвоения (ii).
2X + 3Y = -4 ….. (i) 2X — 2Y = 6 ….. (ii) × 2 …. (iii) Теперь мы можем вычесть два уравнения.
2X + 3Y — (2X — 2Y) = -4 — 6 ….. (i) — (iii) 2X + 3Y — 2X + 2Y = -10 3Y + 2Y = -10 5Y = -10 Y = -2 Теперь у нас есть значение Y.
 Заменив Y в (i) на -2, мы можем получить значение X. 3 × -2) = -4
Заменив Y в (i) на -2, мы можем получить значение X. 3 × -2) = -4 2X — 6 = -4 2X = -4 + 6 2Х = 2 Х = 1 Опять же, у нас есть пара значений, X = 1 и Y = -2 . Их можно проверить, поместив их в (ii).
Проверка значений X = 1, Y = -2 в (ii) дает: X — Y = 1 — (-2) = 1 + 2 = 3 ….. правильно.
Теперь пришло время взглянуть на Пример 2 в верхней части этой страницы. Пример 2: Число умножается само на себя. Трижды вычитается одно и то же число. Наконец, добавляется два. Итого теперь ноль. Какой номер?Это можно записать в виде уравнения:
X 2 — 3X + 2 = 0 Уравнение, в котором X в квадрате встречается с X и числами, называется квадратным уравнением . Квадратные уравнения обычно имеют два ответа, а не один. Другими словами, есть два значения X, которые могут удовлетворять уравнению.
Квадратные уравнения обычно имеют два ответа, а не один. Другими словами, есть два значения X, которые могут удовлетворять уравнению.Существует два метода решения квадратных уравнений. Один называется факторизацией . Уравнение вида
АХ 2 + ВХ + С = 0 (где А, В и С — числа и называются коэффициентами ). можно представить в виде
(X + D) (X + E) = 0 (где D и E — числа). Это процесс проб и ошибок. Для уравнения X 2 — 3X + 2 = 0 это становится
(X — 2)(X — 1) = 0 Примечание. Когда вы умножаете две скобки, вы умножаете каждое слагаемое в первой скобке на каждое слагаемое во второй скобке:(Х — 2)(Х — 1) = (Х × Х) — 2Х — Х + 2 = Х 2 — 3Х + 2 Другие алгебраические расширения можно найти в эссе Треугольник Паскаля. Давайте снова посмотрим на (X — 2) (X — 1) = 0 . Это умножение формы
Давайте снова посмотрим на (X — 2) (X — 1) = 0 . Это умножение формыГ × В = 0 Когда два числа умножаются вместе и дают ноль, либо G должен быть равен нулю, либо H должен быть равен нулю .
Итак, когда (X — 2)(X — 1) = 0 , либо X — 2 = 0 , либо X — 1 = 0 .
Первое выполняется, когда X = 2 , второе — когда X = 1 . Это два значения уравнения X 2 — 3X + 2 .
Проверка путем замены X на 2 дает: 2 2 — (3 × 2) + 2 = 4 — 6 + 2 = 0 …. верно.
Проверка путем замены X на 1 дает: 1 2 — (3 × 1) + 2 = 1 — 3 + 2 = 0 …. верно.
Лучшим методом решения квадратных уравнений является использование приведенной ниже формулы, открытой Омаром Хайямом в 12 веке.
Когда ах 2 + bx + c = 0 ,
Это квадратичная формула . Есть два решения из-за наличия опций «плюс» и «минус». Для уравнения X 2 — 3X + 2 ,
А = 1, В = -3, С = 2 .
Используя приведенные выше квадратные формулы, мы получаем:
. Снова получаем X = 2 и Х = 1 . Пример 11: Решение квадратного уравнения, X 2 — 5Х + 6 = 0 .Коэффициенты А = 1, В = -5, С = 6 .
Используя квадратные формулы, мы получаем:
. В итоге получаем X = 2 и Х = 3 .
Проверка путем замены X на 2 дает:
Пример 12: Решите квадратное уравнение, (X — 1)(X + 2) = -1 — X — 2X 2 .2 2 — (5 × 2) + 6 = 4 — 10 + 6 = 0 …. верно.
Проверка путем замены X на 3 дает:
3 2 — (5 × 3) + 6 = 9 — 15 + 6 = 0 .
 … верно.
… верно.Это уравнение нужно перестроить. Сначала умножаем левую часть:
. (X — 1)(X + 2) , который расширяется до X 2 + X — 2
Полное уравнение теперь принимает вид
X 2 + X — 2 = -1 — X — 2X 2 Получение каждого члена в левой части:
3X 2 + 2X — 1 = 0 А = 3, В = 2, С = -1 .
Используя квадратные формулы, мы получаем:
. Мы получаем X = -1 и Х = 1/3 .
Проверка путем замены X на -1 дает:
Не забывайте всегда проверять свои результаты.3 × -1 2 + (2 × -1) — 1 = 3 — 2 — 1 = 0 …. верно.
Проверка заменой X на 1/3 дает:
3 × (1 / 3) 2 + (2 × (1 / 3)) — 1 = 1 / 3 + 2 / 3 — 1 = 0 .
 … верно.
… верно.
Биквадратные уравнения представляют собой уравнения вида:AX 4 + BX 2 + C = 0 Они являются частным случаем уравнения четвертой степени 9.0029 . По сути, это квадратные уравнения в x 2 .
Пример 13: Решите уравнение X 4 — 3X 2 + 2 + 0.Мы можем использовать квадратичную формулу, положив A = 1, B = -3, C = 2 :
Это дает X 2 = 2 и X 2 = 1 . Это означает, что есть четыре решения, которые являются правильными для уравнения четвертой степени:
Х = +1, -1, √ 2, -√ 2
Возвращаясь к квадратичной формуле:Часть внутри знака квадратного корня называется определителем .  Его значение определяет тип корней.
Его значение определяет тип корней.- b 2 — 4ac > 0 : Уравнение имеет два различных действительных корней.
- b 2 — 4ac = 0 : У уравнения есть один повторяющийся корень.
- b 2 — 4ac < 0 : Уравнение имеет два комплексных корня.
Используя квадратичную формулу и положив A = 1, B = 1, C = 1 :
Это дает Х = 1/2 + я √ 3/2 и Х = 1/2 — я √ 3/2 .
Пара комплексных корней вида а + ib и а — ib называется комплексными сопряженными . Если квадратное уравнение имеет комплексные корни, они всегда будут парой сложных сопряженных уравнений.
Если квадратное уравнение имеет комплексные корни, они всегда будут парой сложных сопряженных уравнений.
Общее кубическое уравнение имеет вид AX 3 + BX 2 + CX + D = 0 . Существует формула для решения этого типа уравнений, но она выходит за рамки этого эссе. Достаточно сказать, что кубическое уравнение должно иметь три корня. Один всегда реален, два других могут быть реальными или сложными.В этом разделе мы рассмотрим корни двух типов кубических уравнений.
Первый тип называется Pure Cubic и имеет вид X 3 — T = 0 , где T — любое действительное число.Корни этого типа задаются как
x = 3 √ T Где ω 2 и ω 3 — комплексные кубические корни из 1:х = ω 2 3 √ T
х = ω 3 3 √ T
ω 2 = (-1 + i √ 3) / 2 Второй тип — Симметричный кубический : X 3 + PX 2 + PX + 1 = 0 .ω 3 = (-1 — i √ 3) / 2

Это можно разложить на множители до (X + 1)(X 2 — X + 1 + PX) = 0 .
Это дает значение x = -1 . Оставшийся квадрат можно решить с помощью квадратичной формулы.
© 2000, 2009 КрысТал
Знакомство с различными типами чисел: действительными, мнимыми, рациональными, иррациональными, трансцендентными. Серия, разработанная Исааком Ньютоном, которая используется для расчетов. Подробнее об индексах: корни и степени. Факториалы. Комбинации. Как решать уравнения, содержащие синусы, косинусы и тангенсы.алгебра | История, определение и факты
математики греко-римского мира
Смотреть все СМИ
- Ключевые люди:
- Джон фон Нейман Сэр Уильям Роуэн Гамильтон Диофант Эмми Нётер Томас Хэрриот
- Похожие темы:
- элементарная алгебра современная алгебра линейная алгебра теорема о рациональном корне биномиальная теорема
Просмотреть весь связанный контент →
Популярные вопросы
Что такое алгебра?
Алгебра — это раздел математики, в котором абстрактные символы, а не числа, обрабатываются или оперируются с помощью арифметики.
 Например, x + y = z или b — 2 = 5 являются алгебраическими уравнениями, а 2 + 3 = 5 и 73 * 46 = 3358 — нет. Используя абстрактные символы, математики могут работать с общими терминами, применимыми гораздо шире, чем конкретные ситуации, связанные с числами.
Например, x + y = z или b — 2 = 5 являются алгебраическими уравнениями, а 2 + 3 = 5 и 73 * 46 = 3358 — нет. Используя абстрактные символы, математики могут работать с общими терминами, применимыми гораздо шире, чем конкретные ситуации, связанные с числами.Чем отличаются алгебра и геометрия?
Алгебра — это раздел математики, в котором арифметические операции и другие формальные операции применяются к абстрактным символам, а не к конкретным числам. Геометрия — это раздел математики, изучающий форму объектов, их пространственные отношения и свойства пространства, в котором находятся объекты.
Резюме
Прочтите краткий обзор этой темы
алгебра , раздел математики, в котором арифметические операции и формальные манипуляции применяются к абстрактным символам, а не к конкретным числам. Представление о существовании такой отдельной дисциплины математики, а также термин алгебра для ее обозначения возникли в результате медленного исторического развития.
 В этой статье представлена эта история, прослеживается эволюция во времени понятия уравнения, систем счисления, символов для передачи математических утверждений и манипулирования ими, а также современного абстрактного структурного взгляда на алгебру. Для получения информации о конкретных разделах алгебры, см. элементарная алгебра, линейная алгебра и современная алгебра.
В этой статье представлена эта история, прослеживается эволюция во времени понятия уравнения, систем счисления, символов для передачи математических утверждений и манипулирования ими, а также современного абстрактного структурного взгляда на алгебру. Для получения информации о конкретных разделах алгебры, см. элементарная алгебра, линейная алгебра и современная алгебра.Возникновение формальных уравнений
Возможно, самым основным понятием в математике является уравнение, формальное утверждение о том, что две части математического выражения равны — как в простом уравнении x + 3 = 5 — и что обе части можно одновременно манипулировать уравнением (складывать, делить, извлекать корни и т. д. с обеих сторон), чтобы «решить» уравнение. Тем не менее, каким бы простым и естественным ни казалось это понятие сегодня, его принятие сначала потребовало развития многочисленных математических идей, каждая из которых требовала времени, чтобы созреть. Фактически, только в конце 16 века закрепилась современная концепция уравнения как единого математического объекта.

Особого внимания заслуживают три основных направления процесса, ведущего к этой консолидации:
Попытки решить уравнения с одной или несколькими неизвестными величинами. При описании ранней истории алгебры слово уравнение часто используется из соображений удобства для описания этих операций, хотя ранние математики не знали о таком понятии.
Эволюция представления о том, что именно считается допустимым числом. Со временем это понятие расширилось, чтобы включить более широкие области (рациональные числа, иррациональные числа, отрицательные числа и комплексные числа), которые были достаточно гибкими, чтобы поддерживать абстрактную структуру символической алгебры.
Постепенное совершенствование символического языка, подходящего для разработки и передачи обобщенных алгоритмов или пошаговых процедур для решения целых категорий математических задач.
Эти три нити прослеживаются в этом разделе, особенно в том, как они развивались на древнем Ближнем Востоке и в Греции, в исламскую эпоху и в эпоху европейского Возрождения.

Викторина по Британике
Дайте определение: математические термины
Вот ваша миссия, если вы решите ее принять: Дайте определение следующим математическим терминам до того, как истечет время.
Решение задач в Египте и Вавилоне
Самый ранний из сохранившихся математических текстов из Египта — это папирус Райнда (ок. 1650 г. до н. э.). Этот и другие тексты свидетельствуют о способности древних египтян решать линейные уравнения с одним неизвестным. Линейное уравнение — это уравнение первой степени, то есть уравнение, в котором все переменные даны только в первой степени. (В сегодняшних обозначениях такое уравнение с одним неизвестным будет 7 x + 3 x = 10.) Свидетельства примерно 300 г. до н.э. указывают на то, что египтяне также знали, как решать задачи, включающие систему двух уравнений с двумя неизвестными. величин, включая квадратные (второй степени или квадраты неизвестных) уравнения. Например, учитывая, что периметр прямоугольного участка земли составляет 100 единиц, а его площадь 600 квадратных единиц, древние египтяне могли найти длину поля l и ширина w .
 (В современных обозначениях они могли решить пару одновременных уравнений 2 w + 2 l = 100 и w l = 600.) Однако на протяжении всего этого периода символы не использовались — задачи формулировались. и решается устно. Типична следующая задача:
(В современных обозначениях они могли решить пару одновременных уравнений 2 w + 2 l = 100 и w l = 600.) Однако на протяжении всего этого периода символы не использовались — задачи формулировались. и решается устно. Типична следующая задача:Метод расчета количества,
умножить на 1 1 / 2 прибавив 4 получилось 10.
Какое количество говорит об этом?
Сначала вы вычисляете разницу между этими 10 и этими 4. Затем получается 6 результатов.
Затем вы делите 1 на 1 1 / 2 . Затем 2 / 3 результатов.
Затем вы вычисляете 2 / 3 из этих 6. Затем 4 результата.
Вот, это 4, количество, которое сказало это.
То, что вы нашли, верно.
Обратите внимание, что за исключением 2 / 3 , для которых существовал специальный символ, египтяне выражали все дробные количества, используя только единичные дроби, то есть дроби, имеющие числитель 1.
 Например, 3 / 4 будет записано как 1 / 2 + 1 / 4 .
Например, 3 / 4 будет записано как 1 / 2 + 1 / 4 .Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Вавилонская математика восходит к 1800 г. до н.э., о чем свидетельствуют клинописные тексты, сохранившиеся на глиняных табличках. Вавилонская арифметика была основана на хорошо разработанной позиционной шестидесятеричной системе счисления, то есть на системе с основанием 60, в отличие от современной десятичной системы, основанной на единицах 10. Вавилоняне, однако, не использовали постоянно ноль. . Большая часть их математики состояла из таблиц, например, для умножения, обратных величин, квадратов (но не кубов), а также квадратных и кубических корней.
Помимо таблиц, многие вавилонские таблички содержали задачи, требующие решения какого-то неизвестного числа. Такие задачи объясняли процедуру решения конкретной проблемы, а не предлагали общий алгоритм решения подобных задач.
 Отправной точкой для задачи могут быть отношения, включающие определенные числа и неизвестное, или его квадрат, или системы таких отношений. Искомым числом может быть квадратный корень из заданного числа, вес камня или длина стороны треугольника. Многие вопросы были сформулированы с точки зрения конкретных ситуаций, таких как разделение поля между тремя парами братьев при определенных ограничениях. Тем не менее их искусственный характер ясно давал понять, что они созданы в дидактических целях. 92 — 4ac}}{2a}$
Отправной точкой для задачи могут быть отношения, включающие определенные числа и неизвестное, или его квадрат, или системы таких отношений. Искомым числом может быть квадратный корень из заданного числа, вес камня или длина стороны треугольника. Многие вопросы были сформулированы с точки зрения конкретных ситуаций, таких как разделение поля между тремя парами братьев при определенных ограничениях. Тем не менее их искусственный характер ясно давал понять, что они созданы в дидактических целях. 92 — 4ac}}{2a}$Число D = b 2 — 4ac называется «дискриминантом» .
Если D < 0, то квадратное уравнение не имеет действительных решений (имеет 2 комплексных решения).
Если D = 0, то квадратное уравнение имеет 1 решение $x = — \frac{b}{2a}$
Если D > 0, то квадратное уравнение имеет 2 различных решения.Пример:
Решим квадратное уравнение: x 2 + 3x — 4 = 0
a = 1, b = 3, c = -4
$x=\frac{-(3) \pm \sqrt{ 3^2 — 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} = $ 92-32$$y=2(x-3)(x+5)$ y-точка пересечения с
$(0, -30)$вершина в
$(-1, -32)$x-отрезков в точках
$(3, 0)$ и $(-5, 0)$Парабола
График квадратного уравнения называется параболой .
Если a < 0, то его вершина направлена вверх: Если a = 0, то график представляет собой не параболу, а прямую линию.
Если a > 0, то его вершина указывает вниз:Вершина параболы $x = -\frac{b}{2a}$.
формулы Виета
Если x 1 и x 2 являются корнями квадратного уравнения ax 2 + bx + c = 0 тогда:
$x_1 + x_2 = -\frac{b}{a}$
$x_1x_2 = \frac{c}{a}$
Эти формулы называются формулами Виета .
Мы можем найти корни x 1 и x 2 квадратного уравнения, решив уравнения уравнений.Задачи на квадратные уравнения
Задача 1. Решите уравнение:
x 2 — 4 = 0
Решение: x 2 — 4 = (x — 2)(x + 2)
(x — 2)(x + 2) = 0
x — 2 = 0 или x + 2 = 0
Корни x = 2 или x = -2Решение 2: a = 1, b = 0, c = -4
D = 0 2 — 4 ⋅ 1 ⋅ (-4) = 16
$x_1 = \frac{-b — \sqrt{D}}{2a} = \frac{- 0 — \sqrt{16}}{2 \cdot 1} = \frac{-4}{2} = -2$
$x_2 = \frac{-b + \sqrt{D}}{2a } = \frac{- 0 + \sqrt{16}}{2 \cdot 1} = \frac{4}{2} = 2$Задача 2.
 Решите уравнение:
Решите уравнение:
3x 2 + 4x + 5 = 0
Решение: дискриминант D = 4 2 — 4⋅3⋅5 = 16 — 60 = -44 Таким образом, квадратное уравнение не имеет действительных корней.Задача 3. Решить уравнение:
х 2 + 4х — 5 = 0; х = ?
Решение: Дискриминант равен 4 2 — (-4⋅1⋅5) = 16 + 20 = 36 > 0
У уравнения два действительных корня: $\frac{-4 \pm \sqrt{36} {2}$
х = 1 или х = -5Задача 4. Решить уравнение:
х 2 + 4х + 4 = 0; х = ?
Решение: Дискриминант равен 4 2 — (4⋅1⋅4) = 16 — 16 = 0
Таким образом, существует одно действительное решение: $x = \frac{-4}{2}$
x = -2Задача 5. Решите уравнение:
x 2 — 13x + 12 = 0
Корни: 1, 12Задача 6.
 Решить уравнение: 92 — 4ac}}{2a}$
Решить уравнение: 92 — 4ac}}{2a}$Квадратные уравнения на нашем математическом форуме
Задачи на квадратные уравнения
Задачи на формулы Виета
Решение уравнений кубической и четвертой степени — 1Форумы, посвященные квадратным уравнениям
«Формула Квартика»
«Формула Квартика»Введение.
Вскоре после открытия метода решения кубического уравнения Лодовико Феррари (1522-1565), ученик Кардано, нашел способ решения уравнения четвертой степени. Его решение является свидетельством как силы, так и ограничений элементарной алгебры.Наша цель — найти два корня уравнения четвертой степени
Затем два других корня (действительные или комплексные) можно найти с помощью полиномиального деления и квадратичной формулы. Решение проходит в два этапа. Во-первых, уравнение четвертой степени «угнетено»; тогда задача сводится к решению родственного кубического уравнения.

Депрессия уравнения четвертой степени.
Уловка, которую мы использовали, чтобы уменьшить кубическое уравнение, работает в основном так же и для уравнения четвертой степени.Применяем замену
к уравнению четвертой степени (1), чтобы получить:
Умножая и упрощая, получаем «вдавленную» квартику
Давайте попробуем это для примера
Наша замена будет х = y -2; расширяя и упрощая, получаем уравнение вдавленной четвертой степени
Решение депрессии квартики.
Нам осталось решить уравнение подавленной четвертой степени вида
Сначала мы переместим y -член на другую сторону.
Далее мы «завершаем квадрат» с левой стороны, но в итоге хотим получить . Для этого добавим термин
с обеих сторон:
Упрощение левой части приводит к
А теперь решающий трюк: используя новое неизвестное z , мы хотим изменить левую часть (5) на
что означает, что мы должны добавить к обеим частям (5), чтобы получить:
Какой беспорядок! Давайте посмотрим, что мы получим для нашего конкретного примера.
 Уравнение (2):
Уравнение (2):«Завершение квадрата» способом, указанным выше, дает:
С
добавление члена к обеим частям (7) приводит к
Левая сторона представляет собой «идеальный квадрат». Следующим шагом будет определение z , чтобы правая сторона тоже выглядела как идеальный квадрат.
Обратите внимание, что правая часть представляет собой квадратичный многочлен от y . Получение идеального квадрата — это еще один способ сказать, что у этого многочлена есть повторяющийся множитель. Квадратичный многочлен имеет повторяющийся множитель, если его дискриминант равен 0. Давайте вычислим дискриминант в нашем примере:
Этот полином называется резольвентным кубическим полиномом для уравнения четвертой степени.
Мы можем найти действительный корень кубической резольвенты; в этом случае Rational Zero Test показывает, что z =-5 является таким корнем.
Где мы? Если z =-5, то
должен быть правильным квадратом.
 Давайте проверим это.
Давайте проверим это.Бинго! К настоящему времени уравнение (7) выглядит так:
Мы почти закончили. Возьмем квадратные корни с обеих сторон:
Мы отбрасываем один из двух вариантов и получаем
Это квадратное уравнение! Его корни
Используя замену x = y -2, мы видим, что наше исходное уравнение
имеет два корня вида
Два других корня можно найти делением многочлена в длину и применением квадратичной формулы.
Позвольте мне закончить, убедив вас в том, что превращение правой стороны в идеальный квадрат всегда равносильно решению кубического уравнения: на последнем общем шаге (уравнение (6)) мы записали наше уравнение четвертой степени с пониженной частотой в виде
Аккуратно записав правую часть в виде многочлена от y , получим
Таким образом, дискриминант правой части равен
кубический многочлен от z .

Таким образом, описанная процедура будет работать в целом. Одно предостережение: уравнение четвертой степени может иметь четыре комплексных корня; поэтому вы должны ожидать, что комплексные числа будут играть гораздо большую роль в целом, чем в моем конкретном примере. При обсуждении общего случая я, например, молчаливо предположил, что C положительный.
Интересный отчет о подходе Эйлера к решению уравнений четвертой степени см. в статье Уравнение четвертой степени: инварианты и Решение Эйлера, раскрытое RWD Nickalls.
Упражнение 1.
Найдите резольвентный кубический многочлен уравнения вдавленной четвертой степениУбедитесь, что z =3 является корнем кубической резольвенты уравнения, затем найдите все корни уравнения четвертой степени.
Ответ.
г. Упражнение 2.
Объясните взаимосвязь метода «заполнение квадрата» и метод «вдавления» кубического или четвертого многочлена.[Назад] [Алгебра] [Тригонометрия] [Комплексные переменные] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра] Домашняя страница S. 


 При этом все эти переменные (а , b и с ) являются коэффициентами вышеприведенного уравнения.
При этом все эти переменные (а , b и с ) являются коэффициентами вышеприведенного уравнения. {2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]
{2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]
 е.
е. Найдите у и подставьте в любое из первоначальных уравнений, найдите х.
Найдите у и подставьте в любое из первоначальных уравнений, найдите х.
 Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.
Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные. Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.
Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В. Решать системы можно несколькими методами.
Решать системы можно несколькими методами. 2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.
2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения. 2=6\)
2=6\)
 2+9x-5=0\)
2+9x-5=0\)
 Актуализация знаний
Актуализация знаний

 Представители групп записывают свои биквадратные уравнения на доске.:
Представители групп записывают свои биквадратные уравнения на доске.: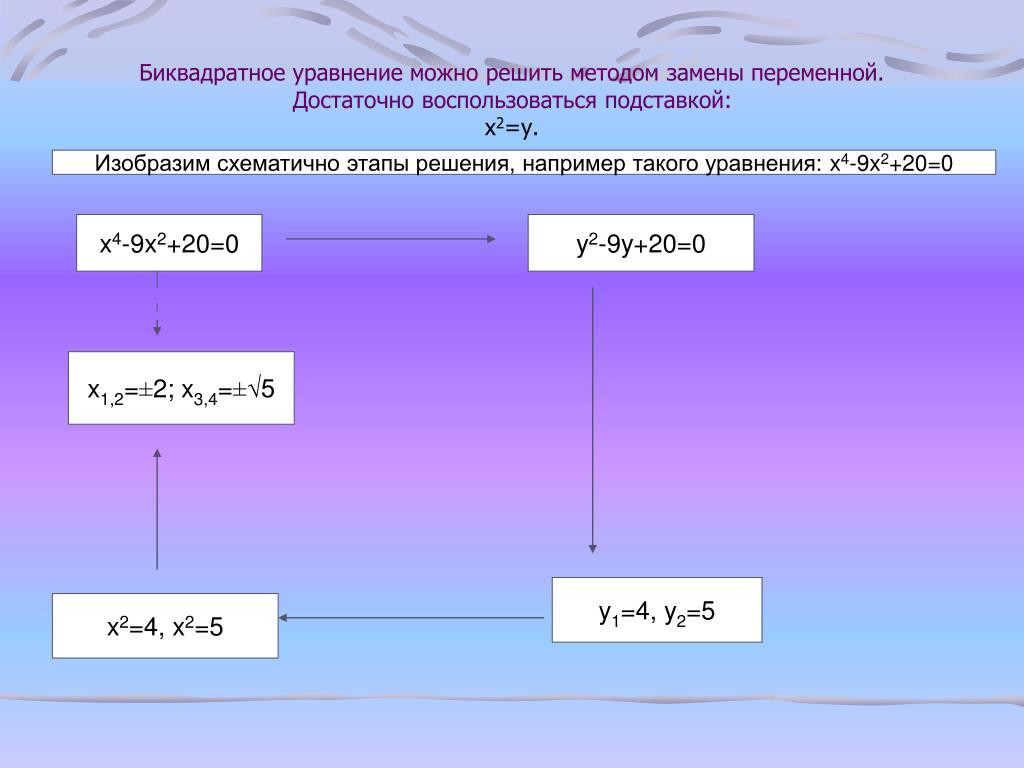
 Поощряется каждый правильный ответ, неуверенно ответившему задается направляющие вопросы.
Поощряется каждый правильный ответ, неуверенно ответившему задается направляющие вопросы.
 Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.




 А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.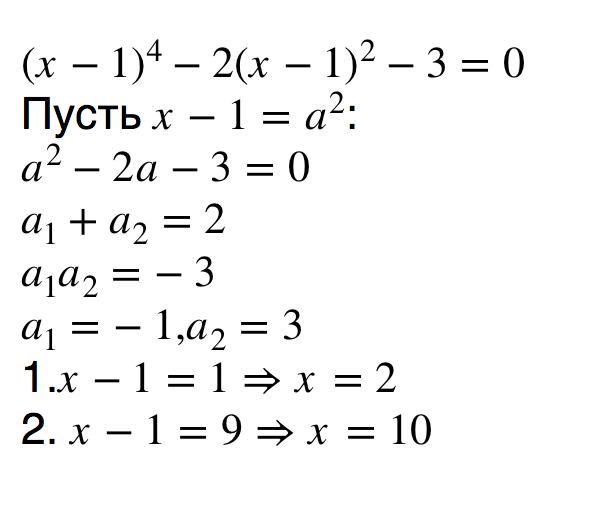
 для вас, что, на мой взгляд, делает его плохим математиком.
для вас, что, на мой взгляд, делает его плохим математиком. Это не влияет на корневые позиции; все, что делал опережающий коэффициент, — это увеличивал ненулевые значения. Относительно нулей нет абсолютно никакой потери общности. Все эти константы $p,q,r$ можно вычислить из исходных коэффициентов $a,b,c,d,e$. Кубического члена по-прежнему нет, а опережающего коэффициента теперь тоже нет.
Это не влияет на корневые позиции; все, что делал опережающий коэффициент, — это увеличивал ненулевые значения. Относительно нулей нет абсолютно никакой потери общности. Все эти константы $p,q,r$ можно вычислить из исходных коэффициентов $a,b,c,d,e$. Кубического члена по-прежнему нет, а опережающего коэффициента теперь тоже нет. Затем мы реализуем метод факторизации Декарта.
Затем мы реализуем метод факторизации Декарта. 2 }$$ 92 =0$$
2 }$$ 92 =0$$ Мы ввели горизонтальный сдвиг $x = z-\frac{b}{4a}$. Выполнение этого последнего шага решит исходную квартику в терминах $ x $, что является решением, которое вам нужно.
Мы ввели горизонтальный сдвиг $x = z-\frac{b}{4a}$. Выполнение этого последнего шага решит исходную квартику в терминах $ x $, что является решением, которое вам нужно. Это также означает, что вам придется решать кубик с комплексными коэффициентами. Это выполнимо, и математика все еще работает нормально.
Это также означает, что вам придется решать кубик с комплексными коэффициентами. Это выполнимо, и математика все еще работает нормально.
 25X 3   —   .85X 2   +   1,45X   —   4,35   =   0
25X 3   —   .85X 2   +   1,45X   —   4,35   =   0
 0625)
0625) 0625)
0625) д   =   4   и   e   =   5
д   =   4   и   e   =   5
 2760
2760 136994
136994
 Эти буквы затем манипулируют в соответствии с определенными правилами, пока не появится ответ. Обычная буква для неизвестного числа — 9.0028 х . Обычно используются маленькие x , но это слишком похоже на знак умножения ( × ), поэтому я буду использовать заглавные X . Два числа, сложенные вместе, показаны как:
Эти буквы затем манипулируют в соответствии с определенными правилами, пока не появится ответ. Обычная буква для неизвестного числа — 9.0028 х . Обычно используются маленькие x , но это слишком похоже на знак умножения ( × ), поэтому я буду использовать заглавные X . Два числа, сложенные вместе, показаны как: Если мы хотим найти значение неизвестного числа X, мы должны получить X с одной стороны уравнения и числа с другой стороны.
Если мы хотим найти значение неизвестного числа X, мы должны получить X с одной стороны уравнения и числа с другой стороны. …. верно. Пример 4: Решите уравнение 2X — 3 = -1
…. верно. Пример 4: Решите уравнение 2X — 3 = -1 
 …. верно.
…. верно. 
 Что делать, если у нас есть два неизвестных числа? Давайте посмотрим на уравнение X + Y = 3 . Это может быть удовлетворено:
Что делать, если у нас есть два неизвестных числа? Давайте посмотрим на уравнение X + Y = 3 . Это может быть удовлетворено:
 Их можно проверить, поместив их в (ii).
Их можно проверить, поместив их в (ii). Заменив Y в (i) на -2, мы можем получить значение X. 3 × -2) = -4
Заменив Y в (i) на -2, мы можем получить значение X. 3 × -2) = -4  Квадратные уравнения обычно имеют два ответа, а не один. Другими словами, есть два значения X, которые могут удовлетворять уравнению.
Квадратные уравнения обычно имеют два ответа, а не один. Другими словами, есть два значения X, которые могут удовлетворять уравнению. Давайте снова посмотрим на (X — 2) (X — 1) = 0 . Это умножение формы
Давайте снова посмотрим на (X — 2) (X — 1) = 0 . Это умножение формы
 … верно.
… верно.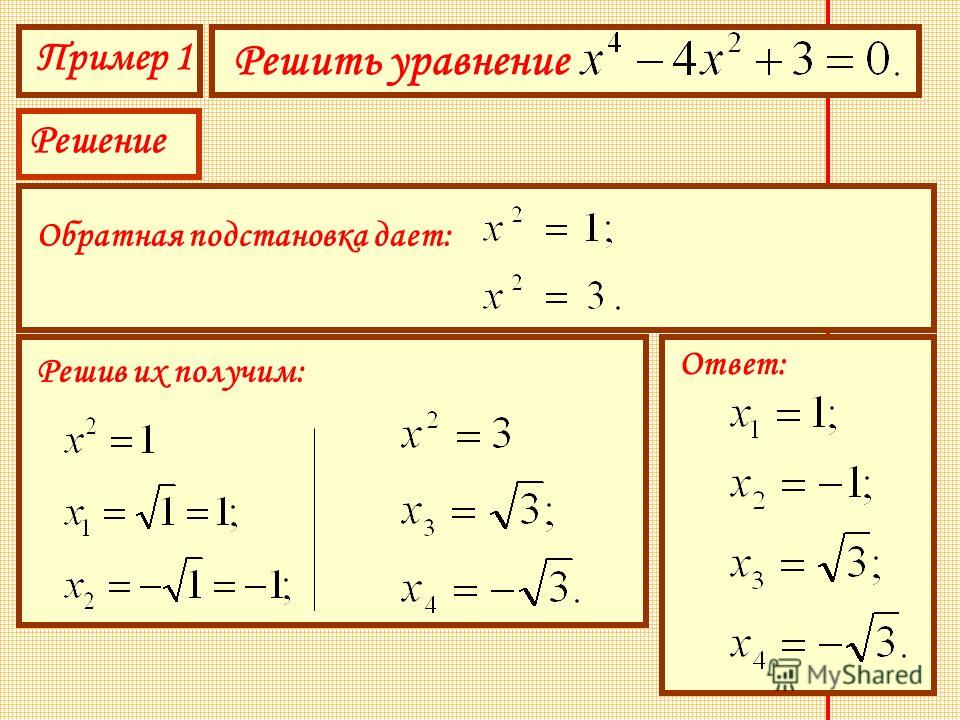 … верно.
… верно. Его значение определяет тип корней.
Его значение определяет тип корней. Если квадратное уравнение имеет комплексные корни, они всегда будут парой сложных сопряженных уравнений.
Если квадратное уравнение имеет комплексные корни, они всегда будут парой сложных сопряженных уравнений.
 Например, x + y = z или b — 2 = 5 являются алгебраическими уравнениями, а 2 + 3 = 5 и 73 * 46 = 3358 — нет. Используя абстрактные символы, математики могут работать с общими терминами, применимыми гораздо шире, чем конкретные ситуации, связанные с числами.
Например, x + y = z или b — 2 = 5 являются алгебраическими уравнениями, а 2 + 3 = 5 и 73 * 46 = 3358 — нет. Используя абстрактные символы, математики могут работать с общими терминами, применимыми гораздо шире, чем конкретные ситуации, связанные с числами. В этой статье представлена эта история, прослеживается эволюция во времени понятия уравнения, систем счисления, символов для передачи математических утверждений и манипулирования ими, а также современного абстрактного структурного взгляда на алгебру. Для получения информации о конкретных разделах алгебры, см. элементарная алгебра, линейная алгебра и современная алгебра.
В этой статье представлена эта история, прослеживается эволюция во времени понятия уравнения, систем счисления, символов для передачи математических утверждений и манипулирования ими, а также современного абстрактного структурного взгляда на алгебру. Для получения информации о конкретных разделах алгебры, см. элементарная алгебра, линейная алгебра и современная алгебра.

 (В современных обозначениях они могли решить пару одновременных уравнений 2 w + 2 l = 100 и w l = 600.) Однако на протяжении всего этого периода символы не использовались — задачи формулировались. и решается устно. Типична следующая задача:
(В современных обозначениях они могли решить пару одновременных уравнений 2 w + 2 l = 100 и w l = 600.) Однако на протяжении всего этого периода символы не использовались — задачи формулировались. и решается устно. Типична следующая задача: Например, 3 / 4 будет записано как 1 / 2 + 1 / 4 .
Например, 3 / 4 будет записано как 1 / 2 + 1 / 4 . Отправной точкой для задачи могут быть отношения, включающие определенные числа и неизвестное, или его квадрат, или системы таких отношений. Искомым числом может быть квадратный корень из заданного числа, вес камня или длина стороны треугольника. Многие вопросы были сформулированы с точки зрения конкретных ситуаций, таких как разделение поля между тремя парами братьев при определенных ограничениях. Тем не менее их искусственный характер ясно давал понять, что они созданы в дидактических целях. 92 — 4ac}}{2a}$
Отправной точкой для задачи могут быть отношения, включающие определенные числа и неизвестное, или его квадрат, или системы таких отношений. Искомым числом может быть квадратный корень из заданного числа, вес камня или длина стороны треугольника. Многие вопросы были сформулированы с точки зрения конкретных ситуаций, таких как разделение поля между тремя парами братьев при определенных ограничениях. Тем не менее их искусственный характер ясно давал понять, что они созданы в дидактических целях. 92 — 4ac}}{2a}$
 Решите уравнение:
Решите уравнение:  Решить уравнение: 92 — 4ac}}{2a}$
Решить уравнение: 92 — 4ac}}{2a}$
 Уравнение (2):
Уравнение (2): Давайте проверим это.
Давайте проверим это.
