Интегрирование по частям. Вторая часть.
Высшая математика » Неопределённые интегралы » Интегрирование по частям » Вторая часть.
Первая часть
Вторая часть
В этой части мы продолжим тему интегрирования по частям в неопределённом интеграле, начатую здесь. Вновь нам будут нужны таблица неопределенных интегралов и таблица производных. Перед прочтением данной страницы рекомендую ознакомиться с предыдущей частью, ибо там были даны полные пояснения к каждому примеру. Здесь же будут затронуты интегралы, которые не подпадают под стандартные правила, указаные в первой части, но, тем не менее, берутся с помощью интегрирования по частям. Мы будем использовать ту же формулу, что и ранее:
$$ \begin{equation} \int u \; dv=u\cdot v-\int v\; du \end{equation} $$
Также рассмотрим интегралы, при вычислении которых получается уравнение относительно исходного интеграла.
Пример №7
Найти $\int\cos\ln x\;dx$.
Решение
Метод решения данного примера аналогичен применённому в предыдущем примере №6:
$$ \int\cos\ln x\;dx=\left | \begin{aligned} & u=\cos\ln x; \; du=-\frac{\sin\ln x}{x}dx.\\ & dv=dx; \; v=x. \end{aligned} \right| =x\cdot \cos\ln x+\int x\cdot\frac{\sin\ln x}{x}dx=\\ =x\cdot \cos\ln x+\int \sin\ln x dx=\left | \begin{aligned} & u=\sin\ln x; \; du=\frac{\cos\ln x}{x}dx.\\ & dv=dx; \; v=x. \end{aligned} \right|=\\ =x\cdot \cos\ln x+x\cdot\sin\ln x-\int x\cdot\frac{\cos\ln{x}}{x}dx =x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx $$
Итак, мы получили уравнение с искомым интегралом:
$$ \int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx $$
Перенося $\int \cos\ln x \;dx$ из правой части в левую, будем иметь:
$$
2\int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x+2C. $$
$$
Деля обе части последнего равенства на $2$, получим:
$$ \int\cos\ln x\;dx=\frac{1}{2}x\cdot \cos\ln x+\frac{1}{2}x\cdot\sin\ln x+C=\frac{x}{2}\cdot (\cos\ln x+\sin\ln x)+C. $$
Ответ: $\int\cos\ln x\;dx=\frac{x}{2}\cdot (\cos\ln x+\sin\ln x)+C$.
Полагаю, что у читателя тут не обойдётся без вопроса, который я изложу ниже.
Вопрос №1
Постойте, тут что-то не сходится. Откуда вообще взялась константа $C$? У нас было равенство
$$ \int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx. $$
Если перенести $\int \cos\ln x \;dx$ в левую часть, то никакой константы не возникнет, а будет вот что:
$$ 2\int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x. $$
Тут вообще нет константы! Как же она возникла в изложенном выше решении?
Ответ
Для того, чтобы разобраться с «внезапно возникшей» контантой, нужно вспомнить, что такое неопределённый интеграл. 3{x}}+\frac{3\tg{x}}{8\cos{x}}+\frac{3}{8}\ln\left|\tg\left(\frac{\pi}{4}+\frac{x}{2}\right)\right|+C
$$
3{x}}+\frac{3\tg{x}}{8\cos{x}}+\frac{3}{8}\ln\left|\tg\left(\frac{\pi}{4}+\frac{x}{2}\right)\right|+C
$$
Ответ:
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Определенный интеграл
Задание для студентов на практическое №3по теме
«Основы интегрального исчисления.Методы нахождения неопределенных интегралов. Вычисление определенных интегралов»
Цель занятия: Научиться решать примеры и задачи по данной теме
Вопросы теории ( исходный уровень)
Первообразная функции и неопределённый интеграл.
Интегрирование.
Методы нахождения неопределенных интегралов: приведение к табличному виду и метод замены переменной, интегрирование по частям.

Определённый интеграл, его применение для вычисления площадей фигур и работы переменной силы.
Вычисление определенных интегралов, правило Ньютона-Лейбница.
Примеры использования интегрального исчисления в медицинских задачах. (самостоятельная подготовка)
Содержание занятия:
1.ответить на вопросы по теме занятия
2.решить примеры
Примеры
Найти интегралы:
1) | 2) | 3) |
4) | 5) | 6) |
7) | 8) | 9) |
| 10) | 11) | 12) |
13) | 14) | 15) |
16) | 17) | 18) |
19) | 20) | 21) |
22) | 23) | 24) |
25) | 26) | 27) |
Вычислить интегралы:
1) | 2) | 3) |
4) | 5) | 6) |
7) | 8) | 9) |
10) | 11) | 12) |
13) | 14) | 15) |
16) | 17) | 18) |
19) | 21) | 22) |
23) | 24) | 25) |
26) | 27) | 28) |
29) | 30) | 31) |
32) | 33) | 34) |
35) | 36) | 37) |
38) |
Тема
Неопределенный интеграл
Функция
F(x),
имеющая данную функцию f(x)
своей производной или
f(x)dx
своим дифференциалом, называется
первообразной данной
функции f(x). Совокупность всех первообразных функций
для
дифференциала f(x)dx
называется неопределенным интегралом
и обозначается символом ∫ f(x)dx.
Совокупность всех первообразных функций
для
дифференциала f(x)dx
называется неопределенным интегралом
и обозначается символом ∫ f(x)dx.
Свойства неопределенного интеграла
∫f(x)dx=F(x)+C
∫[f(x)+φ(x)]dx=∫ f(x)dx+∫φ(x)dx
∫ d(F(x))=F(x)+C
(∫f(x)dx)=f(x)
∫f(x)dx= ∫f(t)dt
d∫f(x)dx=f(x)dx
∫af(x)dx+a∫f(x)dx
Основные интегралы
∫dx=x+C
∫xndx=xn+1/ (n+1) +C (n≠-1)
∫dx/x=ln|x|+C
∫axdx=ax/lna +C
∫exdx=ex+C
∫sin x dx=-cos x +C
∫cos xdx=sin x +C
∫dx/cos2x=tgx+C
∫dx/sin2x=-ctgx+C
∫dx/(1-x2)1/2=arcsinx=-arccosx
∫dx/(1+x2)= arctgx=- arcctgx
Интегрирование по частям
∫ udv = uv—∫ vdu.
Пример
Найти у = ∫ ln хdх.
Полагаем и=lпх, dv = dx, тогда dи =dx/x, v = x
Используя формулу интегрирования по частям, получаем
у = ∫ ln xdx = x ln х-∫ dх = xlnx-x+C
Пример метод непосредственного интегрирования
Найти у= ∫ (1+ 2x2)dx
На основании свойства интеграла суммы запишим
у= ∫ (1+ 2x2)dx = ∫ dx+2 ∫ x2dx =x+2x3/3+C
Пример; метод замены переменной( метод подстановки)
∫tgxdx=∫(sinx/cosx)dx обозначим cosx=t
Продифферинцируем праву и левую часть
-sinxdx=dt найдем dx=dt/(-sinx)
Запишим интеграл через новые переменные
∫(sinx/t) dt/(-sinx) =-∫dt/t= lnt+C или lncosx+C
Определенный интеграл функции f(x) на отрезке [а, b] представляет предел интегральной суммы
lim∑f(ki)Δxi ( от i=1 до n и Δx→0)
где
ki — произвольная точка соответствующего
отрезка.
Формула Ньютона — Лейбница
где F′ — первообразная функцию f(x), т е
F′(x)=f(x)
Некоторые свойства определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми х=а и х=b,
Площадь фигуры, ограниченной двумя кривыми y=.f1(x) и у = = f2(x) [ f’2(x)≥f1(x)] и двумя прямыми х=а и х=b,
Дифференциальные уравнения
Общий вид дифференциального уравнения
F(x ,y,y′,y″,…yn) = О
Общee решение дифференциального уравнения
y=f(x, C1,C2, , Сn)
Общий вид дифференциального уравнения первого порядка
F(x,y,y’) = 0
Общее решение дифференциального уравнения первого порядка
y= f(x,C)
примеры
1 Дифференциальное уравнение типа y’=f(x)
dy/dx=f(х) , dx = f(x)dx
Общее решение
y=∫f(x)dx=F(x)+C
Дифференциальное уравнение типа
у’ = f(y)
dy/dx=f(y), dy/f(y)=dx
Общее решение
∫dy/f(y)=F(y)+C
Дифференциальное уравнение с разделенными переменными
f(x) dx + φ(y)dy = 0
Общее решение
∫f(x) dx + ∫φ(y)dy = C, F(х) + Ф(у) = С
Дифференциальное уравнение с разделяющимися переменными
f(x)φ(y)dx+ψ(x)Ф(y)dy=0
Приведем это уравнение к уравнению с разделенными переменными
(f(x)/ψ(x))dx+(Ф(y)/φ(y))dy=0
Общее решение
∫(f(x)/ψ(x))dx+∫(Ф(y)/φ(y))dy=C, F1(x)+F2(y)=C
Первообразная функции и неопределенный интеграл.
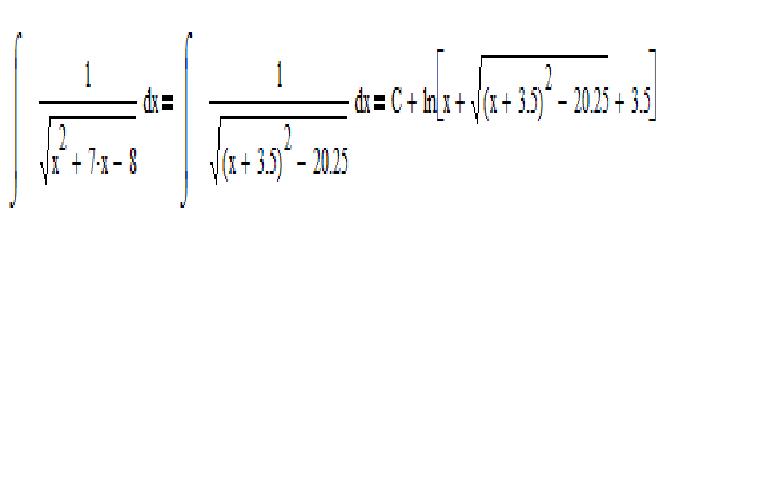
Из школьного курса математики известно, что математические операции образуют пары двух взаимно обратных действий (например, сложение и вычитание, умножение и деление, возведение в целую положительную степень и извлечение корня, логарифмирование и потенцирование).
Дифференцирование дает возможность для заданной функции F(x) находить ее производную F(x) или дифференциал dF = F (x)dx.
Cуществует действие, обратное дифференцированию, интегрирование нахождение функции F(x) по известной ее производной f(x) = F(x) или дифференциалу f(x)dx.
Функцию F(x) называют первообразной функции f(x), если для всех х из области определения
функции F(x)
= f(x) или dF(x)=f(x)dx.
Например, функция F(x) = x5 является первообразной функции f(x) = 5x4 для х , так как при любом х (х5) = 5х4 и dx5=5x4dx.
Для функции f(x) = 5x4 первообразной будет любая функция Ф(х) = х5 + С, где С – произвольное постоянное число, так как производная постоянной равна нулю.
В общем случае, если f(x) имеет первообразную функцию F(x), совокупность F(x) + C также будет первообразной для f(x):
(F(x) + C) = F(x) = f(x).
Cовокупность
первообразных F(x)
+ С для данной функции f(x) или данного дифференциала f(x)dx называют неопределенным
интегралом от
функции f(x)
и обозначают f(x)dx.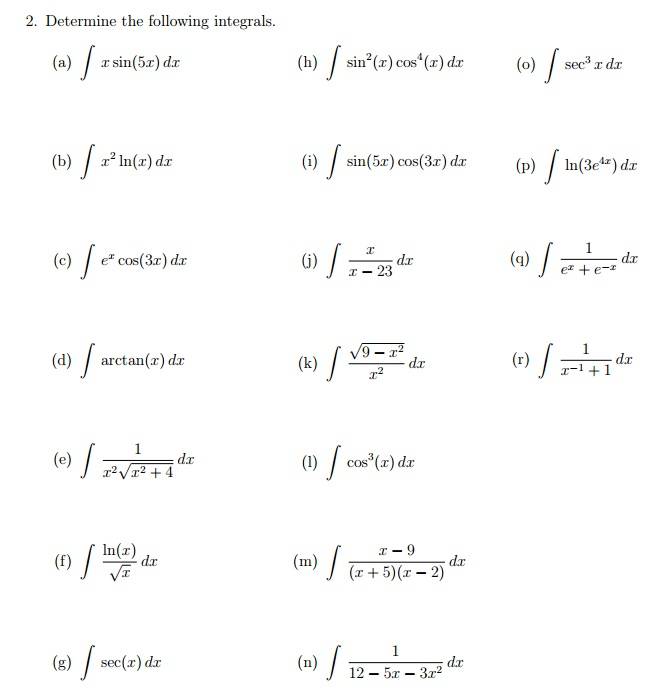
По определению, f(x)dx = F(x) + C (читается «неопределенный интеграл эф от икс дэ икс»).
Выражение f(x)dx называют подынтегральным выражением, функцию f(x) – подынтегральной функцией, а С – постоянной интегрирования.
Вычисление интеграла от данной функции называется интегрированием этой функции.
Пример. Найти неопределенный интеграл от функции f(x) = cos x, если при х = 0 F(0) = 0.
Решение. Функция cos x есть производная от функции sin x,
поэтому cos xdx = sin x + C. Обозначим
искомую первообразную F(x)
= sin x + C. Подставив в последнее выражение начальные
данные x = 0 и F(0)
= 0, получим 0 = sin 0 + C, откуда C = 0. Искомая
первообразная F(x)
= sin x.
Обозначим
искомую первообразную F(x)
= sin x + C. Подставив в последнее выражение начальные
данные x = 0 и F(0)
= 0, получим 0 = sin 0 + C, откуда C = 0. Искомая
первообразная F(x)
= sin x.
В геометрии с помощью неопределенного интеграла по закону углового коэффициента касательной в любой точке кривой можно найти уравнение кривой.
Пример. Угловой коэффициент касательной в любой точке кривой равен её абсциссе, то есть r = x. Составить уравнение кривой.
Решение. Так
как угловой коэффициент r = tg = f(x)
= x, то y= xdx = = x2/2
+ C есть
семейство парабол, отличающихся друг
от друга на постоянную С.
| Определение неопределенного интеграла | |||||||||||||||
| |||||||||||||||
| где F'(x) = f(x), C = const | |||||||||||||||
| |||||||||||||||
Основные свойства неопределенного интеграла | |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
Основные методы интегрирования | |||||||||||||||
| —метод разложения— | |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| —метод подстановки— | |||||||||||||||
| |||||||||||||||
| —метод интегрирования по частям— | |||||||||||||||
| |||||||||||||||
Интегралы некоторых функций | |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
— Что такое $dx$ в интеграции?
Интеграл дает площадь между горизонтальной осью
и кривая. В большинстве случаев это ось x.
В большинстве случаев это ось x.
г
| |
--|-- ----|---- f(x)
/ | \ / |
/ | -------- |
| / | |
-----|------- | |
| | |
| | |
----------|---------------+--------------------|--- -- Икс
а б
9b_a f(x) dx$ Но скажем, вы не хотите использовать интеграл для измерения
область между осью x и кривой. Вместо этого вы просто
вычислить среднее значение графика между a и b
и нарисуйте прямую плоскую линию y = avg(x) (среднее
значение x в этом диапазоне).
Теперь у вас есть такой график:
y
| |
- | - - - | - - f(x)
| / | \ / |
-----|--------------------------------------------------|---- среднее(х)
| / | |
- - -|- - - - | |
| | |
| | |
----------|---------------+--------------------|--- -- Икс
а б
Заключенная область представляет собой прямоугольник:
Площадь = avg(x) w, где w — ширина iof секции
Высота avg(x), а ширина w = b-a или по-английски,
«ширина среза оси x, идущей от a к b».
Но скажем, вам нужна более точная площадь. Вы могли бы сломать
разбить график на более мелкие части и сделать из них прямоугольники.
Скажем, вы делаете 4 равные части:
y
| |
|----|---| |-------|---- f(x)
| | | | |
| | |--------| |
| | | | | |
-----|---------| | | | |
| | | | | |
| | | | | |
----------|---------|----+---|--------|-------|--- -- Икс
а б
94_{n=1}avg(x,n) w$ Но это все еще недостаточно точно. Давайте использовать
бесконечное количество разделов. Теперь наш район
становится суммой бесконечного числа разделов.
Поскольку это бесконечная сумма, мы будем использовать
знак интеграла вместо знака суммы:
Площадь = $\int avg(x) w$
где avg(x) для бесконечно тонкого сечения будет
равна f(x) в этом разделе, а w будет «шириной
бесконечно тонкое сечение оси x."
Таким образом, вместо avg(x) мы можем написать f(x), потому что они
то же самое, если усреднение берется по бесконечно малой ширине.
И мы можем переименовать переменную w во что угодно.
Ширина сечения – это разница между
правая сторона и левая сторона. Разница между
две точки часто называют дельтой этих значений.
Таким образом, разница двух значений x (например, a и b) будет
называться дельта-х. Но это слишком долго, чтобы использовать в
уравнение, поэтому, когда у нас есть бесконечно малая дельта,
это сокращено до dx.
Если мы заменим avg(x) и w этими эквивалентными вещами:
Площадь = $\int f(x) dx$
Итак, что говорит уравнение:
Площадь равна сумме бесконечного числа прямоугольников
которые имеют высоту f(x) и ширину dx (где dx — бесконечно
небольшое расстояние).
Итак, вам нужен dx, потому что иначе вы не суммируете
прямоугольники, и ваш ответ не будет общей площадью.
dx буквально означает «бесконечно малая ширина x».
Это даже означает это в производных. производная от
функция представляет собой наклон графика в этой точке.
Наклон обычно измеряется как разница по оси Y двух
очки, деленные на x разность этих очков:
Наклон = (y2 - y1) / (x2 - x1)
Но чем ближе эти точки, тем меньше эти
получаются отличия. Давайте начнем называть их дельтами,
потому что разница между двумя точками часто
называется дельтой этих значений.
Давайте начнем называть их дельтами,
потому что разница между двумя точками часто
называется дельтой этих значений.
Наклон = дельта-y / дельта-x
Дельты становятся все меньше и меньше, как эти два x,y
точки все ближе и ближе. Когда они
бесконечно маленькое расстояние друг от друга, то дельта-y
а delta-x сокращается до dy и dx:
Slope = dy / dx
Наклон по-прежнему Наклон = (y2 - y1) / (x2 - x1)
но эти точки бесконечно близки друг к другу, поэтому
мы используем dy и dx, чтобы сказать себе, что они
бесконечно близкие или «дифференциальные расстояния».
исчисление - Значение $dx$ в неопределенном интеграле
Заданный вопрос
Изменено
1 год, 6 месяцев назад
Просмотрено
453 раза
$\begingroup$
В этом семестре я впервые сдаю интегральное исчисление. Мы начали с дифференциала (т.е. $dy=f'(x)\,dx$) и сразу после этого с неопределенного интеграла. С тех пор я пытаюсь разобраться в $dx$, когда он является частью неопределенного интеграла (т. е. $\int f(x) \, \boldsymbol{dx}$). Я знаю, что на этот вопрос уже есть миллион ответов, но все они относятся к определенному интегралу, а те, что касаются неопределенных интегралов, говорят только такие вещи, как «это просто синтаксический прием, чтобы сказать вам переменную, которую нужно дифференцировать по отношению к или переменная интегрирования» (Ihf, 2012, Интернет). Мне не нравится этот ответ, особенно потому, что меня учили, что для двух функций $f(x)$, $g(x)$ и первообразной их произведения $\int f(x)g(x)\,dx $, если бы я присвоил $f(x)$ $u$ и $g(x)\,dx$ $dv$ для интегрирования по частям, то мне пришлось бы интегрировать $dv$, чтобы найти $ в$. Это имеет смысл только в том случае, если $dx$ означает что-то само по себе, а не является просто причудливой нотацией, в противном случае мы получили бы что-то вроде следующего: $$\int g(x)\,dx\space dx$$
Мы начали с дифференциала (т.е. $dy=f'(x)\,dx$) и сразу после этого с неопределенного интеграла. С тех пор я пытаюсь разобраться в $dx$, когда он является частью неопределенного интеграла (т. е. $\int f(x) \, \boldsymbol{dx}$). Я знаю, что на этот вопрос уже есть миллион ответов, но все они относятся к определенному интегралу, а те, что касаются неопределенных интегралов, говорят только такие вещи, как «это просто синтаксический прием, чтобы сказать вам переменную, которую нужно дифференцировать по отношению к или переменная интегрирования» (Ihf, 2012, Интернет). Мне не нравится этот ответ, особенно потому, что меня учили, что для двух функций $f(x)$, $g(x)$ и первообразной их произведения $\int f(x)g(x)\,dx $, если бы я присвоил $f(x)$ $u$ и $g(x)\,dx$ $dv$ для интегрирования по частям, то мне пришлось бы интегрировать $dv$, чтобы найти $ в$. Это имеет смысл только в том случае, если $dx$ означает что-то само по себе, а не является просто причудливой нотацией, в противном случае мы получили бы что-то вроде следующего: $$\int g(x)\,dx\space dx$$
После долгих раздумий я наконец нашел способ понять $dx$ как нечто, что не является просто устройством записи. Мои рассуждения таковы:
Мои рассуждения таковы:
- Для заданной функции $f(x)$ пусть $y=f(x)$. Тогда $$\frac{dy}{dx}=f'(x)$$
- Тогда из фундаментальной теоремы исчисления мы знаем, что $$\int\frac{dy}{dx}\,dx=y$$
- Пусть $dy=f'(x)\,dx$. Тогда справедливо равенство $$dy=\frac{dy}{dx}\,dx$$ и $$\int\frac{dy}{dx}\,dx=\int dy=y$$
- Наконец, проинтегрируйте обе части уравнения $dy=f'(x)\,dx$, чтобы из $$\int dy=\int f'(x)\,dx\ следовало y=f(x)$$
Из этого я заключаю, что, интегрируя функцию, мы на самом деле интегрируем дифференциал этой функции. Для меня это имеет смысл, хотя я знаю, что кажущиеся логичными вещи не обязательно логичны. Вот почему я был бы признателен, если бы кто-нибудь мог сказать мне, является ли вышеизложенное математически правильным или чистой тарабарщиной.
PS, я никогда раньше не писал математические доказательства и еще не посещал курсы по доказательствам, так что буду рад любым предложениям.
Артикул: лев. (2012, 9 мая). Что означает $dx$? . Математический стек Exchange. https://math.stackexchange.com/q/143262
(2012, 9 мая). Что означает $dx$? . Математический стек Exchange. https://math.stackexchange.com/q/143262
- исчисление
- интегрирование
- обозначение
- неопределенные интегралы
- дифференциал
$\endgroup$
6 9xf(u)\, du \конец{выравнивание*} для подходящих констант $c$ и $a$, то есть опускаем верхний предел $x$, нижний предел $a$ и аддитивную константу $c$ и используем букву $x$ для переменной интегрирования.
Строго говоря, конечно, есть небольшое несоответствие в использовании одной и той же буквы для переменной интегрирования и верхнего предела $x$, который является независимой переменной в $F(x)$. При использовании
обозначения $\int f(x)\,dx$, мы никогда не должны упускать из виду связанную с ним неопределенность, т. е. тот факт, что символ всегда обозначает одна из примитивных функций только $f$. Формула $F(x) = \int f(x)\,dx$
просто символический способ записи отношения
\начать{выравнивать*}
\color{синий}{\frac{d}{dx}F(x)=f(x)}. \конец{выравнивание*}
\конец{выравнивание*}
$\endgroup$
$\begingroup$
Примечание
В математике может случиться так, что "$\int$" и "$dx$" считаются скобками, заключающими подынтегральную функцию:
$$
\int f(x)\;dx
$$
В физике может быть, что "$\int dx$" используется как оператор, поэтому он предшествует подынтегральной функции:
$$
\инт дх \;f(х)
$$
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Интеграл от 1 - формула, вывод
Прежде чем найти интеграл от 1, давайте вспомним, как мы интегрируем самые простые функции, такие как 1, x, sin x и т. д.? Поскольку интегрирование является обратным процессом дифференцирования, мы можем просто использовать дифференцирование для выполнения интегрирования. то есть, чтобы узнать, каков результат интегрирования 1, мы должны подумать, дифференцируя, какая функция даст 1.
Давайте узнаем больше об интеграле от 1 различными способами его нахождения. Кроме того, мы решим несколько примеров на том же.
| 1. | Что такое интеграл от 1? |
| 2. | Интеграл от 1 с использованием дифференцирования |
| 3. | Интеграл от 1 с использованием степенного правила интегрирования |
| 4. | Определенная интеграция 1 |
5. | Часто задаваемые вопросы по интегралу от 1 |
Что такое интеграл от 1?
Интеграл от 1 относительно x равен x + C. Математически это записывается как ∫ 1 dx = x + C. Здесь
- 1 — подынтегральная функция.
- dx означает, что интегрирование производится по x.
- C – постоянная интегрирования.
Давайте посмотрим, как доказать интегрирование 1 формулы двумя способами:
- с помощью дифференцирования
- с использованием мощного правила интегрирования
Интеграл от 1 с использованием дифференцирования
Для нахождения интеграла от 1 с помощью процесса дифференцирования посмотрите, какое выражение даст 1 при дифференцировании.
d/dx (x) = 1
Взяв интеграл с обеих сторон
∫ d/dx (x) dx = ∫ 1 dx
По основной теореме исчисления интеграл и производная сокращаются. Итак, мы получаем
Итак, мы получаем
x = ∫ 1 dx
Фактически мы добавляем постоянную интегрирования для всех неопределенных интегралов. Таким образом,
∫ 1 dx = x + C.
Следовательно, мы получили формулу интегрирования 1.
Проверка интеграла 1
Чтобы проверить интеграл 1, мы просто продифференцируем результат и посмотрим, вернуть 1. Поскольку ∫ 1 dx = x + C, найдем производную от x + C. Тогда
d/dx (x + C) = d/dx (x) + d/dx (C) (по производным правилам)
= 1 + 0
= 1
Следовательно, интеграл от 1 равен x + C и проверен.
Интеграл от 1 с использованием степенного правила интегрирования
Рассмотрим интеграл ∫ 1 dx. Используя свойства показателей, 1 = x 0 . Тогда интеграл принимает вид ∫ x 0 dx. Используя степенное правило интегрирования,
∫ x n dx = x n + 1 /(n +1) + C
Подставим здесь n = 0,
∫ x 0 dx = x 0 + 1 /(0 +1) + C
∫ 1 dx = x 1 /1 + C
∫ 1 dx = x + C
Следовательно, интеграл от выводится формула.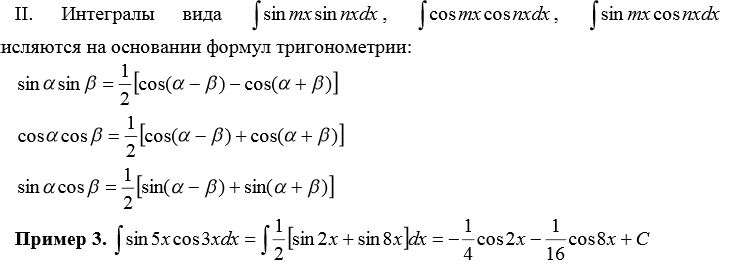
Определенная интеграция 1
Определенный интеграл от 1 — это интеграл от 1 с нижним и верхним пределами. Рассмотрим определенный интеграл с нижним пределом a и верхним пределом b. т. е. ∫ₐ b 1 dx. Поскольку ∫ 1 dx = x + C, определенное значение интеграла получается путем подстановки верхнего и нижнего пределов и вычитания результатов. Затем
∫ₐ b 1 dx = (b + C) - (a + C) = b - a.
Таким образом, определенный интеграл от 1 всегда равен разнице между верхним пределом и нижним пределом.
Важные замечания относительно интеграла от 1:
- Интеграл от 1 равен x + C, т. е. ∫ 1 dx = x + C.
- Следовательно, интеграл любой константы равен ∫ a dx = a ∫ 1 dx = ax + C.
- Определенный интеграл от a до b равен b - a. т. е. ∫ₐ b 1 dx = b - a.
Связанные темы:
- Калькулятор производных
- Производные формулы
- Обратные триггерные производные
- Дифференцирование тригонометрических функций
Часто задаваемые вопросы по интегралу от 1
Каково значение интегрирования 1?
Интегрирование 1 равно x + C. Оно записывается как ∫ 1 dx = x + C, где C – постоянная интегрирования.
Оно записывается как ∫ 1 dx = x + C, где C – постоянная интегрирования.
Как сделать интеграцию 1?
Чтобы найти интеграл от 1, просто найдите формулы производных и посмотрите, дифференцируя, какая функция даст 1. У нас есть d/dx (x + C) = 1, где C — любая константа. Следовательно, интеграл от 1 равен x + C.
Является ли первообразная от 1 равной самой 1?
Нет, первообразная 1 равна x + C. Другое название первообразной — интеграл, поэтому интеграл от 1 равен x + C, который записывается как ∫ 1 dx = x + C.
Чему равен интеграл от 2, если использовать тот факт, что интеграл от 1 равен х?
Дано, что ∫ 1 dx = x + C. Исходя из этого, ∫ 2 dx = 2 ∫ 1 dx = 2x + C.
Как найти определенный интеграл от 1?
Имеем ∫ 1 dx = x + C. Если мы рассмотрим определенный интеграл ∫ₐ b 1 dx и для его вычисления сначала подставим x = b, а затем x = a в результат x + C и найди разницу. Тогда ∫ₐ b 1 dx = (b+C) - (a+C) = b - a.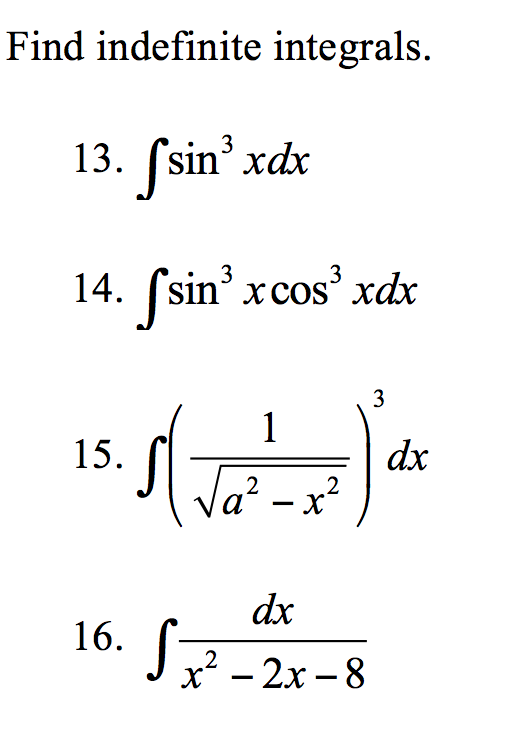
Интегральный ш(х)>
Интеграл cosh(x)>| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
решить левое уравнение = (1/2) е х + (1/2) е -х дх набор замена du= - dx, u= - x = (1/2) e х - (1/2) -е -х дх решить правый интеграл заменить обратно u= - x
= sh x + C Q.  E.D. E.D. | ||||||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
dx в исчислении интегралов и производных: математика
dx в исчислении интегралов и производных: математикаCopyright (c) 1996 Кенни Фелдер
Требуются шрифты
Когда вы впервые изучали исчисление, вы узнали, как вычислять производную и как вычислять интеграл. Вы также узнали некоторые обозначение для того, как представлять эти вещи: f'(x) означало производную, а также dy/dx, а интеграл представлялся чем-то вроде . Ни одно из этих обозначений не имело особого смысла, но вы как бы знали, что они означают, и в конце концов жизнь стала комфортной.
Ни одно из этих обозначений не имело особого смысла, но вы как бы знали, что они означают, и в конце концов жизнь стала комфортной.
И вот однажды ваш профессор сказал что-то вроде "В этом случае мы делим dx на 2". Или, что еще хуже, «давайте умножим обе части уравнения на dx». В этом было так же мало смысла, как добавлять к обеим частям уравнения или говорить: «Мы можем игнорировать ту часть, которая не помещается на странице». И твой разум закружился от вопросов. "Может ли он сделать что? Действительно ли dx означает что-то ? Как и когда вы этим манипулируете? Это будет на тесте?»
Ответ на последний вопрос, боюсь, да. Понимание того, что на самом деле означает dx, — это не просто то, что вы делаете, чтобы чувствовать себя философски чистым. Есть определенные задачи, где вам действительно нужно понимать dx: не брать производную или интеграл, а выяснить, какую производную или интеграл брать! Итак, у вас есть мотивация для просеивания остальной части этого документа. К тому времени, когда вы закончите, я надеюсь, что вы будете достаточно хорошо понимать, что на самом деле означает dx, и будете в некоторой степени готовы начать применять свое понимание для решения проблем.
К тому времени, когда вы закончите, я надеюсь, что вы будете достаточно хорошо понимать, что на самом деле означает dx, и будете в некоторой степени готовы начать применять свое понимание для решения проблем.
Что на самом деле означает dx
Вы помните, что говорили о Dx на курсе предварительного расчета. Он представляет собой расстояние по оси x; или, другими словами, разность между любыми двумя значениями х. Что ж, dx означает то же самое, с одним ключевым отличием: это дифференциальное расстояние , что является причудливым способом сказать очень, очень, очень маленькое. С технической точки зрения, dx — это то, что происходит с Dx в пределе , когда Dx приближается к нулю.Теперь, когда у вас есть величина, ценность которой практически равна нулю, вы мало что можете с ней сделать. 2+dx в значительной степени равно 2. Или, возьмем другой пример, 2/dx увеличивается до бесконечности. Там не очень весело, правда?
Но есть два обстоятельства, при которых члены, включающие dx, могут дать конечное число. Во-первых, когда вы делите два дифференциала; Например, , 2dx/dx=2, а dy/dx может быть чем угодно. Поскольку и верх, и низ близки к нулю, частное может быть некоторым разумным числом. Другой случай — это когда вы складываете 90 519 почти бесконечного числа дифференциалов: 90 520 — это что-то вроде почти бесконечного числа атомов, каждый из которых имеет почти нулевой размер, и в сумме получается баскетбольный мяч. В обоих этих случаях дифференциалы могут дать вам число больше нуля и меньше бесконечности: действительно интересное число. Как вы уже догадались, эти два случая описывают производную и интеграл соответственно. Итак, давайте поговорим о них немного подробнее, по одному.
Во-первых, когда вы делите два дифференциала; Например, , 2dx/dx=2, а dy/dx может быть чем угодно. Поскольку и верх, и низ близки к нулю, частное может быть некоторым разумным числом. Другой случай — это когда вы складываете 90 519 почти бесконечного числа дифференциалов: 90 520 — это что-то вроде почти бесконечного числа атомов, каждый из которых имеет почти нулевой размер, и в сумме получается баскетбольный мяч. В обоих этих случаях дифференциалы могут дать вам число больше нуля и меньше бесконечности: действительно интересное число. Как вы уже догадались, эти два случая описывают производную и интеграл соответственно. Итак, давайте поговорим о них немного подробнее, по одному.
Наклон кривой
Большинство из нас узнало о производных с точки зрения наклона кривой, поэтому я собираюсь начать именно с этого; но я могу использовать несколько иной подход, чем тот, который вы помните. Для начала вспомните, как вы определяете наклон линии. Вы берете любые две точки на линии и определяете наклон линии как Dy/Dx: изменение y, деленное на изменение x, или «подъем по ходу». Наклон физически показывает, насколько быстро движется график вверх. Самое замечательное в линиях то, что не имеет значения где вы выбираете две точки, наклон всегда будет одинаковым.
Наклон физически показывает, насколько быстро движется график вверх. Самое замечательное в линиях то, что не имеет значения где вы выбираете две точки, наклон всегда будет одинаковым.
Теперь, когда вам нужен наклон кривой, вы можете попытаться определить его таким же образом. Проблема в том, что наклон меняется от точки к точке. На приведенной ниже кривой я отметил три точки; и вы можете видеть, что если бы мы вычислили Dy/Dx от A до B, то получили бы отрицательный наклон, от B до C — положительный наклон, а от A до C — нулевой!
Поэтому бессмысленно говорить о «наклоне» этой кривой. С другой стороны, вы, конечно, можете говорить о наклоне на A : он идет вниз. Для количественной оценки этой идеи мы могли бы выбрать две точки, относительно близкие к точке A — одну чуть выше, а другую чуть ниже — и вычислить Dy/Dx в этих двух точках. Чем ближе эти точки к A (и друг к другу), тем точнее они будут описывать наклон в этой точке.
Итак, мы собираемся применить ограничение , , чтобы получить «бесконечно близко» к A. Мы будем говорить о Dy/Dx в точках, очень близких к A, и посмотрим, что происходит с этим отношением, когда Dx приближается к 0. Конечно, Dy также приближается к 0, и отношение этих двух крошечных число приближается к точному наклону в этой точке.
Поскольку теперь у нас есть дифференциальные интервалы (то есть они приближаются к 0), мы обозначаем их буквой d вместо D. Таким образом, мы имеем
Наклон задается дробью dy/dx, именно так вы всегда записывали производную. Но теперь вы видите, что это не просто произвольное обозначение; на самом деле это дробь, как кажется. Это также может помочь объяснить цепное правило: когда они говорят dz/dx = dz/dy * dy/dx, они на самом деле просто перемножают дроби!
Область под кривой
Я говорил о половине обозначений начального исчисления, то есть о постоянно всплывающем dx. Другая половина – это та часть, которая выглядит как вытянутая буква «S».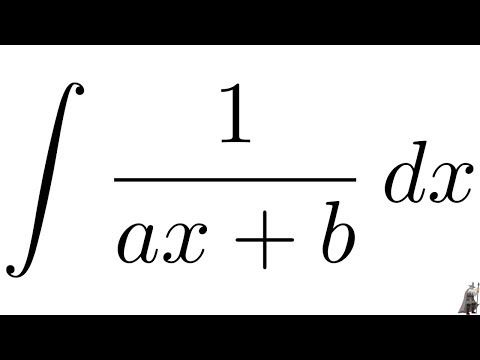 На самом деле так оно и есть: это сумма, как при сложении вещей. В частности, это означает, что вы добавляете фактически бесконечное количество вещей. Конечно, если бы «вещи» имели конечные значения, это всегда давало бы вам бесконечный ответ. Но все дело в наших дифференциальных значениях — каждое из них само по себе приблизительно равно нулю, — так что в сумме они могут составлять разумное конечное число. Всякий раз, когда вы видите, вы должны предполагать, что собираетесь сложить бесконечное количество вещей разного размера.
На самом деле так оно и есть: это сумма, как при сложении вещей. В частности, это означает, что вы добавляете фактически бесконечное количество вещей. Конечно, если бы «вещи» имели конечные значения, это всегда давало бы вам бесконечный ответ. Но все дело в наших дифференциальных значениях — каждое из них само по себе приблизительно равно нулю, — так что в сумме они могут составлять разумное конечное число. Всякий раз, когда вы видите, вы должны предполагать, что собираетесь сложить бесконечное количество вещей разного размера.Итак, для начала рассмотрим всеми любимую интегральную задачу — площадь под кривой. Ради интереса давайте посмотрим на ту же кривую, что и выше, и подумаем о площади под A-C.
Теперь, если бы это был прямоугольник, мы могли бы легко найти площадь: площадь равна произведению ширины на высоту, и все готово. Проблема в том, что чертова высота заставляет 90 519 менять 90 520 на нас, пока мы движемся от А к С.
Итак, чтобы свести к минимуму эту проблему — проблему постоянного изменения высоты — мы сосредоточимся на очень небольшой области графика, где высота относительно стабильна.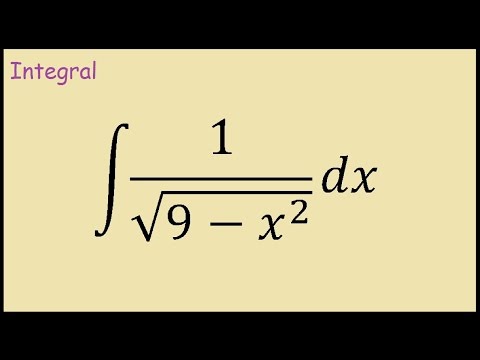 Начните с выбора точки x где-нибудь на нашем графике и другой точки сразу за ней: x+dx. Проведя вертикальные линии в этих двух точках, мы получим небольшую область, заштрихованную темным цветом на рисунке ниже.
Начните с выбора точки x где-нибудь на нашем графике и другой точки сразу за ней: x+dx. Проведя вертикальные линии в этих двух точках, мы получим небольшую область, заштрихованную темным цветом на рисунке ниже.
Если рассматривать эту область как прямоугольник, вычислить ее площадь будет несложно. Высота равна f(x), а ширина равна dx. Конечно, вы можете видеть, что область не является прямоугольником, а высота равна f(x) в крайнем левом углу. Но по мере того, как dx становится меньше — когда мы приближаем правую сторону к левой — изменение высоты становится менее значительным, и область больше напоминает прямоугольник. Когда dx приближается к нулю, это приближение становится совершенным: площадь заштрихованной области равна f(x)dx.
Итак, если площадь этой области равна f(x)dx, какова общая площадь под кривой между A и C? Ясно, что это сумма площадей всех областей между этими двумя точками. Именно это и означает интеграл: в данном случае он означает, что мы суммируем все эти маленькие области между А и С.
Конечно, вы это уже знали. Не понимая, что означает dx или вообще, вы знали, что интеграл даст вам площадь под кривой. Итак, позвольте мне перейти к проблеме, которую вы не может разобраться, не работая напрямую с dx.
Пример, где вам действительно нужно это знать
Каков объем конуса, изображенного ниже?Вам не разрешено искать его: все, что вы знаете, это то, что площадь круга равна pr 2 . Поскольку конус поднимается вверх под углом 45 o , вы можете видеть, что радиус окружности вверху равен h, высоте конуса. Но каков объем?
Общий способ решения подобных проблем — разбить объект на небольшие дифференциальные фрагменты. В этом случае кусок будет представлять собой круглый диск на расстоянии x от земли. Высота диска представляет собой дифференциал dx.
Как и в задаче о площади под кривой, здесь мы собираемся сделать ключевое приближение. Ширина диска неравномерна: сверху он шире, чем снизу. Но когда dx приближается к нулю, эта разница становится несущественной, поэтому мы будем рассматривать эту область как однородный круговой диск. В этот момент найти его объем не так уж сложно. Радиус равен x (опять же, из-за нашего угла 45 o радиус всегда равен расстоянию от земли). Значит, его площадь равна 9 пикселей.0294 2 . Его объем равен площади, умноженной на высоту, которая, как вы видите, равна px 2 dx. Как и следовало ожидать, объем близок к нулю, поскольку сам dx так близок к нулю.
Но когда dx приближается к нулю, эта разница становится несущественной, поэтому мы будем рассматривать эту область как однородный круговой диск. В этот момент найти его объем не так уж сложно. Радиус равен x (опять же, из-за нашего угла 45 o радиус всегда равен расстоянию от земли). Значит, его площадь равна 9 пикселей.0294 2 . Его объем равен площади, умноженной на высоту, которая, как вы видите, равна px 2 dx. Как и следовало ожидать, объем близок к нулю, поскольку сам dx так близок к нулю.
Общий объем — это бесконечное число этих дисков с нулевым объемом, которые добавляются по мере того, как мы поднимаемся по диску от x=0 внизу до x=h вверху. Итак, мы достигли точки, когда мы хотим суммировать бесконечное количество дифференциальных сумм, что и происходит, когда мы интегрируем. Уравнение px 2 dx, которое вы можете вычислить как ph 3 .
Готово!
Если вы следовали этому последнему примеру, вы получили из этой статьи именно то, что я хотел, чтобы вы получили. Целый ряд задач в математике и физике следуют тому же подходу:
Целый ряд задач в математике и физике следуют тому же подходу:- Разделите задачу на дифференциальные суммы
- Решите задачу для каждой дифференциальной суммы
- Интегрируйте, чтобы просуммировать все суммы разностей, и получите ваш ответ
Конечно, есть много вещей, которых у меня нет объяснил. Самый большой из них заключается в том, почему вы суммируете вещи, беря первообразную: может быть, я когда-нибудь напишу об этом еще одну статью. Но как только вы решите несколько подобных задач, вы обнаружите, что целый мир ранее неразрешимых проблем теперь находится в пределах вашей досягаемости.
| Важное примечание, добавленное теми, кто мудрее меня С тех пор, как я впервые опубликовал эту статью, два разных человека написали мне по электронной почте, чтобы сообщить мне, что настоящие математики этого не делают. Игра с dx способами, описанными в этой статье, по-видимому, является одним из тех хитрых трюков, которые используют физики, чтобы доставить математикам головную боль. Я даже не осознавал, что проповедую что-то нестандартное, потому что большая часть моего математического образования исходит из уроков физики. Итак, будьте осторожны. Если вы посещаете уроки физики, материал из этой статьи будет вам очень полезен. Если вы посещаете уроки математики, это может помочь вам обрести некоторую интуицию, но используйте ее осторожно: от вас могут ожидать более строгих методов. Теперь (надеюсь, вам это нравится так же, как и мне) другой человек написал в ответ на эту заметку: «Я заметил примечание внизу страницы о дифференциалах, в котором говорится, что настоящие математики не используют дифференциалы. , что они не являются «строгими».60-е доказали строгую формулировку дифференциалов — формулировку, в которой можно с полной уверенностью выполнять алгебраические операции с бесконечно малыми и бесконечно большими величинами. Это раздел математики, известный как «нестандартный анализ»; на самом деле его используют многие математики, потому что доказательства проще, а теоремы менее многословны в «нестандартной» формулировке. |
Домашняя страница справки Гэри и Кенни Фелдер по математике и физике
www.felderbooks.com/papers Отправить комментарий или вопрос автору
Степенное правило для интегралов
Степенное правило для интегралов позволяет нам находить неопределенные (а позже и определенные) интегралы множества функций, таких как многочлены, функции, содержащие корни, и даже некоторые рациональные функции. Если вы можете записать это с показателями степени, вы, вероятно, сможете применить правило мощности.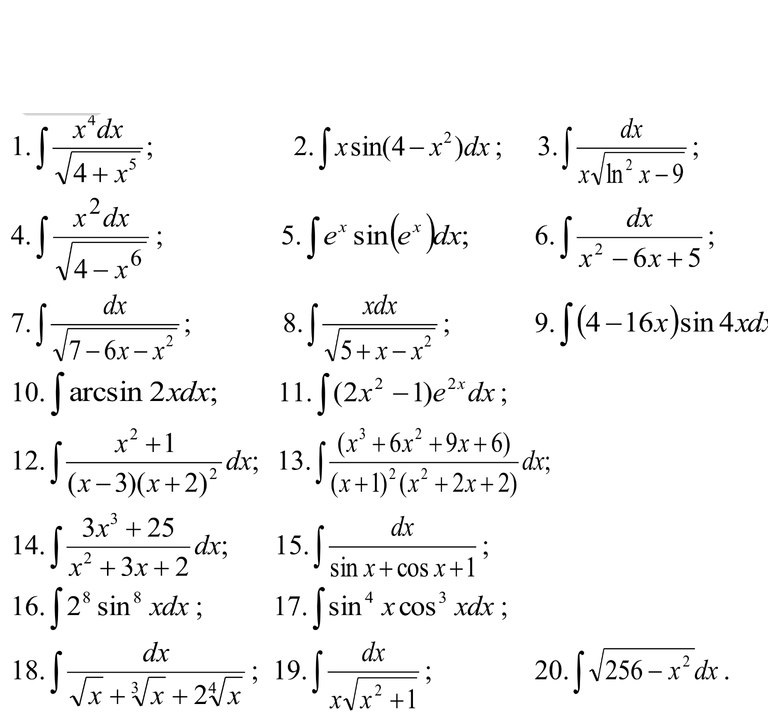 92}{2} – 5x + С}\)
92}{2} – 5x + С}\)
Интегралы радикальных функций (функции с корнями)
Чтобы применить это правило к этому типу функций, вы должны помнить одну очень важную идею из алгебры.
Итак, если мы можем написать функцию с использованием показателей степени, то мы, вероятно, сможем применить степенное правило.
Пример
Найти: \(\displaystyle\int \sqrt{x} + 4 \text{dx}\)
Прежде чем применять какие-либо вычисления, вы можете переписать интеграл, используя приведенное выше правило. Таким образом, у нас есть показатели степени, и мы можем применить правило степени. 9{\ гидроразрыва {7} {4}} + C} \ конец {выравнивание} \)
Вы заметили, что большая часть работы была связана с алгеброй? Это верно для большинства математических задач. Расчетная часть проста, в то время как алгебра требует от вас быть очень осторожным и составляет большую часть проблемы.
Интегралы с отрицательными показателями
Еще одно старое алгебраическое правило позволит нам использовать правило степени, чтобы найти еще больше интегралов. 2} \text{dx}\)
94} + \dfrac{1}{4x} + C}\end{align}\)
2} \text{dx}\)
94} + \dfrac{1}{4x} + C}\end{align}\)
Обратите внимание, что это работает, только если показатель степени не равен –1. Если бы вы попытались применить здесь правило мощности, вы бы в конечном итоге поделили на ноль. Существует другое правило для работы с такими функциями, как \(\dfrac{1}{x}\).
реклама
Резюме
Как вы видели, правило степени можно использовать для нахождения простых интегралов, а также для нахождения гораздо более сложных интегралов. Общая стратегия всегда одна и та же — если у вас еще нет показателей степени, посмотрите, сможете ли вы написать функцию, используя показатели степени. Затем примените правило мощности и упростите.
Ах да, и не забудьте добавить C!
Нужно больше практики?
Пакет задач "Power Rule for Integration" содержит советы и рекомендации по решению рабочих задач, а также множество практических упражнений с полными пошаговыми решениями.
СКАЧАТЬ
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем дополнительные учебные пособия, руководства по калькуляторам и наборы задач.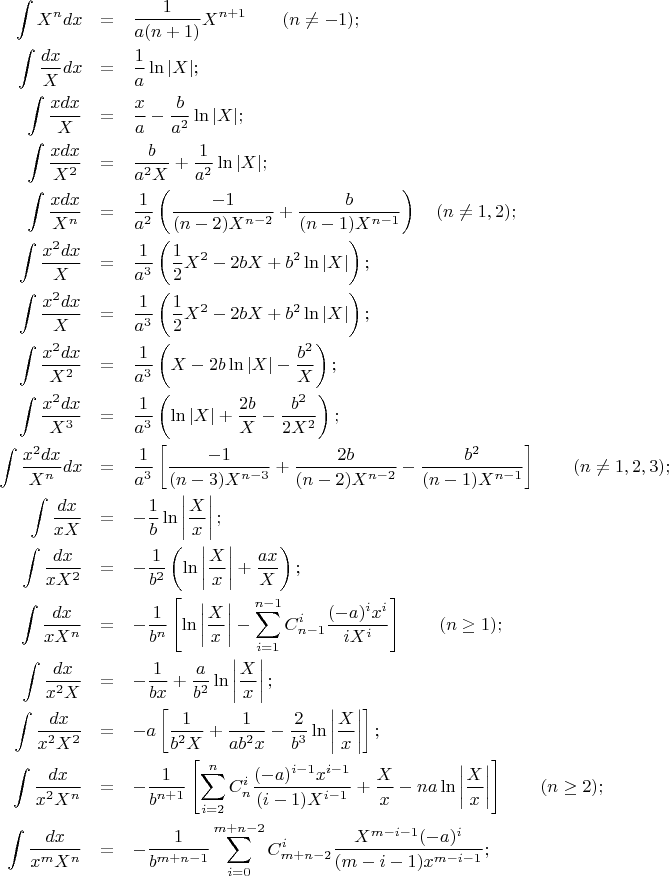


 Давайте начнем называть их дельтами,
потому что разница между двумя точками часто
называется дельтой этих значений.
Давайте начнем называть их дельтами,
потому что разница между двумя точками часто
называется дельтой этих значений. Мы начали с дифференциала (т.е. $dy=f'(x)\,dx$) и сразу после этого с неопределенного интеграла. С тех пор я пытаюсь разобраться в $dx$, когда он является частью неопределенного интеграла (т. е. $\int f(x) \, \boldsymbol{dx}$). Я знаю, что на этот вопрос уже есть миллион ответов, но все они относятся к определенному интегралу, а те, что касаются неопределенных интегралов, говорят только такие вещи, как «это просто синтаксический прием, чтобы сказать вам переменную, которую нужно дифференцировать по отношению к или переменная интегрирования» (Ihf, 2012, Интернет). Мне не нравится этот ответ, особенно потому, что меня учили, что для двух функций $f(x)$, $g(x)$ и первообразной их произведения $\int f(x)g(x)\,dx $, если бы я присвоил $f(x)$ $u$ и $g(x)\,dx$ $dv$ для интегрирования по частям, то мне пришлось бы интегрировать $dv$, чтобы найти $ в$. Это имеет смысл только в том случае, если $dx$ означает что-то само по себе, а не является просто причудливой нотацией, в противном случае мы получили бы что-то вроде следующего: $$\int g(x)\,dx\space dx$$
Мы начали с дифференциала (т.е. $dy=f'(x)\,dx$) и сразу после этого с неопределенного интеграла. С тех пор я пытаюсь разобраться в $dx$, когда он является частью неопределенного интеграла (т. е. $\int f(x) \, \boldsymbol{dx}$). Я знаю, что на этот вопрос уже есть миллион ответов, но все они относятся к определенному интегралу, а те, что касаются неопределенных интегралов, говорят только такие вещи, как «это просто синтаксический прием, чтобы сказать вам переменную, которую нужно дифференцировать по отношению к или переменная интегрирования» (Ihf, 2012, Интернет). Мне не нравится этот ответ, особенно потому, что меня учили, что для двух функций $f(x)$, $g(x)$ и первообразной их произведения $\int f(x)g(x)\,dx $, если бы я присвоил $f(x)$ $u$ и $g(x)\,dx$ $dv$ для интегрирования по частям, то мне пришлось бы интегрировать $dv$, чтобы найти $ в$. Это имеет смысл только в том случае, если $dx$ означает что-то само по себе, а не является просто причудливой нотацией, в противном случае мы получили бы что-то вроде следующего: $$\int g(x)\,dx\space dx$$ Мои рассуждения таковы:
Мои рассуждения таковы: (2012, 9 мая). Что означает $dx$? . Математический стек Exchange. https://math.stackexchange.com/q/143262
(2012, 9 мая). Что означает $dx$? . Математический стек Exchange. https://math.stackexchange.com/q/143262

 Некоторые люди прошли и написали целые вводные тексты по расчету, в которых полностью отказываются от ограничений в пользу гораздо более простого dx, хотя им уделяется очень мало внимания. В использовании дифференциалов нет ничего постыдного." Отдавая должное моим прежним критикам, я должен отметить, что первая девушка, написавшая мне, сказала мне, что я использую "нестандартный анализ", что, как я думал, она имела в виду как критику.
Некоторые люди прошли и написали целые вводные тексты по расчету, в которых полностью отказываются от ограничений в пользу гораздо более простого dx, хотя им уделяется очень мало внимания. В использовании дифференциалов нет ничего постыдного." Отдавая должное моим прежним критикам, я должен отметить, что первая девушка, написавшая мне, сказала мне, что я использую "нестандартный анализ", что, как я думал, она имела в виду как критику.