Лекция 2 — Основы цифровых измерений
С помощью цифровых схем можно производить различные вычисления. Поэтому существует необходимость представлять десятичные числа в виде комбинации 0 и 1. Представление числа только двумя знаками называется бинарным представлением.
Коды, которые используют только два знака, называются бинарными кодами.
Существует множество бинарных кодов. Но на практике применяются только некоторые из них. Бинарные коды имеют регламентированную рядность. Каждая десятичная цифра в определенном коде представляется определенным количеством бинарных разрядов. Бинарный разряд может принимать значение 0 или 1. Бинарный разряд, или базовая единица данных называется битом (от англ.: binary digit — двоичная цифра).
Бит означает один бинарный разряд. Он может быть равен 0 или 1.
2. Структура двоичной системы счисления
Все используемые системы счисления являются позиционными системами счисления. В позиционной системе счисления позиция цифры однозначно связана со значением числа посредством особого фактора увеличения в виде степенного числа.
В десятичной системе счисления каждый разряд числа умножается на 10 в соответствующей степени. Чтобы посчитать от 0 до 9 нужен ноль и девять цифр в колонке единиц. Число десять записывается как 1 в колонке десятков и 0 в колонке единиц.
Если в распоряжении имеются только цифры 0 и 1, то каждый разряд числа умножается на степень числа два.
3. Перевод двоичных чисел в десятичную систему счисления
Перевести двоичное число в десятичное можно следующим образом. Разряды числа, в которых находится 0, не представляют интереса, важны те, где расположена единица.
101102 = 1 · 24 + 0 · 23 + 1 · 22 + 1 · 21 + 0 · 20 = 16 + 0 + 4 + 2 + 0 = 2210.
| 24 = 16 | 23 = 8 | 22 = 4 | 21 = 2 | 20 = 1 |
| 1 | 0 | 1 | 1 | 0 |
4.
Перевод десятичных чисел в двоичную систему счисления
Рассмотрим, как переводится десятичное число в двоичное на примере десятичного числа 900. При преобразовании определим прежде всего единицу с наибольшим значением, а затем единицы с меньшими значениями. Единица со значением 210 = 1024 не подходит, так как 1024 > 900. Следовательно, наибольшая единица будет соответствовать разряду 29 = 512. Вычитаем из 900 число 512 и получаем: 900 — 512 = 388. Подбираем следующий подходящий разряд двоичного числа для десятичного числа 388. Это 28 = 256. Теперь остаток: 388 — 256 = 132. Значит берем 27 = 128. Проводим операцию вычитания: 132 — 128 = 4. Ясно, что 4 = 2
90010 = 512 + 256 + 128 + 4 = 1 · 29 + 1 · 28 + 1 · 27 + 0 · 26 + 0 · 25 + 0 · 24 + 0 · 23 + 1 · 22 + 0 · 21 + 0 · 20 = 11100001002.
2n 29 = 512 28 = 256 27 = 128 26 = 64 25 = 32 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 900 1 1 1 0 0 0 0 1 0 0
5. Вещественные двоичные числа
Двоичные числа, так же как и десятичные, могут быть с дробной частью. Дробная часть пишется после запятой. Первому разряду справа от запятой соответствует 2-1, второму — 2-2 и т.д. Двоичные числа с запятой пересчитывают в десятичные таким же способом, как и двоичные числа без запятой. Можно перевести и дробные десятичные числа в двоичную систему. Например:
22,687510 = 16 + 4 + 2 + 0,5 + 0,125 + 0,0625 = 1 · 24 + 0 · 23 + 1 · 22 + 1 · 21 + 0 · 20 + 1 · 2-1 + 0 · 2-2 + 1 · 2-3 + 1 · 2-4 = 10110,10112.
2n 24 = 16 23 = 8 22 = 4 21 = 2 20 = 1 , 2-1 = 0,5 2-2 = 0,25 2-3 = 0,125 2-4 = 0,0625 22,6875 1 0 1 1 0 , 1 0 1 1
Может быть такая ситуация, что десятичное число с запятой не может быть преобразовано в двоичное число без остатка. В этом случае надо решить, сколько разрядов после запятой следует оставить и после этого закончить перевод числа.
6. Сложение двоичных чисел
Двоичные числа складываются так же, как и десятичные, то есть по разрядам. Сложение начинается с меньших разрядов. При этом действуют следующие правила:
0 + 0 = 0,
0 + 1 = 1,
1 + 0 = 1,
1 + 1 = 10,
1 + 1 + 1 = 11.
За одно действие складываются только два числа. При сложении нескольких чисел сначала складывают первое и второе число, затем прибавляют к результату третье и т.д.
Оба числа пишут поразрядно друг над другом. В случае переноса разряда единица записывается в следующий разряд и учитывается при сложении цифр этого разряда. Иными словами при переносе разряда приходится складывать три двоичных числа.
| 1 | 1 | ||||
| + | 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 0 | |
Для проверки правильности вычислений можно преобразовать двоичные числа в десятичные, провести операцию с ними, а затем перевести результат в двоичную систему счисления.
7. Вычитание двоичных чисел
Непосредственное вычитание
При вычитании действуют следующие правила:
0 — 0 = 0,
1 — 0 = 1,
1 — 1 = 0.
Отрицательный результат операции 0 — 1 пока не рассматриваем.
При вычитании вычитаемое число пишется под уменьшаемым. Вычитание начинается с наименьшего разряда.
| — | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | ||
Здесь не возникло никаких трудностей, так как не было операции 0 — 1. Чтобы проводить такую операции, нужно заимствовать единицу из соседнего старшего разряда. Тогда получаем: 10 — 1 = 1. После чего в старшем разряде получается 0.
Пример:
| 10 | |||||
| — | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | |||
| 1 | 0 | 1 | 0 | 0 | |
Вычитание в дополнительном коде
В компьютерной технике вычитание производится добавлением дополнения к вычитаемому числу. Рассмотрим вычитание с дополнением на примере десятичной системы счисления. Допустим, что автомобиль имеет пятиразрядный спидометр. который в данный момент показывает, что автомобиль уже проехал 95 000 км. Если он проедет еще 15 000 км, то спидометр покажет 10 000 км, так как у него нет шестого разряда, чтобы показать число 110 000. Число 10 000 получается, если из 95 000 вычесть 85 000. Иными словами, разность 95 000 — 85 000 = 10 000 равнозначна при пяти разрядах сумме 95 000 + 15 000 = 10 000.
В двоичной системе вычитание в дополнительном коде производится аналогичным образом. Например, при четырех разрядах надо найти разность 1111 — 111 = 1000 (15 — 7 = 8), это равносильно нахождению суммы 1111 + 1001 = 11000 (15 + 9 = 24), так как пятого разряда нет и мы получим: 1111 + 1001 = 1000 (15 + 9 = 8). Как определить число 1001 (9)? Для того чтобы определить дополнение вычитаемого числа, нужно знать количество разрядов, с которым предстоит работать. В нашем случае их 4 (в компьютерной технике число разрядов, с которыми может работать компьютер, тоже известно заранее). Вычитаемое число 111 в случае четырех разрядов выглядит так: 0111. Проинвертировав это число (то есть поменяв нули и единицы местами), получаем 1000. Это число на 1 меньше искомого дополнения 1001. Следовательно, чтобы найти дополнение нужно выполнить инвертирование вычитаемого числа и затем добавить к нему 1.
В двоичной системе дополнение и вычитаемое число дополняют друг друга при n-разрядном представлении до 2n.
Например, в нашем случае: 1001 + 111 = 10000 (9 + 7 = 16 = 24).
8. Отрицательные двоичные числа
Если вычитаемое число больше, чем уменьшаемое, то в результате получится отрицательное число. Например, 27 — 47 = -20. В двоичной системе счисления этому примеру соответствует разность 11011 — 101111. Проведем вычитание в дополнительном коде. Инвертируем 101111, получаем: 010000. Прибавляем к результату единицу: 01000 + 00001 = 010001. Полученное дополнение складываем с уменьшаемым, приписав уменьшаемому 0 в старшем разряде: 011011 + 010001 = 101100. Если в расчетах используется 6 разрядов, то получится 101100. Дополнительный седьмой разряд будет нужен для определения, является число положительным или отрицательным. Если уменьшаемое число больше вычитаемого, то в седьмом разряде будет 0 (разность положительная), иначе — 1. Таким образом можно определять с помощью седьмого дополнительного разряда, является число положительным (тогда в этом разряде будет 0) или отрицательным (в дополнительном разряде находится 1).
Однако полученное число (1)101100 в десятичной системе счисления равно 44, а вовсе не -20. Но мы-то теперь знаем, что это отрицательное число, а не положительное (каковым является 44), так как в дополнительном разряде расположена 1. Следовательно, его величина определяется иначе. Для этого нужно провести инверсию числа: 010011. А затем добавить к нему единицу: 010011 + 000001 = 010100 (20). Полученный результат как раз и характеризует абсолютную величину отрицательного числа (1)1011002 = -2010 (то есть его модуль).
Цифровая техника всегда имеет известную разрядность (например, 8, 16, 32 или 64 разряда). Поэтому наибольший разряд всегда известен и может рассматриваться как дополнительный знаковый разряд.
Двоичные числа. Язык Си — руководство для начинающих
Двоичные числа. Язык Си — руководство для начинающихВикиЧтение
Язык Си — руководство для начинающих
Прата Стивен
Содержание
Двоичные числа
В основе способа, который мы обычно используем для записи чисел, лежит число 10.
Может быть, вы когда-то слышали, что число 3652 имеет 3 в позиции тысяч, 6 в позиции сотен, 5 в позиции десятков и 2 в позиции единиц. Поэтому мы можем представить число 3652 в виде
3 ? 1000 + 6 ? 100 + 5 ? 10 + 2 ? 1
Однако 1000 — это 10 в кубе, 100 — десять в квадрате, 10 — десять в первой степени, а 1, как принято в математике, 10 (или любое положительное число) в нулевой степени. Следовательно, мы можем записать 3652 как
3 ? 103 + 6 ? 102 + 5 ? 101 + 2 ? 100
Так как наша система записи чисел основывается на степенях десяти, мы можем сказать, что 3652 записывается по основанию 10.
Вероятно, мы создали такую систему потому, что имеем 10 пальцев на руках. Компьютер же, в каком-то смысле, имеет только два «пальца», поэтому его можно установить только в состояние 0 или 1 (выключено или включено). Это делает систему с основанием 2 естественной для компьютера. Как она работает? Используются степени 2 вместо степеней 10.
Например, такое двоичное число, как 1101, означало бы
1 ? 23 + 1 ? 22 + 0 ? 21 + 1 ? 20
В десятичной записи оно становится равным
1 ? 8 + 1 ? 4 + 0 ? 2 + 1 ? 1 = 13
Система с основанием 2 (или «двоичная») позволяет выразите любое число (если у пас достаточно разрядов в двоичной системе, как комбинацию единиц и нулей. Это очень «приятно» для компьютера, особенно если учесть, что у него нет иного выбора. Посмотрим, как работает такой механизм для 1-байтного целого числа.
Можно считать его 8 разрядов пронумерованными слева направо от 7 до 0. Такие «номера разрядов» соответствуют степеням 2. Представьте себе, что байт выглядит примерно так:
Здесь 128 — это 2 в 7-и степени и т. д. Самое большое число, которое может содержать этот байт, имеет во всех разрядах 1 : 11111111. Значение такого двоичного числа
128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
Самое маленькое двоичное число было бы равно 00000000, или просто 0.
Байт может содержать числа от 0 до 255 для всех 256 возможных значений.
14.4.1. Введение в двоичные деревья
14.4.1. Введение в двоичные деревья Массивы являются почти простейшим видом структурированных данных. Их просто понимать и использовать. Хотя у них есть недостаток, заключающийся в том, что их размер фиксируется во время компиляции. Таким образом, если у вас больше данных,
Предикаты: числа
Предикаты: числа В XPath числа хранятся в формате числа с плавающей точкой двойной точности. (Технически все числа XPath хранятся в 64-разрядном формате IEEE числа с плавающей точкой двойной точности, floating-point double.) Все числа хранятся как числа с двойной точностью — даже целые
Числа XPath
Числа XPath
В XPath числа хранятся в формате чисел с плавающей точкой двойной точности.
В соответствии с формальным определением, числа XPath должны храниться в формате 64-разрядных чисел с плавающей точкой двойной точности IEEE 754, и все числа хранятся как числа с плавающей точкой
Абстрактные базы как двоичные интерфейсы
Абстрактные базы как двоичные интерфейсы Оказывается, применение техники разделения интерфейса и реализации может решить и проблемы совместимости транслятора/компоновщика C++. При этом, однако, определение класса интерфейса должно принять несколько иную форму. Как
1. Числа
1. Числа А сейчас, когда вы всё установили, давайте напишем программу! Откройте ваш любимый текстовый редактор и наберите на клавиатуре следующее:puts 1+2Сохраните вашу программу (да, это программа!) под именем calc.rb (.rb – это то, что мы обычно пишем в конце имени программы,
3.
2.1. Двоичные дроби3.2.1. Двоичные дроби Для начала — немного математики. В школе мы проходим два вида дробей простые и десятичные. Десятичные дроби, по сути дела, представляют собой разложение числа по степеням десяти. Так, запись 13,6704 означает число, равное 1?101 + 3?100 + 6?10-1 + 7?10-2 + 0?10-3 + 4?10-4. Но
3.1.6. Двоичные форматы файлов
3.1.6. Двоичные форматы файлов Если в операционной системе применяются двоичные форматы для важных данных (таких как учетные записи пользователей), вполне вероятно, что традиции использования читабельных текстовых форматов для приложений не сформируются. Более подробно
3.1.6. Двоичные форматы файлов
3.1.6. Двоичные форматы файлов
Если в операционной системе применяются двоичные форматы для важных данных (таких как учетные записи пользователей), вполне вероятно, что традиции использования читабельных текстовых форматов для приложений не сформируются.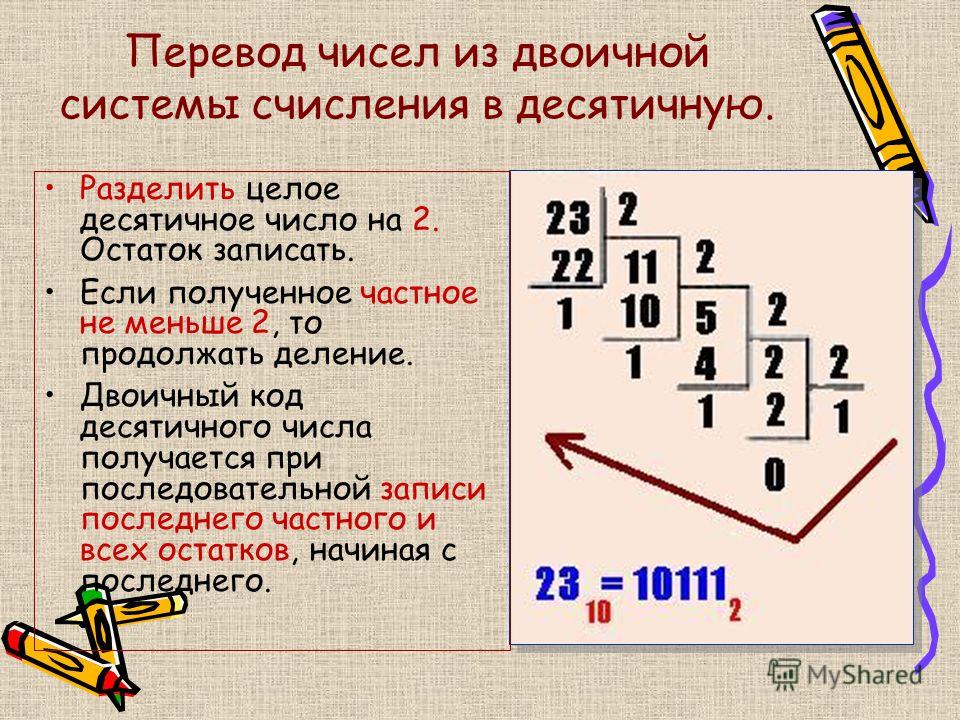
Более подробно о
5.11. Комплексные числа
5.11. Комплексные числа Стандартная библиотека complex предназначена для работы с комплексными числами в Ruby. Большая ее часть не требует пояснений.Для создания комплексного числа применяется следующая несколько необычная нотация:z = Complex(3,5) # 3+5iНеобычно в ней то, что имя метода
Глава 3 Числа
Глава 3 Числа 3.0. Введение Даже если вы не занимаетесь написанием научных или инженерных приложений, вам все равно придется работать с числами. Эта глава содержит решения проблем, часто возникающих при работе с числовыми типами С++.Некоторые из рецептов содержат методики
Простые числа
Простые числа ??** Головоломка 16. Чемпион головоломок.На мой взгляд, наиболее замечательная арифметическая головоломка, над которой мне пришлось особенно долго работать и которая дала мне возможность получить некоторые удовлетворительные результаты, — это, конечно,
ПРИЛОЖЕНИЕ Ж.
ДВОИЧНЫЕ И ДРУГИЕ ЧИСЛА ПРИЛОЖЕНИЕ Ж. ДВОИЧНЫЕ И ДРУГИЕ ЧИСЛА Двоичные числа В основе способа, который мы обычно используем для записи чисел, лежит число 10. Может быть, вы когда-то слышали, что число 3652 имеет 3 в позиции тысяч, 6 в позиции сотен, 5 в позиции десятков и 2 в позиции единиц. Поэтому мы
Двоичные числа с плавающей точкой
Двоичные числа с плавающей точкой Числа с плавающей точкой хранятся в памяти в виде двух частей: двоичной дроби и двоичного порядка. Посмотрим, как это делается. Двоичные дроби Обычную дробь .324 можно представить в виде3/10 + 2/100 + 4/1000,где знаменатели — увеличивающиеся
9.3. Двоичные справочники: добавление и удаление элемента
9.3. Двоичные справочники: добавление и удаление элемента
Если мы имеем дело с динамически изменяемым множеством элементов данных, то нам может понадобиться внести в него новый элемент или удалить из него один из старых.
В связи с этим набор основных операций, выполняемых
Двоичные числа: Введение
Двоичные числа: введениеДвоичная система счисления, используемая для кодирования информации с помощью нулей и единиц, лежит в основе каждого цифрового компьютера.
Что такое двоичный код?
Двоичная система счисления — это система счисления с основанием 2, в которой используются только две цифры (0 и 1). Это система, используемая в основе каждого цифрового компьютера, позволяющая им кодировать информацию, выполнять арифметические операции и выполнять логические процессы управления.
Использование двух цифр вместо, скажем, привычных десяти цифр, используемых в десятичных системах (от 0 до 9), позволяет легко реализовать аппаратное обеспечение с помощью простых состояний схемы «включено» или «выключено» или логических вентилей. Это основа всех цифровых систем.
Понимание двоичных чисел
Чтобы понять двоичные значения, представьте, что каждая цифра (или «бит») двоичной записи представляет собой возрастающую степень числа 2, где крайняя правая цифра представляет 2 0 , а следующая представляет 2 1 , затем 2 2 и так далее.
Для каждого бита 1 или 0 означает, соответствует ли значение возрастающей степени двух суммированию общего числа.
| 2 нет | 2 3 | 2 2 | 2 1 | 2 0 |
| Десятичный | 8 | 4 | 2 | 1 |
В качестве наглядного примера на рис. 2 показано преобразование двоичного значения 1100 в десятичное значение 12. Синие числа представляют двоичное представление, красные числа представляют возрастающую степень числа 2, а зеленые числа представляют десятичные значения.
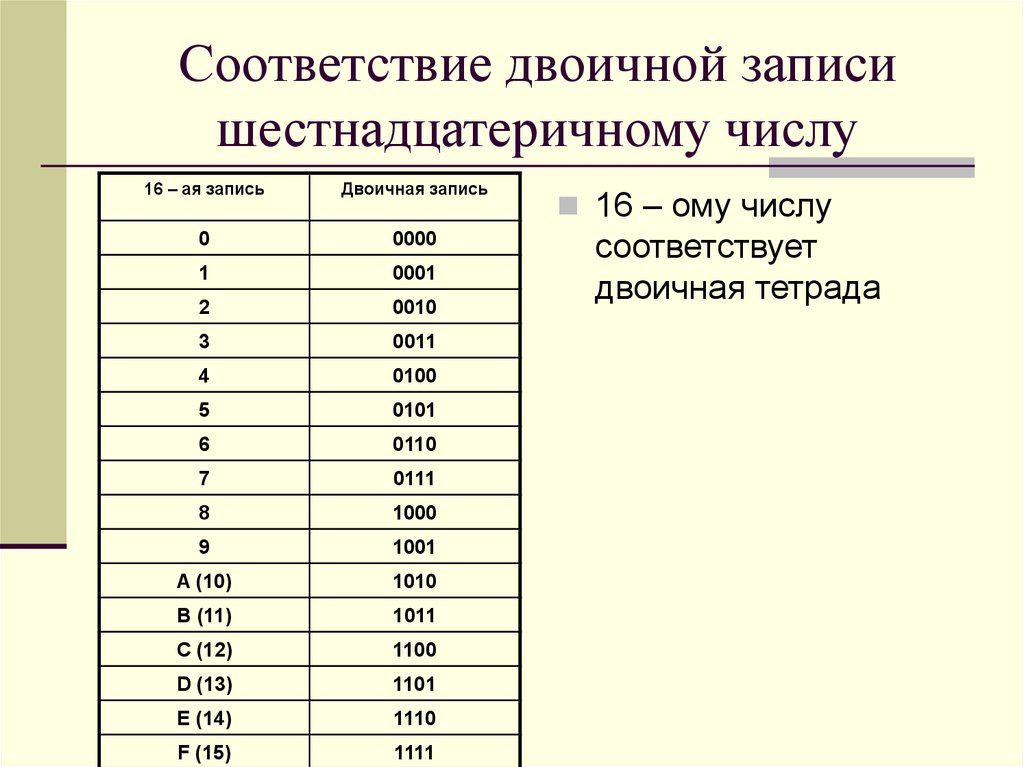
Двоичные значения часто представляются с различной длиной «бит» или размером «слов». В приведенном выше примере значение представлено в 4 битах, называемых «полубайтами». Это означает, что может быть представлено значение от 0 до 15. 8-битные значения, называемые «байтами», могут представлять значения от 0 до 255. На рисунке 3 показано 4-битное двоичное представление для каждого десятичного значения от 0 до 15.
| Десятичный | Двоичный |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
Двоичная таблица 4-битных значений от 0 до 15.Подробнее:
Чтобы узнать больше о вычислительном оборудовании, почему бы не ознакомиться с нашей следующей заметкой: Двоичное сложение с полными сумматорами.
Вам также может понравиться:
Примечание №7
Арифметико-логические единицы (ALU): введение
Примечание №6
Двоичное вычитание с дополнением до двух
Примечание №1
Дух творца: от кухонного стола до микростартапа
Ознакомьтесь с нашими электронными наборами для самостоятельной сборки:
Устаревший продукт
STEM-X1: 4-битный сумматор/вычитатель (DIY Soldering Kit Edition5) 9017
Устаревший продукт
S1-MU: Блок памяти
Устаревший продукт
S1-AU: Арифметический модуль
Все, что вам нужно знать о Binary | Брэндон Скеррит | Заметки по информатике
Фото Антуана Дотри на Unsplash Система счисления — это система чисел, используемая для представления количества объектов.
В англоязычном мире мы используем систему счисления, называемую основанием 10. У нас есть 10 чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, и когда мы хотим посчитать после 9, мы добавляем 1 и 0 вместе, чтобы сделать 10, а затем мы повторяем.
Но мы можем иметь столько чисел, сколько захотим, мы можем иметь от 0 до 8 или от 0 до 1, о чем мы и поговорим.
Двоичная система счисления имеет только 2 числа, 0 и 1. Мы можем считать любое число в двоичной системе счисления. Чтобы сделать двоичные числа более читабельными, вот краткий перевод двоичных чисел в десятичные (десятичные) числа.
0 равно 0, а 1 равно 1. Чтобы получить число 2, пишем «10», потому что физически невозможно написать что-либо > 1, приходится начинать заново в новом столбце. Очень похоже на то, как мы не можем записать 11 как одно число (если только вы не считаете в базовых системах более 10).
Двоичное значение часто используется в логике, 0 представляет False или Off, а 1 представляет True или On.
Относительно легко преобразовать двоичное число в десятичное.
Есть два популярных метода.
Запишите десятичное число и непрерывно делите на 2, чтобы получить результат, а в остатке либо «1», либо «0», пока окончательный результат не будет равен 0.
Это мой любимый метод, но для этого вам нужно знать свои степени двойки.
Степени двойки очень важны в информатике. Двоичный код представлен в виде 2 чисел, поэтому, если у вас есть 3 цепи, у вас будет 2³ числа, от 0 до 7.
Степени двойки:
2, 4, 8, 16, 32, 64, 128, 256 , 512, 1024, 2048, 4096, 8192.
И чтобы получить нечетное число, мы добавляем 1 к списку, так что список чисел, которые нам нужно знать, становится: 1, 2, 4, 8, 16, 32, 64 , 128, 256, 512, 1024, 2048, 4096, 8192.
Хорошо, допустим, мы хотим представить 15 в виде двоичного числа. Сначала нам нужно разделить 15, чтобы его можно было составить из степеней 2 + числа 1. Ближайшая степень двойки, которая меньше 15, равна 8, поэтому мы будем использовать ее. 8 + 4 равно 12. 8 + 4 + 2 равно 14, так что мы почти у цели! Теперь мы просто добавляем 1.
15, представленное как степень двойки, равно 8 + 4 + 2 + 1.
Теперь мы это знаем, мы можем просто преобразовать это.
Двоичный график в степени двойки выглядит следующим образом.
Если число использует 8, поставьте 1 в двоичном поле под ним, чтобы обозначить, что оно использует 8. Однако я предпочитаю использовать этот метод:
И тогда обычно нам нужно было бы инвертировать двоичные числа, но в этом случае, поскольку это всего лишь 1, нам не нужно инвертировать. Если мы не поменяем их местами, то получим неправильное двоичное число, поскольку двоичное число читается с наивысшим порядком слева, а не с низшим. Как и в «10», 1 на целую позицию выше, чем 0; то же самое относится и к бинарному.
Вы можете преобразовать двоичное число в десятичное обратным методом.
Давайте сначала рассмотрим сложение в десятичном виде.
23 + 11
Сначала мы прибавляем 3 + 1, что равно 4. Затем мы прибавляем 2 + 1, что равно 3. Таким образом, ответ равен 34.
Прибавляем справа налево.
Двоичное сложение работает так же.
Мы начнем с добавления одного бита (двоичной цифры).
0 + 0 = 1
и
0 + 1 = 1
и
1 + 1 = 10
1 + 1 переносит нас в следующий столбец.
Попробуйте сами:
111 + 110 = ???
Кроме того, почти все операторы работают так же, как и с двоичными, и с десятичными числами.
Мы можем представить двоичное число, применив к нему «знак».
В двоичном формате числа могут быть 4-битными, 8-битными, 16-битными, 32-битными и так далее. Если у нас есть 8-битное число, оно будет состоять из 8 цифр.
Итак, скажем, у нас есть число 1 в 8-битном двоичном формате, которое будет представлено как: 00000001 чтобы преобразовать это значение в отрицательное, мы добавляем 1 перед ним 10000001
Хотя это иногда вызывает проблемы. Учитывая число 0 в 8-битном двоичном формате: 00000000, мы можем сделать его отрицательным, добавив 1 перед ним.
10000000 Но -0, что это? Ничего. Это невозможно. И вот откуда эта проблема.
Мы можем сделать двоичное число отрицательным, применив к нему дополнение до двух без необходимости подписывать его.
Дополнение до двух — очень простой алгоритм:
- инвертировать все цифры, чтобы 0 стал 1, а 1 стал 0
- добавить +1 к числу
, и это сделает его отрицательным!
Таким образом, учитывая число 15, которое равно 1111, в 8-битном двоичном формате оно будет: 00001111 Итак, чтобы сделать это отрицательным, мы инвертируем все цифры: 11110000, затем мы добавляем 1 к концу 11110001, и теперь это представляет -15 ! Как креативно и круто!
Допустим, у нас есть 2 числа, -3 и -5. В двоичном формате это: 11, 101, и мы хотим сложить их вместе.
Но на этот раз мы можем игнорировать любые переносы, которые идут не в конце.
Итак, мы используем наибольшую степень двойки, которая может поместить в нее и 5, и 3, то есть 8.