Построение графика сложной функции: Построение графиков сложных функций

Исследовательская работа по теме: Построение графиков сложных функций на основе свойства монотонности

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Исследовательская работа по теме:

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА ПО ТЕМЕ:

2. Актуальность выбранной темы

АКТУАЛЬНОСТЬ ВЫБРАННОЙ ТЕМЫ
Умение читать графики функций, т.е. по графику
описывать
свойства
функции
(промежутки
монотонности, экстремальные значения, интервалы
знакопостоянства и т. д.), необходимо и врачу
(кардиограмма),
и
экономисту
(график
производительности труда, курсы валют), метеорологу
(суточное изменение температуры) и другим
специалистам.
Поэтому
в
огромном
море
зависимостей величин необходимо
хорошо
ориентироваться.
Проблема:
Зачастую методами математического анализа в курсе школы
невозможно исследовать функцию и построить график.
Цель:
познакомиться с другими методами исследования функций и
построения графика с тем, чтобы применить их при решении
задач с параметрами;
научиться моделировать условия нахождения значения параметра
для различных математических моделей.
Объект исследования:
Многообразие задач, содержащих параметр.
Предмет исследования:
Сложные функции.
Задачи исследования:
Изучить метод построения графиков сложных функций на основе
свойства монотонности функций.
Применить данный метод при моделировании задач с
параметрами.
Научиться ставить вопросы, имея построенный график сложной
функции (картинку, рисунок).
В курсе алгебры 7-9 классов мы изучали
алгебраические
функции,
т.е.
функции,
заданные аналитическими выражениями, в
записи
которых
использовались
алгебраические операции над числами и
переменной
(сложение,
вычитание,
умножение, возведение в степень, извлечение
квадратного корня). К концу 9 класса у нас
формируется
цепочка
следующих
представлений:
При этом десятиклассник
оказывается
в
двусмысленной ситуации:
в 9 классе он научился
строить график функции и по
графику
перечислять
её
свойства; теперь же от него
требуется
исследовать
функцию и затем строить
график.
А
в
старшей
школе
при
изучении
тригонометрических функций, логарифмических
функций,
показательных и алгебраических
функций высших степеней
формулировка
«исследуйте функцию и постройте её график»
предполагает несколько другой подход:
Сложные функции можно исследовать
разными методами.
Один из методов: построение графиков
сложных
функций
на
основе
монотонности. Математические модели
реальных ситуаций часто бывают
связаны с функциями других классов,
которые
называют
сложными.
Рассмотрим сложную функцию y = f(v(x)).
Напомним, что если внутренняя функция
v(x) и внешняя функция f(v) – монотонны,
то сложная функция y = f(v(x)) также
монотонна.
Пусть, например, v(x) и f(x) – убывают.
Тогда при x1 < x2
v1 = f(x1) > v2 = f(x2).
Неравенство v1 > v2 влечёт за собой неравенство
f(v1) < f(v2), т.е.
f(v(x1)) < f(v(x2)).
Итак, большему значению аргумента (x1 < x2)
соответствует большее значение сложной
функции.
Следовательно, по определению, она является
возрастающей.
Конечно, говоря о монотонности функции, всегда
надо указывать соответствующее множество из
области определения.
АНАЛИТИЧЕСКИЙ АППАРАТ:
найдём производную.
НА ОСНОВЕ МЕТОДА МОНОТОННОСТИ:
D(y):R
Чётная
– внутренняя функция,
— внешняя.
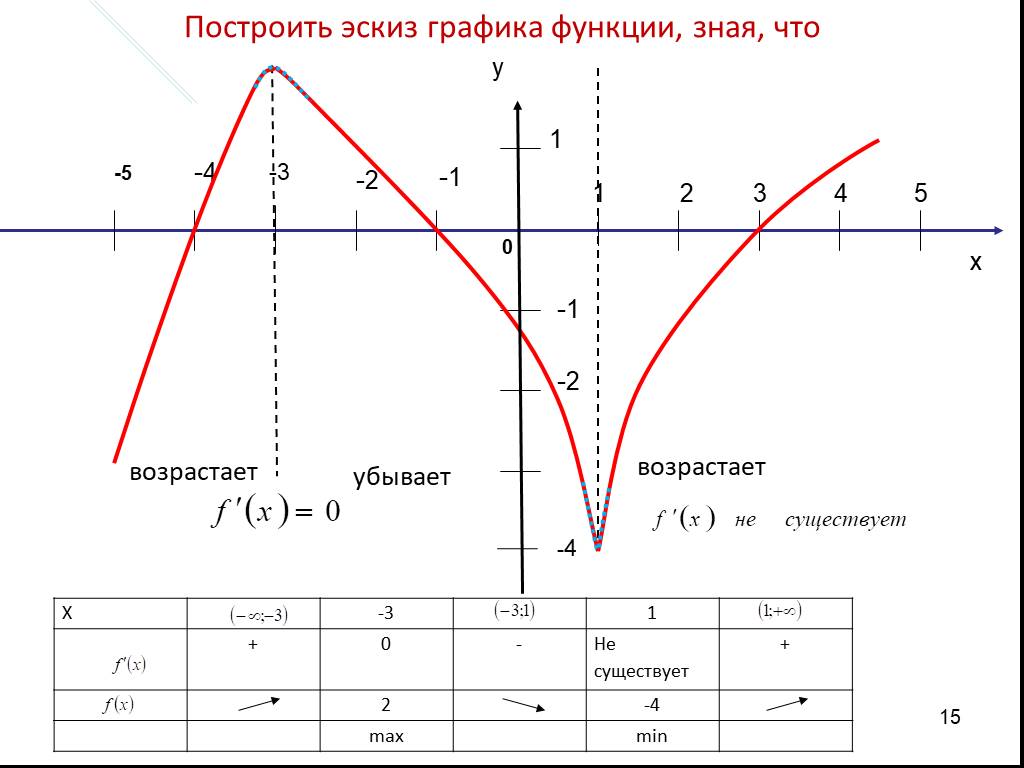
при
Знак y`
Поведение y
+
0
Рассматривается только
,
т.к. функция
чётная, и,
следовательно, её график
симметричен относительно
оси Оy.

12. МОДЕЛИРОВАНИЕ

1)
:
a) При каких значениях a данное уравнение имеет один корень, т.е. горизонтальная
прямая пересекает график 1 раз?
Ответ: a = 1.
a) При каких значениях параметра a данное уравнение не имеет решение, т.е.
горизонтальные прямые не пересекают график?
Ответ: (-∞;0]∩(1;∞).

13. МОДЕЛИРОВАНИЕ

a) При каких значениях параметра a данное уравнение имеет решение, т.е.
горизонтальные прямые пересекают график?
Ответ: (0;1].
Пример 2: Исследовать функцию
и
построить её график.
Можно исследовать функцию методами
математического анализа. Большой сложности
нет. Но объём исследования достаточно
большой: нахождение нулей функции ;
нахождение промежутков возрастания и
убывания…
А можно применить метод на основе свойства
монотонности функций.
А можно применить метод на основе свойства монотонности функций.
2008 г., С3: при каких значениях a неравенство не имеет
решений?
На промежутке (-5;-2] неравенство не
выполняется, т.е. горизонтальные линии не
пересекают полученные области.

English     Русский Правила

График сложных функции

Цель урока:

Систематизировать и расширить знания учащихся по теме: “Графики функций”

Задачи урока:

1. Использовать графики функций в задачах с параметром.
2. Расширить знания при построении графиков функций, связанных с модулем.
3. Исследовать и строить графики суперпозиции функций.
4. Получить новые знания при построении графиков суммы, разности, произведения, частного функций.

План урока:

1. Формулировка темы, цели, задач урока.
2. Обсуждение домашнего задания с приобщением задач с параметром.
3. Исследование и построение графиков функций, связанных с модулем (работа у доски, в парах, в группах).
4. Исследование и построение графиков суммы и произведения функций.
5. Исследование и построение графиков суперпозиции функций.
6. Домашнее задание в виде творческой работы.
7. Итоги урока. Рефлексия.

1. Обсуждение домашнего задания:

Построить график функций и описать свойства:

а)

б)

Правильность построения графиков проверяется с помощью мультимедийного проектора. Свойства функций проговариваются учащимися устно.

Дополнительный вопрос учителя по домашнему заданию:

Найдите все значения параметра a , при каждом из которых уравнение

а)

б)

имеет ровно один, ровно два и ровно один корень.

Вопрос к классу: Сформулируйте определение функции.

2. Построение графиков функций, связанных с модулем (работа в тетрадях).

Построить графики следующих функций:

а)
б)
в)
г)
д)
е)

С помощью ранее построенных графиков, постройте графики следующих функций:

а)
б)
в)
г)
д)
е)

Укажите особенности графиков функций.

Правильность построения графиков проверяется с помощью мультимедийного проектора. Работа в парах, с последующей проверкой и оценкой.

Вывод:

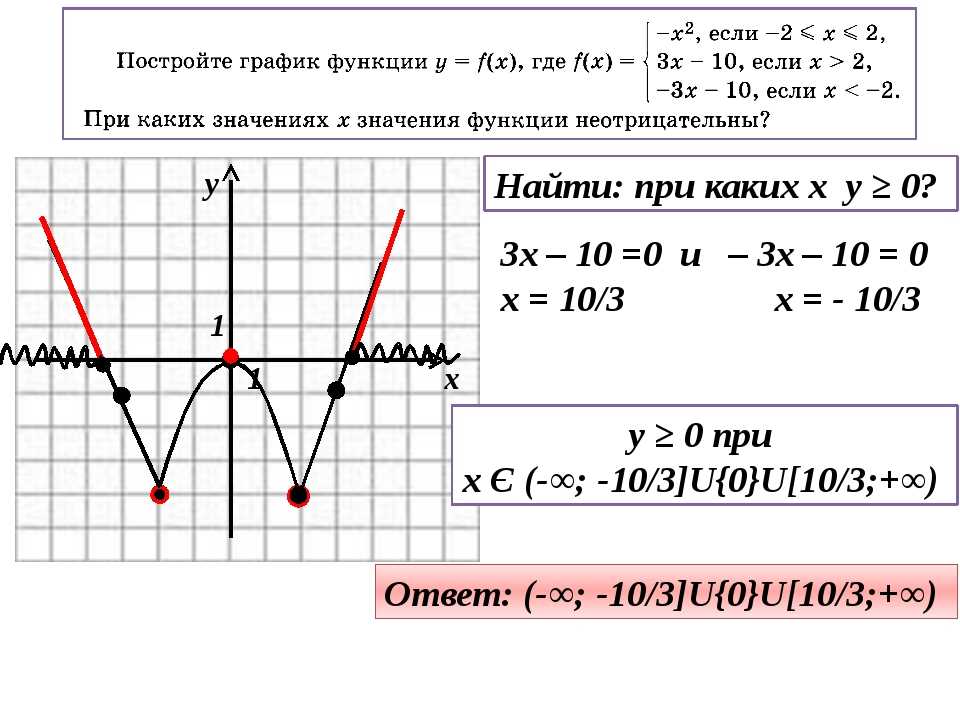
Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОХ или выше, и симметрично отразить относительно оси ОХ ту часть графика функции, которая расположена ниже оси ОХ.

Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОУ или справа от нее, и симметрично отразить эту часть относительно оси ОУ.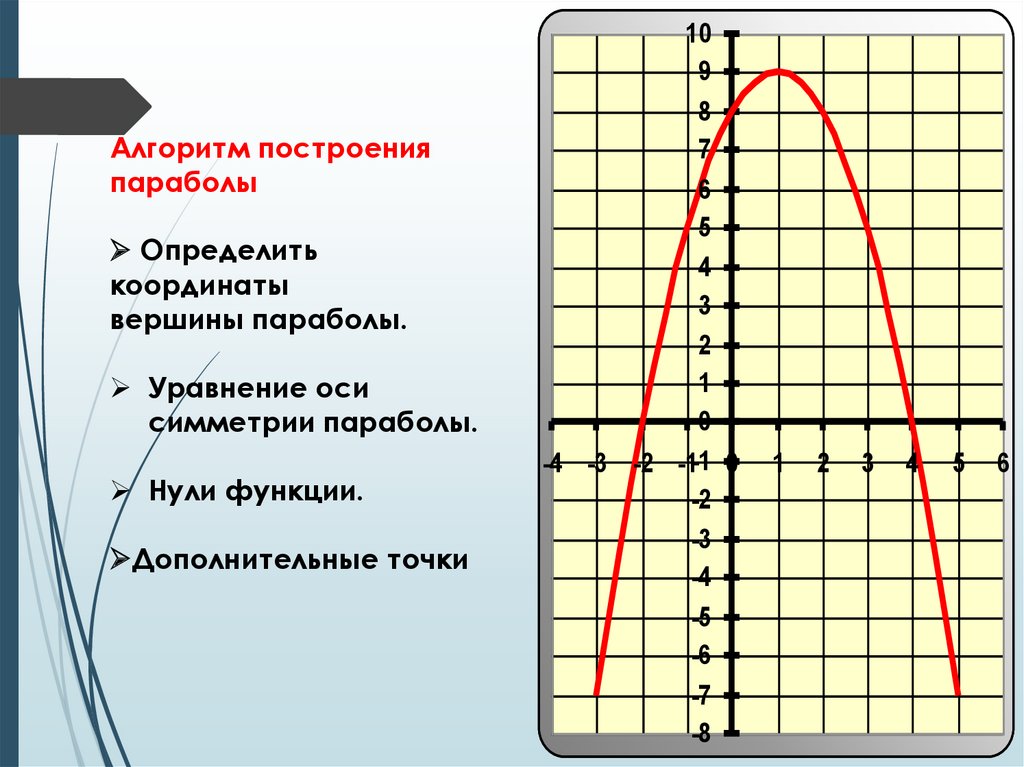

Вопрос классу: Сформулируйте определение графика функции?

Работа в группах.

Построить график и описать свойства следующих функций:

а)
б)
в)
г)
д)

е)
ж)
з)

Работают 6 групп, два — три человека работают у доски. Заранее желательно обсудить какая функция является исходной.

Правильность построения графиков проверяется с помощью мультимедийного проектора.

Учащиеся, работавшие у доски, должны назвать особенности построенных графиков функций. Уполномоченные в группах должны назвать вертикальные и горизонтальные асимптоты для графиков своих функций.

Вопрос классу: Сформулируйте определение сложной функции?

3. Два учащихся выполняют задание у доски:

Построить графики и описать свойства следующих функций:

а)

б)

В это время идет исследование:

Как построить график суммы функций ?

1. Найти область определения функции.
2. Произвести сложение ординат точек графиков.

Например: Постройте график функции

Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.

Проверка с помощью мультимедийного проектора.

Здесь же, с помощью проектора, рассмотреть другой пример графика суммы функций

По аналогии обсудить: как построить график разности функций.

Как построить график произведения функций ?

1. Найти область определения функции.
2. Произвести умножение ординат точек графиков.

Например: Постройте график функции

Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.

Проверка с помощью мультимедийного проектора. С помощью проектора рассмотреть другой пример графика произведения функций

По аналогии обсудить: как построить график частного функций.

Рассмотреть с помощью проектора график функции

4.

С помощью проектора, проверить правильность построения графиков суперпозиции функций (проанализировать работу двух учащихся, которые ранее работали у доски, показать особенности графиков).

Творческое домашнее задание:

Построить графики суммы, разности произведения функций, график сложной функции (подсказка в учебнике после п.2).

Итог урока:

Построение графиков функций один из самых интересных вопросов в курсе алгебры. Графики сложных функций чаще всего получаются очень красивыми и необычными. Поэтому изучение этого материала приносит не только практическую пользу

(например: в физике при изучении волновых явлений), но и эстетическое наслаждение.

Рефлексия:

1. Что вам понравилось (или не понравилось) на уроке?
2. Что нового вы узнали?
3. Ваши пожелания?

Приложение.

Сложный функциональный плоттер

Вы можете использовать этот инструмент для построения графиков функций комплексных, расщепленно-комплексных и двойных чисел, а также их инверсий в 2D и 3D.
Основная цветовая схема и идея были полностью вдохновлены плоттером сложных функций Дэвида Бау, но моя цель состояла в том, чтобы моя версия работала быстрее (используя webgl) и имела больше функций (разделенные комплексные числа, двойные числа, трехмерное построение, инверсии) и была более настраиваемый.

Основное использование

Чтобы ввести функцию, наведите указатель мыши на нижнюю часть окна (или коснитесь на мобильном телефоне) и щелкните 3 горизонтальные полосы, которые отобразят интерфейс для ввода функций и настройки инструмента.
В порядке чтения значки в нижней части экрана: справка, меню (три горизонтальные полосы, упомянутые выше), загрузка фонового изображения (это позволяет вам управлять изображением по вашему выбору с помощью введенной вами функции), загрузка и полноэкранный режим.
Переменная z предоставляет координаты x и y каждого пикселя в форме x + iy.
Любые другие переменные станут переключаемыми значениями в меню, которые вы можете использовать для управления программой.
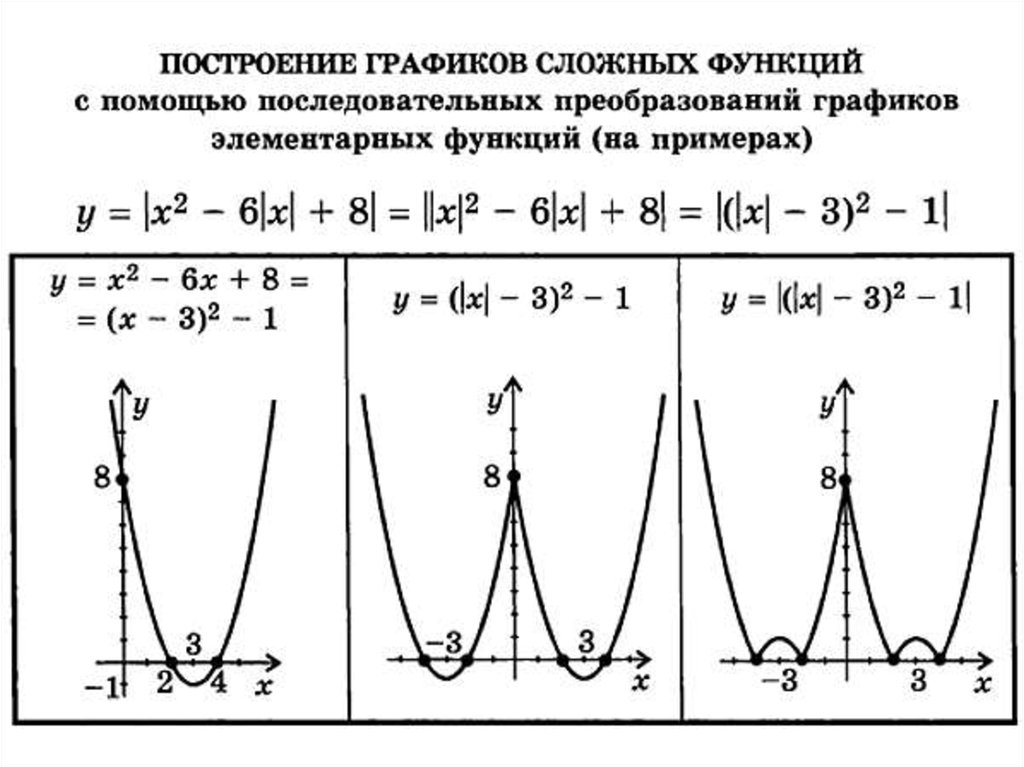
Когда пользователь входит в функцию, каждая точка (x,y) окрашивается в соответствии с тем, где они находятся под f(x+iy). Если вы хотите, чтобы точки окрашивались в зависимости от того, где они возникли, а не где они закончились, включите «инвертировать» в настройках, чтобы численно инвертировать функцию. Это довольно дорого, поэтому подумайте об отключении AA или уменьшении окна, если у вас возникнут проблемы (вы также можете настроить параметры инверсии в меню).

Константы

е
пи или π
i

Операторы и функции

Примечание: ниже u и v используются для представления любого выражения
Группировка (u)
Величина |u| или ‖u‖
Conjuagte u*
Основная арифметика : u+v,u-v,u*v или u⋅v,u/v или u÷v
Для умножения вы также можете просто написать переменные рядом друг с другом, то есть uv или 2uv или 2 u v или ipiuv или i pi u v все действительны и будут вести себя так же, как если бы использовалось *. Обратите внимание, что 2(u) будет работать нормально, но v(u) — это функция, а не умножение (также обратите внимание, что (v)u или (v)(u) будут работать нормально). 9v, ln(u), log(u), log(u,b) (Аргумент b в log может использоваться для указания базы, по умолчанию e)
Факториал : u! (действительно gamma(u+1))

Триггерные функции

: sin(u), cos(u), tan(u)
Обратные триггерные функции : asin(u), acos(u), atan(u)
Гиперболические триггерные функции : sinh(u), ch(u), tanh(u)

Угол : arg(u)
Получить действительные/мнимые компоненты : re(u), im(u)
Знак : sgn(u)
Шаг : шаг(u)
Квадратный корень : sqrt(z) или √(z) (или просто возведение в степень)
Гамма-функция : gamma(u) или Γ(u)
Зета-функция : zeta(u) или ζ(z)

Итерируемая функция {var=update, var=initial, iterations} (Думайте о var=update как о теле цикла for, например, {z’ = z’ +1 , z’ = 0, 5} будет инициализировать z’ значением 0, а затем добавлять к нему единицу в каждой из 5 итераций).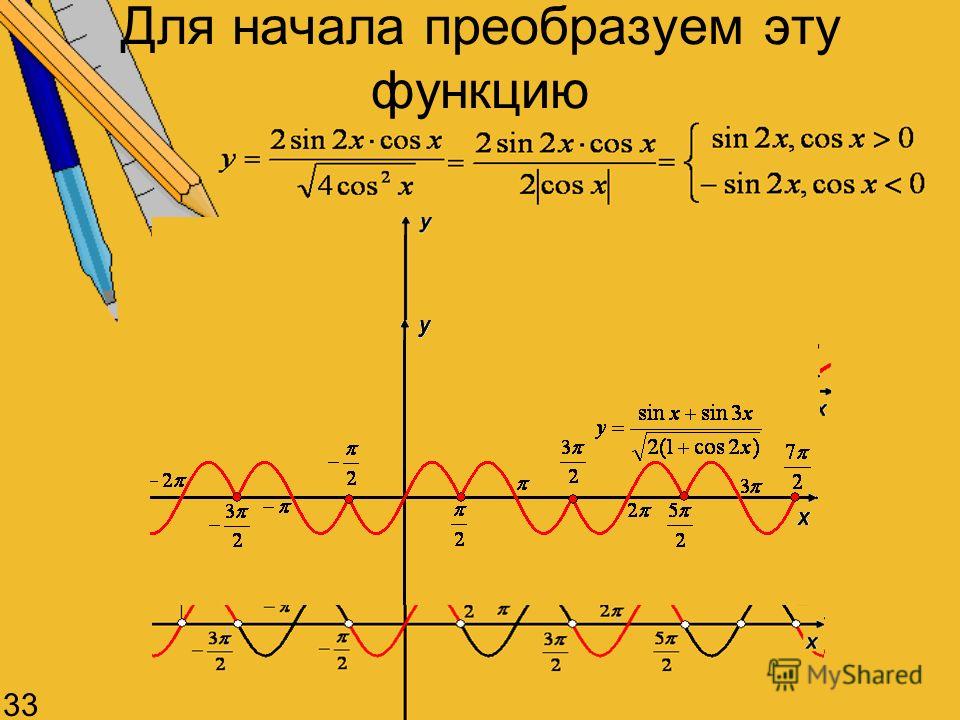 Значение по умолчанию var равно z’, вам не нужно указывать «z’=», если вы планируете использовать z’ (поэтому {z’ +1, 0, 5} также работает), но если вы хотите использовать другую переменную, такую ​​как «y», вам нужно будет указать ее ({y = y +1, y = 0, 5}). Итерации должны быть целым числом

Производная w.r.t z (u)’ (Вы можете вкладывать производные так глубоко, как хотите, но из-за ограничений арифметических операций с плавающей запятой результаты ухудшаются довольно быстро) Обратите внимание на круглые скобки, z’ в итерируемой функции не является производной из з.

Интеграл w.r.t z $(u) или $[нижний](u) или $[нижний, верхний](u). Когда параметры нижней и верхней границы опущены, используются значения по умолчанию 0 и z соответственно. Интегрируется по прямой от нижней до верхней границы. Вы также можете использовать $[lower, upper, variable](u), чтобы указать переменную для интегрирования по отношению к z по умолчанию. Используйте $[lower,upper,variable,iter](u), чтобы указать количество шагов, которые необходимо выполнить при интеграции. Вы можете использовать ∫ вместо $. 9я, 100н).

Прочее

Чтобы сгенерировать парсер для пользовательского ввода, я использовал peg.js. Сгенерированный файл синтаксического анализатора включен вместе с файлом грамматики, который я написал и использовал для создания синтаксического анализатора.

Как построить комплексное число в Python с помощью Matplotlib?

Улучшить статью

Сохранить статью

• Последнее обновление: 03 янв, 2021

Читать

Обсудить

Улучшить статью

Сохранить статью

В этой статье мы узнаем, как построить комплексное число в Python с помощью Matplotlib. Давайте обсудим некоторые концепции:

• Matplotlib : Matplotlib — потрясающая библиотека визуализации на Python для двумерных графиков массивов. Matplotlib — это многоплатформенная библиотека визуализации данных, построенная на массивах NumPy и предназначенная для работы с более широким стеком SciPy. Он был введен Джоном Хантером в 2002 году.
• Комплексное число: Комплексное число — это число, которое может быть выражено в форме a + bi, где a и b — действительные числа, а i — мнимая единица измерения, удовлетворяющее уравнению i2 = −1. Поскольку ни одно действительное число не удовлетворяет этому уравнению, i называется мнимым числом.
• Комплексное число в Python: Комплексное число представляется как «x + yi». Python преобразует действительные числа x и y в комплексные с помощью функции complex(x,y). Доступ к реальной части можно получить, используя функцию real() , а мнимую часть можно представить с помощью imag() .

Подход:

1. Импорт библиотек.
2. Создание данных комплексных чисел
3. Извлечение действительных и мнимых частей из данных комплексных чисел
4. Постройте извлеченные данные.

Примеры:

Чтобы построить комплексные числа, мы должны извлечь их действительную и мнимую части, а также для извлечения и создания данных мы будем использовать некоторые методы, которые объяснены в следующих примерах:

Пример 1: (Простой график с комплексными числами по действительным и мнимым данным)

Python3

import matplotlib. pyplot as plt     data = [ 1 + 2j , - 1 + 4j , 4 + 3j , - 4 , 2 - 1j , 3 + 9j , - 2 + 6j , 5 ]     x = [ele.real for ele in data] y = [ele. imag for ele in data]     plt.scatter(x, y) plt.ylabel( 'Imaginary' ) plt.xlabel( 'Real' ) plt.show()

Output :

Example 2 : (Using numpy for extracting real и воображаемые детали)

Python3

импорт MATPLOTLIB.PYPLOT AS PLT IMPORT 61 IMPORT 61 . 0159 data = np.array([ 1 + 2j , 2 - 4j , - 2j , - 4 , 4 + 1j , 3 + 8j , - 2 - 6j , 5 ] )     x = data.real y = data.imag     plt.plot(x, y, 'g *' ) plt. ylabel( 'Imaginary' ) plt.xlabel( 'Real' ) plt.show()

Output :

Example 3 : (Using numpy for creating data of complex numbers and extracting real and imaginary parts)

Python3

import matplotlib.pyplot as plt Импорт Numpy As NP Данные = NP.Arange ( 8 нп.ранге ( нп.р.0160 1j * np. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт