Карта сайта
Карта сайтаЦвет:C C C
Изображения Вкл. Выкл.
Обычная версия сайта
- Телефон доверия: 8 800 200-01-22
Ошибка 404
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Вопросы для проверки
Формулы тройных углов
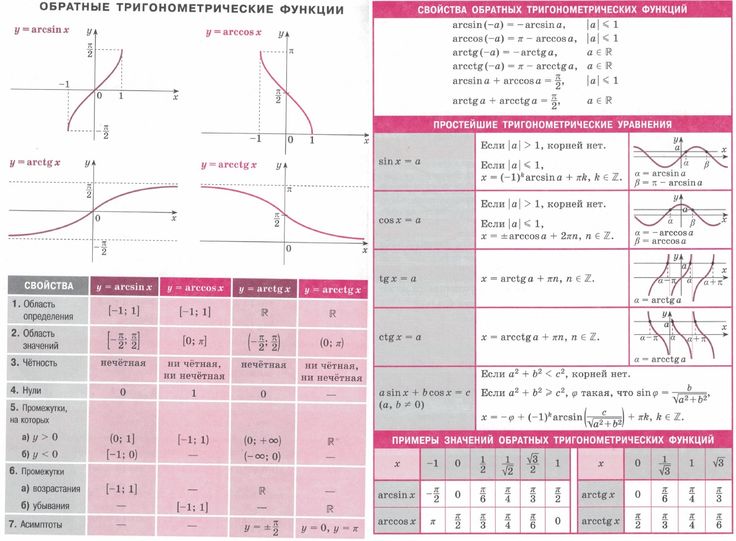
Обратные тригонометрические функции
Некоторые значения тригонометрических функций
таблица 3
Аргумент | ||||
sin | cos | tg | ctg | |
15 | ||||
18 | ||||
36 | ||||
54 | ||||
72 | ||||
75 | ||||
1.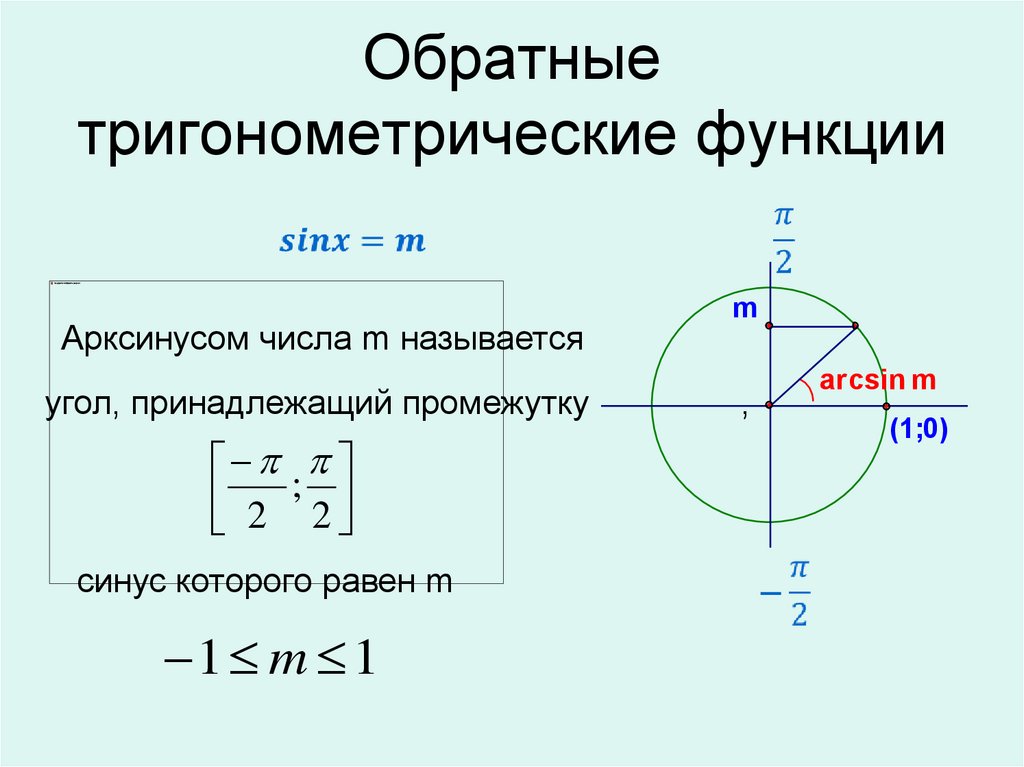 Что
такое числовая окружность?
Что
такое числовая окружность?
2. Перечислите признаки числовой окружности.
3. Какая величина принимается за единицу измерения при градусном измерении углов?
4. Что такое радиан?
5. По каким формулам переводят градусную меру угла в радианную и наоборот?
6. Выразите в радианах углы, равные 30, 45, 60, 90, 180, 270, 360.
8. При каком условии длина дуги равна ее радианной мере?
9. Какой угол называется углом поворота?
10. Какой угол поворота называется положительным? отрицательным?
11. Задайте формулой общий вид углов поворота.
12. Сформулируйте правило «полного оборота».
13. Какие функции называются тригонометрическими?
14. Дайте определение функции синус; косинус; тангенс; котангенс.
15. При каких углах не определен тангенс? котангенс?
16.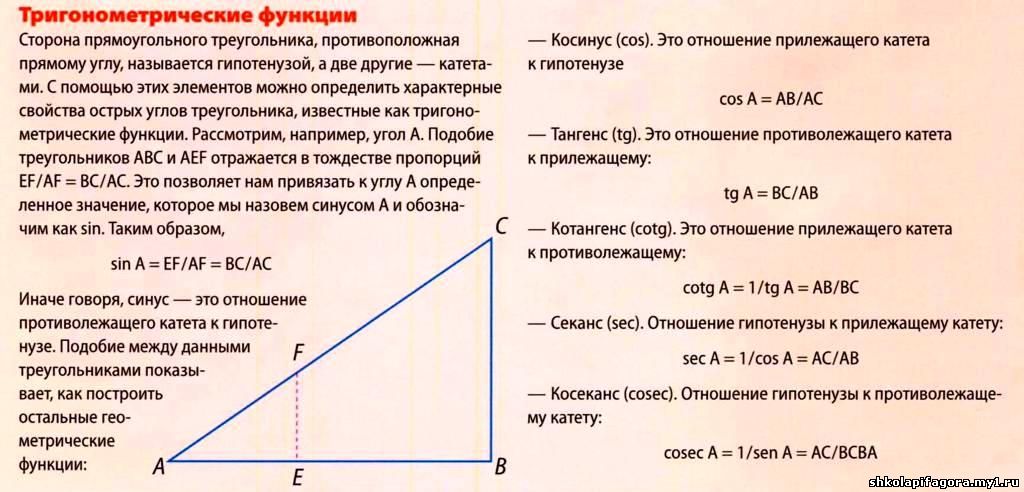 Назовите
значения тригонометрических функций
углов 30,
45,
60.
Назовите
значения тригонометрических функций
углов 30,
45,
60.
17. Какие значения может принимать синус? косинус? тангенс? котангенс?
18. Определите знаки тригонометрических функций в зависимости от того, в какой четверти находится аргумент.
19. Какие из тригонометрических функций являются четными, какие – нечетными?
20. Чему равен период синуса? косинуса? тангенса? котангенса?
1. Числовая прямая
Алгебраические функции — это функции, заданные аналитическим выражением, в записи которого используются алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
у = 2х + 3,
Числовая прямая — это математическая модель для представления чисел, в которой каждое число соответствует точке на прямой, причем расстояние от точки до начала отсчета равно модулю числа:
Признаки числовой прямой:
1) начало отсчета;
2) единичный отрезок;
3) положительное
направление (стрелка).
11. Простейшие тригонометрические неравенства
Чтобы решить простейшее тригонометрическое неравенство нужно:
1. Провести прямую к линии соответствующей функции.
2. Выделить дугу, на которой лежат решения неравенства.
3. Найти концы этой дуги, помня, что обход совершается против часовой стрелки от меньшего числа к большему.
4. Прибавить к концам интервала числа, кратные периоду функции.
Р ешить неравенство .
Решение.
В се решения, удовлетворяющие заданному неравенству, лежат на дуге l. Найдем ее концы:
С учетом периода синуса, запишем ответ:
.
Ответ:
10. Простейшие тригонометрические уравнения
Если правая часть уравнения — отрицательное число, то следует воспользоваться свойствами соответствующих обратных тригонометрических функций, тогда:
При а = 1; 0; –1 решение уравнения записывается в виде (n Z):
Тригонометрические функции и их формулы
В тригонометрии круговые функции также называются тригонометрическими функциями. Определение этих функций в простейшей форме состоит в том, что они демонстрируют тесную связь между сторонами и углами треугольника. Также известные как тригонометрические отношения, они обозначаются косекансом, секансом, котангенсом, тангенсом, косинусом и синусом.
Определение этих функций в простейшей форме состоит в том, что они демонстрируют тесную связь между сторонами и углами треугольника. Также известные как тригонометрические отношения, они обозначаются косекансом, секансом, котангенсом, тангенсом, косинусом и синусом.
- Формула интегрирования
- Формула тригонометрии
- Тригонометрические соотношения
- Триггерные идентификаторы
- Что такое тригонометрические производные
- Высота и расстояние
- Тригонометрическая формула, включающая сумму разностей идентификаторов продуктов
- Теорема Пифагора
- Формула дифференциации
- Основные идентификаторы триггеров
Тригонометрические функции с углами
Любой студент, изучающий эти функции, должен понимать, что существует ряд тригонометрических тождеств и формул. Формулы устанавливают связь между этими функциями.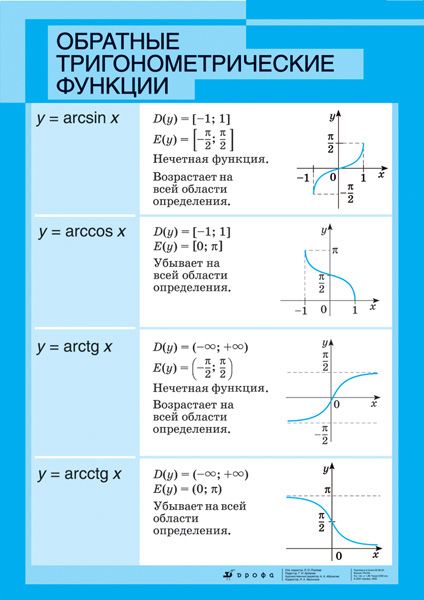
Триггерные функции Таблица
Основная классификация тригонометрических функций включает углы тангенса, косинуса и синуса. Из этих первичных функций можно вывести три функции, которые обозначаются как косеканс, секанс и котангенс.
Тригонометрические функции с графиками
Приведенная выше диаграмма может объяснить три основные тригонометрические функции.
Список тригонометрических функцийСписок дополнительных тригонометрических функций включает секанс, косеканс и котангенс. Эти функции также устанавливаются из первичных функций, таких как синус, косинус и тангенс. Следует отметить, что величины, обратные tan, cos и sin, известны как котангенс (cot), секанс (sec) и косеканс (csc) соответственно.
Формула тригонометрических функцийНиже приведены формулы для некоторых тригонометрических функций. Вот они:
Отношение длины противоположной стороны к длине гипотенузы известно как функция синуса угла. Значение sin должно быть Sin a= Opposite/Hypotenuse=CB/CA.
Значение sin должно быть Sin a= Opposite/Hypotenuse=CB/CA.
Формулу функции cos можно объяснить как отношение длины прилежащей стороны к длине гипотенузы. Функция cos может быть получена из приведенной выше эталонной диаграммы как
Cos a = Adjacent/Hypotenuse = AB/CA.
Формула функции тангенса определяется как отношение длины противоположной стороны прямоугольного треугольника к длине прилежащей стороны. Учащийся должен отметить, что функция тангенса может быть выражена через синус и косинус как их отношение. Следовательно, функция тангенса будет получена как Tan a = Противоположный/Смежный = CB/BA. Кроме того, тангенс можно записать через синус и косинус как Тан а = сина/коза.
Дополнительные функции представлены формулами; они равны:
Cot a = 1/ (tan a) = Смежный/Противоположный = BA/CB
Cosec a = 1/ (sin a) = Гипотенуза/Противоположный = CA/CB
Sec a = 1/ (cos а) = Гипотенуза/Смежная = CA/AB
Существует несколько обратных тригонометрических функций.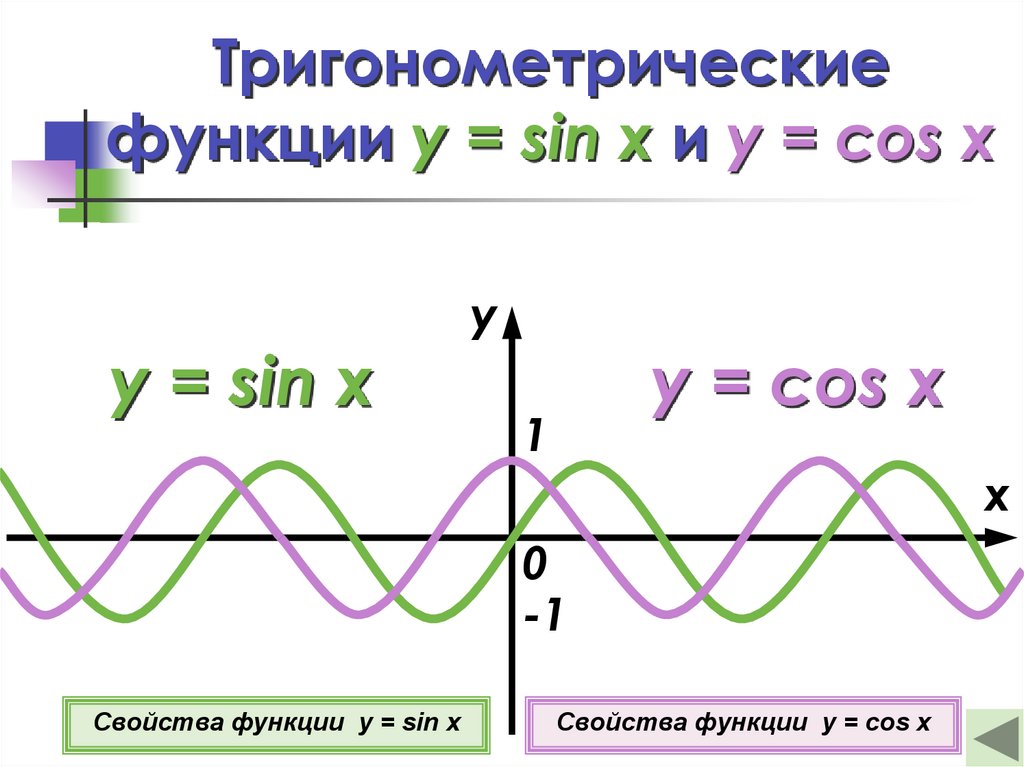 Здесь обратные значения косеканса, секанса, котангенса, тангенса, косинуса и синуса известны как арккосеканс, арксеканс, арккотангенс, арктангенс, арккосинус и арксинус соответственно.
Здесь обратные значения косеканса, секанса, котангенса, тангенса, косинуса и синуса известны как арккосеканс, арксеканс, арккотангенс, арктангенс, арккосинус и арксинус соответственно.
Oikofug касательная на другом конце и оканчивается радиусом; в современном использовании отношение этой линии к радиусу
ˈsi ː kəntсеканс : Первоначально длина прямой линии, проведенной из центра дуги окружности через один конец дуги и оканчивающейся касательной или линией, касающейся дуги на другом конце; в современном использовании отношение этой линии к радиусу
ˈtænʤǝntтангенс : Первоначально длина прямой линии, перпендикулярной радиусу, касающейся одного конца дуги и заканчивающейся секущей, проведенной из центр через другой конец; в современном использовании отношение этой линии к радиусу
Да, эти определения определенно нуждаются в пояснительных диаграммах, и я перейду к этому через минуту.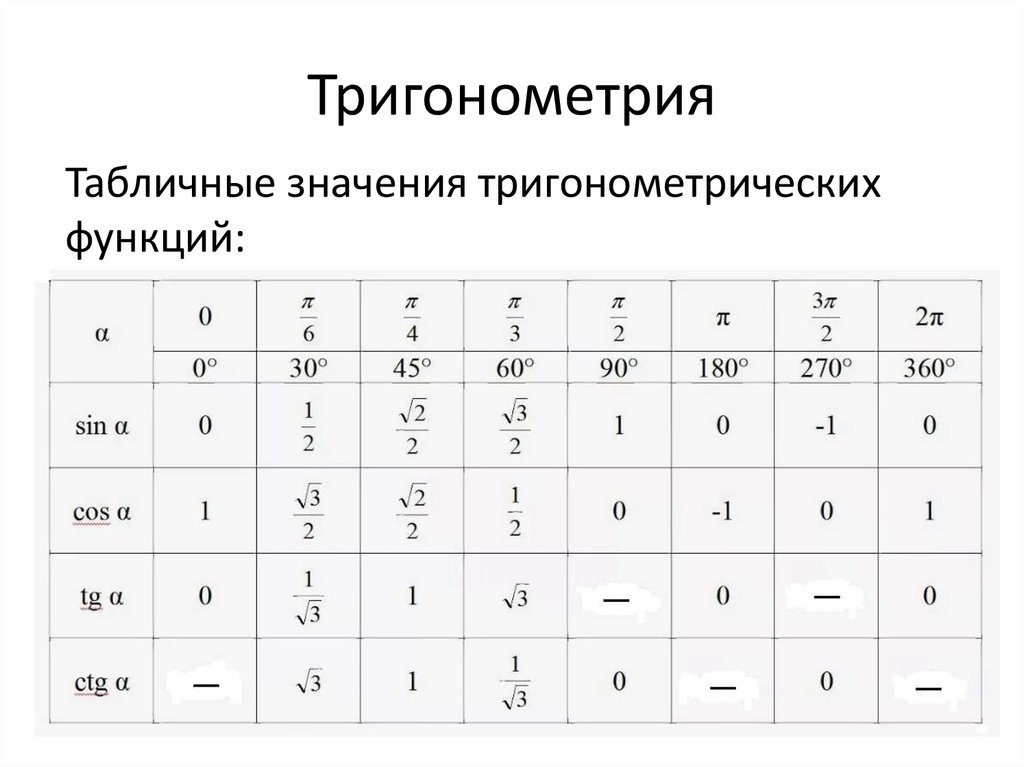 Сначала немного предыстории.
Сначала немного предыстории.
Слово тригонометрия происходит от греческого trigonon «треугольник» и metria «измерение» — это математика измерения треугольника.
Еще в Средние века, до появления электронных калькуляторов и персональных компьютеров, существовали тригонометрические таблицы , в которых перечислялись различные свойства прямоугольных треугольников — вы искали угол треугольника, и таблица давала вам отношение двух его сторон. Для заданного угла можно было узнать об отношениях разных сторон треугольника, проверив соответствующие тригонометрическая функция этого угла — функции с экзотическими названиями неясного происхождения, наподобие перечисленных в заголовке этого поста. У меня до сих пор есть довольно сексуальный набор триггеров. столы, которые я снимаю с полки и время от времени ностальгически глажу.
Самые ранние из известных нам тригонометрических таблиц были составлены греческим астрономом Гиппархом из Никеи, жившим во втором веке до нашей эры. В утерянной работе под названием Ton en kukloi eutheion (О линиях внутри круга) он перечислил длины хорд круга стандартной окружности, которые он установил равными 21600 единицам (количество угловых минут в 360º). Он указал длину хорд, проведенных с регулярным угловым шагом в 45 единиц, что соответствует 7,5º.
В утерянной работе под названием Ton en kukloi eutheion (О линиях внутри круга) он перечислил длины хорд круга стандартной окружности, которые он установил равными 21600 единицам (количество угловых минут в 360º). Он указал длину хорд, проведенных с регулярным угловым шагом в 45 единиц, что соответствует 7,5º.
Вот схема одного такого угла и соответствующей ему хорды:
Одна из хорд ГиппархаУгол в 3600 единиц (от длины окружности 21600, что эквивалентно 60 градусам) дает хорду длиной 3438 единиц
Каждая хорда образует основание равнобедренного треугольника, вписанного в окружность. Если бы вы поняли, что все треугольники с одинаковыми углами имеют стороны в одинаковом соотношении (что и делали древние греки), то вы могли бы использовать данные из таблицы Гиппарха, чтобы вычислить длину сторон 9 треугольников.0099 других равнобедренных треугольников с тем же углом при вершине.
На самом деле таблица Гиппарха работала точно так же, как современная функция синус . Единственные различия между ними заключаются в используемых множителях:
Единственные различия между ними заключаются в используемых множителях:
- Чтобы работать с таблицей Гиппарха, вам нужно сначала вычислить радиус его стандартного круга в 21600 единиц, потому что две стороны его равнобедренного треугольника образованы радиусы стандартной окружности. Современные тригонометрические функции эффективно задают радиус окружности равным единице, что значительно упрощает масштабирование.
- «Значения хорды», указанные Гиппархом для каждого угла, в современных терминах равны удвоенному синусу половины угла.
Если мы вернемся к определению синуса в заголовке этого поста, вы, возможно, увидите, откуда берется «удвоенный синус половины угла». Вот еще раз исходное определение:
.Линия, первоначально определенная как синусДлина прямой линии, проведенной от одного конца дуги окружности параллельно касательной на другом конце и заканчивающейся радиусом
Она составляет половину длины хорды Гиппарха и основана на половине центрального угла хорды
В современных терминах синус центрального угла представляет собой отношение между этой линией и радиус – «противоположная относительно гипотенузы», другими словами
. Из диаграммы должно быть очевидно, что «линия синусоиды» составляет половину длины хорды Гиппарха и основана на половине ее центрального угла.
Из диаграммы должно быть очевидно, что «линия синусоиды» составляет половину длины хорды Гиппарха и основана на половине ее центрального угла.
Sine происходит от латинской sinus , «бухта», и вы можете увидеть небольшую бухту, которая образовалась между линией синуса и дугой окружности.
А вот еще раз исходное определение секущей:
Прямая, первоначально определенная как секансДлина прямой линии, проведенной из центра дуги окружности через один конец дуги и заканчивающейся касательной или линией, касающейся дуги на другом конце
В современных терминах секанс центрального угла есть отношение между этой линией и радиусом – «гипотенуза над соседней», другими словами
Секан происходит от латинского secare , «разрезать», потому что он пересекает дугу окружности.
А тангенс определялся через секанс:
Линия, первоначально определенная как тангенсДлина прямой линии, перпендикулярной радиусу, касающейся одного конца дуги и заканчивающейся секущей, проведенной из центра через другой конец
В современных терминах тангенс центрального угла представляет собой отношение этой линии к радиусу – «противоположный к соседнему», другими словами
Тангенс происходит от латинского tangere «касаться», потому что он просто касается дуги окружности.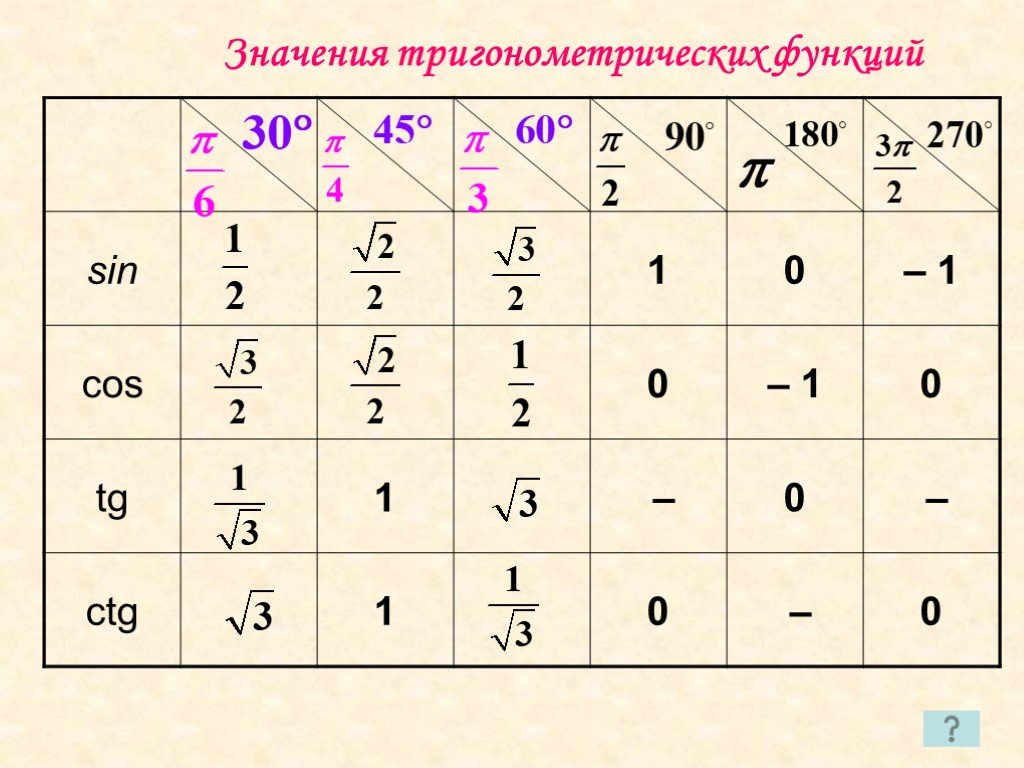
Каждая из этих основных тригонометрических функций имела дополнительную функцию, отмеченную префиксом co-, который происходит от аналогичного латинского префикса, означающего «совместно» или «вместе». Таким образом, у нас также есть косинус , косеканс и котангенс . Я собираюсь пропустить подробное значение этих дополнительных функций, но оказывается, что шесть тригонометрических функций исследуют все возможные отношения трех сторон прямоугольного треугольника. Три из них обратны трем другим:
котангенс = 1/тангенс
косеканс = 1/синус
косинус = 1/секанс
Таким образом, вы можете выполнять тригонометрию, используя всего три функции, по одной из каждой строки выше. Вот почему, когда я учился в школе, я никогда не слышал о секущих — мы использовали синус, косинус и тангенс и брали обратные значения, когда это было необходимо.
Но вернемся к оригинальному трио. У нас есть синус , образующий залив внутри кривой; секанс , разрезающий кривую; и касательной , которая касается кривой.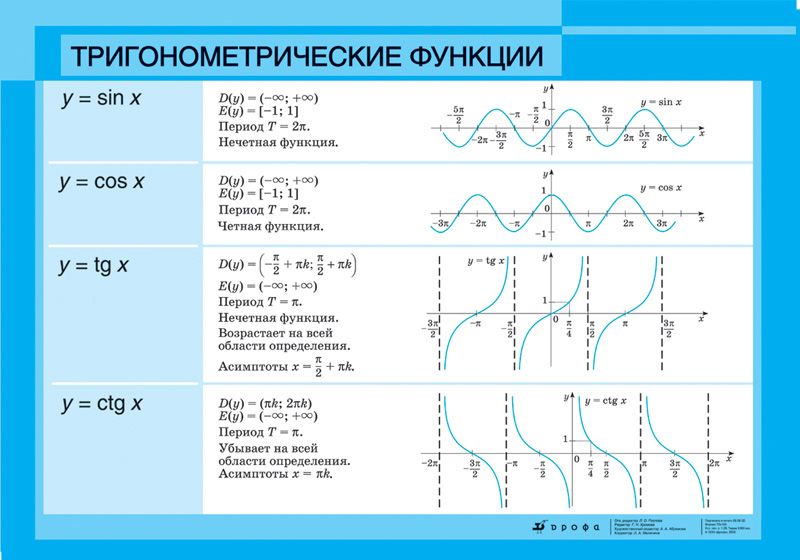 Непонятные названия действительно имеют смысл!
Непонятные названия действительно имеют смысл!
(изображение с камеры Lunar Reconnaissance Orbiter Camera)
Латинское sinus , «залив», в английском языке без изменений в виде пазух в вашей голове, которые могут воспалиться с синусит . Каждая воздушная полость пазухи имеет узкий вход и широкое внутреннее расширение, подобное защищенному заливу. Что-то, что извивается взад и вперед, создавая изгибы, похожие на бухты, это извилистый или извилистый . Акт обматывания синуация . И если мы вводим идею извилистым и запутанным образом, мы внушаем ее.
Латинское secare , «резать», дает нам множество сокращений, оканчивающихся на – sect . Bisect , trisect , quadrisect и quinquesect — это глаголы для разрезания чего-либо на две, три, четыре или пять равных частей. До пересекаются — разрезать что-то, — препарировать, — что-то разрезать, — резектировать, — что-то вырезать, а prosect — что-то заранее разрезать — процесс препарирования образца для анатомической демонстрации. К персекатировать значит резать, к вычищать значит вырезать что-то без запутывания, а секамент это материал, который был отрезан от чего-то другого (например, древесная стружка, оставшаяся от строгания). Если что-то можно вырезать, то это сектиль или сектиль . Сектор и сегмент — обе вещи, отрезанные от большего целого. Секатор является режущим инструментом. Полная этимология слова серп неясна, но вполне возможно, что оно пришло в германские языки из латыни. ( Sect , с другой стороны, скорее всего, произошло от латинского sequi , «следовать».
До пересекаются — разрезать что-то, — препарировать, — что-то разрезать, — резектировать, — что-то вырезать, а prosect — что-то заранее разрезать — процесс препарирования образца для анатомической демонстрации. К персекатировать значит резать, к вычищать значит вырезать что-то без запутывания, а секамент это материал, который был отрезан от чего-то другого (например, древесная стружка, оставшаяся от строгания). Если что-то можно вырезать, то это сектиль или сектиль . Сектор и сегмент — обе вещи, отрезанные от большего целого. Секатор является режущим инструментом. Полная этимология слова серп неясна, но вполне возможно, что оно пришло в германские языки из латыни. ( Sect , с другой стороны, скорее всего, произошло от латинского sequi , «следовать». )
)
Латинское tangere , «касаться», появляется в латинской фразе noli me tangere , «не прикасайся ко мне», который был принят в качестве девиза многими семьями, в том числе Тобинами, Сент-Обинсами, Итерсонами и Грэмами из Пертшира, а также несколькими военными организациями.
Семейный герб и девиз Итерсонов(Источник)
На самом деле это библейская фраза, латинский перевод новозаветного греческого m e mou haptou . Эти слова, по общему мнению, были сказаны перевоплощенным Иисусом Марии Магдалине, и лучшим переводом было бы «не цепляйся за меня».
Степень, в которой noli me tangere повлияла на фразу американских революционеров «Не наступай на меня!» кажется не совсем ясным, хотя в наши дни эти две фразы используются так, как если бы одна была прямым переводом другой. Но «не наступай на меня» на самом деле будет noli me calcare , что является фразой святого Августина, а не Библии.
Флаг Гадсдена революционной Америки(Источник)
Возможно, нынешняя путаница между «не наступай на меня» и noli me tangere был воспитан флагом сепаратистского штата Алабама, который в 1861 году принял свернувшуюся спиралью гремучей змею флага Гадсдена (появляющуюся соответствующим образом из-под хлопкового куста), но заменил noli me tangere на «не наступи на меня».
(Источник)
Тангере является источником материального , относящегося к чему-то, что можно потрогать. Вещи, которые соприкасаются или влияют друг на друга, смежные или контингентные , а болезнь, передающаяся через телесный контакт, считается заразной . Pertingency — акт протягивания руки, чтобы прикоснуться к чему-либо. Что-то, что представляет собой целое число , нетронуто, что означает целое или неповрежденное, поэтому целых числа представляют собой серию целых чисел.
От причастия прошедшего времени tangere происходит латинское tactus , «прикосновение». Такт первоначально означало чувство осязания, прежде чем оно приобрело свое нынешнее значение «чувство того, что уместно». Тактильный по-прежнему относится к чему-то, что связано с прикосновением, а тактичный относится к тому, у кого есть чувство такта.

 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Курсы/ Кружки/ Факультативы
Курсы/ Кружки/ Факультативы