Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376192 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
RU
- Class
RU
1.3. Тригонометрические функции
Тригонометрические функции и опредены на всей числовой оси, переодические, с периодом и не принимают значения по абсолютной величине большие . Отметим также, что функция является нечетной, а функция — четной. Их графики изображены на рис. 7.
Линия, являющаяся графиком функции , называется синусоидой. График функции — тоже синусоида, она получается из графика смещением вдоль влево на отрезок .
Из
рис. 7 видно, что график функции
проходит через точку — начало координат, а функция
проходит через точку
.
Графики обеих функций и
и
пересекают ось
неограниченное число раз, это означает,
что уравнения и имеют бесконечно много корней. Именно,
решение уравнения
имеет вид ,
где — целое число, а решением уравнения
будут число ,
где
— целое число.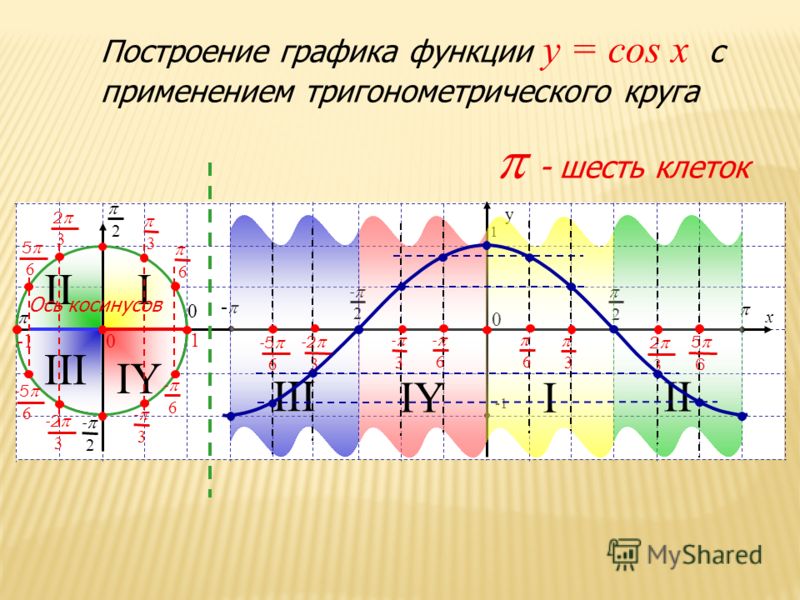
Рис. 7. Графики функции и .
Тангенс и котангенс выражаются формулами и , а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у в знаменателе находится , который обращается в нуль в точках , а будет иметь разрывы там, где синус равен нулю, т.е. в точках ( — целое число).
Обе функции и и являются нечетными и периодическими с периодом . Графики этих функций приведены на рис. 8.
Рис. 8. Графики функции и .
1.4. Обратные тригонометрические функции
Обратные тригонометрические функции ставят в соответствие значению данной тригонометрической функции значение угла. Так, например, есть угол, синус которого равен . Аналогично определяются , и .Полагаем
(1)
(2)
Справедливы следующие формулы сложения обратных тригонометрических функций
Графики
обратных тригонометрических функций
изображены на рис.
9.
Рис. 9. Графики функций , , и .
2. Элементарные преобразования графиков
Допустим, что построен график функции , . Тогда построение графика в общем случае сводится к ряду элементарных преобразований, таких как сдвиг, сжатие, отображение и т.д. графика функции .
Приведем таблицу, в которой описано, как изменяется график функции приопределенном преобразовании функции или ее аргумента (см. таблицу 1).
Таблица 1
№ | Функция | Преобразование, которое следует провести с графиком на плоскости |
1. | , | Сдвиг
вверх по оси
графика функции
на
единиц, если
,
и сдвиг вниз на
единиц, если
. |
2. | , | Сдвиг вправо по оси на единиц, если , сдвиг влево на единиц, если . |
3. | , , | Растяжение вдоль оси относительно в раз, если , сжатие вдоль оси в раз, если . |
4. | , , | Сжатие вдоль оси относительно в раз, если , растяжение вдоль оси в раз, если . |
5. | Симметричное
отображение графика относительно оси
. | |
6. | Часть графика, расположенная ниже оси , симметрично отражается относительно этой оси, остальная часть остается без изменения. | |
7. | Симметричное отображение графика относительно оси . | |
8. | Стирается часть графика функции , лежащая слева от оси , остается часть графика , лежащая справа от оси и на ней; часть графика, расположенная в области , симметрично отображается относительно оси в область . |
Для того, чтобы на практике построить график функции , используя график и элементарные преобразования графика следует использовать такой порядок:
• построить график ;
• построить график функции , для этого сжать или растянуть график вдоль оси и, если, симметрично отобразить относительно ;
• сдвинуть по оси полученный график, так, чтобы получился график функции ;
• построить график функции , для этого сжать или растянуть график вдоль оси и, если , симметрично отобразить относительно оси ;
• сдвинуть
график
на вверх, если ,
и вниз на ,
если .
Пример 1. Построить график функции .
Решение. Сначала преобразуем функцию, вынеся за скобки коэффициент при : . Теперь последовательно выполним преобразования графика функции , который изображен на рис. 7 (см. также рис. 10).
Построим график . Так как больше единицы, то график нужно сжать вдоль в раза (см. преобразование 4 из таблицы 1). Получим
Рис. 10. Графики функций , .
Сдвинем теперь по оси полученный график на вправо (см. преобразование 2 из таблицы 1), получим график функции (см. рис. 11). Наконец, растянем график в раза вдоль (см. преобразование 3 из таблицы 1), чтобы получить требуемый график (см. рис. 11).
Пример 2. Поcтроить график функции
Решение. Построем сначала ,
затем растянем его вдоль оси
в два раза, получим график .
Чтобы теперь получить эскиз ту часть графика, которая находится
выше оси
симметрично отобразим в нижнюю
полуплоскость, оставив без изменения
часть графика
,
которая лежит ниже оси
(см.
рис. 12).
Рис. 11. Графики функций , и .
Рис. 12. Графики функций , и .
Пример 3. Построить график функции .
Решение. Построение эскиза графика функции сводится к следующему (см. рис. 13):
1. строится график ;
2. построенный график сжимается вдоль оси в два раза, получается график ;
3. график симметрично отображается относительно оси , получается график ;
4. наконец, график сдвигается вниз на .
Рис. 13. Графики функций , , и .
5: Графики — триггерные функции и тождества
Графики синуса и косинуса
Ввод x графика соответствует величине угла в радианах на окружности. Результатом является высота графика. Например, когда
π/2 вставляется в базовую функцию синуса (y=sinx), на выходе получается значение y, равное 1, поскольку это значение получается при использовании единичного круга.
Стандартная форма: y=asin(bx+c)+d или y=acos(bx+c)+d
Амплитуда: Амплитуда – это высота графика или расстояние от начала координат до вершины или низа . Алгебраически это |a|.
Период: Период представляет собой длину одного полного цикла на графике (когда график прошел путь от начала к максимуму, к началу от минимума к началу или наоборот). Алгебраически это 2π/|b|.
Фазовый сдвиг: фазовый сдвиг является отправной точкой графика. Алгебраически это -c/b.
Сдвиг по вертикали: Сдвиг по вертикали перемещает график вверх или вниз. Алгебраически это то, чему равно d.
Графические функции синуса и косинуса:
1. Определение амплитуды, периода, фазового и вертикального сдвига
2. Отметьте оси x и y. Ось X должна быть помечена значениями от -4π до 4π, например, 0,π/2,π и т. д. Ось Y должна использовать основные значения, такие как 0, 1, 2 и т. д.
3. Возьмите период и разделите его на 4.
4. Начните строить графики в соответствии с правилом TOBOT и OTOBO.
Если это функция косинуса, начните с Верхней части, нуля, Низа, нуля, Вершины. Если это синусоидальная функция, начните с нуля, Верх, ноль, Низ, ноль.
5. Если член a отрицательный, отразите его по оси x.
Свойства основных синусоидальных и косинусоидальных графиков
Домен: Все действительные числа
Диапазон: [-1,1]
Период: 2π
Амплитуда: 1
Базовый график тангенса
Домен: все действительные числа, кроме x=πn/2, где n нечетно Y-отрезки: (0,0)
Экстремумы: нет
Асимптоты: x= πn/2, где n — нечетное целое число. Асимптоты возникают, когда Cos равен нулю, потому что Tan=Sin/Cos, поэтому, когда Cos=0, функция равна Sin/0, что не определено.
Использование графиков для оценки тригонометрических функций
Чтобы оценить тригонометрическую функцию графически, переведите калькулятор в функциональный режим и убедитесь, что он настроен на измерение в радианах. Затем подставьте обе части данного тригонометрического уравнения и найдите, где они пересекаются в заданной области. Преобразования графиков происходят при изменении значений a, b, c или d основного уравнения При изменении b: Когда вы меняете a: При изменении c: При изменении d: Мы видели, что тригонометрические функции являются периодическими. Мы можем использовать этот факт, чтобы набросать или нарисовать графики тригонометрических функций. 1. Найдите период функции. 2. Выберите подходящий интервал для графика. 3. Исследуйте поведение функции на заданном интервале. Для этого мы проверим значения функции для общих углов, таких как 0°, 30°, 45°, 60°, 90°,… . Это покажет нам, когда функция возрастает, а когда убывает. Мы пишем ⬈, чтобы показать, что функция возрастает на интервале и наоборот, когда она убывает. Для функций sin x и cos x мы можем разделить интервал [0, 2π] на четыре равные части и взять конечные точки интервалов в качестве углов для проверки. 4. Нарисуйте график функции в заданном интервале и скопируйте его любое количество раз, чтобы получить общий график функции. Теперь мы можем посмотреть на графики основных тригонометрических функций. Для ƒ (x) = sin x имеем ƒ: R → [-1, 1]. 1. Период sin x равен 2π. 
Например, если ваша триггерная функция sinx=0,5, когда 0 Преобразования графиков
y=asin(bx+c)+d или y=acos(bx+c)+d.
Горизонтальное сжатие/растяжение связано с периодом графика.
Например, когда базовая функция синуса y=sinx преобразуется в y=sin2x, период становится π, а не 2π.
Увеличение увеличивает высоту графика, а уменьшение уменьшает высоту.
Вертикальное сжатие/растяжение связано с амплитудой графика.
Например, когда y=sinx преобразуется в y=2sinx, высота изменяется с 1 на 2, а диапазон переключается с [-1,1] на [-2,2].
Изменение c влияет на фазовый сдвиг. Это также можно рассматривать просто как сдвиг по горизонтали. Положительное значение c сдвинет график на c единиц вправо, а отрицательное значение c сдвинет график влево.
Изменение d приводит к смещению по вертикали. Положительное значение d сдвинет его вверх, а отрицательное значение сдвинет график вниз. ГРАФИК ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ – ТРИГОНОМЕТРИЯ
Чтобы нарисовать график тригонометрической функции, выполните следующие действия:
Как правило, интервал [0, 2π] является хорошим интервалом для sin x и cos x, (0, π) подходит для ctg x и (-π/2, π/2) подходит для tan x.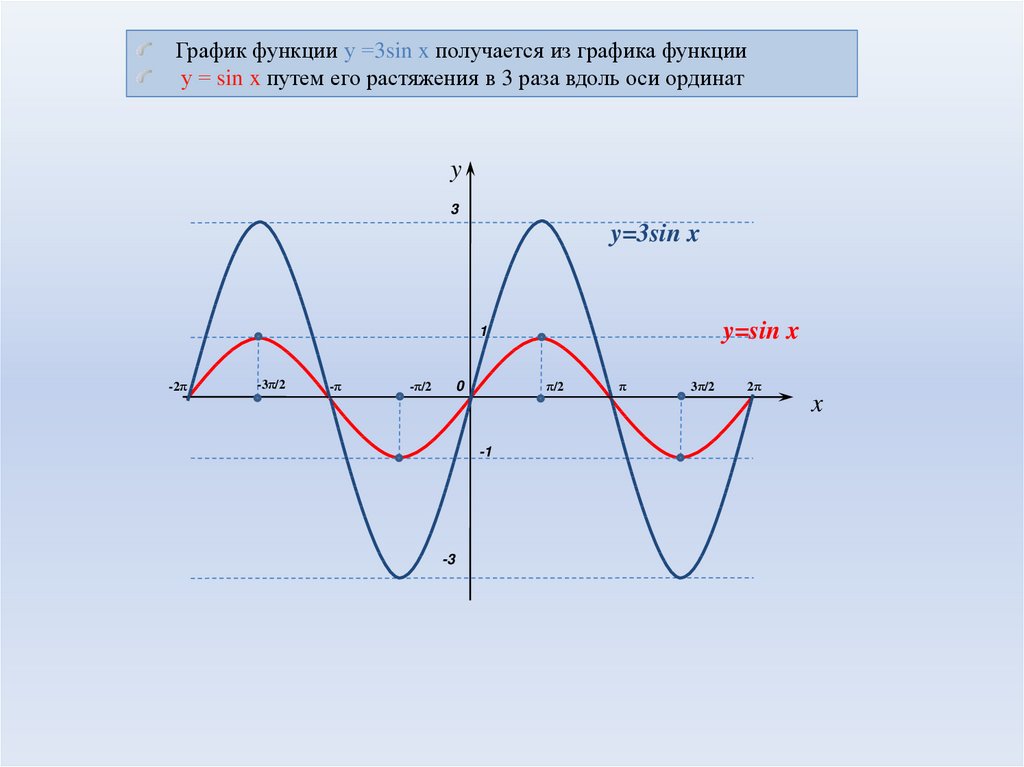
2. Рисуем и рисуем на отрезке [0, 2π].
3. Мы можем использовать квадрантные углы 0, π/2, π, 3π/2 и 2π со значениями 0, 1, 0, -1, 0 соответственно.
4. Теперь мы можем нарисовать график с информацией.
1. Период cos x равен 2π.
2. Построим график на отрезке [0, 2π].
3. Мы можем использовать квадрантные углы 0, π/2, π, 3π/2 и 2π со значениями 0, 1, 0, -1, 0 соответственно.
4. Теперь мы можем нарисовать график с информацией.
2. Построим график на интервале (-π/2, π/2).
3. Используйте специальные углы -π/2, -π/4, 0, π/4 и π/2 со значениями -∞, -1, 0, 1 и ∞ соответственно.
4. Теперь мы можем нарисовать график.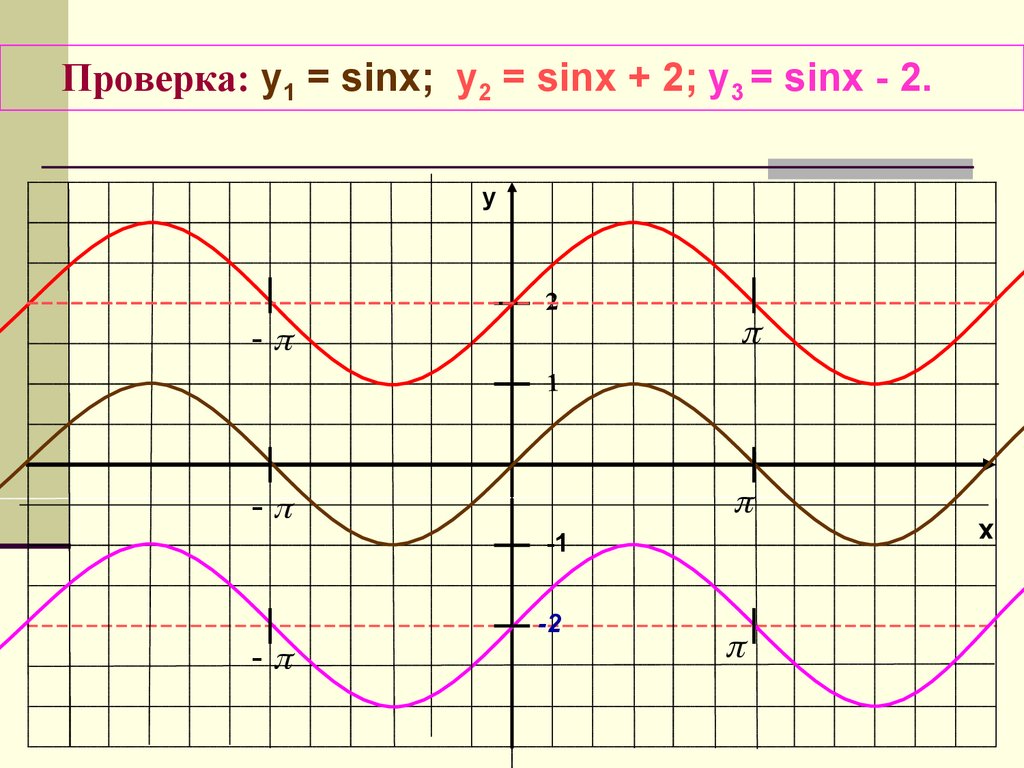
ƒ (x) = COT x ƒ: R — {Kπ} → R.
1. ПЕРИОД из COT x IS IS. π.
2. Построим график на отрезке (0, π).
3. Используйте специальные углы 0, π/4, π/2, 3π/4 и π/2 со значениями ∞, 1, 0, -1, -∞ соответственно.
4. Теперь мы можем нарисовать график.
Мы знаем, что sec x = 1 / cos x. Таким образом, ƒ(x) = sec x не определено, когда cos x = 0, что означает, что функция ƒ: R – {π/2 + kπ} → R – (-1, 1).
1. Период сек x равен 2π.
2. Построим график на интервале (0, 2π).
3. Мы можем использовать квадрантные углы и функцию косинуса, чтобы получить значения.
4. Теперь мы можем нарисовать график.
Мы знаем, что ƒ(x) = csc x и csc x = 1 / sin x, поэтому мы можем сказать, что csc x не определено, когда sin x = 0, что означает ƒ: R – {kπ} → R – (-1, 1).