Биномиальные коэффициенты онлайн: Онлайн калькулятор. Вычисление числа сочетаний из n по k элементов

Содержание

Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.

Сумма двух переменных в степени n

Разность двух переменных в степени n

биномиальный коэффициент

Рейтинг: 0 / 5

Треугольник Паскаля состоит из биномиальных коэффициентов

Таблицу следует читать по строкам. В каждом горизонтальном ряду находятся биномиальные коэффициенты для определенного n , при этом k принимает значения от 0 до n .

Пример чтения строки, для n=4 :

Рейтинг: 5 / 5

В комбинаторике биномиальный коэффициент означает, число всех возможных вариантов выборки k элементов из множества элементов n.

Пример:

Из множества n {1,2,3,4}, выбираем все возможные комбинации из двух элементов, k

{1,2} {1,3} {1,4} {2,3} {2,4} {3,4}

Получается шесть возможных вариантов.

Подставив значения в формулу, проверим полученный результат:

Рейтинг: 5 / 5

Факториал — произведение первых по счету, n натуральных чисел, обозначается n!

для n ϵ N (множество натуральных чисел)

по определению:

Факториал существует только для натуральных чисел и нуля.

пример вычисления факториала:

3!=1·2·3=6

5!=1·2·3·4·5=120

Рейтинг: 0 / 5

Одночлен — произведение числа (коэффициента), одной или несколько переменных и их натуральных степеней.

Многочлен — алгебраическая сумма одночленов.

Двучлен (бином) — многочлен состоящий из двух членов

A. B. C. D — одночлены

Сложение многочленов:

Вычитание многочленов:

Умножение многочлена на одночлен:

Деление многочлена на одночлен:

Умножение многочлена на многочлен:

Рейтинг: 0 / 5

a— основание степени, действительное число ( aϵ R )

n — показатель степени, натуральное число ( n ϵ N )

Произведение степеней с одинаковым основанием:

Деление степеней с одинаковым основанием:

если n > m

если n = m

если n < m

Возведение степени в степень:

Произведение в степени:

Деление в степени:

Рейтинг: 2 / 5

Вопрос №20169 от пользователя Yuriy Kim в испытании «Без двух нулей»

Все топики

Yuriy Kim

Ох и сложное это задание, так и не смог описать алгоритм. Кто пишет что это сочетания вводит в заблуждение. Для сочетания «0011» и «0101» одно и тоже множество. По крайней мере я убедился что дело не в сочетании и размещении как таковых, освежил свою память по курсу Комбинаторика для начинающих Moscow Institute of Physics and Technology. Нашел на просторах интернета точно такую же задачку из уч. пособия Дискретная математика Азарнова Т.В., Булгакова И.Н.

, там есть математическое описание решения (сразу скажу тоже сложное для понимания, но смысл понятен) и если после прочтения вновь посмотреть на решение автора, то можно понять алгоритм:). В общем касательно комбинаторики советую проходить курс включая «Полиномиальный коэффициент» я умер на «Биномиальные коэффициенты» возможно истина кроется в перестановках :).

1 2

Alex Kawperwood

Спасибо за ссылку на курс, лектор веселый 🙂

Задавайте вопросы по уроку
Проверяйте знания в квизах
Проходите практику прямо в браузере
Отслеживайте свой прогресс

Зарегистрируйтесь или войдите в свой аккаунт

Рекомендуемые программы

Профессия

с нуля

Фронтенд-разработчик

Разработка фронтенд-компонентов для веб-приложений

23 марта 10 месяцев

Профессия

Новый с нуля

Онлайн-буткемп. Фронтенд-разработчик

Интенсивное обучение профессии в режиме полного дня

20 апреля 4 месяца

Профессия

Новый с нуля

Аналитик данных

Сбор, анализ и интерпретация данных

дата определяется 9 месяцев

Профессия

с нуля

Python-разработчик

Разработка веб-приложений на Django

23 марта 10 месяцев

Профессия

с нуля

Java-разработчик

Разработка приложений на языке Java

23 марта 10 месяцев

Профессия

с нуля

PHP-разработчик

Разработка веб-приложений на Laravel

23 марта 10 месяцев

Профессия

с нуля

Инженер по тестированию

Ручное тестирование веб-приложений

23 марта 4 месяца

Профессия

с нуля

Node.js-разработчик

Разработка бэкенд-компонентов для веб-приложений

23 марта 10 месяцев

Профессия

с нуля

Fullstack-разработчик

Разработка фронтенд- и бэкенд-компонентов для веб-приложений

23 марта 16 месяцев

Профессия

c опытом

Разработчик на Ruby on Rails

Создание веб-приложений со скоростью света

23 марта 5 месяцев

Профессия

с нуля

Верстальщик

Верстка с использованием последних стандартов CSS

в любое время 5 месяцев

Биномиальное распределение

Чтобы понять биномиальное распределение и биномиальную вероятность, полезно понимать биномиальные эксперименты и некоторые связанные с ними обозначения; так что мы осветить эти темы в первую очередь.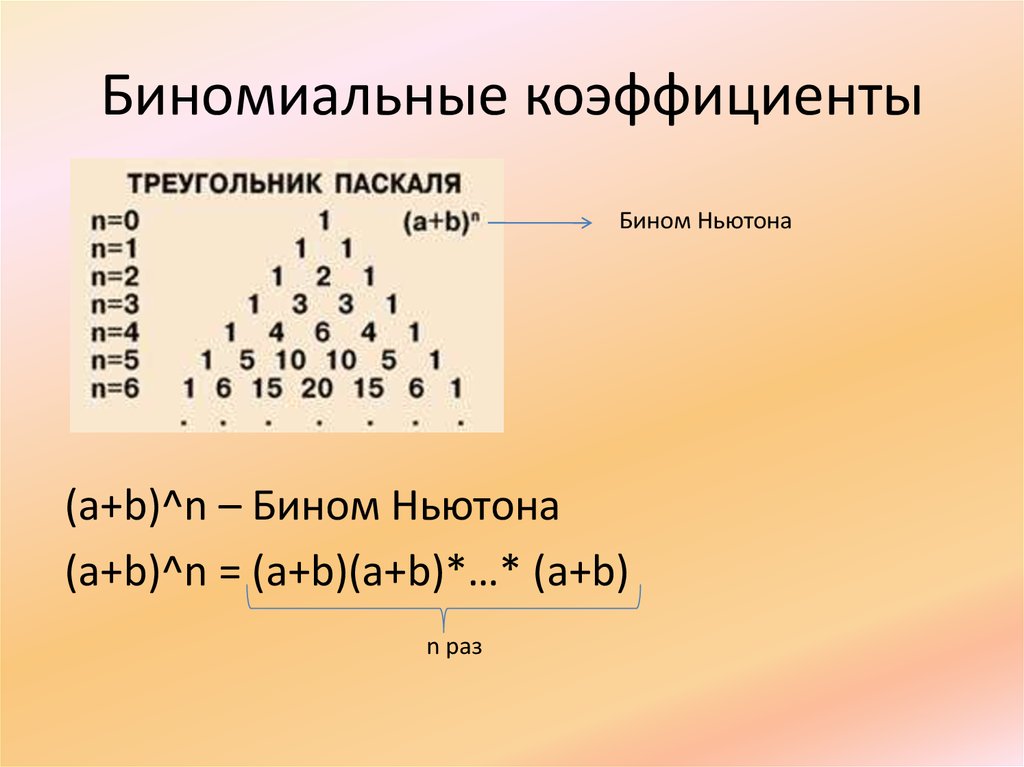

Примечание: Ваш браузер не поддерживает видео HTML5. Если вы просматриваете эту веб-страницу в другом браузере (например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеообработку этого урока.

Биномиальный эксперимент

A Биномиальный эксперимент это статистический эксперимент, обладающий следующими свойствами:

Испытания независимы; то есть результат одного испытания не влияет на результат других испытаний.

Рассмотрим следующий статистический эксперимент. Вы подбрасываете монету 2 раза и считаете количество раз, когда монета падает орлом. Это биномиальный эксперимент потому что:

Испытания независимы; то есть получение орлов на одном испытании не влияет получим ли мы головы на других испытаниях.

Обозначение

Следующие обозначения полезны, когда мы говорим о биномиальной вероятности.

_n C _r : Количество комбинации из n вещей, взятых r за один раз.

Биномиальное распределение

n повторных попыток биномиального эксперимента. Распределение вероятностей биномиальной случайной величины называется биномиальное распределение .

Предположим, мы подбрасываем монету два раза и подсчитываем количество выпавших орлов (успехов). биномиальная случайная величина — это количество орлов, которое может принимать значения 0, 1 или 2. Биномиальное распределение представлено ниже.

Количество головок	Вероятность
0	0,25
1	0,50
2	0,25

Биномиальное распределение обладает следующими свойствами:

Биномиальная формула и биномиальная вероятность

Биномиальная вероятность относится к вероятности того, что биномиальный эксперимент дает ровно x успехов. Например, в приведенной выше таблице мы видим, что биномиальная вероятность получения ровно одного решка в двух бросках монеты равна 0,50.

Учитывая x , n и P , мы можем вычислить биномиальную вероятность по биномиальной формуле:

Биномиальная формула. Предположим, бином эксперимент состоит из n испытаний и дает x успешных результатов. Если вероятность успеха в отдельном испытании равна P , тогда биномиальная вероятность:

б( х ; н, Р ) = _н С _х * Р ^х * (1 — Р) ^{н — х}
или
б( 90 3 х х ; ) = { п! / [ Икс! (н — х)! ] } * P ^x * (1 — P) ^{n — x}

Пример 1

Предположим, что игральную кость подбрасывают 5 раз. Какова вероятность получить ровно 2 четверки?

Решение: Это биномиальный эксперимент, в котором число испытаний равно равно 5, количество успехов равно 2, а вероятность успех в одном испытании составляет 1/6 или около 0,167.

Следовательно, бином вероятность:
б(2; 5, 0,167) = ₅ C ₂ * (0,167) ² * (0,833) ³
B (2; 5, 0,167) = 10 * (0,167) ² * (0,833) ³ 2 * (0,833) ³ * (0,833) ³ 2 * (0,833) 2 * (0,833) ² * (0,833) 5, 0,167) = 0,161
Кумулятивная биномиальная вероятность
Кумулятивная биномиальная вероятность относится к вероятности что биномиальная случайная величина попадает в заданный диапазон (например, больше или равно установленному нижнему пределу и меньше или равно установленному верхнему пределу).
Чтобы вычислить кумулятивную биномиальную вероятность, мы находим сумму соответствующих индивидуальных биномиальных вероятностей, как показано ниже в Примере 2.
Пример 2
Какова вероятность того, что при 100 подбрасываниях монеты выпадет 45 или меньше решек?
Решение: Чтобы решить эту задачу, мы вычисляем 46 отдельных биномиальных вероятностей, используя биномиальную формулу. Сумма всех этих биномиальных вероятностей и есть ответ, который мы искать. Таким образом,
b(x < 45; 100, 0,5) = b(x = 0; 100, 0,5) + b(x = 1; 100, 0,5) + . . . + b(x = 44; 100, 0,5) + b(x = 45; 100, 0,5)
б (х < 45; 100, 0,5) = 0,184
Биномиальный калькулятор
Как вы могли заметить, биномиальная формула требует много времени. вычисления. Биномиальный калькулятор может сделать эту работу за вас — быстро, легко и без ошибок. Используйте биномиальный калькулятор для вычисления биномиала. вероятности и кумулятивные биномиальные вероятности. калькулятор бесплатный. Его можно найти в Stat Trek Главное меню на вкладке Инструменты статистики. Или вы можете нажать кнопку ниже.
Биномиальный калькулятор
Пример 3
Вероятность поступления студента в престижный колледж равна 0,3. Если Подали заявки 5 учеников из одной школы, какова вероятность того, что не более 2 принимаются?
Решение: Чтобы решить эту задачу, мы вычисляем 3 отдельные вероятности, используя биномиальную формулу. Сумма всех этих вероятностей и есть ответ, который мы искать. Таким образом,
б(х < 2; 5, 0,3) = b(x = 0; 5, 0,3) + b(x = 1; 5, 0,3) + b(x = 2; 5, 0,3)
б(х < 2; 5, 0,3) = 0,1681 + 0,3601 + 0,3087
б (х < 2; 5, 0,3) = 0,8369
Пример 4
Какова вероятность того, что мировая серия продлится 4 игры? 5 игр? 6 игр? 7 игр? Предположим, что команды равны.
Решение: Решение этой проблемы требует творческого подхода. биномиальная формула. Если вы можете следовать логике этого решения, у вас есть хорошее понимание материала, изложенного в учебнике, к этому точка.
В мировой серии участвуют две бейсбольные команды. Сериал заканчивается, когда команда-победитель выигрывает 4 игры. Поэтому мы определяем успех как победа команды, которая в конечном итоге становится чемпионом мировой серии.
Для целей данного анализа мы предполагаем, что команды равны. Следовательно, вероятность того, что конкретная команда выиграет конкретную игру, равна 0,5.
Сначала рассмотрим простейший случай. Какова вероятность того, что ряд длится всего 4 игры. Это может произойти, если одна команда выиграет первые 4 игры. Вероятность того, что команда Национальной лиги выиграет 4 игры подряд это:
б(4; 4, 0,5) = ₄ С ₄ * (0,5) ⁴ * (0,5) ⁰ = 0,0625
Точно так же, когда мы вычисляем вероятность того, что команда Американской лиги выиграв 4 игры подряд, мы находим, что он также равен 0,0625. Следовательно, вероятность того, что серия закончится на четыре игры будут 0,0625 + 0,0625 = 0,125; так как сериал закончился бы, если бы либо американская команда, либо команда Национальной лиги выиграли 4 игры подряд.
Теперь займемся поиском вероятности того, что мировой ряд заканчивается в 5 играх. Хитрость в поиске этого решения заключается в том, чтобы признать, что серия может закончиться только через 5 игр, если у одной команды выиграл 3 из первых 4 игр. Итак, сначала найдем вероятность что команда Американской лиги выигрывает ровно 3 из первых 4 игр.
б(3; 4, 0,5) = ₄ С ₃ * (0,5) ³ * (0,5) ¹ = 0,25
Ладно, тут еще кое-что посложнее, так что слушайте. Учитывая, что Команда Американской лиги выиграла 3 из первых 4 игр, команда Американской лиги имеет шанс 50/50 выиграть пятую игру, чтобы закончить серию. Таким образом, вероятность того, что команда Американской лиги выиграет серия в 5 играх 0,25*0,50=0,125. Начиная с Национальной лиги команда также могла выиграть серию из 5 игр, вероятность того, что серия заканчивается в 5 играх будет 0,125 + 0,125 = 0,25.
Остальная часть проблемы будет решена таким же образом. Вы должны найти что вероятность окончания серии в 6 партий равна 0,3125; и вероятность того, что серия закончится в 7 партий, также равна 0,3125.
Последний урок Следующий урок
Калькулятор биномиального распределения
Онлайн-калькулятор биномиального распределения может найти кумулятивную и биномиальную вероятности для заданных значений. Теперь вы можете быстро определить стандартное отклонение, дисперсию и среднее значение биномиального распределения с помощью калькулятора биномиального распределения вероятностей. В следующей статье вы сможете понять, что такое биномиальное распределение, когда и как его применять, а также многое другое, что вам следует знать о распределении вероятностей. Начнем с основ!
Что такое биномиальное распределение?
В статистике биномиальное распределение — это дискретное распределение вероятностей, которое дает только два возможных результата эксперимента: неудачу или успех. Например, если мы подбрасываем монету, может быть только два возможных исхода: решка или орел, а при прохождении любого теста может быть только два исхода: зачет или провал. Это распределение называется биномиальным распределением вероятностей.
В биномиальном распределении используются два параметра p и n. Переменная «n» представляет собой частоту эксперимента, а переменная «p» представляет вероятность результата. Предположим, что кости бросают 10 раз случайным образом, тогда вероятность каждого броска равна 2. Если вы бросите кости 10 раз, вы получите биномиальное распределение с p = ⅙ и n = 10. Исследуйте формулу для расчета распределения два результата в нескольких экспериментах.
Формула биномиального распределения:
Формула биномиального распределения:
$$ P(x) = pr (1 − p) n−r . nCr $$
Или
$$ P(x) = pr (1 − p) n−r . [n!/r!(n−r)!] $$
Где
r = общее количество успешных трасс
n = общее количество событий
p = вероятность успеха
1 – p = вероятность неудачи
nCr = [n!/r!(n−r)]!
Однако онлайн-калькулятор распределения Пуассона определяет вероятность того, что событие произойдет много раз в течение заданных интервалов.
Как рассчитать биномиальное распределение вероятностей?
Вот исчерпывающий пример, который описывает, как работает калькулятор биномиального распределения, который может быть полезен для определения биномиального распределения вручную, если это необходимо.
Пример:
Монета подбрасывается 5 раз с вероятностью 0,13 для количества успехов (x) и условием ровно X успехов P(X = x).
Решение:
Вероятность ровно 3 успеха
$$ P(X = 3) = 0,016629093 $$
Используйте биномиальный калькулятор CDF, чтобы получить стандартное отклонение, дисперсию и среднее значение биномиального распределения на основе количества предоставленных вами следов.
Среднее значение: μ = np = ((5) × (0,13)) = 0,65
Дисперсия:
Стандартное отклонение: σ = np(1 − p) = (5) (0,13) (1 − 0,13) = 0,75199734042083
Заданные значения:
9X⋅ (1 − p) n − X $$
Где,
n = количество испытаний
p = вероятность успеха в одном испытании,
X = количество успехов
в значения для этой задачи, n = 5, p = 0,13 и X = 3:
$$ P (3) = 5! / 3! (5−3)! ⋅ 0,133 ⋅ (1 − 0,13) 5 − 3 $$
После решения выражения:
$$ P (3) = 0,016629093 $$
Калькулятор биномиального распределения Предоставьте таблицу для: n = 5, p = 0,13
$$ P(0) = 0,4984209207 $$
$$ P(1) = 0,3723834465 $$
$$ P(2) = 0,111287007 $$
$$ P(3) = 0,016 $9003 6290903 $ $ P(4) = 0,0012424035 $$
$$ P(5) = 3,71293E−5 $$
Круговая диаграмма для относительной вероятности:
Калькулятор биномиальной вероятности отображает круговую диаграмму для относительной вероятности:
Вероятность против количества успехов График:
Однако онлайн-калькулятор биномиальной теоремы поможет вам найти расширяющиеся биномы для данного биномиального уравнения.
Биномиальное распределение вероятностей:
В распределении вероятностей количество «успехов» в последовательности n экспериментов, где каждый раз задается вопрос «да или нет», тогда результат выражается как логическое значение для успех/да/правда/вероятность p или неудача/нет/ложь/вероятность q = 1-p. Успешный/неудачный модульный тест также называется тестом Бернулли или экспериментом Бернулли, а ряд результатов называется процессом Бернулли. Для n = 1, то есть для одного эксперимента, биномиальное распределение является распределением Бернулли. Биномиальное распределение лежит в основе известного теста биномиальной статистической значимости.
Отрицательное биномиальное распределение:
В вероятности количество успешных результатов в серии одинаково распределенных и независимых распределенных тестов Бернулли до того, как произойдет определенное количество неудач. Это называется отрицательным биномиальным распределением. Количество отказов/ошибок обозначается буквой «r».
Биномиальное распределение Среднее значение и дисперсия:
Для биномиального распределения дисперсия, среднее значение и стандартное отклонение заданного числа успехов выражаются следующей формулой
$$ Дисперсия, σ2 = npq $$
$$ Среднее значение, µ = np $$
$$ Стандартное отклонение σ= √(npq) $$
Эти формулы используются калькулятором биномиального распределения для определения дисперсия, среднее значение и стандартное отклонение.
Где,
p = вероятность успеха
q = вероятность отказа является непрерывным. Это означает, что биномиальное распределение — это ограниченное количество событий, тогда как нормальное распределение имеет бесконечное количество событий. Если размер выборки биномиального распределения очень велик, то кривая распределения биномиального распределения совпадает с кривой нормального распределения.
Свойства биномиального распределения:
Основные свойства биномиального распределения:
Возможны два исхода: успех или неудача, истина или ложь, да или нет.
Существует ‘n’ фиксированное количество n повторных попыток или независимых трейлов.
Каждый трейл имеет разную вероятность неудачи или успеха.
Считайте только количество успешных попыток n, которые являются независимыми испытаниями.
Каждое испытание является независимым испытанием, что означает, что результат одного испытания не влияет на результат другого испытания.
Как работает калькулятор биномиального распределения?
Онлайн-калькулятор биномиального распределения вероятностей находит вероятности для различных условий, используя следующие шаги:
Ввод:
Сначала введите количество следов, вероятность и количество успехов.
Теперь выберем условие для определения биномиального распределения.
Нажмите кнопку «Рассчитать».
Выходные данные:
Калькулятор формулы биномиальной вероятности отображает дисперсию, среднее значение и стандартное отклонение.
Онлайн-биномиальный калькулятор показывает биномиальные коэффициенты, таблицу биномиального распределения, круговую диаграмму и гистограмму для вероятности и количества успешных попыток.
Часто задаваемые вопросы:
Каковы критерии биномиального распределения?
Необходимо указать количество испытаний/испытаний.
Каждое испытание должно быть независимым.
Вероятность успеха в каждом испытании одинакова.
Использование биномиального распределения в реальной жизни.
В реальной жизни можно найти много примеров биномиального распределения. Например, когда новое лекарство используется для лечения болезни, оно либо излечивает болезнь (что является успешным), либо не может вылечить болезнь (что является неудачей).
Вывод:
Используйте этот онлайн-калькулятор биномиального распределения, чтобы оценить совокупные вероятности для биномиального распределения, учитывая количество испытаний (n), количество успешных попыток (X) и вероятность (p) успешного исхода.
No related posts.