Математика. Рациональные числа | Сайт Леонида Некина
В прошлый раз мы познакомились с дробями и упомянули о том, что они тоже называются числами. Речь идет о так называемых рациональных числах. Вообще, рациональным называют такое число, которое можно записать в виде дроби
$\dfrac{\,a\,}{b}$,
где $a$ и $b$ — какие-либо целые числа, причем ${b \ne 0}$. Если $a$ делится нацело на $b$, то число ${\frac{\,a\,}{b}}$ является целым, в противном случае оно называется дробным. (Заметим, что обычно в определении рациональных чисел знаменатель $b$ объявляют не целым, а натуральным числом. Сути дела это нисколько не меняет.) Всякое целое число $a$ является одновременно рациональным, поскольку оно представимо в виде ${\frac{\,a\,}{1}}$.
Почему же дроби называются числами? Потому что их можно складывать между собой, вычитать друг из друга, умножать одно на другое и делить друг на друга, и при этом они ведут себя так же, как и привычные нам целые числа — в том смысле, что все знакомые нам свойства арифметических действий остаются в силе. Давайте в этом убедимся.
Давайте в этом убедимся.
В последующих рассуждениях мы будем считать, что ${\frac{\,a\,}{b}}$, ${\frac{\,c\,}{d}}$ и ${\frac{\,p\,}{q}}$ — это три произвольных рациональных числа (все числители и знаменатели — целые числа, причем знаменатели отличны от нуля). Начнем с умножения, которое мы определим так:
$\Bigl(\dfrac{\,a\,}{b} \dfrac{\,c\,}{d}\Bigr) (…) = \dfrac{\,a\,}{b} \Bigl(\dfrac{\,c\,}{d} (…)\Bigr)$.
Что делает оператор ${\frac{\,c\,}{d}}$? Он находит среди последующих сомножителей число $d$ и заменяет его на число $c$. А что делает произведение операторов ${\frac{\,a\,}{b} \frac{\,c\,}{d}}$? Согласно нашему определению, оно находит числа $d$ и $b$ и заменяет их на $c$ и $a$:
$\Bigl(\dfrac{\,a\,}{b} \dfrac{\,c\,}{d}\Bigr) (b \cdot d \cdot x) = a \cdot c \cdot x$.
Отсюда очевидно, что умножение рациональных чисел осуществляется по такому правилу:
\[ \boxed{\quad \frac{\,a\,}{b} \cdot \frac{\,c\,}{d} = \frac{a\cdot c}{b\cdot d} \quad} \]
Легко убедиться, что такое умножение обладает свойствами коммутативности («переместительности») и ассоциативности («сочетательности»):
$\dfrac{\,a\,}{b}\,\dfrac{\,c\,}{d} = \dfrac{\,c\,}{d}\,\dfrac{\,a\,}{b}; \quad \dfrac{\,a\,}{b}\Big(\dfrac{\,c\,}{d}\,\dfrac{\,p\,}{q}\Big) = \Big(\dfrac{\,a\,}{b}\,\dfrac{\,c\,}{d}\Big)\dfrac{\,p\,}{q}$.
На менее формальном языке это означает, что мы можем произвольно менять порядок вычислений в произведении любого числа сомножителей.
Сокращение дробей. Если у дроби числитель и знаменатель равны между собой, то такая дробь, очевидно, равна единице:
$\dfrac{\,b\,}{b} = 1.$
Отсюда
\[ \boxed{\quad \frac{a\cdot b}{d\cdot b} = \frac{\,a\,}{d} \quad} \]
Таким образом, значение дроби не меняется, если числитель и знаменатель одновременно умножить или поделить на одно и то же число. Например,
$\dfrac{\,2\,}{3} \cdot \dfrac{\,3\,}{5} = \dfrac{2\cdot 3}{3\cdot 5} =\dfrac{\,2\,}{5}$.
Одновременное деление числителя и знаменателя на одно и то же число $b$ называют сокращением дроби на число $b$. Давно нам знакомое правило деления круглых чисел является, по сути дела, частным случаем сокращения на $10$:
$\dfrac{20}{30} = \dfrac{2 \cdot 10}{3 \cdot 10} = \dfrac{\,2\,}{3}$.
Вот еще два полезных соотношения, которые получаются, если числитель и знаменатель дроби одновременно умножить (или поделить) на $-1$:
\[ \boxed{\quad \frac{-a}{-b} = \frac{\,a\,}{b}; \quad \frac{a}{-b} = \frac{-a}{b} \quad} \]
Взаимно обратные дроби. Если целое число $c$ не равно нулю, то у оператора ${\frac{\,c\,}{d} (…)}$, очевидно, имеется взаимно обратный оператор, равный ${\frac{\,d\,}{c} (…)}$. В самом деле
Если целое число $c$ не равно нулю, то у оператора ${\frac{\,c\,}{d} (…)}$, очевидно, имеется взаимно обратный оператор, равный ${\frac{\,d\,}{c} (…)}$. В самом деле
$\dfrac{\,d\,}{c} \dfrac{\,c\,}{d} = \dfrac{\,c\,}{d} \dfrac{\,d\,}{c} = 1$.
В этом случае говорят также о взаимно обратных дробях или взаимно обратных числах.
Деление числа ${\frac{\,a\,}{b}}$ на число ${\frac{\,c\,}{d}}$ определяется как произведение первого числа на число, обратное ко второму. Такое деление может быть записано в виде «многоэтажной» дроби:
\[ \boxed{\quad \cfrac{~~\cfrac{\,a\,}{b}~~}{~~\cfrac{\,c\,}{d}~~} = \frac{\,a\,}{b} \cdot \frac{\,d\,}{c} \quad} \]
Этот же результат мы получим, если просто умножим числитель и знаменатель нашей «многоэтажной» дроби на $bd$:
$\cfrac{~\cfrac{\,a\,}{b}\,\,bd~}{\cfrac{\,c\,}{d}\,\,bd} = \dfrac{\,ad\,}{cb}$.
Сложение и вычитание дробей естественно определить так, чтобы выполнялось свойство дистрибутивности (которые в школе называется распределительным свойством умножения):
\begin{align*} \Bigl(\frac{\,a\,}{b} + \frac{\,c\,}{d}\Bigr) x &= \frac{\,a\,}{b} x + \frac{\,c\,}{d} x. \\ \Bigl(\frac{\,a\,}{b} — \frac{\,c\,}{d}\Bigr) x &= \frac{\,a\,}{b} x — \frac{\,c\,}{d} x. \end{align*}
\\ \Bigl(\frac{\,a\,}{b} — \frac{\,c\,}{d}\Bigr) x &= \frac{\,a\,}{b} x — \frac{\,c\,}{d} x. \end{align*}
Здесь $x$ — любое число или вещь.
Сложение и вычитание дробей с одинаковым знаменателем. Рассмотрим такую цепочку равенств (для удобства здесь каждый знак равенства дополнен подходящим обоснованием):
\begin{align*} &\frac{\,a\,}{b} + \frac{\,c\,}{b} = \\ &=~ a \cdot \frac{\,1\,}{b} + c \cdot \frac{\,1\,}{b} = &&\text{по определению дроби} \\ &=~ (a + c)\cdot \frac{\,1\,}{b} = &&\text{дистрибутивность} \\ &=~ \frac{a + c}{b}.&&\text{по определению дроби} \end{align*}
Заметим, что эта цепочка равенств осталась бы справедливой, если бы мы в ней всюду поменяли знак «плюс» на знак «минус». Таким образом, мы приходим к следующим правилам:
\[ \boxed{ \begin{align*}\quad\frac{\,a\,}{b} + \frac{\,c\,}{b} &= \frac{a + c}{b} \\ \frac{\,a\,}{b} — \frac{\,c\,}{b} &= \frac{a — c}{b}\quad \end{align*} } \]
Сложение и вычитание дробей с разным знаменателем. Если знаменатели у дробей разные, то прежде чем их складывать, их надо заменить дробями с одинаковым знаменателем. Делается это так:
Если знаменатели у дробей разные, то прежде чем их складывать, их надо заменить дробями с одинаковым знаменателем. Делается это так:
$\dfrac{\,a\,}{b} + \dfrac{\,c\,}{d} = \dfrac{a\cdot d}{b\cdot d} + \dfrac{c \cdot b}{d\cdot b}$.
Это называется приведением дробей к одинаковому знаменателю. Точно такую же процедуру надо проделать, если мы имеем дело с вычитанием. Общие правила сложения и вычитания выглядят следующим образом:
\[ \boxed{ \begin{align*}\quad\frac{\,a\,}{b} + \frac{\,c\,}{d} &= \frac{ad + cb}{bd} \\ \frac{\,a\,}{b} — \frac{\,c\,}{d} &= \frac{ad — cb}{bd}\quad \end{align*} }\]
Впрочем, во многих конкретных случаях задача сложения или вычитания дробей с разными знаменателями решается несколько проще. Например:
\[ \frac{\,1\,}{3} + \frac{\,1\,}{6} = \frac{1\cdot 2}{3\cdot 2} + \frac{\,1\,}{6} = \frac{\,2\,}{6} + \frac{\,1\,}{6} = \frac{2 + 1}{6} = \frac{\,3\,}{6} = \frac{1\cdot 3}{2 \cdot 3} = \frac{\,1\,}{2}. \]
Или:
\[ \frac{\,1\,}{4} + \frac{\,1\,}{6} = \frac{1 \cdot 3}{4 \cdot 3} + \frac{1 \cdot 2}{6 \cdot 2} = \frac{\,3\,}{12} + \frac{\,2\,}{12} = \frac{3+2}{12} = \frac{\,5\,}{12}. \]
\]
Противоположные числа. Два рациональных числа называются противоположными, если их сумма равна нулю. Пусть ${\frac{\,a\,}{b}}$ — произвольное рациональное число, тогда число, ему противоположное, обозначается как
$-\dfrac{\,a\,}{b}~~\text{или}~~-(a / b)$.
Очевидно, что
$-\dfrac{\,a\,}{b} = \dfrac{-a}{b} = \dfrac{a}{-b}$.
Нетрудно также убедиться, что разность чисел ${\frac{\,a\,}{b}}$ и ${\frac{\,c\,}{d}}$ равна сумме чисел ${\frac{\,a\,}{b}}$ и ${-\frac{\,c\,}{d}}$. Действительно, складываем ${\frac{\,a\,}{b}}$ и ${-\frac{\,c\,}{d}}$ и получаем тот же результат, как если бы мы вычисляли разность ${\frac{\,a\,}{b} — \frac{\,c\,}{d}}$:
\[\dfrac{\,a\,}{b} + \Big(-\dfrac{\,c\,}{d}\Big) = \dfrac{\,a\,}{b} + \dfrac{-c}{d} = \dfrac{ad + (-c)b}{bd} = \dfrac{ad -cb}{bd}.\]
Немного о терминологии. Какую часть (или какую долю) число $1$ составляет от числа $7$? Разумеется, одну седьмую, то есть ${\frac{\,1\,}{7}}$. В общем случае дробь ${\frac{\,x\,}{y}}$ говорит нам о том, сколько (и каких) частей число $x$ составляет от числа $y$ ($x$ и $y$ — произвольные рациональные числа, ${y \ne 0}$):
В общем случае дробь ${\frac{\,x\,}{y}}$ говорит нам о том, сколько (и каких) частей число $x$ составляет от числа $y$ ($x$ и $y$ — произвольные рациональные числа, ${y \ne 0}$):
число $2$ составляет $\frac{\,2\,}{3}$ (две трети) от числа $3$
или: $\frac{\,2\,}{3}$ (две трети) от числа $3$ равно $2$;
$\frac{\,3\,}{2}$ (три вторых) от числа $\frac{\,1\,}{3}$ равно $\frac{\,3\,}{2} \frac{\,1\,}{3} = \frac{\,1\,}{2}$
или: число $\frac{\,1\,}{2}$ составляет $\frac{\,1\,}{2} \big/ \frac{\,1\,}{3} = \frac{\,3\,}{2}$ (три вторых) от числа $\frac{\,1\,}{3}$.
Число, выражаемое дробью ${\frac{\,x\,}{y}}$, называют отношением чисел $x$ и $y$. Уже знакомое нам слово частное тоже, разумеется, можно употреблять в этом значении.
Числовая прямая. Рациональные числа удобно ассоциировать с точками на бесконечной прямой. Делается это так. Рисуем прямую линию и с помощью засечек отмечаем на ней в произвольных местах две разные точки. Одна из этих точек символизирует число «ноль», другая — число «единица». (Обычно эту линию чертят горизонтально, а единицу располагают правее нуля, но это необязательно.) Расстояние между этими двумя точками принимаем за единичную длину. Далее, мы равномерно покрываем засечками всю нашу прямую, так чтобы расстояние между соседними засечками равнялось единичной длине, и нумеруем их целыми числами.
(Обычно эту линию чертят горизонтально, а единицу располагают правее нуля, но это необязательно.) Расстояние между этими двумя точками принимаем за единичную длину. Далее, мы равномерно покрываем засечками всю нашу прямую, так чтобы расстояние между соседними засечками равнялось единичной длине, и нумеруем их целыми числами.
Помните, когда мы только начинали говорить о целых числах, мы ассоциировали их со ступеньками лестницы, по которой можно было подняться вверх или спуститься вниз? Теперь же наше представление о числах в очередной раз обогатилось, и они предстали перед нами в виде точек на прямой. Но, как и ранее, мы можем с тем же успехом считать, что числа — это команды по перемещению вдоль линии, и представлять их себе не как засечки, а как протяженные отрезки-стрелочки, у которых есть начало и конец, причем начало совпадает с нулем, а конец приходится на ту или иную засечку:
Знак перед числом («минус» или подразумеваемый «плюс») указывает, в какую сторону направлена стрелочка, а «голое» число без знака представляет собой длину отрезка: оно говорит нам о том, сколько единичных длин укладывается между его началом и концом. Но рисовать стрелочки не так удобно, как засечки, поэтому мы будем всё же пользоваться засечками.
Но рисовать стрелочки не так удобно, как засечки, поэтому мы будем всё же пользоваться засечками.
Разделим отрезок между нулем и единицей на две равные части, поставив посередине новую засечку и пометив ее числом $\frac{1}{2}$. Расстояние от нуля до этой засечки задает нам новую длину, равную одной второй от единичной длины. Покроем нашу прямую новой порцией засечек, так чтобы расстояние между соседними засечками равнялось новой длине. Пронумеруем новые засечки целыми числами, приписав к ним через дробную черту знаменатель $2$:
Как и следовало ожидать, часть новых засечек совпала со старыми.
Повторим еще раз эту же процедуру с той разницей, что теперь мы будем делить отрезок между нулем и единицей не на две, а на три части. Для этого нам понадобятся две новые засечки. Берем ту из них, которая ближе расположена к нулю и помечаем ее числом $\frac{1}{3}$. После расстановки и нумерации очередной порции засечек получаем следующую картину (во избежание путаницы тут показаны только дроби со знаменателем $3$):
И так далее и тому подобное. Покажем, пожалуй, еще рисунок с дробями со знаменателем $4$ и на этом остановимся:
Покажем, пожалуй, еще рисунок с дробями со знаменателем $4$ и на этом остановимся:
Каким бы ни было рациональное число ${\frac{\,a\,}{b}}$, для него обязательно найдется соответствующая точка на нашей числовой прямой. Про эту точку тогда говорят, что ее положение равно ${\frac{\,a\,}{b}}$ (или же ее координата равна ${\frac{\,a\,}{b}}$). Следует только заметить, что если нам попадется дробь с отрицательным знаменателем, например $\frac{\,2\,}{-3}$, то, прежде чем откладывать ее на числовой прямой, мы сократим ее на $-1$:
$\dfrac{\,2\,}{-3} = \dfrac{-2}{\,3\,} = -\dfrac{\,2\,}{3}$.
Спрашивается: а как можно поделить отрезок на какое-нибудь заранее заданное число одинаковых частей? Вообще-то, для этого есть специальная процедура, с которой мы познакомимся, когда будем заниматься геометрией. А пока — мы будем делать это «на глазок» или, еще лучше, мы будем чертить наши рисунки на бумаге в клеточку и заранее выбирать длину единичного отрезка таким образом, чтобы его можно было легко разделить «по клеточкам».
Сравнение рациональных чисел. Проще всего сравнивать числа с нулем. Если некоторое рациональное число ${x = \frac{\,a\,}{b}}$ (точнее, соответствующая ему засечка) располагается на нашей числовой прямой справа от нуля (точнее, с той же стороны, что и единица), то про него говорят, что оно положительное и что оно больше нуля: ${\frac{\,a\,}{b} > 0}$. Если же оно расположено с другой стороны, то оно отрицательное и, соответственно, меньше нуля: ${\frac{\,a\,}{b} < 0}$. Вообще, запись
$x > y$
означает, что число $x$ правее (то есть больше) числа $y$, а одинаковая по смыслу запись
$y < x$
означает, что число $y$ левее (то есть меньше) числа $x$.
Пусть $x$ и $y$ — произвольные рациональные числа, так что ${x = \frac{\,a\,}{b}}$ и ${y = \frac{\,c\,}{d}}$. Как определить, которое из них меньше, а которое больше? Если подходить к делу чисто формально, то можно просто посчитать их разность
$x — y = \dfrac{\,a\,}{b} — \dfrac{\,c\,}{d} = \dfrac{ad — cb}{bd}$.
и сравнить ее с нулем. Если окажется, что результат больше нуля, тогда ${x > y}$. Если результат меньше нуля, тогда ${x < y}$. Для полноты картины следует отметить, что результат может оказаться равен нулю. В этом случае ${x = y}$.
Но если проявлять творческий подход, то оказывается, что во многих случаях дроби можно сравнивать не производя никаких вычислений. Например, сразу видно, что
$\dfrac{\,3\,}{7} < \dfrac{\,4\,}{7}$,
потому что у обеих этих дробей знаменатели одинаковы и — что тоже немаловажно — положительны, а числитель у первой дроби меньше, чем у второй. А как быть, если числители одинаковы, но отрицательны? Как сравнить, например,
$\dfrac{3}{-7}$ и $\dfrac{4}{-7}$?
Сделаем знаменатели положительными, сократив каждую из дробей на $-1$, и тогда сразу станет ясно, что
$\dfrac{3}{-7} = \dfrac{-3}{7} > \dfrac{-4}{7} = \dfrac{4}{-7}$.
Также нетрудно видеть, что
$\dfrac{\,1\,}{3} < \dfrac{\,1\,}{2}$ и $-\dfrac{\,1\,}{3} > -\dfrac{\,1\,}{2}$.
Вообще, если у двух положительных дробей числители одинаковы, то меньше та из них, у которых знаменатель больше. У отрицательных дробей — всё наоборот.
Смещение вдоль числовой прямой. Когда мы рассматриваем отдельные рациональные числа, взятые сами по себе, их удобно представлять себе как точки на числовой прямой. Но когда мы переходим к операциям сложения и вычитания, то уместнее говорить о смещениях вдоль этой прямой — точно так же, как мы говорили о прыжках по лестнице, когда имели дело с целыми числами. Пусть, например, нам дан такой пример:
$\dfrac{\,2\,}{3} + \dfrac{\,5\,}{3} = \dfrac{\,7\,}{3}$.
Глядя на числовую прямую, мы можем сказать, что мы начинаем движение из точки $\frac{\,2\,}{3}$, перемещаемся вправо на расстояние $\frac{\,5\,}{3}$ и оказываемся в точке $\frac{\,7\,}{3}$:
Таким образом, первое число в этом примере ($+\frac{\,2\,}{3}$) — это точка, а второе ($+\frac{\,5\,}{3}$) — это команда на смещение. Как мы знаем, числа позволительно интерпретировать и так, и этак. Но если мы хотим единообразия, то мы можем представить себе, что мы начинаем движение из точки $0$ и передвигаемся два раза. Первый раз — на величину $+\frac{\,2\,}{3}$, а второй раз — на величину $+\frac{\,5\,}{3}$. В этом случае оба слагаемых являются командами на смещение. Точка на числовой прямой соответствует тому же числу, что и команда смещения, которая перемещает нас из нуля в эту точку. Если нам даны два рациональных числа, например, $\frac{\,2\,}{3}$ и $\frac{\,7\,}{3}$, то команда, перемещающая нас из первой точки во вторую, — это разность ${\frac{\,7\,}{3} — \frac{\,2\,}{3}}$, в которой из второго числа вычитается первое.
Но если мы хотим единообразия, то мы можем представить себе, что мы начинаем движение из точки $0$ и передвигаемся два раза. Первый раз — на величину $+\frac{\,2\,}{3}$, а второй раз — на величину $+\frac{\,5\,}{3}$. В этом случае оба слагаемых являются командами на смещение. Точка на числовой прямой соответствует тому же числу, что и команда смещения, которая перемещает нас из нуля в эту точку. Если нам даны два рациональных числа, например, $\frac{\,2\,}{3}$ и $\frac{\,7\,}{3}$, то команда, перемещающая нас из первой точки во вторую, — это разность ${\frac{\,7\,}{3} — \frac{\,2\,}{3}}$, в которой из второго числа вычитается первое.
Смещение сохраняет разность между числами. Это значит, что если две точки $x$ и $y$ сместить на одинаковую величину $z$, то разность между новым положением точек останется неизменной:
$(y + z) — (x — z) = y — x$.
Масштабирование. Но числа — это не только точки, не только команды на смещение, это в первую очередь, конечно, операторы умножения, которые меняют количество тех вещей, на которые они действуют. Пока мы имели дело с целыми числами, мы могли только увеличивать это количество, например, из (одной) конфеты сделать $3$ конфеты. Теперь же, благодаря рациональным числам, мы можем менять количество вещей как в сторону увеличения, так и в сторону уменьшения, например, три конфеты превратить снова в одну (с помощью оператора $\frac{\,1\,}{3}$), а из одной конфеты получить половинку (с помощью оператора $\frac{\,1\,}{2}$).
Пока мы имели дело с целыми числами, мы могли только увеличивать это количество, например, из (одной) конфеты сделать $3$ конфеты. Теперь же, благодаря рациональным числам, мы можем менять количество вещей как в сторону увеличения, так и в сторону уменьшения, например, три конфеты превратить снова в одну (с помощью оператора $\frac{\,1\,}{3}$), а из одной конфеты получить половинку (с помощью оператора $\frac{\,1\,}{2}$).
Такие команды умножения (или уменьшения) можно, разумеется, применять и к точкам на числовой прямой. Действие этих команд в таком случае называется масштабированием. Например, применяя команду масштабирования $\frac{\,2\,}{3}$ к точке $\frac{\,4\,}{5}$, мы оказываемся в точке
$\dfrac{\,2\,}{3} \dfrac{\,4\,}{5} = \dfrac{2 \cdot 4}{3 \cdot 5} = \dfrac{8}{15}$.
Точка на числовой прямой соответствует тому же числу, что и команда масштабирования, которую надо применить к единице, чтобы попасть в эту точку.
Масштабирование сохраняет отношение между числами. Если одно и то же масштабирование $s$ применить к двум точкам $x$ и $y$, то отношение между их новым положением останется неизменным:
Если одно и то же масштабирование $s$ применить к двум точкам $x$ и $y$, то отношение между их новым положением останется неизменным:
$\dfrac{sx}{sy} = \dfrac{\,x\,}{y}$.
Абсолютная величина (модуль) числа — это то, что мы называли «голым» числом с отброшенным знаком. Если число отрицательное и перед ним стоит знак «минус», то после отбрасывания знака такое число превращается в противоположное. Если перед числом не стоит никакого знака (а подразумевается «плюс»), то отбрасывать, собственно, нечего и число остается самим собой. Модуль числа $x$ обозначается как $|x|$. Формальное определение модуля выглядит следующим образом:
\[ \boxed{\quad |x| = \begin{cases}\phantom{-}x, ~~\text{если}~~ x \geqslant 0;\\ -x, ~~\text{если}~~ x < 0. \end{cases} \quad} \]
Как мы знаем, всякому рациональному числу $x$ соответствует некоторая точка на числовой прямой. Модуль числа $x$ можно понимать как расстояние от этой точки до отметки «ноль». Расстояние между двумя точками, которые соответствуют некоторым произвольным числам $x$ и $y$, равно:
$|x — y| = \begin{cases}x — y, ~~\text{если}~~ x \geqslant y;\\ y — x, ~~\text{если}~~ x < y. \end{cases}$
\end{cases}$
Расстояние — это величина в любом случае неотрицательная. Расстояние от точки с координатой $x$ до точки с координатой $y$ в точности равно расстоянию от точки с координатой $y$ до точки с координатой $x$. (Ради простоты выражений, допустимо также говорить «расстояние между числами $x$ и $y$».)
Правильные, неправильные и смешанные дроби. Дроби, значение которых по абсолютной величине (по модулю) меньше единицы, называются правильными. Их внешний вид сравнительно легок для восприятия:
$\dfrac{\,1\,}{2},~~ \dfrac{\,3\,}{5},~~ -\dfrac{\,6\,}{7}$ и тому подобное.
Дроби, которые по абсолютной величине больше или равны единице, называются неправильными. Как правило, они воспринимаются на глаз гораздо труднее:
$\dfrac{15}{2},~~ \dfrac{14}{5},~~ -\dfrac{60}{7}$.
Чтобы облегчить восприятие, неправильные дроби часто записывают в виде так называемых смешанных чисел. Делается это следующим образом. Допустим, мы хотим записать в виде смешанного числа дробь
$\dfrac{15}{2}$. 1\!/\!_2}$. Сразу возникает недоуменный вопрос: как же так? Ведь мы до сих пор придерживались обозначений, согласно которым запись ${7\frac{\,1\,}{2}}$ должна означать произведение чисел $7$ и $\frac{\,1\,}{2}$, то есть ${7\cdot\frac{\,1\,}{2}}$, а вовсе не их сумму ${7+\frac{\,1\,}{2}}$. Приходится признать, что такая запись действительно имеет два совершенно разных смысла. Но путаницы всё же, как правило, не возникает, потому что из сопровождающих пояснительных слов бывает ясно, что именно имеется в виду.
1\!/\!_2}$. Сразу возникает недоуменный вопрос: как же так? Ведь мы до сих пор придерживались обозначений, согласно которым запись ${7\frac{\,1\,}{2}}$ должна означать произведение чисел $7$ и $\frac{\,1\,}{2}$, то есть ${7\cdot\frac{\,1\,}{2}}$, а вовсе не их сумму ${7+\frac{\,1\,}{2}}$. Приходится признать, что такая запись действительно имеет два совершенно разных смысла. Но путаницы всё же, как правило, не возникает, потому что из сопровождающих пояснительных слов бывает ясно, что именно имеется в виду.
Отрицательные смешанные числа записываются следующим образом:
$-\dfrac{60}{7} = -8\,\dfrac{\,4\,}{7}$.
Это на самом деле означает:
$-\dfrac{60}{7} = -8 — \dfrac{\,4\,}{7}$.
Здесь $-8$ это целая часть отрицательного числа, а ${-\frac{\,4\,}{7}}$ это дробная часть.
Запись рациональных чисел в виде смешанных дробей облегчает вычисления при выполнении операций сложения и вычитания, например:
\begin{align*} &\frac{15}{2} + \frac{14}{3} = 7\frac{\,1\,}{2} + 4\frac{\,2\,}{3} =\\ &= \Big(7 + 4\Big) + \Big(\frac{\,1\,}{2} + \frac{\,2\,}{3}\Big) =\\ &= \Big(7 + 4\Big) + \Big(\frac{\,3\,}{6} + \frac{\,4\,}{6}\Big) =\\ &= 11 + \frac{\,7\,}{6} = 11 + 1\frac{\,1\,}{6} = 12\frac{\,1\,}{6}. \end{align*}
\end{align*}
Если смешанную дробь требуется перевести обратно в неправильную, то это делается так:
\begin{align*} &12\frac{\,1\,}{6} = \frac{12\cdot 6}{6} + \frac{\,1\,}{6} = \\[1mm] &= \frac{12\cdot 6 + 1}{6} = \frac{72 + 1}{6} = \frac{73}{6}. \end{align*}
Конспект
1. Рациональное число — это дробь ${\frac{\,a\,}{b}}$, где $a$ и $b$ — это целые числа, причем ${b \ne 0}$.
2. Для рациональных чисел определены:
\begin{align*} &\text{умножение} &\dfrac{\,a\,}{b} \dfrac{\,c\,}{d} &= \dfrac{\,ac\,}{bd},\\ &\text{деление} &\dfrac{\,a\,}{b} \Big/ \dfrac{\,c\,}{d} &= \dfrac{\,a\,}{b} \dfrac{\,d\,}{c},\end{align*}
а также сложение и вычитание
\begin{align*} &\frac{\,a\,}{b} + \frac{\,c\,}{b} = \frac{a + c}{b}, &&\frac{\,a\,}{b} — \frac{\,c\,}{b} = \frac{a — c}{b}\\ &\text{(одинаковые числители)},&&\\ &\frac{\,a\,}{b} + \frac{\,c\,}{d} = \frac{ad + cb}{bd}, &&\frac{\,a\,}{b} — \frac{\,c\,}{d} = \frac{ad — cb}{bd}\\ &\text{(разные числители)}. &&\end{align*}
&&\end{align*}
Для сложения и умножения выполняются свойства коммутативности, ассоциативности и дистрибутивности (на школьном языке эти свойства называются переместительным, сочетательным и распределительным).
3. Рациональные числа $x$ и $y$ можно сравнивать между собой: $x$ > $y$, если ${x — y > 0}$; ${x < y}$, если ${x — y < 0}$; ${x = y}$, если ${x — y = 0}$.
4. Пусть $x$ и $y$ — рациональные числа. Результат деления ${\frac{\,x\,}{y}}$ называется их отношением (синоним слову частное). Также говорят, что $x$ составляет ${\frac{\,x\,}{y}}$ (икс игрековых частей) от числа $y$, например, число $2$ составляет $\frac{\,2\,}{3}$ (две третьих) от числа $3$.
5. Всякому рациональному числу ${\frac{\,a\,}{b}}$ можно сопоставить определенную точку на числовой прямой, каковая представляет собой прямую линию, где заранее отмечено положение нуля и единицы. Про эту точку тогда говорят, что ее положение равно ${\frac{\,a\,}{b}}$ (или ее координата равна ${\frac{\,a\,}{b}}$). Оператор сложения ${(…) + x}$, где $x$ — рациональное число, задает операцию смещения вдоль числовой прямой. Оператор умножения $x\,(…)$ задает операцию масштабирования. Смещение сохраняет разность между положениями точек. Масштабирование сохраняет отношение между ними.
Оператор сложения ${(…) + x}$, где $x$ — рациональное число, задает операцию смещения вдоль числовой прямой. Оператор умножения $x\,(…)$ задает операцию масштабирования. Смещение сохраняет разность между положениями точек. Масштабирование сохраняет отношение между ними.
6. Числа ${\frac{\,a\,}{b}}$ и ${-\frac{\,a\,}{b}}$ называются противоположными. Числа ${\frac{\,a\,}{b}}$ и ${\frac{\,b\,}{a}}$ называются взаимно обратными (${a \ne 0}$, ${b \ne 0}$). Абсолютная величина (модуль) числа $x$ — это число $x$ с отброшенным знаком:
\[|x| = \begin{cases}\phantom{-}x, ~~\text{если}~~ x \geqslant 0;\\ -x, ~~\text{если}~~ x < 0. \end{cases}\]
Расстояние между точками на числовой прямой, которым соответствуют числа $x$ и $y$, определяется как ${|y — x|}$.
7. Дроби, которые по абсолютной величине меньше единицы, называются правильными. Дроби, которые по абсолютной величине больше или равны единице, называются неправильными. Неправильную положительную дробь иногда записывают в виде смешанного числа, которое представляет собой сумму натурального числа (целой части) и правильной дроби (дробной части), при этом знак «плюс», который должен был бы стоять между этими двумя частями, опускается, например, ${\frac{\,7\,}{3} = 2\frac{\,1\,}{3}}$. Неправильная отрицательная дробь также может быть записана в виде смешанного числа: ${-2 \frac{\,1\,}{3} = — 2 — \frac{\,1\,}{3} = -\frac{\,7\,}{3}}$.
Неправильная отрицательная дробь также может быть записана в виде смешанного числа: ${-2 \frac{\,1\,}{3} = — 2 — \frac{\,1\,}{3} = -\frac{\,7\,}{3}}$.
Из «бесконечного» сборника типовых упражнений
Простые задания на понимание терминологии
То же, с использованием технологии LaTeX
Перевод смешанной дроби в неправильную
То же, LaTeX
Перевод неправильной дроби в смешанную
То же, LaTeX
Сложение и вычитание смешанных дробей с одинаковыми знаменателями (только положительные числа)
То же, LaTeX
Сложение смешанных дробей с одинаковыми знаменателями (положительные и отрицательные числа)
То же, LaTeX
Сравнение дробей
То же, LaTeX
Сложение и вычитание смешанных дробей с разными знаменателями (только положительные числа)
То же, LaTeX
Сложение смешанных дробей с разными знаменателями (положительные и отрицательные числа)
То же, LaTeX
Умножение и деление дробей
То же, LaTeX
Повторение предыдущего (только положительные числа):
То же, LaTeX
Повторение предыдущего (положительные и отрицательные числа):
То же, LaTeX
Раскрытие скобок в выражениях типа (a ∙/ b) ∙/ (c ∙/ d)
Параллель между сложением-вычитанием и умножением-делением в выражениях типа (a ± b) ± (c ± d) и (a ∙/ b) ∙/ (c ∙/ d)
3 особенности чисел в Python, о которых вы, возможно, не знали / Хабр
Если вы писали код на Python, то весьма высока вероятность того, что вы, хотя бы в одной из своих программ, пользовались числами. Например, это могли быть целые числа для указания индекса значения в списке, или числа с плавающей точкой, представляющие суммы в некоей валюте.
Например, это могли быть целые числа для указания индекса значения в списке, или числа с плавающей точкой, представляющие суммы в некоей валюте.
Но числа в Python — это гораздо больше, чем, собственно, их числовые значения. Поговорим о трёх особенностях чисел в Python, с которыми вы, возможно, не знакомы.
№1: у чисел есть методы
В Python практически всё — это объект. Один из первых объектов, о котором узнаёт тот, кто начинает изучать Python — это str, используемый для представления строк. Возможно, вы сталкивались с использованием методов строк, вроде .lower(), который возвращает новую строку, все символы которой приведены к нижнему регистру:
>>> "HELLO".lower() 'hello'
Числа в Python тоже, как и строки, являются объектами. У них тоже есть методы. Например, целое число можно преобразовать в байтовую строку с помощью метода .to_bytes():
>>> n = 255 >>> n.to_bytes(length=2, byteorder="big") b'\x00\xff'
Параметр length указывает на количество байт, которые нужно использовать при составлении байтовой строки, а параметр byteorder определяет порядок байт. Например, установка параметра
Например, установка параметра «big» приводит к возврату байтовой строки, в которой старший байт расположен первым, а установка этого параметра в значение «little» приводит к тому, что первым идёт младший байт.
255 — это максимальное значение, которое может принимать 8-битное целое число. Поэтому в нашем случае при вызове метода .to_bytes() можно без проблем воспользоваться параметром length=1:
>>> n.to_bytes(length=1, byteorder="big") b'\xff'
А вот если записать в n число 256 и вызвать для него .to_bytes() с параметром length=1, будет выдана ошибка OverflowError:
>>> n = 256 >>> n.to_bytes(length=1, byteorder="big") Traceback (most recent call last): File "<stdin>", line 1, in <module> OverflowError: int too big to convert
Преобразовать байтовую строку в целое число можно, воспользовавшись методом . класса  from_bytes()
from_bytes()int:
>>> int.from_bytes(b'\x06\xc1', byteorder="big") 1729
Методы класса вызывают, используя имя класса, а не его экземпляр. Именно поэтому в предыдущем примере метод .from_bytes() вызывают, обращаясь к int.
Любопытный факт: 1729 — это самое маленькое положительное число, которое можно представить в виде суммы кубов двух положительных чисел двумя способами. Исторический анекдот связывает это число с индийским математиком Сринивасой Рамануджаном, который рассказал о нём своему наставнику Готфри Харолду Харди.
Харди часто навещал Рамануджана, когда тот, умирая, находился в больнице в Патни. Именно в одно из таких посещений произошёл «инцидент» с номером такси. Харди приехал в Патни на такси, воспользовавшись своим излюбленным транспортным средством. Он вошёл в палату, где лежал Рамануджан. Начинать разговор Харди всегда было мучительно трудно, и он произнёс свою первую фразу: «Если не ошибаюсь, то номер такси, на котором я приехал, 1729.
Мне кажется, это скучное число». На что Рамануджан тотчас же ответил: «Нет, Харди! О нет! Это очень интересное число. Это самое малое из чисел, представимых в виде суммы двух кубов двумя различными способами».
Один из способов представления числа 1729 в виде суммы двух кубов — это 13 + 123. Можете отыскать второй способ?
У чисел с плавающей точкой тоже есть методы. Возможно, самый полезный из них — это .is_integer(). Его используют для проверки того, есть ли у числа с плавающей точкой дробная часть:
>>> n = 2.0 >>> n.is_integer() True >>> n = 3.14 >>> n.is_integer() False
Вот — интересный метод .as_integer_ratio(). Он, вызванный для числа с плавающей точкой, возвращает кортеж, содержащий числитель и знаменатель дроби, представляющей это число:
>>> n.as_integer_ratio() (1, 2)
Правда, из-за ошибки представления чисел с плавающей точкой, иногда этот метод возвращает неожиданные результаты:
>>> n = 0.SyntaxError: invalid syntax >>> 3.14.is_integer() False
Полный список методов числовых Python-типов можно найти в документации.
№2: числа обладают иерархией
В математике числа обладают естественной иерархией. Например, все натуральные числа являются целыми, а все целые числа — рациональными. Все рациональные числа — это вещественные числа, а все вещественные числа — это комплексные числа.
Похожие рассуждения применимы и к представлению чисел в Python. Здесь «числовая башня» выражается через абстрактные типы, содержащиеся в модуле numbers.
Числовая башня
Все числа в Python являются экземплярами класса Number:
>>> from numbers import Number >>> # Целые числа являются наследниками Number >>> isinstance(1729, Number) True >>> # Числа с плавающей точкой являются наследниками Number >>> isinstance(3.14, Number) True >>> # Комплексные числа являются наследниками Number >>> isinstance(1j, Number) True
Если нужно узнать о том, является ли некое Python-значение числовым, но при этом неважно то, каким именно числовым типом оно представлено, воспользуйтесь конструкцией isinstance(value, Number).
В Python имеется четыре дополнительных абстрактных типа, иерархия которых, начиная с наиболее общего числового типа, выглядит так:
Класс
Complexиспользуется для представления комплексных чисел. Тут имеется один встроенный конкретный тип —complex.Класс
Real— это представление вещественных чисел. Его единственный встроенный конкретный тип —float.Класс
Rationalпредставляет рациональные числа. Его единственным встроенным конкретным типом являетсяFraction.Класс
Integralприменяют для представления целых чисел. В нём имеется два встроенных конкретных типа —intиbool.
Так, погодите, а значения типа bool — это разве числа? Да — числа. Можете это проверить, воспользовавшись REPL:
>>> import numbers >>> # Комплексные числа являются наследниками Complex >>> isinstance(1j, numbers.Complex) True >>> # Комплексные числа не являются наследниками Real >>> isinstance(1j, numbers.Real) False >>> # Числа с плавающей точкой являются наследниками Real >>> isinstance(3.14, numbers.Real) True >>> # Числа с плавающей точкой не являются наследниками Rational >>> isinstance(3.14, numbers.Rational) False >>> # Объекты Fractions - это не наследники Rational >>> from fractions import Fraction >>> isinstance(Fraction(1, 2), numbers.Rational) True >>> # Объекты Fractions - это не наследники Integral >>> isinstance(Fraction(1, 2), numbers.Integral) False >>> # Целые числа - это наследники Integral >>> isinstance(1729, numbers.Integral) True >>> # Логические значения - это наследники Integral >>> isinstance(True, numbers.Integral) True >>> True == 1 True >>> False == 0 True
Всё это, на первый взгляд, выглядит вполне нормально. Правда, порядок несколько нарушает то, что значения типа
Правда, порядок несколько нарушает то, что значения типа bool являются числами.
Странность Python: так как тип bool относится к классу Integral (на самом деле он — прямой наследник int), со значениями True и False можно вытворять довольно необычные вещи.
Например, True можно использовать в роли индекса для того чтобы получить второй элемент итерируемого объекта. А если поделить число на False — будет выдана ошибка ZeroDivisionError.
Попробуйте выполнить «False»[True] и 1 / False в REPL!
Но если присмотреться к числовым типам поближе, окажется, что в иерархии Python-чисел имеется пара своеобразных моментов.
Числа типа Decimal не укладываются в иерархию
Как уже было сказано, в «числовой башне» Python есть 4 конкретных числовых типа, соответствующих четырём абстрактным типам: complex, float, Fraction и int. Но в Python имеется и пятый числовой тип, представленный классом
Но в Python имеется и пятый числовой тип, представленный классом Decimal. Этот тип используется для точного представления десятичных чисел и для преодоления ограничений арифметических операций с плавающей точкой.
Можно предположить, что числа типа Decimal являются наследниками Real, но это, на самом деле, не так:
>>> from decimal import Decimal
>>> import numbers
>>> isinstance(Decimal("3.14159"), numbers.Real)
FalseЕдинственный класс, наследником которого является класс Decimal — это Number:
>>> isinstance(Decimal("3.14159"), numbers.Complex)
False
>>> isinstance(Decimal("3.14159"), numbers.Rational)
False
>>> isinstance(Decimal("3.14159"), numbers.Integral)
False
>>> isinstance(Decimal("3.14159"), numbers.Number)
TrueЛогично то, что класс Decimal не является наследником Integral. В некоторой степени смысл есть и в том, что Decimal не является наследником Rational. Но почему
Но почему Decimal
Real или Complex?Ответ кроется в исходном коде CPython:
Объекты Decimal обладают всеми методами, определёнными в классе Real, но эти объекты не должны регистрироваться в виде наследников Real, так как Decimal-числа не взаимодействуют с двоичными числами с плавающей точкой (например, результат операции Decimal(‘3.14’) + 2.71828 не определён). Но ожидается, что числа, классы которых являются наследниками абстрактного класса Real, способны взаимодействовать друг с другом (то есть — R1+R2 должно вычисляться в том случае, если числа R1 и R2 представлены типами, являющимися наследниками Real).
Получается, что объяснение странностей сводится к особенностям реализации.
Числа с плавающей точкой — странные создания
А вот числа с плавающей точкой, с другой стороны, реализуют абстрактный базовый класс Real. Они используются для представления вещественных чисел.
>>> 0.1 + 0.1 + 0.1 == 0.3 False
Числа с плавающей точкой хранятся в памяти в виде двоичных дробей. Это приводит к появлению некоторых проблем. Например, у дроби 1/3 нет конечного десятичного представления (после десятичной точки идёт бесконечное множество троек). А у дроби 1/10 нет конечного представления в виде двоичной дроби.
Другими словами, в компьютере нельзя совершенно точно представить число 0,1 — если только этот компьютер не обладает бесконечной памятью.
Со строго математической точки зрения все числа с плавающей точкой — это рациональные числа, за исключением float(«inf») и float(«nan»). Но программисты используют их в роли аппроксимаций вещественных чисел и воспринимают их, по большей части, как вещественные числа.
Странность Python: float(«nan») — это особое значение с плавающей точкой, представляющее собой «не число». Такие значения часто обозначают как NaN. Но, так как float — это числовой тип, isinstance(float(«nan»), Number) возвращает True.
Получается, что «не числа» — это числа.
В общем, числа с плавающей точкой — странные создания.
№3: набор числовых типов Python можно расширять
Абстрактный числовой базовый тип Python позволяет программисту создавать собственные абстрактные и конкретные числовые типы.
В качестве примера рассмотрим класс ExtendedInteger, который реализует числа в форме a+b√p, где a и b — целые числа, а p — простое число (обратите внимание: класс не обеспечивает то, что число p является простым):
import math import numbers class ExtendedInteger(numbers.Real): def init(self, a, b, p = 2) -> None: self.a = a self.b = b self.p = p self._val = a + (b * math.sqrt(p)) def repr(self): return f"{self.class.name}({self.a}, {self.b}, {self.p})" def str(self): return f"{self.a} + {self.b}√{self.p}" def trunc(self): return int(self._val) def float(self): return float(self._val) def hash(self): return hash(float(self._val)) def floor(self): return math.floor(self._val) def ceil(self): return math.ceil(self._val) def round(self, ndigits=None): return round(self._val, ndigits=ndigits) def abs(self): return abs(self._val) def floordiv(self, other): return self._val // other def rfloordiv(self, other): return other // self._val def truediv(self, other): return self._val / other def rtruediv(self, other): return other / self._val def mod(self, other): return self.
_val % other def rmod(self, other): return other % self._val def lt(self, other): return self._val < other def le(self, other): return self._val <= other def eq(self, other): return float(self) == float(other) def neg(self): return ExtendedInteger(-self.a, -self.b, self.p) def pos(self): return ExtendedInteger(+self.a, +self.b, self.p) def add(self, other): if isinstance(other, ExtendedInteger): # Если оба экземпляра имеют одно и то же значение p, # вернуть новый экземпляр ExtendedInteger if self.p == other.p: new_a = self.a + other.a new_b = self.b + other.b return ExtendedInteger(new_a, new_b, self.p) # В противном случае вернуть значение типа float else: return self._val + other._val # Если other - значение класса Integral, прибавить значение other к значению self.
a elif isinstance(other, numbers.Integral): new_a = self.a + other return ExtendedInteger(new_a, self.b, self.p) # Если other - значение класса Real, вернуть значение типа float elif isinstance(other, numbers.Real): return self._val + other._val # Если тип other неизвестен, позволить другим принять решение # о том, что делать в такой ситуации else: return NotImplemented def radd(self, other): # Сложение коммутативно, поэтому прибегнуть к add return self.add(other) def mul(self, other): if isinstance(other, ExtendedInteger): # Если оба экземпляра имеют одно и то же значение p, # вернуть новый экземпляр ExtendedInteger if self.p == other.p: new_a = (self.a * other.a) + (self.b * other.b * self.p) new_b = (self.a * other.b) + (self.b * other.a) return ExtendedInteger(new_a, new_b, self.
p) # в противном случае вернуть значение типа float else: return self._val * other._val # Если other - значение класса Integral, умножить его компоненты a и b на other elif isinstance(other, numbers.Integral): new_a = self.a * other new_b = self.b * other return ExtendedInteger(new_a, new_b, self.p) # Если other - значение класса Real, вернуть значение типа float elif isinstance(other, numbers.Real): return self._val * other # Если тип other неизвестен, позволить другим принять решение # о том, что делать в такой ситуации else: return NotImplemented def rmul(self, other): # Умножение коммутативно, поэтому прибегнуть к mul return self.mul(other) def pow(self, exponent): return self._val ** exponent def rpow(self, base): return base ** self._val
Для того чтобы обеспечить правильность реализации интерфейса Real конкретным типом — нужно создать реализации множества методов, в именах которых есть два символа подчёркивания. Ещё нужно поразмыслить о том, как методы вроде
Ещё нужно поразмыслить о том, как методы вроде .add() и .mul() взаимодействуют с другими типами, являющимися наследниками Real.
Обратите внимание: вышеприведённый пример не создавался в расчёте на его полноту или абсолютную правильность. Его цель — продемонстрировать читателю возможности работы с числами.
При наличии реализации ExtendedInteger можно заниматься следующими вычислениями:
>>> a = ExtendedInteger(1, 2) >>> b = ExtendedInteger(2, 3) >>> a ExtendedInteger(1, 2, 2) >>> # Проверяем то, что a - это наследник Number >>> isinstance(a, numbers.Number) True >>> # Проверяем то, что a - это наследник Real >>> isinstance(a, numbers.Real) True >>> print(a) 1 + 2√2 >>> a * b ExtendedInteger(14, 7, 2) >>> print(a * b) 14 + 7√2 >>> float(a) 3.8284271247461903
Иерархия числовых типов в Python — довольно гибкая структура. Но, конечно, всегда стоит очень внимательно относиться к реализации типов, являющихся наследниками встроенных абстрактных базовых типов Python. Нужно обеспечить их корректную работу друг с другом.
Но, конечно, всегда стоит очень внимательно относиться к реализации типов, являющихся наследниками встроенных абстрактных базовых типов Python. Нужно обеспечить их корректную работу друг с другом.
В документации по Python можно найти несколько советов по реализации собственных типов, которые стоит прочесть тому, кто решит заняться созданием собственных числовых типов. Такому человеку ещё полезно будет ознакомиться с реализацией Fraction.
Итоги
Вот — те три особенности Python-чисел, которые мы здесь обсуждали:
У чисел есть методы, как и у практически всех остальных объектов в Python.
Числа обладают иерархией, даже несмотря на то, что их чёткие взаимоотношения несколько портит наличие типов
Decimalиfloat.Программисты могут создавать собственные числовые типы, которые вписываются в иерархию числовых типов Python.
Может быть, вы узнали из этого материала не только об этих особенностях чисел, но и ещё о чём-нибудь, что вам пригодится.
Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.
Присоединяйтесь к нашей команде.
Что такое каждое натуральное число?
Натуральные числа включают в себя все целые числа, кроме числа 0 . Другими словами, все натуральные числа являются целыми числами, но все целые числа не являются натуральными числами. Натуральные числа = {1,2,3,4,5,6,7,8,9,…..}
Запрос на удаление |
Посмотреть полный ответ на byjus. com
com
Каждое натуральное число является действительным числом?
Натуральные числа также называют счетными числами, потому что они не включают ноль или отрицательные числа. Они являются частью действительных чисел, включая только положительные целые числа, но не ноль, дроби, десятичные дроби и отрицательные числа.
Запрос на удаление |
Просмотреть полный ответ на cuemath.com
Является ли 1 натуральным числом?
Натуральные числа — это все числа 1, 2, 3, 4… Это числа, которые вы обычно считаете, и они будут продолжаться до бесконечности. Целые числа — это все натуральные числа, включая 0, например. 0, 1, 2, 3, 4… Целые числа включают в себя все целые числа и их отрицательные эквиваленты, например. …
Запрос на удаление |
Посмотреть полный ответ на mathplanet.com
Является ли 0 натуральным числом Да или нет?
Натуральные числа — это подмножество действительных чисел, которые включают только положительные целые числа, такие как 1, 2, 3, 4, 5, 6, а затем исключают отрицательные числа, ноль, десятичные дроби и дроби. Они не содержат отрицательных чисел или нуля.
Они не содержат отрицательных чисел или нуля.
|
Посмотреть полный ответ на geeksforgeeks.org
Все ли натуральные числа являются целыми?
Отсюда можно сделать вывод, что все натуральные числа являются целыми. Ответ на утверждение «всякое натуральное число является целым числом, истинно или ложно» верен.
Запрос на удаление |
Посмотреть полный ответ на unacademy.com
Что такое натуральные числа?
Каждое ли натуральное число является дробью?
Натуральные числа являются частью действительных чисел, включая только положительные целые числа, но не ноль, дроби, десятичные дроби и отрицательные числа. Из определения натуральных чисел мы видим, что натуральные числа не могут быть дробями, тогда как рациональные числа являются дробными числами.
Из определения натуральных чисел мы видим, что натуральные числа не могут быть дробями, тогда как рациональные числа являются дробными числами.
|
Посмотреть полный ответ на cuemath.com
Каждое ли натуральное число является рациональным?
Все натуральные числа, целые числа и целые числа являются рациональными числами, потому что их можно записать в форме pq, где q не равно нулю.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Является ли минус 1 натуральным числом?
Натуральные числа являются частью действительных чисел, которые включают только положительные целые числа, то есть 1, 2, 3, 4,5,6, ………. кроме нуля, дробей, десятичных и отрицательных чисел. Примечание. Натуральные числа не включают отрицательные числа или ноль.
Запрос на удаление |
Посмотреть полный ответ на byjus. com
com
Почему 1 не является простым числом?
1 можно разделить только на одно число, на 1, поэтому с этим определением 1 не является простым числом.
Запрос на удаление |
Полный ответ на wgtn.ac.nz
Является ли натуральное число бесконечностью?
Множество натуральных чисел бесконечно.
Запрос на удаление |
Посмотреть полный ответ на сайте quantamagazine.org
Почему 0 натуральный?
Ноль не является положительным или отрицательным. Хотя ноль не является положительным числом, он все же считается целым числом. Статус нуля как целого числа и тот факт, что это не отрицательное число, заставляет некоторых математиков считать его натуральным числом.
Запрос на удаление |
Полный ответ см. на сайте Study.com
Является ли Пи действительным числом?
Пи нельзя выразить простой дробью, значит, это иррациональное число. Мы знаем, что каждое иррациональное число является действительным числом. Итак, Пи — действительное число.
Мы знаем, что каждое иррациональное число является действительным числом. Итак, Пи — действительное число.
|
Посмотреть полный ответ на byjus.com
Является ли 1 A полностью реальным числом?
Тип числа, который мы обычно используем, например, 1, 15,82, -0,1, 3/4 и т. д. Положительные или отрицательные, большие или маленькие, целые числа, дроби или десятичные числа — все это действительные числа. Их называют «действительными числами», потому что они не являются мнимыми числами.
Запрос на удаление |
Посмотреть полный ответ на mathsisfun.com
Почему ноль — это целое число?
Ноль не является дробью или десятичной дробью какого-либо числа. Это ни положительно, ни отрицательно. Ноль подчиняется правилу целых чисел. Это сумма любого числа и его отрицательного члена.
Запрос на удаление |
Просмотреть полный ответ на byjus. com
com
Является ли 5 реальным или натуральным числом?
Число 5 присутствует в действительных числах. Следовательно, число 5 является рациональным, целым, целым и действительным числом.
Запрос на удаление |
Посмотреть полный ответ на vedantu.com
Является ли 0 четным или нечетным?
Для математиков ответ прост: ноль — четное число.
Запрос на удаление |
Посмотреть полный ответ на bbc.com
Почему 1111 не является простым числом?
Нет, 1111 не простое число. Число 1111 делится на 1, 11, 101, 1111. Чтобы число считалось простым, оно должно иметь ровно два делителя. Поскольку 1111 имеет более двух делителей, то есть 1, 11, 101, 1111, это не простое число.
Запрос на удаление |
Посмотреть полный ответ на cuemath. com
com
Какое самое маленькое простое число?
Простое число должно иметь ровно два делителя (1 и само число). Таким образом, число 2 является наименьшим простым числом, так как его единственные делители — 1 и 2.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Сколько будет 0 минус любое число?
Как и при сложении, если из любого числа вычесть 0, получится та же сумма. Например, 12-0 = 12. Если вы вычитаете, вам может понадобиться заимствование для решения задачи.
Запрос на удаление |
Посмотреть полный ответ на blog.prepscholar.com
Является ли 0,1 естественным?
Целые числа Пример
Все перечисленные ниже не являются целыми числами: Десятичные числа: 0,1, 5,23, 15,999, 1,7 2 . Дроби: ½, 1/27, 2 ½, 99/100. Отрицательные числа: -10, -99, -521.
|
Посмотреть полный ответ на statshowto.com
Является ли 0,5 натуральным числом?
Следовательно, 1 и 5 — натуральные числа, а 0,5 и 45 — нет.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Все ли натуральные числа иррациональны?
На самом деле, мы можем сказать, что натуральное число n может быть выражено как n = n/1, что есть не что иное, как частное двух целых чисел. Следовательно, каждое натуральное число является рациональным числом.
Запрос на удаление |
Посмотреть полный ответ на Learncbse.in
Является ли 2 единственным четным простым числом?
Единственное четное простое число 2. Все остальные простые числа нечетные. С юмором это означает, что 2 — самое «странное» простое число.
|
Посмотреть полный ответ на mathworld.wolfram.com
Является ли 0 рациональным числом?
Да, 0 — рациональное число. Поскольку мы знаем, рациональное число может быть выражено как p/q, где p и q — целые числа, а q не равно нулю. Таким образом, мы можем выразить 0 как p/q, где p равно нулю, а q — целое число.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
← Предыдущий вопрос
Какой шампунь избавляет от чесотки?
Следующий вопрос →
Сколько вам платят за то, что вы сообщаете о нарушениях?
В чем разница между целым числом и целым числом?
`;
Наука
Факт проверен
Г.
 Визен
Визен Разница между целым числом и целым числом, к сожалению, во многом зависит от того, кто говорит о рассматриваемых числах. Это связано с тем, что существует много разногласий по поводу того, что представляет собой этот тип числа, что привело к путанице и разочарованию среди студентов, изучающих математику. Однако целые числа легче понять, поскольку набор целых чисел просто относится ко всем натуральным числам, включая отрицательные, положительные и ноль. Часто говорят, что эти числа относятся только к положительным натуральным числам, хотя иногда включается и ноль, а некоторые люди используют термин «целое число» как синоним «целого числа».
Понять разницу между целым числом и целым числом может быть сложно, поскольку это зависит от того, как человек использует термин «целое число». Легче всего начать с определения того, что такое целые числа, поскольку существует общепринятое определение «целого числа». Целые числа — это натуральные числа, включая отрицательные, нулевые и положительные числа. Это только натуральные числа, и они не включают в себя дроби, десятичные дроби, иррациональные числа, мнимые числа или что-либо еще, что не может быть выражено как простое натуральное число.
Легче всего начать с определения того, что такое целые числа, поскольку существует общепринятое определение «целого числа». Целые числа — это натуральные числа, включая отрицательные, нулевые и положительные числа. Это только натуральные числа, и они не включают в себя дроби, десятичные дроби, иррациональные числа, мнимые числа или что-либо еще, что не может быть выражено как простое натуральное число.
Однако применительно к этим целым числам целые числа могут быть намного сложнее. Многие люди считают целыми числами только положительные целые числа, также называемые счетными числами, и в этом случае ноль не будет целым числом. Другие рассматривают эти числа как неотрицательные целые числа, которые включают все положительные целые числа, но включают ноль, поскольку это не отрицательное число. Чтобы еще больше усугубить эту путаницу, есть также люди, которые используют термины «целое число» и «целое число» как синонимы, имея в виду, что при таком использовании не будет никакой разницы между этими двумя терминами.
Другие рассматривают эти числа как неотрицательные целые числа, которые включают все положительные целые числа, но включают ноль, поскольку это не отрицательное число. Чтобы еще больше усугубить эту путаницу, есть также люди, которые используют термины «целое число» и «целое число» как синонимы, имея в виду, что при таком использовании не будет никакой разницы между этими двумя терминами.
Вот почему этот термин не часто используется в курсах более высокого уровня и в дискуссиях по математике, поскольку разные люди могут понимать его по-разному.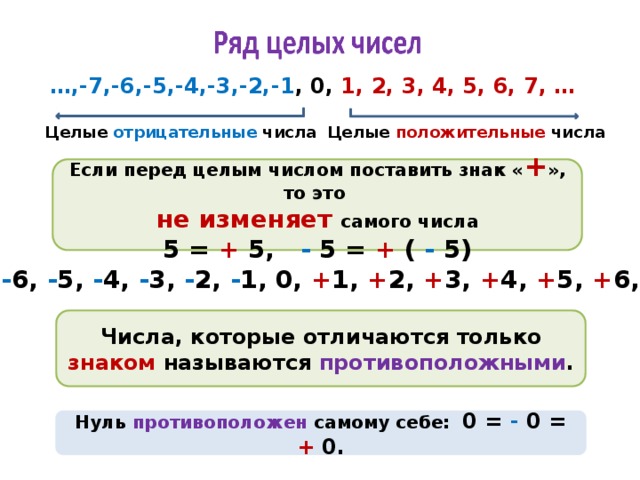


 SyntaxError: invalid syntax
>>> 3.14.is_integer()
False
SyntaxError: invalid syntax
>>> 3.14.is_integer()
False Complex)
True
>>> # Комплексные числа не являются наследниками Real
>>> isinstance(1j, numbers.Real)
False
>>> # Числа с плавающей точкой являются наследниками Real
>>> isinstance(3.14, numbers.Real)
True
>>> # Числа с плавающей точкой не являются наследниками Rational
>>> isinstance(3.14, numbers.Rational)
False
>>> # Объекты Fractions - это не наследники Rational
>>> from fractions import Fraction
>>> isinstance(Fraction(1, 2), numbers.Rational)
True
>>> # Объекты Fractions - это не наследники Integral
>>> isinstance(Fraction(1, 2), numbers.Integral)
False
>>> # Целые числа - это наследники Integral
>>> isinstance(1729, numbers.Integral)
True
>>> # Логические значения - это наследники Integral
>>> isinstance(True, numbers.Integral)
True
>>> True == 1
True
>>> False == 0
True
Complex)
True
>>> # Комплексные числа не являются наследниками Real
>>> isinstance(1j, numbers.Real)
False
>>> # Числа с плавающей точкой являются наследниками Real
>>> isinstance(3.14, numbers.Real)
True
>>> # Числа с плавающей точкой не являются наследниками Rational
>>> isinstance(3.14, numbers.Rational)
False
>>> # Объекты Fractions - это не наследники Rational
>>> from fractions import Fraction
>>> isinstance(Fraction(1, 2), numbers.Rational)
True
>>> # Объекты Fractions - это не наследники Integral
>>> isinstance(Fraction(1, 2), numbers.Integral)
False
>>> # Целые числа - это наследники Integral
>>> isinstance(1729, numbers.Integral)
True
>>> # Логические значения - это наследники Integral
>>> isinstance(True, numbers.Integral)
True
>>> True == 1
True
>>> False == 0
True a = a
self.b = b
self.p = p
self._val = a + (b * math.sqrt(p))
def repr(self):
return f"{self.class.name}({self.a}, {self.b}, {self.p})"
def str(self):
return f"{self.a} + {self.b}√{self.p}"
def trunc(self):
return int(self._val)
def float(self):
return float(self._val)
def hash(self):
return hash(float(self._val))
def floor(self):
return math.floor(self._val)
def ceil(self):
return math.ceil(self._val)
def round(self, ndigits=None):
return round(self._val, ndigits=ndigits)
def abs(self):
return abs(self._val)
def floordiv(self, other):
return self._val // other
def rfloordiv(self, other):
return other // self._val
def truediv(self, other):
return self._val / other
def rtruediv(self, other):
return other / self._val
def mod(self, other):
return self.
a = a
self.b = b
self.p = p
self._val = a + (b * math.sqrt(p))
def repr(self):
return f"{self.class.name}({self.a}, {self.b}, {self.p})"
def str(self):
return f"{self.a} + {self.b}√{self.p}"
def trunc(self):
return int(self._val)
def float(self):
return float(self._val)
def hash(self):
return hash(float(self._val))
def floor(self):
return math.floor(self._val)
def ceil(self):
return math.ceil(self._val)
def round(self, ndigits=None):
return round(self._val, ndigits=ndigits)
def abs(self):
return abs(self._val)
def floordiv(self, other):
return self._val // other
def rfloordiv(self, other):
return other // self._val
def truediv(self, other):
return self._val / other
def rtruediv(self, other):
return other / self._val
def mod(self, other):
return self. _val % other
def rmod(self, other):
return other % self._val
def lt(self, other):
return self._val < other
def le(self, other):
return self._val <= other
def eq(self, other):
return float(self) == float(other)
def neg(self):
return ExtendedInteger(-self.a, -self.b, self.p)
def pos(self):
return ExtendedInteger(+self.a, +self.b, self.p)
def add(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = self.a + other.a
new_b = self.b + other.b
return ExtendedInteger(new_a, new_b, self.p)
# В противном случае вернуть значение типа float
else:
return self._val + other._val
# Если other - значение класса Integral, прибавить значение other к значению self.
_val % other
def rmod(self, other):
return other % self._val
def lt(self, other):
return self._val < other
def le(self, other):
return self._val <= other
def eq(self, other):
return float(self) == float(other)
def neg(self):
return ExtendedInteger(-self.a, -self.b, self.p)
def pos(self):
return ExtendedInteger(+self.a, +self.b, self.p)
def add(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = self.a + other.a
new_b = self.b + other.b
return ExtendedInteger(new_a, new_b, self.p)
# В противном случае вернуть значение типа float
else:
return self._val + other._val
# Если other - значение класса Integral, прибавить значение other к значению self. a
elif isinstance(other, numbers.Integral):
new_a = self.a + other
return ExtendedInteger(new_a, self.b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val + other._val
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def radd(self, other):
# Сложение коммутативно, поэтому прибегнуть к add
return self.add(other)
def mul(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = (self.a * other.a) + (self.b * other.b * self.p)
new_b = (self.a * other.b) + (self.b * other.a)
return ExtendedInteger(new_a, new_b, self.
a
elif isinstance(other, numbers.Integral):
new_a = self.a + other
return ExtendedInteger(new_a, self.b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val + other._val
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def radd(self, other):
# Сложение коммутативно, поэтому прибегнуть к add
return self.add(other)
def mul(self, other):
if isinstance(other, ExtendedInteger):
# Если оба экземпляра имеют одно и то же значение p,
# вернуть новый экземпляр ExtendedInteger
if self.p == other.p:
new_a = (self.a * other.a) + (self.b * other.b * self.p)
new_b = (self.a * other.b) + (self.b * other.a)
return ExtendedInteger(new_a, new_b, self. p)
# в противном случае вернуть значение типа float
else:
return self._val * other._val
# Если other - значение класса Integral, умножить его компоненты a и b на other
elif isinstance(other, numbers.Integral):
new_a = self.a * other
new_b = self.b * other
return ExtendedInteger(new_a, new_b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val * other
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def rmul(self, other):
# Умножение коммутативно, поэтому прибегнуть к mul
return self.mul(other)
def pow(self, exponent):
return self._val ** exponent
def rpow(self, base):
return base ** self._val
p)
# в противном случае вернуть значение типа float
else:
return self._val * other._val
# Если other - значение класса Integral, умножить его компоненты a и b на other
elif isinstance(other, numbers.Integral):
new_a = self.a * other
new_b = self.b * other
return ExtendedInteger(new_a, new_b, self.p)
# Если other - значение класса Real, вернуть значение типа float
elif isinstance(other, numbers.Real):
return self._val * other
# Если тип other неизвестен, позволить другим принять решение
# о том, что делать в такой ситуации
else:
return NotImplemented
def rmul(self, other):
# Умножение коммутативно, поэтому прибегнуть к mul
return self.mul(other)
def pow(self, exponent):
return self._val ** exponent
def rpow(self, base):
return base ** self._val